Взаимное расположение прямых и плоскосте в пространстве

1.

2.

- Образовательные:
1) сформировать представление о взаимных
расположениях прямых, прямых и плоскостей в
окружающем мире;
2) изучить понятия параллельных, скрещивающихся
прямых в пространстве; параллельности прямой и
плоскости, параллельности плоскостей и свойств;
3) формировать навыки чтения и построения
чертежей, применения, полученных теоретических
знаний при решении задач;

3.

- Развивающие:
1) развивать пространственное воображение у
обучающихся, умение переносить
пространственные ситуации на плоскость,
интерес к предмету, математическую речь.
- Воспитательные:
воспитывать у обучающихся культуру
математической речи, аккуратность в
построении чертежа, формировать культуру
общения.
- Методическая цель:
показать формы и методы активизация
мыслительной деятельности студентов.

4.

5. Проверь себя:

ЗАДАНИЕ 1.
Впишите слова, пропущенные в предложениях.
1)
Через три точки,
единственная плоскость.
2)
Если
точки прямой принадлежат плоскости, то и вся
прямая принадлежит плоскости.
3)
Две различные плоскости могут иметь только одну общую
.
4)
Через прямую и не лежащую на ней точку проходит
.
5)
Через две
плоскость.
на одной прямой, проходит
прямые проходит единственная

6.

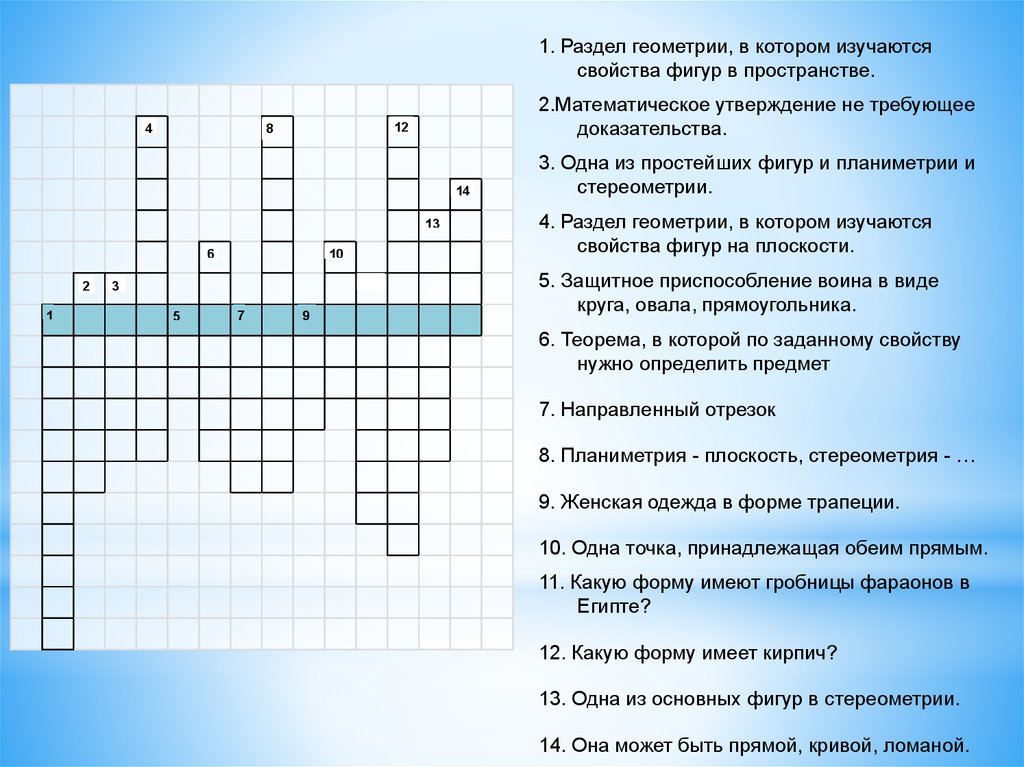
1. Раздел геометрии, в котором изучаются
свойства фигур в пространстве.
4
2.Математическое утверждение не требующее
доказательства.
12
8
14
13
6
2
1
10
3
5
7
9
3. Одна из простейших фигур и планиметрии и
стереометрии.
4. Раздел геометрии, в котором изучаются
свойства фигур на плоскости.
5. Защитное приспособление воина в виде
круга, овала, прямоугольника.
6. Теорема, в которой по заданному свойству
нужно определить предмет
7. Направленный отрезок
8. Планиметрия - плоскость, стереометрия - …
9. Женская одежда в форме трапеции.
10. Одна точка, принадлежащая обеим прямым.
11. Какую форму имеют гробницы фараонов в
Египте?
12. Какую форму имеет кирпич?
13. Одна из основных фигур в стереометрии.
14. Она может быть прямой, кривой, ломаной.

7.

8
п
12
л
р
а
а
о
р
4
п
н
с
а
1
3
п
м
л
н
п
л
о
и
в
а ю щ и
е
с
я
о
р
7
б
11
9
с
к
р
е щ и
т
с
я
т
и
з
е
н
б
а
р
л
к
е
и
м
р
т
н
к
с
к
я
а
е
о
р
о
а
и
а
т
т
а
м
п
с
е
м
я
я
к
о
в
и
и
т
о
а
р
о
д
п
ь
а
е
м
е
т
р
и
л
л
10
т
р
5
13
и
п
а
14
п
6
и
2
п
д

8.

а
b
а
b
а

9.

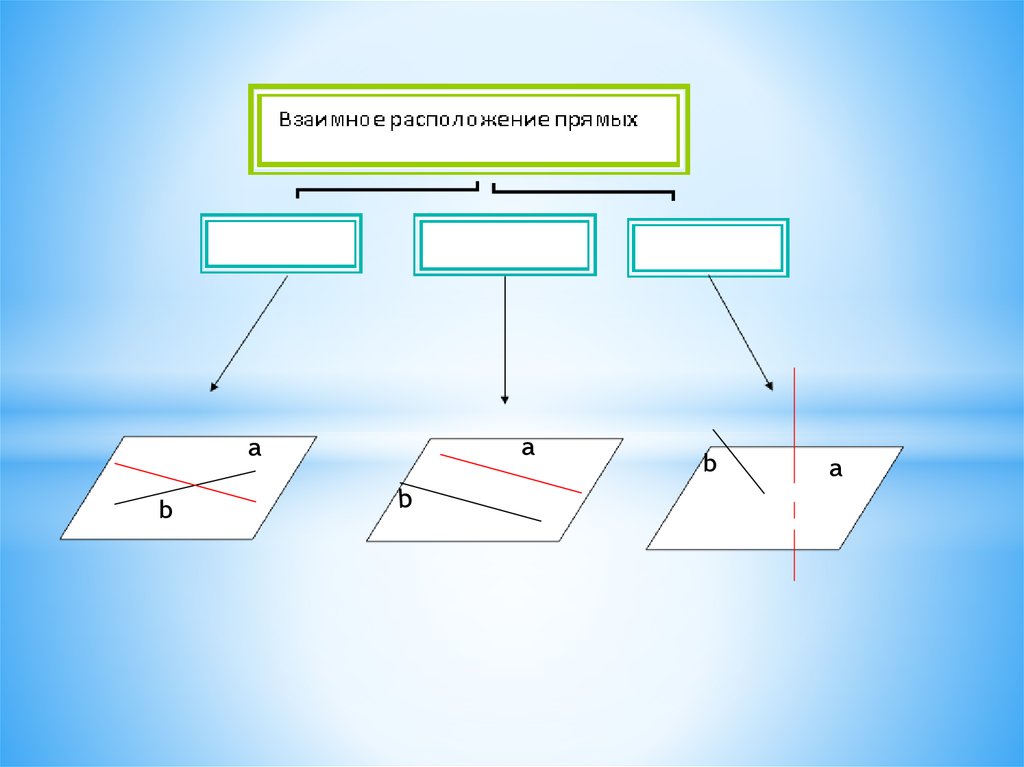
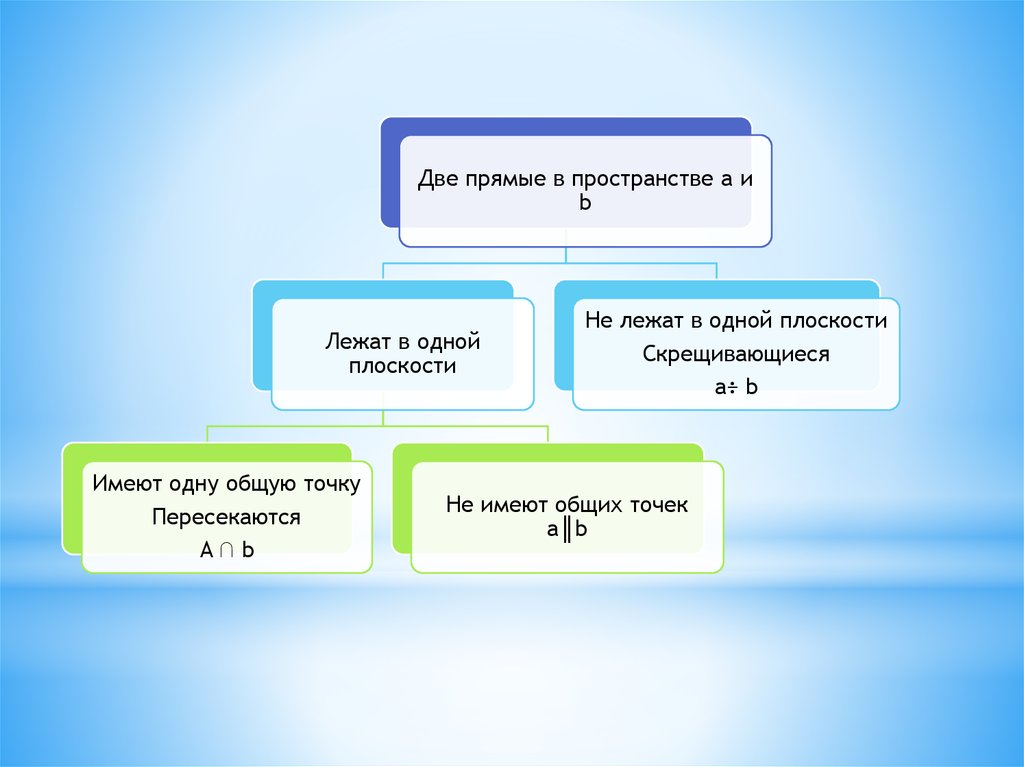
Две прямые в пространстве a и
b
Лежат в одной
плоскости
Имеют одну общую точку
Пересекаются
A∩b
Не лежат в одной плоскости
Скрещивающиеся
a÷ b
Не имеют общих точек
a║b

10.

Одной из достопримечательностью Старого Оскола являются
купеческие домики XIX века. К примеру, дом № 66, в котором
сейчас располагается Промышленная палата.

11.

А это современное здание Железнодорожного вокзала Старого
Оскола. Оно признано одним из самых необычных в стране.

12.

13.

14.

Пример скрещивающихся прямых в пространстве

15.

B1
K
A1
C1
D1
N
M
B
C
A
D
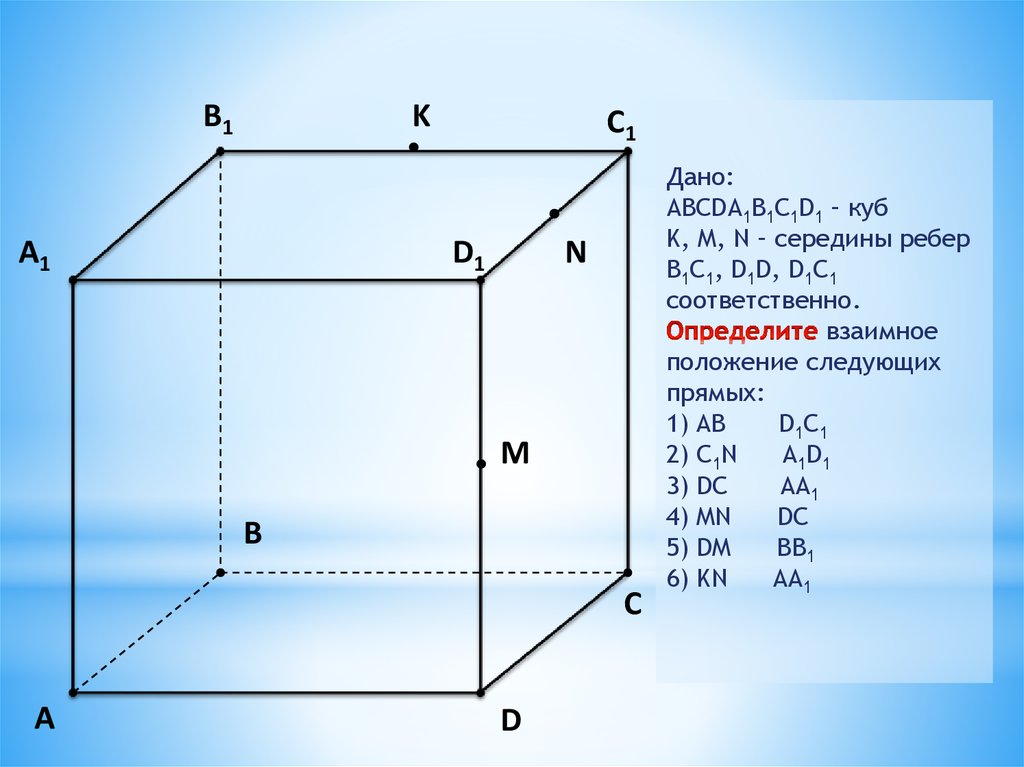
Дано:
ABCDA1B1C1D1 – куб
K, M, N – середины ребер
B1C1, D1D, D1C1
соответственно.
взаимное
положение следующих
прямых:
1) AB
D1C1
2) C1N
A1D1
3) DC
AA1
4) MN
DC
5) DM
BB1
6) KN
AA1

16.

B1
K
A1
C1
D1
N
M
B
C
A
D
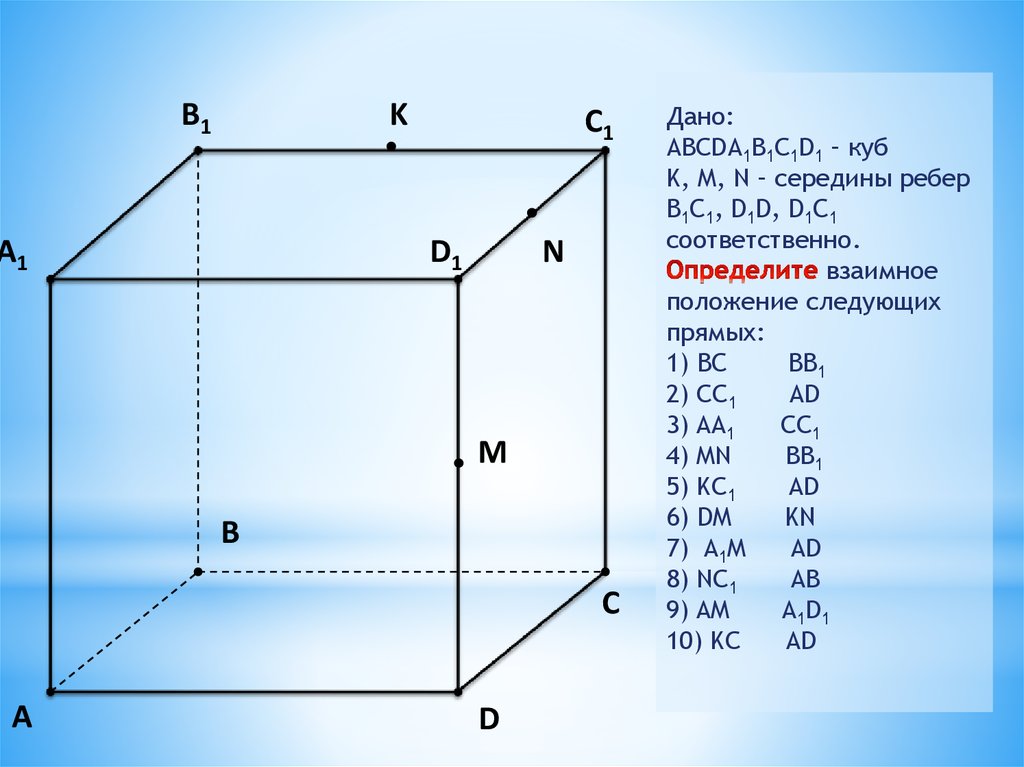
Дано:
ABCDA1B1C1D1 – куб
K, M, N – середины ребер
B1C1, D1D, D1C1
соответственно.
взаимное
положение следующих
прямых:
1) BC
BB1
2) CC1
AD
3) AA1
CC1
4) MN
BB1
5) KC1
AD
6) DM
KN
7) A1M
AD
8) NC1
AB
9) AM
A1D1
10) KC
AD

17. Проверь себя

1.
ПЕРЕСЕКАЮТСЯ (
2.
ПАРАЛЛЕЛЬНЫ (
3.
СКРЕЩИВАЮТСЯ (
)
)
)

18.

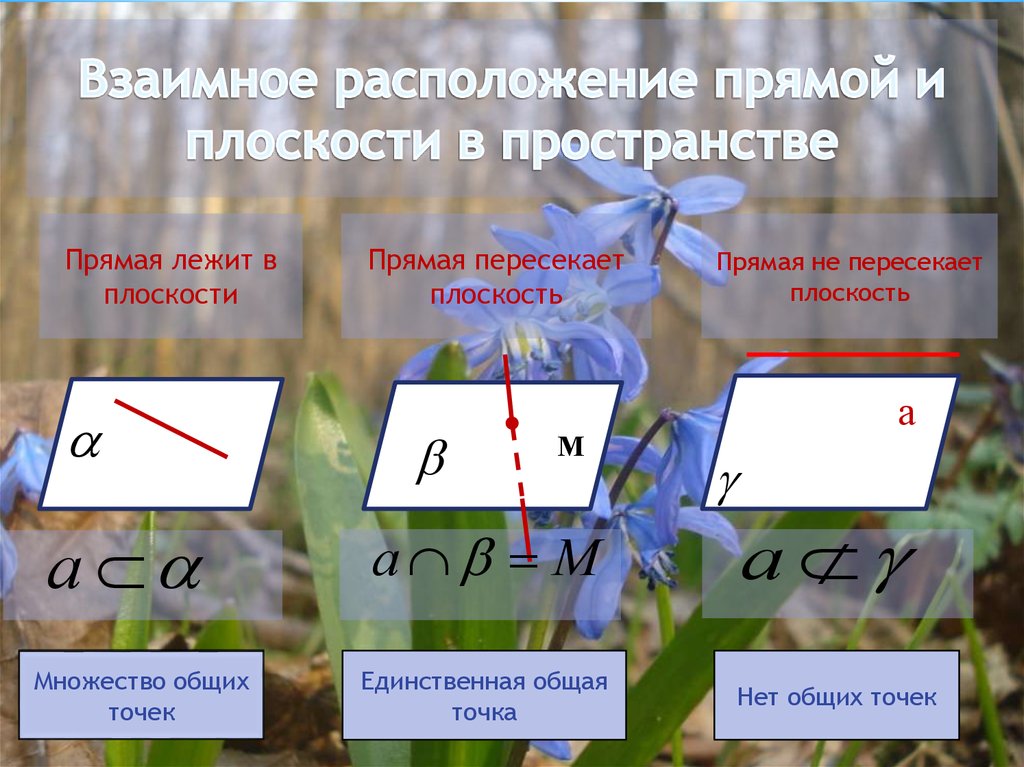
Прямая лежит в
плоскости
а
Множество общих
точек
Прямая пересекает
плоскость
М
а М
Единственная общая
точка
Прямая не пересекает
плоскость
а
а
Нет общих точек

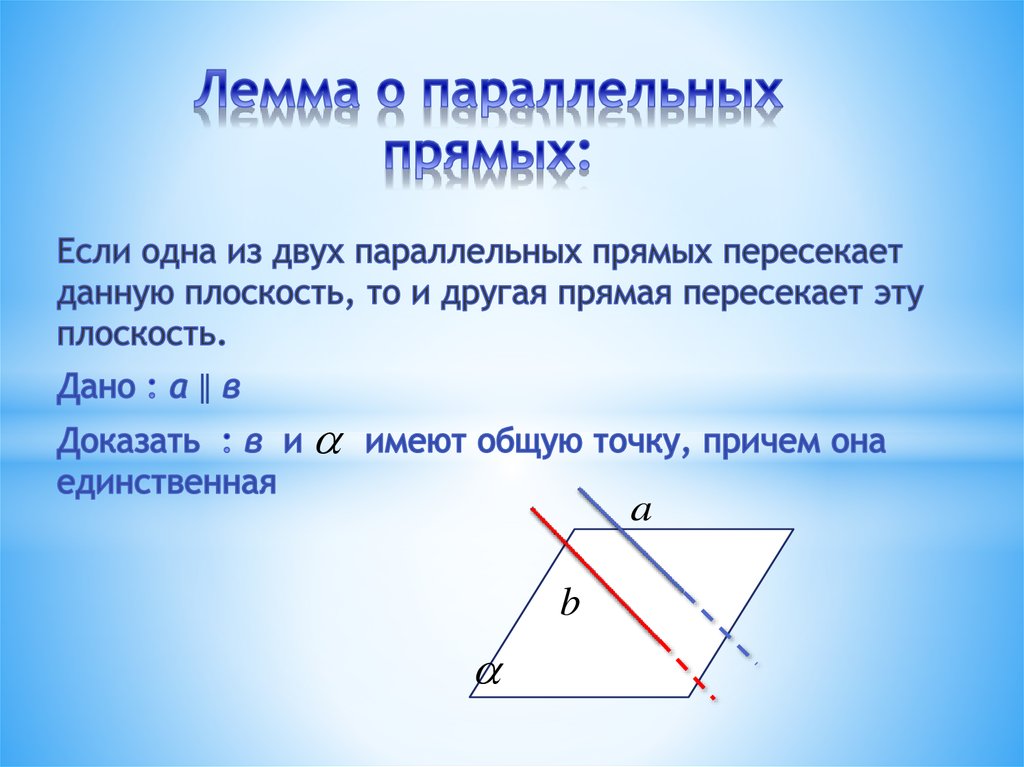
19. Лемма о параллельных прямых:

ǁ
a
b

20.

Т.
a
b
a
a | | b a | |
b
Если прямая, не лежащая в
данной плоскости,
параллельна какойнибудь прямой, лежащей
в этой плоскости, то она
параллельна данной
плоскости.

21.

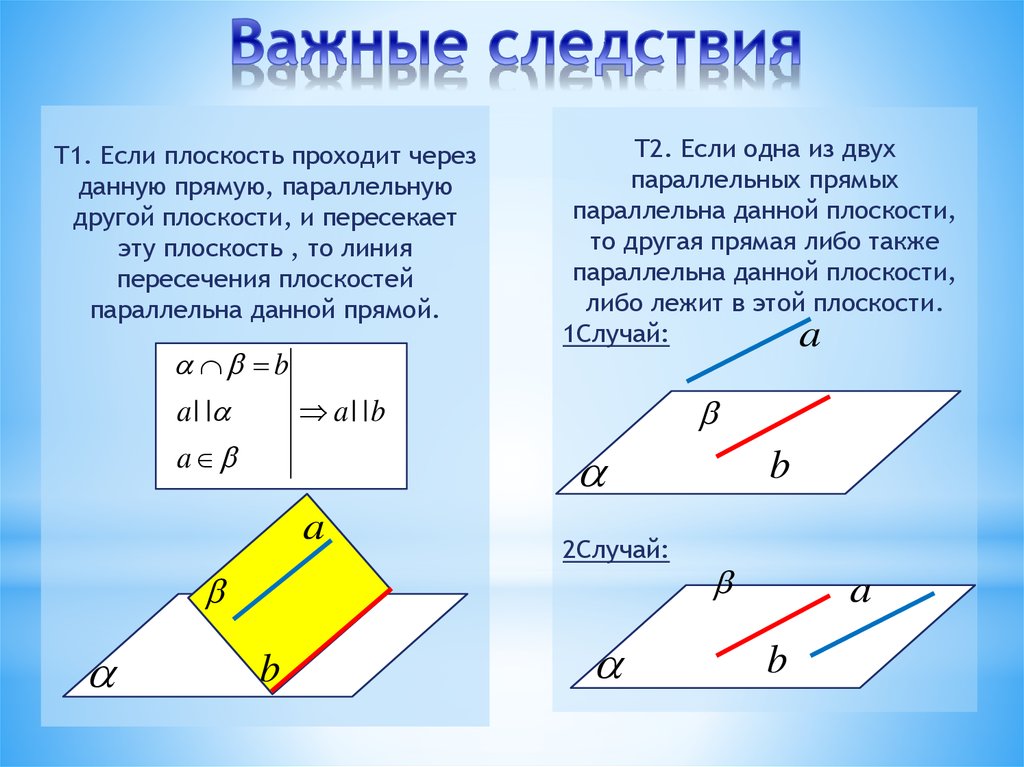
Т1. Если плоскость проходит через
данную прямую, параллельную
другой плоскости, и пересекает
эту плоскость , то линия
пересечения плоскостей
параллельна данной прямой.
b
a | |
a | |b
a
a
Т2. Если одна из двух
параллельных прямых
параллельна данной плоскости,
то другая прямая либо также
параллельна данной плоскости,
либо лежит в этой плоскости.
1Случай:
a
2Случай:
b
b
a
b

22. Водопад Эйшера

23.

24.

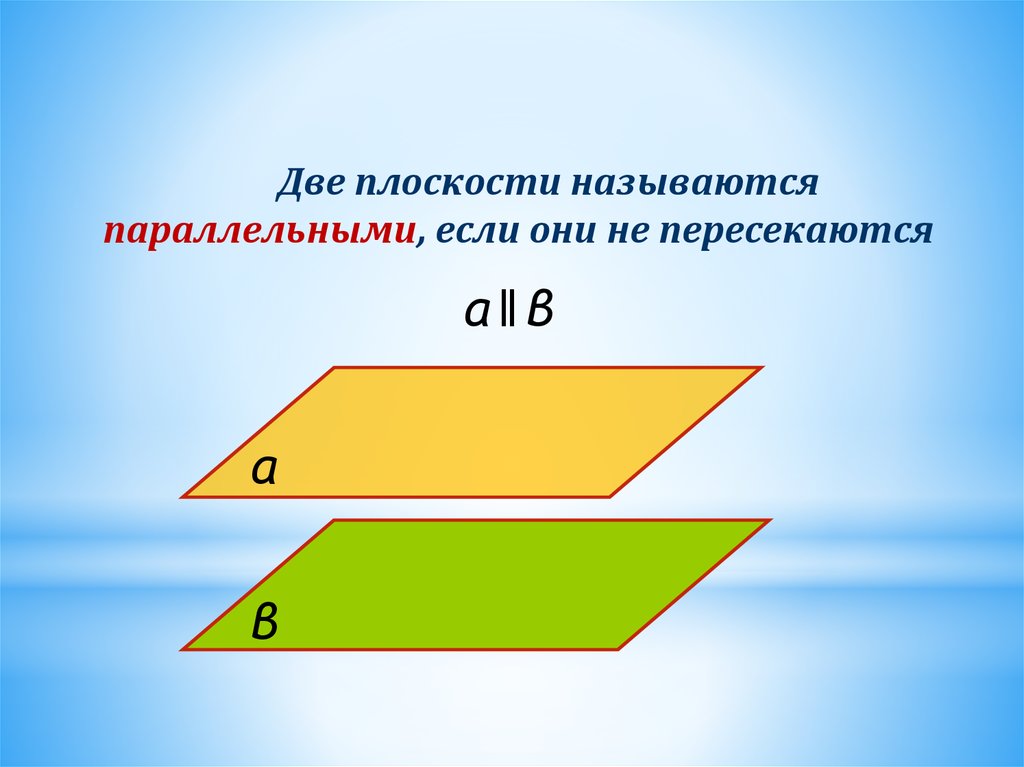
Две плоскости называются
параллельными, если они не пересекаются
α‖β
α
β

25.

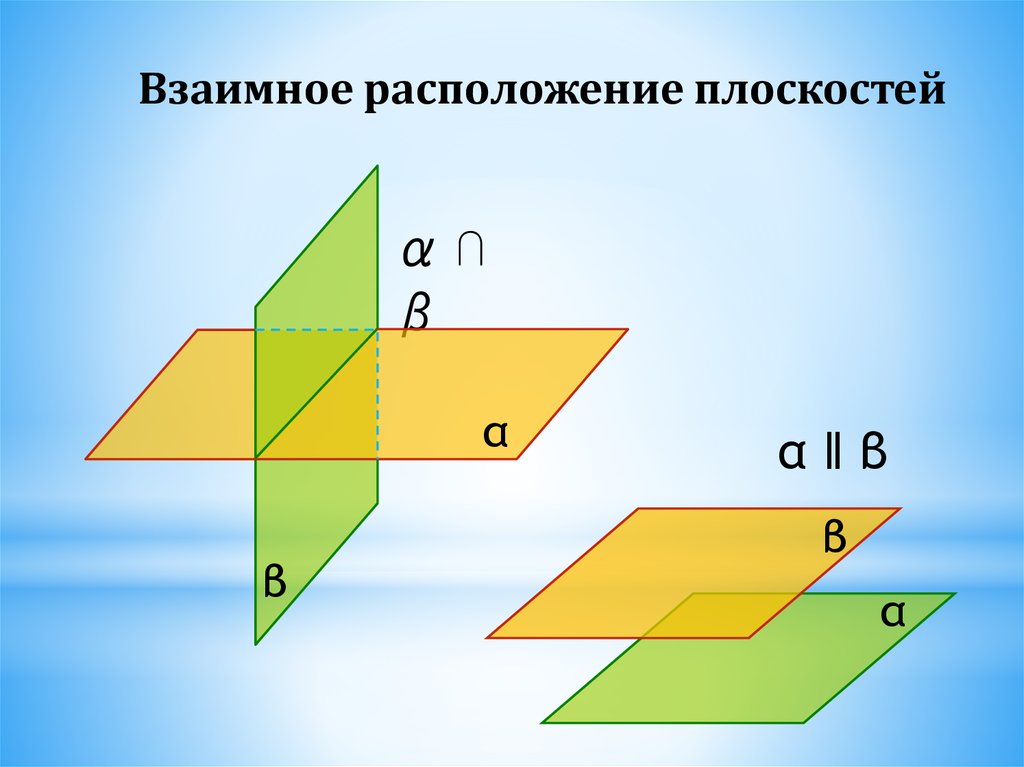
Взаимное расположение плоскостей
α⋂
β
α
β
α‖β
β
α

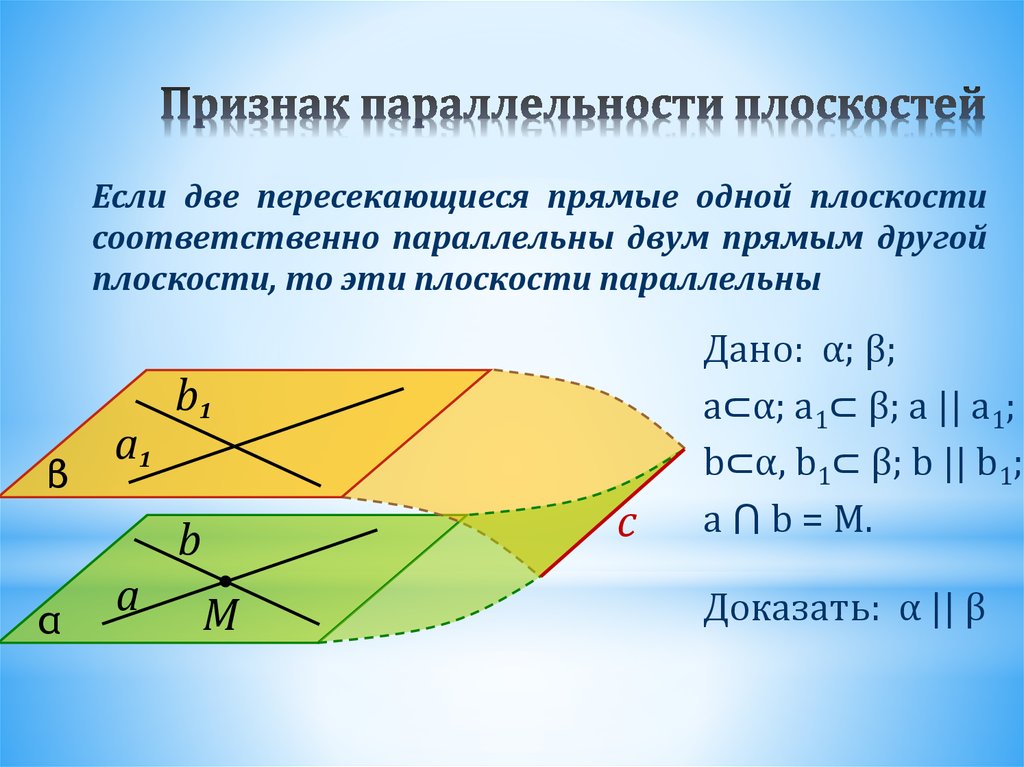
26. Признак параллельности плоскостей

Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны
β
a1
b1
с
b
α
a
М
Дано: α; β;
a⊂α; a1⊂ β; a || a1;
b⊂α, b1⊂ β; b || b1;
a ⋂ b = M.
Доказать: α || β

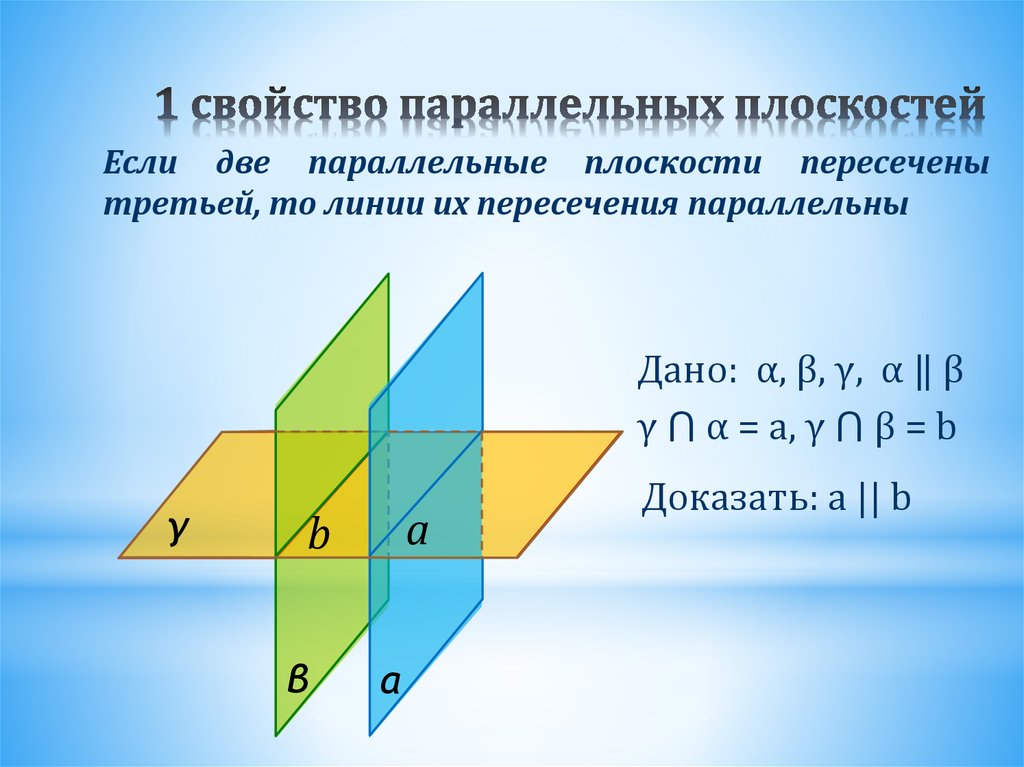
27. 1 свойство параллельных плоскостей

Если две параллельные плоскости пересечены
третьей, то линии их пересечения параллельны
Дано: α, β, γ, α ‖ β
γ ⋂ α = a, γ ⋂ β = b
γ
a
b
β
α
Доказать: a || b

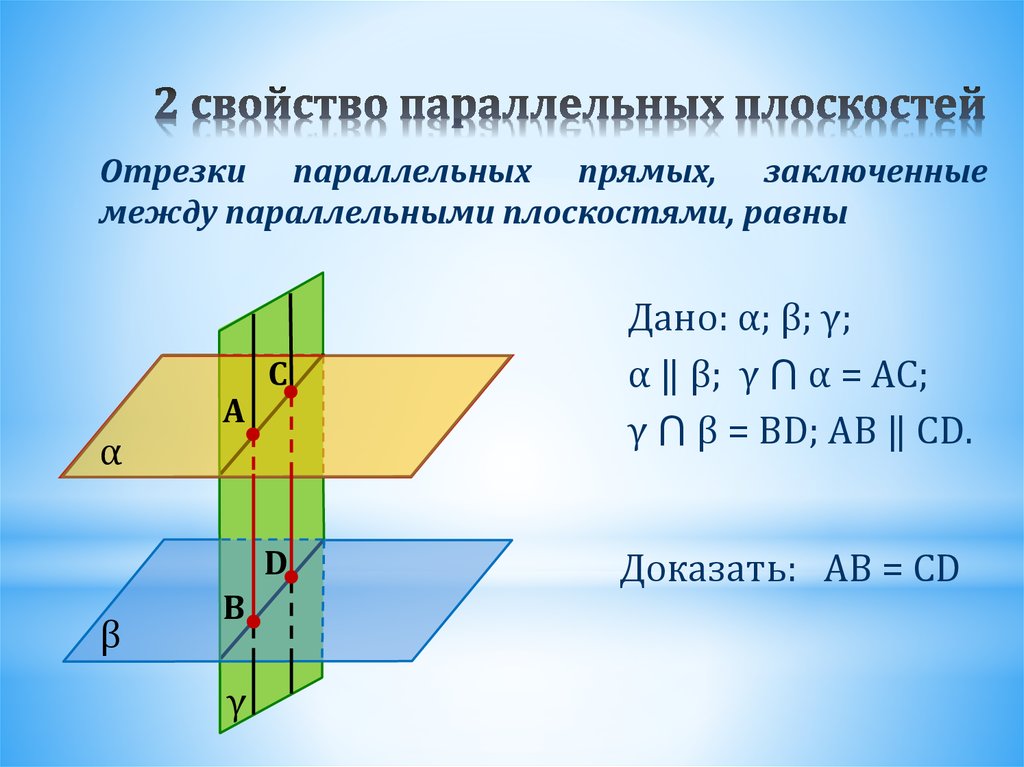
28. 2 свойство параллельных плоскостей

Отрезки параллельных прямых, заключенные
между параллельными плоскостями, равны
α
β
A
B
γ
C
Дано: α; β; γ;
α ‖ β; γ ⋂ α = AC;
γ ⋂ β = BD; AB ‖ CD.
D
Доказать: AB = CD

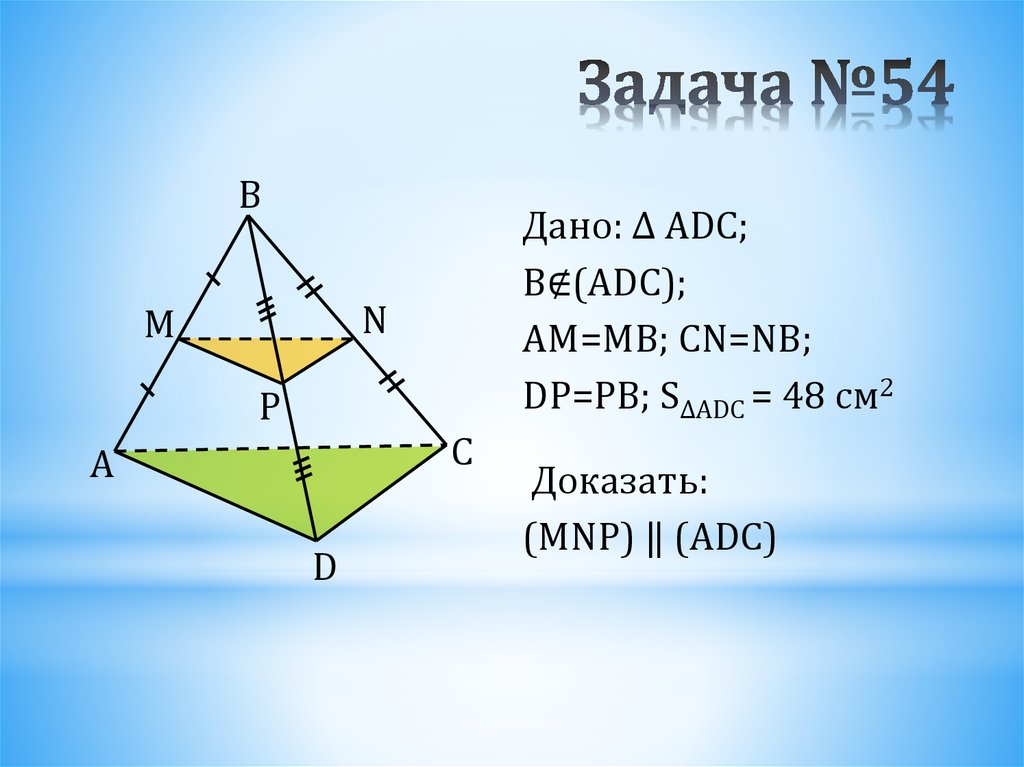
29. Задача №54

B
Дано: ∆ ADC;
B∉(ADC);
AM=MB; CN=NB;
DP=PB; S∆ADC = 48 см2
N
M
P
C
A
D
Доказать:
(MNP) ‖ (ADC)

30. Задание по теме на закрепление

ЗАДАНИЕ ПО ТЕМЕ НА
ЗАКРЕПЛЕНИЕ
1. Замените верным словом ошибку
в утверждении:
«Прямая, не лежащая в данной
плоскости, параллельна ей, если эта
прямая параллельна любой прямой,
лежащей в данной плоскости».
Ответ:___________________________
________________________________
2. Продолжите мысль:
«Если две плоскости пересекаются и
одна из этих плоскостей проходит
через прямую, параллельную другой
плоскости, то линия пересечения
этих плоскостей…»
Ответ:___________________________
________________________________
3. В признаке параллельности двух
плоскостей какими должны быть
прямые одной плоскости,
соответственно параллельные прямым
другой плоскости?
Ответ:______________________________
_____________________________
4. Каким свойством обладают две
параллельные плоскости,
пересеченные третьей?
Ответ:______________________________
_____________________________
5. Сколько плоскостей, параллельных
данной плоскости, можно провести
через точку, не лежащую на данной
плоскости?
Ответ:______________________________
_____________________________

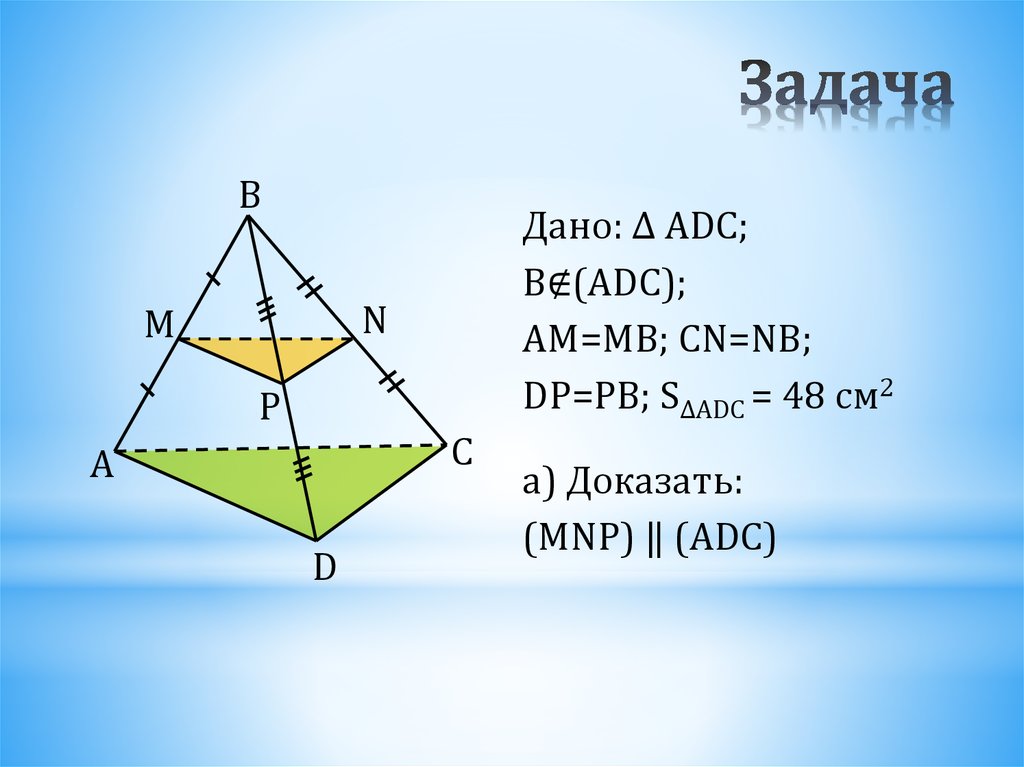
31. Задача

B
Дано: ∆ ADC;
B∉(ADC);
AM=MB; CN=NB;
DP=PB; S∆ADC = 48 см2
N
M
P
C
A
D
а) Доказать:
(MNP) ‖ (ADC)

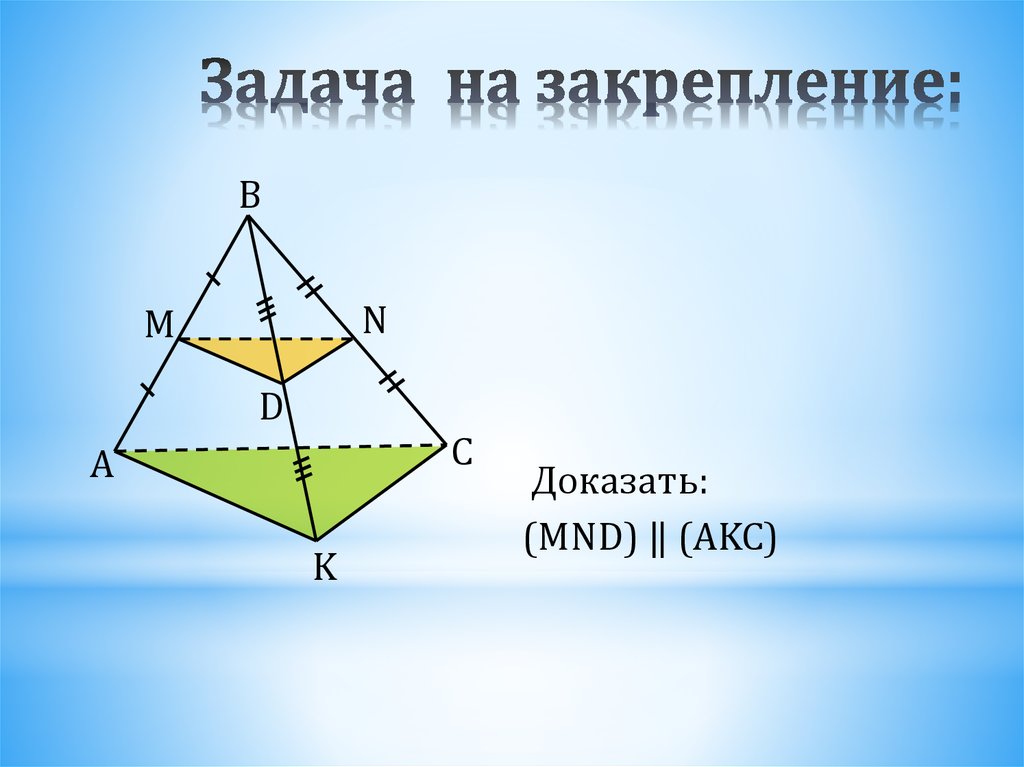
32. Задача на закрепление:

B
N
M
D
C
A
K
Доказать:
(MND) ‖ (AKC)

33. Проверь себя:

1. Замените верным словом ошибку в утверждении:
Ответ: «Прямая, не лежащая в данной плоскости,
параллельна ей,
если эта прямая параллельна
прямой, лежащей в данной плоскости».
2. Ответ: «Если две плоскости пересекаются и одна из этих
плоскостей проходит через прямую, параллельную другой
плоскости, то линия пересечения этих плоскостей
»
3. Ответ: Если две
прямые одной плоскости
параллельны двум пересекающимся прямым другой
плоскости, то такие плоскости параллельны.
4. Ответ: Линии пересечения плоскостей
5. Ответ:
.
.

34. Проверь себя:

ЗАДАЧА
Дано:
АМ=МВ,
BD=DK
BN=NC
Доказать, что MND||AKC.
Решение:
1
a) B ∆ ABC: MN – средняя линия, MN║AC, MN = AC .
B ∆BCK: DN– средняя линия , DN║KC, DN =
2
1
KC .
2
По теореме:Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой плоскости, то эти
плоскости параллельны.
Плоскости MDN и AKC параллельны.
∟MND = ∟ACK – как углы с соответственно параллельными
сторонами.

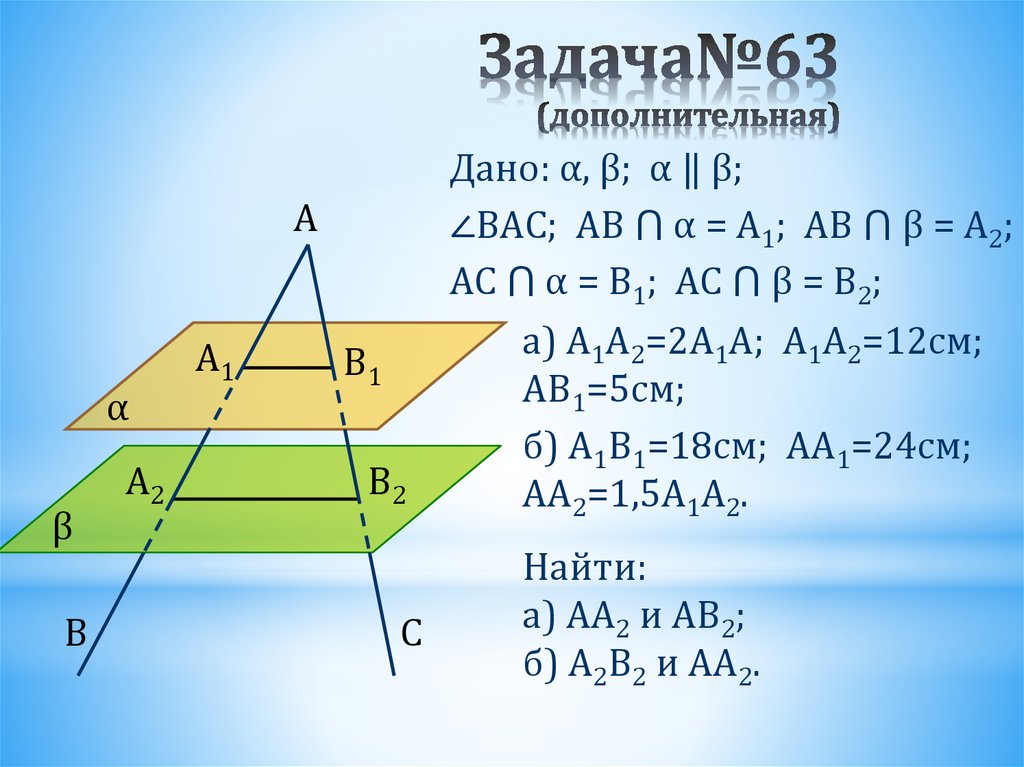
35. Задача№63 (дополнительная)

A
α
β
B
A2
A1
B1
B2
C
Дано: α, β; α ‖ β;
∠BAC; AB ⋂ α = A1; AB ⋂ β = A2;
AC ⋂ α = B1; AC ⋂ β = B2;
а) A1A2=2A1A; A1A2=12см;
AB1=5см;
б) A1B1=18см; AA1=24см;
AA2=1,5A1A2.
Найти:
а) AA2 и AB2;
б) A2B2 и AA2.

36.

1. Плоскости параллельны, прямая mлежит в плоскости