Similar presentations:
Символы математической логики
1. Символы математической логики
Кванторы- общности
- существования
Связки
- конъюнкция (и)
- дизъюнкция (или)
- импликация (если…, то…)
- эквиваленция (если и только
если…, то…
- отрицание (неверно, что…)
2. Понятие множества
Под множеством понимается совокупность некоторыхобъектов. Объекты, которые образуют множество,
называются элементами или точками, этого множества.
Множества обозначаются прописными буквами, а их
элементы – строчными.
а А
а А
А В
Ø
- принадлежит
- не принадлежит
- подмножество
- пустое множество
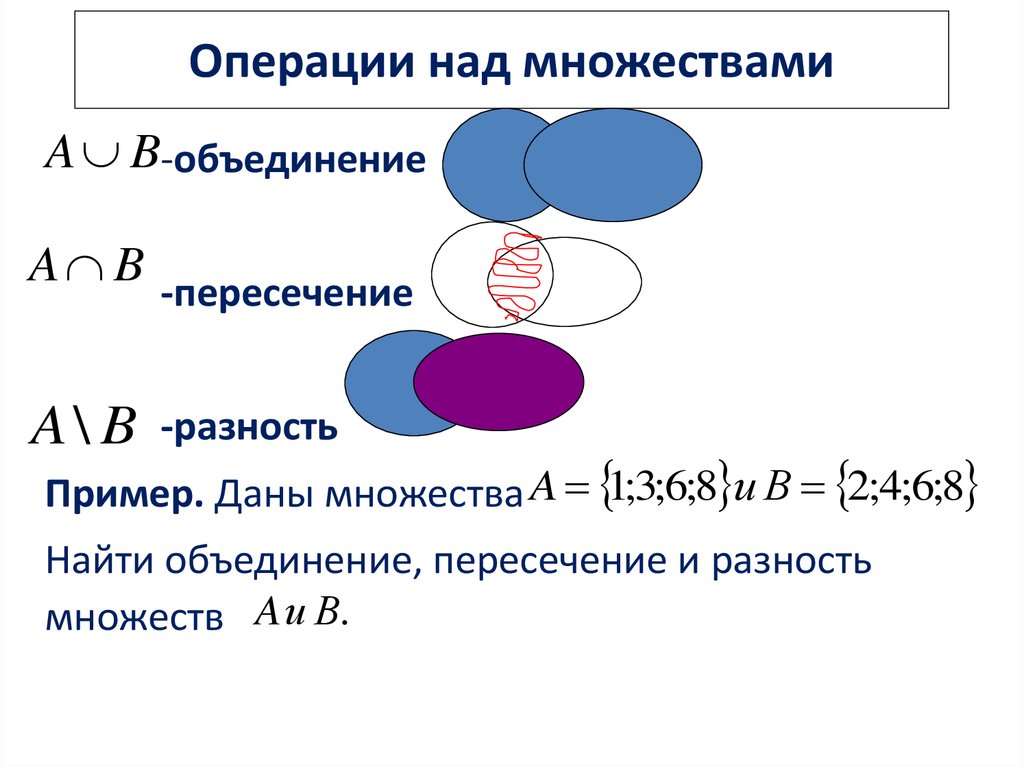
3. Операции над множествами
A B-объединениеA B
A\ B
-пересечение
-разность
Пример. Даны множества A 1;3;6;8 и В 2;4;6;8
Найти объединение, пересечение и разность
множеств A и В.
4. Последовательность. Предел последовательности.
• Определение 1. Если по некоторому законукаждому натуральному числу n N поставлено в
соответствие вполне определенное число а n , то
говорят, что дана числовая последовательность аn :
а1 , а2 ,.....аn ,...
словами, числовая последовательность эта функция
аn f (n).
натурального аргумента
а1 , а2 ,.....аn ,... называются членами
последовательности, а число аn общим
членом.
n
Пример. аn 1 /( 2n 1).
5.
• Определение 2. Число A называется пределомчисловой последовательности аn , если для любого
сколь угодно малого положительного числа 0 ,
найдется такой номер N , зависящий от , N N ( ),
что для всех членов последовательности с номерами
n N справедливо аn A .
Предел числовой последовательности обозначается
lim an A или
an при n .
n
Последовательность, имеющая предел, называется
сходящейся, а в противном случае - расходящейся.
6. Функция. Способы задания функции.
• Определение 3. Если каждому элементу х измножества X по некоторому правилу
соответствует единственный элемент у из
множества Y , то говорят, что на множестве X
задана функция y f (x) переменной х .
При этом множество X называется областью
определения функции, а множество Y –
областью значений функции.
x- называется независимой переменной или
аргументом, у - зависимой переменно, буква f –
обозначает закон соответствия.
7. Существует несколько способов задания функции.
• Аналитический способ, если функция заданаформулой вида y f (x).
• Табличный способ, если функция задана в виде
таблицы.
• Графический способ, если функция изображена
в виде в виде графика-множества точек ( x, y )
плоскости, абсциссой которых есть значения
аргумента x , о ординаты - соответствующие им
значения функции y .
• Словесный способ, если функция описана
правилом ее составления, например функция
Дирихле: f ( x ) 1, если x рационально; и
f ( x) 0, если x нерационально.
8.
• Функция может быть задана программой,вычисляющей ее значения с помощью
компьютера.
Основные свойства функций.
1. Четность и нечетность. Функция y f (x)
называется четной, если для любых значений x
из любой области определения f ( x) f ( x), и
нечетной, если f ( x) f ( x).
Функция, не являющаяся ни четной, ни нечетной,
называется функцией общего вида.
График четной функции симметричен
относительно оси ординат.
График нечетной функции симметричен
относительно начала координат.
9.
• 2. Монотонность. Функция y f (x)называется возрастающей (убывающей) на
промежутке X, если большему значению
аргумента из этого промежутка соответствует
большее (меньшее) значение функции.
Функции возрастающие или убывающие
называются монотонными.
• 3. Ограниченность. Функция y f (x)
называется ограниченной на промежутке X,
если существует такое положительное число
M 0, что f ( x) M для любого x X .
В противном случае функция называется
неограниченной.
10.
• 4. Периодичность. Функция y f (x)называется периодической с периодом T
если для любых x из области определения
f ( x T ) f ( x).
функции
0,
11. Основные элементарные функции
• 1) Степенная функция: y x , гдеЕе область определения и множество значений
зависят от α .
Например:
а)
y x : D x
2
2
2
Е
х
0;
; ,
б)
y x : D x 0; , Е ( х ) 0;
в)
y x : D x 3 ; ,
3
E x 3 ; .
12.
• 2. Показательная функция: y a , гдеa 0, a 1; D a x ; , E a x 0; .
x
3) Логарифмическая функция: y log a x, где
a 0, a 1;
4) Тригонометрические функции:
а)
D sin x ; ,E sin x 1; 1 ;
y sin x :
б) y cos x : D cos x ; , E cos x 1; 1 ;
в) y tg x : D tg x x x n, n Z , E tg x R ;
2
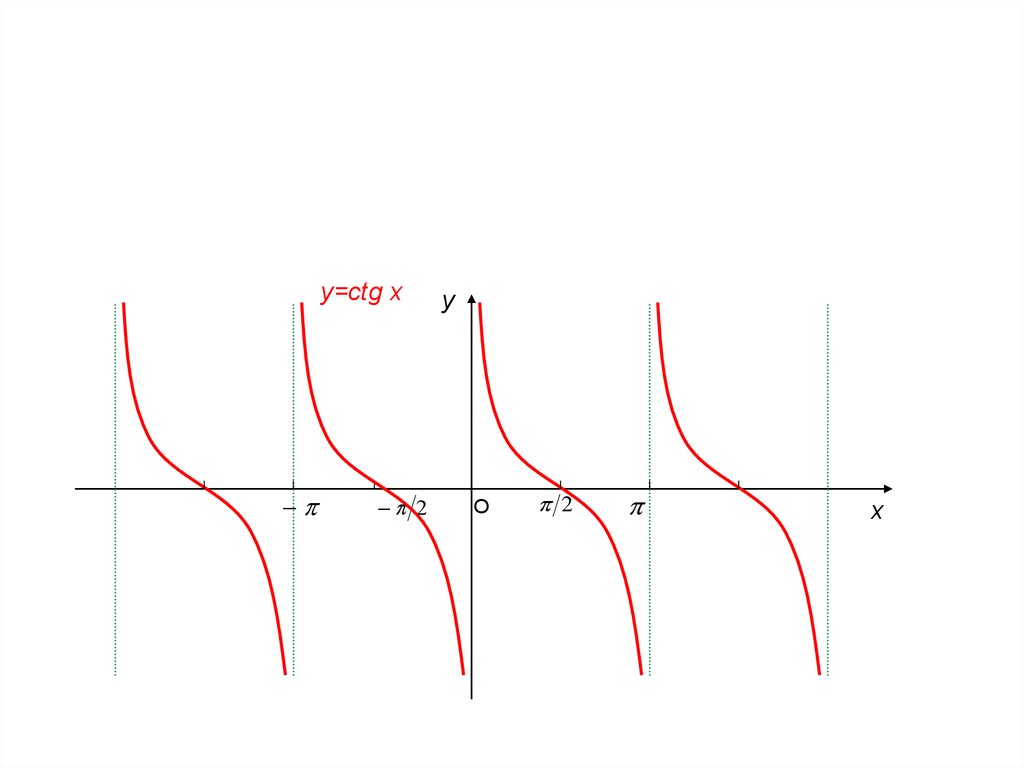
E ctg x R .
г) y ctg x : D ctg x x x n, n Z ,
13.
• 5) Обратные тригонометрические функции:а) y arcsin x : D arcsin x 1;1 E arcsin x ; ;
2 2
,
б) y arccos x : D arccos x 1;1 E arccos x 0; ;
,
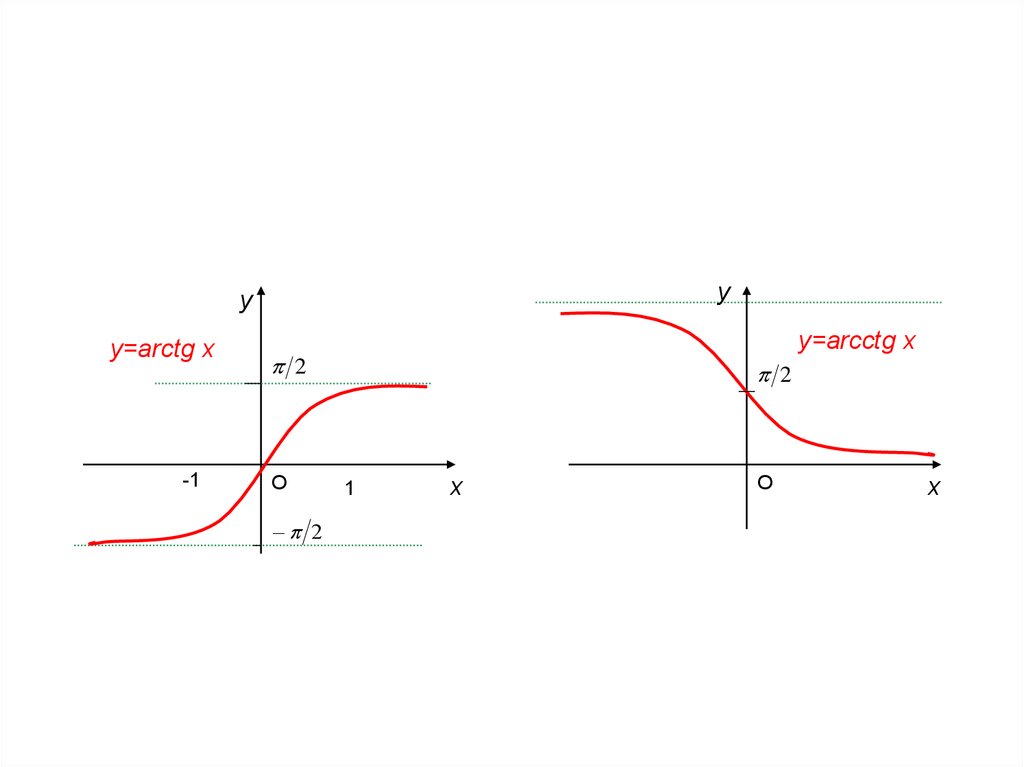
в) y arctg x : D arctg x ; E arctg x ; ;
2 2
г) y=arcctg x: D arcctg x ; , Е arcctg x 0; .
14.
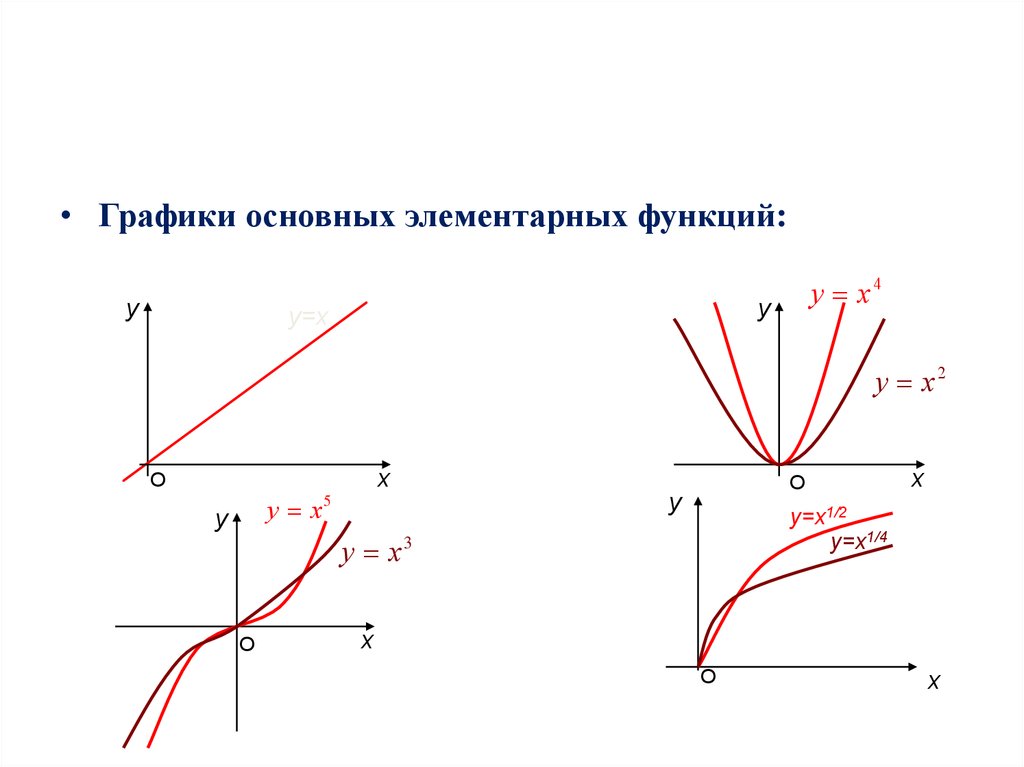
• Графики основных элементарных функций:у
y x4
у
у=х
y x2
х
О
у х
у
5
О
у
у=х1/2
у=х1/4
у х3
О
х
х
О
х
15.
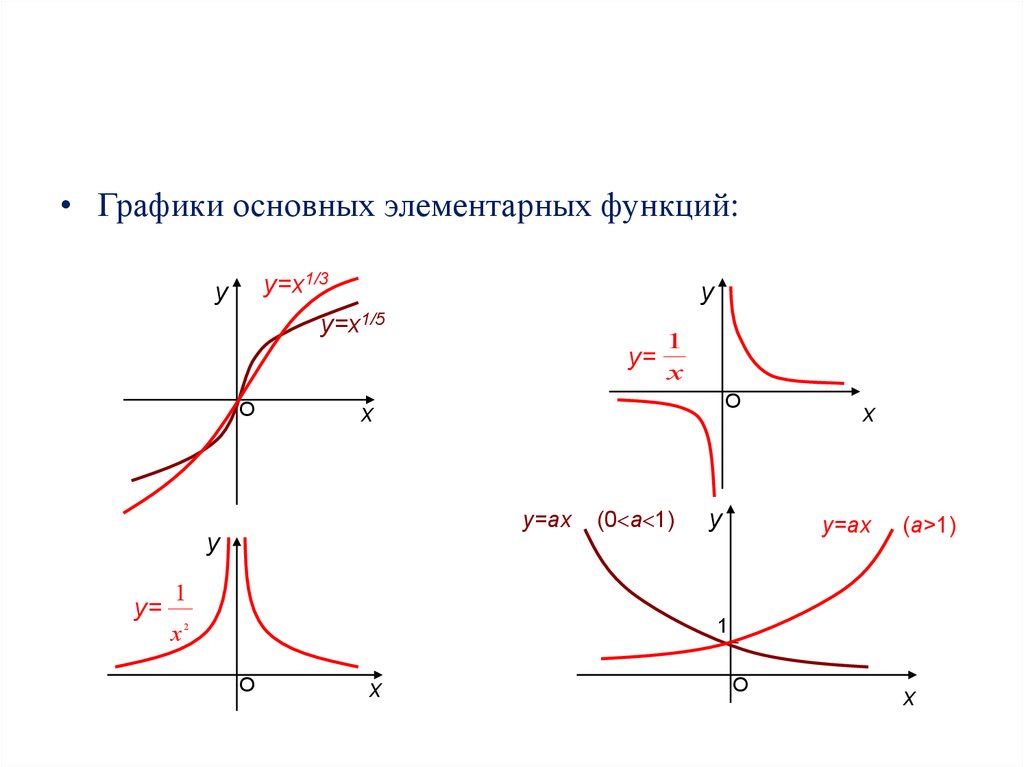
• Графики основных элементарных функций:у=х1/3
у
у
у=х1/5
у=
О
О
х
у=ax
у
у=
1
х
(0 а 1)
у
х
у=ax
(а>1)
1
1
х2
О
х
О
х
16. ФУНКЦИЯ. ПРЕДЕЛ ФУНКЦИИ 2. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
• Графики основных элементарных функций:у
О
у log a x a 1
у
1
х
у log a x 0 a 1
О
1
х
17.
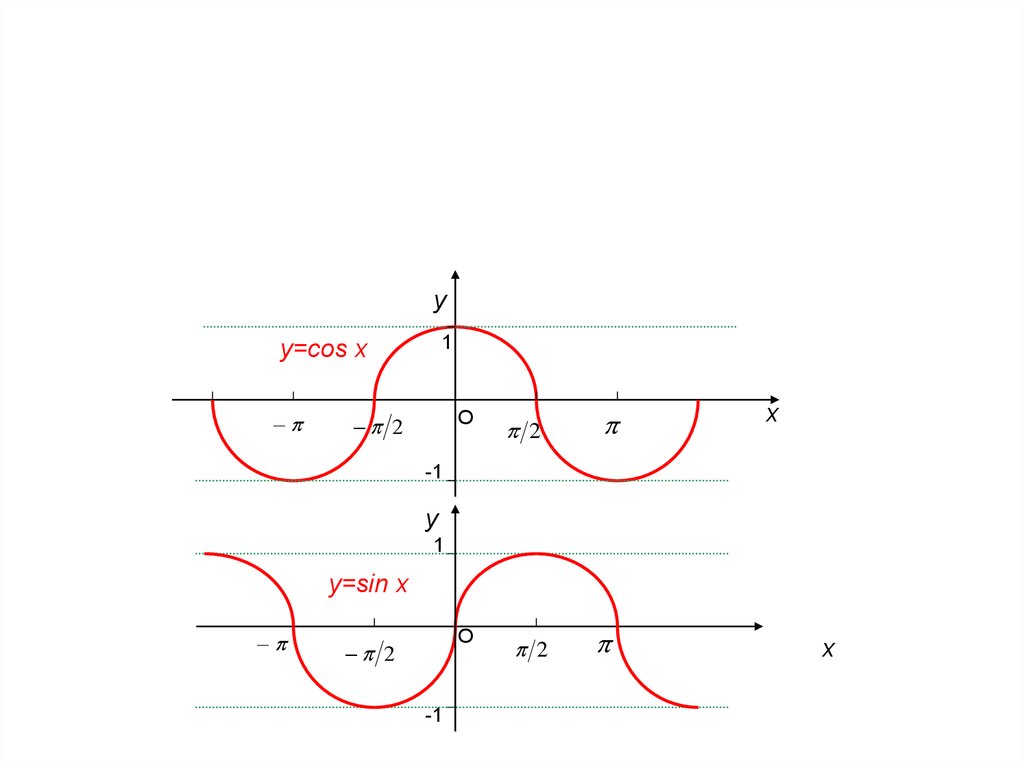
у1
y=соs x
О
2
2
х
-1
у
1
y=sin x
О
2
-1
2
х
18.
y=tg xу
2
О
2
х
19.
y=сtg x2
у
О
2
х
20.
уу
у=arcsin x
-1
у=arccos x
2
О
2
2
1
х
-1
О
1
х
21.
уу
у=arctg x
-1
у=arcctg x
2
О
2
2
1
х
О
х















 mathematics
mathematics








