Теория алгоритмов. (Глава 4)

1.

Глава 4.
ТЕОРИЯ
АЛГОРИТМОВ
Слово
алгоритм
(алгорифм)
происходит
от
имени
узбекского
математика Аль-Хорезми, который в IХ
веке
систематизировал
правила
арифметических операций. Полное имя:
Аль-Хорезми
Абу
Абдалла
Мухаммед бен Муса аль - Маджуси.
«Китаб
мухтасар
аль-джебр
ва-лмукабала (Краткая книга восполнения и
протовоставлнения)»
Аль-Хорезми
1

2.

ПОНЯТИЕ АЛГОРИТМА
Под алгоритмом понимают точное предписание о выполнении в
определенном порядке системы операций для решения всех задач
некоторого данного типа.
Характеристика алгоритма:
алгоритм задается как инструкция конечных размеров;
имеется вычислитель;
имеется множество входных данных;
имеется возможность запоминания;
вычисления проводятся только по заданным
инструкциям;
в результате получается множество выходных данных.
Алгоритм обладает свойствами массовости, общедоступности и
механистичностью.
2

3.

АЛФАВИТ, СЛОВА, АЛГОРИТМ В АЛФАВИТЕ
Алфавит – конечное
(называемых буквами).
Примеры:
множество
{А, Б, В, Г, Д};
различных
{ , , , , };
символов
{0, , &, 1}.
Слово в алфавите – конечная последовательность букв этого
алфавита.
Примеры: А = {a, b, c, d}. P = abb, Q = dda, PQ = abbdda.
P = P = P.
Алгоритм в алфавите А перерабатывает слово (слова) из А в
слово (слова) этого алфавита.
3

4.

АЛГОРИТМ В АЛФАВИТЕ.
ВПОЛНЕ ЭКВИВАЛЕНТНЫЕ АЛГОРИТМЫ
Под алгоритмом A в алфавите А понимается алгоритм, входами
и выходами которого являются слова в алфавите А.
A (Р) = Q
Слова в алфавите А
Алгоритм A применим к слову Р, если преобразование
Р
заканчивается через конечное число шагов: Q = A ( Р ). Если процесс
преобразования бесконечен, то алгоритм не применим к этому слову.
Два алгоритма A и B в одном и том же алфавите С наз-ся
вполне эквивалентными в алфавите D (D C), если для слова Р в
алфавите D оба алгоритма либо не применимы к Р, либо применимы
и их результаты совпадают:
P в D:
A ( P ) B ( P ).
4

5.

НОРМАЛЬНЫЙ АЛГОРИТМ ( АЛГОРИТМ А. А. МАРКОВА )
А - алфавит, не содержащий в качестве букв символов " " и " ".
Р и Q - слова в алфавите А.
P 1 Q 1
P 2 Q 2
В=
.......... ........
P n Q n
Пусть А = { a, b, c }
Р Q - простая подстановка;
Р Q - заключительная подст-ка;
Р ( ) Q - любая из Р Q или Р Q.
n 1, Pi и Qi , ( 1 i n ) - слова в А.
и
a a
В = cc ( )c
b c
Если Ro = bb,
сb – по (3)
сс - по (3)
с - по (2) Следовательно: В ( R o ) = с.
(1)
(2)
(3)
5

6.

ПРИМЕР НОРМАЛЬНОГО АЛГОРИТМА
Пусть А = { a, b, c }
и
β a
β b
В = β c
β
Λ
aβ ( 1)
bβ ( 2 )
cβ ( 3 )
где А.
a (4)
β
(5)
Алгоритм:
(x A ) (1*)
β x xβ
В* β ( )a
(2*)
Λ β
(3*)
Здесь x x для обозначения подстановок (1) - (3) из В.
6

7.

ПРИМЕР НОРМАЛЬНОГО АЛГОРИТМА
Пусть М = { 1, * }.
Число 0 обозначим словом 0
число 1 обозначим словом 1
.............................
число n обозначим словом n =
= 1,
= 11,
111
...
1 .
n 1 единиц
вектор (n1 , n2 ,..., nk ) n1 n2 ... nk (n1 , n2 ,..., nk ) . Напр.
(1, 2, 3 ) = 11*111*1111.
α 11
A0 =
α1
Λ
α1
1
α
применим только к тем словам в алфавите М, которые суть цифры,
переводит n в 0 и A0 не применим к пустому слову.
Нормальный алгоритм: A1 = α 1 11
Λ α
преобразует n в n 1 и A1 не применим к пустому слову.
7

8.

ФУНКЦИИ ЧАСТИЧНО - ВЫЧИСЛИМЫЕ
И ВЫЧИСЛИМЫЕ ПО МАРКОВУ
Частично определенная функция f(x1,x2,…,xn) называется частично
вычислимой по Маркову, если существует нормальный алгоритм B
над М = { 1, * }:
В(( k1, k2 ,..., k n )) = f ( k1 , k 2 ,..., k n )
тогда и только тогда, когда хотя бы одна из частей этого равенства
определена.
n - аргументная функция f вычислима по Маркову, когда норм.
алгоритм, позволяющий вычислить значение f (x1 , x2 ,..., x n ) для
совокупностей значений x 1 , x 2 ,..., x n .
f ( x ) = 0, ( x ) = x + 1, x ( x 0 ) - функции вычислимыми по Маркову.
Замыкание алгоритма:
P 1 Q 1
P Q
2
2
A
.......... .......
P n Q n
его замыкание:
Алгоритмы A и А вполне эквивалентны.
P 1 Q 1
P Q
2
2
А .......... .......
P Q
n
n
Λ Λ
8

9.

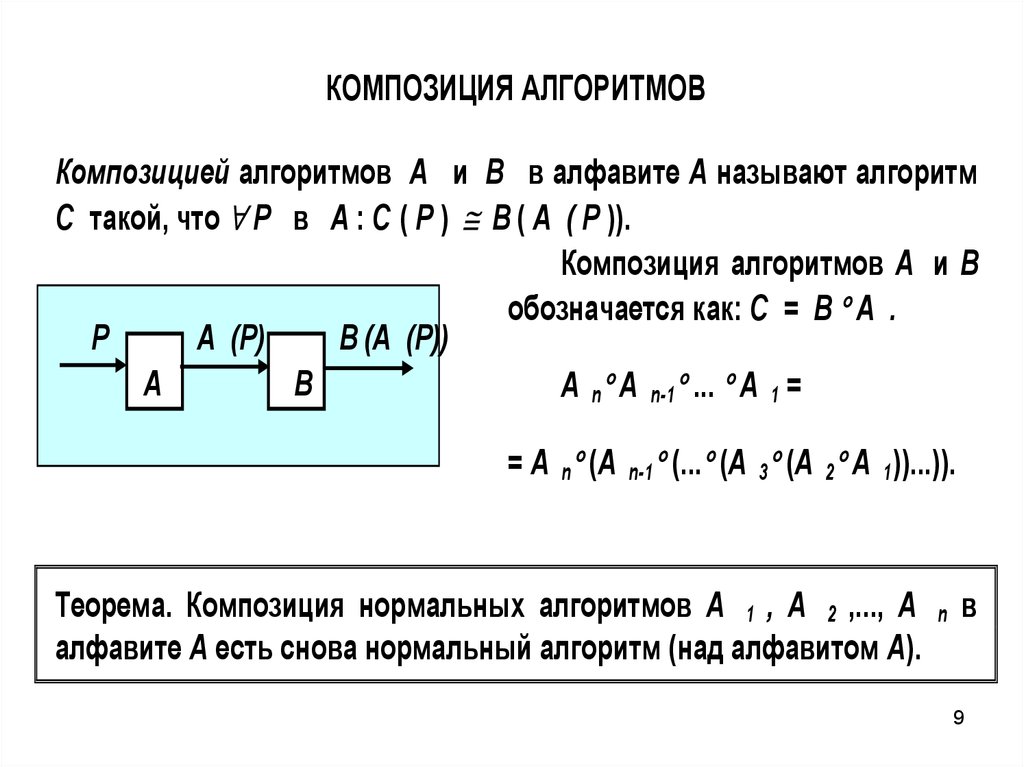
КОМПОЗИЦИЯ АЛГОРИТМОВ
Композицией алгоритмов A и B в алфавите А называют алгоритм
C такой, что P в А : C ( P ) B ( A ( P )).
Композиция алгоритмов A и B
обозначается как: C = B A .
Р
A (Р)
B (A (Р))
A
B
A n A n-1 ... A 1 =
= A n (A
n-1
(... (A 3 (A 2 A 1))...)).
Теорема. Композиция нормальных алгоритмов A 1 , A 2 ,..., A
алфавите А есть снова нормальный алгоритм (над алфавитом А).
n
в
9

10.

КОМПОЗИЦИЯ АЛГОРИТМОВ
aα α a
α a α a
a b a b
a β β a
C βa β a
ab ab
αβ Λ
β
B
α
A
a A
a A
a, b A
a A
a A
a, b A
1
2
3
4
5
6
7
8
9
10

11.

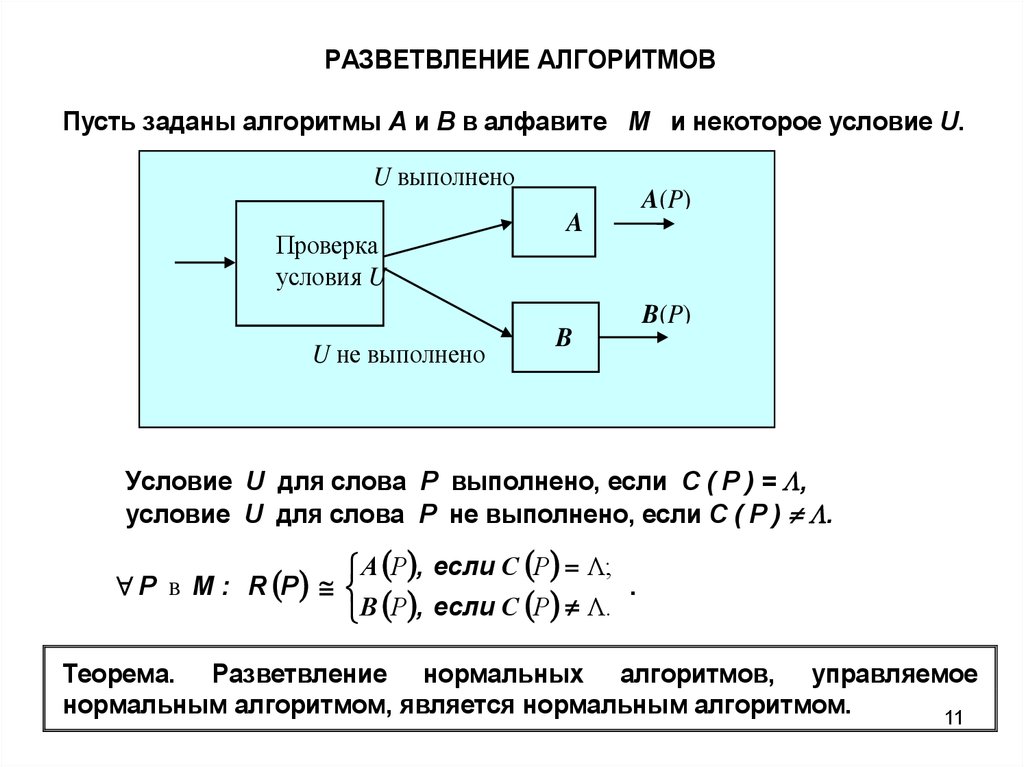
РАЗВЕТВЛЕНИЕ АЛГОРИТМОВ
Пусть заданы алгоритмы A и B в алфавите М и некоторое условие U.
U выполненo
Проверка
условия U
U не выполнено
A
B
A(P)
B(P)
Условие U для слова Р выполнено, если C ( Р ) = ,
условие U для слова Р не выполнено, если C ( Р ) .
A P , если С P Λ;
.
P в М : R P
B P , если С P Λ.
Теорема. Разветвление нормальных алгоритмов, управляемое
нормальным алгоритмом, является нормальным алгоритмом.
11

12.

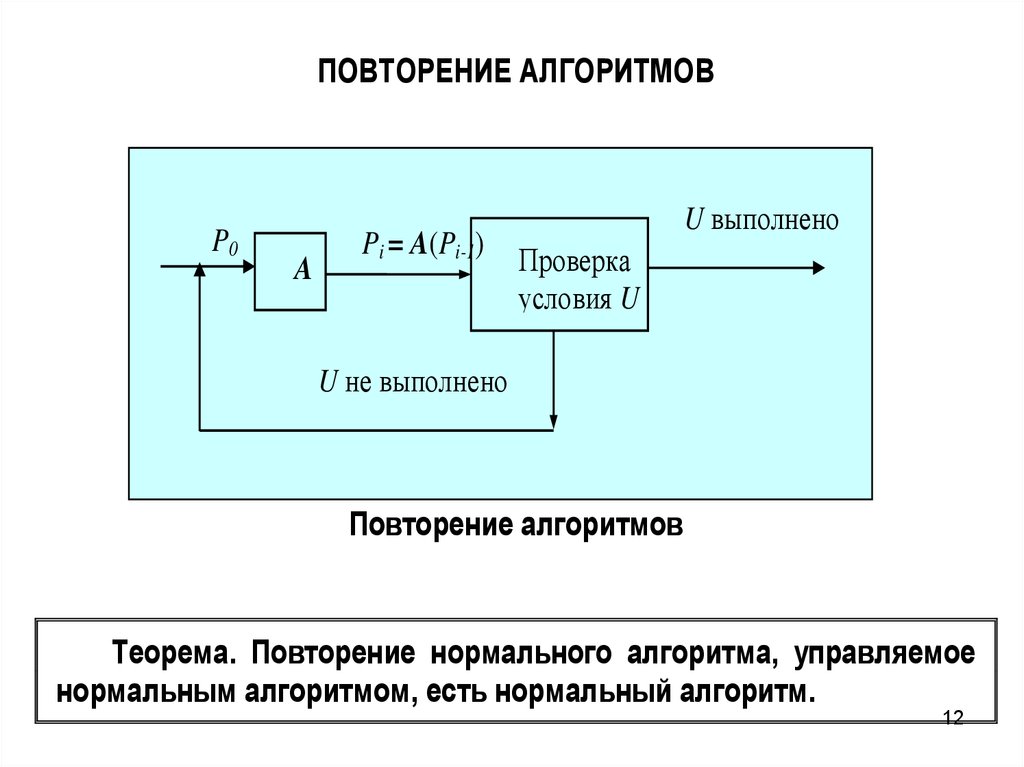
ПОВТОРЕНИЕ АЛГОРИТМОВ
P0
A
Pi = A(Pi-1)
U выполнено
Проверка
условия U
U не выполнено
Повторение алгоритмов
Теорема. Повторение нормального алгоритма, управляемое
нормальным алгоритмом, есть нормальный алгоритм.
12

13.

МАШИНА ТЬЮРИНГА
S0
q0
А = { S 0 , S 1 ,.., S
алфавит машины
{ q 0 , q 1 ,..., q
внутренних состояний.
} – (внешний)
n
m
} - множество
Действия машины:
1) головка стирает символ Si и записывает там же символ Sk;
2) головка перемещается в соседний слева квадрат;
3) головка перемещается в соседний справа квадрат;
4) машина останавливается.
В случаях 1) - 3) машина переходит во внутреннее состояние qr и
готова к действию в следующий момент времени t + 1.
1) qj Si Sk qr;
2) qj Si L qr;
3) qj Si R qr.
13

14.

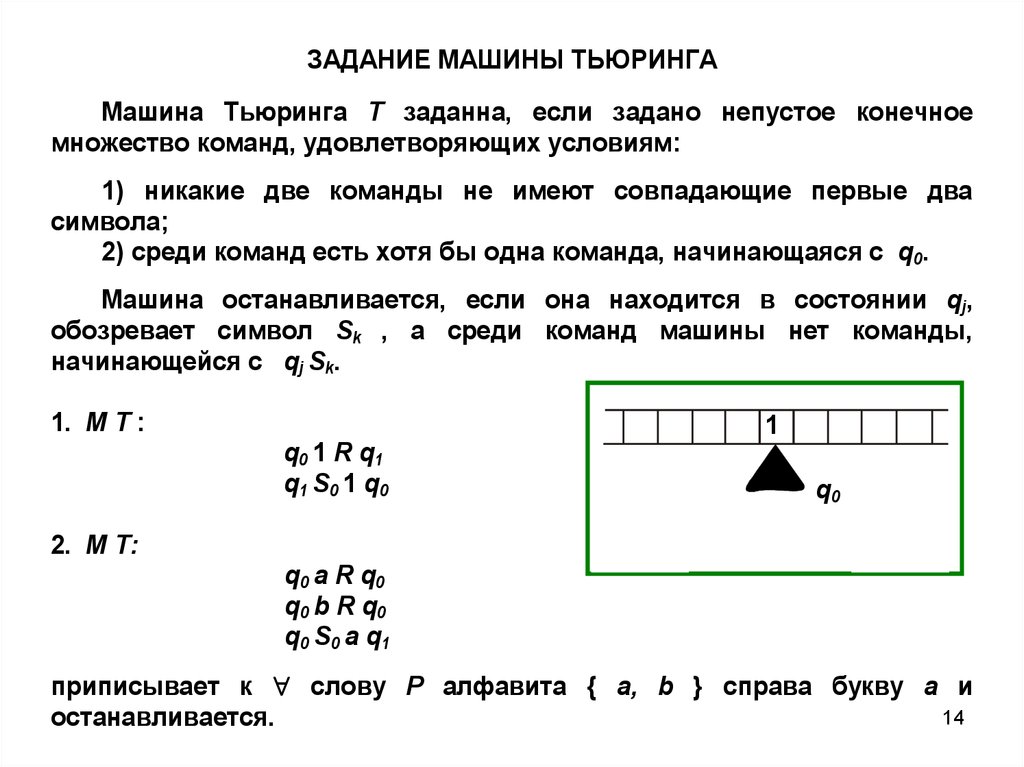
ЗАДАНИЕ МАШИНЫ ТЬЮРИНГА
Машина Тьюринга Т заданна, если задано непустое конечное
множество команд, удовлетворяющих условиям:
1) никакие две команды не имеют совпадающие первые два
символа;
2) среди команд есть хотя бы одна команда, начинающаяся с q0.
Машина останавливается, если она находится в состоянии qj,
обозревает символ Sk , а среди команд машины нет команды,
начинающейся с qj Sk.
1. М Т :
1
q0 1 R q1
q1 S0 1 q0
q0
2. М Т:
q0 a R q0
q0 b R q0
q0 S0 a q1
приписывает к слову Р алфавита { a, b } справа букву а и
14
останавливается.

15.

АЛГОРИТМ ТЬЮРИНГА. ВЫЧИСЛИМОСТЬ ПО ТЬЮРИНГУ
Частично определённая арифметическая функция f ( x 1 , x 2 ,..., x n )
наз-ся частично вычислимой по Тьюрингу если машина Тьюринга Т с
алфавитом М, включающим 1 и *, такая, что для натуральных k1, k2
,..., kn и некоторых r и m имеем:
AT ,М ( k1 , k 2 ,..., k n ) S0r f ( k1 , k 2 ,..., k n ) S0m (S0i S0S0 ...S0 ),
i раз
т. и т. т., когда определена хотя бы одна из частей этого равенства.
Арифметическая функция f ( x 1 , x 2 ,..., x n ) наз-ся вычислимой по
Тьюрингу, если машина Тьюринга Т с алфавитом М, включающим 1 и
*, такая, что для натуральных k 1 , k 2 ,..., k n найдутся r и m:
AТ ,М ( k1 , k2 ,..., kn ) S0r f ( k1 , k2 ,..., kn ) S0m .
15

16.

СВЯЗЬ МЕЖДУ
МТ И НОРМАЛЬНЫМИ АЛГОРИТМАМИ
Теорема. Пусть Т - машина Тьюринга с алф. М. Тогда нормальный
алгоритм B над А, вполне эквивалентный относительно М алгоритму
Тьюринга AT, М..
Следствие. Всякая частично вычислимая (вычислимая) по Тьюрингу
функция является частично вычислимой (вычислимой) по Маркову.
Пусть f ( x
1
, x
2
,..., x
n
) вычислима по Тьюрингу: AT,
М
( k1 , k 2 ,...,k n ) =
R1 f ( k1 , k 2 ,...,k n ) R2. Тогда нормальный алгоритм B: B A T, A :
AT, М (( k1 , k 2 ,...,k n ) ) B(( k1 , k 2 ,...,k n ) ) R1 f ( k1 , k 2 ,...,k n ) R2.
α S0 α
α 1 1
B1 α
α Λ
Λ α
α α
α 1 1α
B2 αS0 α
α Λ
Λ α
C = B 2 B 1 B.
B1 R1f k1, k2 ,..., kn R2 f k1, k2 ,..., kn R2 ;
B2 f k1, k2 ,..., kn R2 f k1, k2 ,..., kn .
Тогда:
B k1, k2 ,..., kn AT,М k1, k2 ,..., kn R1 f k1, k2 ,..., kn R2 ,
16

17.

ОСНОВНАЯ ГИПОТЕЗА ТЕОРИИ АЛГОРИТМОВ
(ПРИНЦИП НОРМАЛИЗАЦИИ ИЛИ ТЕЗИС ЧЕРЧА)
Для всякого алгоритма В в алфавите М существует вполне
эквивалентный ему нормальный алгоритм С над М, т.е.
P
в М:
В ( Р ) С ( Р ).
Иначе эта гипотеза формулируется так:
Всякий алгоритм может быть задан посредством некоторой
машины Тьюринга и реализован в этой машине.
17

18.

АЛГОРИТМИЧЕСКИ РАЗРЕШИМЫЕ ПРОБЛЕМЫ:
-сложение двух и более заданных чисел;
-решение в радикалах уравнений от одной переменной не выше
четвертой степени;
-решение систем линейных уравнений с n неизвестными;
-и т. д.
АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ:
1. Проблема диофантовых корней (10-ая проблема Гильберта)
Р n ( х 1 , х 2 ,…, х m ) = 0
В 1970 году советским математиком Ю.В. Матиясевичем было доказано,
что эта проблема алгоритмически неразрешима.
2. Проблема распознавания применимости. А ( Р ) -- ?
Теорема. Не существует нормального алгоритма B, который позволил
бы выяснить, применим или нет произвольный нормальный алгоритм
A к произвольному слову Р.
18

19.

АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ:
3. Проблема эквивалентности слов: для любых двух слов в
данном алфавите требуется указать, эквивалентны они или нет проблема эквивалентности слов. Марков и Пост доказали, что данная
проблема алгоритмически неразрешима.
4. Проблема неразрешимости логики предикатов. Черчем
доказано, что не существует алгоритма, который для любой формулы
логики предикатов устанавливает, логически общезначима она или нет.
5. Проблема остановки. Тьюрингом доказано, что не существует
алгоритма, позволяющего выяснить: остановится или нет
произвольная программа для произвольного заданного входа. Для
теоретического программирования означает, что не существует общего
метода проверки программ на наличие в них бесконечных циклов.
6. Не существует алгоритма, позволяющего установить, вычисляет
ли некоторая программа постоянную нулевую функцию Z(x) = 0. Тогда
проблема вычисляют ли две произвольные программы одну и ту же
одноаргументную функцию, тоже алгоритмически неразрешима.
19

20.

РЕКУРСИВНЫЕ ФУНКЦИИ
Исходные функции:
1) нуль функция: Z(x) = 0 при x ( x 0 ),
2) функция прибавления единицы: N ( x ) = x + 1 при x ( x 0 ),
3) проектирующая функция Jin ( x 1 , x 2 ,..., x n ) = xi при x1, x2 ,..., xn 0.
Правила для получения новых функций:
Подстановка: f ( x 1 , x 2 ,..., x n ) =
g ( h 1 ( x 1 , x 2 ,..., x n ),..., h m ( x 1 , x 2 ,..., x n )).
Рекурсия:
f ( x1, x2 ,..., xn , 0 ) = g ( x1, x2,..., xn ),
а)
f ( x1, x2,..., xn, y + 1 ) = h ( x1, x2, ..., xn, y, f ( x1, x2,..., xn , y )),
для n = 0:
f ( 0 ) = k, где k - Const,
б)
f ( y + 1 ) = h ( y, f ( y )).
- оператор: пусть g ( x1, x2,..., xn, y ) такова, что для x1, x2,..., xn у:
g ( x1, x2,..., xn, y ) = 0. Обозначим через y (g ( x1, x2,..., xn, y ) = 0 )
наименьшее значение у, при котором g(x1, x2,..., xn, y) = 0. Полагаем:
f ( x1, x2,..., xn ) = y ( g ( x1, x2,..., xn, y ) = 0 ).
20

21.

РЕКУРСИВНЫЕ ФУНКЦИИ
Функция называется примитивно рекурсивной, если она может
быть получена из исходных функций 1), 2) и 3) с помощью конечного
числа подстановок и рекурсий.
Функция f называется общерекурсивной, если она может быть
получена из исходных функций 1), 2) и 3) с помощью конечного числа
подстановок, рекурсий и - оператора. Общерекурсивные функции
иногда называют рекурсивными функциями.
Частичная функция называется частично рекурсивной, если она
может быть получена из исходных функций 1), 2) и 3) с помощью
конечного числа подстановок, рекурсий и ‘ -оператора, где ‘ оператор определяется как и -оператор, но при некоторых значениях
x1, x2 ,..., xn может и не существовать у такого, что g ( x1, x2 ,..., xn , y) = 0.
21

22.

Теорема. Следующие функции являются примитивно рекурсивными:
1) х + у;
2) х у;
3) х у;
4)
(х) =
х - 1 , если х > 0,
0 , если х = 0;
5)
x - y, x y,
х-y=
0, x < y;
6)
7)
Sg (x) =
8)
0, x = 0,
1, x 0;
x-y =
x - y, x y
y - x, x < y;
1, x = 0,
sg*(x) =
9) rm ( x, y ) = остатку от деления у на х;
10) qt ( x, y ) = частному от деления у на х;
11) х ! ;
12) min ( x, y);
14) max ( x, y);
15) max ( x1, x2,..., xn ).
0, x 0;
13) min ( x1, x2,..., xn );
22

23.

ТЕОРИЯ АЛГОРИТМОВ
Известные советские математики Успенский В. А. и Семенов А. Л. в
обзоре основных достижений теории алгоритмов пишут:
“Алгоритмические
обучения
и
концепции играют в процессе
воспитания
современного
человека
фундаментальную роль, сравнимую лишь с ролью
письменности”.
23