Similar presentations:
Логическое следствие и метод резолюций. (Глава 3)
1.
Глава 3ЛОГИЧЕСКОЕ СЛЕДСТВИЕ И
МЕТОД РЕЗОЛЮЦИЙ
1
2.
Логическое следствие и проблемадедукции в логике высказываний
А
В означает, что из А лог. следует В.
Т. 3.1. Если А
В и В
С , то А
С.
А означает, что А - тавтология
(логически общезначима).
Т. 3.2.
А
В
(А В).
А1 , А2 ,…, А m ╞ В
2
3.
ПРОБЛЕМА ДЕДУКЦИИ В ЛОГИКЕ ВЫСКАЗЫВАНИЙА1 , А2 ,…, А m ╞ В
Теорема 3.4. Если формула
А1 & А2 &…& А m & В
является противоречием, то
А1 , А2 ,…, А m ╞ В.
?
4.
РЕЗОЛЬВЕНТА ДИЗЪЮНКТОВ ЛОГИКИ ВЫСКАЗЫВАНИЙP
Q
– дизъюнкт.
R
литерал литерал литерал
P и
P
контрарные.
Пусть в D1 есть L , а в D2 - L
R = (D1 - L) (D2 - L) - бинарная резольвента D1 и D2.
1. Пусть D1 = P Q,
D2 =
P T,
2. Пусть D1 = P Q
( D1 = P Q ),
D2 = Q T
( D2 = Q T ),
тогда R = Q T.
R = P T
(R=P T)
Теорема 3.5. Пусть для дизъюнктов D1 и D2 существует
резольвента R. Тогда R есть логическое следствие из D1 и D2.
4
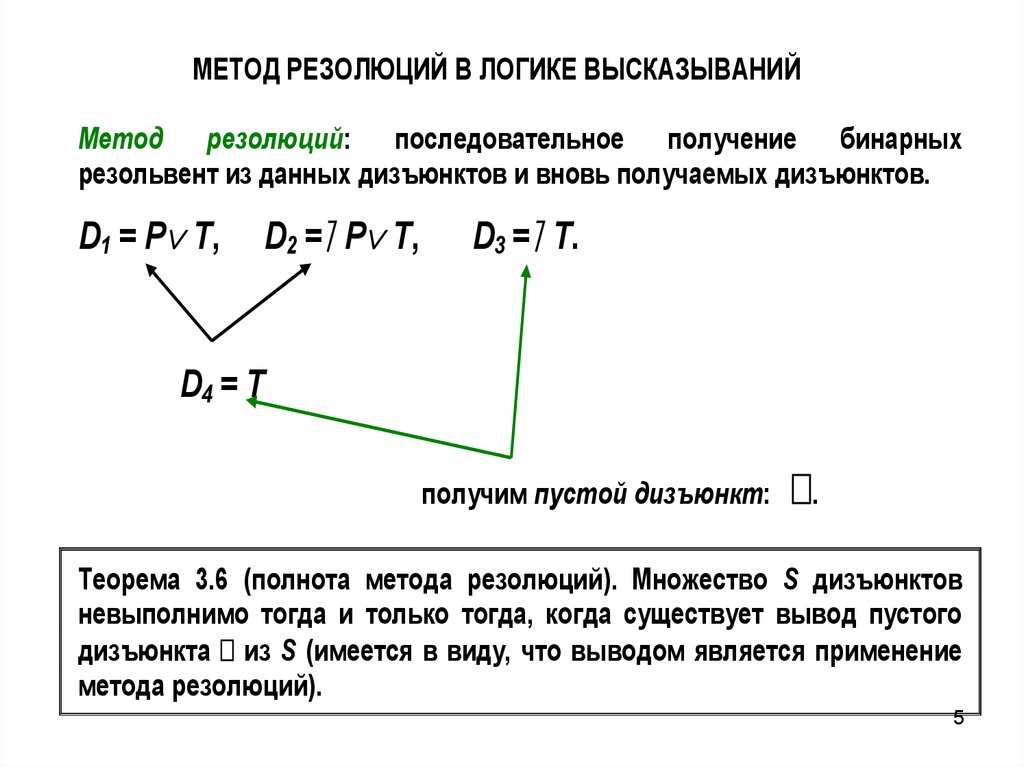
5.
МЕТОД РЕЗОЛЮЦИЙ В ЛОГИКЕ ВЫСКАЗЫВАНИЙМетод резолюций: последовательное получение бинарных
резольвент из данных дизъюнктов и вновь получаемых дизъюнктов.
D1 = P T,
D2 = P T,
D3 = Т.
D4 = Т
получим пустой дизъюнкт:
.
Теорема 3.6 (полнота метода резолюций). Множество S дизъюнктов
невыполнимо тогда и только тогда, когда существует вывод пустого
дизъюнкта из S (имеется в виду, что выводом является применение
метода резолюций).
5
6.
МЕТОД НАСЫЩЕНИЯ УРОВНЯ. S = { D1 , D2 ,…,D k }. Строим S0, S1, S2, …1) S 0 = S;
2) если S n-1 построено, то S n = резольвенты Dj и Dk: j < k :
Dj ( S 0 S 1 … S n-1 ),
Dk S n-1 , n = 1, 2,…
Пр.: S = { P Q, P Q, P Q, P Q }.
(1) P Q;
(2) P Q;
(3) P Q;
(4) P Q;
_____________________________
S1: (5) Q
из (1) и (2);
(6) P
из (1) и (3);
(7) Q Q
из (1) и (4);
(8) P P
из (1) и (4);
(9) Q Q
из (2) и (3);
(10) P P из (2) и (3);
(11) P
из (2) и (4);
(12) Q
из (3) и (4);
_____________________________
S2: (13) P Q
из (1) и (7);
(14) P Q
из (1) и (8);
(15) P Q
из (1) и (9);
(16) P Q
из (1) и (10);
(17) Q
из (1) и (11);
На 39 шаге получим:
(39)
из (5) и (12).
S0 :
6
7.
СТРАТЕГИЯ ВЫЧЕРКИВАНИЯD* = D D’
D* - наддизъюнктом для D
Строим ( S 0 S 1 … S n-1 ) находим резольвенты R для
Di ( S0 S1 … Sn-1) и Dk Sn-1, i<k.
R записываем, если она не тавтология и не наддизъюнкт
существующего дизъюнкта.
S0: (1) P Q,
(2) P Q,
(3) P Q,
(4) P Q,
______________________________________________
S1: (5) Q
(6) P
(7) P
(8) Q
из (1) и (2),
из (1) и (3),
из (2) и (4),
из (3) и (4),
_______________________________________________
S2:
(9)
из (5) и (8).
7
8.
ЛОК-РЕЗОЛЮЦИЯРассмотрим:
P Q,
(1) 1 P 2 Q,
(2) 3 P 4 Q.
Получаем лок-резольвенту :
(3) 2 Q 4 Q Q .
P Q.
Введем индексы:
Пример: (1) 1 P 2 Q,
(2) 3 P 4 Q,
(3) 5 P 6 Q,
(4) 7 P 8 Q.
(5) 2 Q
(6) 2 Q 8 Q
(7) 4 Q 6 Q
(8) 4 Q
(9)
из
из
из
из
из
(1)
(1)
(2)
(2)
(5)
и
и
и
и
и
(3),
(4).
(3),
(4),
(8).
Теорема 3.7. Пусть S - множество дизъюнктов, в котором каждая
литера индексирована целым числом. Если S противоречиво, то
имеется лок-вывод пустого дизъюнкта из S.
8
9.
МЕТОД РЕЗОЛЮЦИЙ ДЛЯ ХОРНОВСКИХ ДИЗЪЮНКТОВХорновские дизъюнкты: А, А, А С В, А В С D.
S множество хорновских дизъюнктов без тавтологий.
0
1. Полагаем, что S = S.
n-1
n-1
2. Пусть S , n 1, построено. Выбираем из S
D1 и D2 :
D1 - унитарный позитивный дизъюнкт, например, D1 = Р;
D2 - дизъюнкт, содержащий литеру Р.
Вычисляем резольвенту R для дизъюнктов D1 и D2 и
n
\ { D2 } ) { R }. Повторяем до тех пор, пока
S = (S
n-1
получим
либо в S
n-1
не D1 и D2 указанных видов.
9
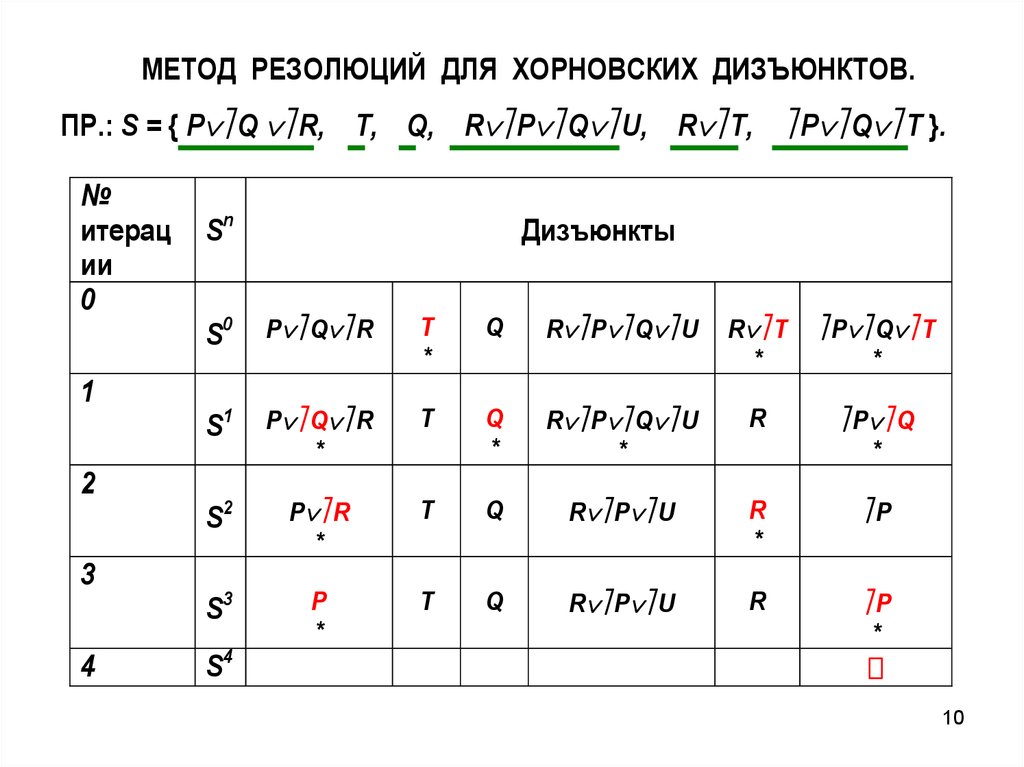
10.
МЕТОД РЕЗОЛЮЦИЙ ДЛЯ ХОРНОВСКИХ ДИЗЪЮНКТОВ.ПР.: S = { P Q R, T, Q, R P Q U, R T, P Q T }.
№
итерац
ии
0
Sn
Дизъюнкты
S0
P Q R
T
*
Q
R P Q U
R T
*
P Q T
*
S1
P Q R
*
T
Q
*
R P Q U
*
R
P Q
*
S2
P R
*
T
Q
R P U
R
*
P
S3
P
*
T
Q
R P U
R
P
*
1
2
3
4
S4
10
11.
РЕШЕНИЕ ПРОБЛЕМЫ ДЕДУКЦИИ В ЛОГИКЕ ВЫСКАЗЫВАНИЙА1 , А2 ,…, А m ╞ В
1. Строим формулу:
приводим ее к к.н.ф.:
(1)
С = А1 & А2 &…& А
m
& В
и
С = D1 & D2 &…& D k .
2. Применяем к S = {D1 , D2 ,…, D k } метод резолюций. Если
получим пустой дизъюнкт, то ( 1 ) имеет место, если пустой дизъюнкт
получить нельзя, то ( 1 ) не имеет места.
Множество дизъюнктов S = { D1 , D2 ,…, D k } наз-ся невыполнимым
если С невыполнима ( является противоречием ).
11
12.
ЛОГИЧЕСКОЕ СЛЕДСТВИЕ И ПРОБЛЕМА ДЕДУКЦИИВ ЛОГИКЕ ПРЕДИКАТОВ
Будем рассматривать только замкнутые формулы логики предикатов.
Проблема дедукции логики предикатов:
А1 , А2 ,…, А m ╞ В
Строим:
?
С = А1 & А2 &…& А m & В
и приводим ее к
предваренной нормальной форме (пренексной нормальной форме):
Пусть
Q
x i
i = x ;
i
C Q1 Q 2...Q n D
префикс
матрица
12
13.
СКОЛЕМОВСКАЯ СТАНДАРТНАЯ ФОРМАA Q1 x1 Q2 x2…Qn xn D
префикс
матрица
А = x y ( P (x, y ) Q (x, a )) А S = y (P (c, y ) Q (c, a )).
x y z ( P (x, y, z ) Q (a, b, x, y ))
z (P (c, d, z ) Q (a, b, c, d )).
А = x y z ( P( x, y ) Q ( f1 ( a ), y)).
Аs = x z ( P ( x, f2 (x) ) Q ( f1(a), f2 ( x ))).
13
14.
СКОЛЕМОВСКАЯ СТАНДАРТНАЯ ФОРМАА
не всегда
Аs
Теорема 3.8. Формула A является противоречием т. и т. т., когда её
стандартная форма As является противоречием.
’
Сл. 3.1. Если А противоречие, и Аs = (Q1 ,…,Q n ) D1 & D2 &…& Dm, то
А ~ D1 & D2 &,…,& Dm.
Сл. 3.2. Пусть As – стандартная форма для A и пусть A –противоречие.
Тогда As ~ A.
14
15.
ПРОЦЕСС «СКОЛЕМИЗАЦИИ» (ЗАМКНУТОЙ) ФОРМУЛЫа) исходная формула:
В = x y(Р(х) Q(у)) y xR(х,у);
б) переименовываем перемен.:
В = x y(Р(х) Q(у)) z wR(z,w);
в) переносим отрицание:
В = x y(Р(х) Q(у)) z w R(z,w);
г) выносим кванторы за скобки: В = x y z w((Р(х) Q(у)) R(z,w));
д) приводим матрицу к к.н.ф.:
В = x y z w(( Р(х) R(z,w))& (Q(y) R(z,w)));
е) удаляем кванторы , вводя сколемовские функции
В = x z(( Р(х) R(z,g(x,z))&(Q(f(x)) R(z, g(x,z)))).
Формула В имеет дизъюнкты:
x z( Р(х) R(z,g(x,z)) и x z(Q(f(x)) R(z, g(x,z)))
Их записываем в виде:
Р(х) R(z,g(x,z)
и
Q(f(x)) R(z, g(x,z)).
15
16.
ДИЗЪЮНКТЫ ЛОГИКИ ПРЕДИКАТОВЭлементарную формулу или её отрицание называют литералом (литерой)
в логике предикатов.
Дизъюнктом в логике предикатов считают дизъюнкцию литералов, при
этом все переменные связаны кванторами всеобщности.
х y z ( P(х) Q(с,у)
литерал
литерал
R(z) )
– дизъюнкт.
литерал
P(x) и P(с) не являются контрарными,
но
P(с) и P(с) - контрарные.
Иногда литералы или дизъюнкты называют клаузами
предложение, являющееся частью сложного предложения).
(clause
–
16
17.
ДИЗЪЮНКТ ЛОГИКИ ПРЕДИКАТОВДизъюнктом или клаузой в логике предикатов наз. выражение вида:
х1 х2 … хk (C1 C2 … Cn),
где Ci , 1 i n – литералы, а х1, х2, …, хk все переменные
встречающиеся в Ci, 1 i n. При n = 0 получим пустой дизъюнкт,
который обозначается символом .
Дизъюнкт
содержит
кванторы
общности
по
всем
переменным из C1 C2 … Cn. Для краткости дизъюнкт пишут
без кванторов:
C1 C2 … Cn
17
18.
УНИФИКАЦИЯдизъюнкт
дизъюнкт
S = { P(x, f(y), b) P(x, f(a), b), P(c, f(a), b) }
литерал
литерал
литерал
Подстановочный частный случай литерала получается
при подстановке в литералы термов вместо переменных.
Пусть L = P( x, f(y), b). Тогда:
Подстановки:
1 = { z/x, w/y };
2 = { a/y };
3 = { g(z)/x, a/y };
L1 = P( z, f(w), b),
L2 = P( x, f(a), b),
L3 = P( g(z), f(a), b).
L 1 L1 ,
L 3 L3 ,
L 2 L2 .
Множество { Li } литералов унифицируемо, если подстановка ,
что ( L1 ) = ( L2 ) = … = ( Ln ) . и - унификатор для { Li }.
18
19.
АЛГОРИТМ УНИФИКАЦИИ1) Начинает работу с пустой подстановки , если унификатор, то
завершаем, иначе переходим к 2);
2) Пусть на k-ом шаге получена k. Если k – унификатор, то
завершаем, иначе строится множество рассогласования.
Пример: { P (a, f(a, g(z)), h(x)), P (a, f( a, u), g(w)) }.
W = { g(z), u }.
Тогда:
k+1 = k { g(z) / u }.
Теорема 3.9. Описанный алгоритм находит наиболее общий
унификатор для множества унифицируемых литералов и сообщает о
неудаче, если литералы неунифицируемы.
19
20.
МЕТОД РЕЗОЛЮЦИЙ В ЛОГИКЕ ПРЕДИКАТОВПусть в D1 есть литера L1 , в D2 - литера L2 .
Если L1 и L2 имеют унификатор θ, то новый дизъюнкт R:
R = ((D1 )θ - (L1 )θ ) ((D2 )θ - (L2 )θ )
называется бинарной резольвентой D1 и D2 .
Резольвента дизъюнктов D1 и D2 :
1) бинарная резольвента D1 и D2,
2) бинарная резольвента D1 и склейки D2,
3) бинарная резольвента D2 и склейки D1,
4) бинарная резольвента склейки D1 и склейки D2.
Метод резолюций в логике предикатов: последовательное
получение резольвент из заданных дизъюнктов и вновь
получаемых дизъюнктов.
Теорема 3.10 (полнота метода резолюций). Множество S
дизъюнктов невыполнимо тогда и только тогда, когда существует
вывод пустого дизъюнкта из S.
20
21.
О РЕАЛИЗАЦИИ МЕТОДА РЕЗОЛЮЦИЙВыбор, в какой последовательности строить резольвенты для
множества дизъюнктов S очень важен так как:
1) для невыполнимого множества дизъюнктов S можно никогда не
завершить процесс построения непустых резольвент;
2) если в процессе построения резольвент из S не использовать все
дизъюнкты из S, то процесс построения резольвент может
завершится за конечное число шагов без получения пустого
дизъюнкта, так как из невыполнимости множества S не следует (в
общем случае) невыполнимость части S.
21
22.
РЕШЕНИЕ ПРОБЛЕМЫ ДЕДУКЦИИ В ЛОГИКЕ ПРЕДИКАТОВА1 , А2 ,…, А m ╞ В
1.
Строим: С = А1 & А2 &…&
предваренной нормальной форме:
(1)
А m& В
и приводим ее к
С Q1 x1 Q2 x2…Qn xn D
префикс
матрица
2. Строим сколемовскую нормальную форму:
(Q1 x1 Q2 x2…Qn xn)* D1 & D2 &…& D k .
3. Применяем к S = {D1 , D2 ,…, D k } метод резолюций. Если
получим пустой дизъюнкт, то ( 1 ) имеет место, если пустой дизъюнкт
получить нельзя, то ( 1 ) не выполняется.
22
23.
ПРИЛОЖЕНИЕ МЕТОДА РЕЗОЛЮЦИЙ ДЛЯ АНАЛИЗАСИЛЛОГИЗМОВ АРИСТОТЕЛЯ
x (M(x) P(x));
x (M(x) P(x));
x (M(x) & P(x));
x (M(x) & P(x)).
А : Всякий М есть Р
Е : Всякий М не есть Р
Некоторый М есть Р
I:
O : Некоторый М не есть Р
Силлогизм Барбара по 1-ой фигуре: Выяснить следует ли из
x (S(x) P(x)),
формула
x (P(x) Q(x))
x (S(x) Q(x)),
Если С = ( x (S(x) P(x))) & ( x (P(x) Q(x))) & x (S(x) Q(x))
- противоречие, то силл. правильный. Из С получим:
1) S(x) P(x),
2) P(у) Q(у),
3) S(a),
4) 7 Q(a),
S
5) P(a) из 3) и 1),
6) P(a) из 4) и 2),
из 5) и 6).
7)
Следовательно, силлогизм правильный.
P
Q
23
24.
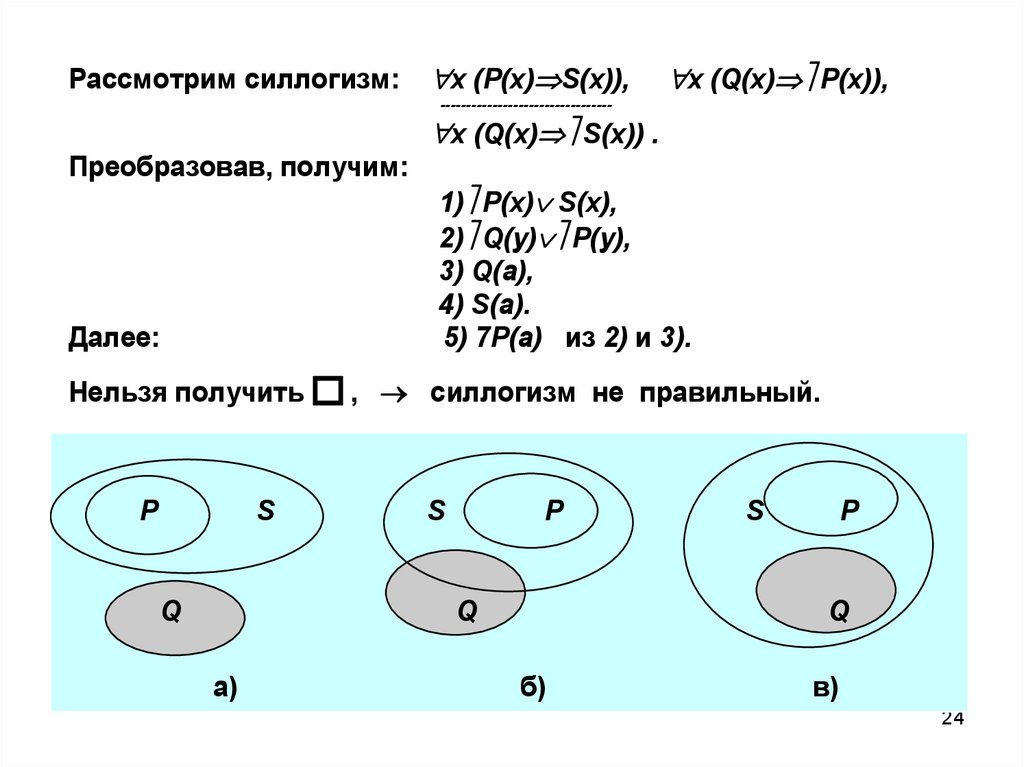
Рассмотрим силлогизм:x (P(x) S(x)),
x (Q(x) P(x)),
---------------------------------
x (Q(x) S(x)) .
Преобразовав, получим:
Далее:
Нельзя получить
P
S
Q
1) P(x) S(x),
2) Q(y) P(у),
3) Q(a),
4) S(a).
5) 7P(a) из 2) и 3).
, силлогизм не правильный.
S
P
Q
а)
S
P
Q
б)
в)
24
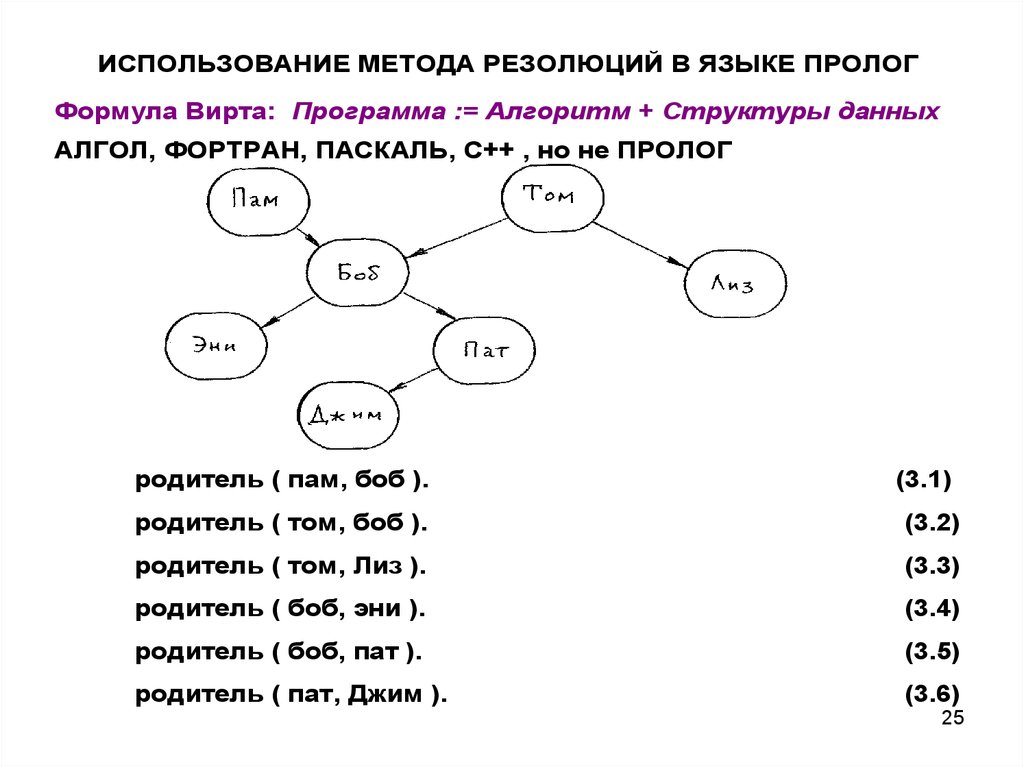
25.
ИСПОЛЬЗОВАНИЕ МЕТОДА РЕЗОЛЮЦИЙ В ЯЗЫКЕ ПРОЛОГФормула Вирта: Программа := Алгоритм + Структуры данных
АЛГОЛ, ФОРТРАН, ПАСКАЛЬ, C++ , но не ПРОЛОГ
родитель ( пам, боб ).
(3.1)
родитель ( том, боб ).
(3.2)
родитель ( том, Лиз ).
(3.3)
родитель ( боб, эни ).
(3.4)
родитель ( боб, пат ).
(3.5)
родитель ( пат, Джим ).
(3.6)
25
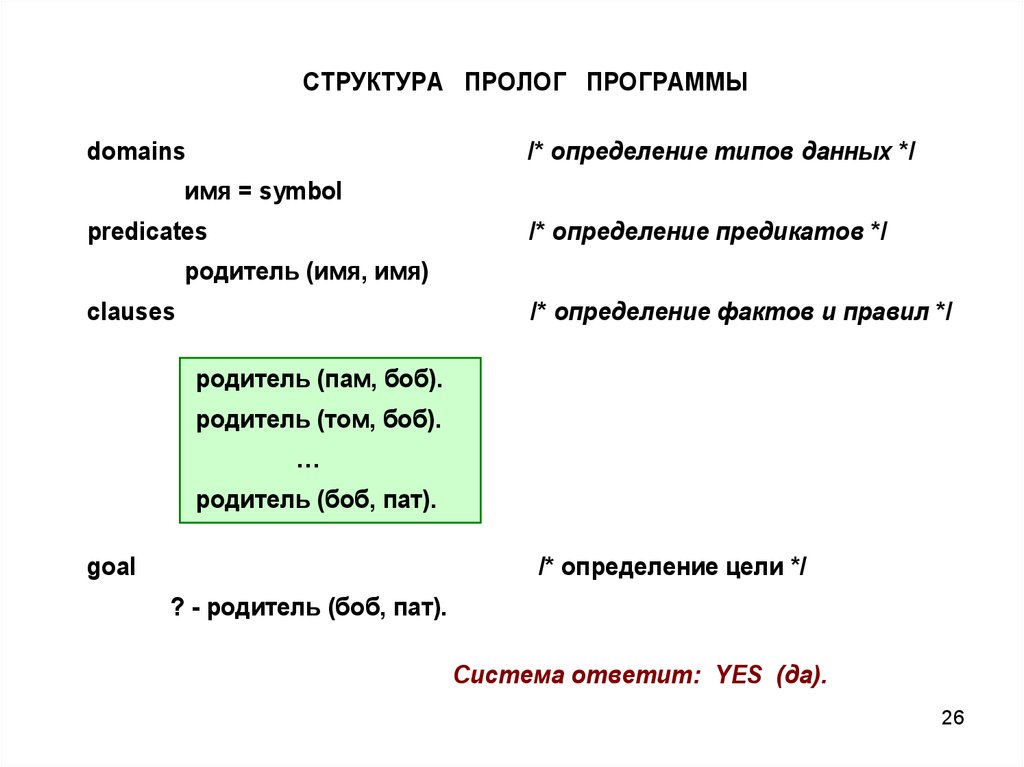
26.
СТРУКТУРА ПРОЛОГ ПРОГРАММЫ/* определение типов данных */
domains
имя = symbol
/* определение предикатов */
predicates
родитель (имя, имя)
/* определение фактов и правил */
clauses
родитель (пам, боб).
родитель (том, боб).
…
родитель (боб, пат).
/* определение цели */
goal
? - родитель (боб, пат).
Система ответит: YES (да).
26
27.
ВВЕДЕНИЕ И ИСПОЛЬЗОВАНИЕ ПРАВИЛ В ПРОЛОГЕВведем отношение дети.
дети (лиз, том).
дети (боб, пам). …
Правило:
Для всех Х и Y
Y дети Х, если
Х является родителем для Y.
дети (Y,Х): - родитель (Х,Y).
(3.20)
Является ли Лиз дитем для Тома: ? - дети (лиз, том).
дети (лиз, том).
(3.21)
Из (3.20):
родитель(Х,Y) дети(Y,Х).
(3.22)
Из (3.21) и (3.22) получим: родитель (том, лиз).
Из последнего и (3.12), получим
, следовательно: YES (да).
27
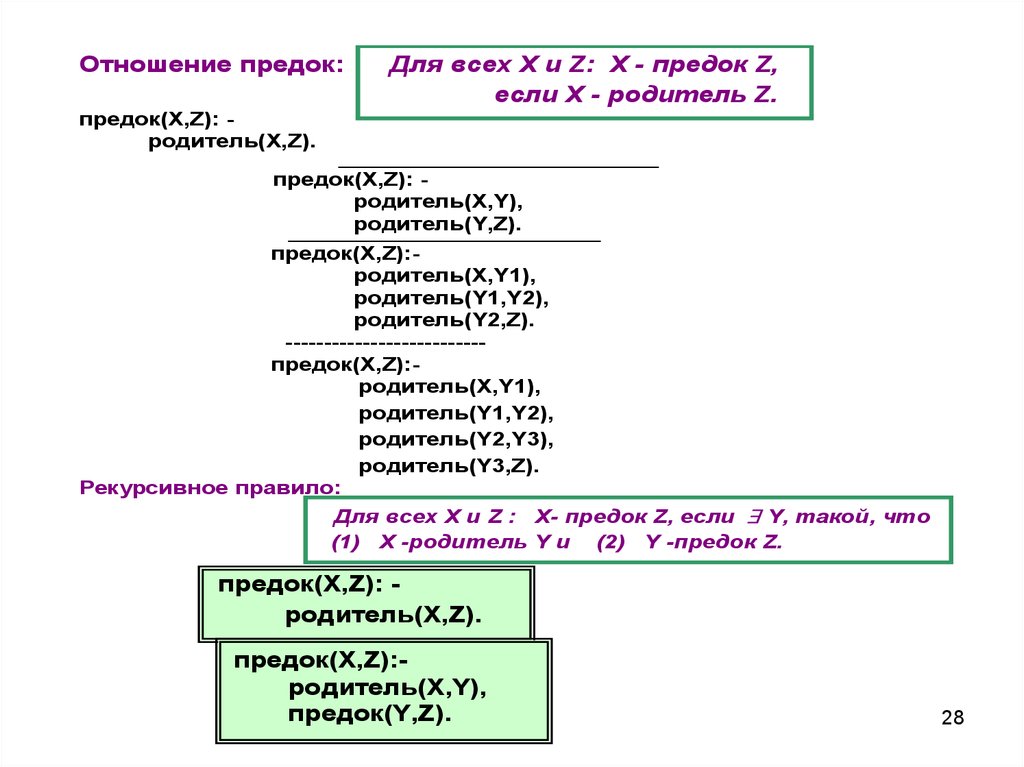
28.
Отношение предок:Для всех Х и Z: X - предок Z,
если X - родитель Z.
предок(Х,Z): родитель(X,Z).
предок(Х,Z): родитель(X,Y),
родитель(Y,Z).
предок(X,Z):родитель(X,Y1),
родитель(Y1,Y2),
родитель(Y2,Z).
-------------------------предок(Х,Z):родитель(Х,Y1),
родитель(Y1,Y2),
родитель(Y2,Y3),
родитель(Y3,Z).
Рекурсивное правило:
Для всех X и Z : Х- предок Z, если Y, такой, что
(1) Х -родитель Y и (2) Y -предок Z.
предок(Х,Z): родитель(Х,Z).
предок(X,Z):родитель(Х,Y),
предок(Y,Z).
28
29.
О ВОЗМОЖНОСТЯХ ПРОЛОГАВ ПРОЛОГе имеются (нелогические) операторы, позволяющие
управлять решением задачи, отсекая ненужные ветви поиска. Может
оказаться, что теряется нужный для дальнейшего дизъюнкт, и процесс
поиска может либо не завершится, либо привести к неправильному
результату.
Нужно помнить о неразрешимости логики предикатов. Из этого
следует, что для решения некоторой задачи, возможно, не существует
разрешающей процедуры и алгоритм, основанный на методе резолюций,
не сможет решить рассматриваемую задачу, и будет считать
безостановочно.
Считается (принято думать), что задача, сформулированная на
некотором языке программирования, должна быть решена компьютером,
тогда как имеются проблемы, для которых нет алгоритмического решения,
и которые, таким образом, не могут быть решены компьютером.
29























 mathematics
mathematics








