Пример применения алгоритма резолюций. Хорновские БЗ. Алгоритм прямого и обратного вывода. Лекция 3

1. Лекция №3

• Пример применения алгоритма резолюций
• Хорновские БЗ.
• Алгоритм прямого и обратного вывода.
• Логика предикатов как язык представления
знаний. Синтаксис и семантика.
• Алгоритм унификации в логике предикатов

2. Пример применения метода резолюции

• БЗ = (B1,1 (P1,2 P2,1)) B1,1
• α = P1,2
(B1,1 (P1,2 P2,1)) ≡
(B1,1 (P1,2 P2,1)) ((P1,2 P2,1) B1,1) ≡
(B1,1 (P1,2 P2,1)) ((P1,2 P2,1) B1,1) ≡
(( P1,2 P2,1) B1,1) (P1,2 P2,1 B1,1) ≡
( P1,2 B1,1) ( P2,1 B1,1) (P1,2 P2,1 B1,1)

3. Пример применения метода резолюции

БЗ =
( P1,2 B1,1) ( P2,1 B1,1) (P1,2 P2,1 B1,1) B1,1
α = P1,2

4. Хорновские базы знаний

Хорновские дизъюнкты являются дизъюнкциями
литералов, среди которых положительным
является один и только один литерал.
Хорновский дизъюнкт A B C,
эквивалентен импликации
(A B) C,
Т.е. может интерпретироваться в виде правила
«Если А и В, то С»
Базы знаний, состоящие из хорновских
дизъюнктов, называются базами знаний в
хорновской форме.

5. Почему хорновские базы знаний получили широкое распространение?

1) Дизъюнкт с одним положительным
литералом эквивалентен импликации
антецедент консеквент
где антецедент – коньюнкция положительных
литералов, консеквент – единственный
положительный литерал.
A B C … F G
Выражения такого вида очень хорошо
подходят для описания ситуации во многих
предметных областях. Хорновские дизъюнкты
образуют основу для логического
программирования.

6. Почему хорновские базы знаний получили широкое распространение?

2) Логический вывод с использованием
хорновских дизъюнктов может
осуществляться с помощью алгоритма
прямого логического вывода и обратного
логического вывода. Оба эти алгоритма
являются очень естественными для
человеческого восприятия.

7. Почему хорновские базы знаний получили широкое распространение?

3) Получение логических следствий
помощью хорновских дизъюнктов может
осуществляться за время, линейно
зависящее от размера базы знаний. Это
означает, что процедура логического
вывода оказывается весьма
недорогостоящей применительно ко
многим базам знаний, встречающимся
на практике.

8. Терминология хорновской логики

Единственный положительный литерал
хорновского дизъюнкта называется заголовком
(головой), остальные литералы образуют тело
выражения. Например, для дизъюнкта A B
C заголовком является литерал C, конъюнкция
A B составляет тело выражения. Если дизъюнкт
не содержит отрицательных литералов (включает
только голову), то он называется фактом. Факт
просто утверждает справедливость некоторого
высказывания. Полный дизъюнкт, включающий и
голову, и тело, называется правилом. Правило
утверждает справедливость некоторого
высказывания, являющегося головой, при условии
истинности конъюнкции высказываний,
составляющих тело хорновского дизъюнкта.

9. Алгоритмы прямого и обратного логического вывода

Основываются на применении
правила Modus Ponens :
α1, … ,αn,
α1 … αn β
—————————————————
β

10. Алгоритм прямого логического вывода

• Начинает свою работу с известных фактов,
содержащихся в БЗ.
• Если для некоторой импликации становятся истинными
все предпосылки, то ее заключение добавляется к базе
знаний в соответствии с правилом Modus Ponens.
• Процесс продолжается до тех пор, пока:
- к базе знаний добавляется изначально заданный
запрос q (алгоритм достигает успеха в доказательстве
q),
- новые факты не добавляются в базу знаний (алгоритм
достиг фиксированной точки). Если при достижении
фиксированной точки исходный запрос q не достигнут,
то последний не может быть выведен из базы знаний.

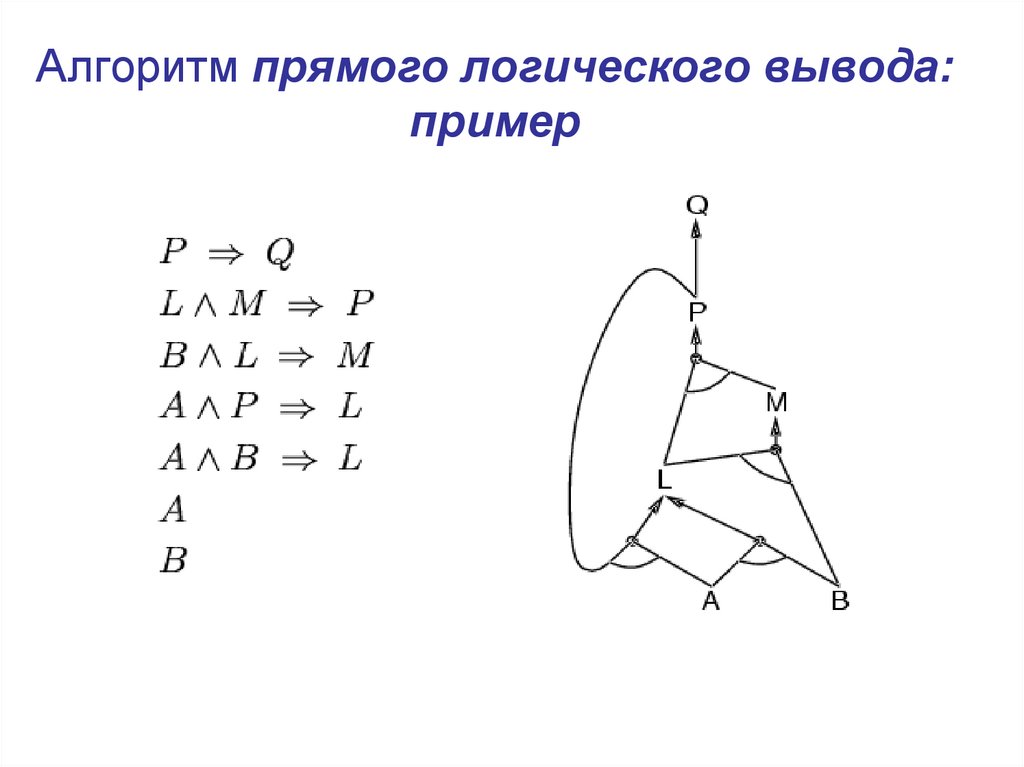
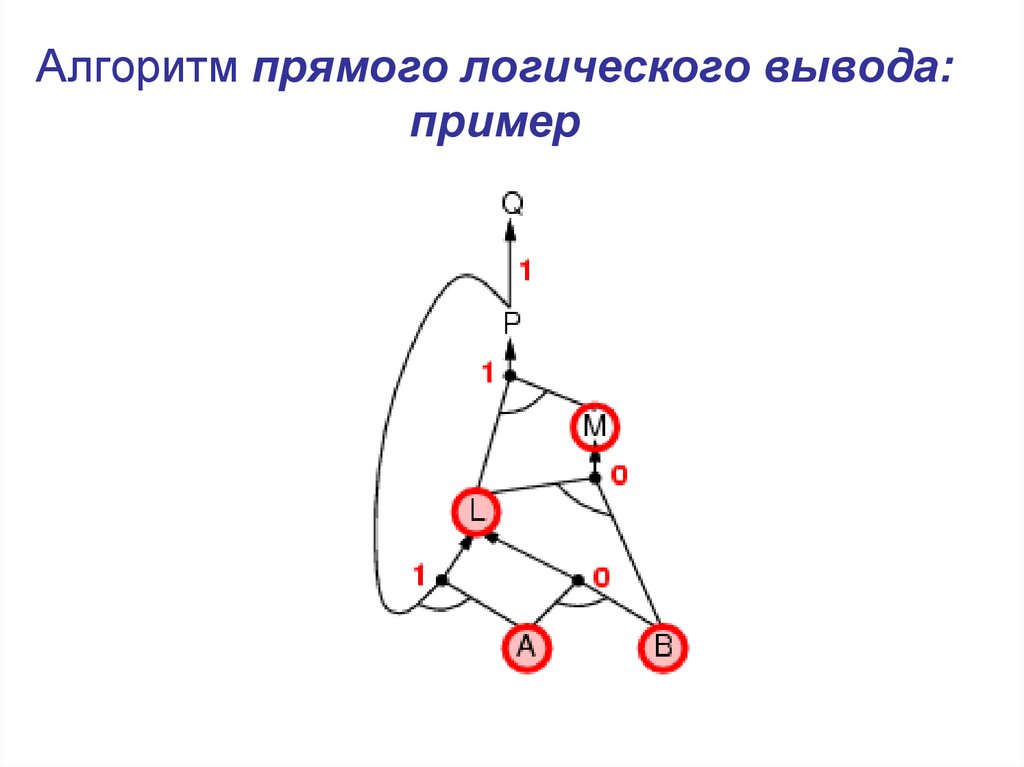
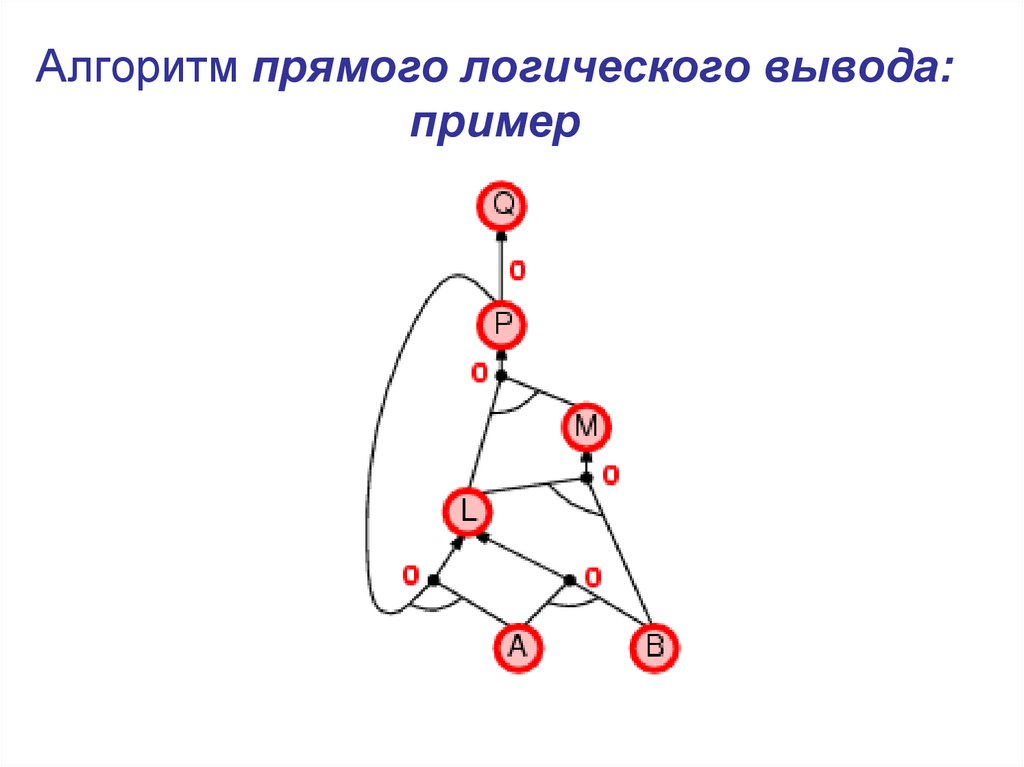
11. Алгоритм прямого логического вывода: пример

12. Алгоритм прямого логического вывода: пример

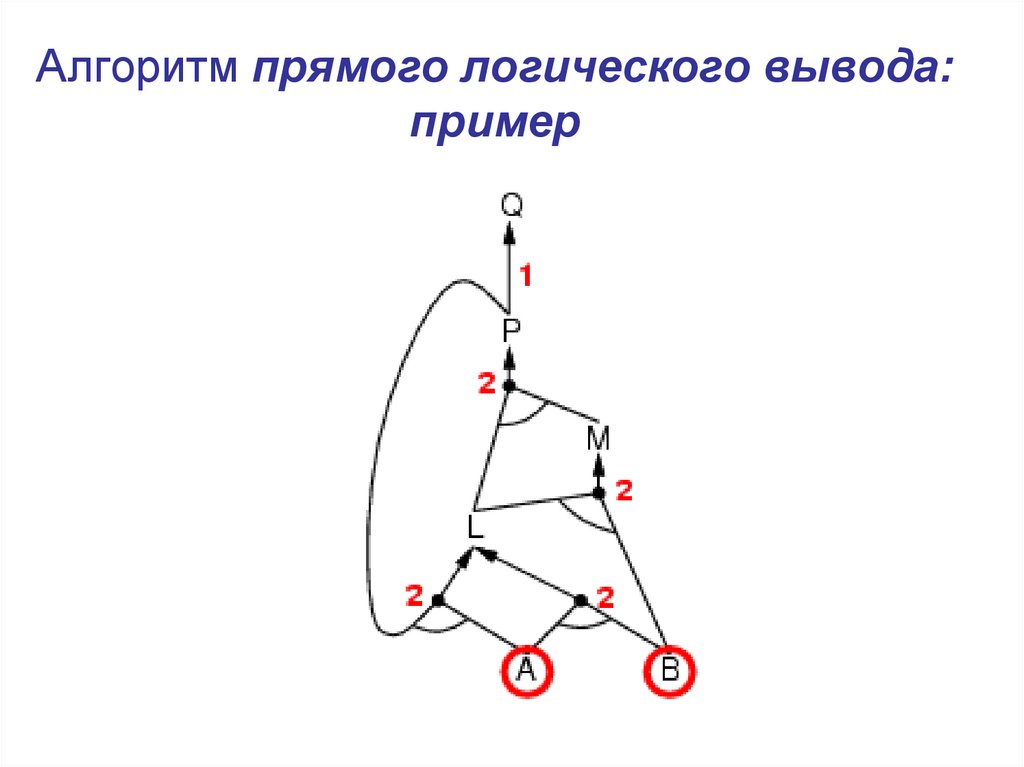
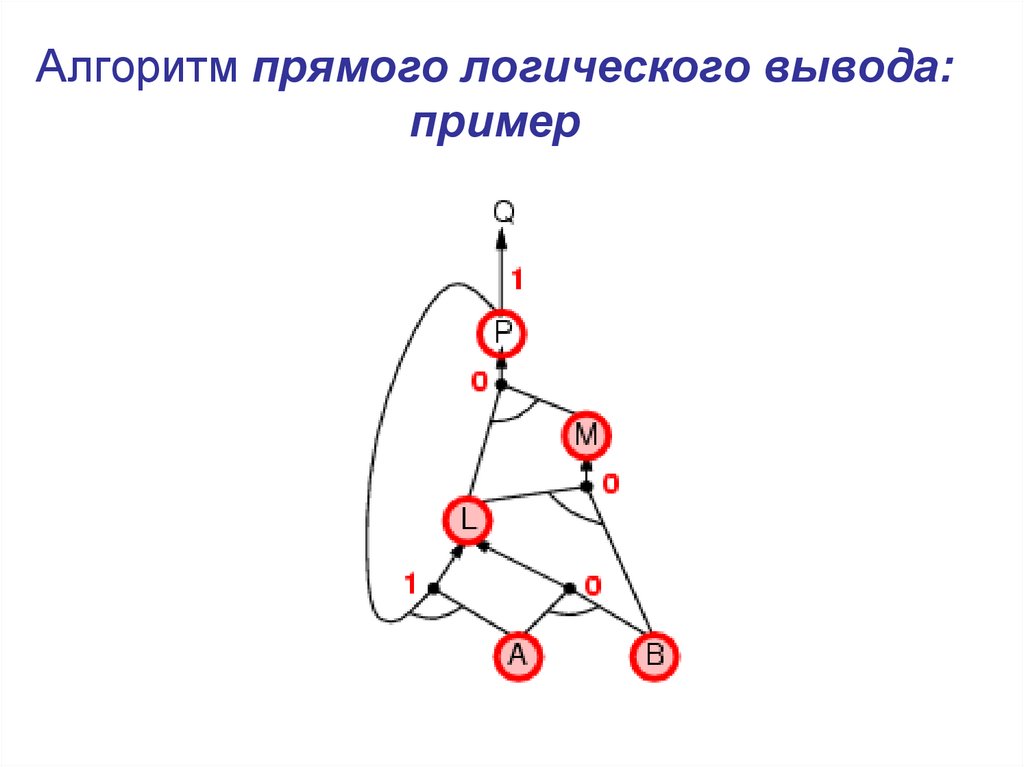
13. Алгоритм прямого логического вывода: пример

14. Алгоритм прямого логического вывода: пример

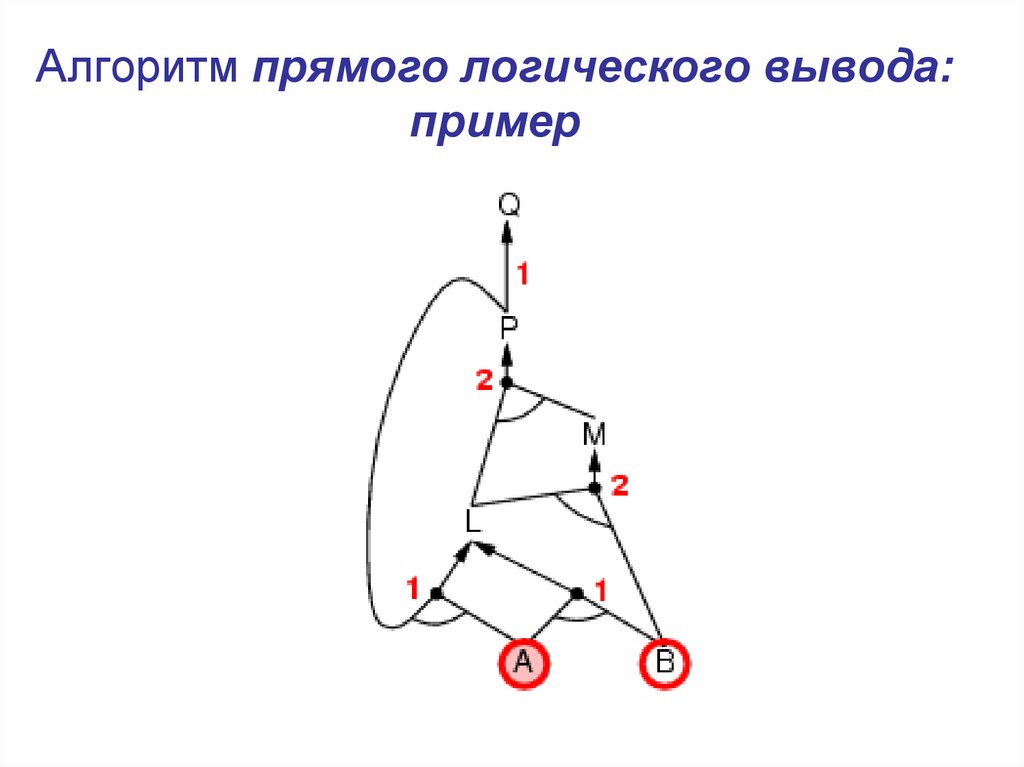
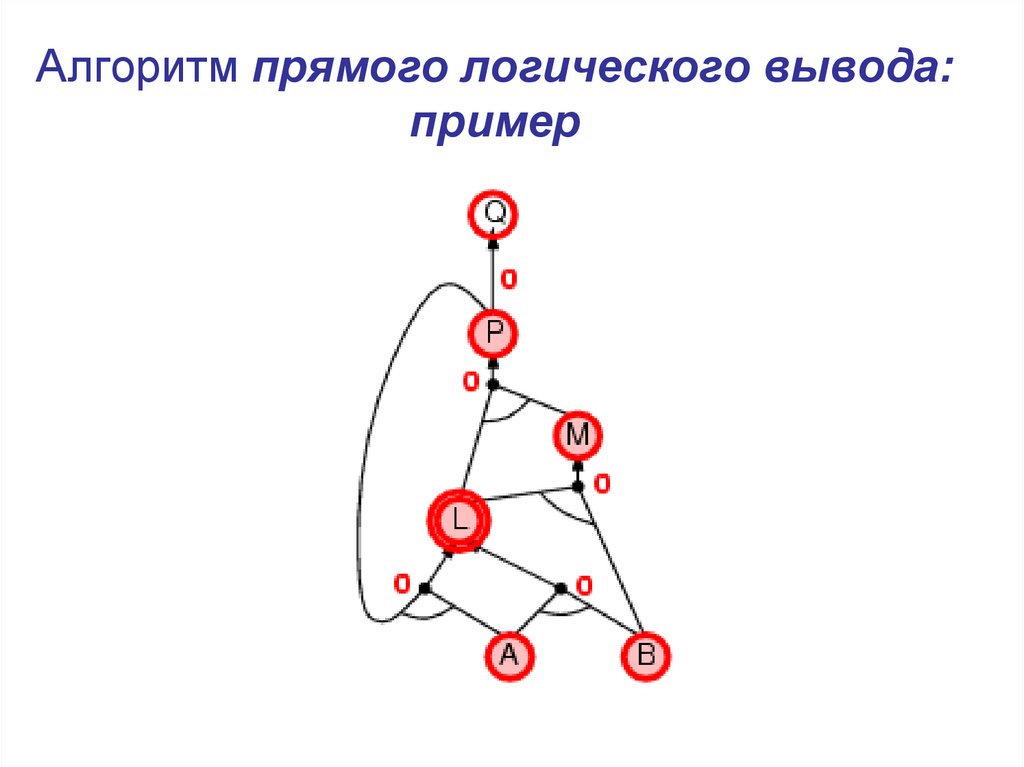
15. Алгоритм прямого логического вывода: пример

16. Алгоритм прямого логического вывода: пример

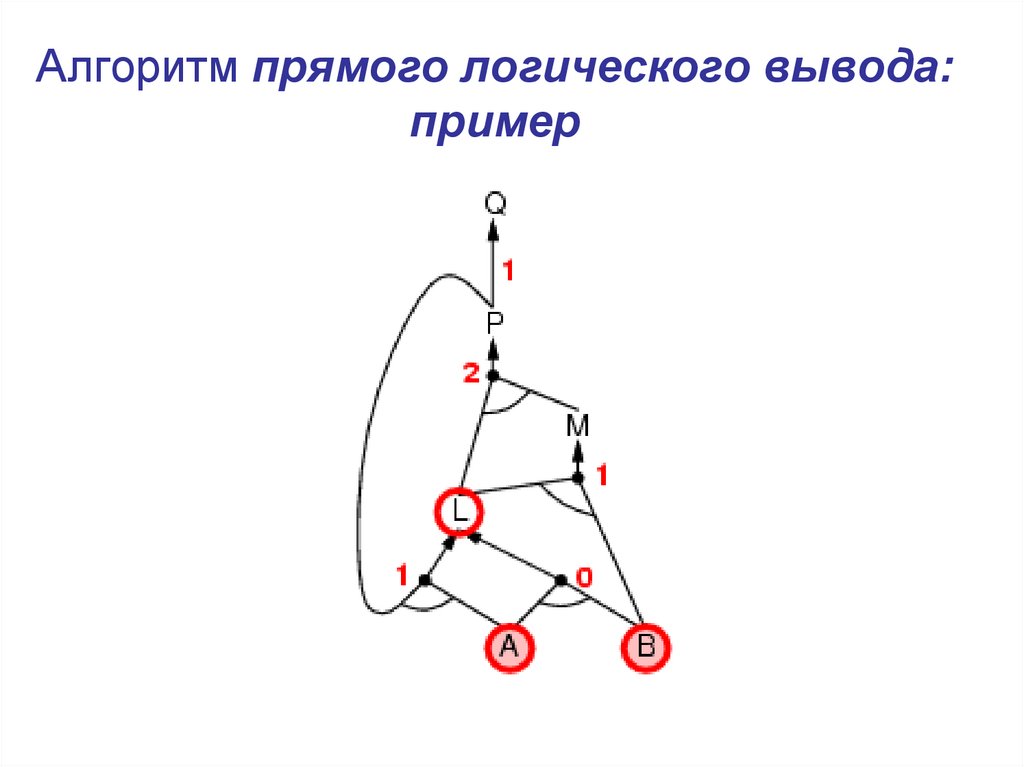
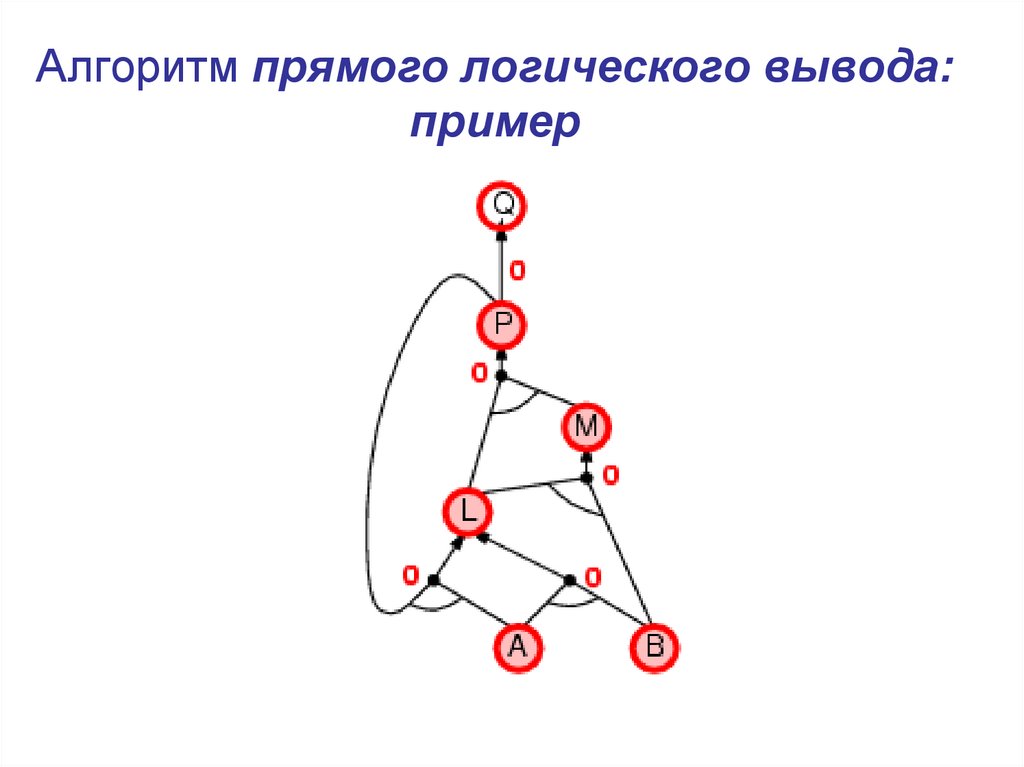
17. Алгоритм прямого логического вывода: пример

18. Алгоритм прямого логического вывода: пример

19. Алгоритм прямого логического вывода: пример

20. Алгоритм обратного логического вывода

• Действует в обратном направлении от запроса
к данным.
• Если запрос q содержится среди фактов, то на
этом алгоритм завершает работу.
• В противном случае алгоритм использует те
импликации в базе знаний, для которых q
является заключением:
- Если все посылки найденной импликации
являются фактами, то выводим q и
заканчиваем доказательство.
- Иначе ищем импликации для
доказательства посылок.

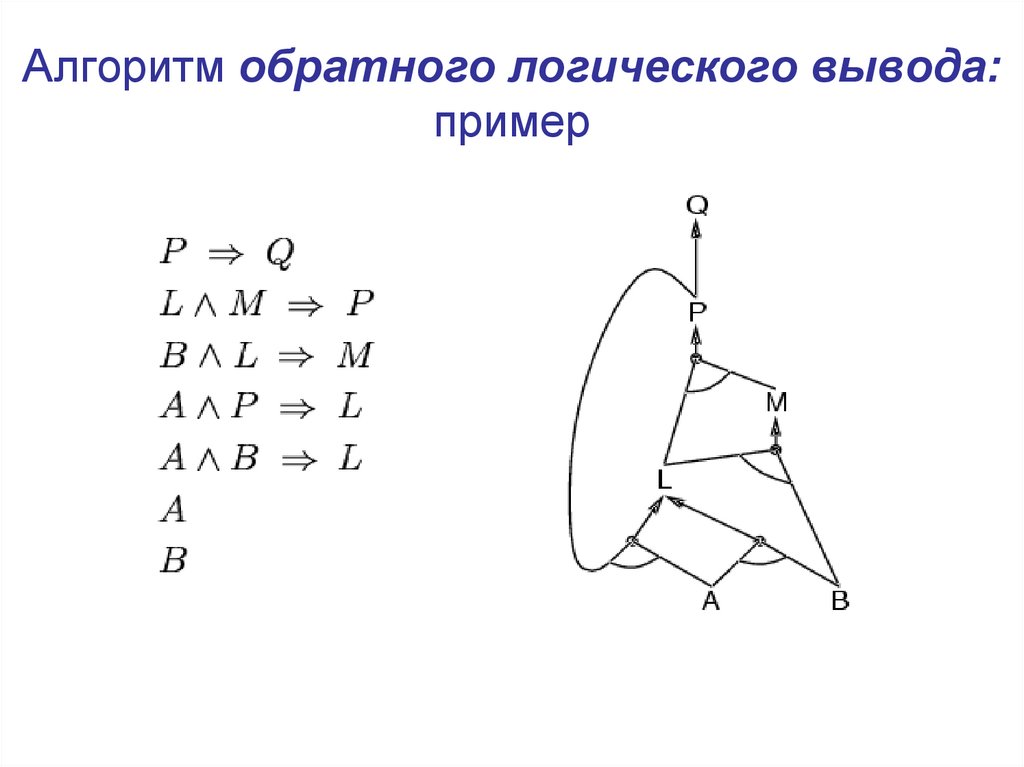
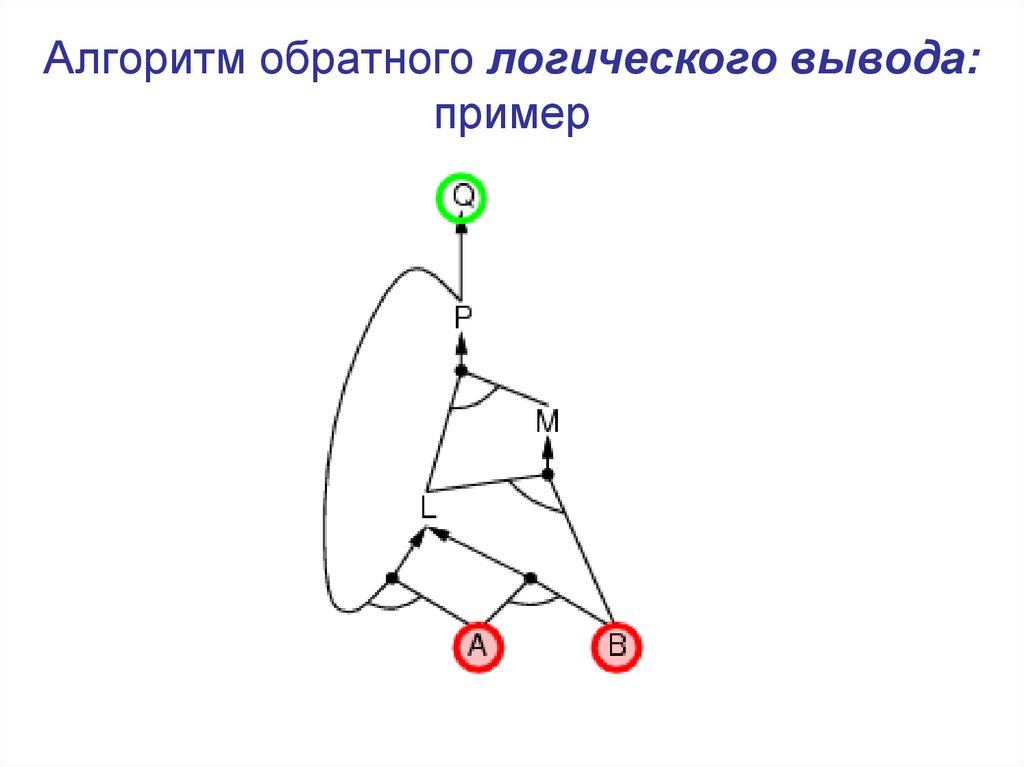
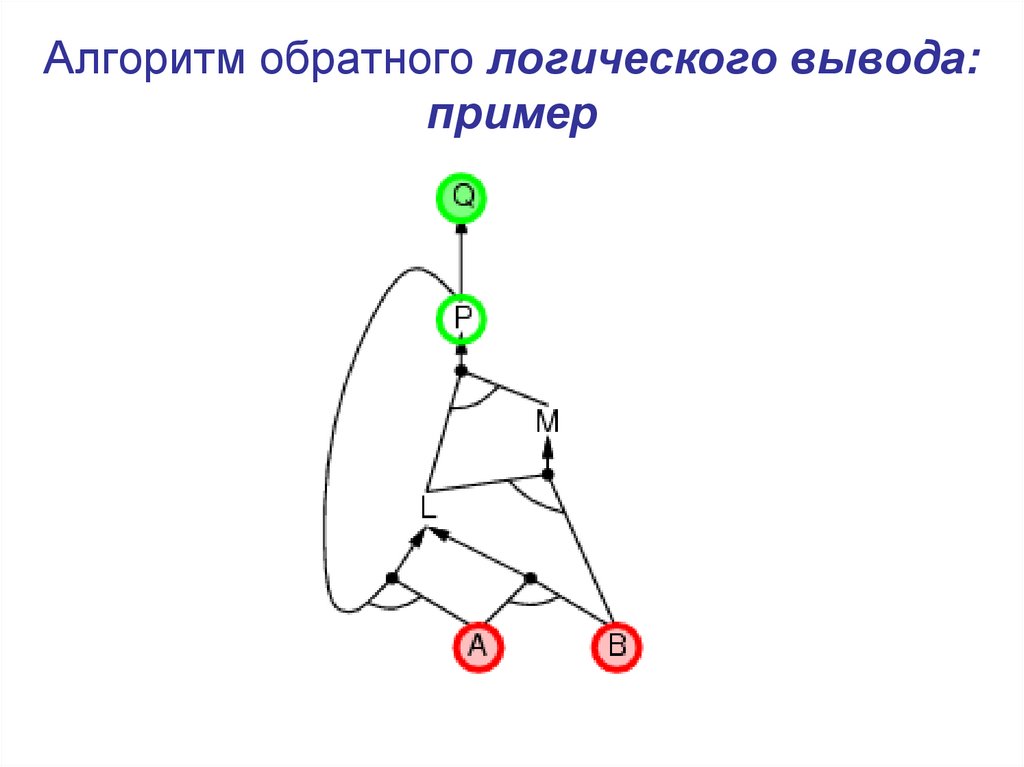
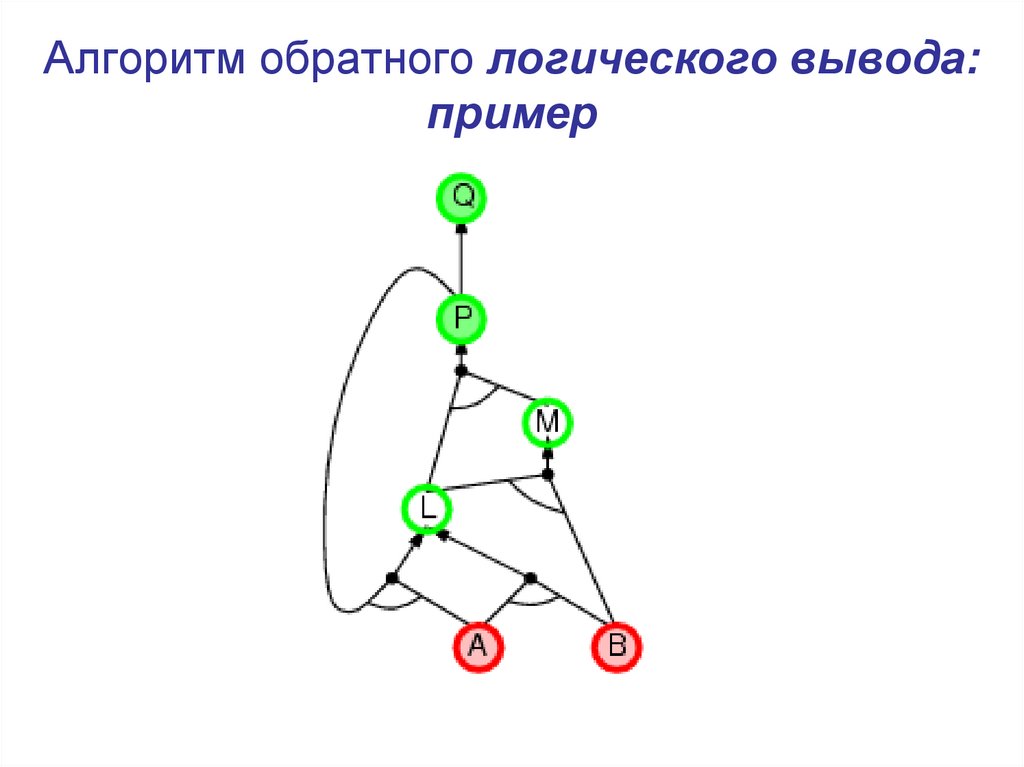
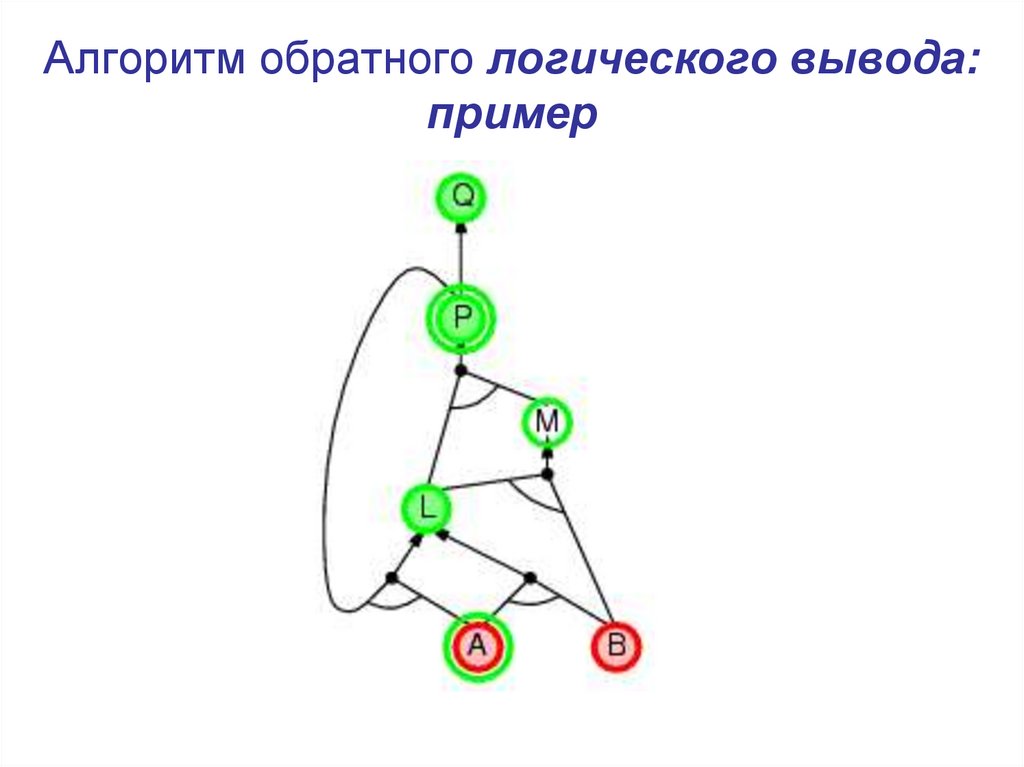
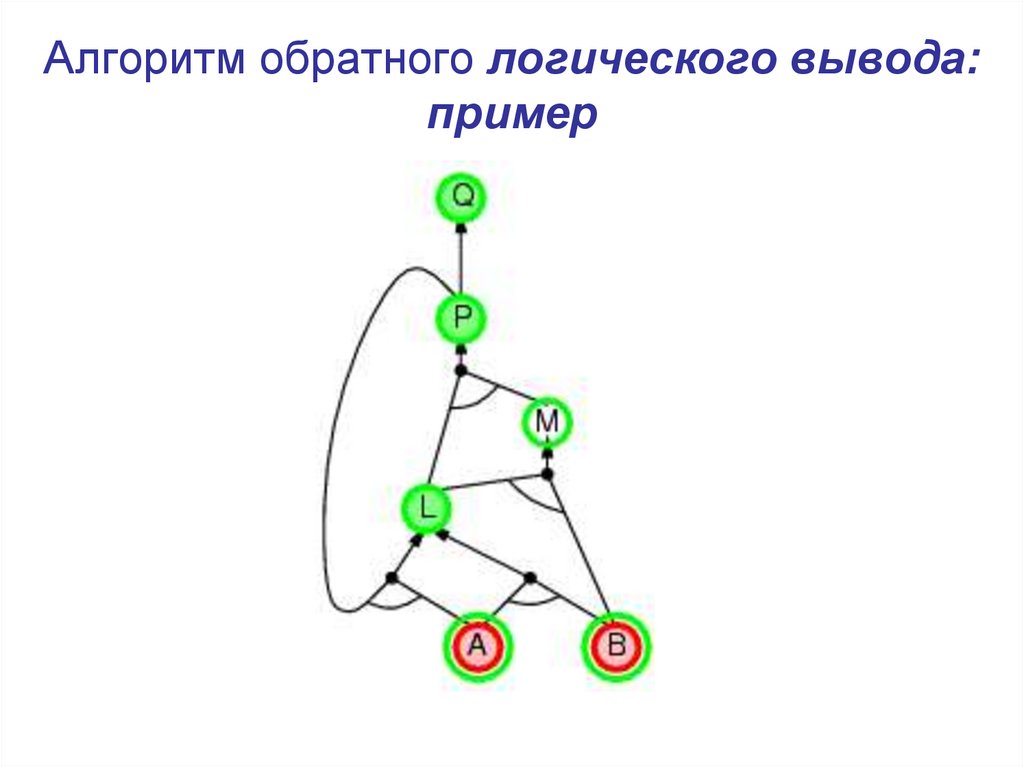
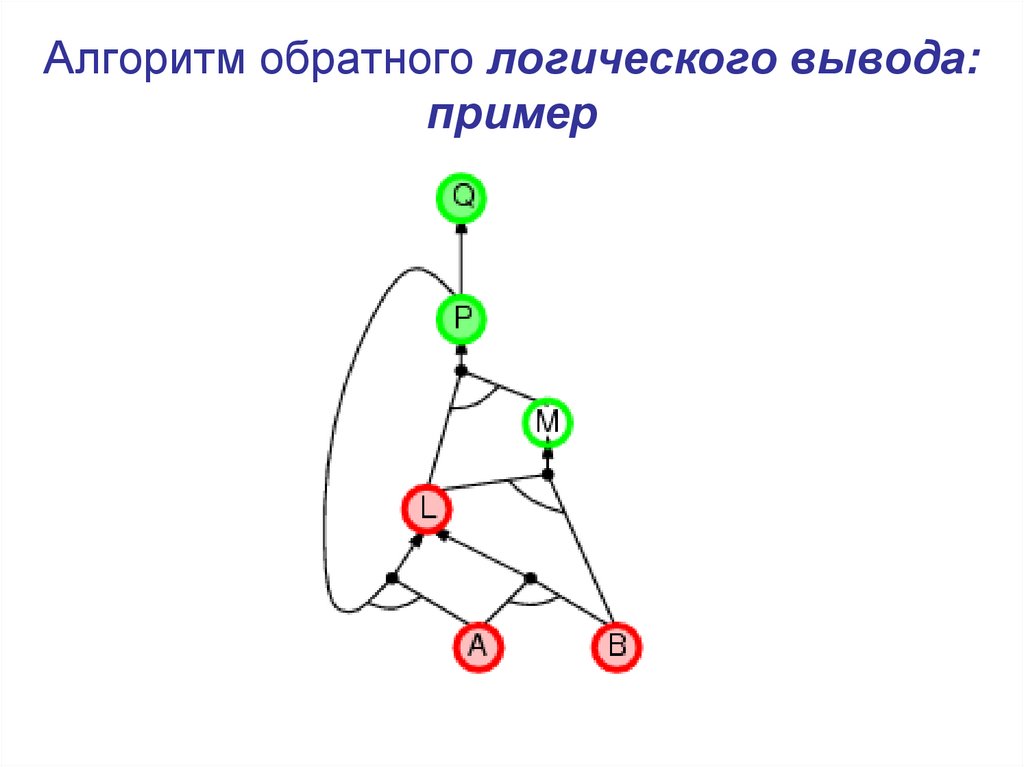
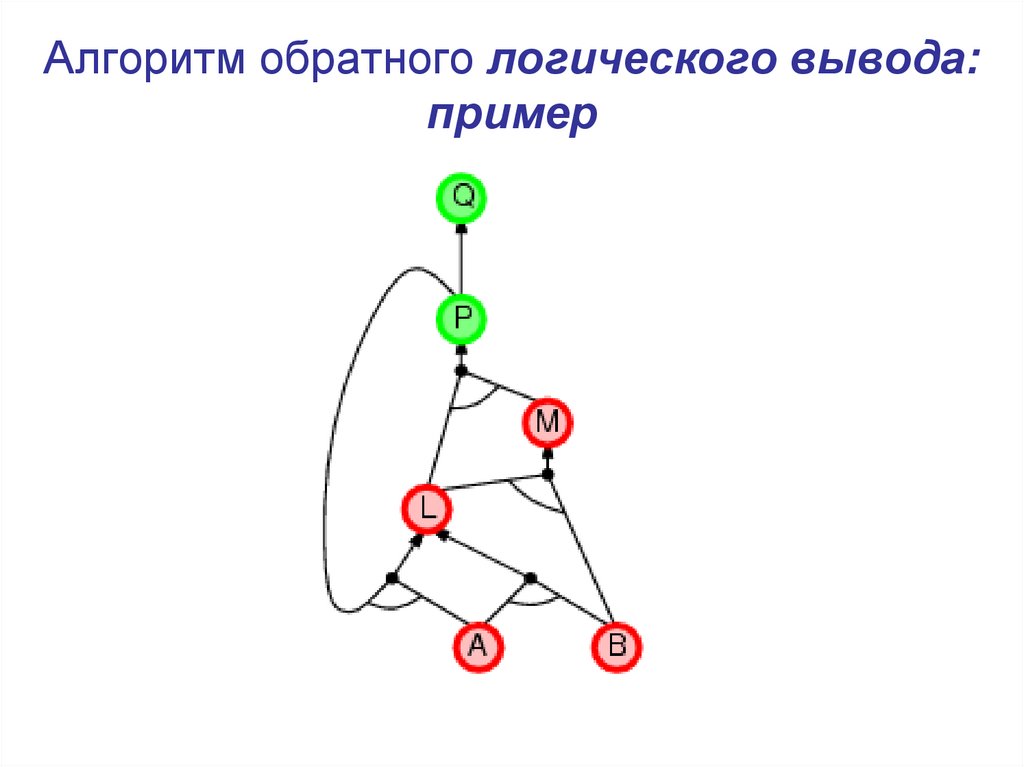
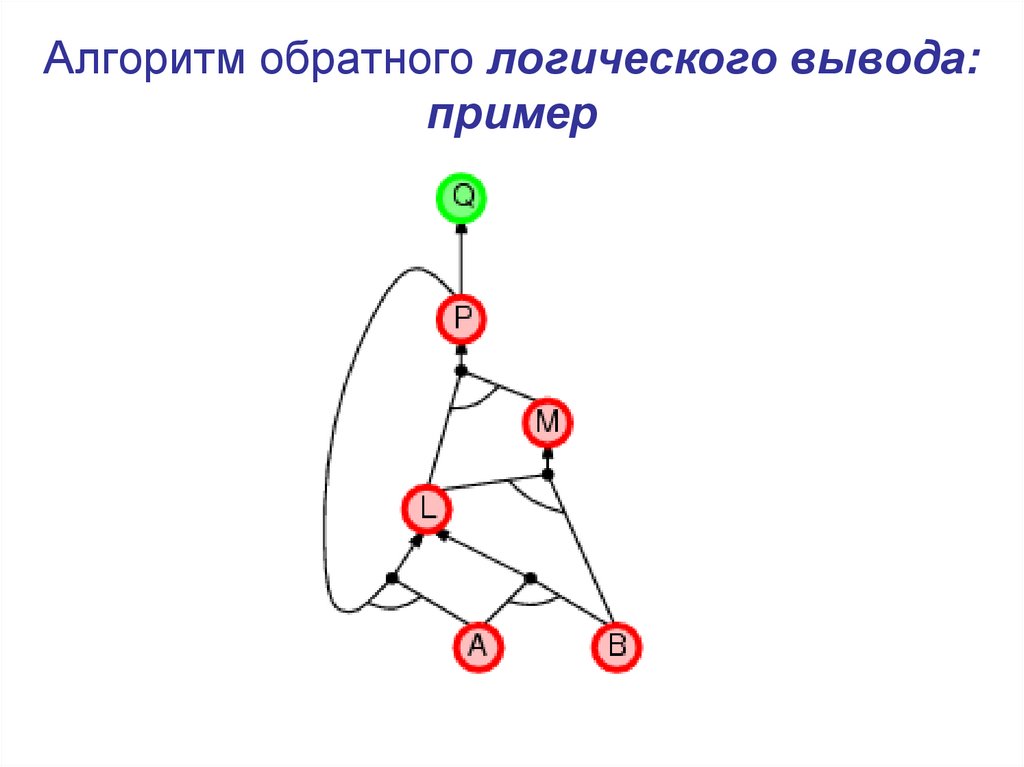
21. Алгоритм обратного логического вывода: пример

22. Алгоритм обратного логического вывода: пример

23. Алгоритм обратного логического вывода: пример

24. Алгоритм обратного логического вывода: пример

25. Алгоритм обратного логического вывода: пример

26. Алгоритм обратного логического вывода: пример

27. Алгоритм обратного логического вывода: пример

28. Алгоритм обратного логического вывода: пример

29. Алгоритм обратного логического вывода: пример

30. Алгоритм обратного логического вывода: пример

31. Алгоритм обратного логического вывода: пример

32. Логика предикатов в сравнении с логикой высказываний

• Логика высказываний предполагает, что
мир состоит из фактов;
• Логика предикатов (как и естественный
язык) предполагает, что мир содержит:
– Объекты: люди, дома, числа, цвета, мячи, …
– Отношения: являться красным, круглым,
быть братом, больше чем, лежит между,
является частью, принадлежит, …
– Функции: отец, лучший друг, плюс, …

33. Синтаксис логики предикатов: основные элементы

• Константы KingJohn, 2, NUS,...
• Предикаты Brother, >,...
• Функции
Sqrt, LeftLegOf,...
• Переменные x, y, a, b,...
• Связки
, , , ,
• Равенство =
• Кванторы ,

34. Синтаксис логики предикатов: атомарные высказывания

Атомарное высказывание =
predicate (term1,...,termn)
or term1 = term2
Терм
=
function (term1,...,termn)
or constant or variable

35. Синтаксис логики предикатов: сложные высказывания

• Сложные высказывания получаются из
атомарных с помощью связок
S, S1 S2, S1 S2, S1 S2, S1 S2,
Например,
Брат(KingJohn,Richard)
Брат(Richard,KingJohn)
>(1,2) ≤ (1,2)
>(1,2) >(1,2)

36. Семантика логики предикатов: определение истинности

• Предложения являются истинными относительно
модели и интерпретации
• Модель содержит объекты (domains) и отношения
между ними (predicates)
• Интерпретация устанавливает ссылки на:
constant symbols →
predicate symbols →
function symbols
→
objects
relations
functional relations
• Атомарное предложение predicate(term1,...,termn)
истинно тогда и только тогда когда объекты, на
которые указывают термы term1,...,termn,, находятся в
отношении, на которое указывает предикатный
символ predicate.

37. Вывод в логике предикатов: метод пропозиционализации

Идея метода пропозиционализации:
преобразование высказываний в логике
первого порядка в высказывания,
представленные в логике высказываний,
и дальнейшее использование
пропозиционального логического
вывода. Применение данного метода
основано на применении двух простых
правил конкретизации.

38. Метод пропозиционализации: правила конкретизации

1)
2)
конкретизация высказывания с квантором
всеобщности, согласно которому из высказывания
x P(x) выводится любое высказывание
P(A),P(B),P(C),…, полученное в результате
подстановки основного терма (терма, не
содержащего переменную) вместо переменной,
связанной квантором всеобщности.
конкретизация высказывания с квантором
существования. Согласно этому правилу из
высказывания x P(x) выводится высказывание
P(C), где C - некоторая новая константа с
уникальным именем, которая называется
сколемовской константой (имя сколемовской
константы не должно встречаться нигде ранее).

39.

Метод пропозиционализации является довольно
неэффективным, так как генерирует
множество нерелевантных
пропозициональных высказываний, не
участвующих в процессе дальнейшего
логического вывода. Более эффективные
алгоритмы появились после 1960-х годов,
когда были предложены алгоритм
унификации, метод резолюции и обобщенное
правило Modus Ponens. Основная идея этих
методов - не сводить базу знаний первого
порядка к пропозициональной базе знаний, а
обобщить правила вывода логики
высказываний до логики первого порядка.

40. Унификация

Унификация применяется к множеству
термов или предикатов.
Унификация позволяет отождествлять
термы или предикаты путем замены
свободных переменных на термы.
Унификация может быть успешной или
неуспешной.
В случае успешной унификации мы
получаем унификатор – множество
подстановок переменных, при которых
термы становятся тождественными.

41. Унификация

Подстановкой (унификатором) называется
множество пар вида ={x1/t1, x2/t2 ,…, xn/tn},
где i ti - терм, xi - переменная, не входящая
в терм ti , причем xi xj для любых i j.
Подстановка может применяться к терму,
предикату, высказыванию или к их множеству.
Результат применения подстановки к
выражению обозначается Subst( , ) (или
) и называется примером выражения.
Пример получается путем одновременной
замены каждой переменной xi из на терм ti .

42. Унификация

Например, подстановкой для двух выражений
King(x) and Greedy(x) и
King(John) and Greedy(y)
является
θ = {x/John,y/John}
Унификатор выражений:
p
Knows(John,x)
Knows(John,x)
Knows(John,x)
Knows(John,x)
Unify( , ) = if =
q
Knows(John,Jane)
Knows(y,OJ)
Knows(y,Mother(y))
Knows(x,OJ)

43. Унификация

Например, подстановкой для двух выражений
King(x) and Greedy(x) и King(John) and Greedy(y)
является
θ = {x/John,y/John}
Унификатор выражений: Unify( , ) = if =
p
Knows(John,x)
Knows(John,x)
Knows(John,x)
Knows(John,x)
q
Knows(John,Jane)
Knows(y,OJ)
Knows(y,Mother(y))
Knows(x,OJ)
{x/Jane}

44. Унификация

Например, подстановкой для двух выражений
King(x) and Greedy(x) и King(John) and Greedy(y)
является
θ = {x/John,y/John}
Унификатор выражений: Unify( , ) = if =
p
Knows(John,x)
Knows(John,x)
Knows(John,x)
Knows(John,x)
q
Knows(John,Jane)
Knows(y,OJ)
Knows(y,Mother(y))
Knows(x,OJ)
{x/Jane}
{x/OJ,y/John}

45. Унификация

Например, подстановкой для двух выражений
King(x) and Greedy(x) и King(John) and Greedy(y)
является
θ = {x/John,y/John}
Унификатор выражений: Unify( , ) = if =
p
Knows(John,x)
Knows(John,x)
Knows(John,x)
Knows(John,x)
q
Knows(John,Jane)
{x/Jane}
Knows(y,OJ)
{x/OJ,y/John}
Knows(y,Mother(y)) {y/John,x/Mother(John)}
Knows(x,OJ)

46. Унификация

Например, подстановкой для двух выражений
King(x) and Greedy(x) и King(John) and Greedy(y)
является
θ = {x/John,y/John}
Унификатор выражений: Unify( , ) = if =
p
Knows(John,x)
Knows(John,x)
Knows(John,x)
Knows(John,x)
q
Knows(John,Jane)
{x/Jane}
Knows(y,OJ)
{x/OJ,y/John}
Knows(y,Mother(y)) {y/John,x/Mother(John)}
Knows(x,OJ)
{fail}

47. Наибольший общий унификатор

• Для унификации выражений Knows(John,x) и
Knows(y,z) можно использовать подстановки
θ1 = {y/John, x/z }
или
θ2 = {y/John, x/John, z/John}
• Унификатор θ1 = {y/John, x/z } является более общим ,
чем унификатор θ2 = {y/John, x/John, z/John}, так как
θ2 = Subst ( { z/John }, θ1 ) = θ1 { z/John }
Утверждение: Для любой унифицируемой пары
выражений существует единственный наибольший
общий унификатор (НОУ), уникальный с точностью до
переименования переменных
НОУ= { y/John, x/z }

48. Алгоритм унификации

Пусть S - конечное множество простых выражений.
Определим
DS(S)
множество
рассогласований.
Для
этого зафиксируем самую
левую позицию, на которой
не во всех выражениях из S
стоит один и тот же символ. Занесем в DS(S) первые
слева термы выражений из S, начинающиеся с
данной
позиции.
Например,
S={ P(F(x),H(y),A), P(F(x),z,A), P(F(x),H(y),B) }.
Множество
рассогласований
для
S:
DS(S)={H(y),z}.

49. Алгоритм унификации

Опишем алгоритм поиска НОУ для конечного мн-ва S:
Шаг 0. Полагаем θ0=E(тожд-я подст.), Sθ0=Subst(θ0,S)=S
Шаг k. Если Sθk - множество, состоящее из одного элемента, то
останов, θk - наибольший общий унификатор для S. В
противном случае строим мн-во рассогласований DS(Sθk) и
переходим к шагу k+1.
Шаг k+1. Если во множестве DS(Sθk) найдутся переменная x и
терм t, такие, что x не входит в t, то осуществляем композицию
подстановок θk+1= θk{x/t}. Увеличиваем k=k+1 и идем на шаг k.
Если такой пары x/t нельзя подобрать в множестве DS(Sθk), то
останов, множество выражений S не унифицируемо.

50. Алгоритм унификации (пример)

1. S={Q(a,x,f(g(z))), Q(z,f(y),f(y)}
2. S={Q(y,y), Q(z,f(z)}

51. Алгоритм унификации (вариант2)

52. Алгоритм унификации (вариант2)