Similar presentations:
Теорія відношень
1. Розділ 2. Теорія відношень
2. 2.1. Поняття відношення. Задання відношень
декартів добуток множинбінарне відношення
способи задання відношень
окремі випадки відношень
3.
Відношення реалізують у математичнихтермінах на абстрактних множинах реальні
зв'язки між реальними об'єктами.
Декартовим добутком множин Х1 Х2 ... Хn
називається множина всіх можливих
упорядкованих наборів (х1, х2, ..., хn) з n елементів
(які називають кортежами довжини n), в яких
перший елемент належить множині Х1, другий —
множині Х2, n-й — множині Хn.
Декартів добуток Х Х ... Х, в якому одна й та ж
множина Х помножується n раз сама на себе,
називають декартовим степенем множини і
позначають Хn.
4.
Приклад.Нехай A={a1, a2, a3}, B={b1, b2}, C={c1, c2}. Тоді
A B={(a1,b1), (a1,b2), (a2,b1), (a2,b2), (a3,b1), (a3,b2)}.
B A={(b1,a1), (b1,a2), (b1,a3), (b2,a1), (b2,a2), (b2,a3)}.
A B C={(a1,b1,c1), (a1,b1,c2), (a1,b2,c1), (a1,b2,c2),
(a2,b1,c1), (a2,b1,c2), (a2,b2,c1), (a2,b2,c2),
(a3,b1,c1), (a3,b1,c2), (a3,b2,c1), (a3,b2,c2)}.
B2={(b1,b1), (b1,b2), (b2,b1), (b2,b1)}.
Порядок проходження пар може бути довільним, але
розміщення елементів у кожній парі визначається
порядком
проходження
множин,
що
перемножуються, тобто A B B A якщо A B.
5.
n-арне відношення R на множинах Х1, Х2,..., Хn –це підмножина декартова добутку цих n множин:
R Х1 Х2 ... Хn
Якщо R – бінарне відношення на множинах X, Y, то
факт (x,y) R часто записується у вигляді xRy
Приклад.
Нехай A={a1, a2, a3}, B={b1, b2}, C={c1, c2}. Тоді
A B C={(a1,b1,c1), (a1,b1,c2), (a1,b2,c1), (a1,b2,c2),
(a2,b1,c1), (a2,b1,c2), (a2,b2,c1), (a2,b2,c2),
(a3,b1,c1), (a3,b1,c2), (a3,b2,c1), (a3,b2,c2)}.
R1, R2 A B C
R1={(a1,b1,c1),(a2,b1,c1),(a2,b1,c2),(a3,b2,c1),(a3,b2,c2)}.
R2={(a2,b2,c1), (a2,b2,c2), (a3,b1,c1)}.
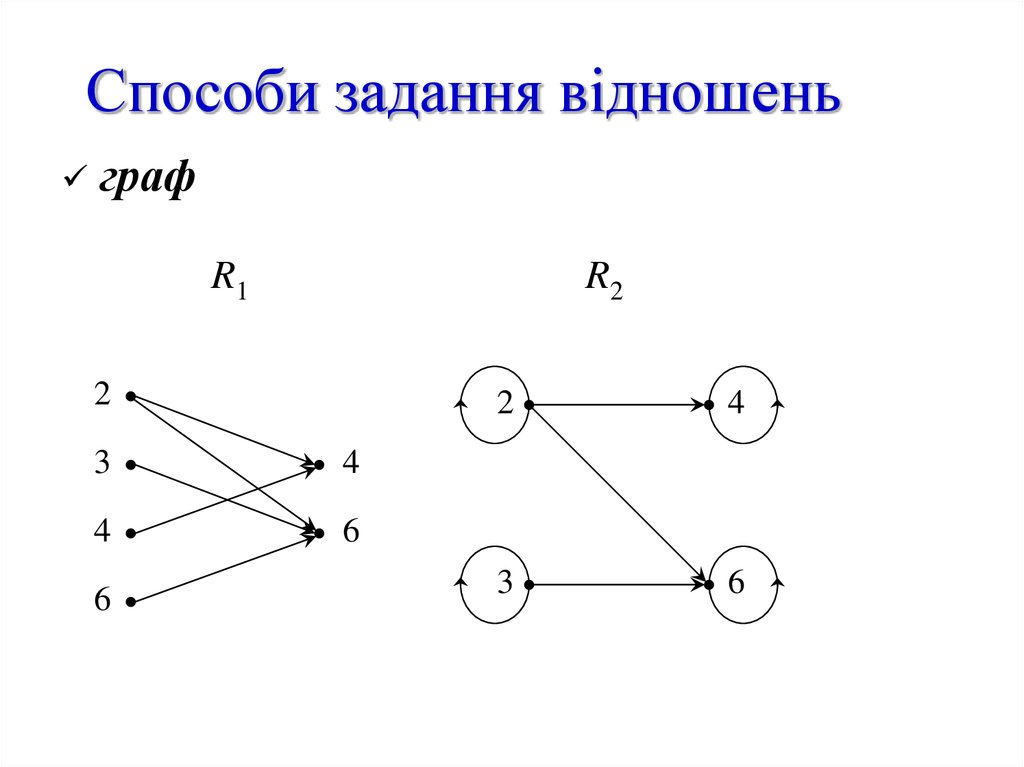
6. Способи задання відношень
Нехай A={2, 3, 4, 6}, B={4, 6}.R1 A B, R2 A А
R1, R2 – бути дільником
список
R1 = {(2,4),(2,6),(3,6),(4,4),(6,6)},
R2 = {(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(6,6)}
7. Способи задання відношень
матриця (таблиця) W=W(R);wij=1, якщо (xi, yj) R і wij=0, якщо (xi, yj) R
R1
4
6
R2
2
3
4
6
2
1
1
2
1
0
1
1
3
0
1
3
0
1
0
1
4
1
0
4
0
0
1
0
6
0
1
6
0
0
0
1
8. Способи задання відношень
графR1
R2
2
3
4
4
6
6
2
4
3
6
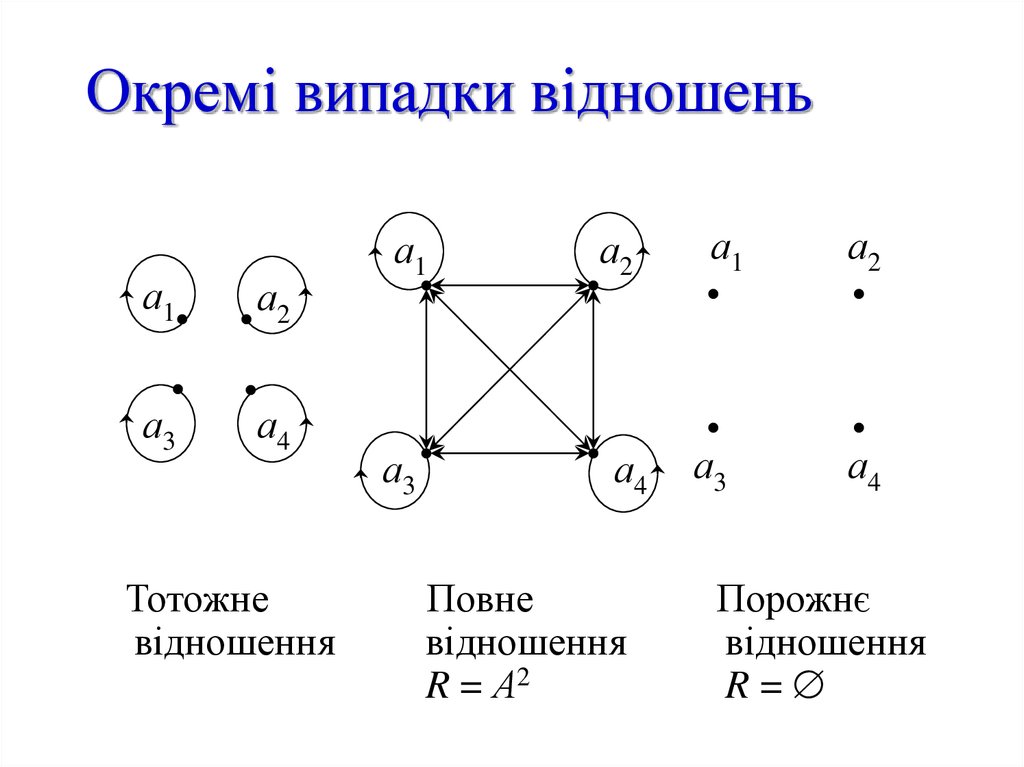
9. Окремі випадки відношень
а1а2
а3
а4
Тотожне
відношення
а1
а3
а2
а4
Повне
відношення
R = А2
а1
а3
а2
а4
Порожнє
відношення
R=
10. 2.2. Операції над відношеннями
обернене відношеннякомпозиція відношень
степінь відношення
переріз відношення
фактор-множина
11.
Нехай A={2, 3, 4, 6},R1, R2 A А
R1 = {(2,4),(2,6),(4,3),(3,6),(6,6)},
R2 = {(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(6,6)}
R1
2
3
4
6
2
0
0
0
0
3
0
0
1
0
4
1
0
0
0
6
1
1
0
1
R2
2
3
4
6
2
1
0
0
0
3
0
1
0
0
4
1
0
1
0
6
1
1
0
1
2
4
2
4
3
6
3
6
12. об’єднання R1 R2
об’єднання R1 R2R1 R2 = {(2,2),(2,4),(2,6),(3,3),(3,6),(4,3),(4,4),(6,6)}
R1 R2
2
3
4
6
2
1
0
1
1
3
0
1
0
1
4
0
1
1
0
6
0
0
0
1
2
4
3
6
13. перетин R1 R2
перетин R1 R2R1 R2 = {(2,4),(2,6),(3,6),(6,6)}
R1 R2
2
3
4
6
2
0
0
1
1
3
0
0
0
1
4
0
0
0
0
6
0
0
0
1
2
4
3
6
14. різниця R1\ R2
R1\ R2 = {(3,4)}R1\ R2
2
3
4
6
2
0
0
0
0
3
0
0
0
0
4
0
1
0
0
6
0
0
0
0
2
4
3
6
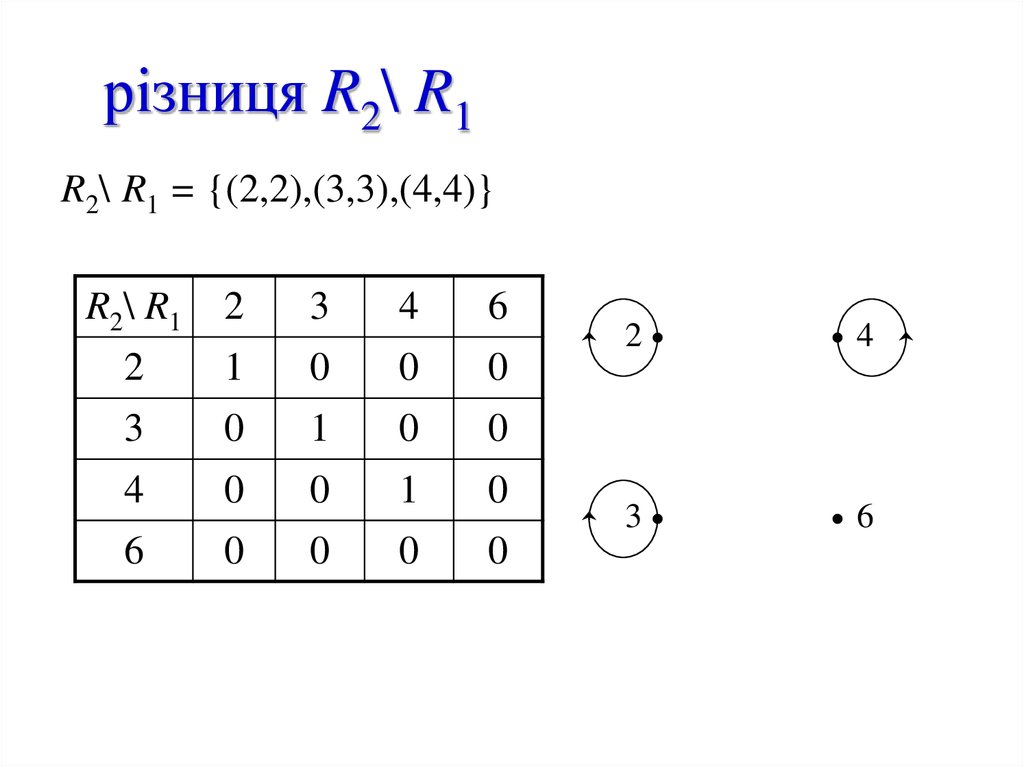
15. різниця R2\ R1
R2\ R1 = {(2,2),(3,3),(4,4)}R2\ R1
2
3
4
6
2
1
0
0
0
3
0
1
0
0
4
0
0
1
0
6
0
0
0
0
2
4
3
6
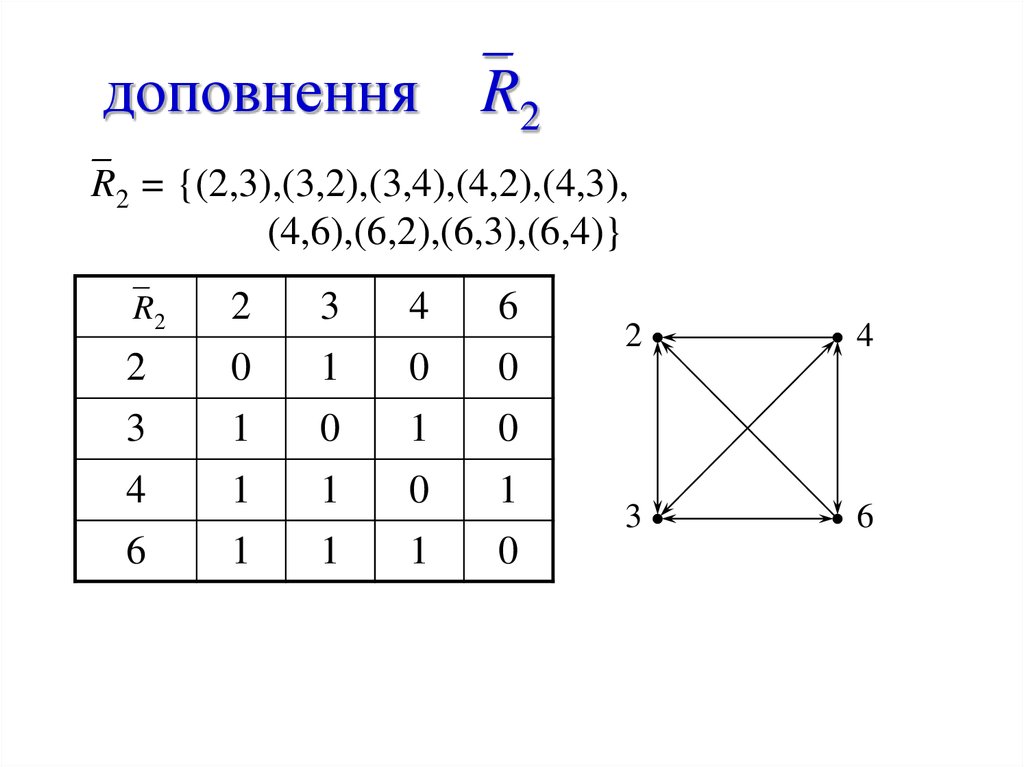
16. доповнення R2
доповнення R2R2 = {(2,3),(3,2),(3,4),(4,2),(4,3),
(4,6),(6,2),(6,3),(6,4)}
R2
2
3
4
6
2
0
1
0
0
3
1
0
1
0
4
1
1
0
1
6
1
1
1
0
2
4
3
6
17. обернене R1-1
R1-1 = {(3,4),(4,2),(6,2),(6,3),(6,6)}R1-1
2
3
4
6
2
0
0
0
0
3
0
0
1
0
4
1
0
0
0
6
1
1
0
1
2
4
3
6
18. композиція
Нехай R і S — відношення, такі, що R X Y,S Y Z, де X, Y, Z — деякі множини.
Композицією відношень R і S називається
відношення S°R, що складається з упорядкованих
пар (х, z), х X, z Z, для яких існує елемент у Y,
такий, що виконуються умови (х, у) R, (у, z) S.
Зауваження: для пари (х, z) S°R «проміжних»
елементів Y може бути кілька, однак їх кількість
(якщо вона не нульова) не впливає на вид
композиції S°R.
19.
Властивості композиції відношень :не виконується закон комутативності
S°R R°S
виконується закон асоціативності
S°(R°D) = (S°R)°D = S°R°D
правило розрахунку оберненого відношення
(S°R)-1 = R-1°S-1
Матриця композиції відношень S°R утворюється
як добуток матриць відношень S і R з подальшою
заміною відмінних від нуля елементів одиницями.
20. композиція R1 R2
композиція R1 R2R1 R2 = {(2,3),(2,4),(2,6),(4,3),(3,6),(6,6)}
R1 R2
2
2
0
1
1
1
3
0
0
0
1
4
0
1
0
0
6
0
0
0
1
3
4
6
R2
R1
2
3
4
6
2
3
4
6
R1 R2
2
4
3
6
21. степінь Rn
n-й степінь відношення R X X позначаєтьсяRn і визначається рекурсивно так:
R0 — тотожне відношення на множині X;
Rn = Rn-1 ° R, для n = 1, 2, …
Із визначення маємо:
R1 = R,
R2 = R ° R,
R3 = R2 ° R .
Графічне трактування степеня відношення:
в графі відношення Rn є дуга з х в у, якщо в графі
R з вершини х у вершину у веде хоча б один
маршрут довжини n (що складається з n дуг).
22. степінь R12 , R13
R12 = {(2,3),(2,6),(3,6),(4,6),(6,6)}R13 = {(2,6),(3,6),(4,6),(6,6)}
R12
R1
R13
2
4
2
4
2
4
3
6
3
6
3
6
23. переріз R(x), фактор-множина
Нехай R X Y—відношення на множинах X і Y.Перерізом відношення R(x) за х X є множина
R(x) Y, що складається з елементів у Y, таких, що
(х, у) R.
Об'єднання перерізів за елементами деякої
підмножини Z X називається перерізом R(Z)
відносно підмножини Z.
Множина, що складається з перерізів відношення
R X Y за кожним елементом з X, називається
фактор-множиною множини Y за відношенням R
Y/R = {R(x), x X}.
24. перерізи R2 (x)
R22
3
4
6
2
1
0
0
0
3
0
1
0
0
4
1
0
1
0
6
1
1
0
1
R2 (2) = {2,4,6}
R2 (3) = {3,6}
R2 (4) = {4}
R2 (6) = {6}
фактор-множина
А/R2 = {R2 (x), x А} = {{2,4,6}, {3,6}, {4}, {6}}




















 mathematics
mathematics








