Дискретні структури. Бінарні відношення. Лекція 2

1. Дискретні структури

Лекція 2
Бінарні відношення
2.1. Поняття бінарного відношення.
2.2. Властивості бінарних відношень.
2.3. Види бінарних відношень.
2.4. Операції над бінарними відношеннями.
2.5. Відображення множин.

2. 2.1. Поняття бінарного відношення

Визначення. Декартовим добутком множин X і Y називається
множина X*Y всіх впорядкованих пар (x, у) таких, що x X, у Y.
Визначення. Відношенням між множинами X і Y (або відношенням
з X в Y) називається будь-яка підмножина R декартового добутку
X*Y. Якщо множини X і Y збігаються, то відношення між
множинами X і Y називають бінарним відношенням на множині
X.
Приклад. Нехай X = {а, b, с, d}, Y = {1, 2, 3, 4, 5}. Тоді множина
комбінацій R={(а, 1), (b, 2), (с, 3), (d, 4)} є відношенням з X в Y.
Зазвичай відношення задаються не шляхом задання підмножини R
декартового добутку X*Y, а шляхом задання властивості пар (x,
у), що належать цій підмножині R.
Приклад. Відношення R = {(4, 4), (3, 3), (2, 2), (4, 2)} на множині X
= {4, 3, 2} можна визначити як властивість "Ділиться" на цій
підмножині цілих чисел.

3.

Приклади відношень з курсу математики є:
на множині цілих чисел Z
- відношення "ділиться",
"ділить", "рівно", "більше", "менше", "взаємно прості";
на множині прямих простору - відношення "паралельні",
"взаємно
перпендикулярні",
"схрещуються",
"перетинаються", "збігаються";
на множині окружності площини - відношення
"перетинаються", "торкаються", "концентричні".

4.

Приналежність комбінації (x, у) відношенню R, часто
позначають за допомогою так званої інфіксної форми
запису: x R y.
Приклад. x >у, а = b, m||l, а ┴b і т.п.
Відношення можуть задаватися формулами:
1) у = x2 +5x - 6 - задаються бінарні відношення на множині
дійсних чисел;
2) x +у = любов - задаються бінарні відношення на безлічі
людей.

5.

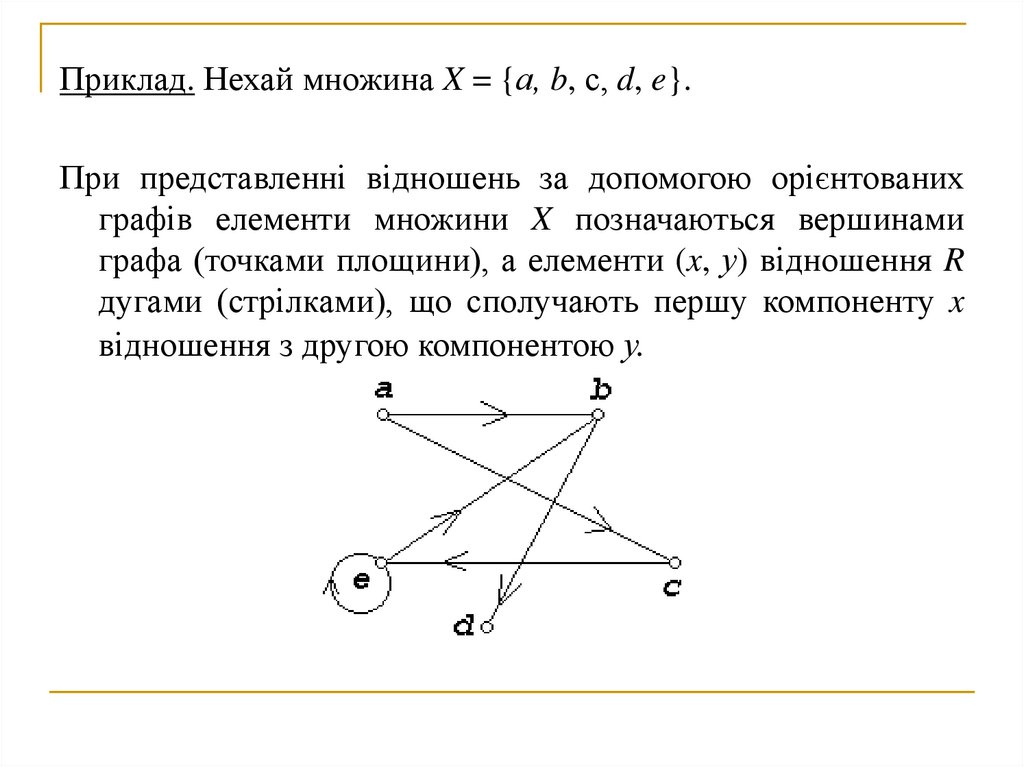
Приклад. Нехай множина X = {а, b, с, d, e}.
При представленні відношень за допомогою орієнтованих
графів елементи множини X позначаються вершинами
графа (точками площини), а елементи (x, у) відношення R
дугами (стрілками), що сполучають першу компоненту x
відношення з другою компонентою у.

6.

Для бінарних відношень, визначених на скінченій множині,
часто використовується матричний спосіб представлення.
Для цього необхідно визначити матрицю відношення A =
[aij] наступним чином:
1, якщо ( x i , x j ) належить R
a ij
0, якщо ( x i , x j ) неналежить R
Таким чином, матриця відношення R, представленого графом
має вигляд

7. 2.2. Властивості бінарних відношень

1.Рефлексивність
x A xRx
2.Іррефлексивність
x A xRx
3.Симетричність
xRy yRx
4.Антисиметричність
xRy yRx x y
5.Транзитивність
xRy, yRz xRz

8. 2.3. Види бінарних відношень

Відношення еквівалентності: рефлексивне, симетричне та транзитивне.
Приклад. Відношення рівнозначності формул, подібності геометричних
фігур, належності студентів до однієї групи.
Відношення сумісності: рефлексивне та симетричне.
Приклад. Відношення близькості чисел, знайомства людей.
Відношення часткового порядку: рефлексивне, антисиметричне
транзитивне.
Приклад. Відношення та для дійсних чисел, та для множин.
та
Відношення повного порядку: іррефлексивне, антисиметричне
транзитивне.
Приклад. Відношення та для дійсних чисел, и для множин.
та

9. 2.4. Операції над бінарними відношеннями

Визначення. Перетином двох відношень R та S називається
множина впорядкованих комбінацій, які належать як R, так і S.
Визначення. Об’єднанням двох відношень R та S називається
множина впорядкованих комбінацій, які належать R або S.
Визначення. Різницею двох відношень R та S називається
множина впорядкованих комбінацій, які належать R, але не
належать S.

10. 2.5. Відображення множин

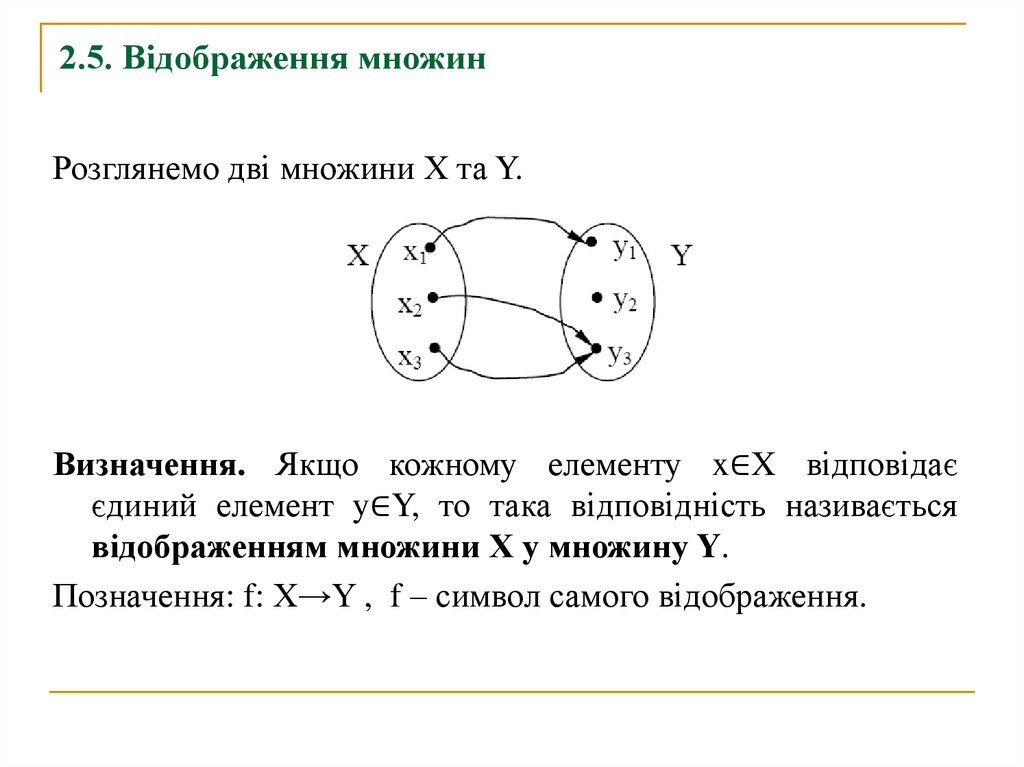
Розглянемо дві множини Х та Y.
Визначення. Якщо кожному елементу x∈X відповідає
єдиний елемент y∈Y, то така відповідність називається
відображенням множини Х у множину Y.
Позначення: f: X→Y , f – символ самого відображення.

11.

Визначення. Якщо при відображенні f кожний елемент
множини Y є образом хоча б одного елементу з Х, то f
називають відображенням Х на Y або сюр’єнцією.
Визначення. Якщо при відображенні f всі різні елементи
множини Х переходять в різні елементи множини Y, то
відношення f називають ін’єнцією.

12.

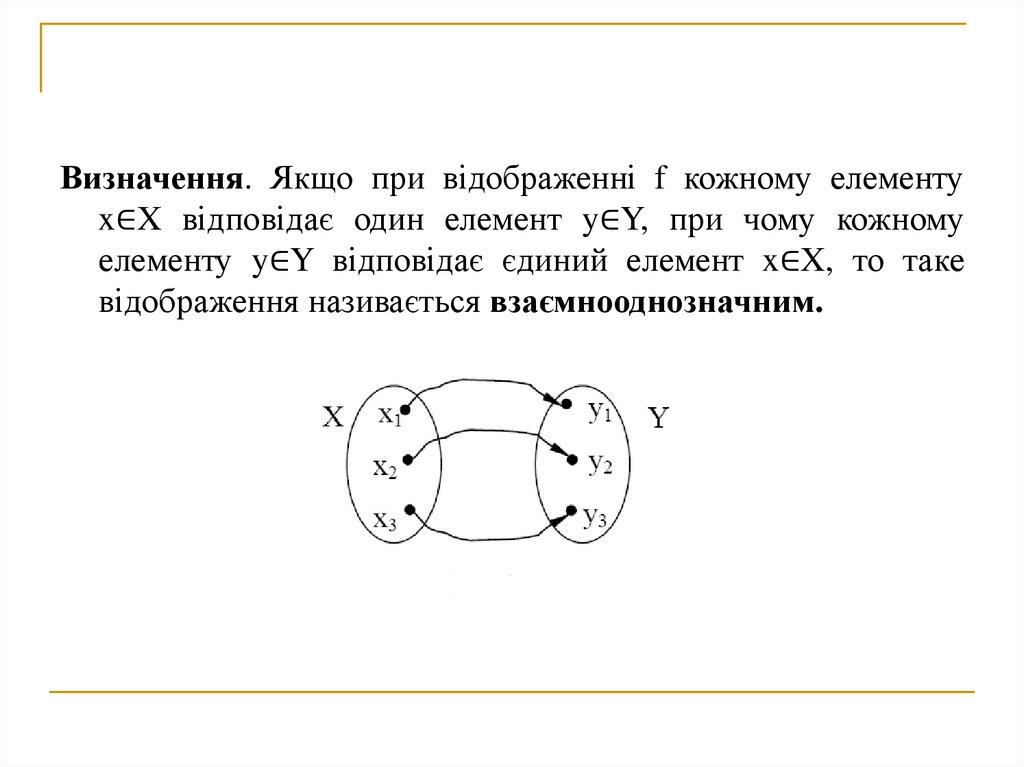
Визначення. Якщо при відображенні f кожному елементу
x∈X відповідає один елемент y∈Y, при чому кожному
елементу y∈Y відповідає єдиний елемент x∈X, то таке
відображення називається взаємнооднозначним.