Вычислительная механика. Формирование глобальных векторов и матриц МКЭ

1. Лекция Вычислительная механика Формирование глобальных векторов и матриц МКЭ

К.т.н., доцент каф. ВМиМ
Каменских Анна Александровна
239-15-64

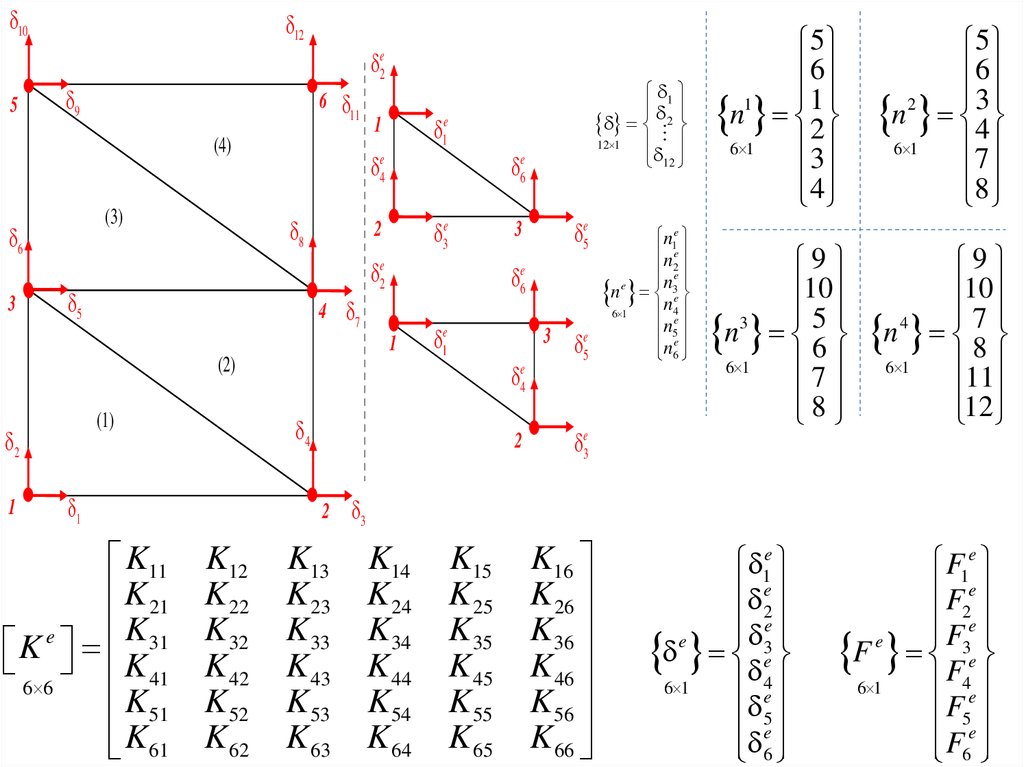
2.

10
12
5
9
6
11
(4)
(3)
6
3
e
2
1e
1
e4
8
e6
3e
2
e6
4 7
1
(2)
(1)
2
1
K11
K 21
K e K31
K 41
6 6
K51
K
61
1e
3
e4
4
1
5e
3
e2
5
1
2
12 1
12
2
5e
3e
n1e
n2e
e
ne nn34e
6 1
e
n5e
n6
5
6
1
1
n
2
6 1
3
4
5
6
3
2
n
4
6 1
7
8
9
10
n3 56
6 1
7
8
9
10
n4 78
6 1
11
12
2 3
K12
K 22
K32
K 42
K52
K 62
K13
K 23
K33
K 43
K53
K 63
K14
K 24
K 34
K 44
K 54
K 64
K15
K 25
K 35
K 45
K 55
K 65
K16
K 26
K 36
K 46
K 56
K 66
1e
e2
e
e
e34
6 1
e
5e
6
F1e
F2e
F e
e
F F34e
6 1
e
F5e
F6

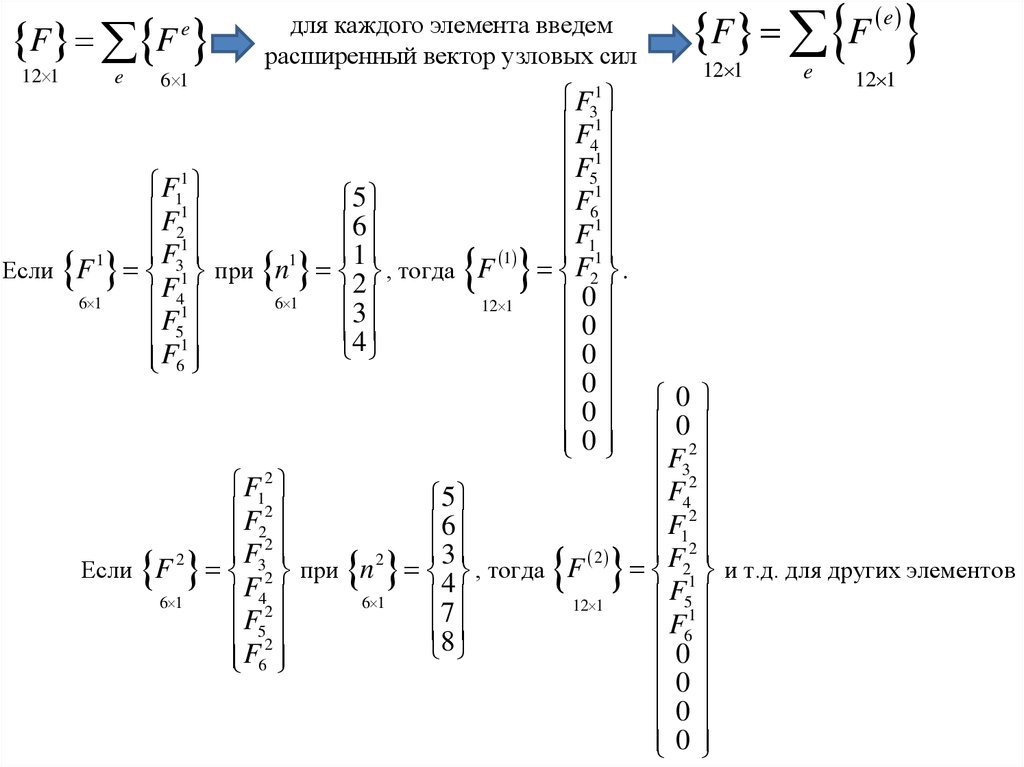
3.

F F
12 1
e
e
6 1
для каждого элемента введем
расширенный вектор узловых сил
12 1
e
e
12 1
1
F1
5
F21
6
F 1
1
1
1
1
Если F 31 при n , тогда F
.
2
F
6 1
6 1
3
12 1
41
4
F51
F6
0
0
2
F3
2
F 2
F1
5
F42
F22
6
12
2
2
F
3
2
2
F21 и т.д. для других элементов
Если F 32 при n , тогда F
4
F
6 1
6 1
F51
7
12 1
42
F6
8
F52
0
F6
0
0
0
F
F
F
F
F
F
0
0
0
0
0
0
F
F
1
3
1
4
1
5
1
6
1
1
1
2

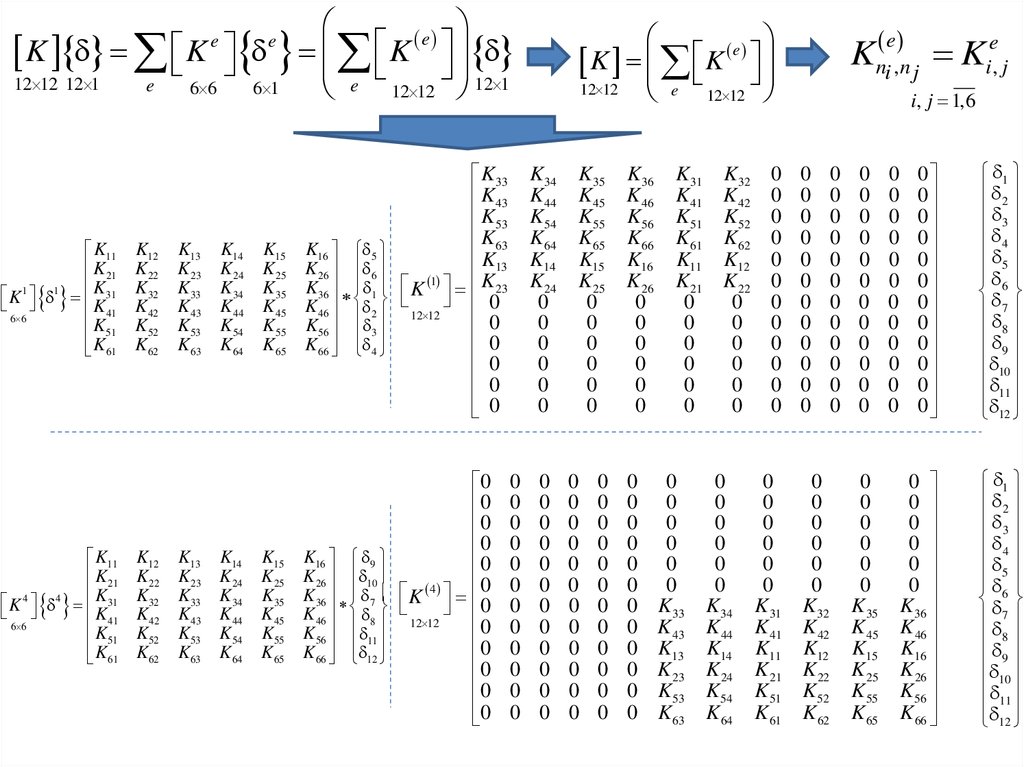
4.

e
K K K
12 12 12 1
e
6 6
6 1
e 12 12 12 1
e
K11 K12
K 21 K 22
1
1
K K31 K32
K 41 K 42
6 6
K51 K52
K
61 K 62
K11
K 21
4
4
K K31
K 41
6 6
K51
K
61
K12
K 22
K32
K 42
K52
K 62
K13
K 23
K33
K 43
K53
K 63
K13
K 23
K33
K 43
K53
K 63
e
K K
12 12
e 12 12
e
K14
K 24
K34
K 44
K54
K 64
K14
K 24
K34
K 44
K54
K 64
K15
K 25
K35
K 45
K55
K 65
K15
K 25
K35
K 45
K55
K 65
K16 5
K 26 6
K36 1
K 46 2
K56 3
K 66 4
K 33
K 43
K 53
K 63
K13
K 1 K 23
0
12 12
0
0
0
0
0
K16 9
K 26 10
K36 7
K 46 8
K56 11
K 66 12
0
0
0
0
0
K 4 0
0
12 12
0
0
0
0
0
K 34
K 44
K 54
K 64
K14
K 24
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 35
K 45
K 55
K 65
K15
K 25
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 36
K 46
K 56
K 66
K16
K 26
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 31
K 41
K 51
K 61
K11
K 21
0
0
0
0
0
0
0
0
0
0
0
0
K 33
K 43
K13
K 23
K 53
K 63
K 32
K 42
K 52
K 62
K12
K 22
0
0
0
0
0
0
0
0
0
0
0
0
K 34
K 44
K14
K 24
K 54
K 64
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 31
K 41
K11
K 21
K 51
K 61
Kn i , n j Kie, j
e
i, j 1,6
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 32
K 42
K12
K 22
K 52
K 62
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
K 35
K 45
K15
K 25
K 55
K 65
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
11
12
0
0
0
0
0
0
K 36
K 46
K16
K 26
K 56
K 66
1
2
3
4
5
6
7
8
9
10
11
12

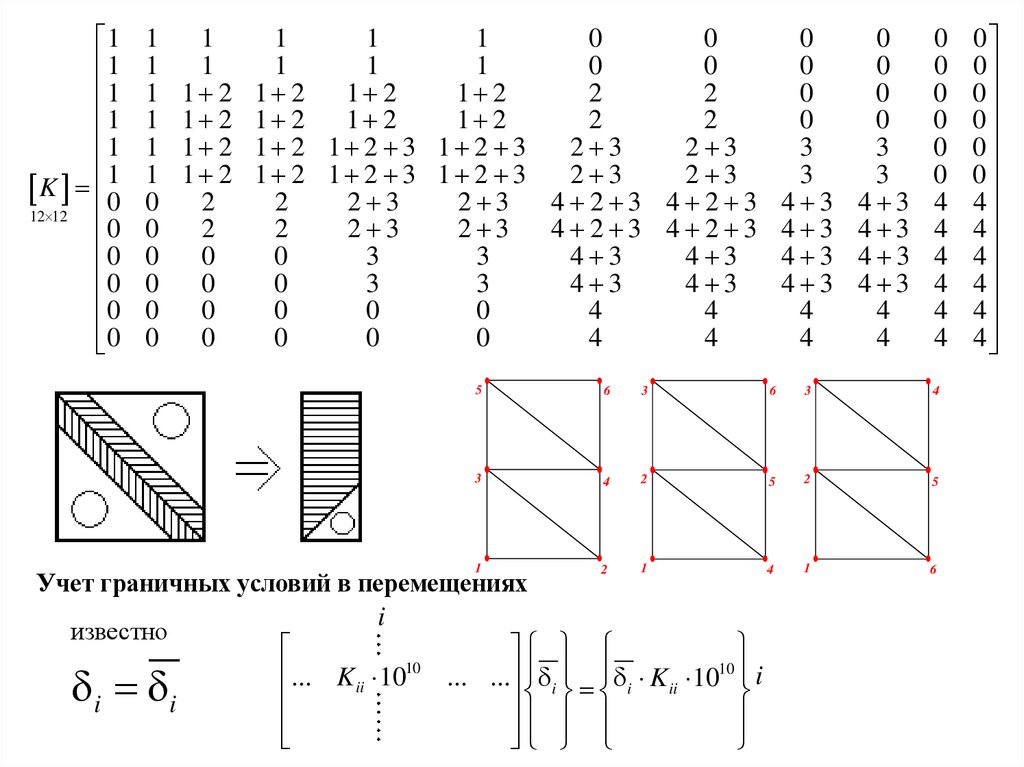
5.

1
1
1
1
1
1
K
0
12 12
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
1
1
1 2
1 2
1 2
1 2
2
2
0
0
0
0
1
1
1
0
0
1
1
1
0
0
1 2
1 2
1 2
2
2
1 2
1 2
1 2
2
2
1 2 1 2 3 1 2 3
2 3
2 3
1 2 1 2 3 1 2 3
2 3
2 3
2
2 3
2 3
4 2 3 4 2 3
2
2 3
2 3
4 2 3 4 2 3
0
3
3
4 3
4 3
0
3
3
4 3
4 3
0
0
0
4
4
0
0
0
4
4
i i
i
0
0
0
0
3
3
4 3
4 3
4 3
4 3
4
4
0
0
0
0
0
0
4
4
4
4
4
4
5
6
3
6
3
4
3
4
2
5
2
5
1
2
1
4
1
6
Учет граничных условий в перемещениях
известно
0
0
0
0
3
3
4 3
4 3
4 3
4 3
4
4
10
10
... K ii 10
... ... i i Kii 10 i
0
0
0
0
0
0
4
4
4
4
4
4