Несобственные интегралы. Приложения определенного интеграла. Приближенное вычисление определенного интеграла
Несобственные интегралы.
Несобственные интегралы.
Несобственные интегралы.
Несобственные интегралы.
Пример
Пример
Пример
Признаки сходимости несобственных интегралов первого рода.
Признаки сходимости несобственных интегралов первого рода.
2) Несобственные интегралы II - ого рода (интегралы от неограниченных (разрывных) функций).
Несобственные интегралы II - ого рода (интегралы от неограниченных (разрывных) функций).
Признаки сходимости несобственных интегралов второго рода.
Признаки сходимости несобственных интегралов второго рода.
Пример.
Пример.
Пример.
Геометрические приложения определенного интеграла.
Пример.
Геометрические приложения определенного интеграла.
Площадь плоской фигуры
Площадь плоской фигуры
Пример
Площадь плоской фигуры
II. Вычисление дуги плоской кривой
II. Вычисление дуги плоской кривой
III. Вычисление объема тела
III. Вычисление объема тела
Пример
Пример.
Пример.
Пример.
2.01M
Category: mathematicsmathematics
Similar presentations:
Несобственные интегралы
Несобственные интегралы
Несобственные интегралы
Несобственные интегралы
Несобственные интегралы
Несобственные интегралы
Определение определённого интеграла (Лекция 2)
Определение определённого интеграла (Лекция 2)
Определённый интеграл
Определённый интеграл
Определённый интеграл. Задача о площади криволинейной трапеции
Определённый интеграл. Задача о площади криволинейной трапеции
Несобственные интегралы. Лекция 6
Несобственные интегралы. Лекция 6
Интегралы. Неопределенный интеграл. Определенный интеграл
Интегралы. Неопределенный интеграл. Определенный интеграл
Несобственные интегралы
Несобственные интегралы
Несобственные интегралы (лекция 7)
Несобственные интегралы (лекция 7)

Несобственные интегралы. Приложения определённого интеграла. (Лекция 4)

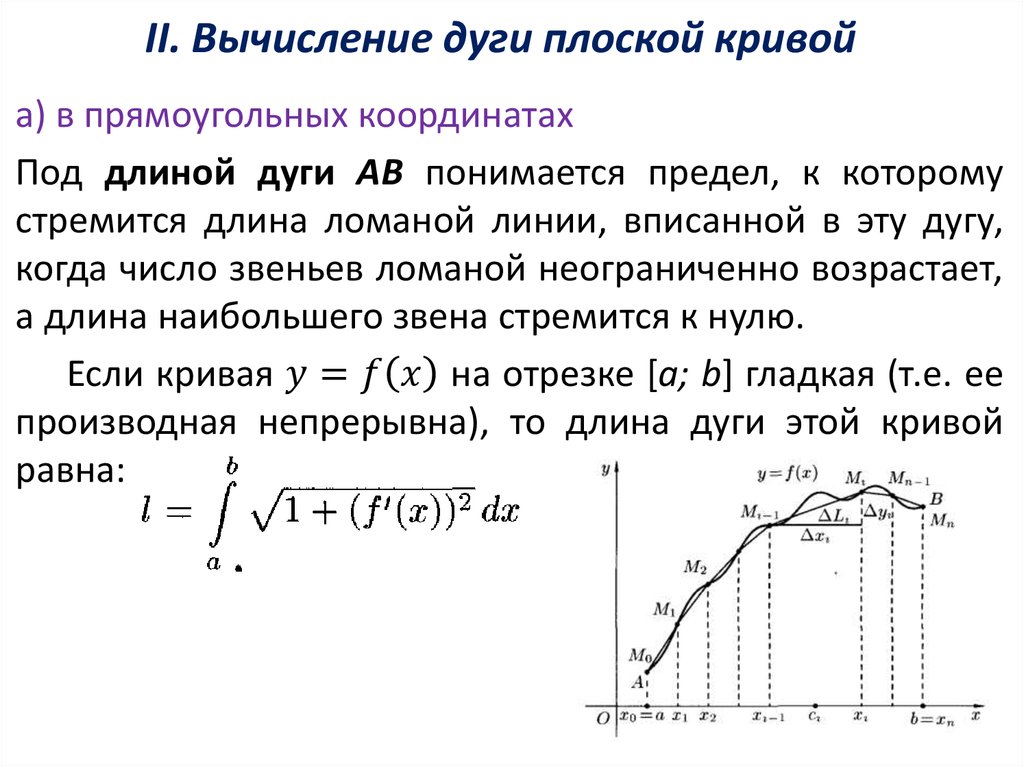
1. Несобственные интегралы. Приложения определенного интеграла. Приближенное вычисление определенного интеграла

Лекция № 4

2. Несобственные интегралы.

1) Несобственный интеграл I - ого рода (с бесконечными
пределами интегрирования).
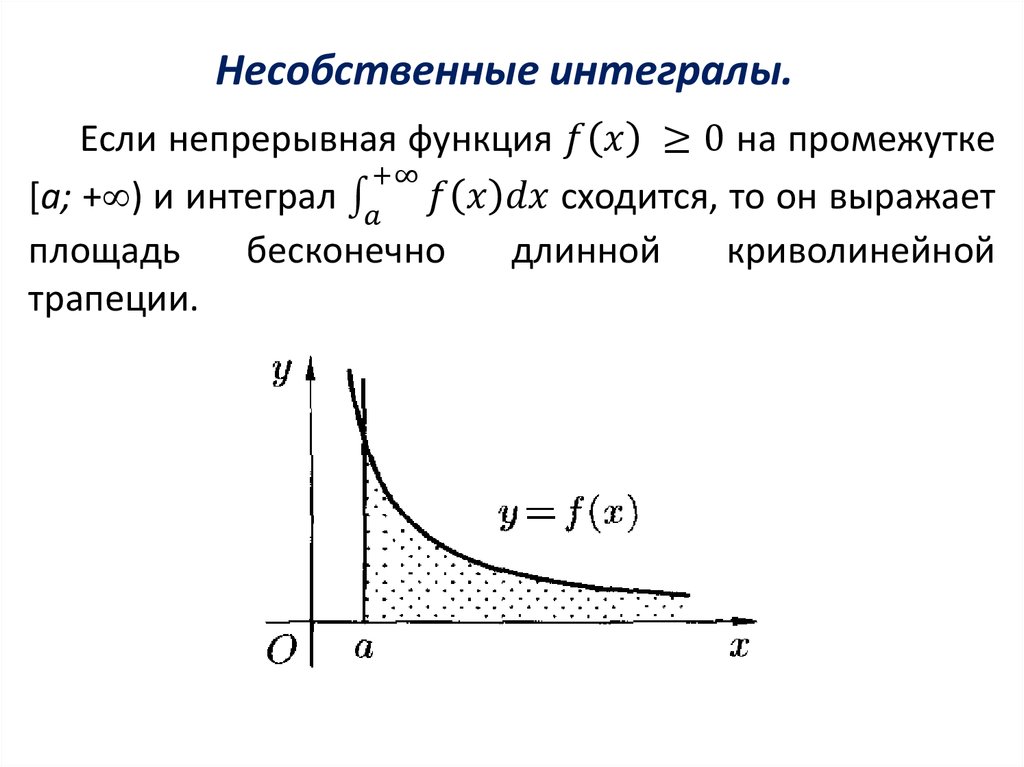
Опр. Пусть функция f(x) непрерывна на промежутке [a; + ).
Несобственным интегралом первого рода от функции
f(x) на промежутке [a; +∞) называется предел
English     Русский Rules