Теория электромагнитного поля

1. ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени С.М. Кирова Кафедра биологической и медицинской физики

ЛЕКЦИЯ № 9
по дисциплине «Физика, математика»
на тему: «Основы теории электромагнитного
поля»
для курсантов и студентов I курса по
специальности «Лечебное дело»

2. 1. Электрическое поле. Его основные характеристики. Потенциальное и вихревое электрические поля.

• Все тела в природе способны
электризоваться, то есть приобретать
электрический заряд.
• Наличие электрического заряда
проявляется в том, что заряженное тело
взаимодействует с другими заряженными
телами.

3.

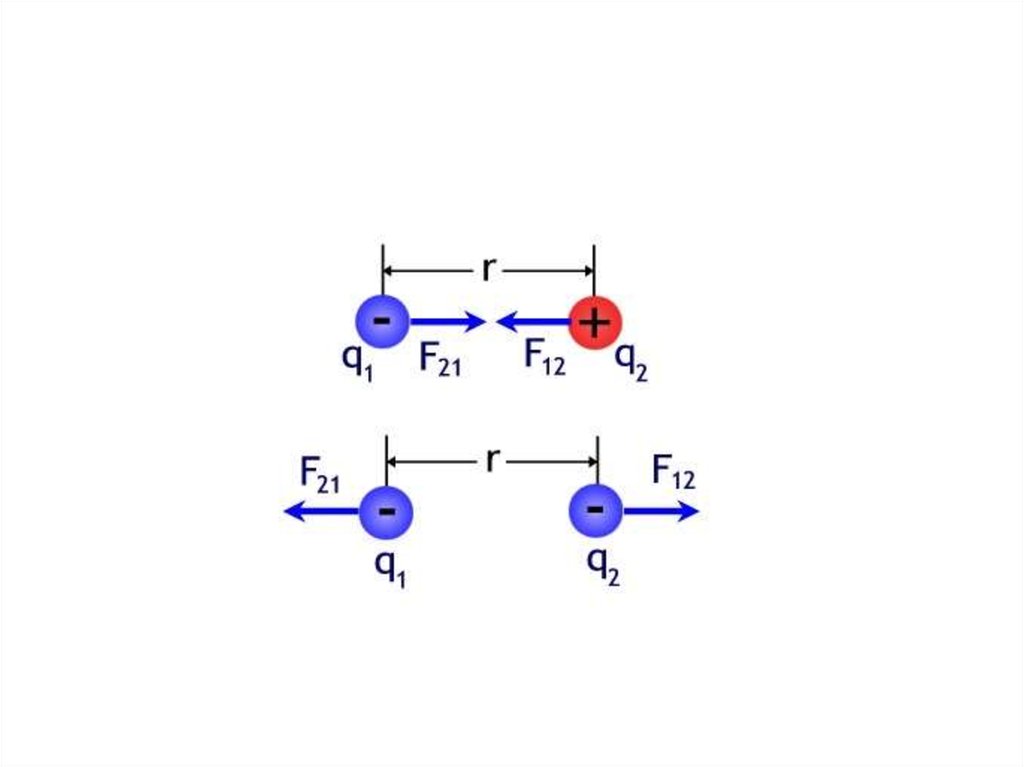
• Опыт показал, что между
наэлектризованными телами имеется либо
притяжение, либо отталкивание.
• Это объясняется тем, что имеется два вида
электрических зарядов, условно
называемых положительными и
отрицательными.
• Одноименные заряды отталкиваются,
разноименные – притягиваются.

4.

• Электрический заряд обозначается буквой
q, единица измерения заряда – кулон (Кл).
• Электрический заряд любой системы тел
состоит из целого числа элементарных
зарядов.
• Элементарный заряд - это наименьший
встречающийся в природе электрический
заряд, равный 1,6·10-19 Кл.

5.

• Наименьшей по массе устойчивой
частицей, имеющей отрицательный
элементарный заряд, является электрон
(m = 9,1·10-31 кг).
• У электрона существует и античастица,
имеющая положительный элементарный
заряд – позитрон.

6.

• Суммарный заряд электрически
изолированной системы не изменяется при
любых процессах, происходящих в этой
системе. Это положение известно под
названием закона сохранения заряда:
q = q1 + q2 + q3 +…+ qn = const

7.

• Силы электростатического взаимодействия
заряженных тел подчиняются закону
Кулона, поэтому их часто называют
кулоновскими силами.

8.

• Закон Кулона. Сила взаимодействия двух
неподвижных точечных зарядов прямо
пропорциональна величине каждого из
зарядов и обратно пропорциональна
квадрату расстояния между ними.
q1q2
1 q1q2
F 12
k 2
2
4 0 r12
r12

9.

12
1
8
,
85
10
Ф
м
где 0
– электрическая
постоянная,
k 9 10 9 Н м 2 Кл 2
– коэффициент
пропорциональности, или константа
Кулона,
• ε – относительная диэлектрическая
проницаемость среды.
• Сила направлена вдоль прямой,
соединяющей заряженные тела.

10.

11.

• Сам по себе закон Кулона не дает
представления о том, каков механизм
взаимодействия зарядов. Физическую
картину взаимодействия электрических
зарядов раскрывает так называемая теория
близкодействия.

12.

• Согласно этой теории вокруг каждого
заряда существует электрическое поле.
• Взаимодействие электрических зарядов q1
и q2 есть результат действия поля заряда q1
на заряд q2 и поля заряда q2 на заряд q1.

13.

• Определение:
Электрическое поле есть особый вид
материи, посредством которого
осуществляются силовые воздействия на
электрические заряды, находящиеся в
этом поле.

14.

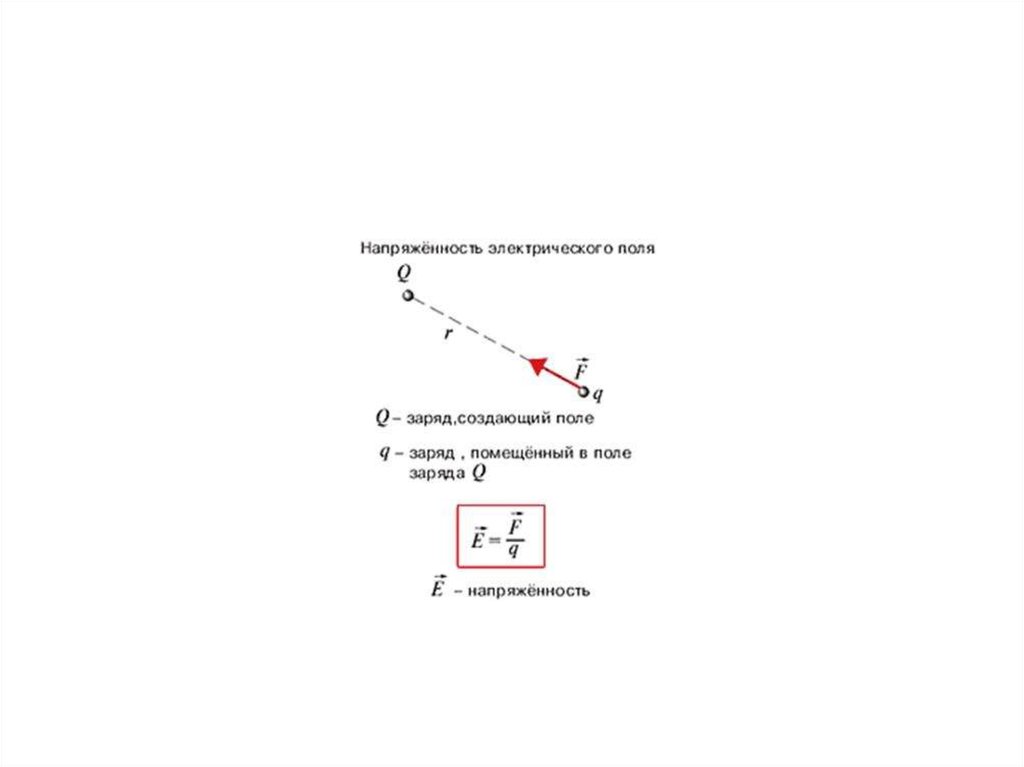
• Силовой характеристикой электрического поля
служит вектор напряженности электрического
поля.
• Он численно равен и совпадает по направлению с
силой, действующей на единичный
положительный заряд, помещенный в данную
точку поля:
• Размерность напряженности ЭП: Н/Кл.

15.

• Напряженность поля, создаваемого
точечным зарядом:
,
• где r – расстояние от заряда до
рассматриваемой точки.

16.

17.

• Однородным называют электрическое
поле, векторы напряженности которого
одинаковы во всех точках поля.
• Приблизительно однородным является
электрическое поле между двумя
разноименно заряженными
металлическими пластинами,
расположенными параллельно друг другу.

18.

• Для графического изображения
электростатического поля в пространстве
применяется метод силовых линий, или
линий напряженности.
• Силовыми линиями называются линии,
касательные к которым в каждой точке
совпадают с направлением вектора
напряженности в этой точке.

19.

• Следует помнить, что:
• 1) силовые линии электростатического поля не
пересекаются друг с другом;
• 2) имеют начало на положительном заряде и
конец на отрицательном или уходят на
бесконечность, т.е. являются незамкнутыми;
• 3) густота силовых линий пропорциональна
величине напряженности электростатического
поля.

20.

21.

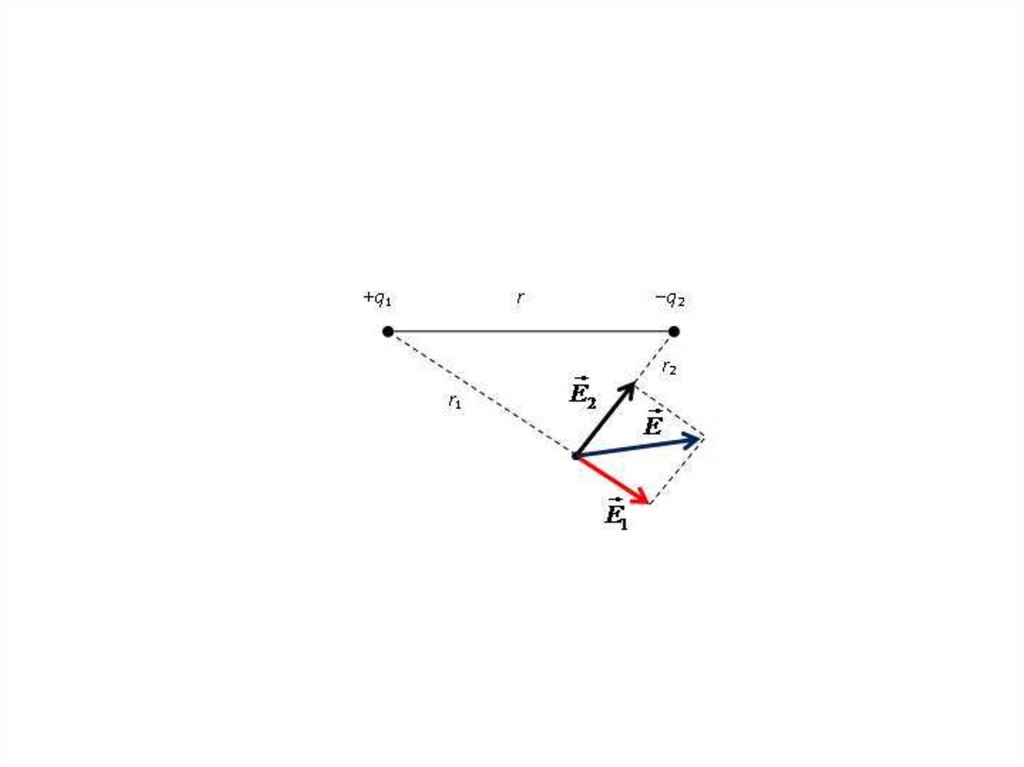
• Принцип суперпозиции электрических
полей: напряженность электрического
поля системы точечных зарядов равна
векторной сумме напряженностей полей
каждого из зарядов в отдельности:
E E1 E2 ... En или
n
Е Еi
i 1

22.

23.

• Помимо силовой характеристики
электрического поля существует и
характеристика его источников электрическое смещение, или вектор
электрической индукции (D) , который
зависит от того, каким образом и в каком
количестве источники ЭП расположены в
пространстве.
D = ε0εE [Кл.м-2]

24.

• Существуют два вида электрических полей:
а) потенциальное ЭП;
б) вихревое ЭП.

25.

• Потенциальное ЭП – это
электростатическое поле, т.е. поле,
созданное системой неподвижных
электрических зарядов.
• Важной характеристикой потенциального
ЭП является потенциал электрического
поля (электрический потенциал).
• Это энергетическая характеристика
потенциального ЭП.

26.

• Потенциал электрического поля –
скалярная физическая величина, численно
равная отношению потенциальной энергии
(+) электрического заряда, помещенного в
данную точку поля, к величине этого
заряда:
• Единица измерения: 1 вольт (В) = 1 Дж/Кл.

27.

• Другими словами, потенциал
электрического поля в данной точке равен
работе сторонних сил по переносу
единичного положительного точечного
заряда от точки, потенциал которой принят
равным нулю (обычно этой точкой является
бесконечность), в данную точку поля.

28.

• Разность потенциалов – величина, равная
работе А1,2 , которую совершают силы
электрического поля при перемещении
единичного положительного заряда q из
точки с потенциалом φ1 в точку с
потенциалом φ2:

29.

• Работа электростатического поля при
перемещении заряда q из точки с
потенциалом 1 в точку с потенциалом 2:
А1,2 = q·( 1 - 2)

30.

• Работа электростатического поля не зависит
от вида траектории перемещения заряда, а
определяется только исходным и
конечным положением перемещенного
заряда.
• Соответственно, при перемещении заряда
по замкнутому контуру полная работа
электростатического поля равна нулю.

31.

• Такое поле называется потенциальным.
• Электростатическое поле – потенциальное
поле.

32.

• Кроме потенциальных ЭП, существуют
также вихревые электрические поля.
• Их силовые линии замкнуты, т.е. не имеют
ни начала, ни конца, а работа по
перемещению заряда по замкнутому
контуру не равна нулю и зависит от
траектории движения заряда.
• Источником вихревых ЭП является
переменное магнитное поле.

33. Связь между разностью потенциалов и напряженностью ЭП

• Между напряженностью ЭП и потенциалом
существует определенная связь. Вектор
напряженности Е численно равен
градиенту потенциала, но направлен в
противоположную сторону, т.е. в сторону
падения потенциала:
или

34.

• Напряженность однородного поля
численно равна разности потенциалов на
единице длины линии напряженности.

35.

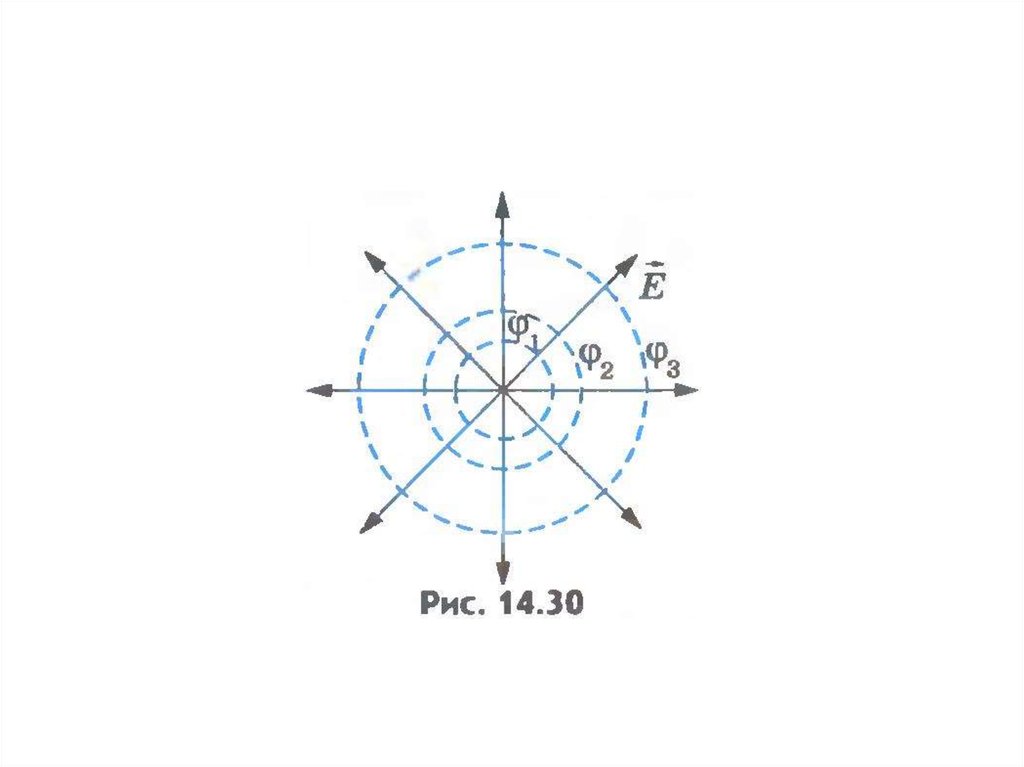
• Воображаемую поверхность, все точки
которой имеют одинаковый потенциал,
называют эквипотенциальной
поверхностью.
• Силовые линии и эквипотенциальные
поверхности взаимно перпендикулярны.
• При перемещении заряда по
эквипотенциальной поверхности работа не
совершается.

36.

• Потенциал поля точечного заряда q на
расстоянии r от него:
• Эквипотенциальная поверхность поля
точечного заряда на расстоянии r от
заряда – поверхность сферы радиуса r.

37.

38.

• Принцип суперпозиции электрических
полей – потенциал поля системы точечных
зарядов φ в некоторой точке пространства
равен алгебраической сумме потенциалов,
создаваемых каждым из зарядов в этой
точке:

39. Электрическая емкость

• Электрическая емкость проводника C –
количественная мера его способности
удерживать электрический заряд.
• Электрическая емкость уединенного
проводника равна отношению заряда
проводника q к его потенциалу φ :
[1 Кл/В = 1 Ф]

40.

• Электрическая емкость проводника
определяется его формой,
геометрическими размерами и свойствами
окружающей среды (диэлектрической
проницаемостью ).
• Емкость уединенного шара, погруженного в
однородный безграничный диэлектрик с
проницаемостью ε, равна
C 4 0 R

41.

• Однако уединенные проводники обладают
небольшой емкостью.
• Для накопления большого по величине
заряда применяют конденсаторы.
• Конденсатором называют устройство из
двух проводников (обкладок), разделенных
слоем диэлектрика, толщина которого мала
по сравнению с размерами проводников.

42.

• Плоский конденсатор – система из двух
плоских параллельных металлических
пластин, расположенных на расcтоянии d,
с площадью S каждая, разделенных
диэлектриком с диэлектрической
проницаемостью .

43.

• Электроемкость конденсатора –
отношение заряда одной из его обкладок к
разности потенциалов между обкладками:
,
где φ1 и φ2 – потенциалы пластин,
U – напряжение на конденсаторе.

44.

• Конденсаторы различаются по форме
(плоские, сферические, цилиндрические), а
также по материалу, используемому в
качестве изолирующей прокладки
(парафинированная бумага, полистирол,
слюда, керамика).

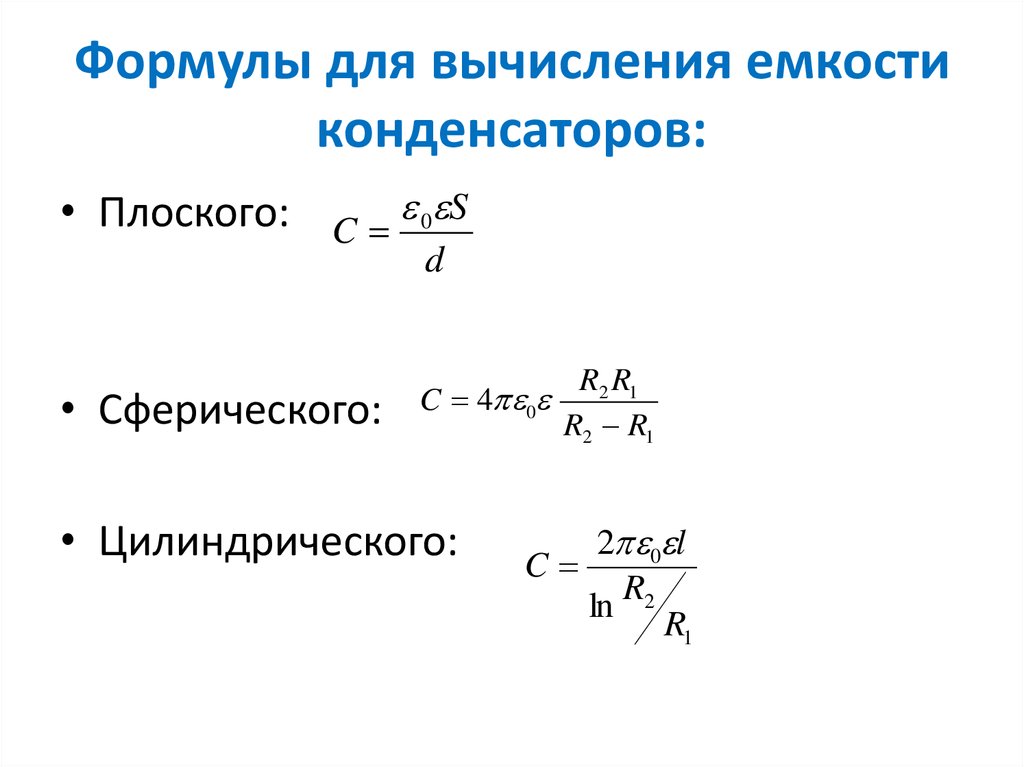
45. Формулы для вычисления емкости конденсаторов:

• Плоского: C 0 S
d
• Сферического:
R2 R1
C 4 0
R2 R1
• Цилиндрического:
2 0 l
C
R
ln 2
R1

46. Энергия электрического поля

• Электрическое поле является носителем
энергии.
• В общем случае количественной
характеристикой электрического поля
служит объемная плотность энергии.

47.

• Объемная плотность энергии
электростатического поля ω – физическая
величина, равная отношению энергии
электростатического поля W,
сосредоточенного в некотором объеме V к
этому объему:

48. Энергия плоского конденсатора.

• Исходя из величины работы А,
совершаемой электрическим полем при
разрядке конденсатора:
• получим формулу для энергии
заряженного конденсатора:

49. 2. Магнитное поле и его характеристики

• Магнитные явления были известны
человечеству давно (намагниченные тела,
постоянные магниты, компас и т. д.).
• Впоследствии выяснилось, что в пространстве
вокруг движущихся заряженных тел,
движущихся заряженных частиц, а также
вокруг проводников, по которым текут
постоянные токи, возникает особого вида
поле, называемое магнитным полем.

50.

• Таким образом, источниками магнитного
поля являются движущиеся электрические
заряды (следовательно, и проводники с
токами).
• Магнитное поле постоянных магнитов
также создается электрическими
микротоками, циркулирующими внутри
молекул вещества (гипотеза Ампера).

51.

• Определение: Магнитное поле есть
особый вид материи, посредством
которого осуществляются силовые
воздействия на движущиеся
электрические заряды, находящиеся в
этом поле, и другие тела, обладающие
магнитным моментом.

52.

• Для описания магнитного поля необходимо
ввести силовую характеристику поля,
аналогичную вектору напряженности
электрического поля. Такой
характеристикой является вектор
магнитной индукции B.

53.

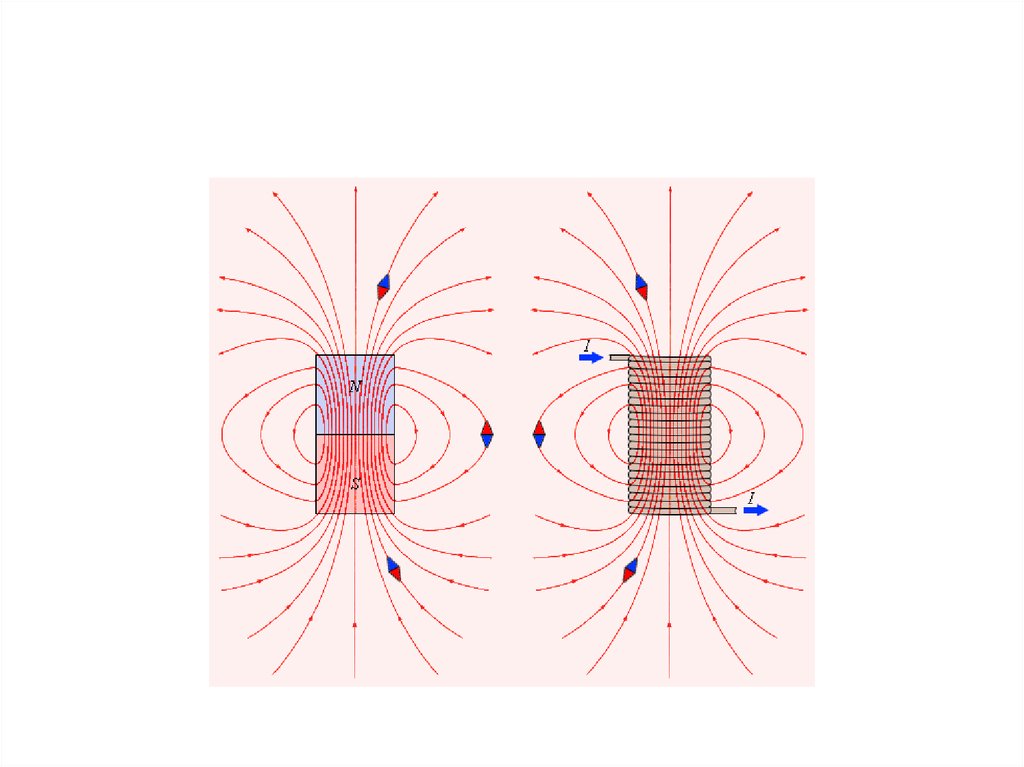
• За положительное направление вектора B
принимается направление от южного
полюса S к северному полюсу N магнитной
стрелки, свободно устанавливающейся в
магнитном поле.

54.

• Таким образом, исследуя магнитное поле,
создаваемое током или постоянным
магнитом, с помощью маленькой
магнитной стрелки, можно в каждой точке
пространства определить направление
вектора B.
• Такое исследование позволяет представить
пространственную структуру магнитного
поля.

55.

• Аналогично силовым линиям в
электростатике можно построить линии
магнитной индукции, в каждой точке
которых вектор B направлен по касательной
к ним.
• Линии магнитной индукции всегда
замкнуты, они нигде не обрываются.
Поэтому магнитное поле является
вихревым силовым полем.

56.

57.

• Для того чтобы количественно описать
магнитное поле, нужно указать способ
определения не только направления
вектора B, но и его модуля.
• Известно, что на заряд, движущийся в
магнитном поле, действует сила Лоренца,
численно равная:

58.

• Здесь
q – величина заряда,
v – его скорость,
В – величина вектора магнитной индукции,
α – угол между векторами v и В.

59.

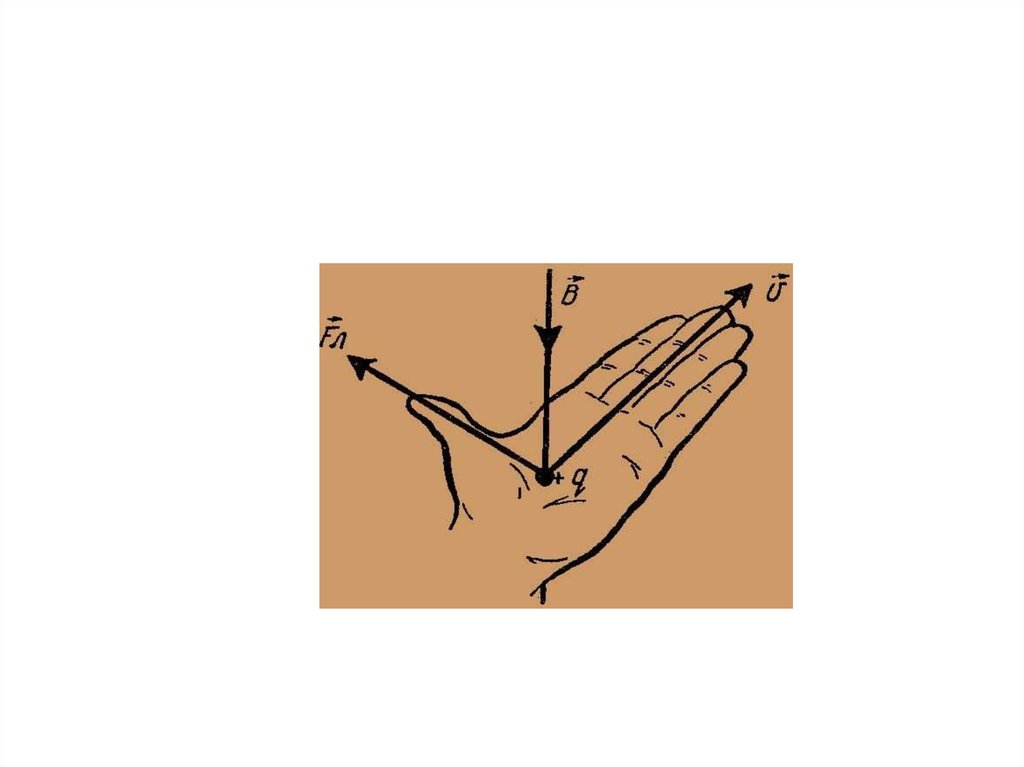
• Направление силы Лоренца определяют по
правилу левой руки:

60.

61.

• Сила Лоренца (магнитная сила) всегда
перпендикулярна плоскости, в которой
лежат векторы v и В.
• Этим она отличается от электрической
силы, которая направлена так же, как
вектор Е.

62.

• Из формулы Лоренца можно дать
определение магнитной индукции В:
• Вектор магнитной индукции численно
равен силе, действующей на единичный
положительный заряд, двигающийся с
единичной скоростью перпендикулярно
линиям магнитной индукции:

63.

• Единицей магнитной индукции В является
тесла (Тл).
• Для характеристики магнитного поля
источника в любой среде используют
векторную физическую величину –
напряженность магнитного поля :
Н
В
0

64.

• где μ – относительная магнитная
проницаемость среды, а μ0 – магнитная
постоянная, равная 12,57 ·10-7 Гн·м-1.
• Единица напряженности магнитного поля –
1 А·м-1.

65. Действие магнитного поля на проводник с током. Закон Ампера.

• А.М. Ампером было установлено силовое
воздействие магнитного поля на
прямолинейный участок проводника с
током I длиной l , расположенный в
однородном магнитном поле под углом к
магнитной индукции В .

66.

• Сила, действующая в этом случае на
участок проводника со стороны магнитного
поля, вычисляется по формуле:
F IBl sin

67.

• Из курса элементарной физики известно, что
направление действия силы F определяется по
правилу левой руки: если ладонь левой руки
расположить так, чтобы перпендикулярная к
проводнику составляющая вектора В входила в
ладонь, а четыре вытянутых пальца указывали
бы направление тока, то отогнутый на 900
большой палец укажет направление силы,
действующей со стороны поля на проводник с
током.

68.

• Эта сила называется силой Ампера.
• Она достигает максимального по модулю
значения Fmax, когда проводник с током
ориентирован перпендикулярно линиям
магнитной индукции.

69.

• Одним из важных примеров магнитного
взаимодействия является взаимодействие
параллельных токов.
• Закономерности этого явления были
экспериментально установлены Ампером.

70.

• Если по двум параллельным проводникам
электрические токи текут в одну и ту же
сторону, то наблюдается взаимное
притяжение проводников.
• В случае, когда токи текут в противоположных
направлениях, проводники отталкиваются.
• Взаимодействие токов вызывается их
магнитными полями: магнитное поле одного
тока действует силой Ампера на другой ток и
наоборот.

71.

72.

• Опыты показали, что модуль силы,
действующей на отрезок длиной Δl
каждого из проводников, прямо
пропорционален силам тока I1 и I2 в
проводниках, длине отрезка Δl и обратно
пропорционален расстоянию R между
ними:
0 I1 I 2 l
F
2 R

73. Закон Био-Савара-Лапласа

• Позволяет вычислить напряженность
магнитного поля, создаваемого
постоянным током.
• Ж.Б. Био и Ф. Савар (1820 г.) установили
этот закон, экспериментально определяя
действие токов различной формы на
магнитную стрелку.

74.

• П.С. Лаплас проанализировал полученные
данные и нашел, что напряженность
магнитного поля любого тока
складывается из напряженностей полей,
создаваемых его отдельными
элементами.

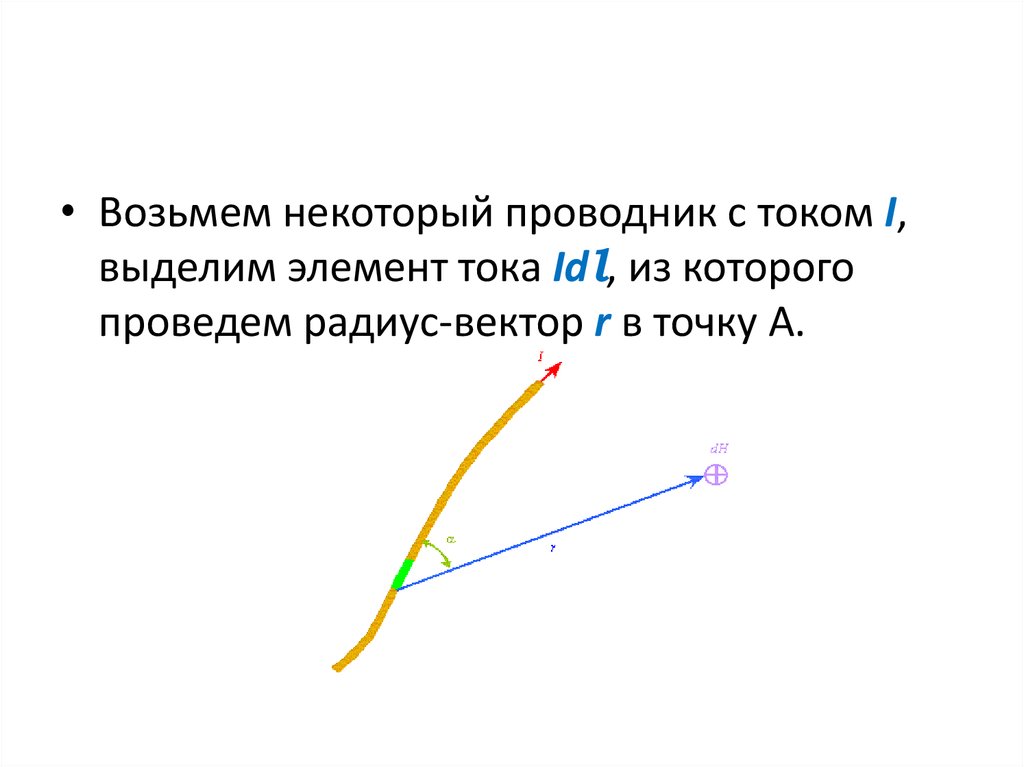
75.

• Возьмем некоторый проводник с током I,
выделим элемент тока Idl, из которого
проведем радиус-вектор r в точку А.

76.

• В точке А элемент тока создает магнитное
поле, напряженность которого dH
определяется законом Био-Савара-Лапласа:

77.

• k – коэффициент пропорциональности,
зависящий от выбора единиц.
• В системе СИ
• k = 1/(4π), поэтому:

78.

• Интегрируя эту формулу, находим
напряженность поля, создаваемого током
любой формы:

79.

• Так, напряженность магнитного поля в
центре кругового тока:

80.

• Напряженность магнитного поля,
созданного бесконечным прямолинейным
проводником с током в любой точке,
удаленной от проводника на расстояние b:

81.

• Напряженность магнитного поля соленоида
(однородного):
• где N – число витков; l – длина соленоида.

82. Энергия магнитного поля

• Поскольку магнитное поле является
силовым полем, то оно обладает
определенной энергией.
• Объемная плотность энергии магнитного
поля вычисляется по формуле: