464.05K

Categories: $mathematics$ mathematics

economics

Эконометрика. Модели обработки остатков ARMA. Лаговые модели

1.

Эконометрика-1
Филатов Александр Юрьевич
(Главный научный сотрудник, доцент ШЭМ ДВФУ)
[email protected]
http://vk.com/alexander.filatov, http://vk.com/baikalreadings
Лекции 7.1-7.2
Модели обработки остатков ARMA.
Лаговые модели

2.

Модели обработки остатков
2
Из исходного временного ряда yt исключаем всю неслучайную составляющую, в частности, тренд и сезонность, и переходим к ряду остатков t.
В отличие от пространственных выборок во временных рядах остатки тоже можно моделировать.
Автоковариационная и автокорреляционная функция:
Частная автокорреляционная функция – устранено влияние всех промежуточных членов ряда между t и t+ :

3.

Авторегрессия первого порядка.
Марковский процесс AR(1)
3
Марковский процесс AR(1):
Идентификация модели: найти и
Домножим на t, t–1, t–2 и т.д. и перейдем к математическим ожиданиям:
………………………………………………………………
Итоговые формулы:

4.

Авторегрессия второго порядка.
Процесс Юла AR(2)
4
Процесс Юла AR(2):
Идентификация модели: найти
и
…………………………………………………………………………………
Итоговые формулы:

5.

Авторегрессия порядка p: AR(p)
Общий вид авторегрессионной модели AR(p):
Идентификация модели: найти
5
и
…………………………………………………………………………………
Матричная форма:
Итоговые формулы:

6.

Модели скользящего среднего
Общий вид модели MA(q):
6
Частные случаи:
Двойственность в представлении моделей AR(p) и MA(q):
Аналогично, AR(p) ~ MA(+ ), MA(q) ~ AR(+ ).
Стационарность и обратимость:
Ряд AR(p) стационарен, если все корни характеристического уравнения
по модулю больше единицы.
Ряд MA(q) стационарен всегда, но обратим (представим в виде AR(p)),
если все корни
по модулю больше единицы.

7.

Скользящее среднее
первого порядка: MA(1)
7
Модель MA(1):
Идентификация модели: найти
и
Выбираем из двух корней тот, который удовлетворяет
условию | | < 1.

8.

Скользящее среднее
порядка q: MA(q)
8
Модель MA(q):
Идентификация модели: найти
и
Идентификация модели осуществляется с помощью решения системы
квадратичных уравнений

9.

9
Выявление порядка модели
с помощью коррелограмм
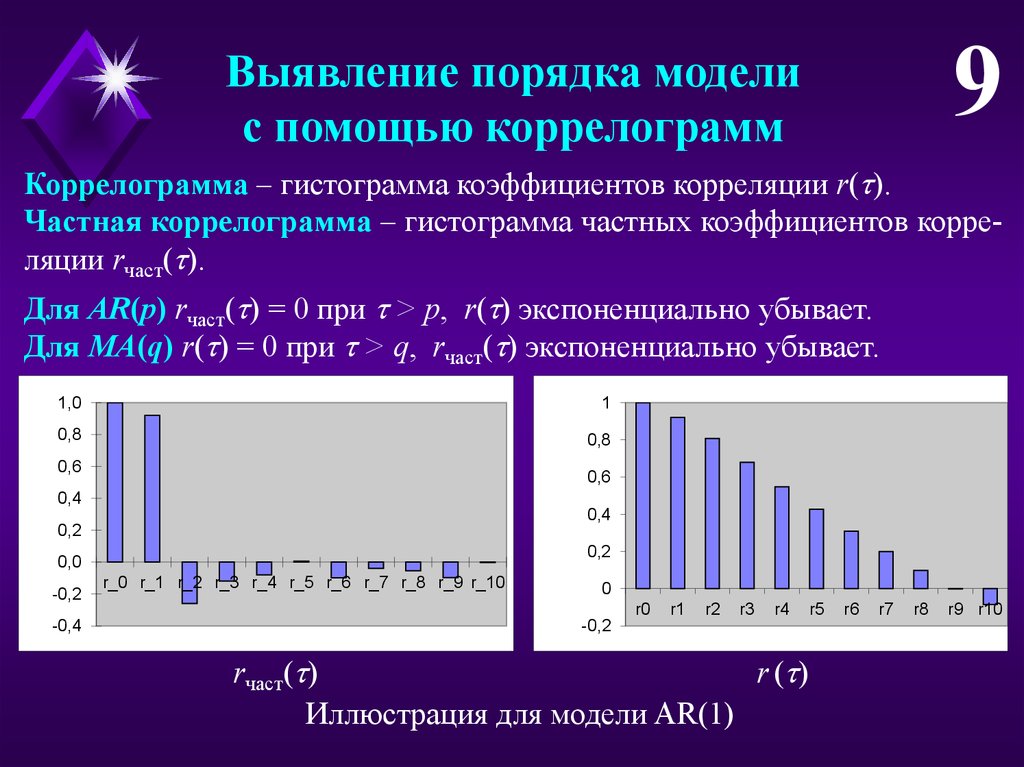
Коррелограмма – гистограмма коэффициентов корреляции r( ).
Частная коррелограмма – гистограмма частных коэффициентов корреляции rчаст( ).
Для AR(p) rчаст( ) = 0 при > p, r( ) экспоненциально убывает.
Для MA(q) r( ) = 0 при > q, rчаст( ) экспоненциально убывает.
1,0
1
0,8
0,8
0,6
0,6
0,4
0,4
0,2
0,2
0,0
-0,2
-0,4
r_0 r_1 r_2 r_3 r_4 r_5 r_6 r_7 r_8 r_9 r_10
0
-0,2
r0
r1
r2
r3
r4
rчаст( )
r ( )
Иллюстрация для модели AR(1)
r5
r6
r7
r8
r9 r10

10.

10
Авторегрессионные модели
со скользящими средними в остатках
Модель ARMA(p, q):
Замечание:
t – не зависит от будущих t, но зависит от прошлых и текущих.
Идентификация модели: найти
,
и
Этап 1: нахождение α1,…,αp из системы линейных уравнений порядка p.
Подставляем выборочные значения r(k) и находим α1,…,αp.

11.

Авторегрессионные модели
со скользящими средними в остатках
11
Этап 2: нахождение 1,…, q из системы нелинейных уравнений порядка q.
Протиражируем соотношение (0) для t+1,…, t+q.
Умножаем (0) на (1), (2),…,(q), переходим к математическому ожиданию.
Получаем систему из q квадратных уравнений с q неизвестными. Находим из нее 1,…, q.
Замечание: удобно идентифицировать модель ARMA(p, 1), для q ≥ 2 используются численные методы.

12.

Операторы F+ и F_
сдвига во времени
Оператор «вперед»: F+ t = t+1;
Оператор «назад»: F_ t = t–1.
Свойства:
1. F+ F_ = 1, F+(F_ t) = F+ t–1 = t.
2.
3.
ARMA(p, q):
Оператор «дельта»: = 1 – F_:
t = t – t–1.
12

13.

Проблема перепараметризации
Пример модели ARMA(2, 1):
13
Часто множители не идентичны, но близки между собой:
Можно ожидать нестабильность оценок параметров. Если сокращение
на похожие множители кажется некорректным, можно использовать сумму бесконечно убывающей геометрической прогрессии:

14.

Проверка возможности
упрощения модели ARMA(p,q)
Представление модели ARMA(p,q) в еще одной форме:
zi (α) – корни характеристического уравнения AR-модели,
zj ( ) – корни характеристического уравнения MA-модели.
Пример:
14

15.

Многомерный временной ряд.
Лаговые модели
15
Многомерный временной ряд:
Можно учитывать лаг – запаздывание во времени.
## Инфляция негативно влияет на экономический рост не сразу, а спустя
некоторое время.
Лаг может быть распределенным – наблюдается распределенный во
времени эффект воздействия.
## Зависимость расходов населения y(t) от наблюдаемых доходов x(t).
k – доля дохода, которая тратится через k периодов после получения.
Если наблюдаемый доход равен истинному, k = 1, k [0; 1]
Если наблюдаемый доход меньше истинного, k > 1
## Зависимость объемов основных фондов y(t) от инвестиций x(t).

16.

Регрессионные модели
с распределенными лагами
16
Проблемы использования обычных регрессионных моделей:
1. Неизвестен период распределенного во времени воздействия T.
2. Как правило, значение T достаточно велико.
3. Малое по сравнению с числом параметров модели число наблюдений.
4. Высокая степень корреляции между объясняющими переменными.
Решение проблемы – особая структура модели!
Общий случай – зависимость большого числа коэффициентов дистрибутивной лаговой модели 0, 1,…, T от малого числа параметров α1,…, αm.
Частные случаи:
1. Экспоненциальное убывание силы воздействия – модель Койка.
2. Полиномиальная лаговая структура Ширли Алмон.

17.

Модель Койка
17
Предположения модели:
1. Период распределенного во времени воздействия велик, в пределе равен бесконечности.
2. Сила воздействия экспоненциально убывает.
Умножим исходную модель на λ и введем задержку на один период:
Вычтем второе неравенство из первого:
Итоговая модель:
Преимущества модели:
1. Бесконечное число параметров меняется на три: α, θ0, .
2. Исчезает проблема мультиколлинеарности.
3. Модель из дистрибутивно-лаговой превращается в авторегрессию.

Эконометрика. Модели обработки остатков ARMA. Лаговые модели

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.