Сезонные модели ARMA. Модели с авторегрессионной условной гетероскедастичностью (ARCH). Лекция 4 (часть 4)

1. Лекция 4 (часть 4)

Сезонные модели ARMA. Модели
с авторегрессионной условной
гетероскедастичностью (ARCH)

2. Цель лекции

Цель лекции - формирование теоретических
знаний о моделях стационарных временных
рядов, позволяющих прогнозировать соиальноэкономические
явления
и
процессы
на
краткосрочную
перспективу,
а
также
формирование навыков реализации указанных
моделей и методов в пакетах прикладных
программ
2

3. План лекции

1. Авторегрессионная модель с условной
гетероскедастичностью
2. Модификации авторегрессионной модели с
условной гетероскедастичностью
3. Тестирование условной дисперсии
4. Аддитивные сезонные модели ARMA
5. Мультипликативные сезонные модели ARMA
3

4. Реализуемые компетенции

ОПК-1 готовностью к самостоятельной работе
ОПК-2 способностью использовать современные математические методы и
современные прикладные программные средства и осваивать современные технологии
программирования
ПК-1 способностью использовать стандартные пакеты прикладных программ для
решения практических задач на электронных вычислительных машинах, отлаживать,
тестировать прикладное программное обеспечение
ПК-9 способностью выявить естественнонаучную сущность проблем, возникающих в
ходе профессиональной деятельности, готовностью использовать для их решения
соответствующий естественнонаучный аппарат
ПК-10 готовностью применять математический аппарат для решения поставленных
задач, способностью применить соответствующую процессу математическую модель и
проверить ее адекватность, провести анализ результатов моделирования, принять
решение на основе полученных результатов
ПК-11 готовностью применять знания и навыки управления информацией
ПК-12 способностью самостоятельно изучать новые разделы фундаментальных наук
4

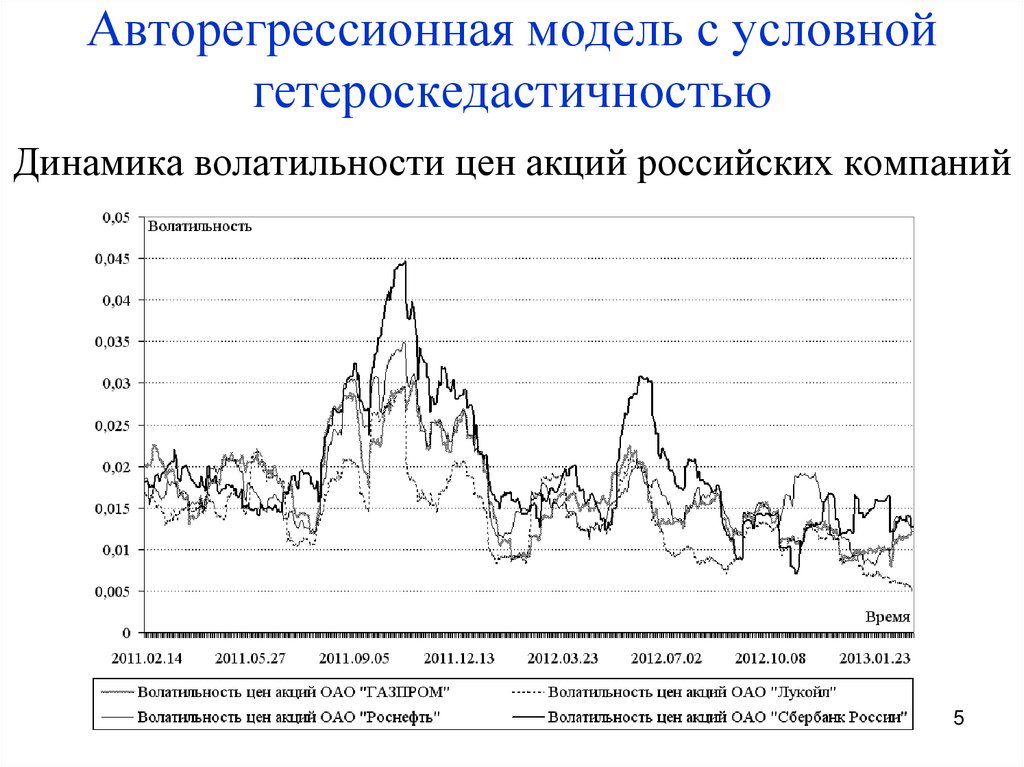
5. Авторегрессионная модель с условной гетероскедастичностью Динамика волатильности цен акций российских компаний

5

6. Авторегрессионная модель с условной гетероскедастичностью

Простейшей моделью является модель с авторегрессионной условной
гетероскедастичностью,
предложенная
Энглом
[http://wolfweb.unr.edu/~zal/STAT758/Engle82.pdf]. В этой модели безусловная
дисперсия M (u t2 ) var( u t ) является
постоянной, а условная дисперсия
M(u 2t I t 1 ) , где I t 1 - совокупность информации, известной на момент t-1,
включающей значения xt и лаговые значения yt и xt, то есть
I t 1 (x t , x t 1 ,..., y t 1 , y t 2 ,...) , изменяется во времени.
Обозначая условную дисперсию через h 2 t , в простейшем случае
модель АРСН (1) можно записать как
y t 1 2 x t u t
h 2t var( u t ) 0 1u 2t 1
,
(1)
где 1 >0.
Последнее уравнение означает следующее: если ошибка в предыдущий
момент была большой, то и дисперсия текущей ошибки будет увеличенной.
Если же 1 =0, то это означает, что эффекта АРСН не наблюдается, дисперсия
постоянна, т есть имеет место гомоскедастичность и можно применять
обычные методы оценивания, например МНК.
6

7. Авторегрессионная модель с условной гетероскедастичностью

Модель Энгла была расширена до включения большего числа лагов
остаточного члена. В этом общем случае спецификация модели АРСН(q)
имеет вид:
y t x t u t
(2)
q
h var( u t I t 1 ) 0 i u 2t i
2
t
i 1
то есть математическое
условной дисперсии равно безусловной дисперсии.
Безусловная дисперсия остатков постоянна и равна
М (h ) М (М (u t I t 1 )) М (ut2 ) ,
2
t
2
ожидание
q
M (h ) M ( 0 i ut2 i )
2
t
(3)
i 1
q
2 0 i 2
(4)
i 1
q
(1 i ) 0
2
(5)
i 1
M(u 2t ) var( u t )
0
q
1 i
>0,
(6)
i 1
так как дисперсия величина положительная.
7

8. Авторегрессионная модель с условной гетероскедастичностью

При применении ARCH-моделей к реальным данным было замечено,
что модель ARCH(1) не дает достаточно длительных кластеров волатильности,
а только порождает большое число выбросов. Для корректного описания
данных требуется довольно большая длина лага q, что создает трудности при
оценивании. В частности, зачастую нарушается условие неотрицательности
оценок коэффициентов i . Поэтому Р. Энгл наложил на коэффициенты лага
ограничение, состоящее в том, что они линейно убывают до нуля. Веса лага при
этом задаются соотношением
j
q 1 j
0,5q(q 1)
(7)
так чтобы их сумма равнялась 1, а коэффициенты берутся равными j j .
Получается следующая модель с двумя параметрами 0 и :
ht2 0 ( 1 ut2 1 ... q ut2 q ).
(8)
8

9. 2 Модификации ARCH Модель GARCH

В отличие от ARCH позволяет строить модели с меньшим числом
параметров. Модель GARCH(p,q) – обобщенная модель АРСН, введенная
Болерслевым является особым случаем модели ARCH(p,q), в уравнении
которой есть авторегрессия и скользящая средняя
q
h var( u t I t 1 ) 0 i u
2
t
i 1
p
2
t i
i h 2t i
(9)
i 1
Безусловная дисперсия остатков постоянна и равна
var( u t )
0
q
p
i 1
i 1
1 i i
(10)
9

10. 2 Модификации ARCH Недостатки модели GARCH

1. «левередж-эффект» (leverage effect). Будущие
значения волатильности отрицательно коррелируют с
текущей отдачей или можно сказать об отрицательной
корреляции между остатками в текущий момент и
условной дисперсией в последующий. Корреляция между
этими величинами, однако, игнорируется GARCH
моделью.
2. Применительно к процессам типа GARCH
различные определения стационарности не согласованы.
3. ограничения области допустимых значений
параметров модели и создают трудности при оценивании
GARCH модели
Данные недостатки учтены в экспоненциальной
модели.
10

11. 2 Модификации ARCH Модель GARCH-М

Обобщенная модель ARCH в среднем значении обозначается
GARCH(p,q)-М
Имеет следующую спецификацию
y t x t h 2t u t
(11)
где из выражения (9), то есть
q
h var( u t I t 1 ) 0 i u
2
t
i 1
p
2
t i
i h 2t i
(12)
i 1
Таким образом, среднее значение зависимой переменной уt в момент t
зависит от условной дисперсии остаточного члена ut, представляемой в свою
очередь, моделью АРСН. Необходимое условие ковариационной
состоятельности (4) состоит в том, чтобы
q
p
<1.
i 1
i
i 1
i
(13)
В дополнение к ограничениям (11) и (13) Болерслев предполагает
i 0, i 1,2,..., q i 0, i 1,2,..., p .
также,
что
Этих
дополнительных
ограничений достаточно для того, чтобы условная дисперсия была
положительной, но они не являются необходимыми.
11

12. 2 Модификации ARCH Модель АGARCH и AGARCH-M

Модель GARCH(p,q), в которой условная стандартная ошибка ut в
выражении y t x t u t определяется как
q
p
h t var( u t I t 1 ) 0 i u t i i h t i
i 1
(14)
i 1
Называется абсолютной GARCH и обозначается АGARCH(p,q).
Модель АGARCH(p,q)-М – модель АGARCH(p,q) в среднем значении и
специфицируется уравнениями (11-14).
Модель ЕGARCH(p,q) – это экспоненциальная модель
АGARCH(p,q), в которой логарифм условной дисперсии ошибки уравнения
y t x t u t имеет следующую спецификацию
q
q
p
u t i
u t i
*
ln h 0 i (
) i (
) i ln h 2t i
h t i
h t i
i 1
i 1
i 1
2
t
(15)
где
u
M t .
ht
(16)
Значение зависит от функции плотности вероятностей, которая по
предположению, описывает стандартизированные возмущения t
ut
. Эта
ht
модель, разработанная Нельсоном, допускает асимметричные воздействия
прошлых ошибок на условные дисперсии ошибок.
12

13. 3 Проверка ARCH- эффекта

Процедура предложена Энглом и состоит из следующих шагов:
1.
Строим модель регрессии для получения ряда остатков z t . В
случае, если на условную гетероскедастичность проверяется
одномерный временной ряд, то этот шаг опускается.
2.
МНК оцениваются параметры модели:
zt2 1 zt2 1 ... p zt2 p vt ,
(17)
где vt - остатки, удовлетворяющие свойствам белого шума.
3.
Проверяем гипотезу об адекватности модели:
H 0 1 ... p 0
H1 12 ... p2 0
с помощью обычного критерия Фишера-Снедекора.
Если Но отвергается, то делается вывод о наличии условной
гетероскедастичности, с длиной наибольшего лага p.
13

14. Задание на практическое занятие

Записать общий вид:
- квадратическая GARCH (QGARCH)
пороговая модель GARCH (Threshold
GARCH, TGARCH)
14

15. Аддитивные сезонные модели

Зачастую наблюдаемый временной ряд содержит сезонность. Для
стационарных рядов с сезонностью разработаны модели авторегрессии
скользящего среднего. Идея состоит в том, чтобы включать в модель
составляющие с соответствующими сезонности лагами.
Например, для помесячных данных сезонная модель авторегрессии 1го порядка САР(1) (SAR(1)):
t k t k t ,
(18)
или с использованием оператора сдвига
1 L , 1
k
k
t
t
k
(19)
где k – период сезонности (k=12 для помесячных данных и 4 для
квартальных данных).
15

16. Аддитивные сезонные модели

Соответственно модель сезонного скользящего среднего
порядка ССС(1) (или SMA(1)):
t t k t k ,
или
t 1 k Lk t , k 1
Сезонные АР и СС модели порядков pk и qk имеют вид:
t k t k 2k t 2 k ... pk t p k t ,
или
1 L L ... L
k
k p
k 2
k
pk
2k
t
t
1-го
(20)
(21)
(22)
(23)
и
t t k t k 2k t 2 k ... qk t qk ,
t 1 k Lk 2k Lk ... qk Lk t
2
qk
(24)
(25)
16

17. Аддитивные сезонные модели

Представленные
модели
являются
несезонных и сезонных изменений
аддитивными.
Комбинации
в рамках аддитивных моделей
реализуются следующим образом:
САРСС(1, 1)(1,0):
t 1 t 1 k t k t 1 t 1
(26)
общий вид САРСС(p,q)( pk,qk):
t 1 t 1 ... p t p k t k ... pk t pk
t 1 t 1 ... q t q k t k ... qk t qk
.
(27)
17

18. Мультипликативные сезонные модели

При построении моделей типа АРСС одним из критериев их
качества является минимум параметров (принцип «экономности»). Это
способствует повышению устойчивости модели, а часто ведет и к
уменьшению ошибки прогноза. Поэтому плодотворной оказалась идея
уменьшения числа параметров модели, описывающей процессы с
сезонными колебаниями, путем учета взаимосвязей не только между
соседними значениями процесса, но и между его значениями,
разделенными периодом колебания.
Реализация этой идеи также показала возможность рассмотрения
моделей с сезонными колебаниями как специфической подгруппы
моделей
АРСС.
Модели
данной
подгруппы
называют
мультипликативными.
18

19. Мультипликативные сезонные модели

Если временной ряд характеризуется сезонной составляющей с
периодом k, то в таком ряду обычно выделяют два различных типа
взаимосвязей между переменными – текущую и сезонную. Текущая
взаимосвязь, как и ранее, характерна для соседних значений временного
ряда yt и yt–1, yt–2,...,
сезонная – для значений, разделенных периодом
колебаний yt и yt–k.
В мультипликативных моделях, в отличие от аддитивных,
допускается взаимодействие составляющих АР или СС на лагах, например,
t-1 и t-k. Для этого берется сезонная разность: t t k 1 Lk t k t и в
предположении стационарности разности s y t к ней подбирается модель из
класса АРСС(p,q). Например,
k t 1k k t 1 t ,
(28)
или
1 1k L 1 Lk t t .
(29)
Идентификация и оценивание параметры сезонных моделей
осуществляется также как и в обычных моделях АР, СС и АРСС.
19

20. Задание на практическое занятие

Записать
общий
вид
моделей
САРСС((1,1)(0,1), САРСС(p,0)( 0,qk)
20

21. Литература к лекции

Engle, R. Autoregressive conditional heteroscedasticity with estimates of
variance of United Kingdom inflation // Econometrica. – 1982. – № 50.
– P. 987-1008.
Шепард Н. Статистические аспекты моделей типа ARCH и
стохастическая волатиль- ность / Н. Шепард // Обозрение
прикладной и промышленной математики. – 1996. – Т. 3, вып. 6. –
С. 764–826.
Канторович, Г. Г. Анализ временных рядов// Экономический
журнал ВШЭ– 2002 г. – №1, с.85-116.
Эдуардо Росси Эконометрический ликбез:волатильность / Э.Росси
// Квантиль. – 2010. - №8. – С. 1-67.
Лукашин, Ю. П. Адаптивные методы краткосрочного
прогнозирования временных рядов [Текст] : учеб. пособие для
вузов / Ю. П. Лукашин. - М. : Финансы и статистика, 2003. - 416 с.
21