Согласованный фильтр

1. СОГЛАСОВАННЫЙ ФИЛЬТР

2. СХЕМЫ КОРРЕЛЯТОРА И СФ (предыдущая лекция)

СФ

3. СФ КАК КОРРЕЛЯТОР

1.Отношение сигнал/шум на выходе СФ при t=t0 равно
отношению сигнал/шум на выходе коррелятора с опорным
сигналом, равным sвх (t )
2.Сигналы на выходе СФ и коррелятора не совпадают по
форме

4. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СИГНАЛА НА ВЫХОДЕ СФ

ПРВ сечения СП:
w( yвых ; t0 )
Yвых (t0 ) sвых (t0 ) Nвых (t0 )
СФ является НЧ фильтром, в котором происходит нормализация
белого шума, т.е. ПРВ СП на выходе СФ является гауссовской
Если на входе СФ действуют сигнал и шум (H1)
МО СП( t=to):
(t0 ) M [Yвых (t0 )] M [sвых (t0 ) Nвых (t0 )]
вых
my
M [sвых (t0 )] M [ Nвых (t0 )] sвых (t0 ) BEsвх
Дисперсия СП:
N0 2
B Es
Dy (t0 ) D[Yвых (t0 )] D[sвых (t0 ) Nвых (t0 )] Dn
вх
вых
вых 2

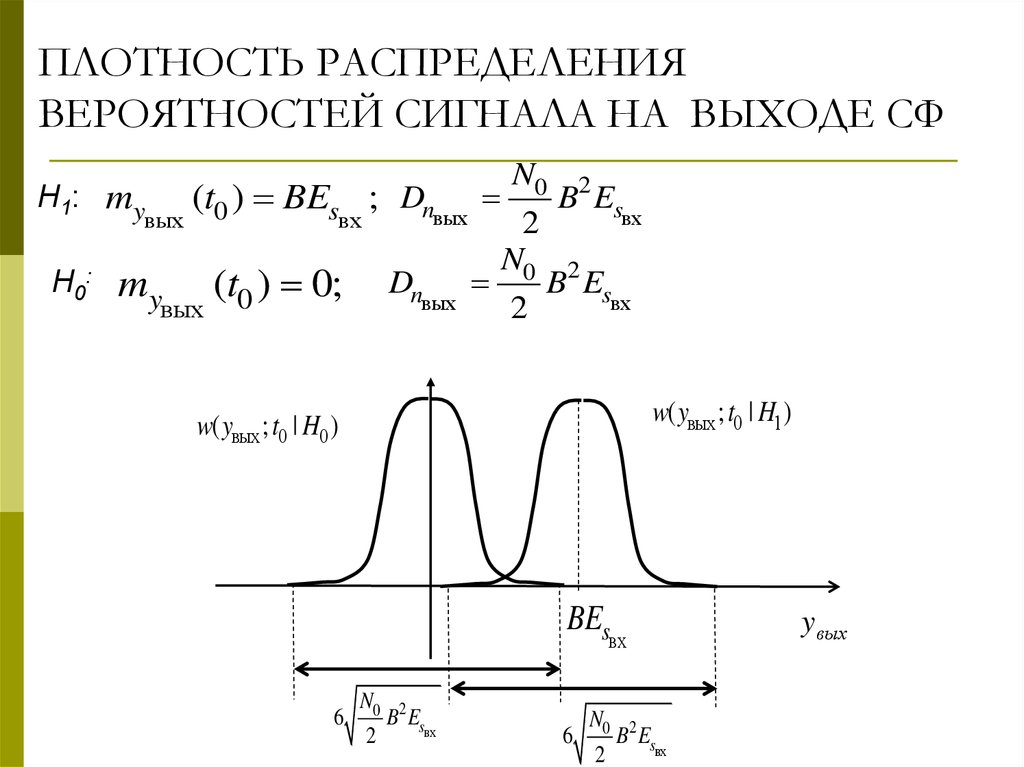
5. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СИГНАЛА НА ВЫХОДЕ СФ

N0 2
H1: my (t0 ) BEs ; Dn
B Es
вых
вх
вых
вх
2
N0 2
:
H0 m
Dn
B Es
yвых (t0 ) 0;
вых
вх
2
w( yвых ; t0 | H1)
w( yвых ; t0 | H0 )
BEs
вх
6
N0 2
B Es
вх
2
6
N0 2
B Es
вх
2
yвых

6. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

7. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

СПМ аддитивного шума
Nвх (t ) :
Gn ( f ) const
вх
Наблюдаемый сигнал:
Yвх (t ) sвх (t ) Nвх (t )
«Выбеливающий» линейный фильтр преобразует окрашенный
шум NВХ(t) в белый шум N1(t)
N0
Gn ( f )
1
2

8. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

Реакция «выбеливающего» фильтра:
Y1 (t ) Lвф [Y (t )] s1 (t ) N1 (t )
s1 (t ) sвх (t )
s1 (t )
sвх (t )
Nвх (t )
СФ для
s1(t)
Выб.
фильтр
N1 (t )
СФ для
sвх (t)

9. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

КЧХ фильтра, согласованного с s1(t)
Hcф1 ( f ) BS1* ( f )exp( j 2 ft1 )
S1 ( f ) F{s1 (t )}
t1
–длительность сигнала
s1 (t )
АЧХ «выбеливающего» фильтра должна удовлетворять условию:
2
Cвф
(f
N0
)Gn ( f )
вх
2
Свф ( f )
N0
2Gn ( f )
вх

10. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

Пример. Найти KЧХ фильтра, преобразующего в белый шум СП с
СПМ
Gnвх ( f )
2
2 4 2 f 2
2
2 2
N
N
(
4
f )
2
0
0
Свф ( f )
2Gn ( f )
2 2
вх
H вф ( f )
N0
( j 2 f )
4

11. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

Спектральная плотность сигнала на выходе «выбеливающего»
фильтра:
S1 ( f ) Hвф ( f )Sвх ( f )
КЧХ фильтра, согласованного с s1(t) (шум - белый)
Нсф1 ( f ) BS1* ( f ) exp( j 2 ft1 )
*
*
BHвф
( f ) Sвх
( f ) exp( j 2 ft1 )
КЧХ фильтра, согласованного с sвх(t) ) (шум - небелый)
2
*
BС
(
f
)
S
Hсф ( f ) Hвф ( f ) Hсф1 ( f )
вф
вх ( f )exp( j 2 ft1 )

12. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ПРИ НЕБЕЛОМ ШУМЕ

Вывод: КЧХ СФ не зависит от ФЧХ выбеливающего фильтра
N0
*
Hсф ( f ) B
Sвх
( f )exp( j 2 ft1 )
2Gn ( f )
вх
2
Свф
(f)
Отношение сигнал/шум:
2
qсф
2 Es
1
N0
Es
1
| Hвф ( f ) Sвх ( f ) |2 df

13. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ

Критерий: минимум среднего
квадрата ошибки

14. НОРБЕРТ ВИНЕР (1894−1964)

Американский учёный, выдающийся математик
и философ, основоположник кибернетики и
теории искусственного интеллекта.
Во время второй мировой войны перед
американским математиком Н. Винером встала
задача отделения полезного сигнала от шума
при решении задач автоматизации систем ПВО,
использующих радиолокационную технику.
В 1942 г. Н. Винер решил эту задачу, допустив что искомая система
должна быть линейной с постоянными параметрами, время
наблюдения бесконечно, входной и желаемый выходной сигналы
системы являются стационарными и стационарно связанными
случайными процессами, система минимизирует средний квадрат
ошибки между желаемым и реальным выходными сигналами.
В 1942-м году сотрудник Винера Джулиан Бигелоу (Julian Bigelow)
построил прототип прибора, позволявшего следить за самолетом в
течение десяти секунд и предсказывать затем его местонахождение
двадцатью секундами позже

15. РУДОЛЬФ ЭМИЛЬ КАЛМАН (RUDOLPH EMIL KALMAN) (19.05.1930)

Фильтра Калмана (конец 1958-го — начало
1959) - эффективный рекурсивный фильтр.
Когда Калман придумал свой фильтр, то
встретился с таким скептицизмом, что был
вынужден опубликовать первые работы о
нем в журнале, связанном с механикой,
хотя сам занимался электротехникой.
Основываясь на предшествующих работах Винера, Колмогорова,
Шеннона и др. Калман разработал технику оценки вектора состояния
системы управления с использованием неполных и неточных
(зашумленных) измерений, используемую в частности, в системах
навигации.
Широко используется в инженерных и эконометрических
приложениях: от радаров и систем технического зрения до оценок
параметров макроэкономических моделей

16. ФИЛЬТР ВИНЕРА

17. ФИЛЬТР ВИНЕРА

1. Априорная информация
Наблюдаемый сигнал:
X(t)
Y (t ) [ X (t ), N (t )], t
N(t)
Канал
Xˆ (t )
Пр. У
X(t) и N(t) стационарно связанные (необязательно
гауссовские) СП с нулевыми математическими ожиданиями.
Ky( ) и Kxy( ) - полагаются известными.

18. ФИЛЬТР ВИНЕРА

2. Критерий оптимальности: минимум
среднеквадратической ошибки оценивания
M [ 2 (t )] M [( X (t ) X (t ))2 ] min
3. Ограничения на синтез ОС: линейный фильтр с
постоянными параметрами
HВ ( f ) CВ ( f )exp( j В ( f ))
hВ ( )

19.

СИНТЕЗ НЕКАУЗАЛЬНОГО
СТАЦИОНАРНОГО ЛФ
X (t )
hВ ( )
hВ ( )Y (t )d
- ИХ, минимизирующая СКО
h( ) hВ ( ) h ( )
- произвольная ИХ ЛС
2
2
M [ (t )] M ( X (t ) (hВ ( ) h ( ))Y (t )d )
2
M ( X (t ) hВ ( )Y (t )d )
M [ 2 (t )] min
M [ 2 (t )]
0
0

20.

СИНТЕЗ НЕКАУЗАЛЬНОГО
СТАЦИОНАРНОГО ЛФ
K xy ( )
hВ ( 1 ) K y ( 1 )d 1
Gxy ( f ) F{Kxy ( )};
Gxy ( f ) HВ ( f )Gy ( f )
hВ ( ) K y ( )
F{hВ ( ) K y ( )} HВ ( f )Gy ( f )
HВ ( f )
Gxy ( f )
Gy ( f )

21. АНАЛИЗ ФИЛЬТРА ВИНЕРА

M [ (t ) ] M [( X (t ) X (t )) ]
2
Dx
2
Gx ( f )df ;
Dx
Gx ( f )df
M [ 2 (t )]min Dx Dx
M [ (t )]min Dx Dx
2
Gy ( f ) | H В ( f ) |2 df
(Gx ( f ) Gy ( f ) | H В ( f ) |2 )df
HВ ( f )
M [ 2 (t )]min
| Gxy ( f ) |2
df
Gx ( f )
Gy ( f )
Gxy ( f )
Gy ( f )

22.

ВЫВОДЫ
Для отыскания оптимальной линейной оценки
необходимо знать только Ky(t) и Kxy(t) (или
Gy(f) и Gxy(f) ).
Для вычисления минимальной
среднеквадратической ошибки также необходимо
знать эти характеристики и Gx(f).
Любые другие статистические характеристики
сигнала и помехи оказываются бесполезными.

23.

ВЫВОДЫ
Для всех гауссовских и негауссовских
процессов, имеющих одинаковые Ky(t), Kx(t) и
Kxy(t) , оптимальный линейный фильтр является
одинаковым и обладает одинаковой
среднеквадратической ошибкой.
Если сообщение , помеха и наблюдаемый
сигнал являются совместно гауссовскими
стационарно связанными СП, то фильтр Винера
является абсолютно оптимальным

24. ФИЛЬТР ВИНЕРА ДЛЯ СИГНАЛА, НЕКОРРЕЛИРОВАННОГО С АДДИТИВНОЙ ПОМЕХОЙ

Оцениваемый процесс X(t) и шум N(t) являются
некоррелированными СП с нулевыми МО и Y (t ) X (t ) N (t )
N(t)
X(t)
+
Y(t)
Xˆ (t )
Пр. У
K y ( ) K x ( ) K ( )
Gy ( f ) Gx ( f ) G ( f )
K xy ( ) M [ X (t )Y (t )]
M [ X (t )( X (t ) N (t ))] Kx ( )
Gxy ( f ) Gx ( f )

25. ФИЛЬТР ВИНЕРА ДЛЯ СИГНАЛА, НЕКОРРЕЛИРОВАННОГО С АДДИТИВНОЙ ПОМЕХОЙ

HВ ( f )
Gyx ( f )
M [ 2 (t )]min
Gx ( f )
HВ ( f )
Gx ( f ) G ( f )
Gy ( f )
| Gyx ( f ) |2
df
Gx ( f )
Gy ( f )
M [ (t )]min
2
Gx ( f )G ( f )
Gx ( f ) G ( f )
df

26. ВЫВОДЫ

1. Поскольку СПМ являются вещественными и четными
функциями, то
- КЧХ фильтра Винера также является вещественной и
четной:
H В ( f ) CВ ( f );
- ФЧХ фильтра Винера тождественно равна нулю на
всех частотах:
( f ) 0.
Фильтр Винера не вносит фазовых искажений в
наблюдаемый сигнал и тем самым максимально сохраняет
форму оцениваемого сигнала.

27.

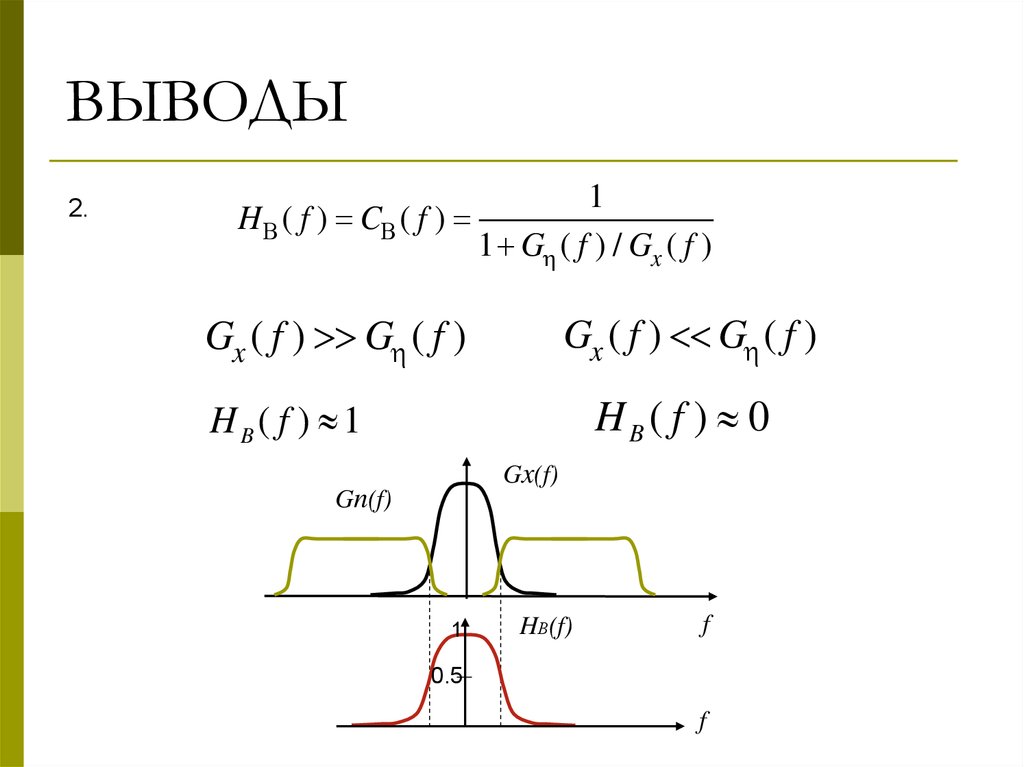
ВЫВОДЫ
2.
1
H В ( f ) CВ ( f )
1 G ( f ) / Gx ( f )
Gx ( f ) G ( f )
Gx ( f ) G ( f )
HB( f ) 0
HB( f ) 1
Gx(f)
Gn(f)
1
HВ(f)
f
0.5
f

28.

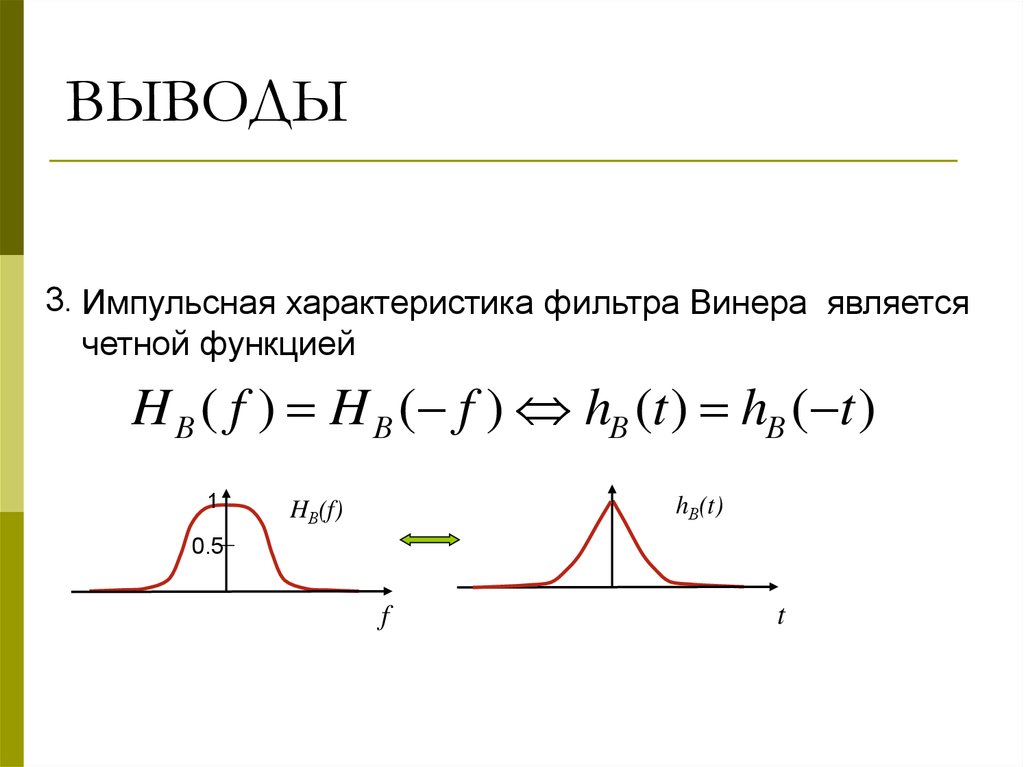
ВЫВОДЫ
3. Импульсная характеристика фильтра Винера является
четной функцией
H В ( f ) H В ( f ) hВ (t ) hВ ( t )
1
hВ(t)
HВ(f)
0.5
f
t

29.

ВЫВОДЫ
4. Величина среднеквадратической ошибки не превышает
дисперсии шума:
M [ (t )2 ]min
1 G
G ( f )
( f
X (t ) Y (t ) X (t ) N (t )
) / Gx ( f )
df
G ( f )df D
M [ (t ) ]min Dn
2
Использование фильтра Винера не может привести к
увеличению среднеквадратической ошибки

30.

ВЫВОДЫ
5.
M [ (t )]min 0
2
- при отсутствии шума;
- СПМ сигнала и помехи не перекрываются на всех
частотах.
Gx ( f )Gn ( f ) 0
G ( f )G ( f )
x
M [ 2 (t )]min
df
G ( f ) G ( f )
x
Gn(f)
Gx(f)
1 при Gx ( f ) 0,
HВ ( f )
0 при Gx ( f ) 0.
1
HВ(f)
f
f

31.

ВЫВОДЫ
6. Если СПМ сообщения и помехи перекрываются,
например, при f1<f<f2 , то СКО фильтрации не равна
нулю.
Ошибка фильтрации возникает как от пропускания помехи
в частотном диапазоне f1<f<f2 , так и от ослабления
сигнала в этом же частотном диапазоне.
Чем выше уровень СПМ помехи в диапазоне перекрытия,
тем сильнее искажение информационного сигнала.