Статистические характеристики шума на выходе БВЧ. Квазигармоническое колебание. Белый шум

1.

10.1. Статистические характеристики
шума на выходе БВЧ
Квазигармоническое
колебание
Белый шум
БВЧ
АЧХ БВЧ
f0
w(u )
Плотность вероятности напряжения шума
"правило 3-х -м"
(нормальное распределение)
w u =
1
U ш 2
e
P u 3U ш , 3U ш 0,997
u2
2U ш2
3U ш
u
0
3U ш
1

2.

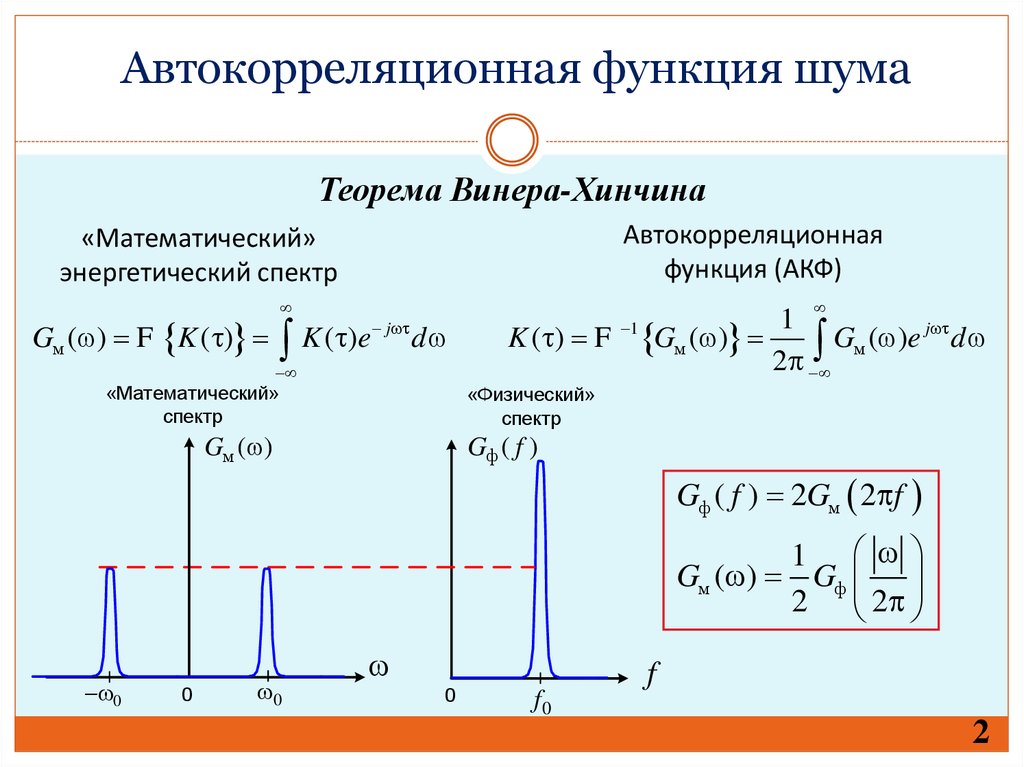
Автокорреляционная функция шума
Теорема Винера-Хинчина
Автокорреляционная
функция (АКФ)
«Математический»
энергетический спектр
Gм ( ) F K ( )
K ( )e
j
d
K ( ) F
«Математический»
спектр
1
1
Gм ( ) Gм ( )e j d
2
«Физический»
спектр
Gм ( )
Gф ( f )
Gф ( f ) 2Gм 2 f
1
Gм ( ) Gф
2 2
0
0
0
0
f0
f
2

3.

Автокорреляционная функция шума
1
1
j
K ( )
G
(
)
e
d
2
Gм ( )cos d Gф ( f )cos 2 f df
м
2
2 0
0
Приближённое выражение при симметричной АЧХ БВЧ
АЧХ БВЧ: K ( f ) K 0 ( f )
Энергетический Gф ( f ) G0 K 02 2 ( f )
спектр:
0
f0
K ( ) G0 K 02 2 f cos 2 f df G0 K 02
2НЧ F cos 2 f 0 2 F dF
2
2
2
G0 K 0 НЧ F cos 2 F dF cos 2 f 0 НЧ F sin 2 F dF sin 2 f 0
2
2
2G0 K 0 НЧ ( F )cos 2 F dF cos 2 f 0
0
3

4.

Автокорреляционная функция шума
K ( ) U ш2 ( )cos 2 f 0
U ш2 K (0) G0 K02 ш дисперсия шума на выходе БВЧ
2
2
( )
НЧ F cos 2 F dF огибающая нормированной АКФ
Пш 0
U
( )
K ( )
2
ш
( )
1
0
0
4

5.

10.2. Воздействие сигнала и шума
на линейный АД
Статистические характеристики
низкочастотных квадратурных составляющих шума
Шум - квазигармоническое колебание:
u (t ) U (t )cos 0t (t )
U (t )cos (t ) cos 0t U (t )sin (t ) sin 0t U шc (t ) cos 0t U шs (t ) sin 0t
Свойства квадратурных составляющих шума:
1) U шs (t ), U шc (t ) нормальные случайные процессы с нулевым математическим ожиданием:
U шs (t ) U шc (t ) 0
2
2
2) Дисперсия U шs (t ) U шc (t ) U ш2
3) АКФ KU с ( ) KU s ( ) U ш2 ( ) K ( ) KU c ( )cos 0 KU s ( )cos 0
ш
ш
ш
ш
4) В совпадающие моменты времени U шс (t )U шs (t ) 0
5) Огибающая U (t )
U
с
ш
(t ) U шs (t )
2
2
5

6.

Статистические характеристики
огибающей шума на выходе БВЧ
Распределение Релея w(U )
Мода: U mod U ш
Среднее значение: U
U
e
2
Uш
U2
2
2U ш
w(U )
, U 0
U ш 1,25U ш U mod
2
U
0
U mod
4 2
4
U ш 0,43U ш2
СКО: U
U ш 0,66U ш
2
2
АКФ: KU ( ) U (t ) U (t ) U (t ) U (t ) U2 U ( )
Нормированная огибающая АКФ:
Дисперсия: U2
2
2
2
1 2
1 4
1 3 6
U ( )
( )
( )
( )
4 2
2
4
2
4
6
0,915 2 ( ) 0,057 4 ( ) 0,014 6 ( )
2 ( )
6

7.

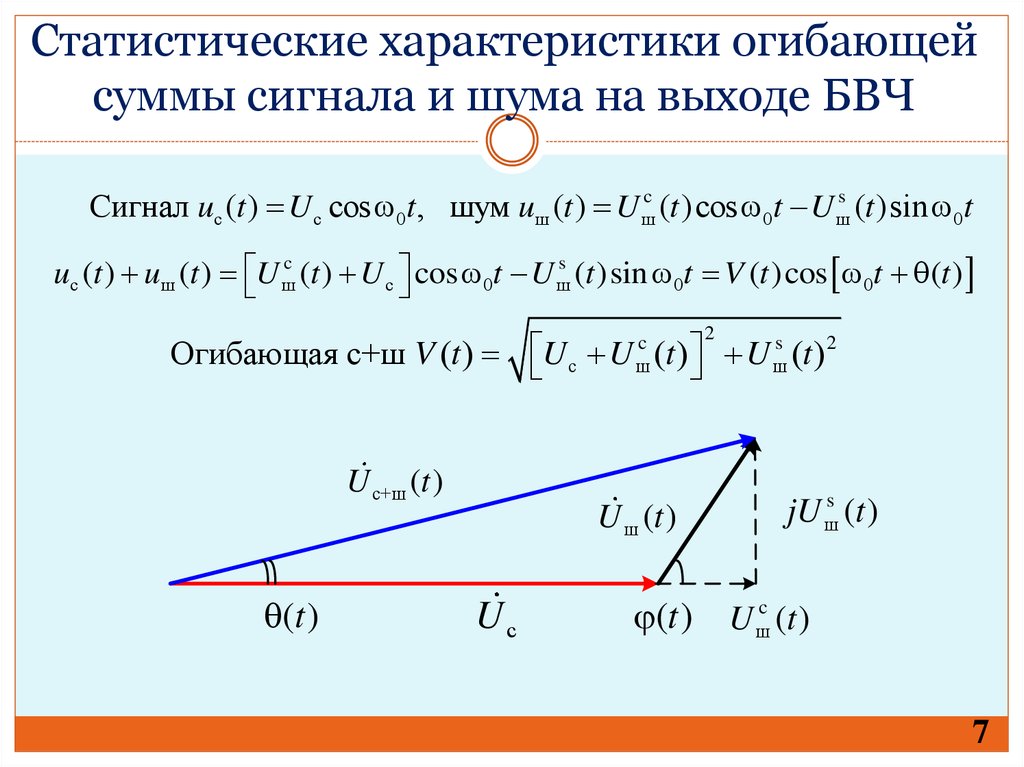
Статистические характеристики огибающей
суммы сигнала и шума на выходе БВЧ
Сигнал uс (t ) U с cos 0t , шум uш (t ) U шc (t )cos 0t U шs (t )sin 0t
uс (t ) uш (t ) U шc (t ) U с cos 0t U шs (t )sin 0t V (t )cos 0t (t )
2
Огибающая с+ш V (t ) U с U (t ) U шs (t ) 2
c
ш
U с+ш (t )
U ш (t )
(t )
Uс
jU шs (t )
(t ) U шc (t )
7

8.

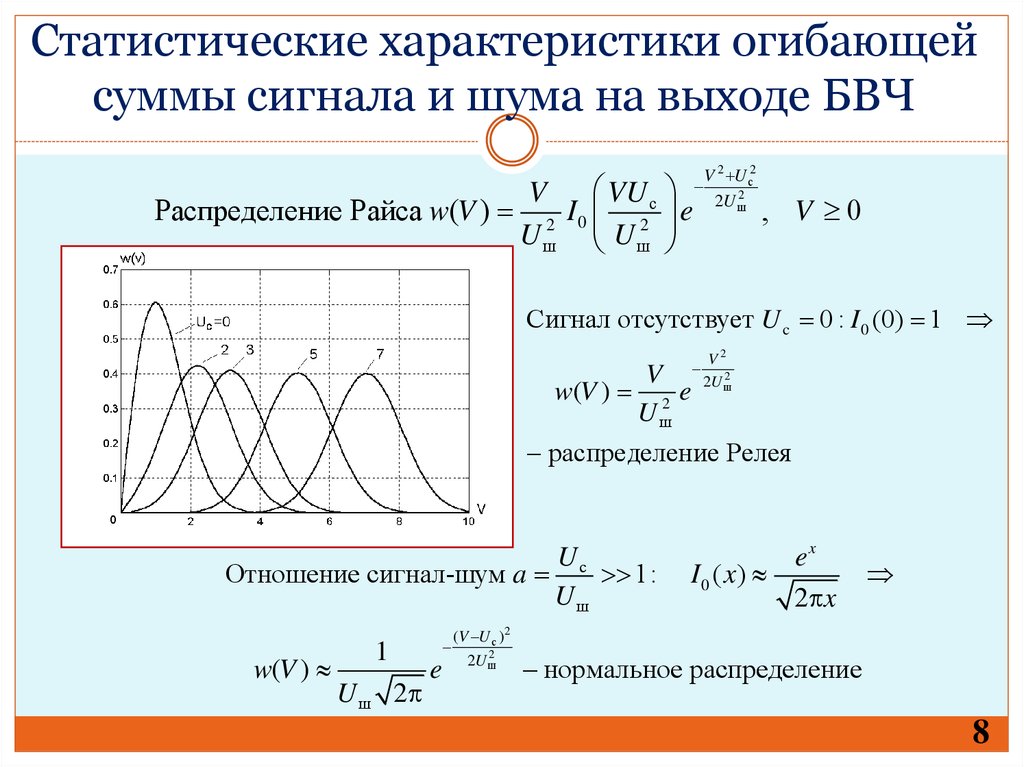
Статистические характеристики огибающей
суммы сигнала и шума на выходе БВЧ
Распределение Райса w(V )
VU с
V
I
e
2 0
2
Uш Uш
V 2 U с2
2U ш2
, V 0
Сигнал отсутствует U c 0 : I 0 (0) 1
w(V )
V
e
U ш2
V2
2U ш2
распределение Релея
U
Отношение сигнал-шум a с 1:
Uш
w(V )
1
U ш 2
e
(V U с )2
2U ш2
I 0 ( x)
ex
2 x
нормальное распределение
8

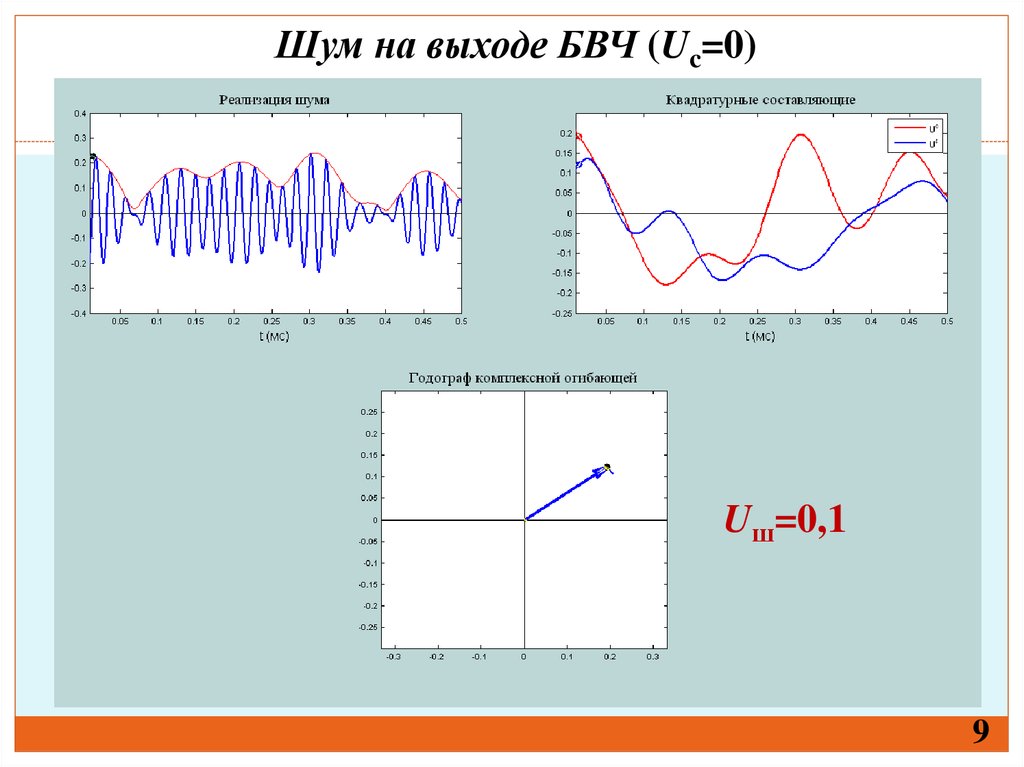
9.

Шум на выходе БВЧ (Uc=0)
Uш=0,1
9

10.

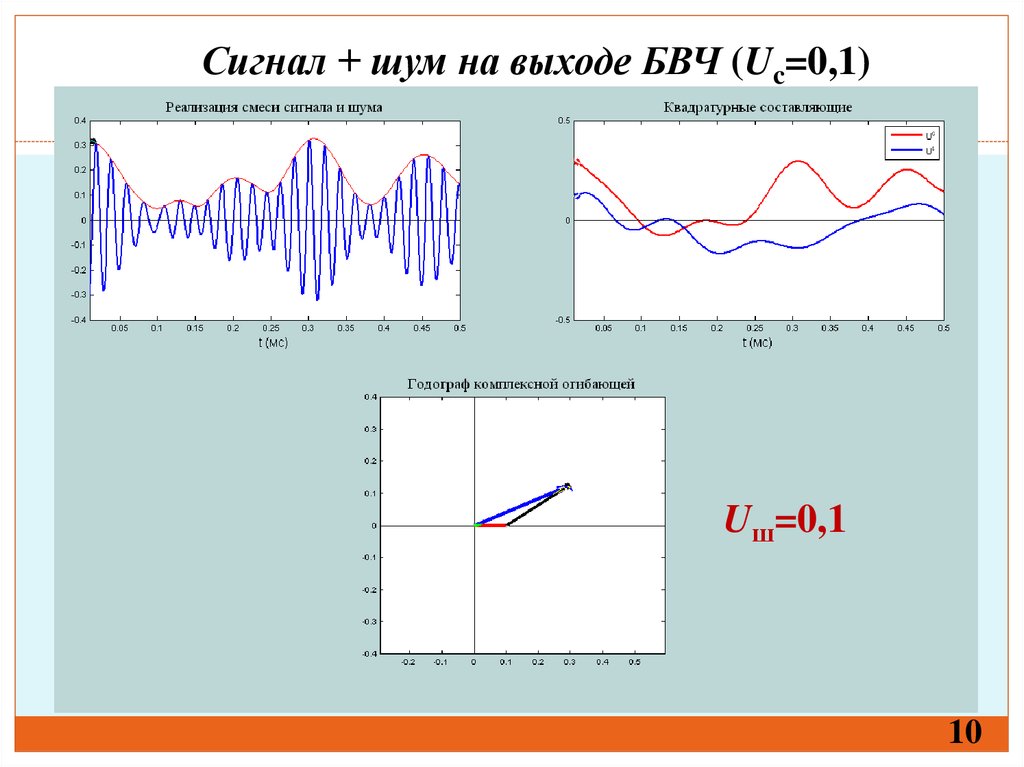
Сигнал + шум на выходе БВЧ (Uc=0,1)
Uш=0,1
10

11.

Сигнал + шум на выходе БВЧ (Uc=0,2)
Uш=0,1
11

12.

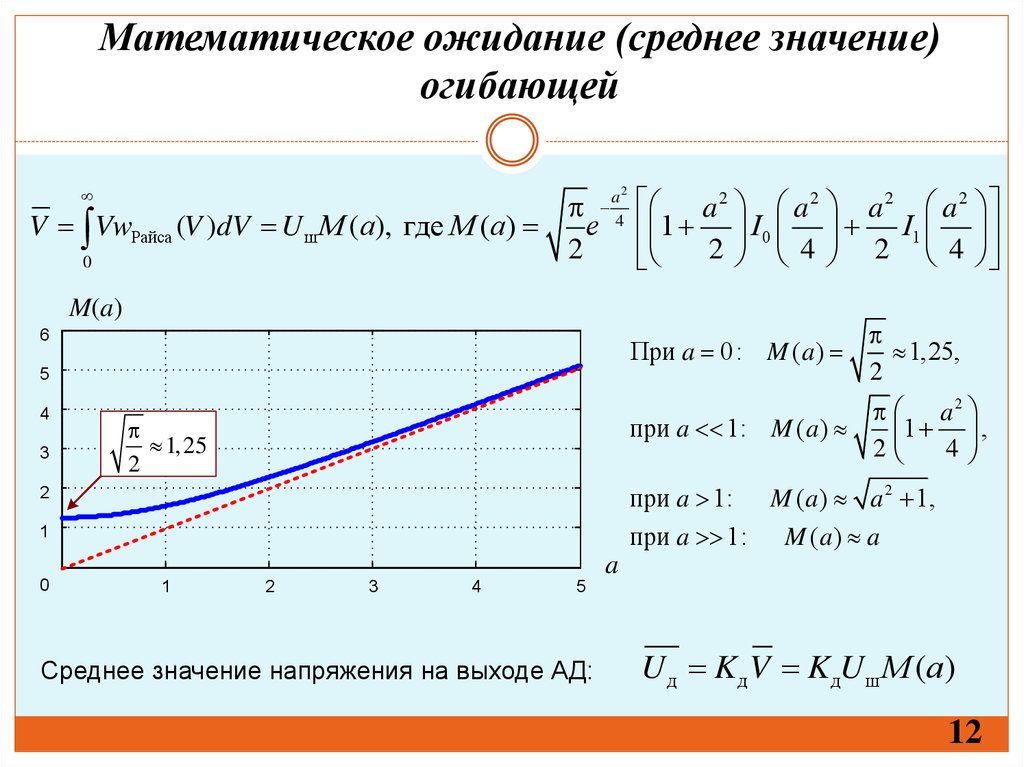
Математическое ожидание (среднее значение)
огибающей
V VwРайса (V )dV U ш М (a), где M (a)
e
2
0
a2
4
a 2 a 2 a 2 a 2
1 I 0 I1
2 4 2 4
M(a)
6
При a 0 : M (a)
5
4
3
a2
при a 1: M (a )
1 ,
2
4
1,25
2
2
при a 1:
1
при a 1:
0
1,25,
2
M (a ) a 2 1,
M (a) a
a
1
2
3
4
5
Среднее значение напряжения на выходе АД:
U д Kд V KдU ш М (a)
12

13.

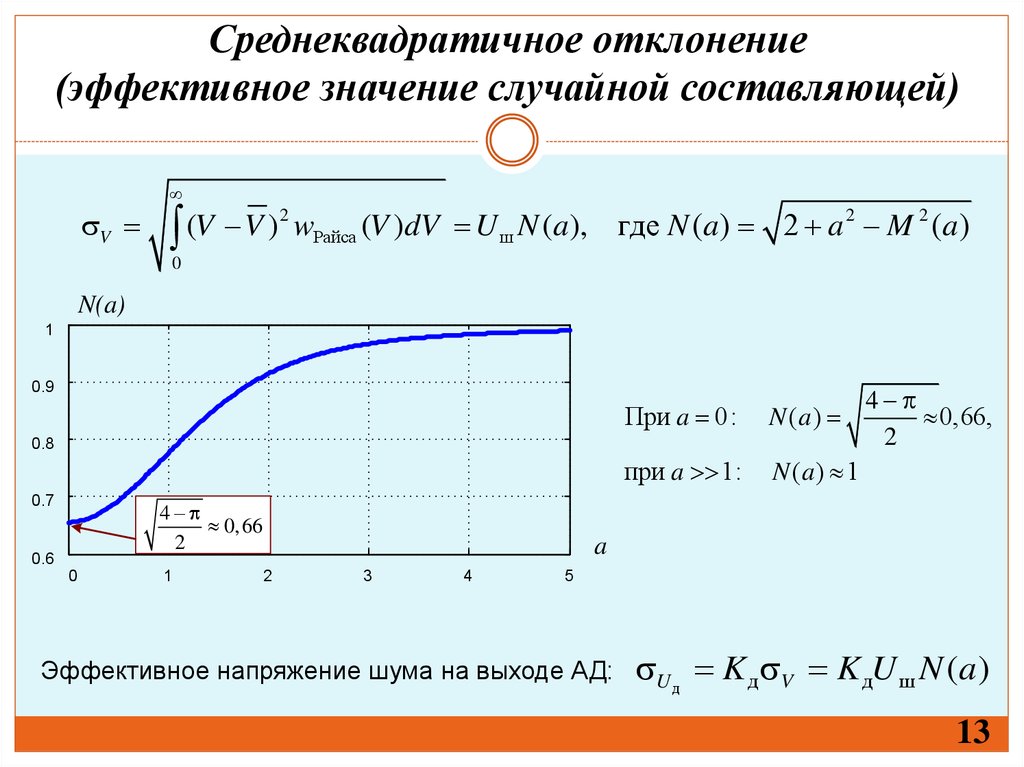
Среднеквадратичное отклонение
(эффективное значение случайной составляющей)
V
2
2
2
(
V
V
)
w
(
V
)
dV
U
N
(
a
),
где
N
(
a
)
2
a
M
(a )
Райса
ш
0
N(a)
1
0.9
При a 0 :
N (a)
при a 1:
N (a) 1
0.8
0.7
4
0,66
2
0.6
0
1
4
0,66,
2
a
2
3
4
5
Эффективное напряжение шума на выходе АД:
U д K д V K дU ш N (a )
13

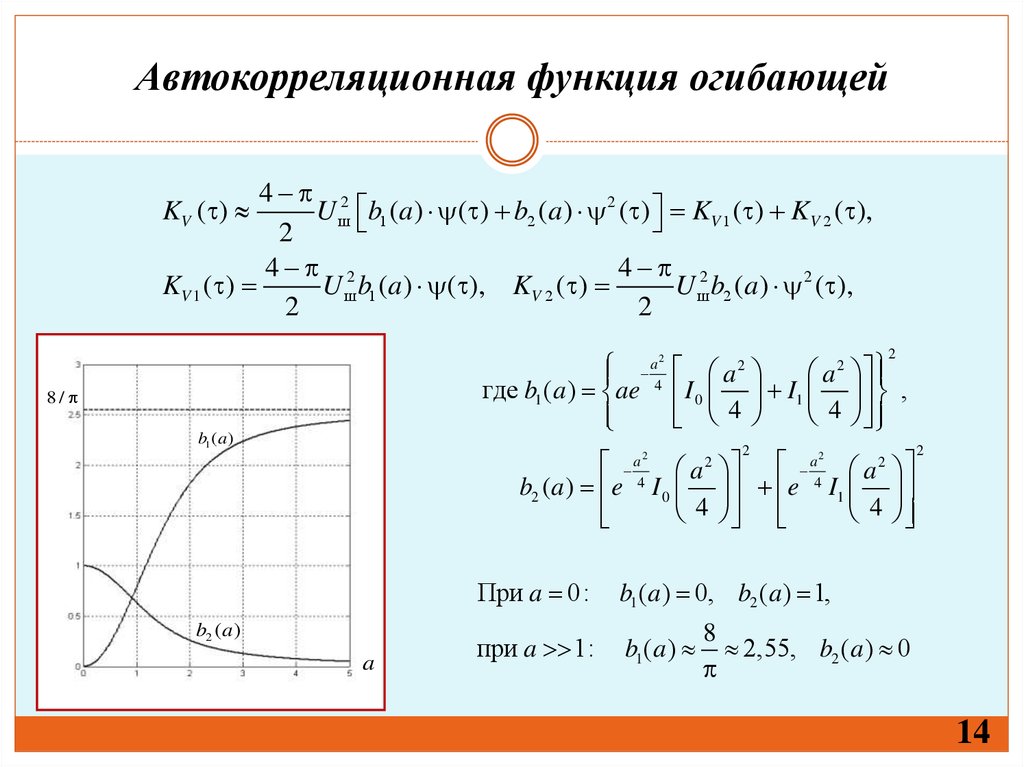
14.

Автокорреляционная функция огибающей
4 2
U ш b1 (a ) ( ) b2 (a ) 2 ( ) KV 1 ( ) KV 2 ( ),
2
4 2
4 2
KV 1 ( )
U ш b1 (a ) ( ), KV 2 ( )
U ш b2 (a) 2 ( ),
2
2
KV ( )
2
a a 2
a 2
4
где b1 (a ) ae I 0 I1 ,
4
4
2
8/
b1 (a )
2
a a2 a a2
b2 (a ) e 4 I 0 e 4 I1
4
4
2
b2 (a )
a
2
При a 0 :
b1 (a) 0, b2 (a) 1,
при a 1:
b1 (a)
2
8
2,55, b2 (a) 0
14

15.

Энергетический спектр огибающей
«Математический» спектр огибающей:
GVм ( ) F KV ( ) F KV 1 ( ) F KV 2 ( ) GV 1м ( ) GV 2м ( )
4
4
4
GV 1м ( ) F
b1 (a) U ш2 ( )
b1 (a)F KU с ( )
b1 (a)GU с м ( )
ш
ш
2
2
2
K с ( )
Uш
4
4
GV 2м ( ) F
b2 (a) U ш2 2 ( )
b2 (a)F KU с ( ) KU с ( )
2
ш
ш
2U ш
2
2
1
K с ( )
2
U ш Uш
4
b2 (a) GU с м ( ) GU с м ( )
2
ш
ш
2U ш
«Физический» спектр огибающей: GV ( f ) 2GVм 2 f GV 1 ( f ) GV 2 ( f )
15

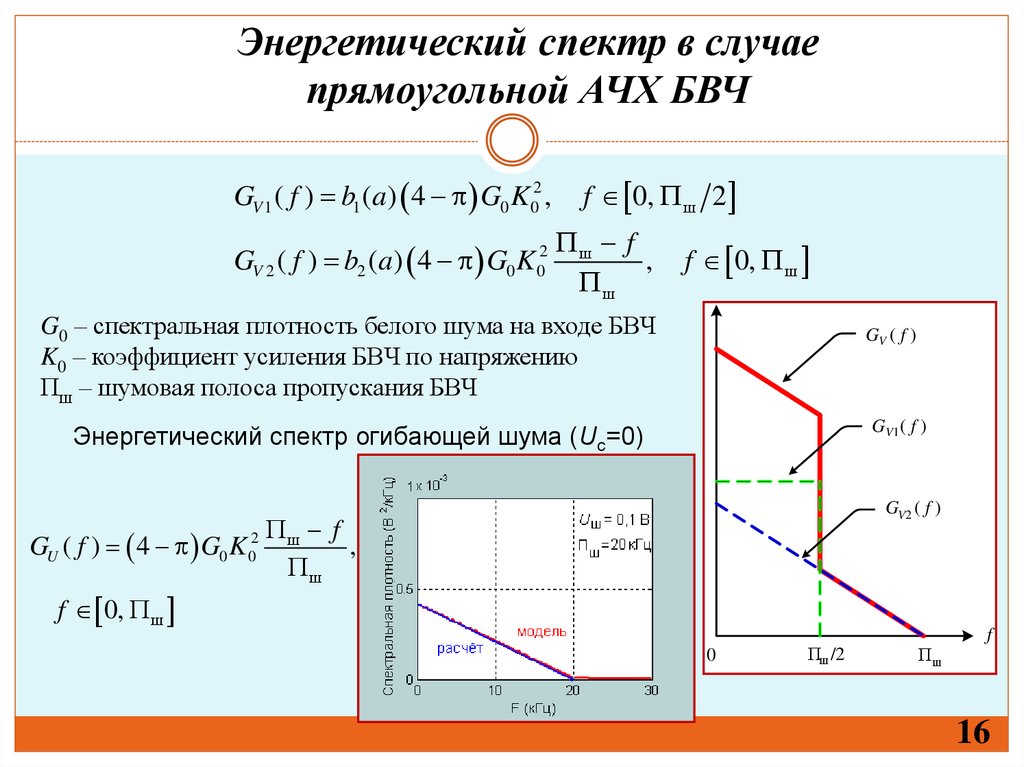
16.

Энергетический спектр в случае
прямоугольной АЧХ БВЧ
GV 1 ( f ) b1 (a) 4 G0 K 02 ,
GV 2 ( f ) b2 (a) 4 G0 K 02
f 0, ш 2
ш f
,
ш
f 0, ш
G0 – спектральная плотность белого шума на входе БВЧ
K0 – коэффициент усиления БВЧ по напряжению
Пш – шумовая полоса пропускания БВЧ
GV ( f )
GV1( f )
Энергетический спектр огибающей шума (Uс=0)
GU ( f ) 4 G0 K 02
f 0, ш
GV2 ( f )
ш f
,
ш
0
Пш /2
Пш
f
16

17.

Отношение сигнал-шум на выходе
линейного АД
Сигнал на выходе АД – приращение постоянной составляющей
выходного напряжения, обусловленное модуляцией сигнала.
Шум – случайная составляющая выходного напряжения.
U д
Детекторная характеристика при наличии шума – зависимость
Условия расчёт отношения сигнал-шум на выходе АД:
U д K д V U
K д M a U ш
Uш
2
U д
1) на входе АД: АМ сигнал с коэфф. модуляции m;
Pнесущей
q
2) отношение сигнал-шум на входе АД: вх
Pшума.вх
P1-й гарм.
q
3) отношение сигнал-шум на выходе АД: вых
Pшума.вых
a 1: qвых m 2
0
U д U с
Uс
qвх2 1,8m 2 qвх2
2 4
a 1: qвых m 2 qвх
17

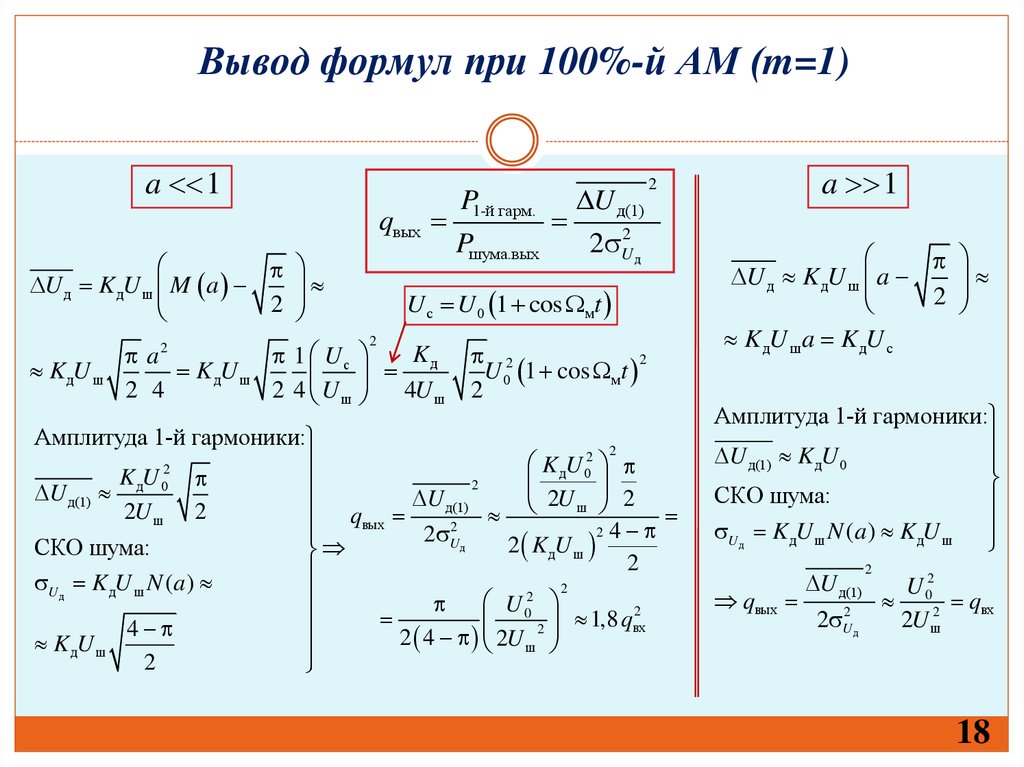
18.

Вывод формул при 100%-й АМ (m=1)
a 1
qвых
U д K дU ш M a
2
Pшума.вых
U д(1)
Kд
a2
1 Uс
K дU ш
2 4
2 4 U ш 4U ш
a 1
2
2 U2 д
U с U 0 1 cos мt
2
K дU ш
P1-й гарм.
2
2
U 0 1 cos мt
2
Амплитуда 1-й гармоники:
2
K дU 02
2
KU
2
U д(1) д 0
U
2
U
д(1)
ш
2
q
2U ш 2
вых
2 4
2 U2 д
2
K
U
СКО шума:
д ш
2
U д K дU ш N (a )
2
U 02
1,8 qвх2
2
4
2 4 2U ш
K дU ш
2
U д K дU ш a
2
K дU ш a K дU с
Амплитуда 1-й гармоники:
U д(1) K дU 0
СКО шума:
U д K дU ш N (a ) K дU ш
qвых
U д(1)
2 U2 д
2
U 02
qвх
2
2U ш
18

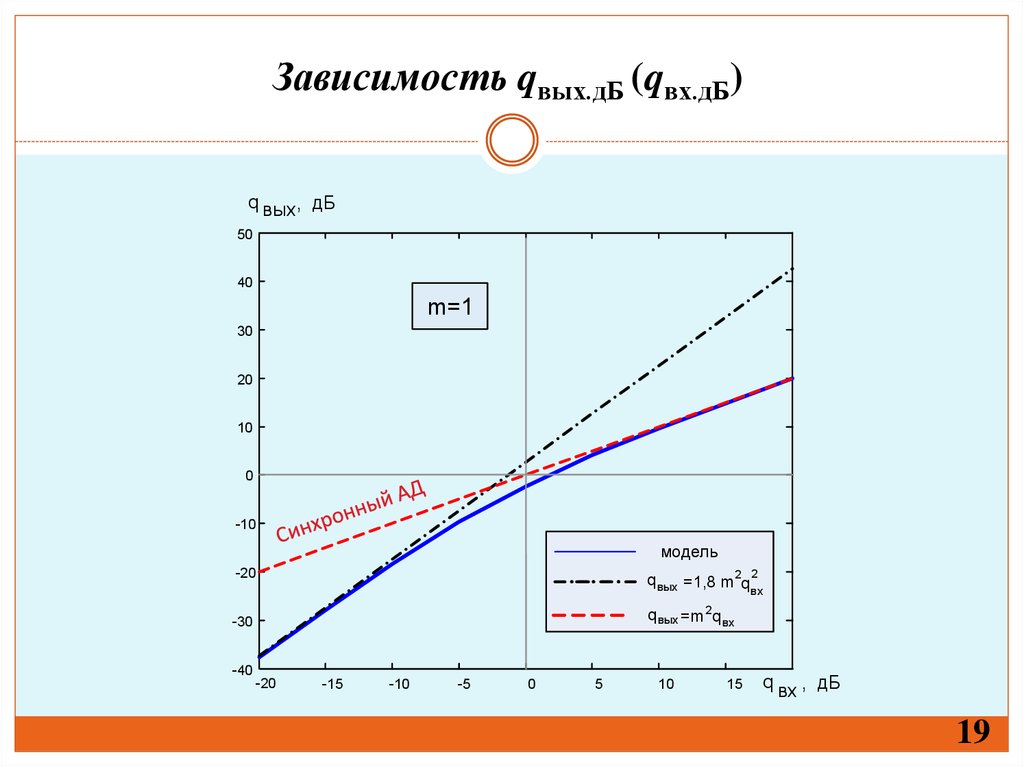
19.

Зависимость qвых.дБ (qвх.дБ)
q вых , дБ
50
40
m=1
30
20
10
0
-10
модель
-20
q вых =1,8 m2q 2
вх
q вых =m 2q вх
-30
-40
-20
-15
-10
-5
0
5
10
15
q вх , дБ
19

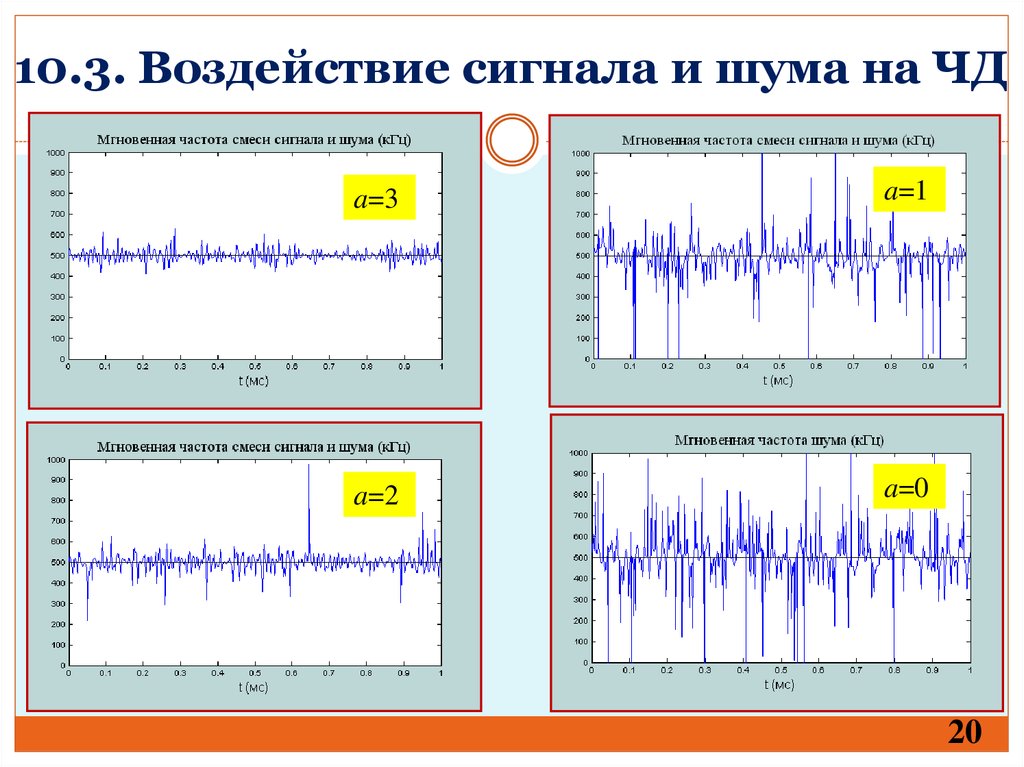
20.

10.3. Воздействие сигнала и шума на ЧД
a=3
a=1
a=2
a=0
20

21.

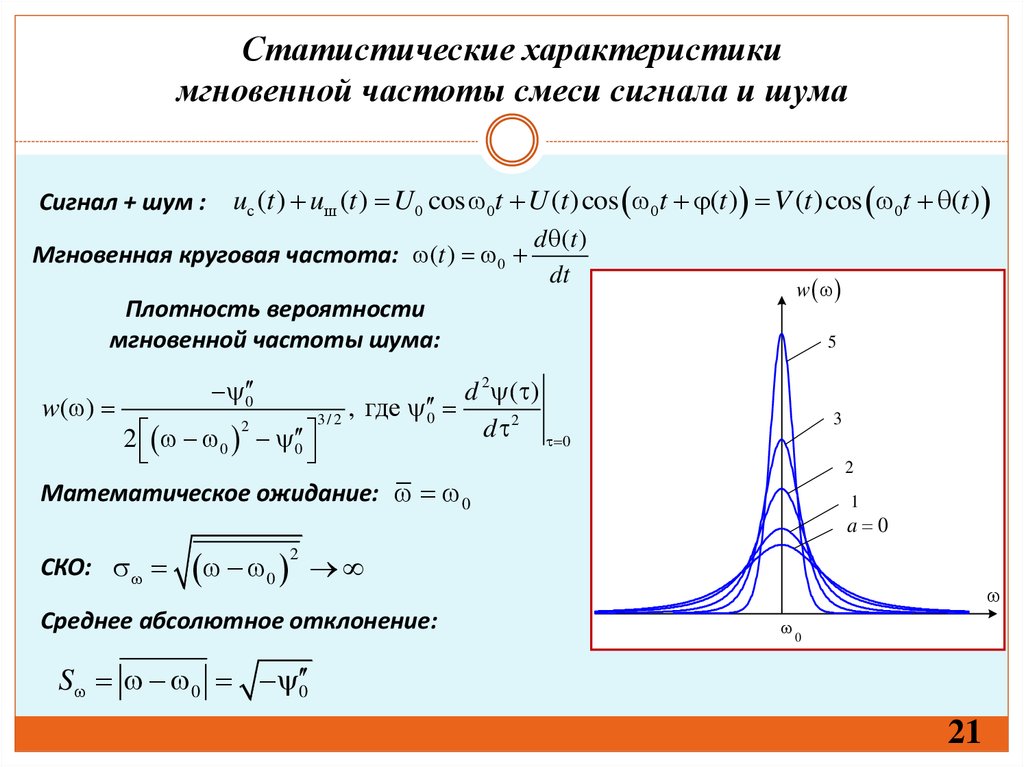
Статистические характеристики
мгновенной частоты смеси сигнала и шума
Сигнал + шум :
uс (t ) uш (t ) U 0 cos 0t U (t )cos 0t (t ) V (t )cos 0t (t )
Мгновенная круговая частота: (t ) 0
d (t )
dt
Плотность вероятности
мгновенной частоты шума:
w
5
0
d 2 ( )
w( )
, где 0
3/ 2
2
2
d
0
2 0 0
3
2
Математическое ожидание: 0
СКО:
0
2
1
a 0
Среднее абсолютное отклонение:
0
S 0 0
21

22.

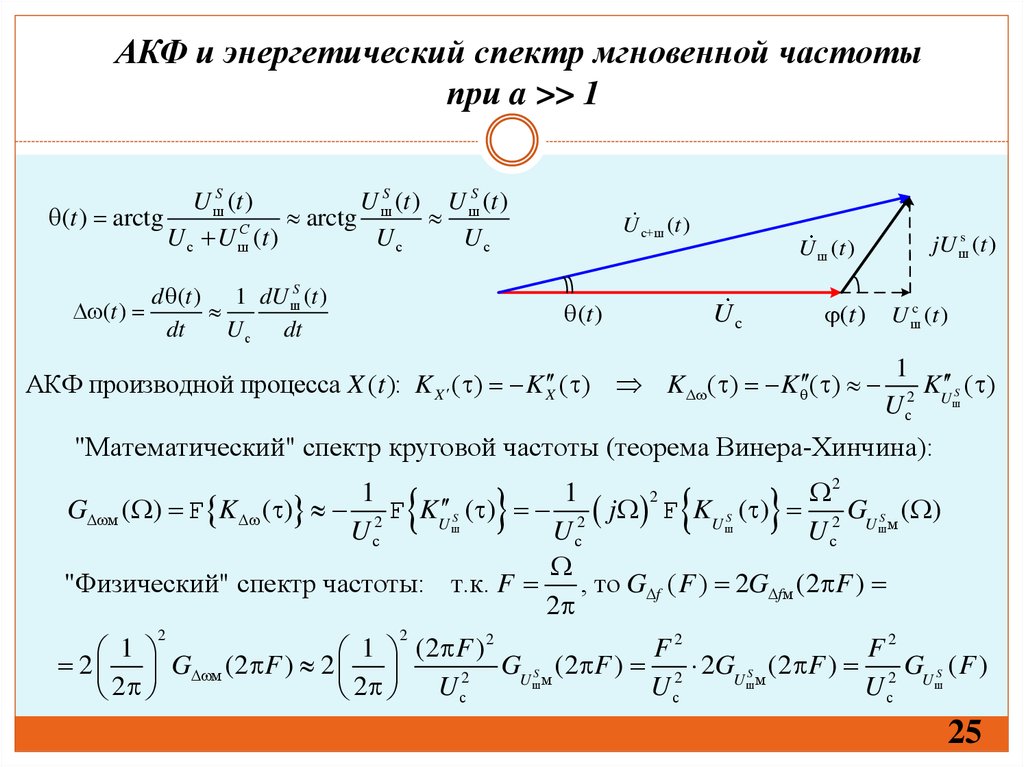
АКФ и энергетический спектр мгновенной частоты
при a >> 1
U шS (t )
U шS (t ) U шS (t )
(t ) arctg
arctg
С
U с U ш (t )
Uс
Uс
d (t ) 1 dU шS (t )
(t )
dt
U с dt
U с+ш (t )
U ш (t )
(t )
(t )
Uс
АКФ производной процесса X (t ): K X ( ) K X ( ) K ( ) K ( )
jU шs (t )
U шc (t )
1
KU S ( )
2
ш
Uс
"Математический" спектр круговой частоты (теорема Винера-Хинчина):
1
1
2
2
G м ( ) F K ( ) 2 F KU S ( ) 2 j F KU S ( ) 2 GU S м ( )
ш
ш
Uс
Uс
Uс ш
"Физический" спектр частоты: т.к. F
, то G f ( F ) 2G fм (2 F )
2
2
F2
F2
1
1 (2 F )
2 G м (2 F ) 2
GU S м (2 F ) 2 2GU S м (2 F ) 2 GU S ( F )
2
ш
ш
ш
Uс
Uс
2
2 U с
2
2
25

23.

Энергетический спектр мгновенной частоты
смеси сигнала и шума (прямоугольная АЧХ БВЧ)
22

24.

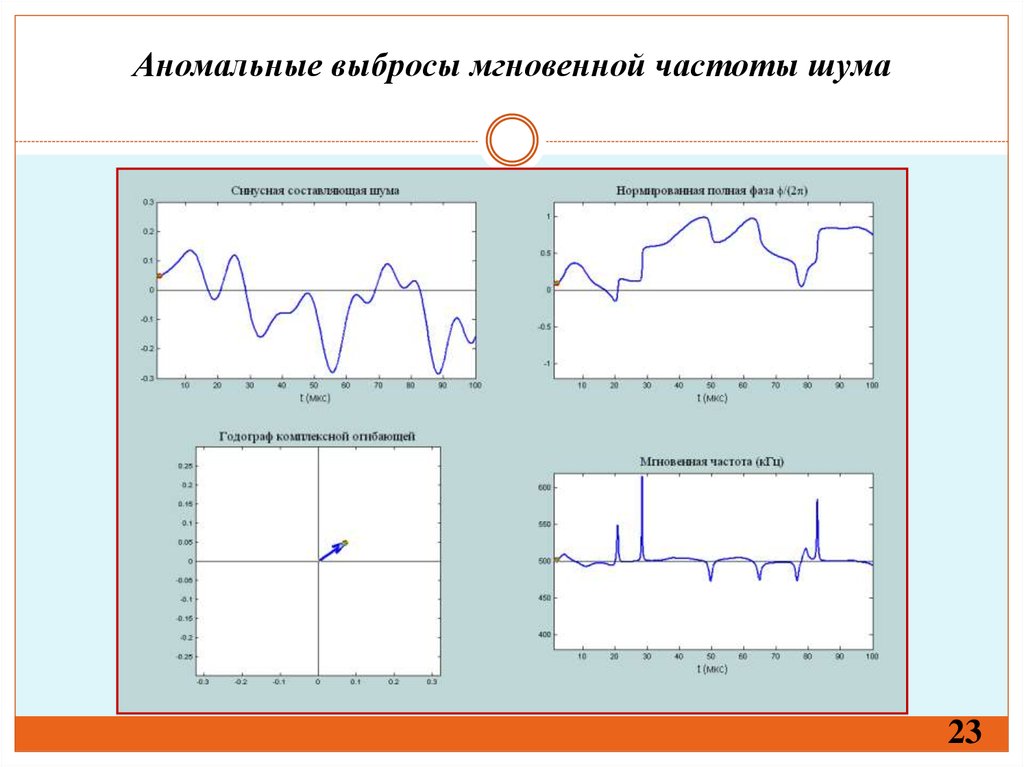
Аномальные выбросы мгновенной частоты шума
23

25.

Аномальный выброс
24

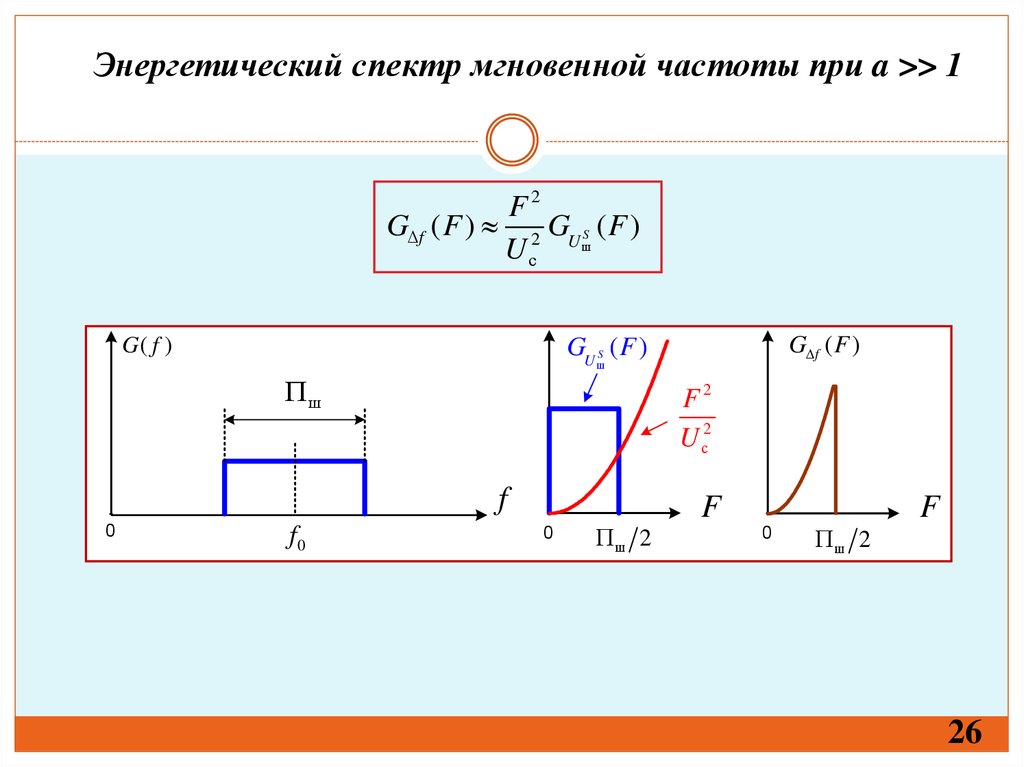
26.

Энергетический спектр мгновенной частоты при a >> 1
F2
G f ( F ) 2 GU S ( F )
Uс ш
G f ( F )
GU S ( F )
G( f )
ш
ш
F2
U с2
f
0
f0
0
ш 2
F
0
ш 2
F
26

27.

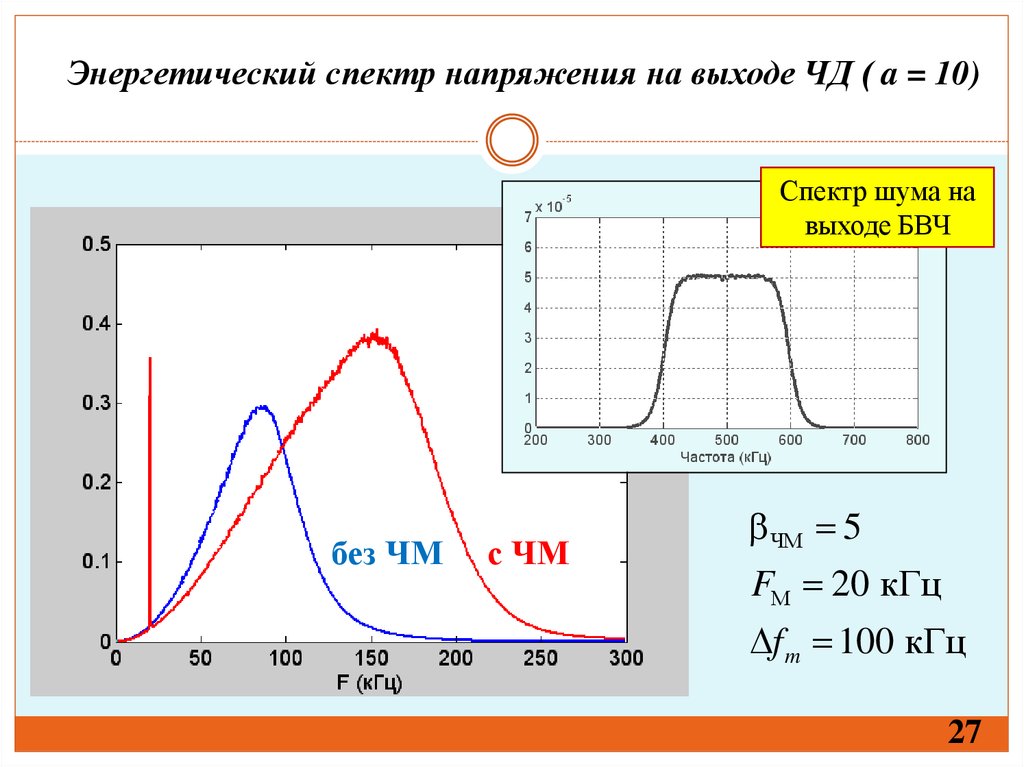
Энергетический спектр напряжения на выходе ЧД ( a = 10)
Спектр шума на
выходе БВЧ
без ЧМ
с ЧМ
ЧМ 5
FМ 20 кГц
f m 100 кГц
27

28.

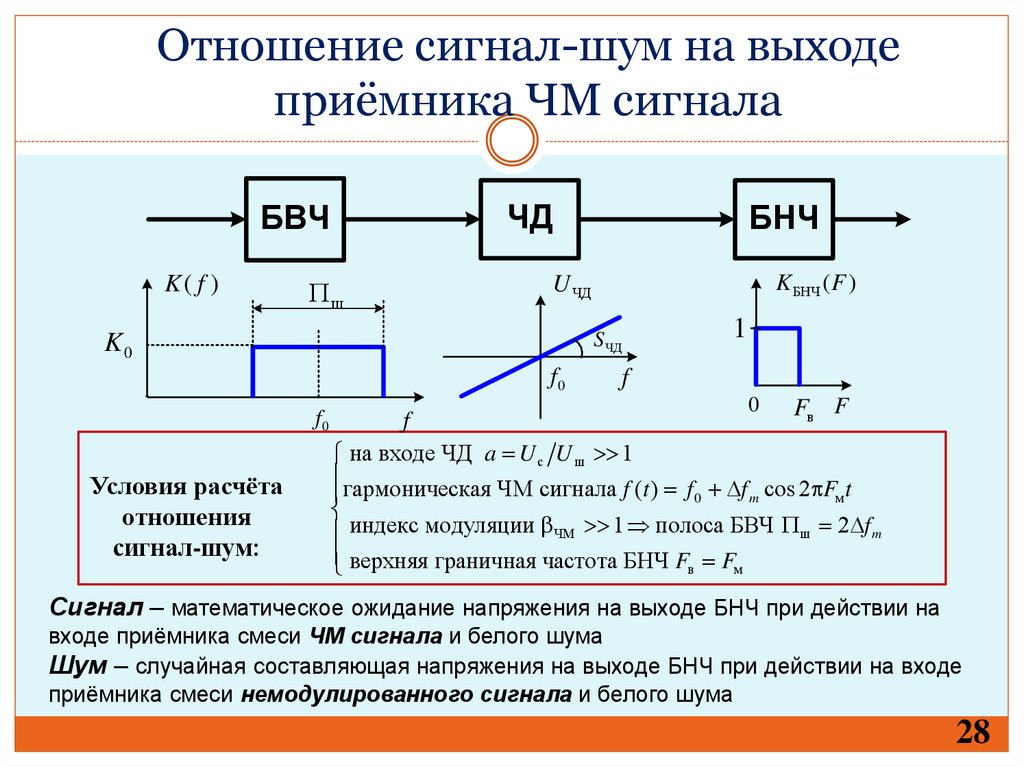
Отношение сигнал-шум на выходе
приёмника ЧМ сигнала
ЧД
БВЧ
K( f )
ш
K БНЧ ( F )
U ЧД
SЧД
K0
f0
f0
Условия расчёта
отношения
сигнал-шум:
БНЧ
1
f
0
Fв F
f
на входе ЧД a U с U ш 1
гармоническая ЧМ сигнала f (t ) f 0 f m cos 2 Fм t
индекс модуляции ЧМ 1 полоса БВЧ ш 2 f m
верхняя граничная частота БНЧ Fв Fм
Сигнал – математическое ожидание напряжения на выходе БНЧ при действии на
входе приёмника смеси ЧМ сигнала и белого шума
Шум – случайная составляющая напряжения на выходе БНЧ при действии на входе
приёмника смеси немодулированного сигнала и белого шума
28

29.

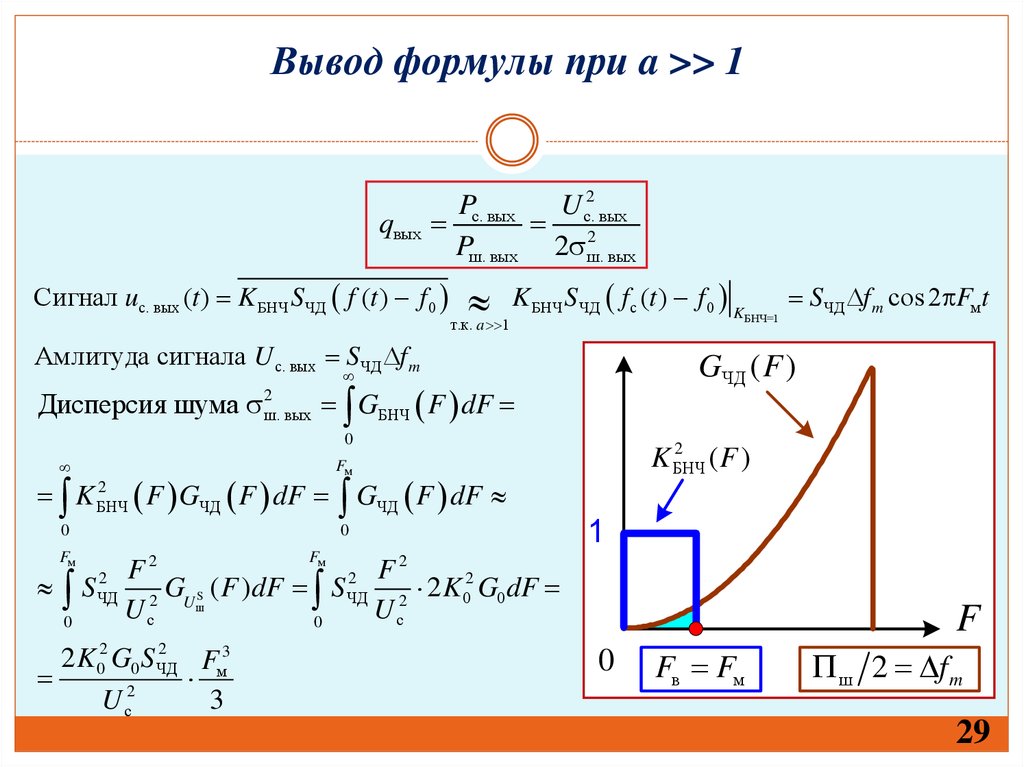
Вывод формулы при a >> 1
qвых
Pс. вых
U с.2 вых
2
Pш. вых 2 ш.
вых
Сигнал uс. вых (t ) K БНЧ SЧД f (t ) f 0
т.к. a 1
K БНЧ SЧД f с (t ) f 0 K
Амлитуда сигнала U с. вых SЧД f m
2
Дисперсия шума ш.
вых GБНЧ F dF
0
0
0
2
K БНЧ
F GЧД F dF GЧД F dF
Fм
S
0
SЧД f m cos 2 Fмt
GЧД ( F )
Fм
БНЧ=1
2
K БНЧ
(F )
1
Fм
2
ЧД
2
F2
2 F
2
G
(
F
)
dF
S
2
K
G0 dF
S
ЧД
0
2
2
Uш
Uс
Uс
0
2
2 K 02 G0 SЧД
Fм3
2
Uс
3
F
0
Fв Fм
ш 2 f m
29

30.

Вывод формулы при a >> 1
(окончание)
qвых
2
с. вых
2
ш. вых
U
2
S
f
ЧД
m
2
2
0
0 ЧД
2
с
2K G S
2
U
SЧД f m
2
2
2 K 02 G0 SЧД
Fм3
2
2
Uс
3
2
Fм3
3
Влияние формы АЧХ БНЧ
f m
f m
U с2 2
3 2
3ЧМ 3qвх 3ЧМ
K 0 БВЧG0 ш
qвых 3qвх 3ЧМ
(при a 1)
30

31.

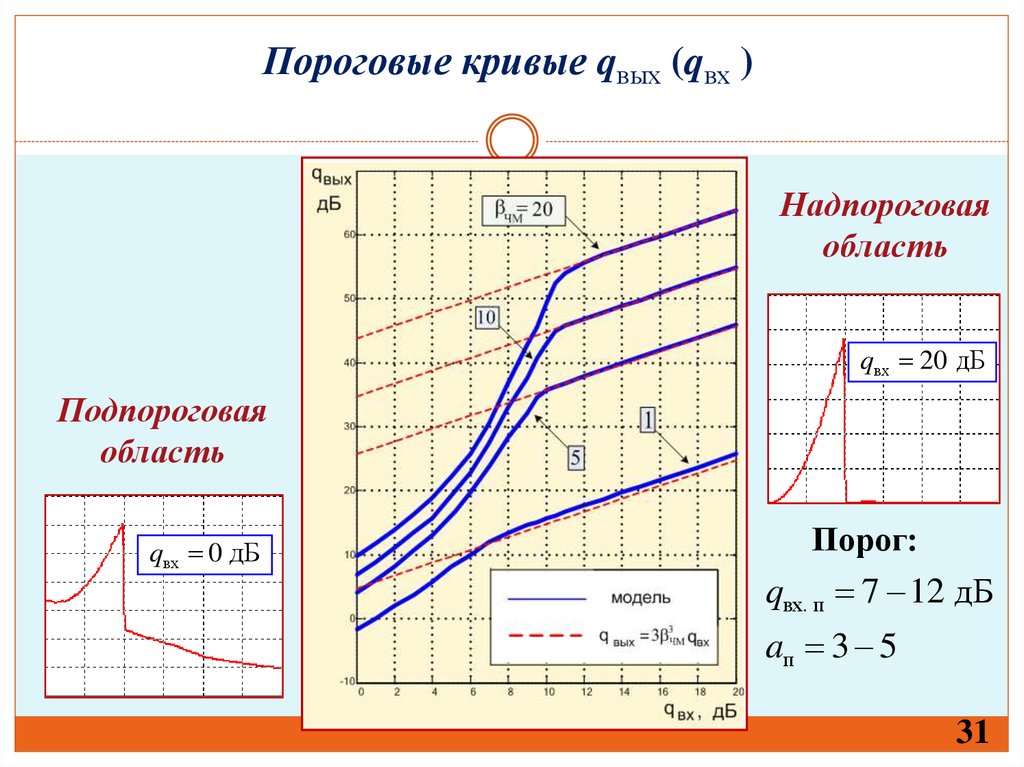
Пороговые кривые qвых (qвх )
Надпороговая
область
qвх 20 дБ
Подпороговая
область
qвх 0 дБ
Порог:
qвх. п 7 12 дБ
aп 3 5
31

32.

Методы повышения качества
приёма ЧМ сигнала
Задача
Метод
1. Выравнивание отношения сигналшум на выходе приёмника в
интервале частот
Предыскажение модулирующего
колебания и частотная коррекция
демодулированного колебания
2. Уменьшение порогового
отношения сигнал-шум путём
увеличения амплитуды несущей
Синхронный приём (регенерация
несущей)
3. Уменьшение порогового
отношения сигнал-шум путём
уменьшения мощности шума на
входе ЧД
Приём с обратной связью по частоте
(ОСЧ)
32

33.

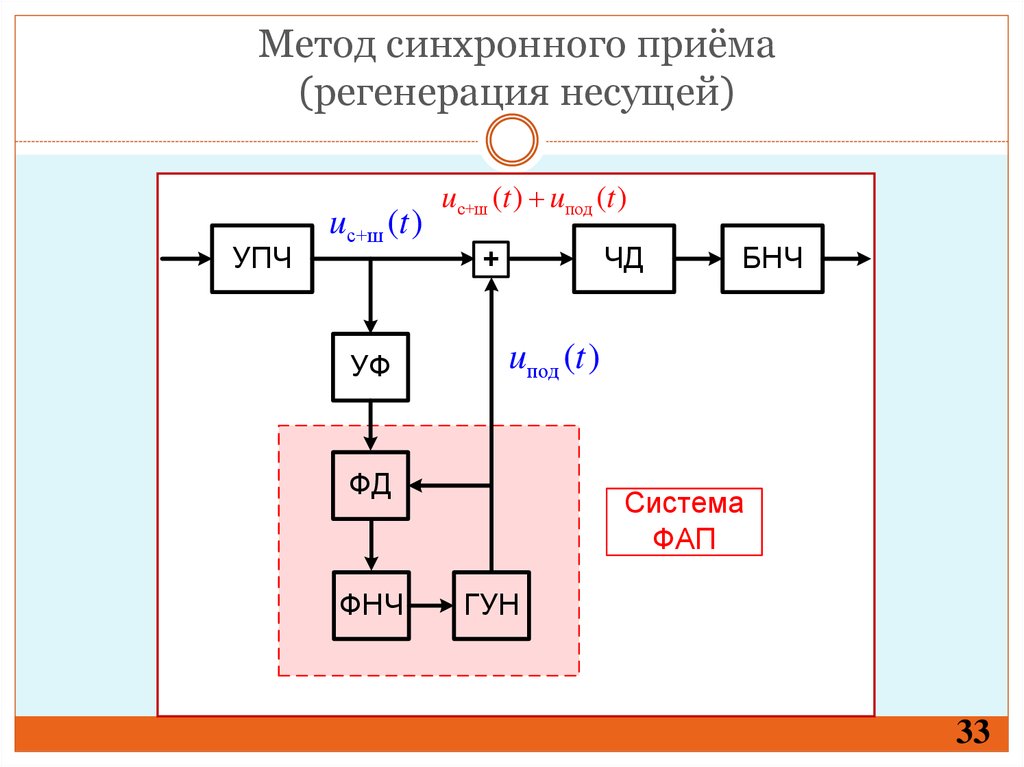
Метод синхронного приёма
(регенерация несущей)
УПЧ
uс+ш (t )
uс+ш (t ) uпод (t )
ЧД
+
УФ
uпод (t )
ФД
ФНЧ
БНЧ
Система
ФАП
ГУН
33

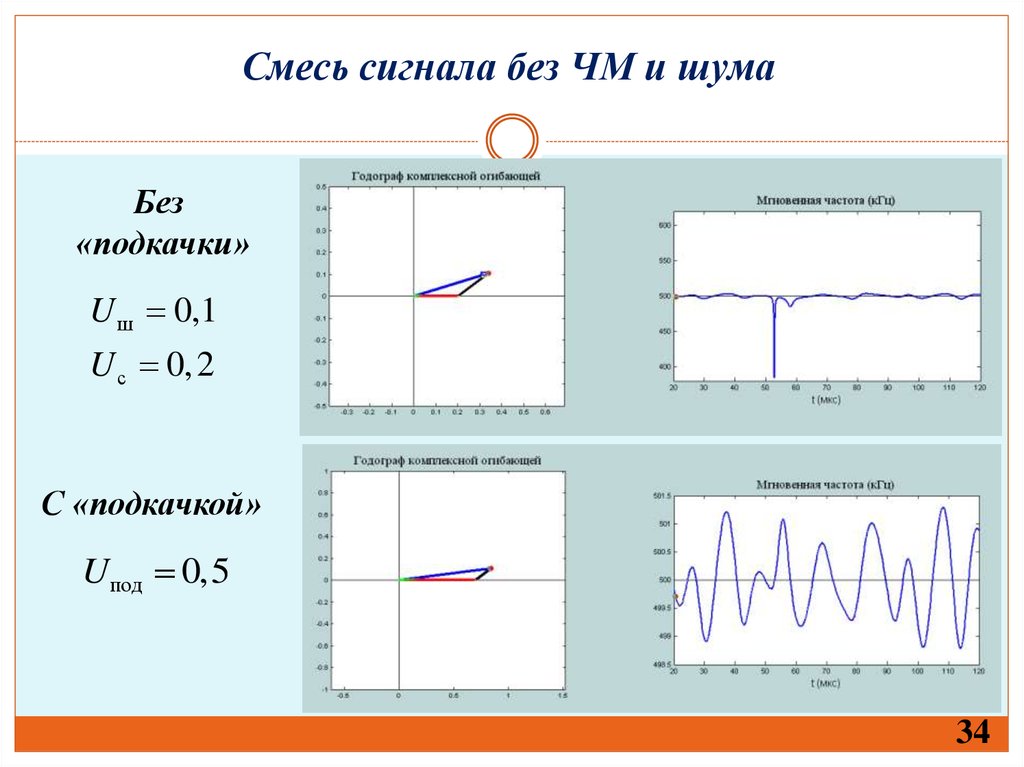
34. Смесь сигнала без ЧМ и шума

Без
«подкачки»
U ш 0,1
U с 0, 2
С «подкачкой»
Uпод 0,5
34

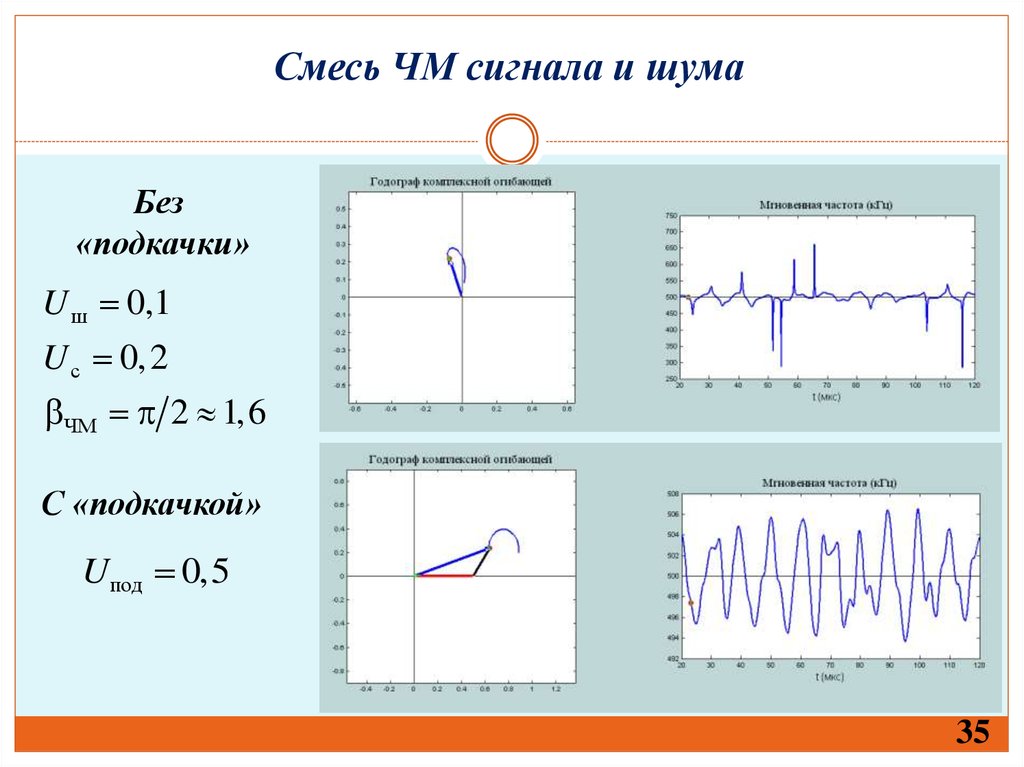
35. Смесь ЧМ сигнала и шума

Без
«подкачки»
U ш 0,1
U с 0, 2
ЧМ 2 1,6
С «подкачкой»
Uпод 0,5
35

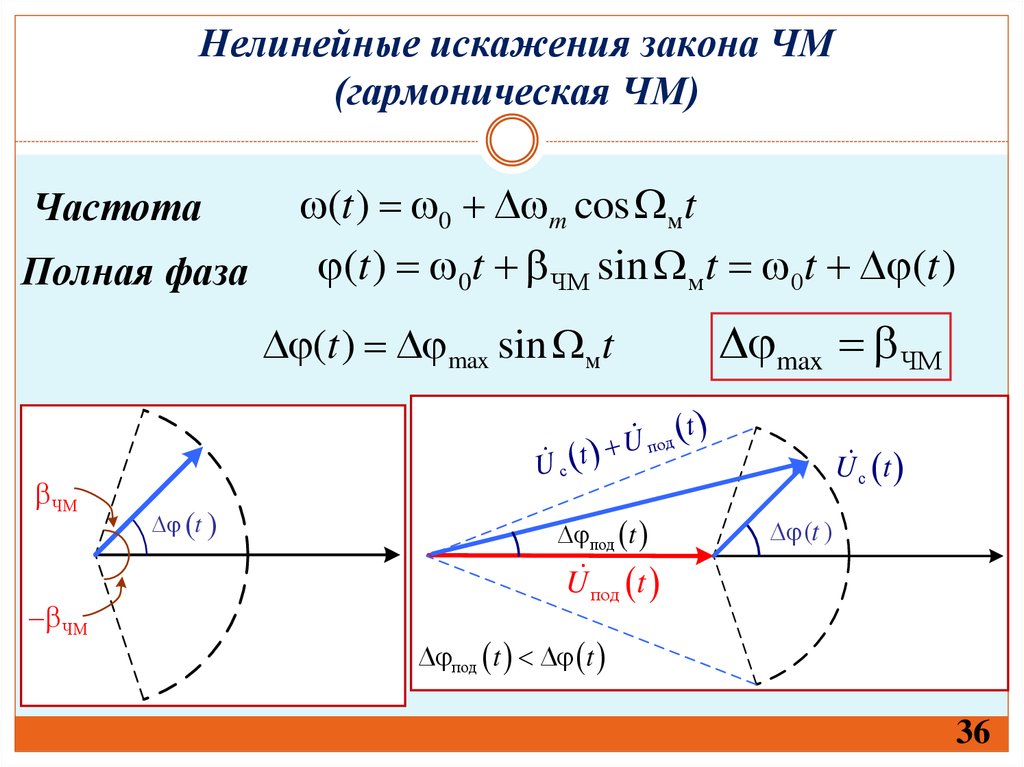
36. Нелинейные искажения закона ЧМ (гармоническая ЧМ)

Частота
Полная фаза
(t ) 0 m cos мt
(t ) 0t ЧМ sin мt 0t (t )
max ЧМ
(t ) max sin мt
ЧМ
ЧМ
Uс
t
U
под
t
под t
t
Uс t
t
U под t
под t t
36

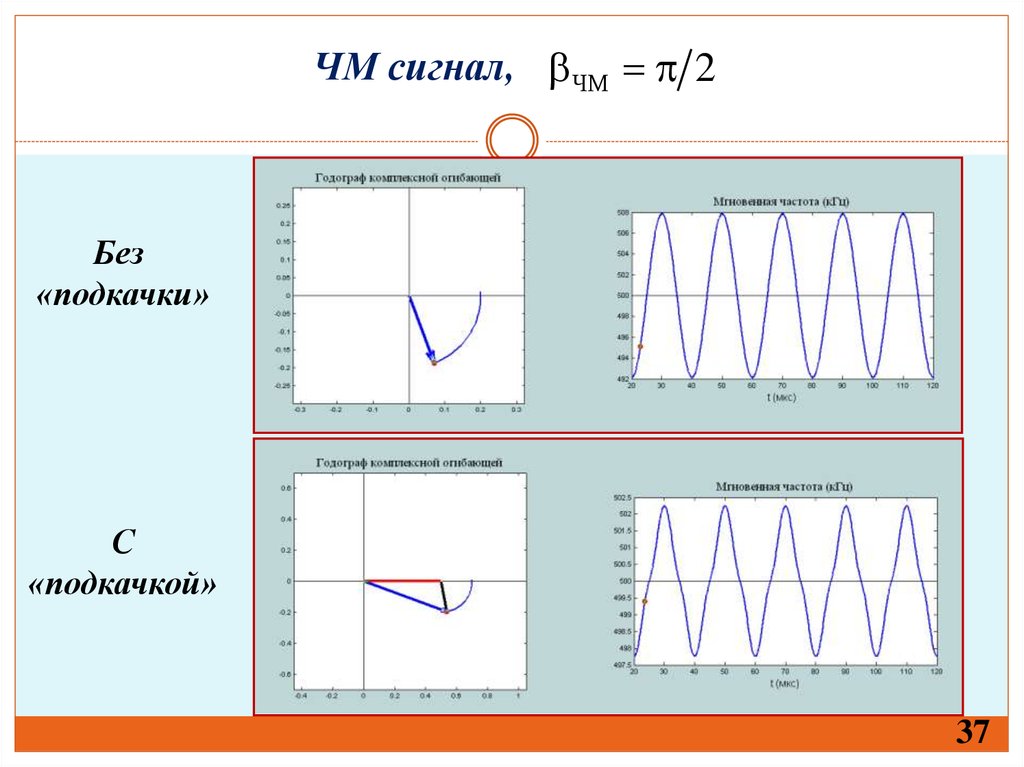
37. ЧМ сигнал,

ЧМ 2
Без
«подкачки»
С
«подкачкой»
37

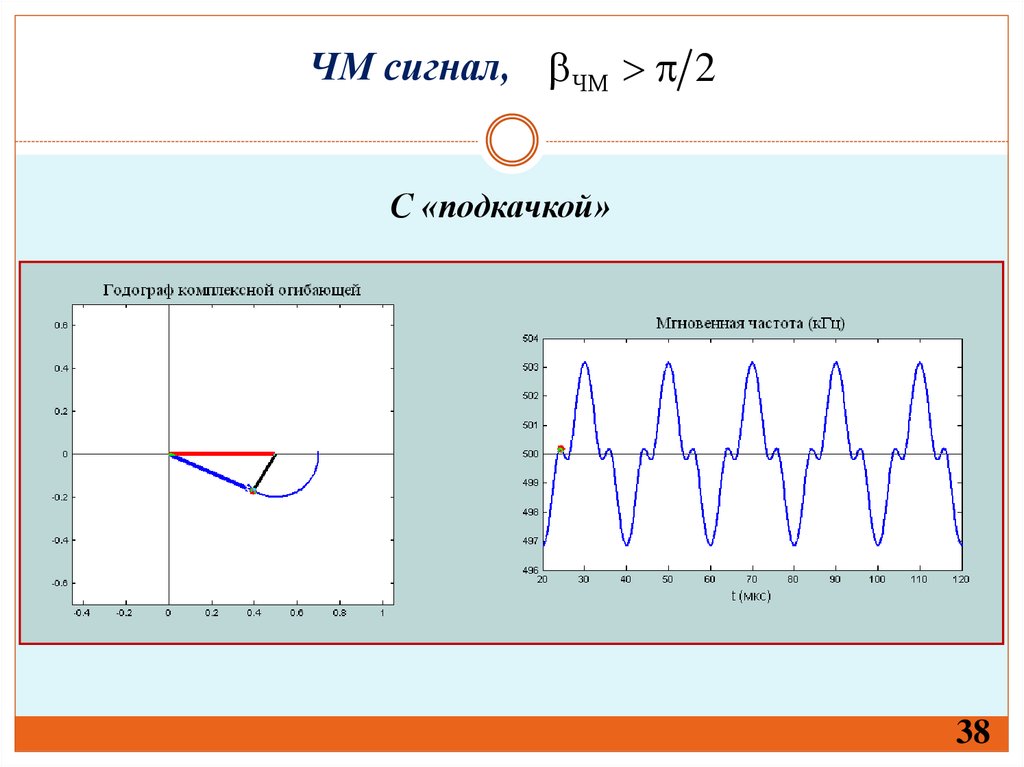
38. ЧМ сигнал,

ЧМ 2
С «подкачкой»
38

39.

Приём с обратной связью по частоте (ОСЧ)
uс+ш (t )
ЧМ
УПЧ
(t )
uс+ш
ЧМ ЧМ
См
ГУН
УФ
УПТ
ЧД
ФНЧ
БНЧ
Система
ЧАП
УФ УПЧ
39