Similar presentations:
Цифровые сигналы
1. ЦИФРОВЫЕ СИГНАЛЫ
2. ЦИФРОВЫЕ СИГНАЛЫ
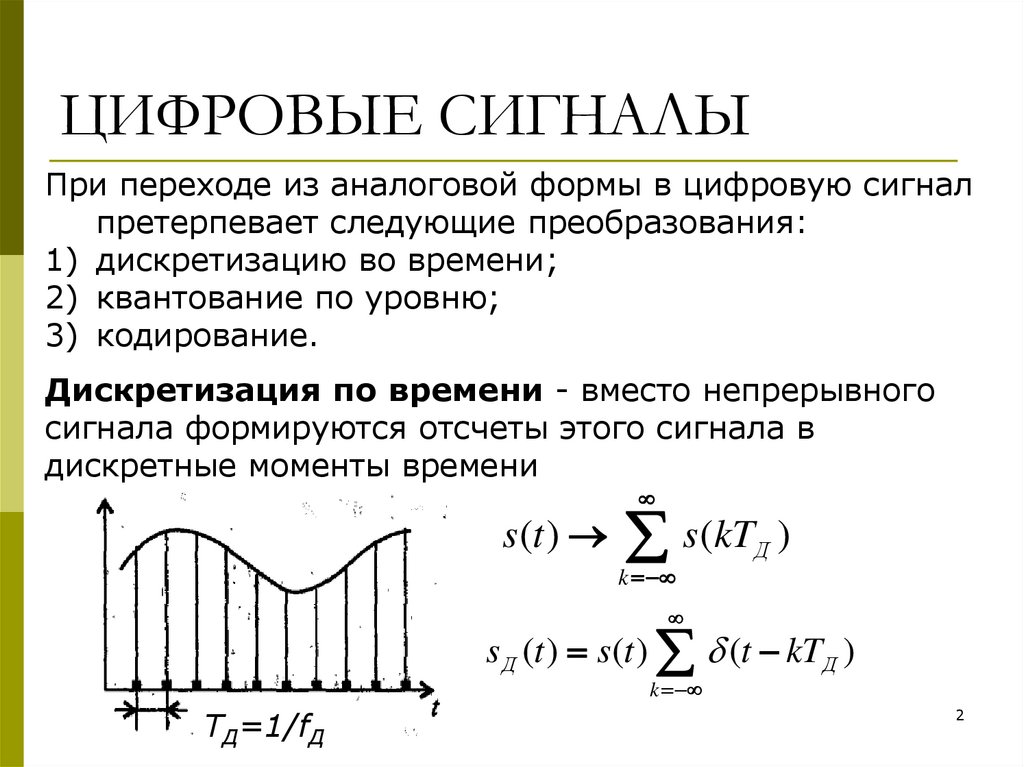
При переходе из аналоговой формы в цифровую сигналпретерпевает следующие преобразования:
1) дискретизацию во времени;
2) квантование по уровню;
3) кодирование.
Дискретизация по времени - вместо непрерывного
сигнала формируются отсчеты этого сигнала в
дискретные моменты времени
s (t )
s(kT
k
Д
)
s Д (t ) s(t ) (t kTД )
k
TД=1/fД
2
3. ДИСКРЕТИЗАЦИЯ СИГНАЛА ПО ВРЕМЕНИ
Сигнал, описываемый непрерывной функцией s(t) сограниченным спектром, полностью определяется своими
значениями sД(t) взятыми через интервал времени
TД=1/(2fв) ,где fв – верхняя частота s(t).
1
f Д 2 fВ
TД
Спектр дискретного сигнала
1
SД ( f )
TД
S ( f kf
k
Д
)
3
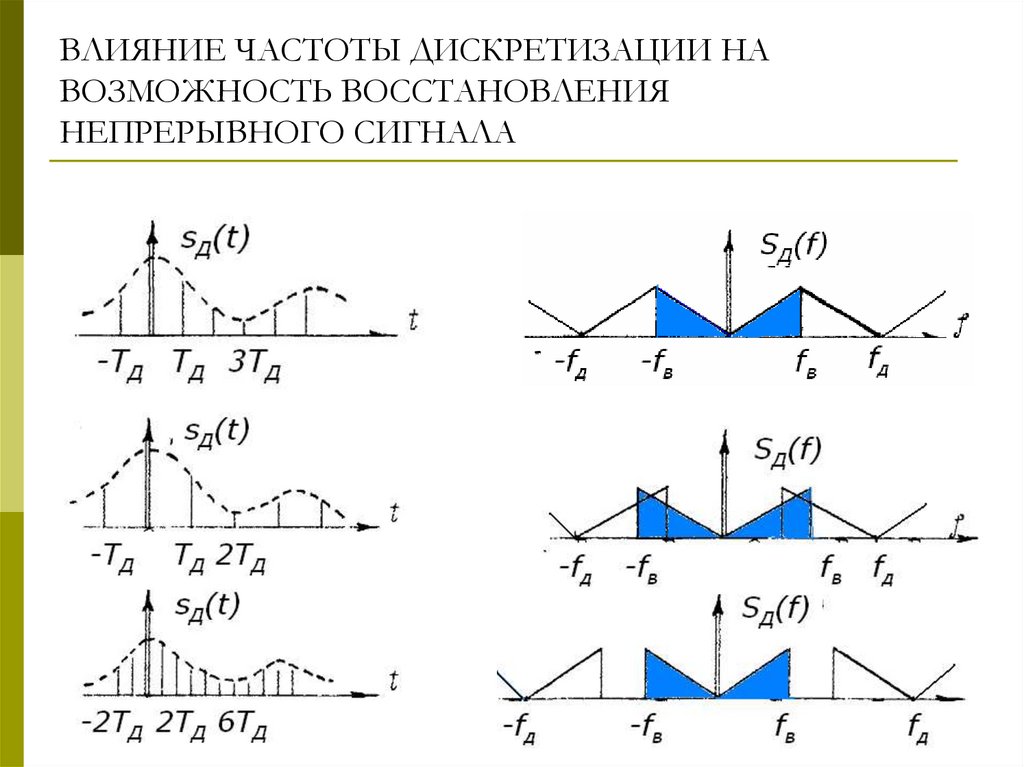
4. ВЛИЯНИЕ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ НА ВОЗМОЖНОСТЬ ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНОГО СИГНАЛА
45. ПРОБЛЕМА НАЛОЖЕНИЯ СПЕКТРОВ
4 t3 t
6 t
4 t
5
6. ПРОБЛЕМА НАЛОЖЕНИЯ СПЕКТРОВ
наложение спектровИз лекций
Tomas Svoboda
предварительная НЧ фильтрация
2
t
2 fв
6
7.
ПРОБЛЕМА НАЛОЖЕНИЯСПЕКТРОВ
наложение спектров
Из лекций
Tomas Svoboda
предварительная НЧ фильтрация
4
t
2 fв
7
8.
ПРОБЛЕМА НАЛОЖЕНИЯСПЕКТРОВ
наложение спектров
Из лекций
Tomas Svoboda
предварительная НЧ фильтрация
6
t
2 fв
8
9. ПОЛОСА РАСФИЛЬТРОВКИ
Полоса расфильтровкиf р ( f Д fВ ) fВ f Д 2 fВ ;
f Д 2 fВ
fр 0
Частоту дискретизации обычно выбирают с некоторым
запасом
f Д 2(1 ) f в ; 0 0.5 - коэффициент запаса
9
10. ПРИМЕР
Пример . Найти частоту дискретизации, периоддискретизации и полосу расфильтровки для телефонного
сигнала, при коэффициенте запаса 0.18
f Д 2(1 ) f в ;
f р f Д 2 fВ ;
Для телефонного сигнала fв=3.4 кГц;
fд=2*3.4*(1+0.18)=8кГц;
TД=125мкс;
fр=8-2*3.4=1.2 кГц
10
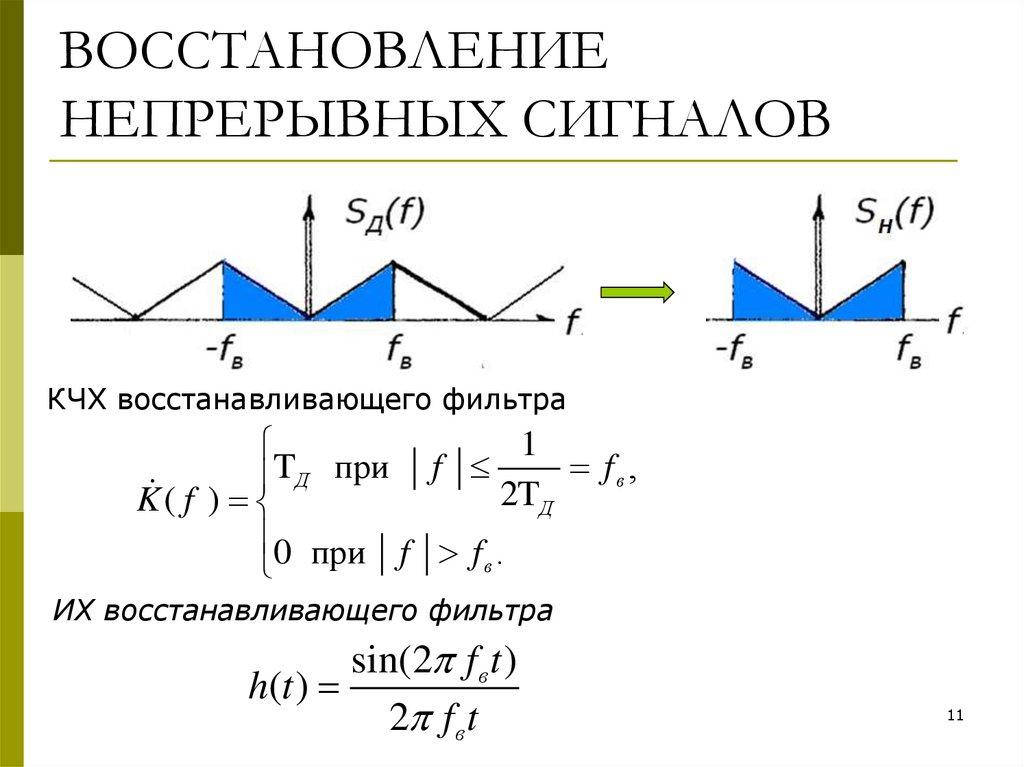
11. ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
КЧХ восстанавливающего фильтра1
T
при
f
fв ,
Д
2TД
K( f )
0 при f f .
в
ИХ восстанавливающего фильтра
sin(2 f в t )
h(t )
2 f в t
11
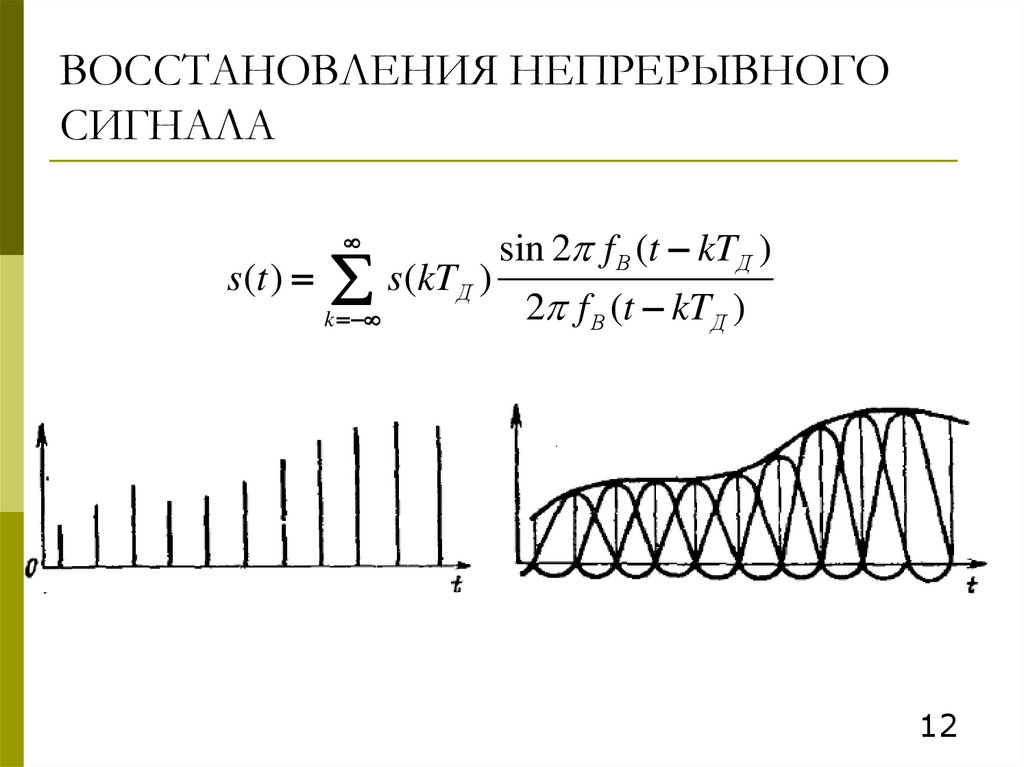
12. ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНОГО СИГНАЛА
s (t )s(kT
k
Д
)
sin 2 f В (t kTД )
2 f В (t kTД )
12
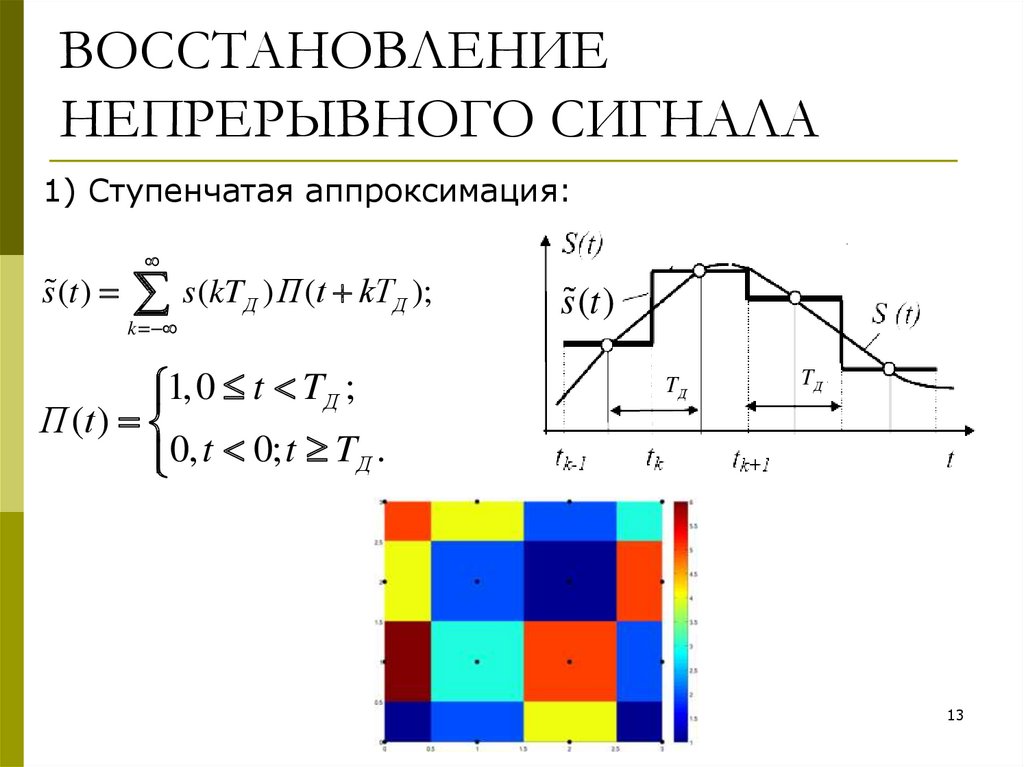
13. ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНОГО СИГНАЛА
1) Ступенчатая аппроксимация:s (t )
s(kT
k
Д
) П (t kTД );
1, 0 t TД ;
П (t )
0, t 0; t TД .
s (t )
TД
TД
13
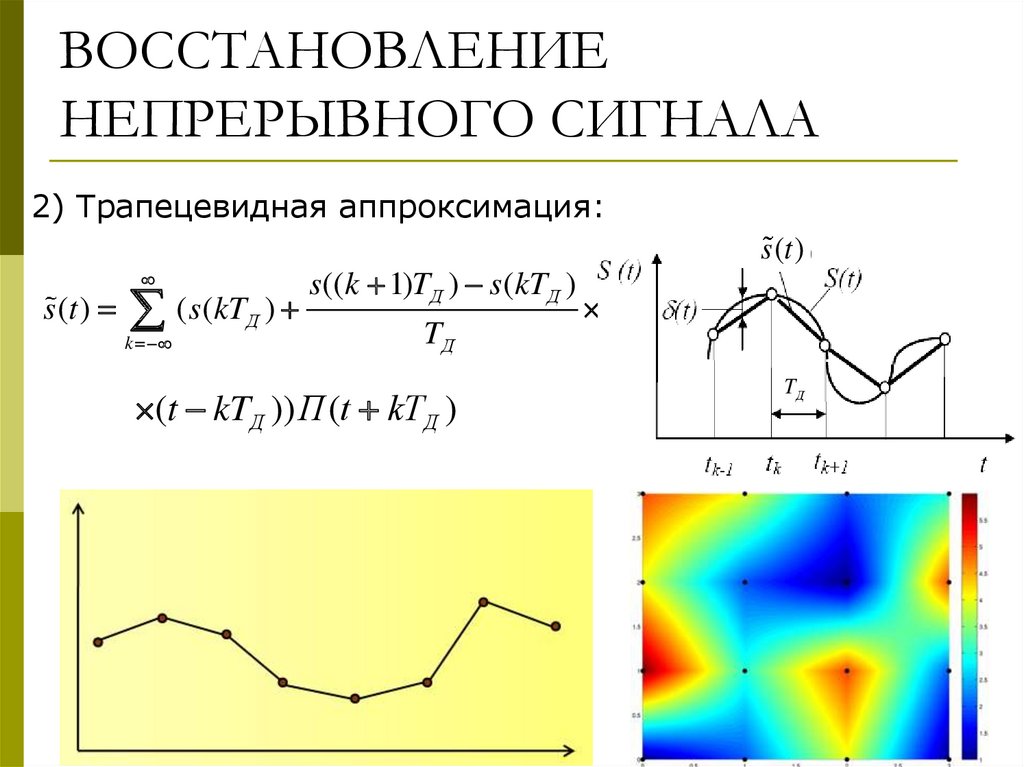
14. ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНОГО СИГНАЛА
2) Трапецевидная аппроксимация:s (t )
(s(kT
k
Д
)
s ((k 1)TД ) s (kTД )
TД
(t kTД )) П (t kTД )
s (t )
TД
14
15. ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНОГО СИГНАЛА
Метод «ближайшегососеда»
А.C. Крылов
Лаборатория математических
методов обработки
изображений,МГУ
Билинейная
интерполяция
Бикубическая
интерполяция
15
16.
ПРОБЛЕМА НАЛОЖЕНИЯСПЕКТРОВ
наложение спектров
Из лекций
Tomas Svoboda
предварительная НЧ фильтрация
6
t
2 fв
16
17. ПОГРЕШНОСТИ ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНОГО СИГНАЛА
Нормированная СКО восстановления2
s 2 (t )
(s(t ) s (t ))
s 2 (t )
2
1T
lim (s(t ) s (t )) 2 dt
T T 0
1T
lim (s(t )) 2 dt
T T 0
Нормированная СКО, обусловленная ограничением полосы
сигнала
02
2
s (t )
Gs ( f )df
fВ
Gs ( f )df
0
17
18. ПРИМЕР
Найти верхнюю частоту ограничения полосы сигнала,если нормированная СКО равна 1% и СПМ сигнала
x
G( f
(2 f )
f э
2
02
2
s (t )
x
df
f В (2 f )
0.01
x
df
0 (2 f )
Gs ( f )df
fВ
Gs ( f )df
0
1
df
2
2 f B
f В (2 f )
1 arctg (
)
1
df
0 (2 f )
f B 10.15 20.3 f э
18
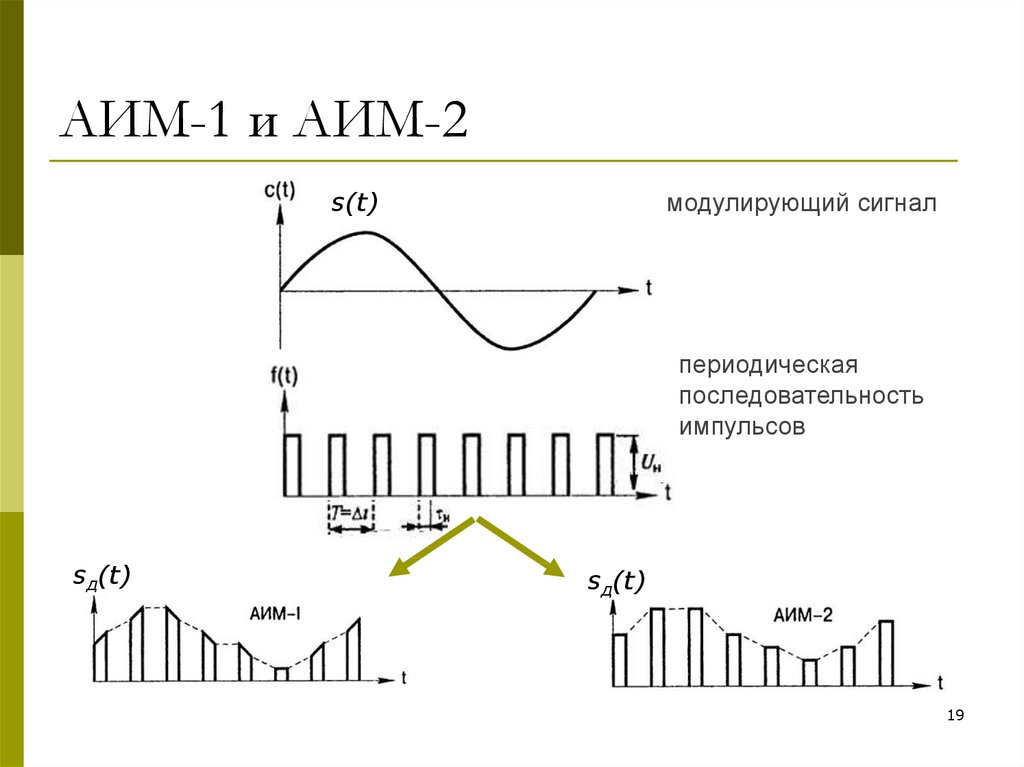
19. АИМ-1 и АИМ-2
s(t)модулирующий сигнал
периодическая
последовательность
импульсов
sд(t)
sд(t)
19
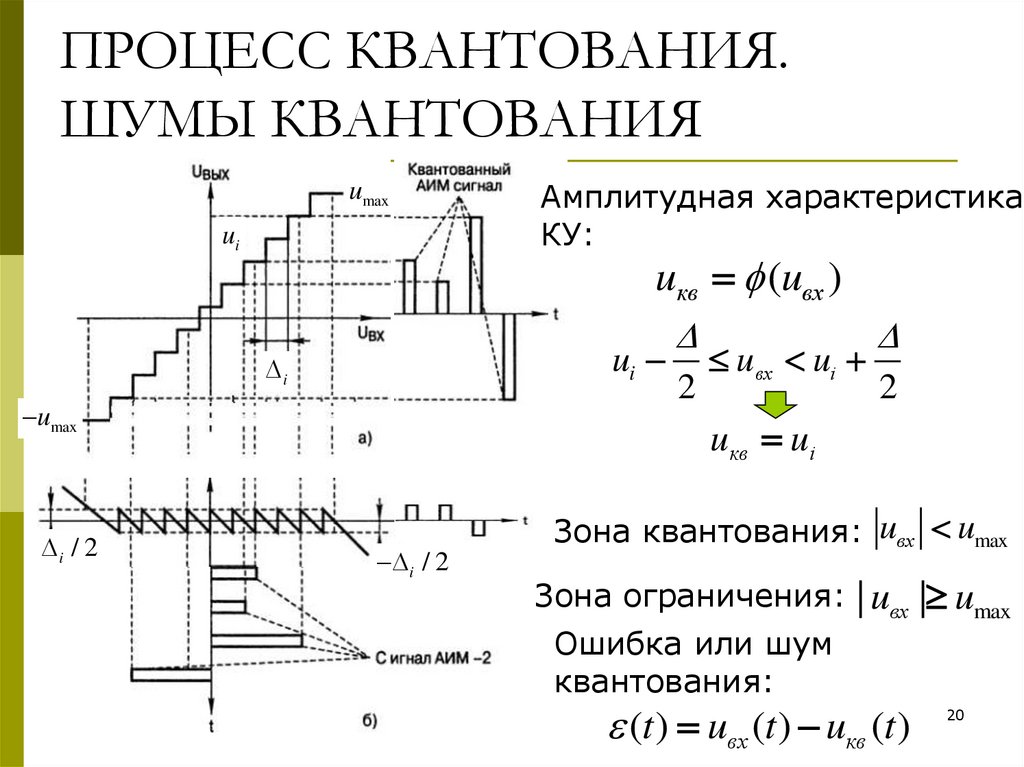
20. ПРОЦЕСС КВАНТОВАНИЯ. ШУМЫ КВАНТОВАНИЯ
umaxui
uкв (uвх )
ui
i
umax
i / 2
Амплитудная характеристика
КУ:
2
uвх ui
2
uкв ui
i / 2
Зона квантования: uвх umax
Зона ограничения:
| uвх | umax
Ошибка или шум
квантования:
(t ) uвх (t ) uкв (t )
20
21. КВАНТОВАНИЕ ПО УРОВНЮ
1. Значения отсчетов округляются до ближайшегоразрешенного уровня.
2. Отсчеты имеют строго фиксированные значения из
числа заранее известных.
3. Каждому разрешенному уровню можно сопоставить
определенное число.
Диапазон отсчетов сигнала : 2umax
Шаг квантования - размер отдельных участков на
которые разбивается непрерывный динамический
диапазон отсчетов сигнала
Число разрешенных уровней квантования:
2umax
M
1
2umax
M
21
22. ОЦЕНКА ШУМОВ ПРИ КВАНТОВАНИИ
Квантование называется равномерным, если величинашага квантования постоянная величина.
Квантование называется неравномерным, если
величина шага квантования изменяется с изменением uвх
Вероятность появления сигнала с уровнем, лежащим в
пределах i-го шага квантования
pi P(ui uвх ui )
2
2
ui
i
2
ui
i
2
w(uвх )duвх w(ui ) i
23. ОЦЕНКА ШУМОВ ПРИ КВАНТОВАНИИ
Мгновенная мощность шума квантования, развиваемая наединичном сопротивлении, при квантовании сигналов,
лежащих в пределах i-го шага квантования:
Wмгн,i (uвx ui )
2
Мощность шума квантования при квантовании
сигналов, лежащих в пределах i-го шага квантования:
ui
Wi
i
2
ui
i
2
(uвx ui )2 w(uвх )duвх
i 2
pi
12
i 2
pi
Полная мощность шума квантования: Wкв Wi
i 1
i 1 12
M
M
23
24. МОДЕЛЬ ШУМА
1. Шум квантования является стационарным белымшумом
2. Шум квантования не коррелирован с входным
сигналом
3. Распределение шума равномерно в любом
интервале квантования
4. Диапазон квантования установлен таким
образом, что он превышает размах сигнала.
- диапазон квантования используется
полностью;
- количество отсчетов, не попадающих в него,
24
достаточно мало
25. ОЦЕНКА ШУМОВ ПРИ РАВНОМЕРНОМ КВАНТОВАНИИ
iПри равномерной шкале квантования:
i 2
Wкв
pi
i 1 12
2
Wкв
12
M
Отношением сигнал-шум квантования (ОСШК):
Wcp
2
c
q
2
Wcp
Wкв
12
2
c
2
Отношением сигнал-шум квантования в дБ
(защищенность сигнала от шума квантования):
Aкв 10 lg
Wcp
Wкв
10lg(12
2
c
2
)
26. ОЦЕНКА ШУМОВ ПРИ РАВНОМЕРНОМ КВАНТОВАНИИ
Число уровней квантования :2umax
M
2umax
2umax
M
1
Защищенность
Aкв 10lg(12
c2
2
) 10 lg(12M
10lg 3 10lg M 20lg
2
umax
Aкв 4.77 20lg M 20lg
Пример.
umax 4 c
c
umax
c
2
4u
2
c
2
max
)
M 2B
4, 77 6 B 20lg
Aкв 6B 7.2
umax
c
26
27. ПРИМЕР
Найти защищенность от шумов квантованиягармонического сигнала со случайной фазой при M=16
1
2
c
2
2
0
2
A
A2 cos(2 f 0t ) 2 d
2
AКВ (дБ ) 6 B 4, 77 20lg
umax A
umax
c
6 4 4.77 20 lg 2 25.7дБ
28. ОПРЕДЕЛЕНИЕ ЧИСЛА УРОВНЕЙ КВАНТОВАНИЯ
Aкв 4.77 20 lg M 20 lgumax
c
;
0.05( Aкв 4.77 20lg
M 10
umax
Aкв 4, 77 6 B 20lg
;
c
umax
c
)
umax
1
B ( Aкв 4.77 20 lg
)
6
c
28
29. ПРИМЕР
Определить число уровней квантования двухдвуполярных сигналов, если:
1. мощность первого сигнала на 30дБ больше
мощности второго сигнала;
2. защищенность: AКВ 25 дБ;
3. пик-фактор слабого и сильного сигналов: 18дБ.
На сколько отличается защищенность первого
сигнала от второго?
29
30. ПРИМЕР
У сигналов одинаковый пик-фактор20lg
umax,1
с ,1
20lg
umax,2
с,2
18дБ ;
Mощность первого сигнала на 30дБ больше
мощности второго сигнала:
с ,1
20 lg
30дБ ;
c ,2
Следовательно:
umax,1 umax,2 ;
Примем для квантователя:
umax umax,1 ;
30
31. ПРИМЕР
Число разрядов квантования (максимальное)umax
1
B ( Aкв 4.77 20 lg
)
6
c ,2
20lg
umax
20lg
umax,1
20lg
umax,1 c ,1
c ,2 c,1
c ,2
umax,1
c ,1
18 30 48дБ
20 lg
20 lg
c ,1
c ,2
c,2
1
B (25 4.77 48) 11.3 12
6
31
32. ПРИМЕР
Защищенность для каждого из сигналовB 12
Для слабого сигнала
AКВ ,2 (дБ ) 6 B 4, 77 20 lg
umax
c ,2
72 4, 77 48 28.77
Для сильного сигнала
AКВ ,1 (дБ ) 6 B 4, 77 20 lg
umax
c ,1
72 4, 77 18 58.77
32
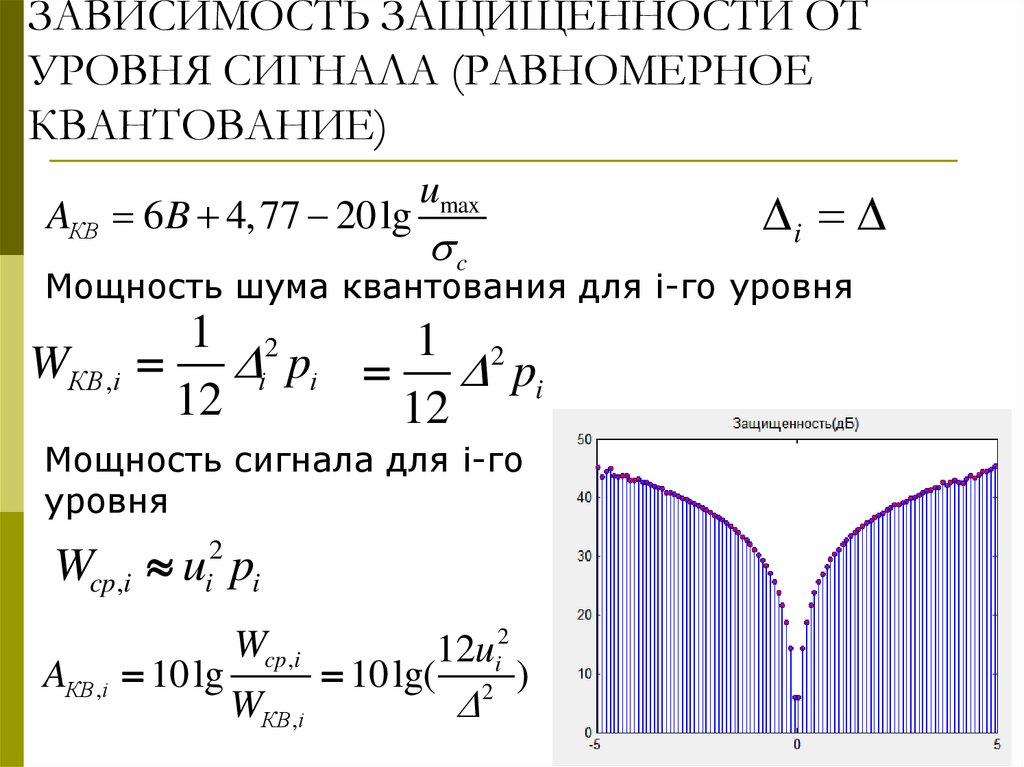
33. ЗАВИСИМОСТЬ ЗАЩИЩЕННОСТИ ОТ УРОВНЯ СИГНАЛА (РАВНОМЕРНОЕ КВАНТОВАНИЕ)
AКВ 6 B 4, 77 20lgumax
c
i
Мощность шума квантования для i-го уровня
WКВ ,i
1 2
1
i pi 2 pi
12
12
Мощность сигнала для i-го
уровня
Wcp,i ui2 pi
AКВ ,i 10 lg
Wcp ,i
WКВ ,i
12ui2
10 lg( 2 )
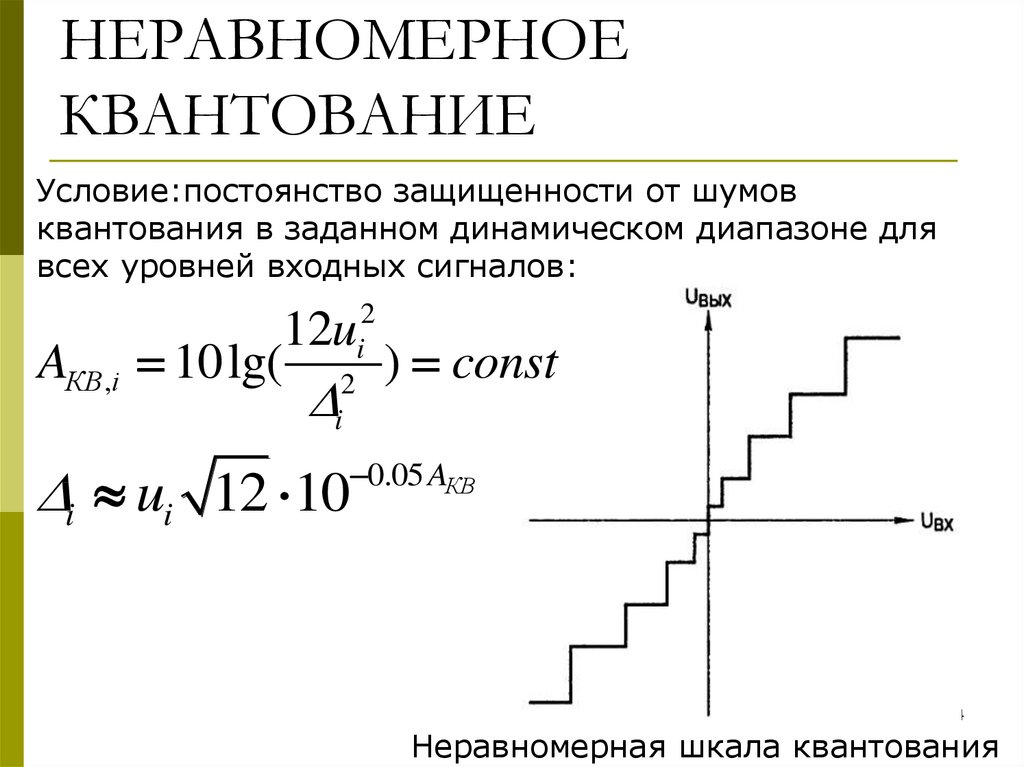
34. НЕРАВНОМЕРНОЕ КВАНТОВАНИЕ
Условие:постоянство защищенности от шумовквантования в заданном динамическом диапазоне для
всех уровней входных сигналов:
AКВ ,i
2
i
12u
10lg( 2 ) const
i
i ui 12 10
0.05 AКВ
34
Неравномерная шкала квантования
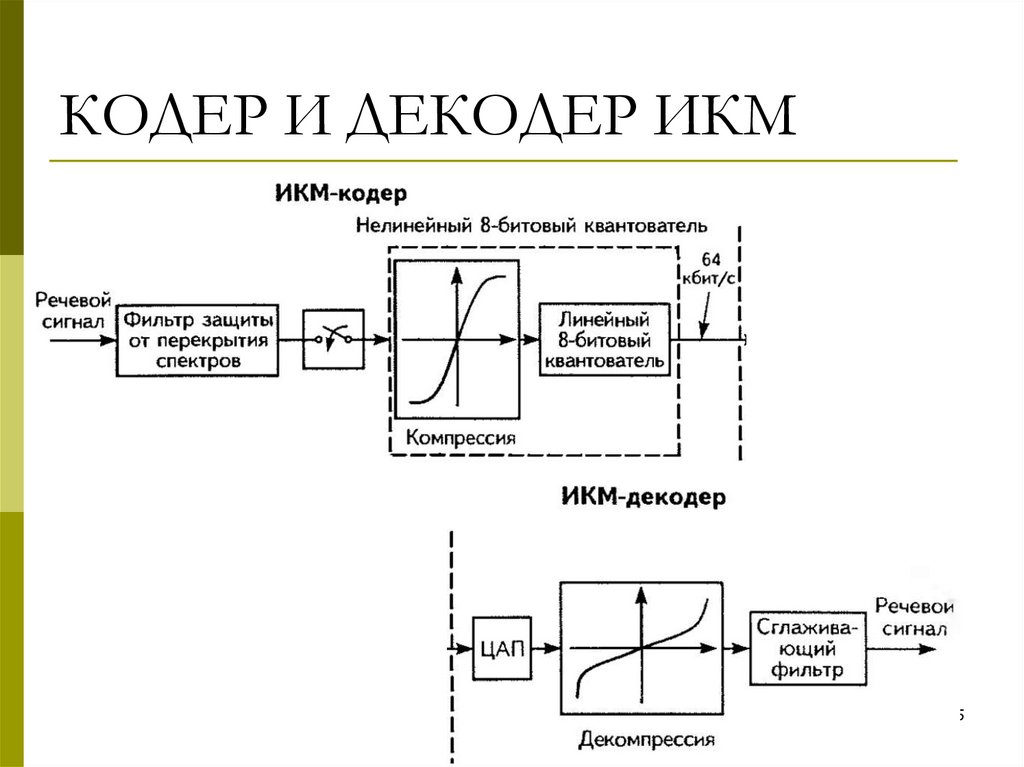
35. РЕАЛИЗАЦИЯ НЕРАВНОМЕРНОГО КВАНТОВАНИЯ
Компандирование – процесс сжатия (компрессии), азатем расширения (экспандирования)
uвых ,к (uвх ,к ) uвых ,э (uвх ,к ) 1
U
U (t )
Uˆ (t )
U
35
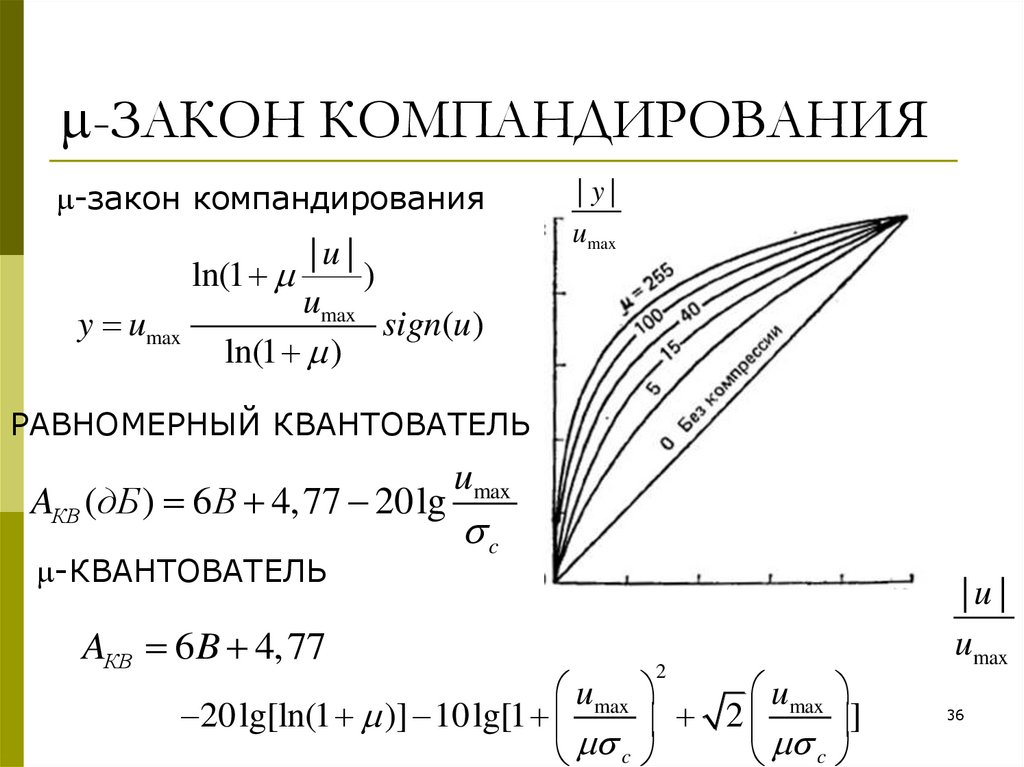
36. -ЗАКОН КОМПАНДИРОВАНИЯ
-ЗАКОН КОМПАНДИРОВАНИЯ-закон компандирования
y umax
|u|
ln(1
)
umax
sign(u )
ln(1 )
| y|
umax
РАВНОМЕРНЫЙ КВАНТОВАТЕЛЬ
AКВ (дБ ) 6 B 4, 77 20lg
-КВАНТОВАТЕЛЬ
AКВ 6 B 4, 77
umax
c
2
umax
umax
20 lg[ln(1 )] 10 lg[1
2
]
c
c
|u|
umax
36
37.
umaxc
umax
c
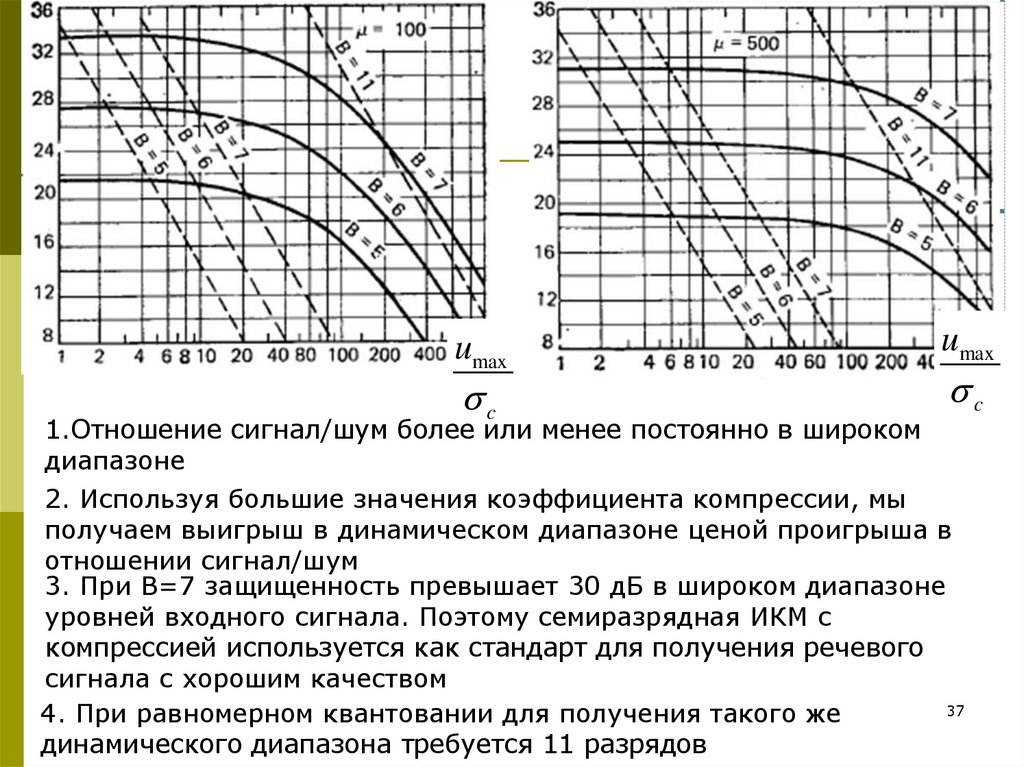
1.Отношение сигнал/шум более или менее постоянно в широком
диапазоне
2. Используя большие значения коэффициента компрессии, мы
получаем выигрыш в динамическом диапазоне ценой проигрыша в
отношении сигнал/шум
3. При В=7 защищенность превышает 30 дБ в широком диапазоне
уровней входного сигнала. Поэтому семиразрядная ИКМ с
компрессией используется как стандарт для получения речевого
сигнала с хорошим качеством
37
4. При равномерном квантовании для получения такого же
динамического диапазона требуется 11 разрядов
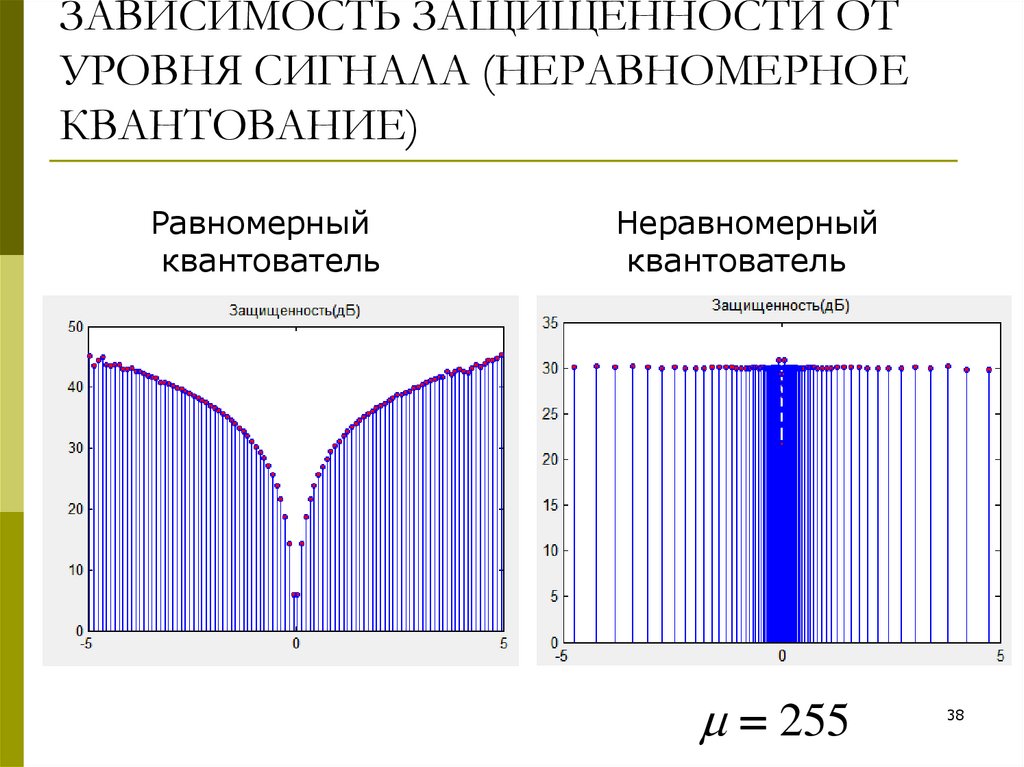
38. ЗАВИСИМОСТЬ ЗАЩИЩЕННОСТИ ОТ УРОВНЯ СИГНАЛА (НЕРАВНОМЕРНОЕ КВАНТОВАНИЕ)
Равномерныйквантователь
Неравномерный
квантователь
255
38
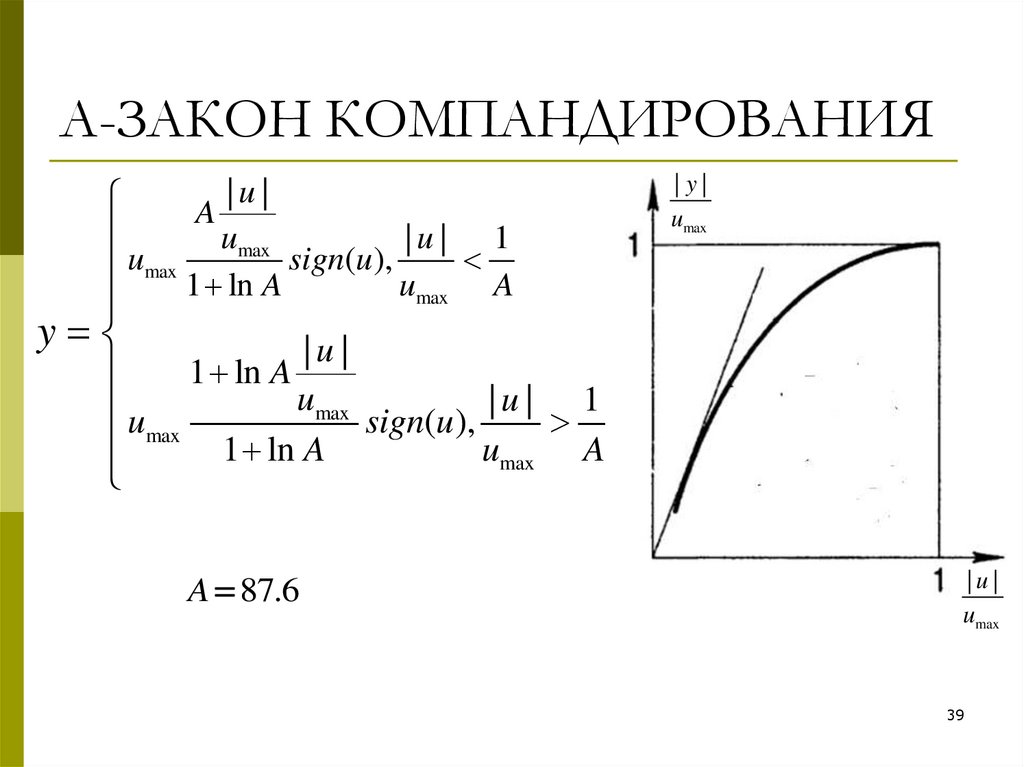
39. A-ЗАКОН КОМПАНДИРОВАНИЯ
|u|A
umax umax sign(u ), | u | 1
umax A
1 ln A
| y|
umax
y
|u|
1 ln A
umax
|u| 1
sign(u ),
umax
1 ln A
umax A
A 87.6
|u|
umax
39
40. ВЫИГРЫШ В ЗАЩИЩЕННОСТИ ПРИ НЕРАВНОМЕРНОМ КВАНТОВАНИИ ДЛЯ СЛАБЫХ СИГНАЛОВ (U<1/A )
ВЫИГРЫШ В ЗАЩИЩЕННОСТИ ПРИНЕРАВНОМЕРНОМ КВАНТОВАНИИ ДЛЯ
СЛАБЫХ СИГНАЛОВ (U<1/A )
При равномерном квантовании
WКВ , р
2
12
При неравномерном квантовании для слабых сигналов
WКВ ,н
2
min
min
12
Выигрыш в защищенности за счет неравномерного
квантования
2
2
12u
12u
A 10 lg 2 10 lg 2
min
A
min
1 ln A
A 87.6
20 lg
min
A 24дБ
40
41. ШУМЫ ОГРАНИЧЕНИЯ
Мгновенное значение шума ограничения:огр
u umax ; u umax
u umax ; u umax
Вероятность появления шума ограничения
poгр
umax
w(u )du
w(u )du
umax
Вероятность появления шума ограничения
(для симметричных распределений):
poгр 2
umax
w(u )du
41
42. ПРИМЕР. Мощность шума ограничения (для симметричных распределений)
Woгр2
poгр
(u umax )2 w(u)du
umax
Равномерное распределение:
1
,|u | ,
c
w( u )
2
12
0,|u | ;
/2
1
/ 2 U огр
poгр 2 du 2
U огр
1 2
U огр
1
U огр
3 c
42
43. ПРИМЕР
Гауссовское:poгр 2
w( u )
Лапласа:
U огр
u ;
u2
U огр
exp( 2 )du =2(1 Ф(
))
2
2
2 c
c
c
U огр
poгр 2
u2
w( u )
exp( 2 )
2 c
2 c2
1
1
,
,.
2
2
exp( |u |)
u
exp( | u |)du
= exp( U огр ) = exp(
c =
2U огр
c
)
2
43
44. ШУМЫ ОГРАНИЧЕНИЯ
Мощность шума ограничения и квантования(для симметричных распределений):
Woгр
2
poгр
(u umax ) w(u)du
2
umax
2
Wкв
1 poгр
umax
(u (u ))2 w(u)du
0
Мощность общего шума, возникающего при квантовании:
Wкв , s poгрWогр (1 poгр )Wкв
44






























 physics
physics








