Similar presentations:
Преобразование подобия
1.
КРУЖОК ПОГЕОМЕТРИИ
Январь, 2018
9 КЛАСС
Занятие 5.
Преобразование подобия
А. Блинков, г. Москва
w w w. m c c m e. r u
2.
Январь, 2018Пример 1
Являются ли подобными:
а) два прямоугольника, отличных от квадрата: картина
в рамке и картина без рамки, если ширина рамки
всюду одинакова (см. рис);
б) литровая и пол-литровая бутылки колы?
3.
Январь, 2018Пример 2
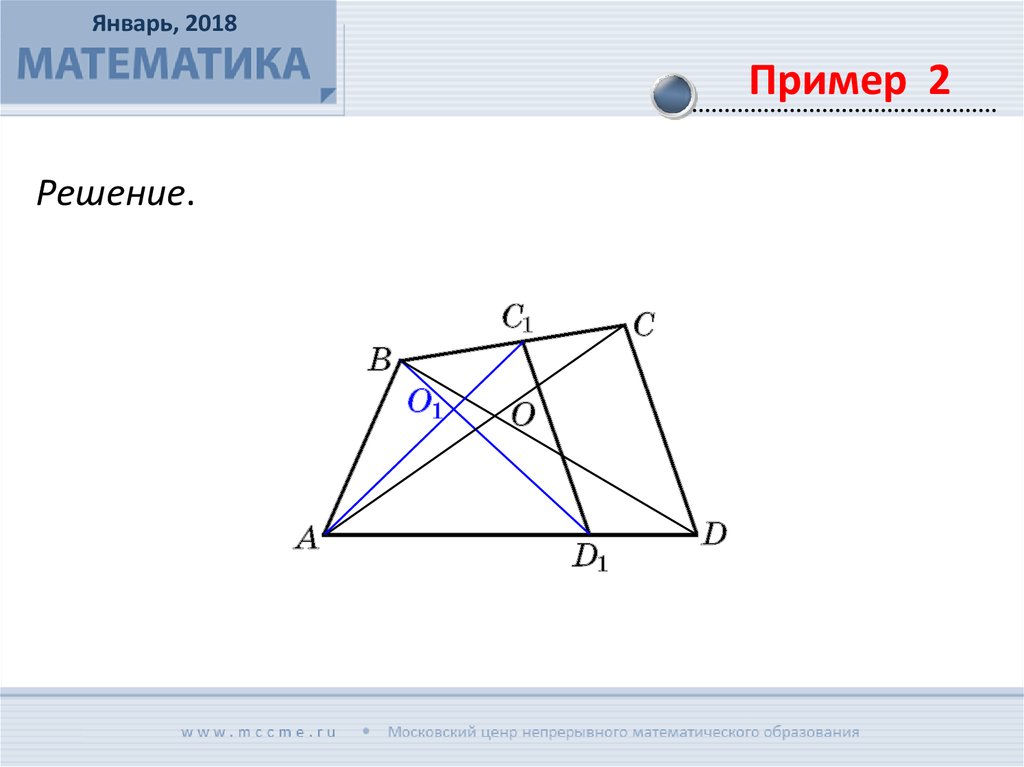
Докажите, что два четырехугольника подобны, если
у них соответственно равны три угла и углы между
диагоналями.
4.
Январь, 2018Пример 2
Решение.
5.
Январь, 2018Задача 1
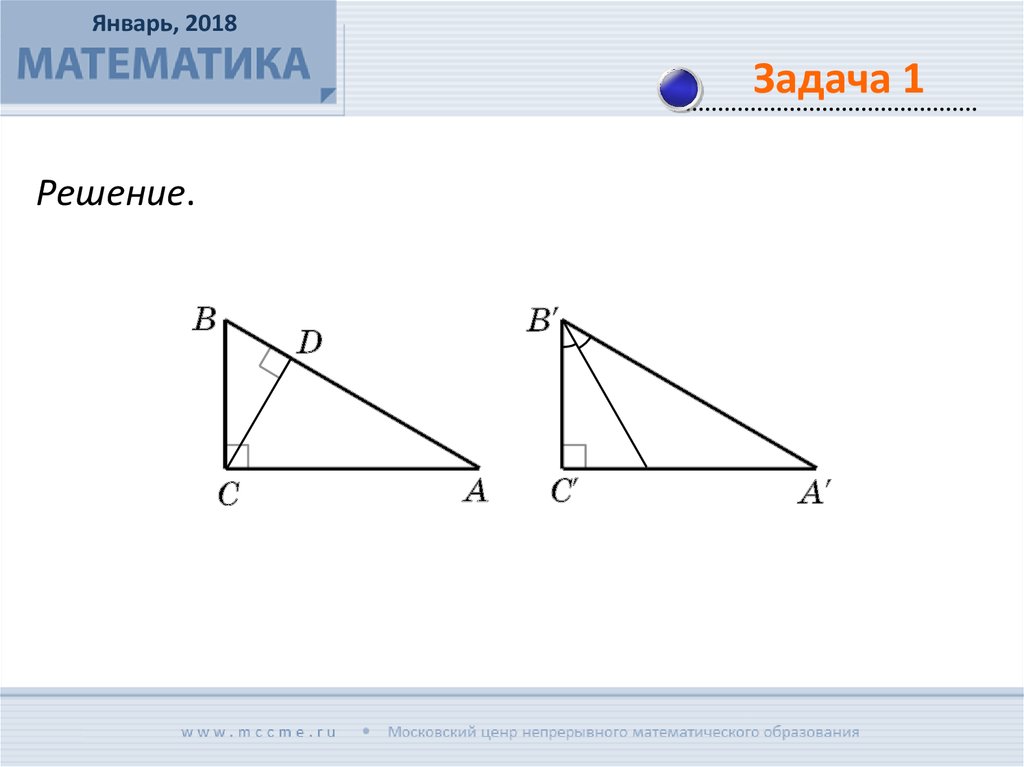
Каждый из двух подобных треугольников разрезали на
два треугольника так, что одна из получившихся частей
одного треугольника подобна одной из частей другого
треугольника. Обязательно ли подобны оставшиеся
части?
6.
Январь, 2018Задача 1
Решение.
7.
Январь, 2018Задача 2
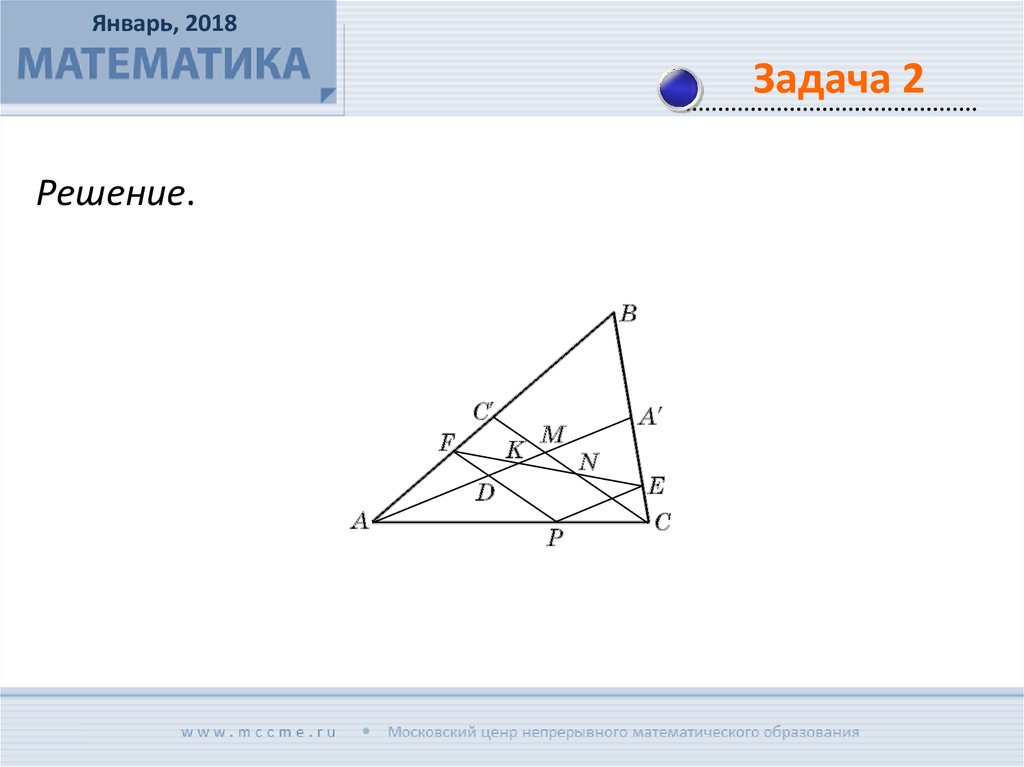
Через произвольную внутреннюю точку Р стороны АС
треугольника АВС проведены прямые, параллельные
его медианам AA' и СС'. Эти прямые пересекают
стороны ВС и АВ в точках Е и F соответственно.
Докажите, что отрезок ЕF делится медианами AA’ и СС’
на три равные части.
8.
Январь, 2018Задача 2
Решение.
9.
Январь, 2018Задача 3
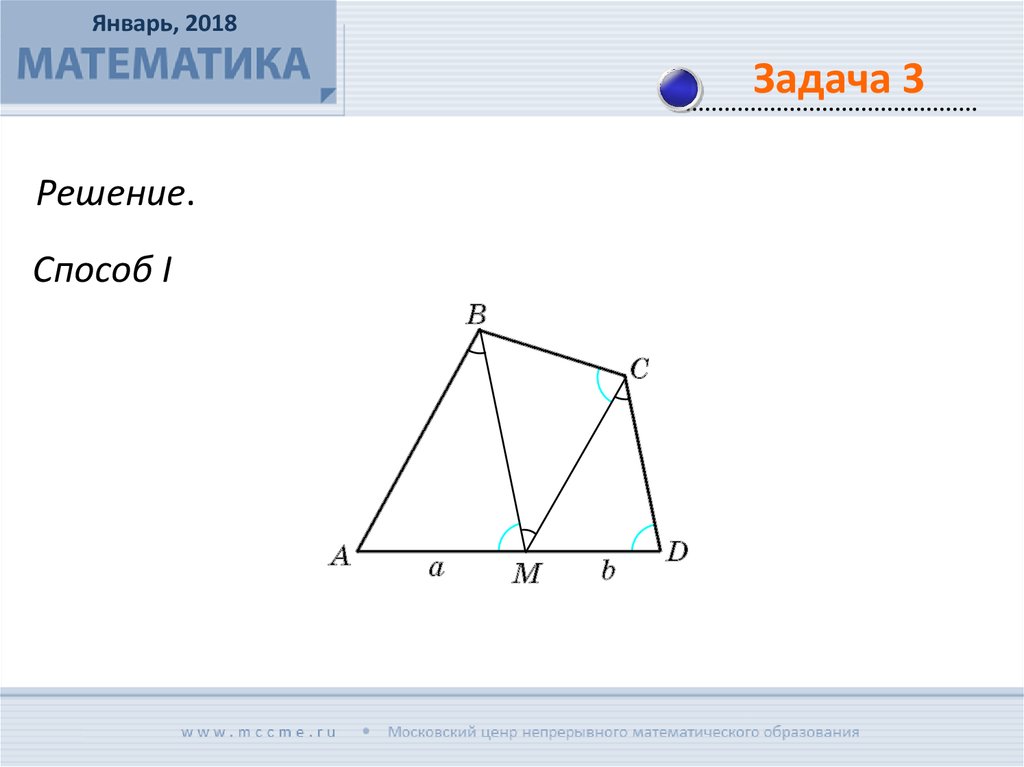
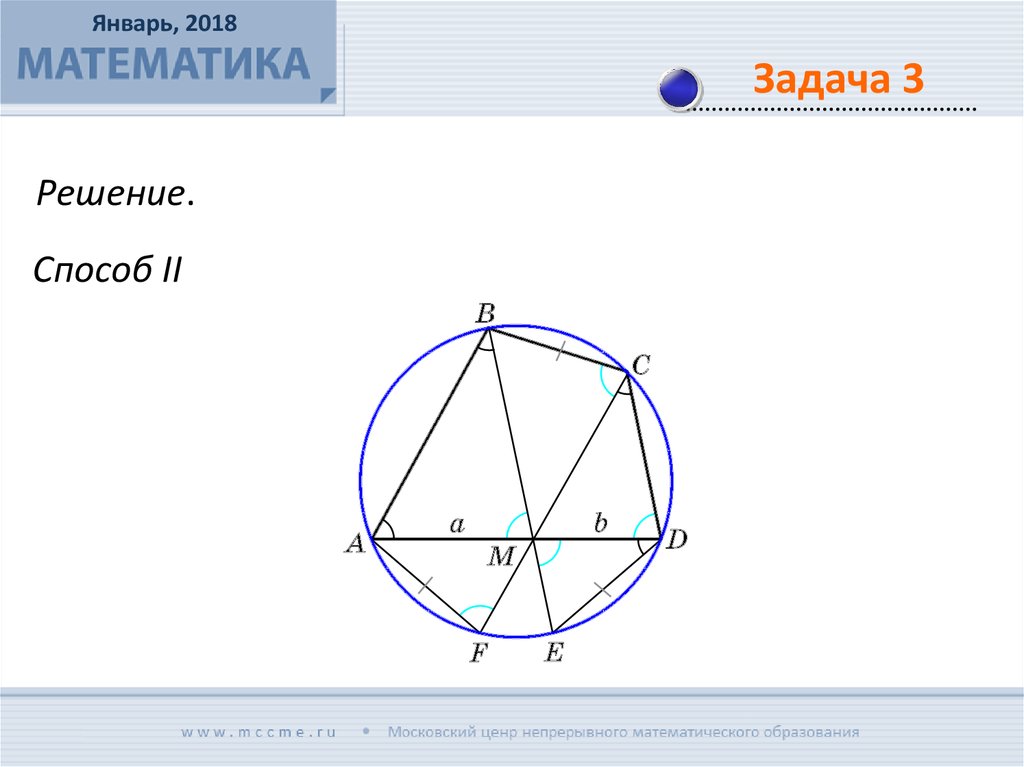
Во вписанном четырехугольнике АВСD точка М лежит
на стороне AD, причем BM ǁ CD и CM ǁ BA. Найдите ВС,
если АМ = а, DM = b.
10.
Январь, 2018Задача 3
Решение.
Способ I
11.
Январь, 2018Задача 3
Решение.
Способ II
12.
Январь, 2018Задача 4
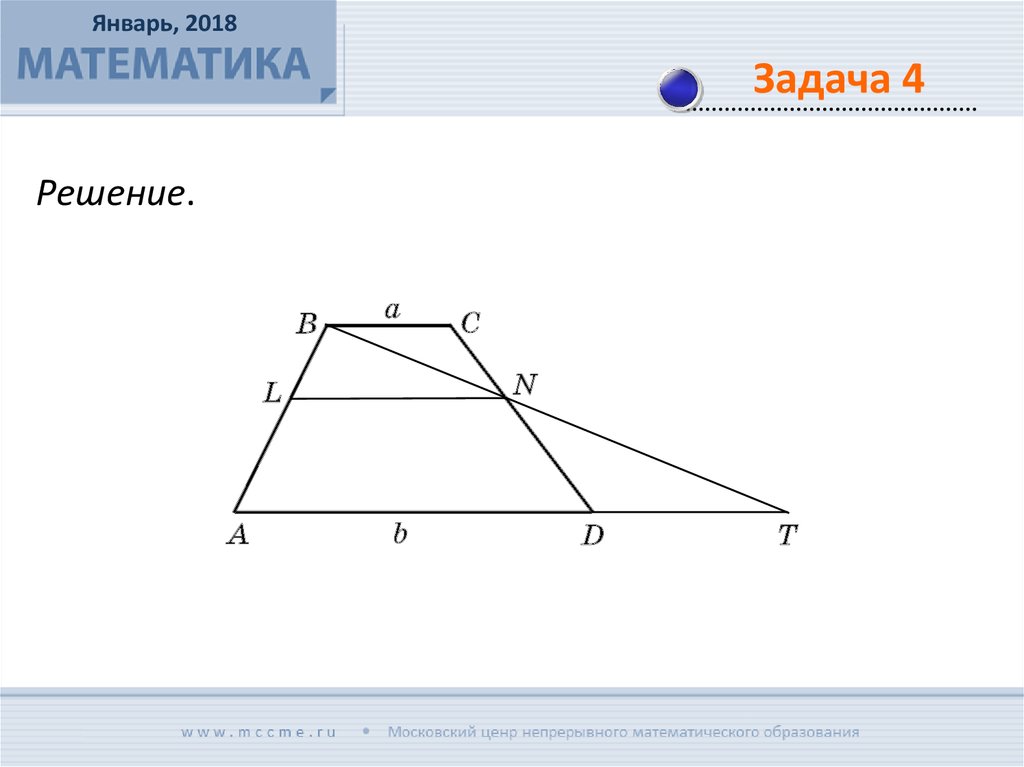
В трапеции АВСD с основаниями ВС = а и AD = b
проведен отрезок LN = ab с концами на боковых
сторонах. Докажите, что он разделил трапецию на две
подобные.
13.
Январь, 2018Задача 4
Решение.
14.
Январь, 2018Задача 5
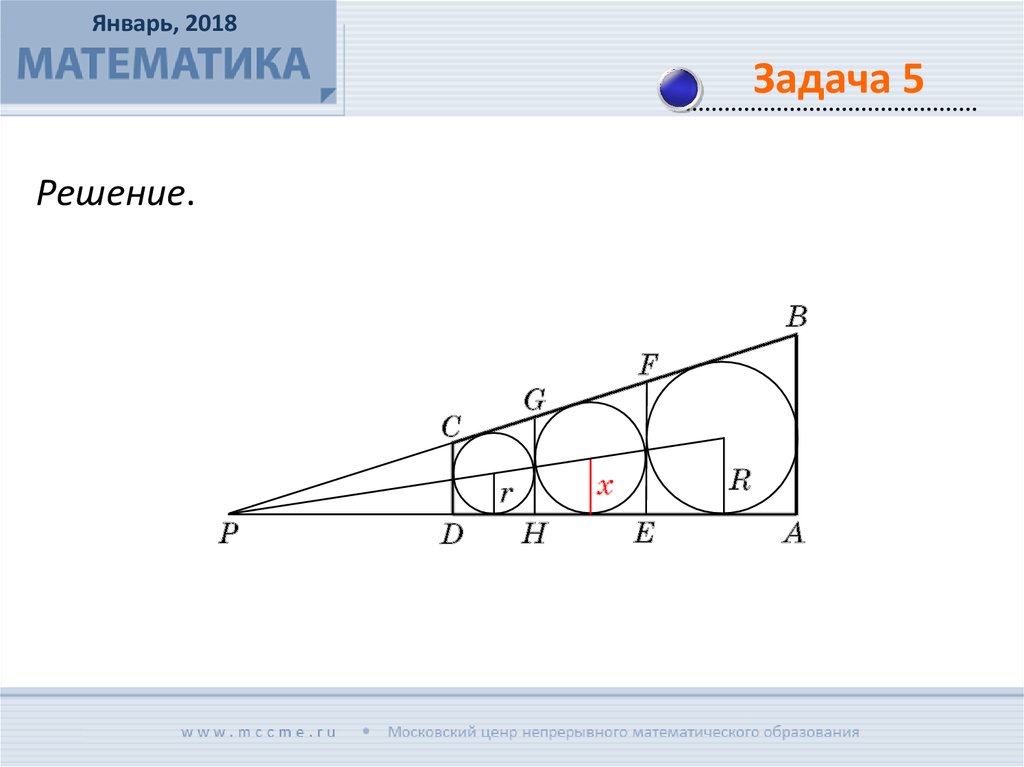
Трапеция разделена на три трапеции прямыми,
параллельными основаниям. Известно, что в каждую
из трех получившихся трапеций можно вписать
окружность. Найдите радиус окружности, вписанной
в среднюю трапецию, если радиусы окружностей,
вписанных в две крайние, равны R и r.
15.
Январь, 2018Задача 5
Решение.
16.
Январь, 2018Задача 6
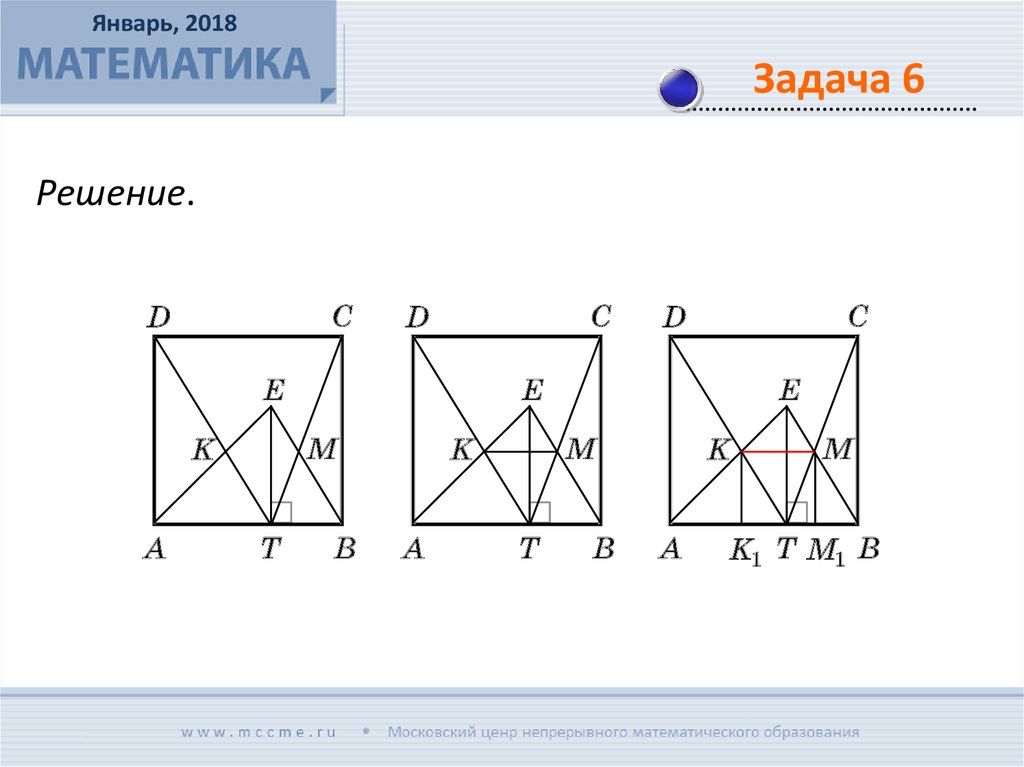
Внутри квадрата ABCD взята точка Е, ET – высота
треугольника АВЕ, K – точка пересечения прямых DT и
AE, М – точка пересечения прямых СТ и ВЕ. Докажите,
что отрезок KМ является стороной квадрата,
вписанного в треугольник АВЕ.
17.
Январь, 2018Задача 6
Решение.
18.
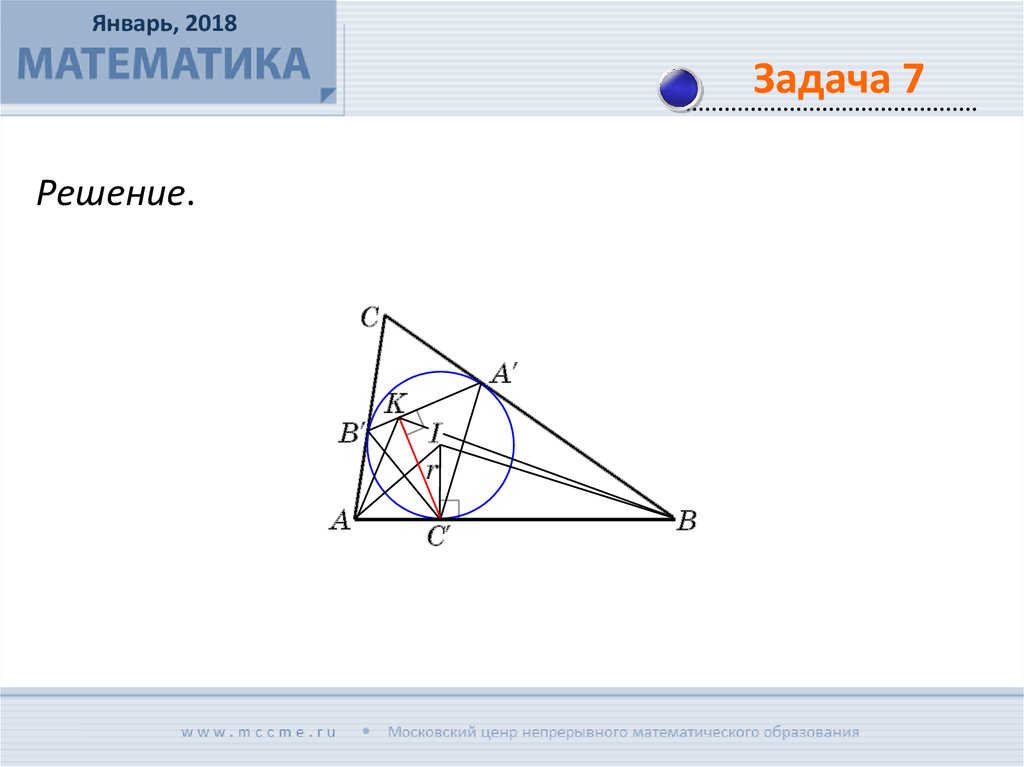
Январь, 2018Задача 7
Вписанная окружность треугольника ABC касается его
сторон ВС, АС и АВ в точках A', B' и C' соответственно.
Точка K – проекция точки C' на прямую A'B'. Докажите,
что KC' – биссектриса угла AKB.
19.
Январь, 2018Задача 7
Решение.
20.
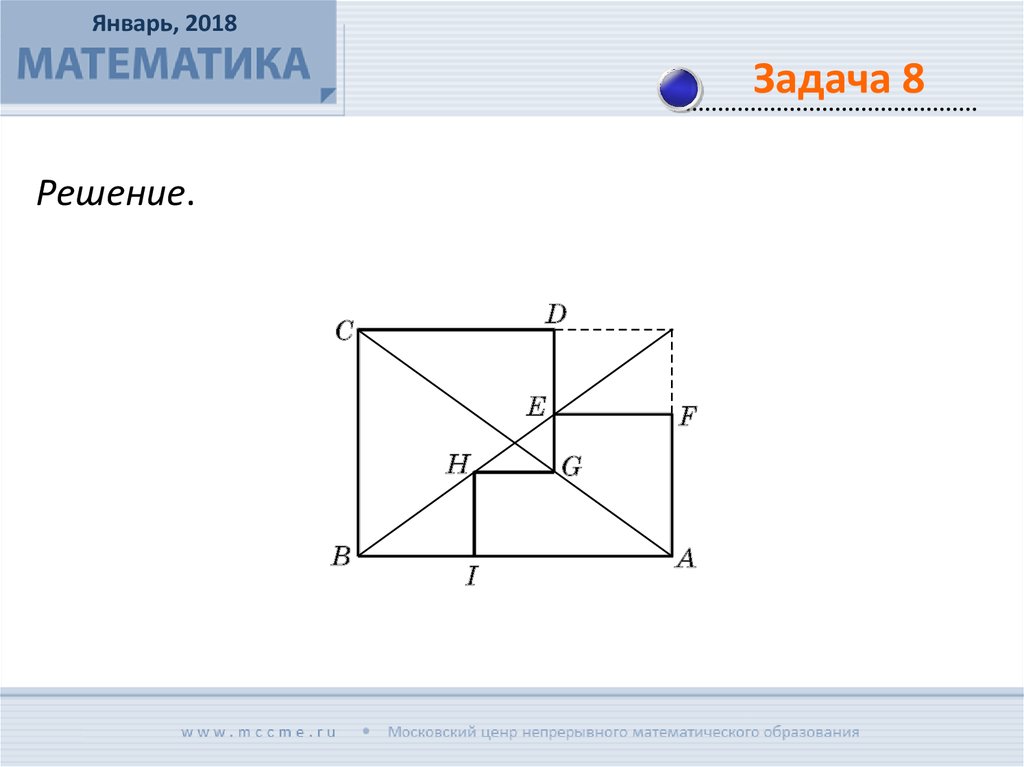
Январь, 2018Задача 8
Докажите, что существует такой невыпуклый
шестиугольник, у которого каждый угол равен либо
90°, либо 270°, что его можно разрезать на два
подобных
ему
и
неравных
между
собой
шестиугольника.
21.
Январь, 2018Задача 8
Решение.











 mathematics
mathematics








