Options

1.

22.1 Options
22.2 Call Options
22.3 Put Options
22.4 Selling Options
22.5 Stock Option Quotations
22.6 Combinations of Options
22.7 Valuing Options
22.8 An Option‑Pricing Formula
22.9 Stocks and Bonds as Options
22.10 Capital-Structure Policy and Options
22.11 Mergers and Options
22.12 Investment in Real Projects and Options
22.13 Summary and Conclusions

2. 22.1 Options

• Many corporate securities are similar to the stock
options that are traded on organized exchanges.
• Almost every issue of corporate stocks and bonds
has option features.
• In addition, capital structure and capital budgeting
decisions can be viewed in terms of options.

3. 22.1 Options Contracts: Preliminaries

• An option gives the holder the right, but not the
obligation, to buy or sell a given quantity of an asset on
(or perhaps before) a given date, at prices agreed upon
today.
• Calls versus Puts
– Call options gives the holder the right, but not the
obligation, to buy a given quantity of some asset at some
time in the future, at prices agreed upon today. When
exercising a call option, you “call in” the asset.
– Put options gives the holder the right, but not the obligation,
to sell a given quantity of an asset at some time in the
future, at prices agreed upon today. When exercising a put,
you “put” the asset to someone.

4. 22.1 Options Contracts: Preliminaries

• Exercising the Option
– The act of buying or selling the underlying asset through
the option contract.
• Strike Price or Exercise Price
– Refers to the fixed price in the option contract at which
the holder can buy or sell the underlying asset.
• Expiry
– The maturity date of the option is referred to as the
expiration date, or the expiry.
• European versus American options
– European options can be exercised only at expiry.
– American options can be exercised at any time up to
expiry.

5. Options Contracts: Preliminaries

• In-the-Money
– The exercise price is less than the spot price of
the underlying asset.
• At-the-Money
– The exercise price is equal to the spot price of
the underlying asset.
• Out-of-the-Money
– The exercise price is more than the spot price of
the underlying asset.

6. Options Contracts: Preliminaries

• Intrinsic Value
– The difference between the exercise price of the
option and the spot price of the underlying
asset.
• Speculative Value
– The difference between the option premium and
the intrinsic value of the option.
Option
Premium
=
Intrinsic
Value
Speculative
+
Value

7. 22.2 Call Options

• Call options gives the holder the right, but not the
obligation, to buy a given quantity of some asset
on or before some time in the future, at prices
agreed upon today.
• When exercising a call option, you “call in” the
asset.

8. Basic Call Option Pricing Relationships at Expiry

• At expiry, an American call option is worth the
same as a European option with the same
characteristics.
• If the call is in-the-money, it is worth ST - E.
• If the call is out-of-the-money, it is worthless.
CaT = CeT = Max[ST - E, 0]
• Where
ST is the value of the stock at expiry (time T)
E is the exercise price.
CaT is the value of an American call at expiry
CeT is the value of a European call at expiry

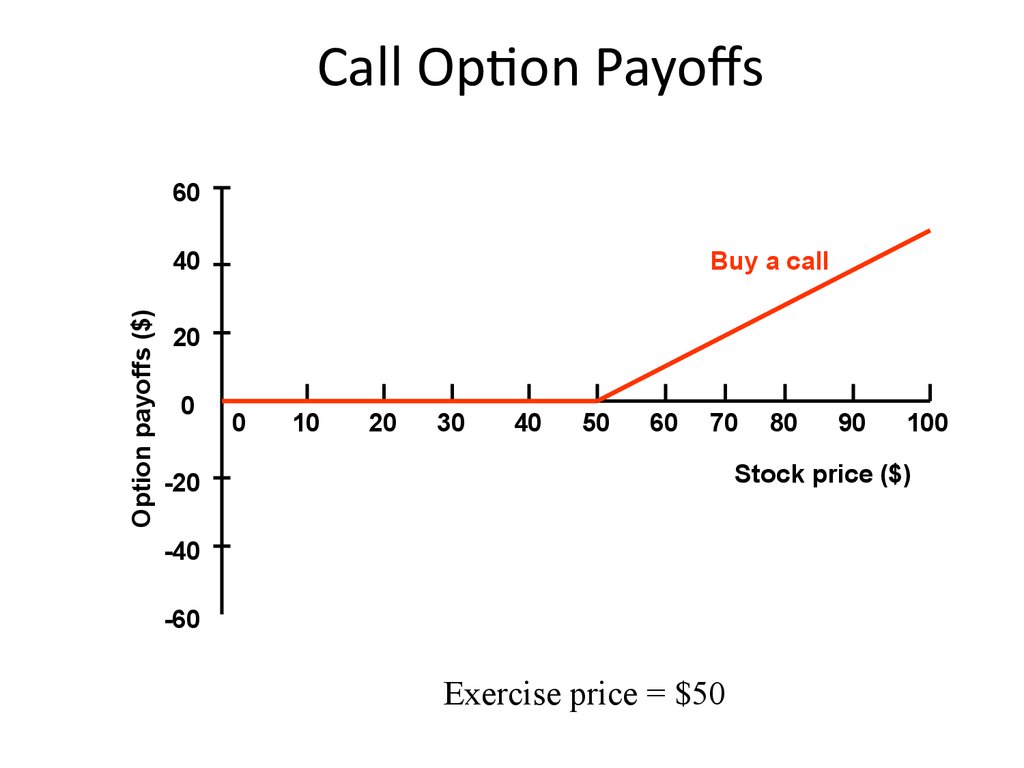
9. Call Option Payoffs

60
Option payoffs ($)
40
Buy a call
20
0
0
10
20
30
40
50
60
70
80
90
100
Stock price ($)
-20
-40
-60
Exercise price = $50

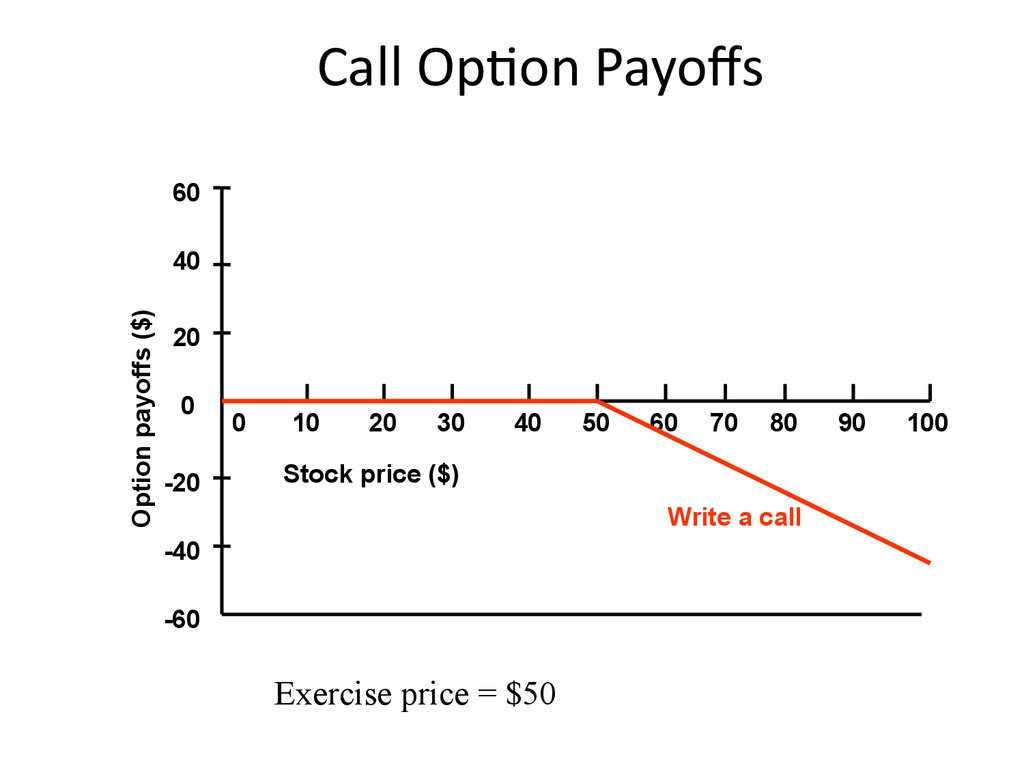
10. Call Option Payoffs

60
Option payoffs ($)
40
20
0
-20
0
10
20
30
40
50
60
70
80
Stock price ($)
Write a call
-40
-60
Exercise price = $50
90
100

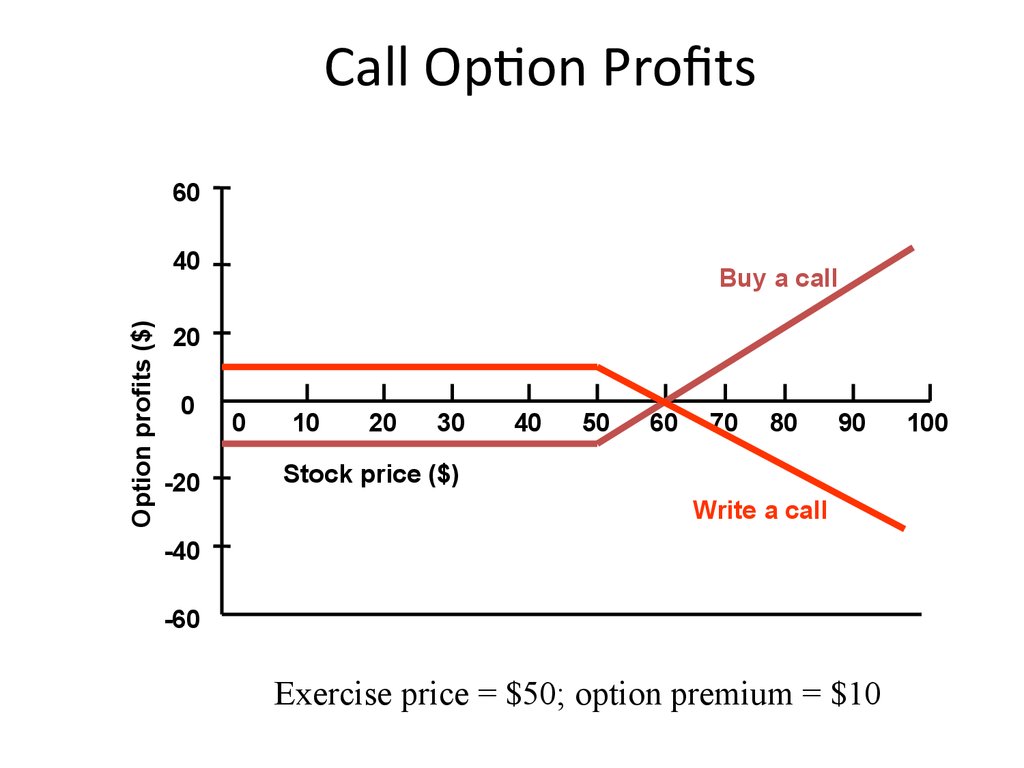
11. Call Option Profits

60
Option profits ($)
40
Buy a call
20
0
-20
0
10
20
30
40
50
60
70
80
90
Stock price ($)
Write a call
-40
-60
Exercise price = $50; option premium = $10
100

12. 22.3 Put Options

• Put options give the holder the right, but not the
obligation, to sell a given quantity of an asset on
or before some time in the future, at prices
agreed upon today.
• When exercising a put, you “put” the asset to
someone.

13. Basic Put Option Pricing Relationships at Expiry

• At expiry, an American put option is worth the
same as a European option with the same
characteristics.
• If the put is in-the-money, it is worth E - ST.
• If the put is out-of-the-money, it is worthless.
PaT = PeT = Max[E - ST, 0]

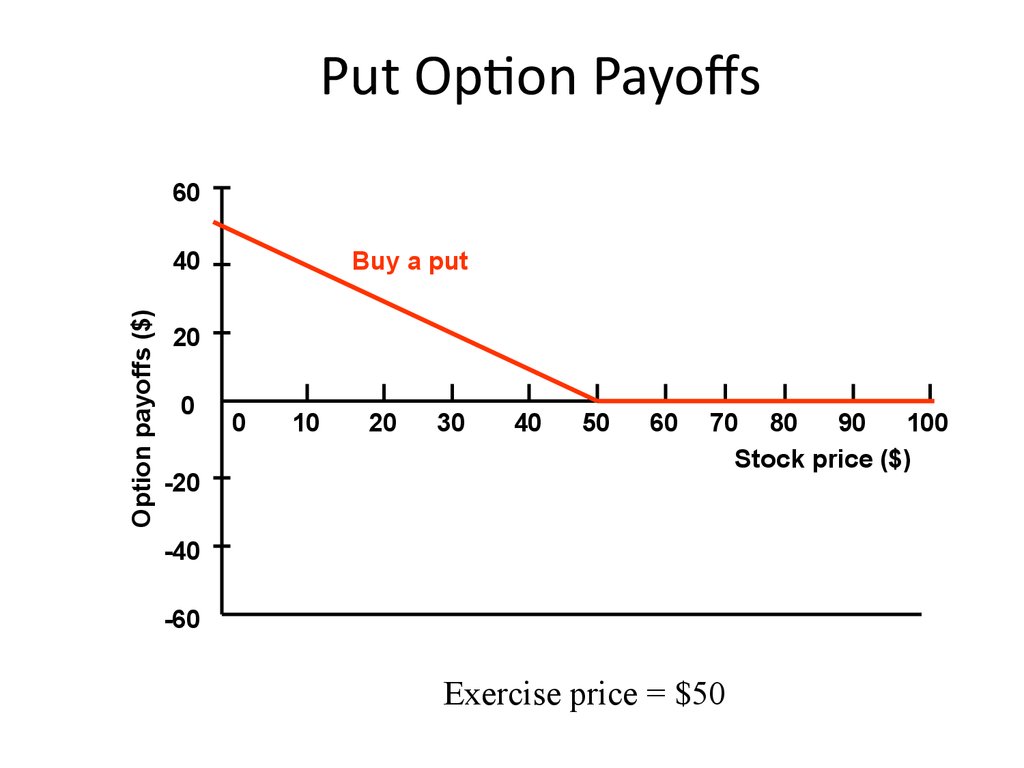
14. Put Option Payoffs

60
Option payoffs ($)
40
Buy a put
20
0
-20
0
10
20
30
40
50
60
70 80
90
100
Stock price ($)
-40
-60
Exercise price = $50

15. Put Option Payoffs

60
Option payoffs ($)
40
20
0
0
10
20
30
-20
-40
40
50
60
70 80
90
100
Stock price ($)
write a put
-60
Exercise price = $50

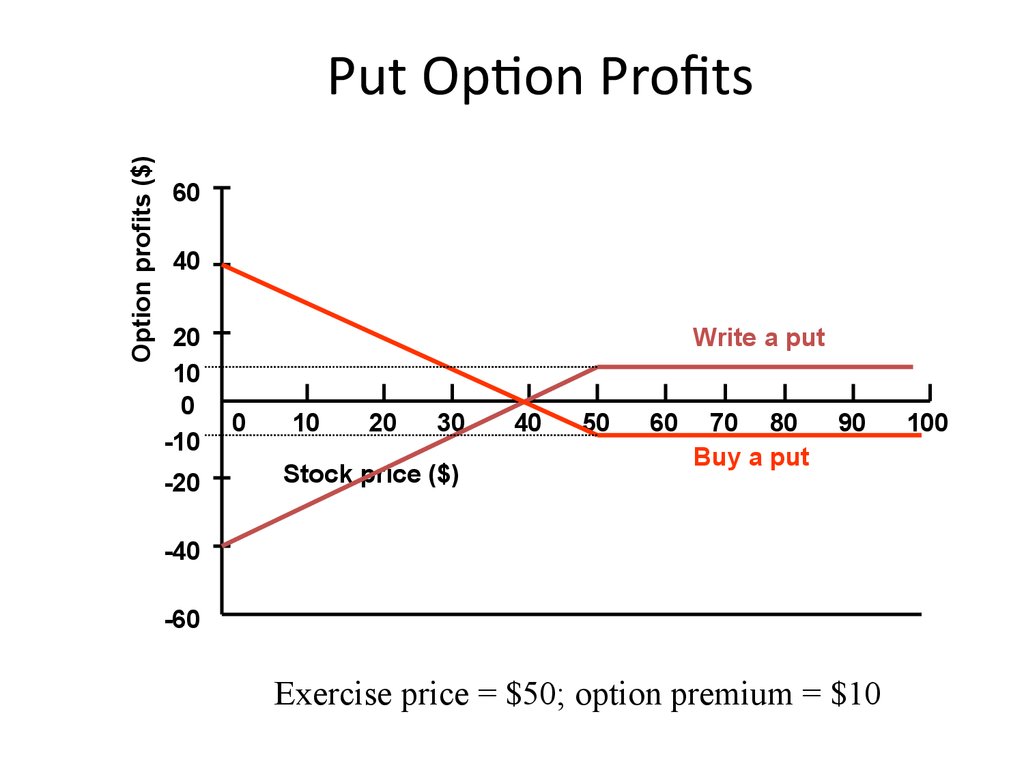
16. Put Option Profits

Option profits ($)
Put Option Profits
60
40
20
10
0
-10
-20
Write a put
0
10
20
30
Stock price ($)
40
50
60
70 80
Buy a put
90
-40
-60
Exercise price = $50; option premium = $10
100

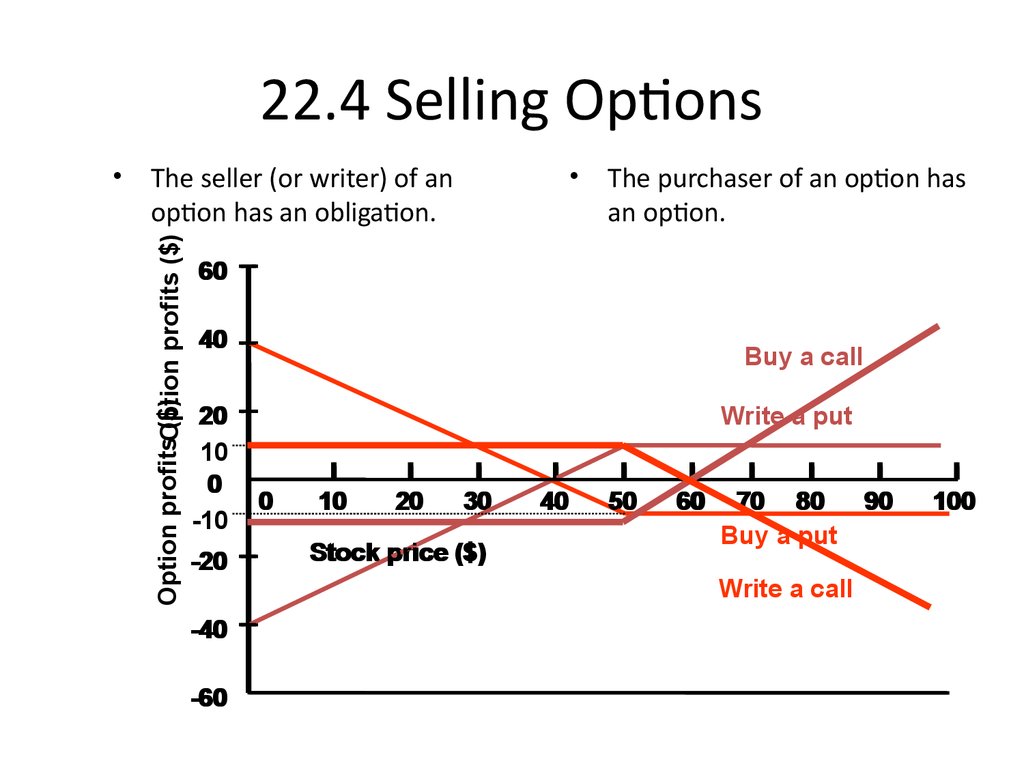
17. 22.4 Selling Options

The seller (or writer) of an
option has an obligation.
Option profitsOption
($)
profits ($)
The purchaser of an option has
an option.
60
40
20
10
0
-10
-20
-40
-60
Buy a call
Write a put
0
10
20
30
Stock price ($)
40
50
60
70 80
Buy a put
Write a call
90
100

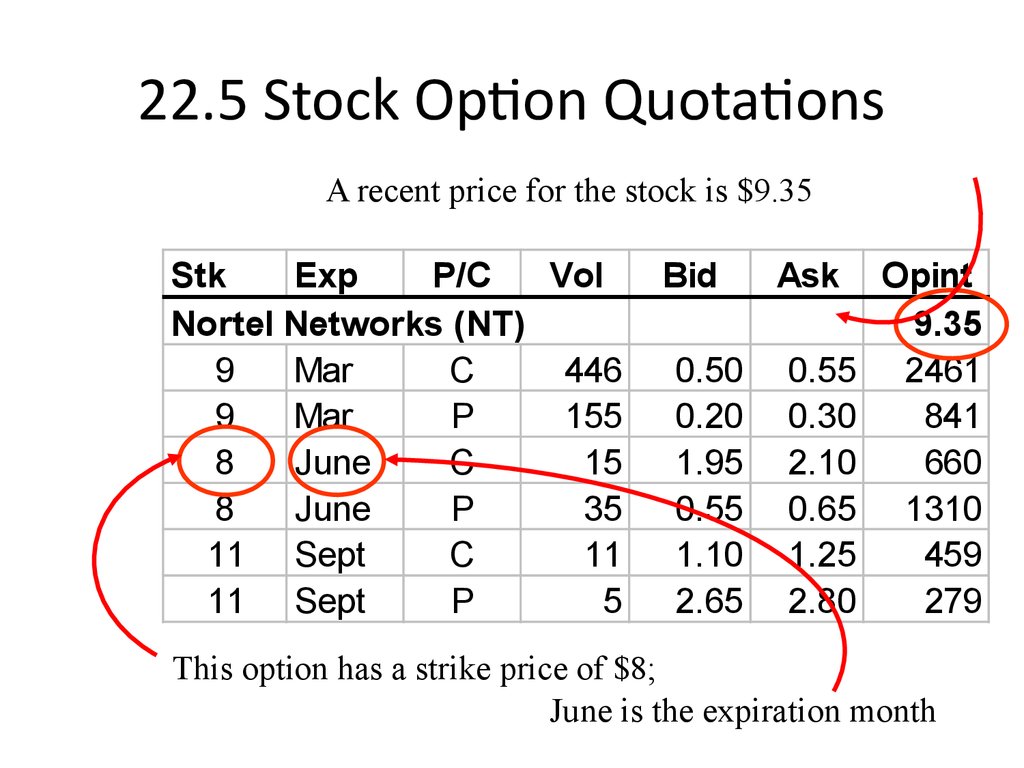
18. 22.5 Stock Option Quotations

Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279

19. 22.5 Stock Option Quotations

A recent price for the stock is $9.35
Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279
This option has a strike price of $8;
June is the expiration month

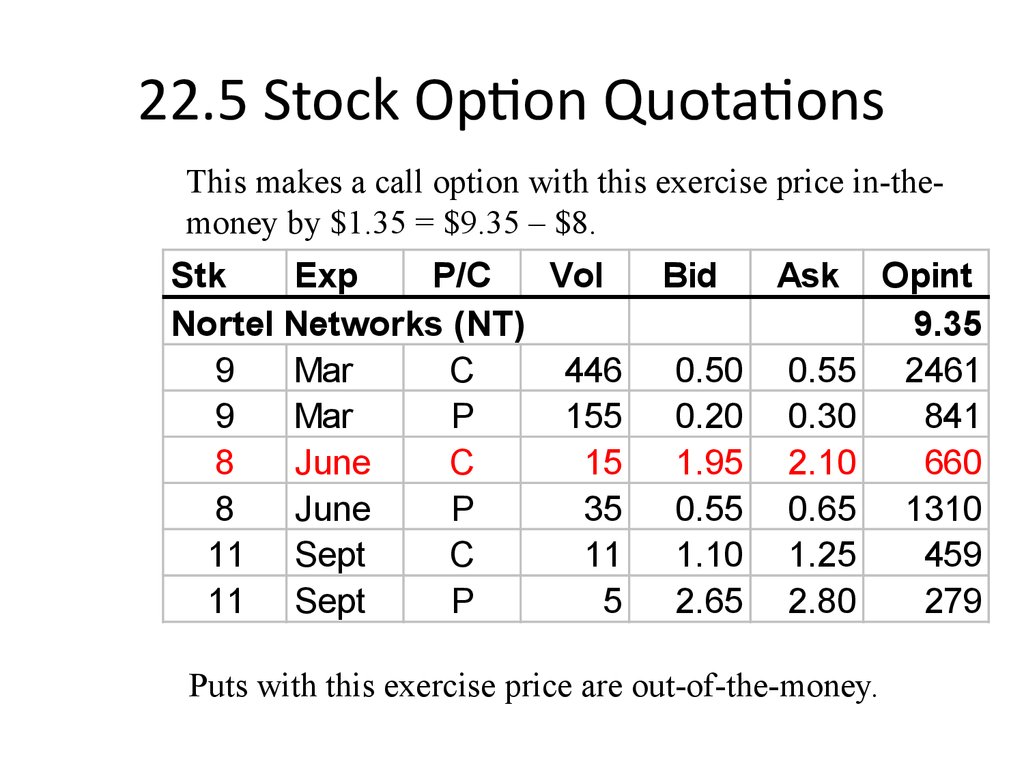
20. 22.5 Stock Option Quotations

This makes a call option with this exercise price in-themoney by $1.35 = $9.35 – $8.
Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Puts with this exercise price are out-of-the-money.
Opint
9.35
2461
841
660
1310
459
279

21. 22.5 Stock Option Quotations

Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279
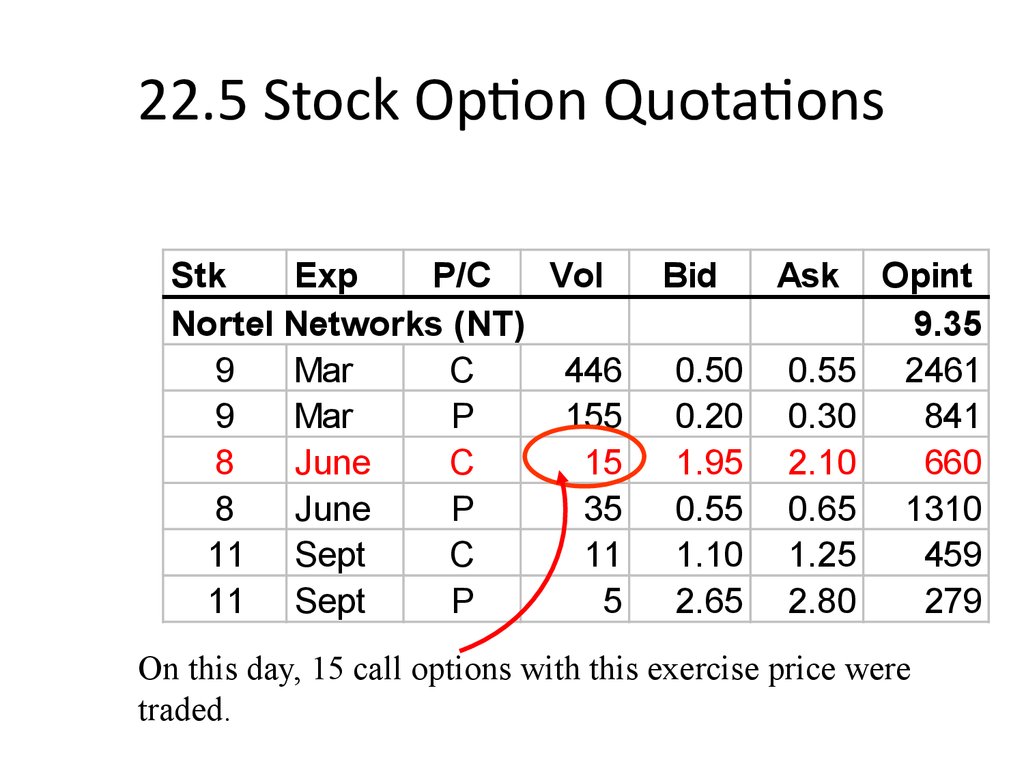
On this day, 15 call options with this exercise price were
traded.

22. 22.5 Stock Option Quotations

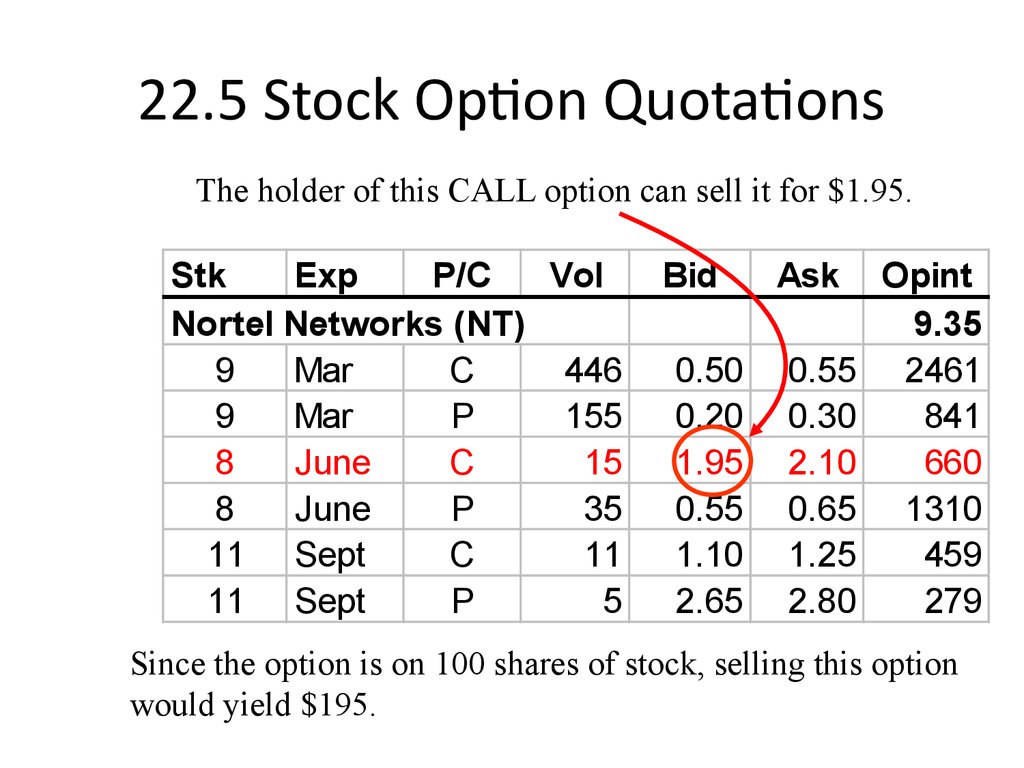
The holder of this CALL option can sell it for $1.95.
Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279
Since the option is on 100 shares of stock, selling this option
would yield $195.

23.

22.5 Stock Option Quotations
Buying this CALL option costs $2.10.
Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279
Since the option is on 100 shares of stock, buying this option
would cost $210.

24. 22.5 Stock Option Quotations

Stk
Exp
P/C
Vol
Nortel Networks (NT)
9
Mar
C
446
9
Mar
P
155
8
June
C
15
8
June
P
35
11 Sept
C
11
11 Sept
P
5
Bid
0.50
0.20
1.95
0.55
1.10
2.65
Ask
0.55
0.30
2.10
0.65
1.25
2.80
Opint
9.35
2461
841
660
1310
459
279
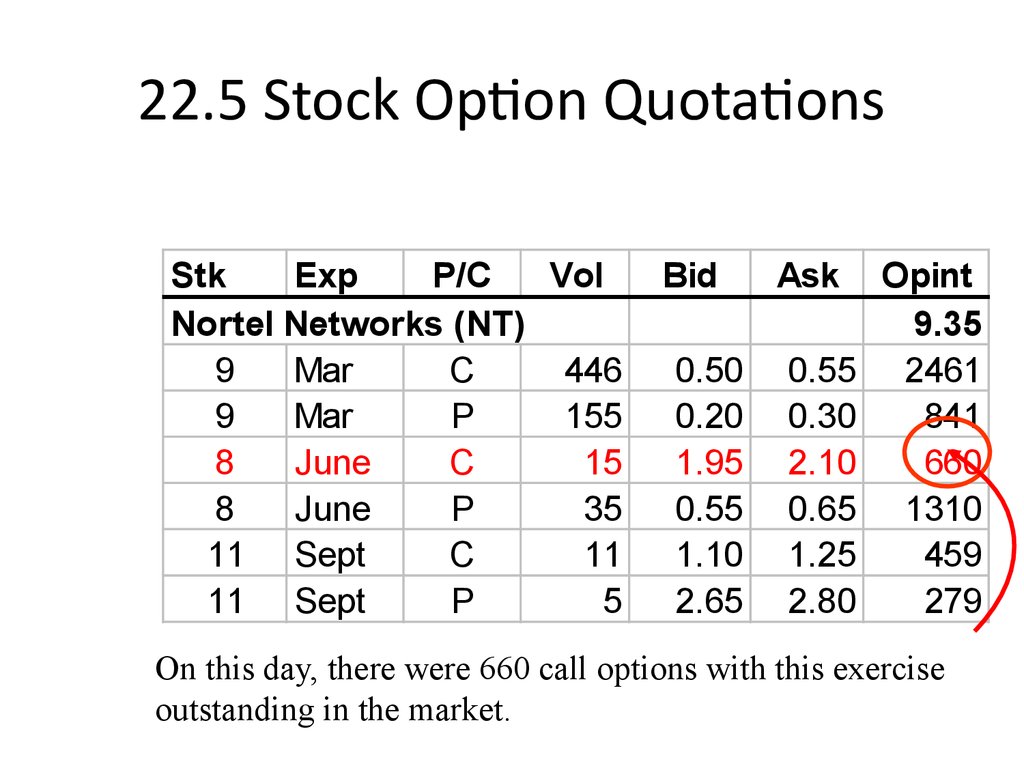
On this day, there were 660 call options with this exercise
outstanding in the market.

25. 22.6 Combinations of Options

• Puts and calls can serve as the building blocks
for more complex option contracts.
• If you understand this, you can become a
financial engineer, tailoring the risk-return
profile to meet your client’s needs.

26. Protective Put Strategy: Buy a Put and Buy the Underlying Stock: Payoffs at Expiry

Value at
expiry
Protective Put strategy has
downside protection and
upside potential
$50
Buy the
stock
Buy a put with an exercise
price of $50
$0
$50
Value of
stock at
expiry

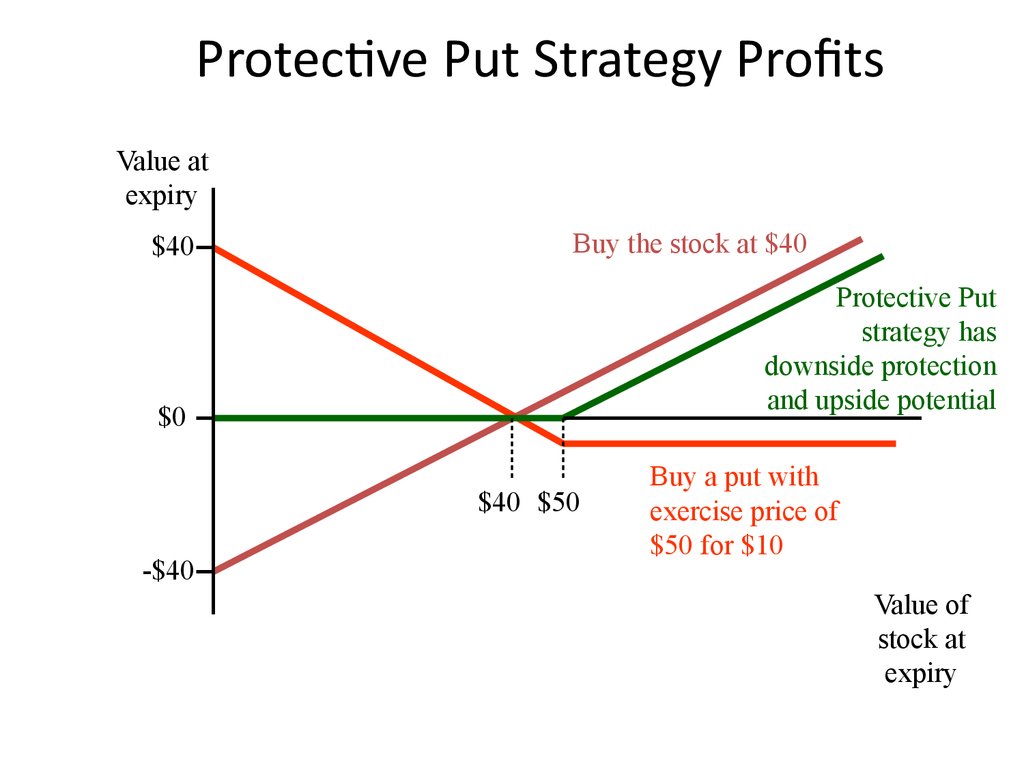
27. Protective Put Strategy Profits

Value at
expiry
$40
Buy the stock at $40
Protective Put
strategy has
downside protection
and upside potential
$0
$40 $50
-$40
Buy a put with
exercise price of
$50 for $10
Value of
stock at
expiry

28. Covered Call Strategy

Value at
expiry
$40
Buy the stock at $40
Covered call
$10
$0
Value of stock at expiry
$30 $40 $50
-$30
-$40
Sell a call with
exercise price of
$50 for $10

29. Long Straddle: Buy a Call and a Put

Value at
expiry
Buy a call with an
exercise price of
$50 for $10
$40
$30
$0
-$10
-$20
$30 $40 $50 $60
Buy a put with an
$70 exercise price of
$50 for $10
A Long Straddle only makes money if the
stock price moves $20 away from $50.
Value of
stock at
expiry

30. Short Straddle: Sell a Call and a Put

Value at
expiry
$20
$10
$0
A Short Straddle only loses money if the stock
price moves $20 away from $50.
Sell a put with exercise price of
$50 for $10
Value of stock at
expiry
-$30
-$40
$30 $40 $50 $60 $70
Sell a call with an
exercise price of $50 for $10

31. Long Call Spread

Value at
expiry
Buy a call with an
exercise price of
$50 for $10
$5
$0
-$5
-$10
long call spread
$50 $60
Value of
stock at
expiry
$55
Sell a call with exercise
price of $55 for $5

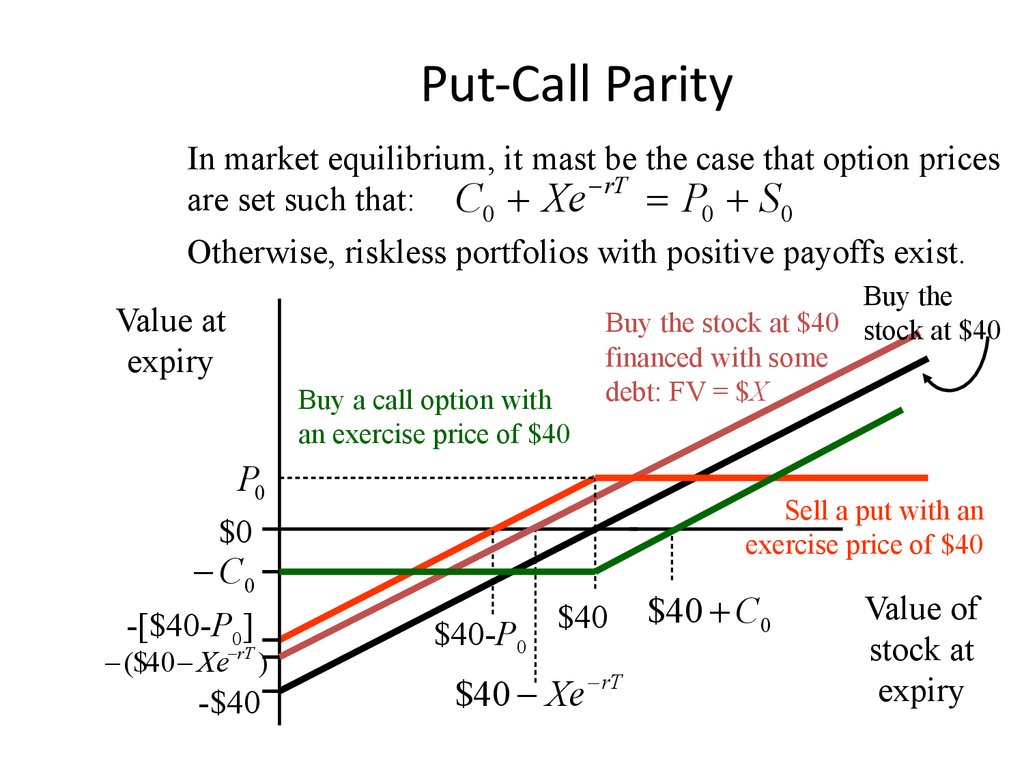
32. Put-Call Parity

In market equilibrium, it mast be the case that option prices
rT
are set such that: C0 Xe
P0 S0
Otherwise, riskless portfolios with positive payoffs exist.
Value at
expiry
Buy a call option with
an exercise price of $40
Buy the
Buy the stock at $40 stock at $40
financed with some
debt: FV = $X
P0
Sell a put with an
exercise price of $40
$0
C0
-[$40-P0]
rT
($40 Xe )
-$40
$40-P0
$40
$40 Xe rT
$40 C0
Value of
stock at
expiry

33. 22.7 Valuing Options

• The last section
concerned itself with
the value of an option
at expiry.
• This section considers
the value of an option
prior to the expiration
date.
• A much more
interesting question.

34. Option Value Determinants

Call
1.
2.
3.
4.
5.
Stock price
Exercise price
Interest rate
Volatility in the stock price
Expiration date
Put
+
–
+
+
+
–
+
–
+
+
The value of a call option C0 must fall within
max (S0 – E, 0) < C0 < S0.
The precise position will depend on these factors.

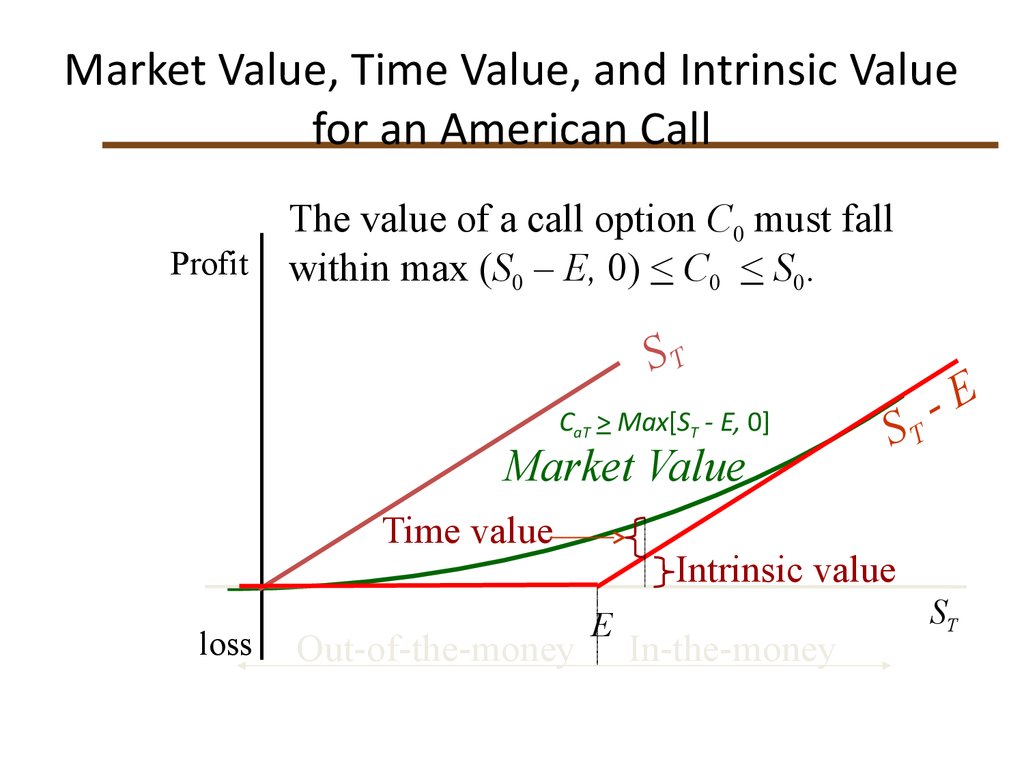
35. Market Value, Time Value, and Intrinsic Value for an American Call

Profit
The value of a call option C0 must fall
within max (S0 – E, 0) < C0 < S0.
ST
CaT > Max[ST - E, 0]
Market Value
Time value
loss
Out-of-the-money
ST
-E
Intrinsic value
E
In-the-money
ST

36. 22.8 An Option‑Pricing Formula

• We will start with a
binomial option pricing
formula to build our
intuition.
• Then we will graduate
to the normal
approximation to the
binomial for some realworld option valuation.

37. Binomial Option Pricing Model

Suppose a stock is worth $25 today and in one period will
either be worth 15% more or 15% less. S0= $25 today and in
one year S1 is either $28.75 or $21.25. The risk-free rate is 5%.
What is the value of an at-the-money call option?
S0
S1
$28.75
$25
$21.25

38. Binomial Option Pricing Model

1. A call option on this stock with exercise price
of $25 will have the following payoffs.
2. We can replicate the payoffs of the call
option. With a levered position in the stock.
S0
S1
C1
$28.75
$3.75
$21.25
$0
$25

39. Binomial Option Pricing Model

Borrow the present value of $21.25 today and
buy one share.
The net payoff for this levered equity portfolio
in one period is either $7.50 or $0.
TheS levered equity
portfolio
has portfolio
twice the C
S
debt
(
)
=
0
1
1
option’s payoff$28.75
so the
portfolio
is worth$3.75
twice
- $21.25
= $7.50
the call option value.
$25
$21.25- $21.25 =
$0
$0

40. Binomial Option Pricing Model

The levered equity portfolio value today is
today’s value of one share less the present value
of a $21.25 debt:
$21.25
$25
S0
( S1 - debt
)=
(1 rf )
portfolio C1
$28.75- $21.25 = $7.50
$3.75
$25
$21.25- $21.25 =
$0
$0

41. Binomial Option Pricing Model

We can value the option today
as half of the value of the
1
$21.25
levered equity portfolio: C0 2 $25 (1 r )
f
S0
( S1 - debt
)=
portfolio C1
$28.75- $21.25 = $7.50
$3.75
$25
$21.25- $21.25 =
$0
$0

42. The Binomial Option Pricing Model

If the interest rate is 5%, the call is worth:
1
$21.25 1
$25 20.24 $2.38
C0 $25
2
(1.05) 2
S0
( S1 - debt
)=
portfolio C1
$28.75- $21.25 = $7.50
$3.75
$25
$21.25- $21.25 =
$0
$0

43. The Binomial Option Pricing Model

If the interest rate is 5%, the call is worth:
1
$21.25 1
$25 20.24 $2.38
C0 $25
2
(1.05) 2
S0
C0
( S1 - debt
)=
portfolio C1
$28.75- $21.25 = $7.50
$3.75
$25 $2.38
$21.25- $21.25 =
$0
$0

44. Binomial Option Pricing Model

The most important lesson (so far) from the binomial
option pricing model is:
the replicating portfolio intuition.
Many derivative securities can be valued by
valuing portfolios of primitive securities
when those portfolios have the same
payoffs as the derivative securities.

45. The Risk-Neutral Approach to Valuation

The Risk-Neutral
Valuation
Approach
to
S(U), V(U)
q
S(0), V(0)
1- q
S(D), V(D)
We could value V(0) as the value of the
replicating portfolio. An equivalent method is
qvaluation
V (U ) (1 q) V ( D)
risk-neutral
V (0)
(1 rf )

46. The Risk-Neutral Approach to Valuation

The Risk-Neutral
Valuation
Approach
to
S(U), V(U)
q
q is the risk-neutral
probability of an
“up” move.
S(0), V(0)
1- q
S(D), V(D)
S(0) is the value
of
the
underlying
S(U) and S(D) are the values of the asset in
asset
the
next today.
period following an up move and a
down move, respectively.
V(U) and V(D) are the values of the asset in the next period
following an up move and a down move, respectively.

47. The Risk-Neutral Approach to Valuation

S(U), V(U)
q
V (0)
S(0), V(0)
q V (U ) (1 q) V ( D)
(1 rf )
1- q
S(D), V(D)
• The key to finding q is to note that it is
already impounded into an observable
q S (U ) (1 q) S ( D)
S (0) the value of S(0):
security price:
(1 r )
f
A minor bit of algebra yields: q
(1 rf ) S (0) S ( D)
S (U ) S ( D)

48. Example of the Risk-Neutral Valuation of a Call:

Suppose a stock is worth $25 today and in
one period will either be worth 15% more
or 15% less. The risk-free rate is 5%. What is
the value of an at-the-money
call
option?
$28.75 $25 (1.15)
The binomial tree would look like this:
q
$25,C(0)
$28.75,C(D)
$21.25 $25 (1 .15)
1- q
$21.25,C(D)

49. Example of the Risk-Neutral Valuation of a Call:

The next step would be to compute the risk
(1 r ) S (0) S ( D)
neutral probabilities
q
f
S (U ) S ( D)
q
(1.05) $25 $21.25
$5
2 3
$28.75 $21.25
$7.50
2/3
$28.75,C(D)
$25,C(0)
1/3
$21.25,C(D)

50. Example of the Risk-Neutral Valuation of a Call:

After that, find the value of the call in the up state and down
state.
C (U ) $28.75 $25
2/3
$25,C(0)
$28.75, $3.75
C ( D) max[$25 $28.75,0]
1/3
$21.25, $0

51. Example of the Risk-Neutral Valuation of a Call:

Finally, find the value of the call at time 0:
q C (U ) (1 q) C ( D)
C (0)
(1 rf )
C ( 0)
2 3 $3.75 (1 3) $0
(1.05)
$
2
.
50
C
(
0
)
$
2
.
38
(
1
.
05
)
2/3
$28.75,$3.75
$25,$2.38
$25,C(0)
1/3
$21.25, $0

52. Risk-Neutral Valuation and the Replicating Portfolio

This risk-neutral result is consistent with
valuing the call using a replicating portfolio.
2 3 $3.75 (1 3) $0 $2.50
C0
$2.38
(1.05)
1.05
1
$21.25 1
$25 20.24 $2.38
C0 $25
2
(1.05) 2

53. The Black-Scholes Model

The Black-Scholes Model is
C0 S N(d1 ) Ee rT N(d 2 )
Where
C0 = the value of a European option at time t = 0
r = the risk-free interest rate.
σ2
ln(S / E ) (r )T
2
d1
T
d 2 d1 T
N(d) = Probability that a
standardized, normally
distributed, random
variable will be less than
or equal to d.
The Black-Scholes Model allows us to value options in the
real world just as we have done in the two-state world.

54. The Black-Scholes Model

Find the value of a six-month call option on
Microsoft with an exercise price of $150.
The current value of a share of Microsoft is
$160.
The interest rate available in the U.S. is r = 5%.
The option maturity is six months (half of a
year).
The volatility of the underlying asset is 30% per
annum.
Before we start, note that the intrinsic value of

55. The Black-Scholes Model

Let’s try our hand at using the model. If you
have a calculator handy, follow along.
First calculate d1 and d2
ln(S / E ) (r .5σ 2 )T
d1
T
ln(160 / 150) (.05 .5(0.30) 2 ).5
d1
0.5282
0.30 .5
Then,
d 2 d1 T 0.52815 0.30 .5 0.31602

56. The Black-Scholes Model

C0 S N(d1 ) Ee rT N(d 2 )
d1 0.5282
N(d1) = N(0.52815) = 0.7013
d 2 0.31602
N(d2) = N(0.31602) = 0.62401
C0 $160 0.7013 150e .05 .5 0.62401
C0 $20.92

57. Another Black-Scholes Example

22.9 Stocks and Bonds as Options
• Levered Equity is a Call Option.
– The underlying asset comprises the assets of the
firm.
– The strike price is the payoff of the bond.
• If at the maturity of their debt, the assets of the
firm are greater in value than the debt, the
shareholders have an in-the-money call, they will
pay the bondholders, and “call in” the assets of the
firm.
• If at the maturity of the debt the shareholders have
an out-of-the-money call, they will not pay the
bondholders (i.e., the shareholders will declare
bankruptcy), and let the call expire.

58. 22.9 Stocks and Bonds as Options

• Levered Equity is a Put Option.
– The underlying asset comprise the assets of the firm.
– The strike price is the payoff of the bond.
• If at the maturity of their debt, the assets of the
firm are less in value than the debt, shareholders
have an in-the-money put.
• They will put the firm to the bondholders.
• If at the maturity of the debt the shareholders have
an out-of-the-money put, they will not exercise the
option (i.e., NOT declare bankruptcy) and let the
put expire.

59. 22.9 Stocks and Bonds as Options

• It all comes down to put-call parity.
C0 S P0 X e
Value of a
call on the
firm
Value of
= the firm
Stockholder’s
position in terms
of call options
rT
Value of a
+ put on the –
firm
Stockholder’s
position in terms
of put options
Value of a
risk-free
bond

60. 22.9 Stocks and Bonds as Options

22.10 Capital-Structure Policy and
Options
• Recall some of the agency costs of debt: they can
all be seen in terms of options.
• For example, recall the incentive shareholders in
a levered firm have to take large risks.

61. 22.10 Capital-Structure Policy and Options

Balance Sheet for a Company in
Distress
Assets BVMV Liabilities BVMV
Cash $200 $200 LT bonds $300 ?
Fixed Asset $400 $0 Equity $300 ?
Total $600 $200 Total $600 $200
What happens if the firm is liquidated today?
The bondholders get $200; the shareholders get nothing.

62. Balance Sheet for a Company in Distress

Selfish Strategy 1: Take Large Risks
(Think of a Call Option)
The Gamble
Probability Payoff
Win Big
10%
$1,000
Lose Big
90%
$0
Cost of investment is $200 (all the firm’s cash)
Required return is 50%
$100
NPV $200
1.50 × 0.10 +
Expected CF from the Gamble = $1000
NPV $133
$0 = $100

63. Selfish Strategy 1: Take Large Risks (Think of a Call Option)

Selfish Stockholders Accept
Negative NPV Project with Large
• Expected cash flowRisks
from the Gamble
– To Bondholders = $300 × 0.10 + $0 = $30
– To Stockholders = ($1000 - $300) × 0.10 + $0 =
$70
PV of Bonds Without the Gamble = $200
PV of Stocks Without the Gamble = $0
PV of Bonds With the Gamble = $30 / 1.5 = $20
PV of Stocks With the Gamble = $70 / 1.5 = $47
The stocks are worth more with the high risk project because
the call option that the shareholders of the levered firm hold
is worth more when the volatility is increased.

64. Selfish Stockholders Accept Negative NPV Project with Large Risks

22.11 Mergers and Options
• This is an area rich with optionality, both in the
structuring of the deals and in their execution.

65. 22.11 Mergers and Options

22.12 Investment in Real Projects & Options
• Classic NPV calculations typically ignore the
flexibility that real-world firms typically have.
• The next chapter will take up this point.

66. 22.12 Investment in Real Projects & Options

22.13 Summary and Conclusions
• The most familiar options are puts and calls.
– Put options give the holder the right to sell stock
at a set price for a given amount of time.
– Call options give the holder the right to buy stock
at a set price for a given amount of time.
• Put-Call parity
C0 X e
rT
S P0

67. 22.13 Summary and Conclusions

• The value of a stock option depends on six factors:
1. Current price of underlying stock.
2. Dividend yield of the underlying stock.
3. Strike price specified in the option contract.
4. Risk-free interest rate over the life of the contract.
5. Time remaining until the option contract expires.
6. Price volatility of the underlying stock.
• Much of corporate financial theory can be presented
in terms of options.
1. Common stock in a levered firm can be viewed as
a call option on the assets of the firm.
2. Real projects often have hidden options that