Similar presentations:
Introduction to Risk, Return, and the Opportunity Cost of Capital
1.
Principles ofCorporate
Finance
Seventh Edition
Richard A. Brealey
Chapter 7
Introduction to Risk, Return,
and the Opportunity Cost of
Capital
Stewart C. Myers
Slides by
Matthew Will
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
2. Topics Covered
7- 2Topics Covered
75 Years of Capital Market History
Measuring Risk
Portfolio Risk
Beta and Unique Risk
Diversification
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
3.
7- 3The Value of an Investment of $1 in 1926
1000
6402
S&P
Small Cap
Corp Bonds
Long Bond
T Bill
2587
64.1
Index
48.9
16.6
10
1
0.1
1925
1940
Source: Ibbotson Associates
McGraw Hill/Irwin
1955
1970
1985
2000
Year End
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
4.
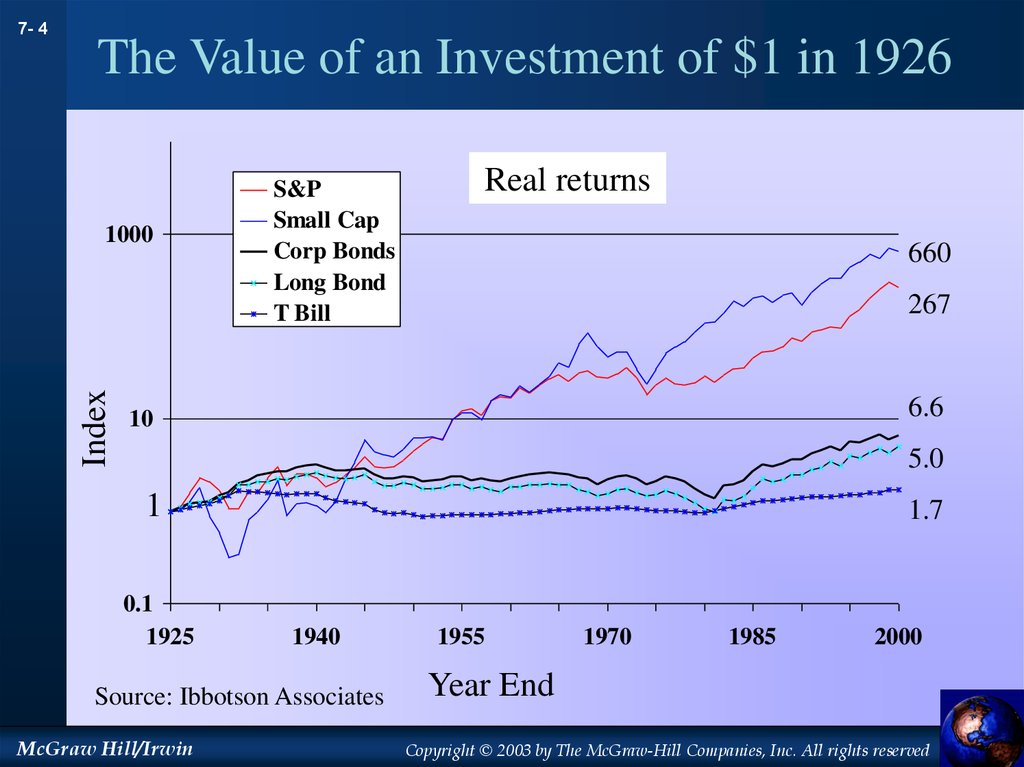
7- 4The Value of an Investment of $1 in 1926
Index
1000
S&P
Small Cap
Corp Bonds
Long Bond
T Bill
Real returns
660
267
6.6
10
5.0
1
0.1
1925
1.7
1940
Source: Ibbotson Associates
McGraw Hill/Irwin
1955
1970
1985
2000
Year End
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
5.
7- 5Rates of Return 1926-2000
40
20
0
95
90
85
80
75
70
65
60
55
50
45
40
35
26
-60
Common Stocks
Long T-Bonds
T-Bills
20
-40
00
-20
30
Percentage Return
60
Year
Source: Ibbotson Associates
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
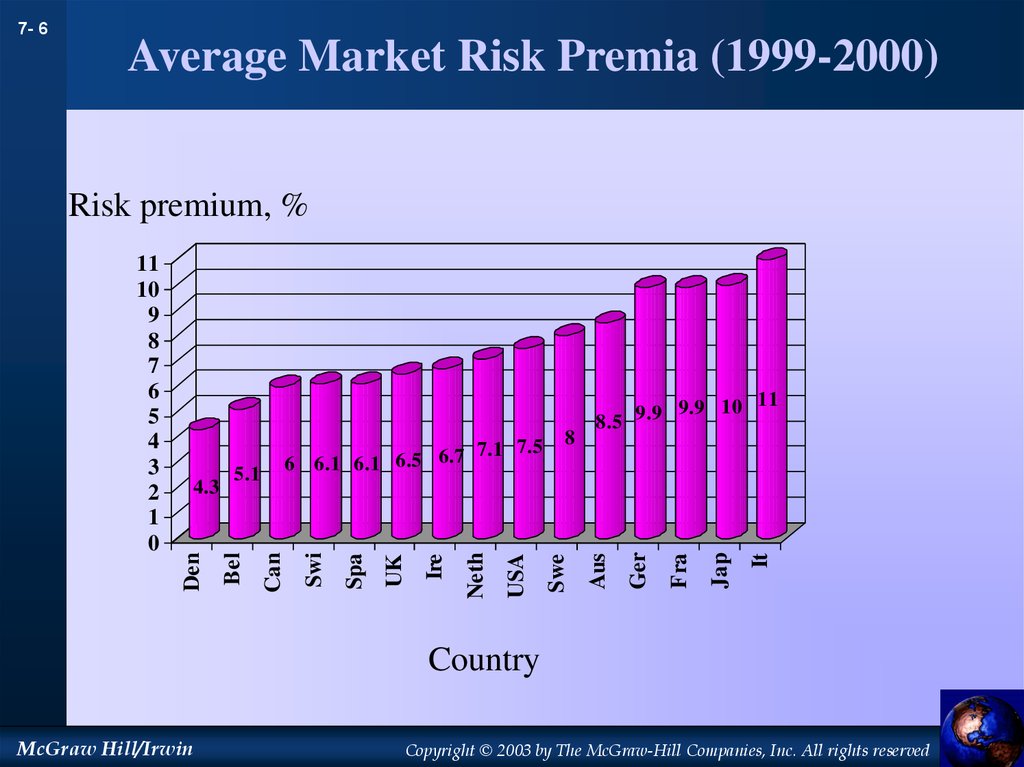
6. Average Market Risk Premia (1999-2000)
7- 6Average Market Risk Premia (1999-2000)
Risk premium, %
It
Jap
Fra
Ger
9.9 10 11
9.9
8.5
Aus
8
Swe
USA
Neth
Ire
UK
Spa
Swi
7.1 7.5
6 6.1 6.1 6.5 6.7
Can
5.1
Bel
4.3
Den
11
10
9
8
7
6
5
4
3
2
1
0
Country
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
7. Measuring Risk
7- 7Measuring Risk
Variance - Average value of squared deviations from
mean. A measure of volatility.
Standard Deviation - Average value of squared
deviations from mean. A measure of volatility.
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
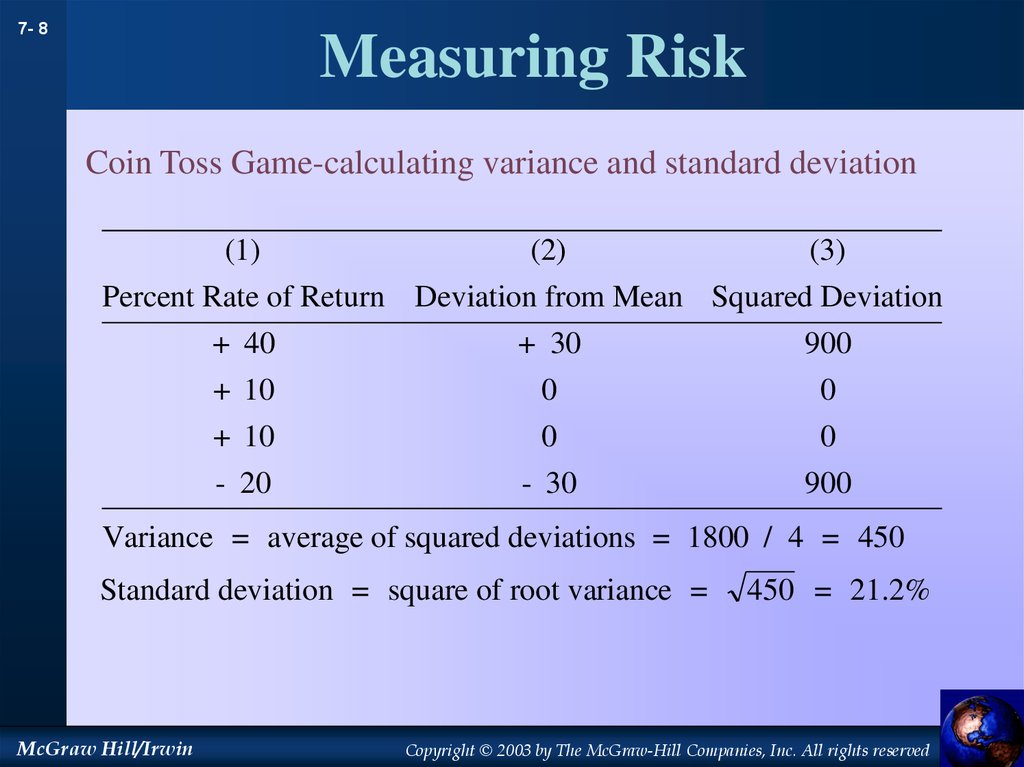
8. Measuring Risk
7- 8Measuring Risk
Coin Toss Game-calculating variance and standard deviation
(1)
(2)
(3)
Percent Rate of Return Deviation from Mean Squared Deviation
+ 40
+ 30
900
+ 10
0
0
+ 10
0
0
- 20
- 30
900
Variance = average of squared deviations = 1800 / 4 = 450
Standard deviation = square of root variance =
McGraw Hill/Irwin
450 = 21.2%
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
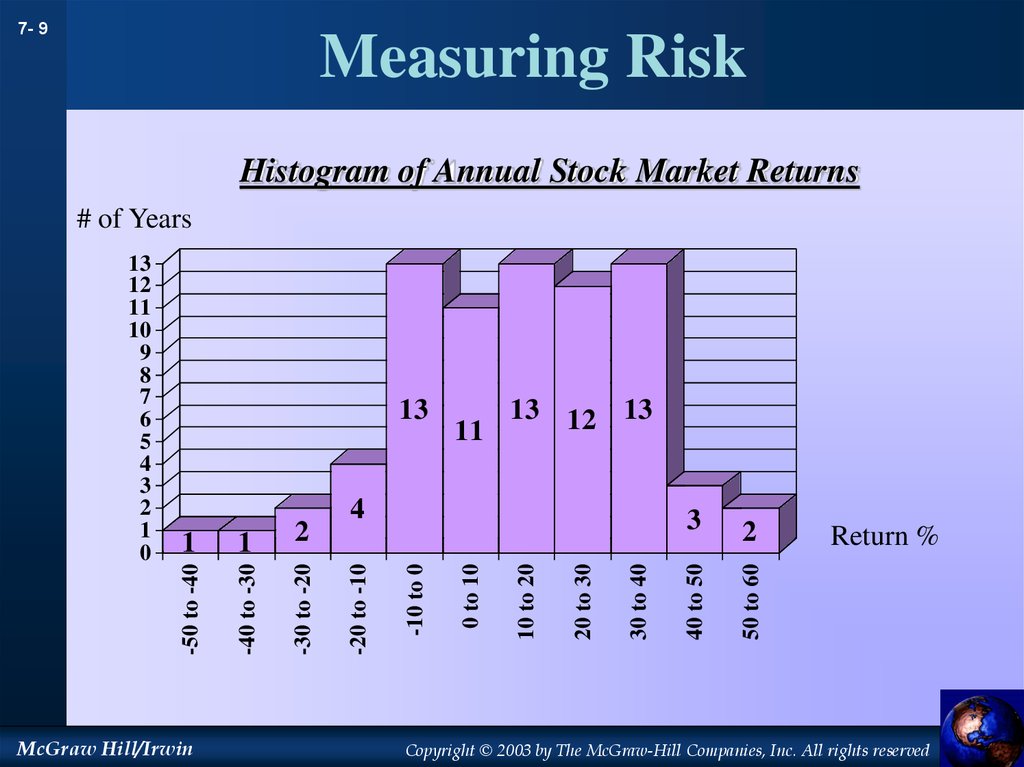
9. Measuring Risk
7- 9Measuring Risk
Histogram of Annual Stock Market Returns
# of Years
2
Return %
50 to 60
40 to 50
30 to 40
20 to 30
10 to 20
0 to 10
-30 to -20
McGraw Hill/Irwin
3
-10 to 0
1
13 12 13
11
4
-20 to -10
1
2
-40 to -30
13
-50 to -40
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
10. Measuring Risk
7- 10Measuring Risk
Diversification - Strategy designed to reduce risk by
spreading the portfolio across many investments.
Unique Risk - Risk factors affecting only that firm.
Also called “diversifiable risk.”
Market Risk - Economy-wide sources of risk that
affect the overall stock market. Also called
“systematic risk.”
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
11. Measuring Risk
7- 11Measuring Risk
Portfolio rate
of return
(
(
=
+
McGraw Hill/Irwin
)(
)(
fraction of portfolio
in first asset
fraction of portfolio
in second asset
x
x
rate of return
on first asset
rate of return
)
)
on second asset
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
12. Measuring Risk
7- 12Portfolio standard deviation
Measuring Risk
0
5
10
15
Number of Securities
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
13. Measuring Risk
7- 13Portfolio standard deviation
Measuring Risk
Unique
risk
Market risk
0
5
10
15
Number of Securities
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
14. Portfolio Risk
7- 14Portfolio Risk
The variance of a two stock portfolio is the sum of these
four boxes
Stock 1
Stock 1
Stock 2
McGraw Hill/Irwin
x 12σ 12
x 1x 2σ 12
x 1x 2ρ 12σ 1σ 2
Stock 2
x 1x 2σ 12
x 1x 2ρ 12σ 1σ 2
x 22σ 22
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
15. Portfolio Risk
7- 15Portfolio Risk
Example
Suppose you invest 65% of your portfolio in CocaCola and 35% in Reebok. The expected dollar
return on your CC is 10% x 65% = 6.5% and on
Reebok it is 20% x 35% = 7.0%. The expected
return on your portfolio is 6.5 + 7.0 = 13.50%.
Assume a correlation coefficient of 1.
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
16. Portfolio Risk
7- 16Portfolio Risk
Example
Suppose you invest 65% of your portfolio in Coca-Cola and 35% in
Reebok. The expected dollar return on your CC is 10% x 65% = 6.5%
and on Reebok it is 20% x 35% = 7.0%. The expected return on your
portfolio is 6.5 + 7.0 = 13.50%. Assume a correlation coefficient of 1.
Coca - Cola
Coca - Cola
Reebok
McGraw Hill/Irwin
x 12 σ12 (.65) 2 (31.5) 2
x 1 x 2 ρ12 σ1σ 2 .65 .35
1 31.5 58.5
Reebok
x 1 x 2 ρ12 σ1σ 2 .65 .35
1 31.5 58.5
x 22 σ 22 (.35) 2 (58.5) 2
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
17. Portfolio Risk
7- 17Portfolio Risk
Example
Suppose you invest 65% of your portfolio in Coca-Cola and 35% in
Reebok. The expected dollar return on your CC is 10% x 65% = 6.5%
and on Reebok it is 20% x 35% = 7.0%. The expected return on your
portfolio is 6.5 + 7.0 = 13.50%. Assume a correlation coefficient of 1.
Portfolio Valriance [(.65) 2 x(31.5) 2 ]
[(.35) 2 x(58.5) 2 ]
2(.65x.35x 1x31.5x58. 5) 1,006.1
Standard Deviation 1,006.1 31.7 %
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
18. Portfolio Risk
7- 18Portfolio Risk
Expected Portfolio Return (x 1 r1 ) ( x 2 r2 )
Portfolio Variance x12σ 12 x 22σ 22 2( x1x 2ρ 12σ 1σ 2 )
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
19. Portfolio Risk
7- 19Portfolio Risk
The shaded boxes contain variance terms; the remainder
contain covariance terms.
1
2
3
STOCK
To calculate
portfolio
variance add
up the boxes
4
5
6
N
1
2
3
4
5
6
N
STOCK
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
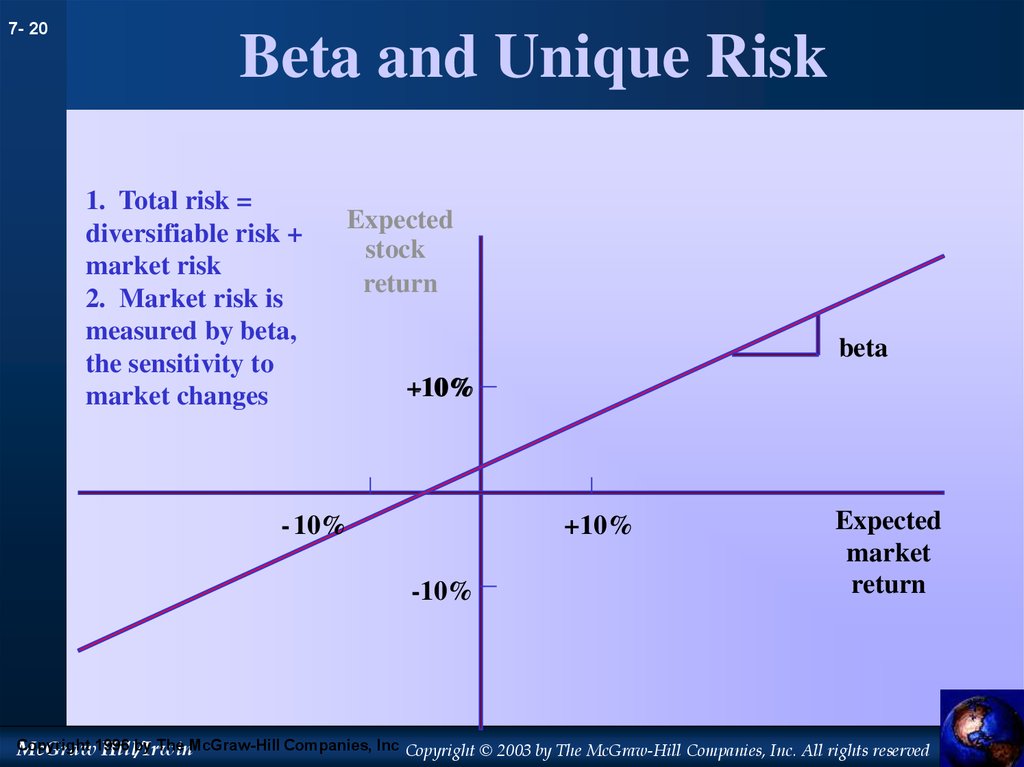
20. Beta and Unique Risk
7- 20Beta and Unique Risk
1. Total risk =
diversifiable risk +
market risk
2. Market risk is
measured by beta,
the sensitivity to
market changes
Expected
stock
return
beta
+10%
-10%
- 10%
+10%
-10%
Expected
market
return
Copyright
by The McGraw-Hill Companies, Inc Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
McGraw1996
Hill/Irwin
21. Beta and Unique Risk
7- 21Beta and Unique Risk
Market Portfolio - Portfolio of all assets in the
economy. In practice a broad stock market
index, such as the S&P Composite, is used
to represent the market.
Beta - Sensitivity of a stock’s return to the
return on the market portfolio.
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
22. Beta and Unique Risk
7- 22Beta and Unique Risk
im
Bi 2
m
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved
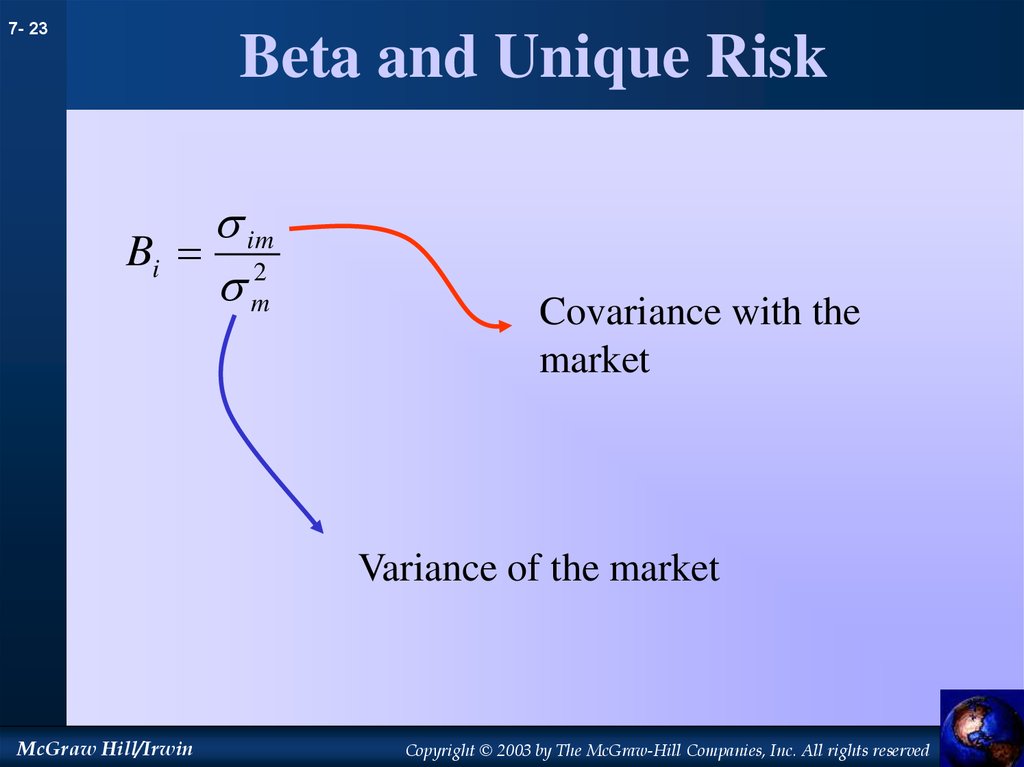
23. Beta and Unique Risk
7- 23Beta and Unique Risk
im
Bi 2
m
Covariance with the
market
Variance of the market
McGraw Hill/Irwin
Copyright © 2003 by The McGraw-Hill Companies, Inc. All rights reserved

















 finance
finance








