Общее повторение алгебры

1.

Повторение курса
алгебры

2. НОД и НОК

НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Пример:
Например, найдём НОД для чисел 28 и 16. В первую очередь, раскладываем эти числа на
простые множители:
Получили два разложения
и
Берем только повторяющие множители в первом и втором разложении.
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4
без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4

3. НОД и НОК

Пример:
Найдём НОК для чисел 9 и 12.
Разложим на множители число 9:
Разложим на множители число 12
Выпишем первое разложение: 3 × 3
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом
разложении нет двух двоек. Их и допишем: 3 × 3 × 2 × 2
Теперь перемножаем эти множители:
3 × 3 × 2 × 2 = 36
Получили ответ 36. Значит наименьшее общее кратное для чисел 9 и 12 это число 36.
НОК (9 и 12) = 36

4. Формулы сокращенного умножения

5. Квадратные уравнения

6.

7.

8.

9.

10.

11.

Тригонометрия

12.

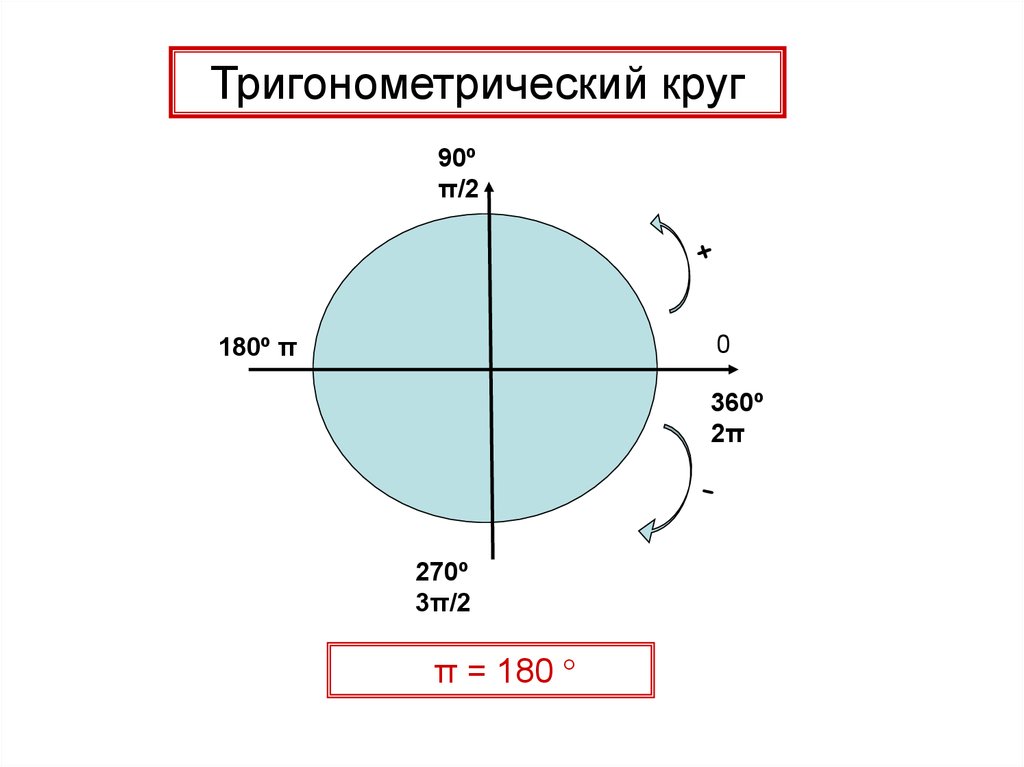
Тригонометрический круг
90º
π/2
180º π
0
360º
2π
270º
3π/2
π = 180 °

13.

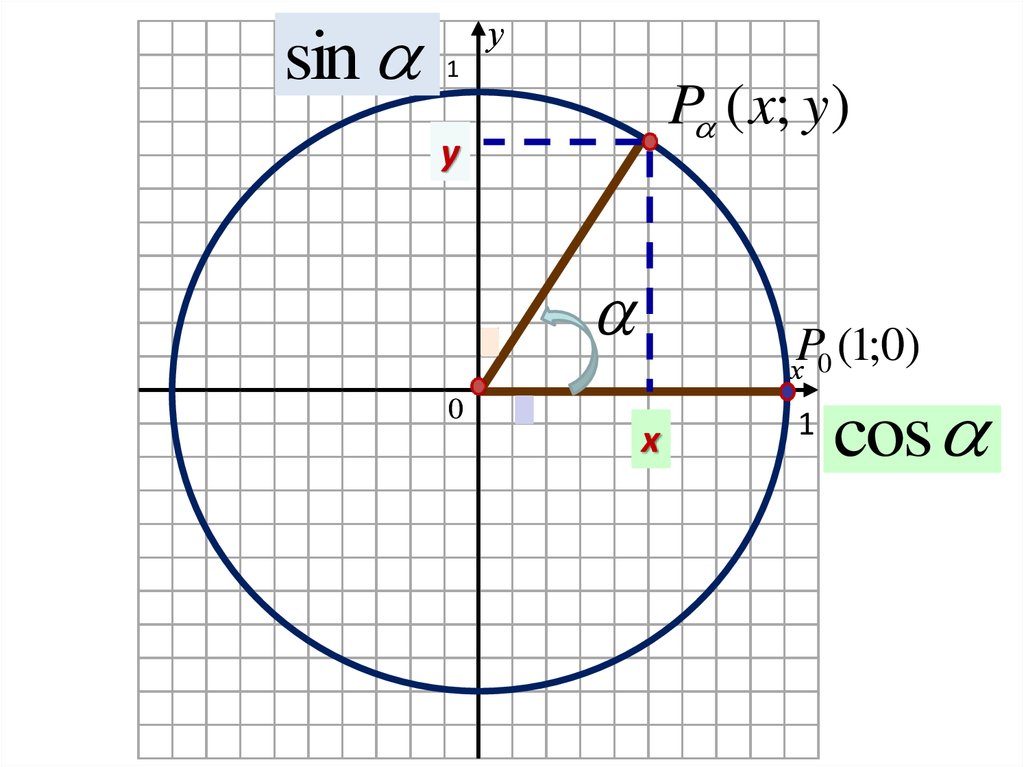
sin
у
1
P ( x; y)
у
1
0
P (1;0)
х 0
1
х
1
cos

14.

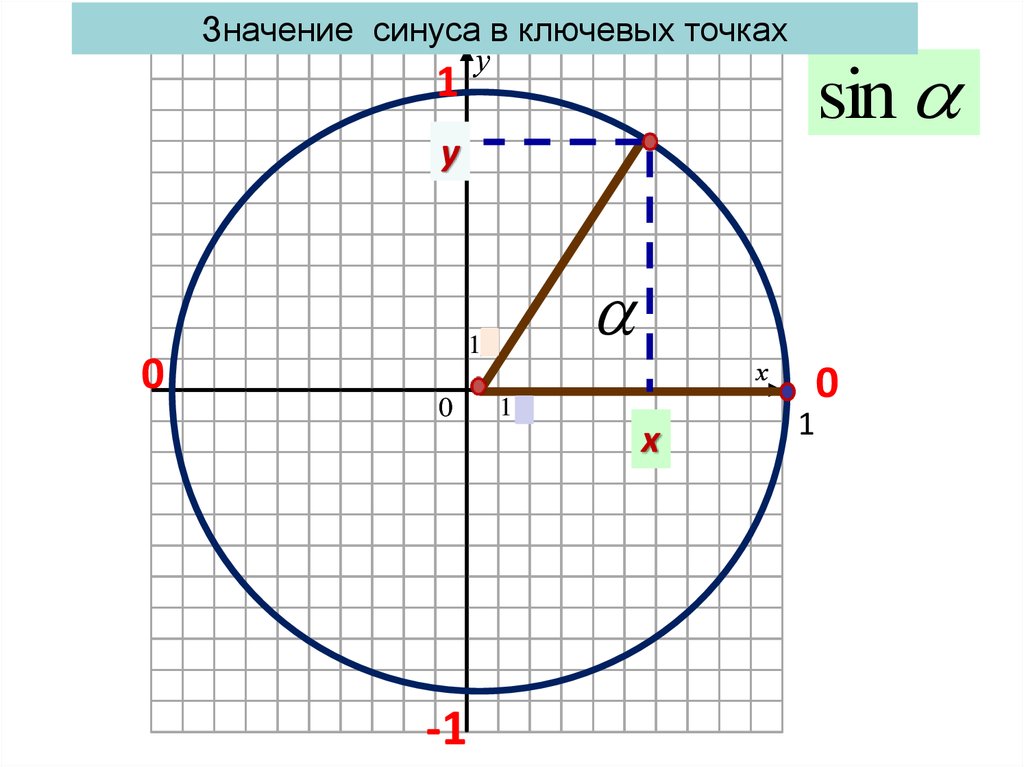
Значение синуса в ключевых точках
у
sin
1
у
0
1
0
х
1
х
-1
0
1

15.

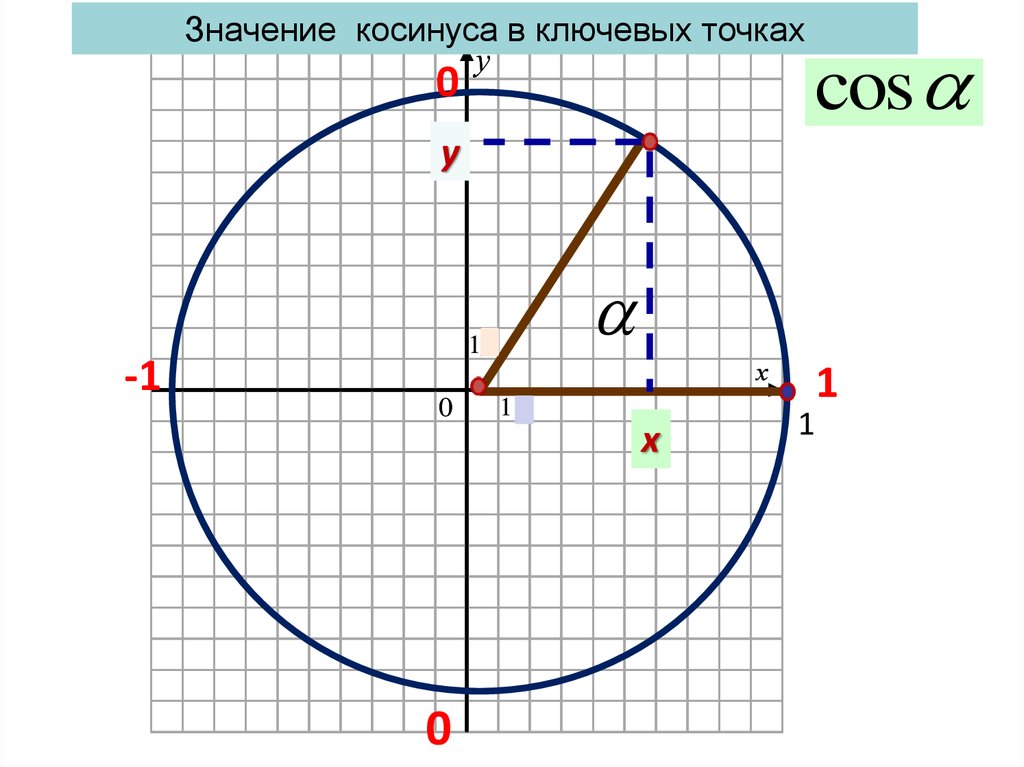
Значение косинуса в ключевых точках
у
0
cos
у
-1
1
0
х
1
х
0
1
1

16.

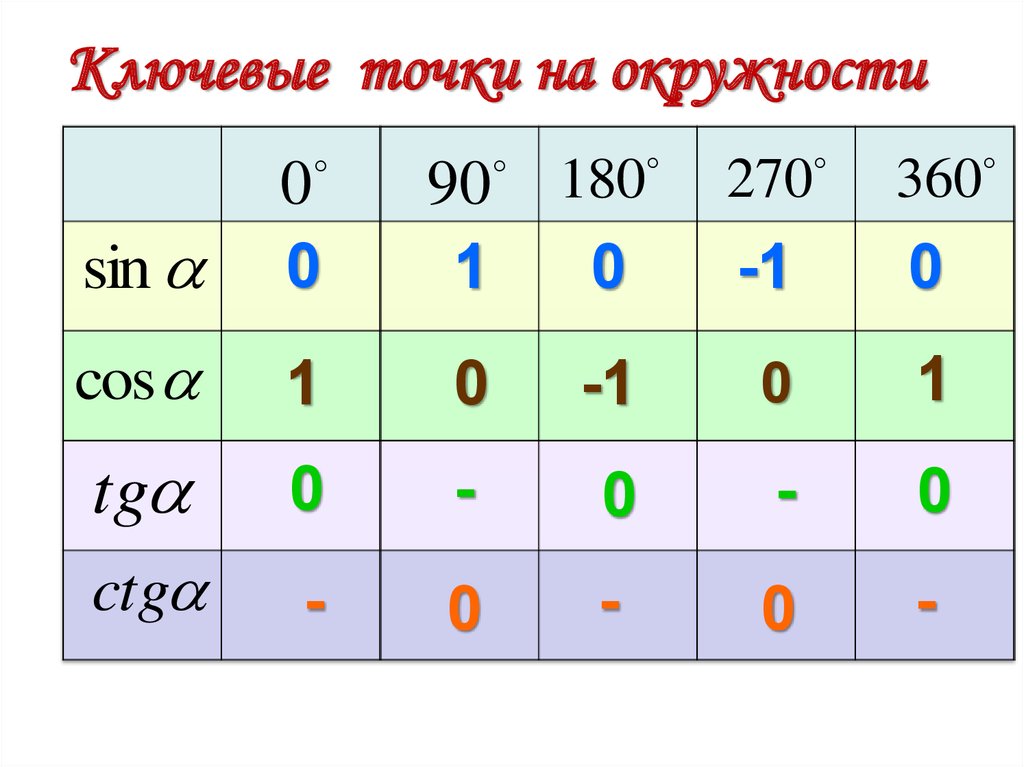
Ключевые точки на окружности
180
270
0
-1
0
0
-1
0
1
0
-
0
-
0
-
0
-
0
-
sin
0
0
90
1
cos
1
tg
ctg
360

17.

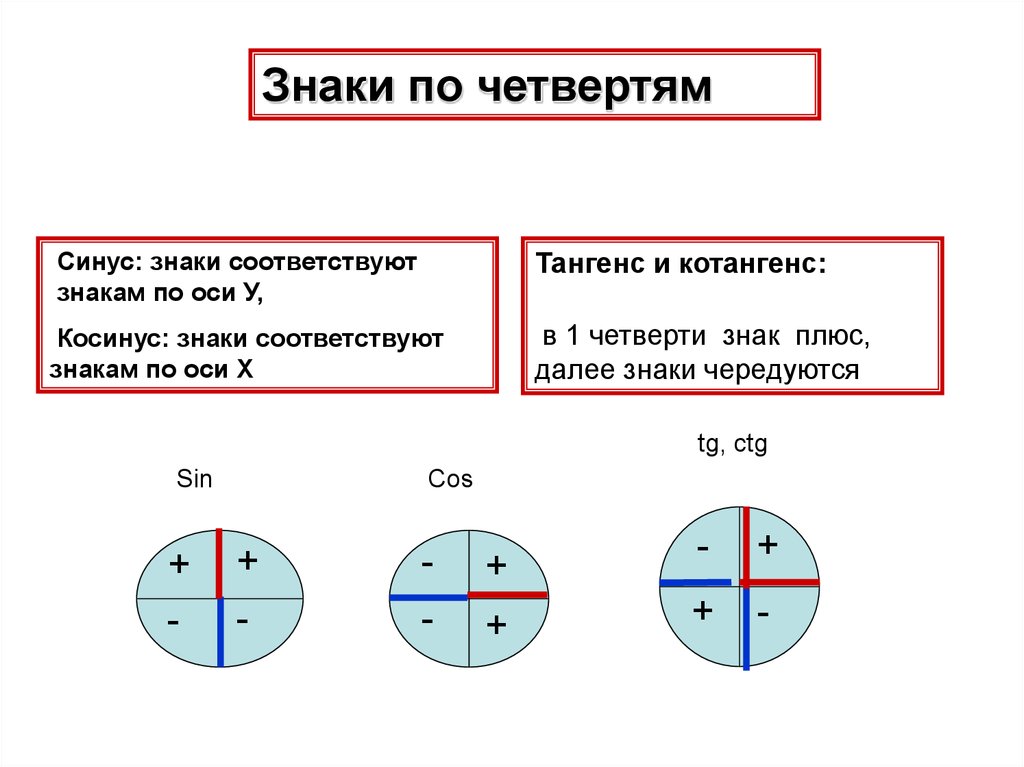
Знаки по четвертям
Синус: знаки соответствуют
знакам по оси У,
Тангенс и котангенс:
Косинус: знаки соответствуют
знакам по оси Х
в 1 четверти знак плюс,
далее знаки чередуются
tg, ctg
Sin
+
-
Cos
+
-
-
+
+
-
+
+
-

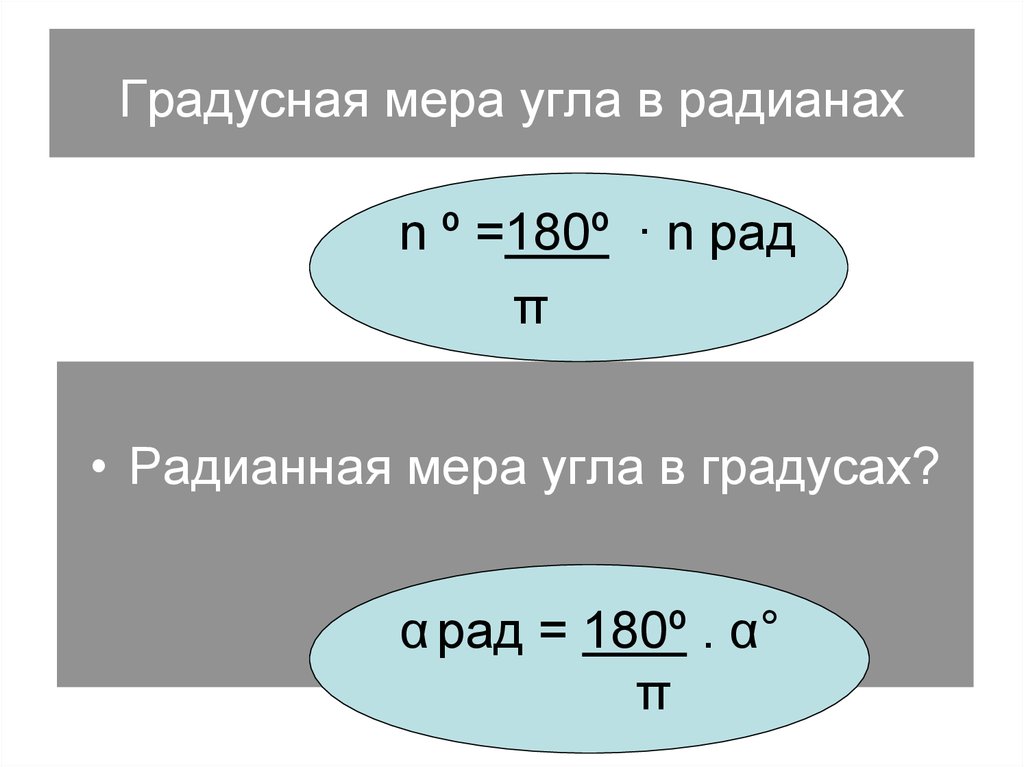
18. Градусная мера угла в радианах

n º =180º ∙ n рад
π
• Радианная мера угла в градусах?
α рад = 180º . α°
π

19. Таблица

20.

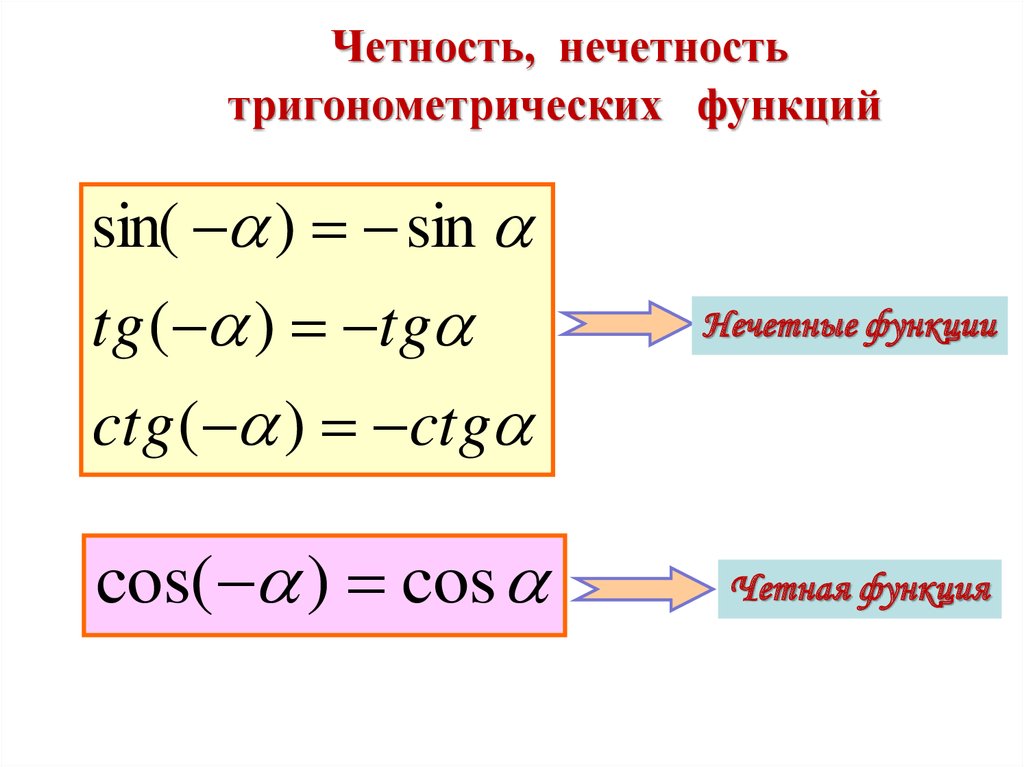
Четность, нечетность
тригонометрических функций
sin( ) sin
tg ( ) tg
Нечетные функции
ctg ( ) ctg
cos( ) cos
Четная функция

21.

Основные тригонометрические
формулы

22.

Формулы сложения

23.

Формулы двойного угла

24.

Формулы преобразования суммы в
произведение

25.

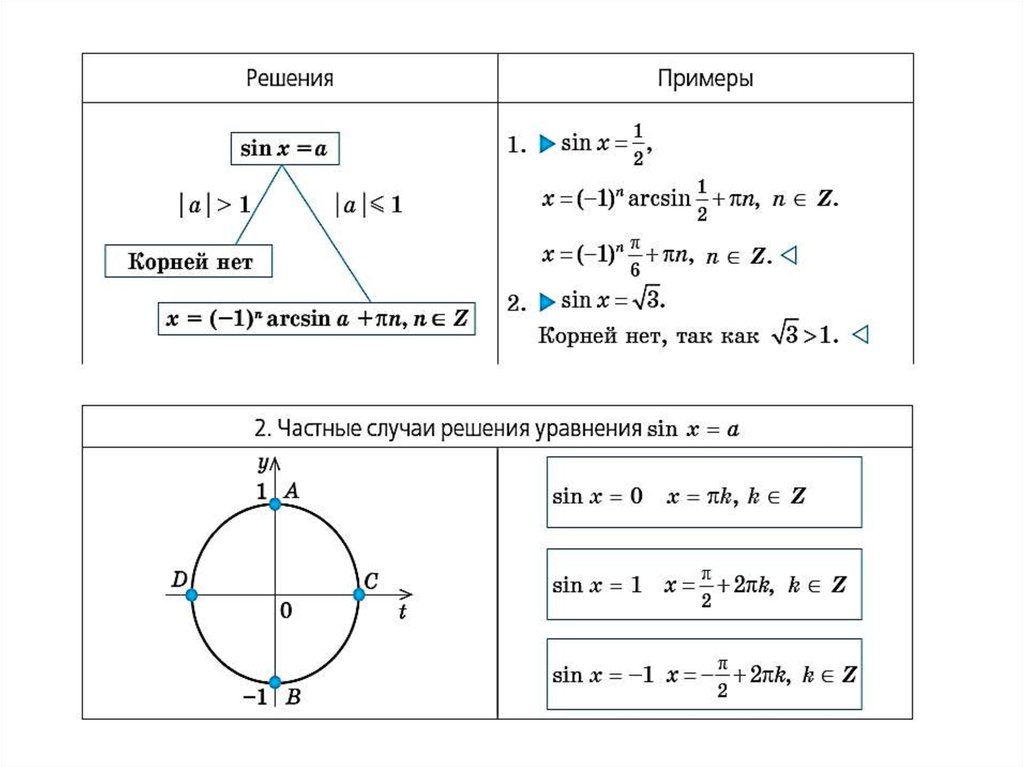
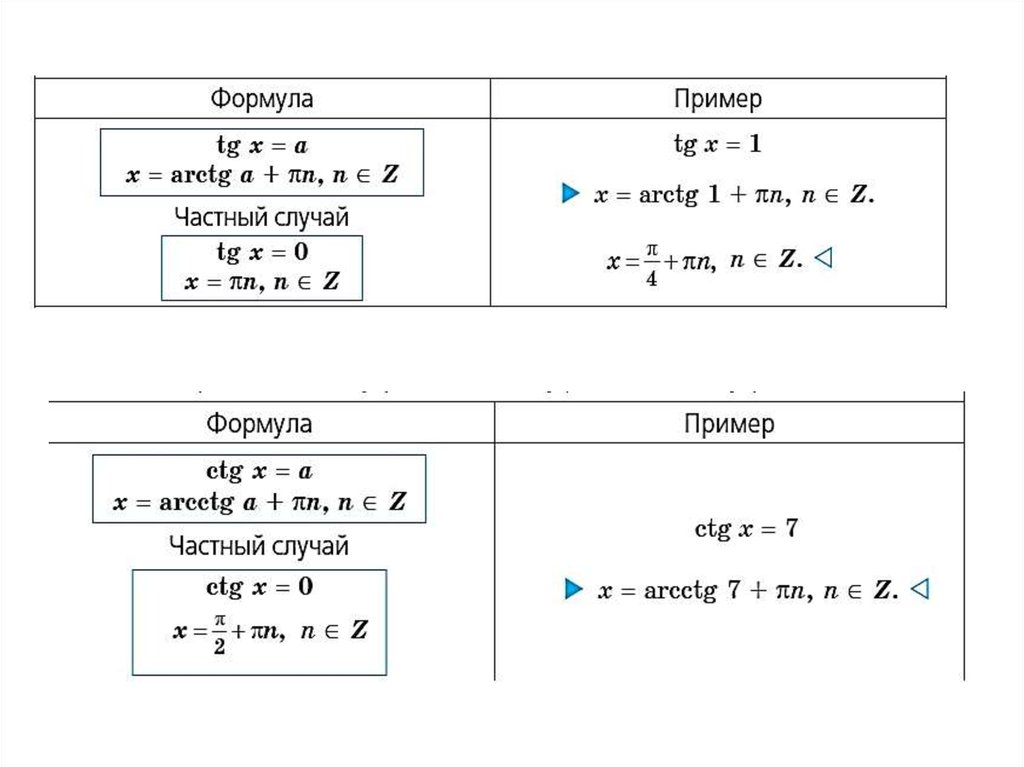
Простейшие тригонометрические
уравнения

26.

27.

Тригонометрические уравнения

28.

29.

Тригонометрические уравнения,
решаемые выненсением за скобки….
cos2 x - 2cosx = 0.
cosx(cos x – 2) = 0.
сosx=0
или
cos x – 2 = 0.

30.

Тригонометрические уравнения,
приводимые к квадратным

31.

Тригонометрические уравнения,
приводимые к квадратным
6cos2 x + 5 sin x – 7 = 0.
6(1-sin2 x) + 5 sin x – 7 = 0.
6sin2 x - 5 sin x +1 = 0.
1
Далее применяем формулу

32.

Однородные тригонометрические
уравнения 1 степени
sin x – 2 cos x = 0..

33.

Однородные тригонометрические
уравнения 2 степени
sin2 x – 6 sin x cos x + 5 cos2 x = 0.

34.

Степени и корни

35.

Свойства корней n-й степени

36.

Решение иррациональных уравнений
1)
2n
f ( x) a, a const 0,
2)
2n
f ( x) a, a const 0 f ( x) a 2n
2n
f ( x) 2 n ( x),
f ( x) ( x)
( x) 0.
3)
4)
2n
f ( x)
2n
решений нет
f ( x) ( x),
( x)
f ( x) 0 или ( x) 0.

37.

Решение иррациональных уравнений
1)
2n
f ( x) a, a const 0,
2)
2n
f ( x) a, a const 0 f ( x) a 2n
2n
f ( x) 2 n ( x),
f ( x) ( x)
( x) 0.
3)
4)
2n
f ( x)
2n
решений нет
f ( x) ( x),
( x)
f ( x) 0 или ( x) 0.

38.

Проверка:

39.

- верно
неверно

40.

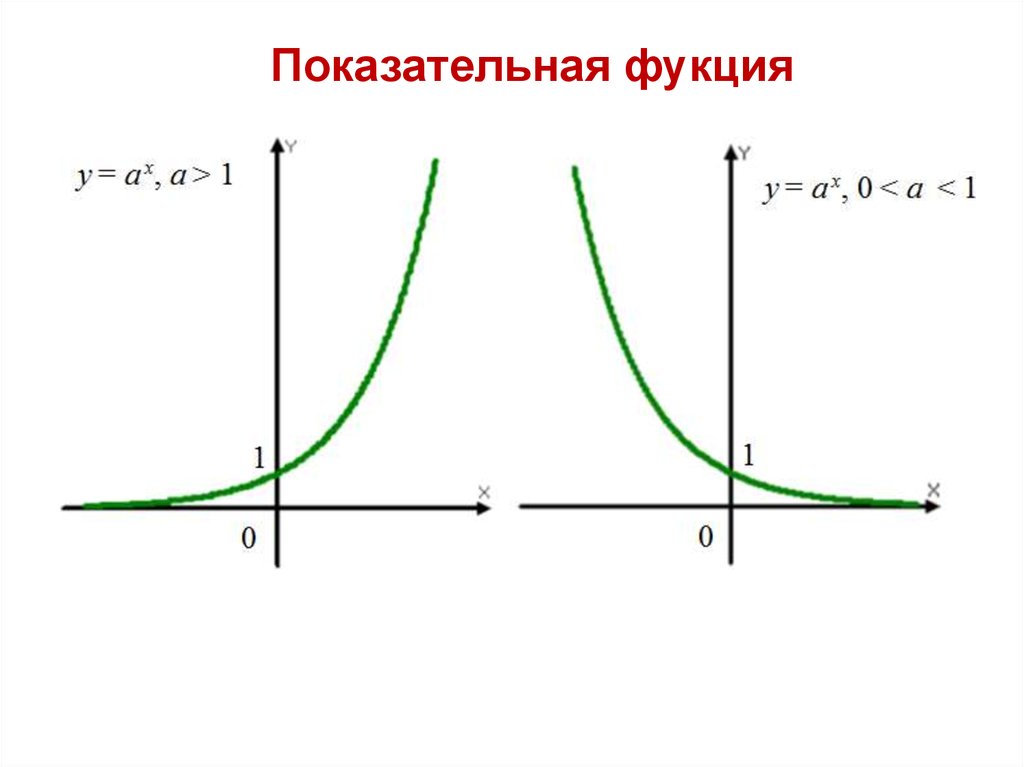
Показательная фукция

41.

Показательные уравнения
.
1) a
f ( x)
2
2)
a
x 1
1 a
1, 2
f ( x)
2
x 1
a
2
f ( x)
x 1
g ( x)
x 2 2
a f ( x) 0
0
2 , x 1 0......
0
f ( x) g ( x)
, x 1 x 2......
2

42.

Показательные уравнения
.
3)
2
4)
Вынесение за скобки общего
множителя
x 2
2 12,
x
2 (2 1) 12.....
x
2
Приведение к квадратному
уравнению
4 3 2 4 0,
x
x
2 3 2 4 0,
2x
Пусть 2 t , тогда....
x
x

43.

Показательные уравнения
.
5)
Однородные уравнения
5 4 3 6 9 0,
х
x
x
,
Делим обе части на 4 или на 9
x
x
Плучаем... уравнение..квадратное...

44.

Показательные уравнения
.
6) 2
x 2
2
2 x
15
2
2
2 2 x 15 0
2
4
x
4 2 x 15 0
2
x
Пусть 2 t , тогда
2
x
4
4 t 15 0 | t
t
2
4t 15t 4 0......

45.

Показательные неравенства
1)
a
f ( x)
a
g ( x)
,
если 0 a 1, то f ( x) g ( x)
0,2
x 1
0,2
x2 2
Так как 0,2 1, то
x 1 x 2......
2

46.

Показательные неравенства
1)
a
f ( x)
a
g ( x)
,
если a 1, то f ( x) g ( x)
2
x 1
2
x2 2
Так как 2 1, то
x 1 x 2......
2

47.

Логарифмическая функция
у log x, а 0, а 1
a

48.

Основные свойства логарифмов
1. log a 1 0
2. log a a 1
3. log a ( xy) log a x log a y
x
4. log a log a x log a y
y
5. log a x p p log a x
log b x
6. log a x
log b a
7.log a g x 1 log a x
g
1
8.log a b
log b a

49.

Логарифмические уравнения
1)
log a f ( x) b f ( x) a
b
log 2 ( x 4) 5 x 4 2 ......
5
f ( x) g ( x)
2) log a f ( x) log a g ( x)
f ( x) 0 или g ( x) 0
2
x 4 x 1
2
log 2 ( x 4) log 2 ( x 1)
x 4 0.....

50.

3)
Приведение к квадратному
уравнению
log 22 x 5 log 2 x 4 0
Пусть log 2 x t......
4)
Применение свойств
логарифмов
log a f ( x) log a g ( x) log a h( x),
log a ( f ( x) g ( x)) log a h( x),
f ( x ) g ( x ) h( x )
f ( x) 0
g ( x) 0
h( x) 0......

51.

Логарифмические уравнения
5)
log g ( x )
f ( x) g ( x) a
f ( x) a g ( x) 0
g ( x) 1
x 4 x2
log x ( x 4) 2 x 0
x 1

52.

Логарифмические неравенства
log a f ( x) log a g ( x)
Если a 1, то f ( x) g ( x)
x 4 x 1
log 2 ( x 4) log 2 ( x 1) 2
x 1 0....
2
2
(обязательно проверяем меньшее в системе…)

53.

Логарифмические неравенства
log a f ( x) log a g ( x)
Если 0 a 1, то f ( x) g ( x)
x 4 x 1
log 2 ( x 4) log 2 ( x 1)
3
3
x 4 0....
2
2
(обязательно проверяем меньшее в системе…)

54.

Логарифмические неравенства
log g ( x ) f ( x) log g ( x ) g ( x)
g ( x) 1
0 g ( x) 1,
f ( x) g ( x) f ( x) g ( x)
или
f ( x) 0
f ( x) 0
g ( x) 0
g ( x) 0