Инерциальные и неинерциальные системы отсчета. Принцип относительности. Преобразования Галилея

1.

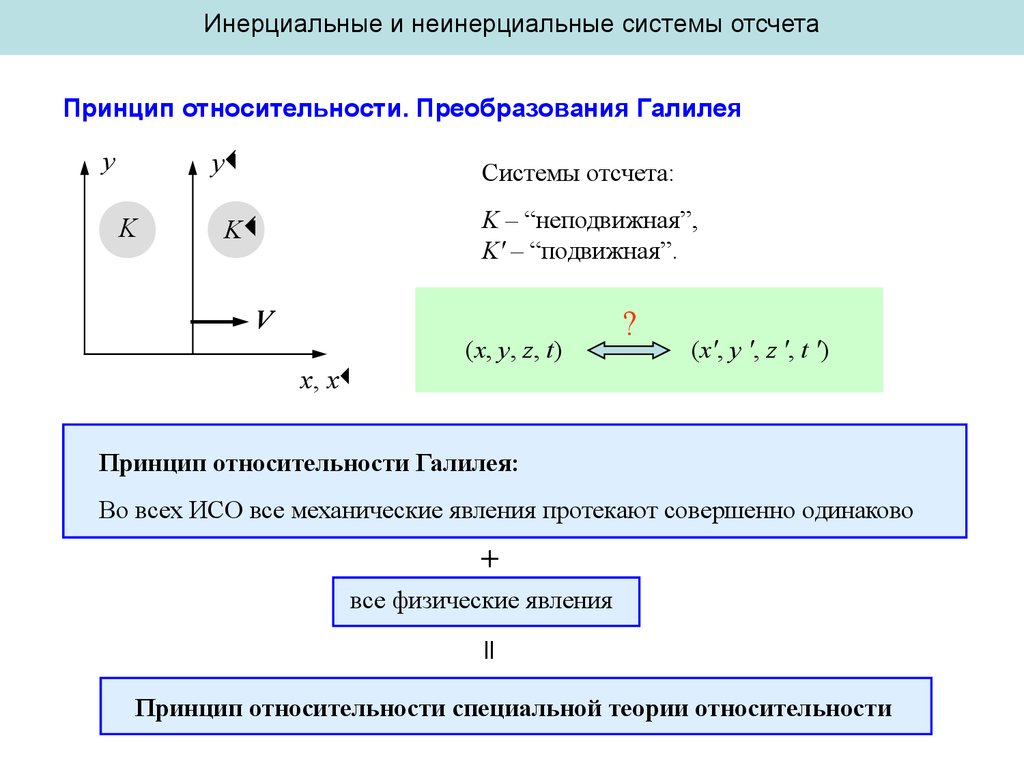
Инерциальные и неинерциальные системы отсчета
Принцип относительности. Преобразования Галилея
y
y
K
Системы отсчета:
K – “неподвижная”,
K' – “подвижная”.
K
V
x, x
(x, y, z, t)
?
(x', y ', z ', t ')
Принцип относительности Галилея:
Во всех ИСО все механические явления протекают совершенно одинаково
+
все физические явления
=
Принцип относительности специальной теории относительности

2.

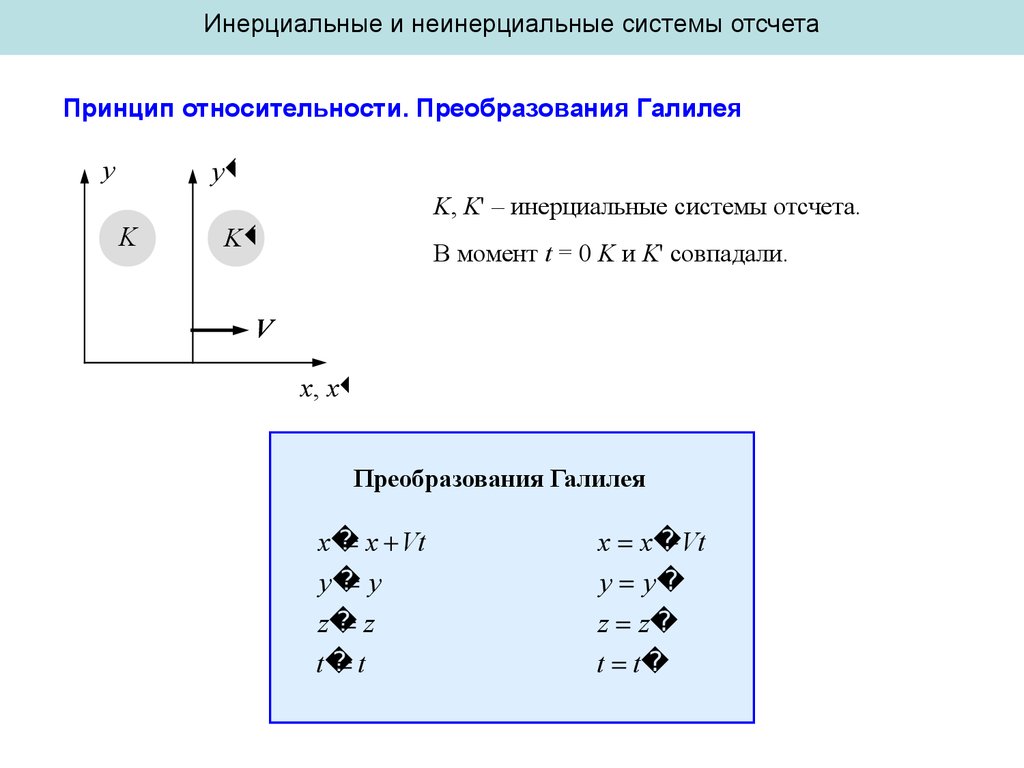
Инерциальные и неинерциальные системы отсчета
Принцип относительности. Преобразования Галилея
y
y
K, K' – инерциальные системы отсчета.
K
K
В момент t = 0 K и K' совпадали.
V
x, x
Преобразования Галилея
x
x Vt
y
y
z
z
t
t
x x
Vt
y y
z z
t t

3.

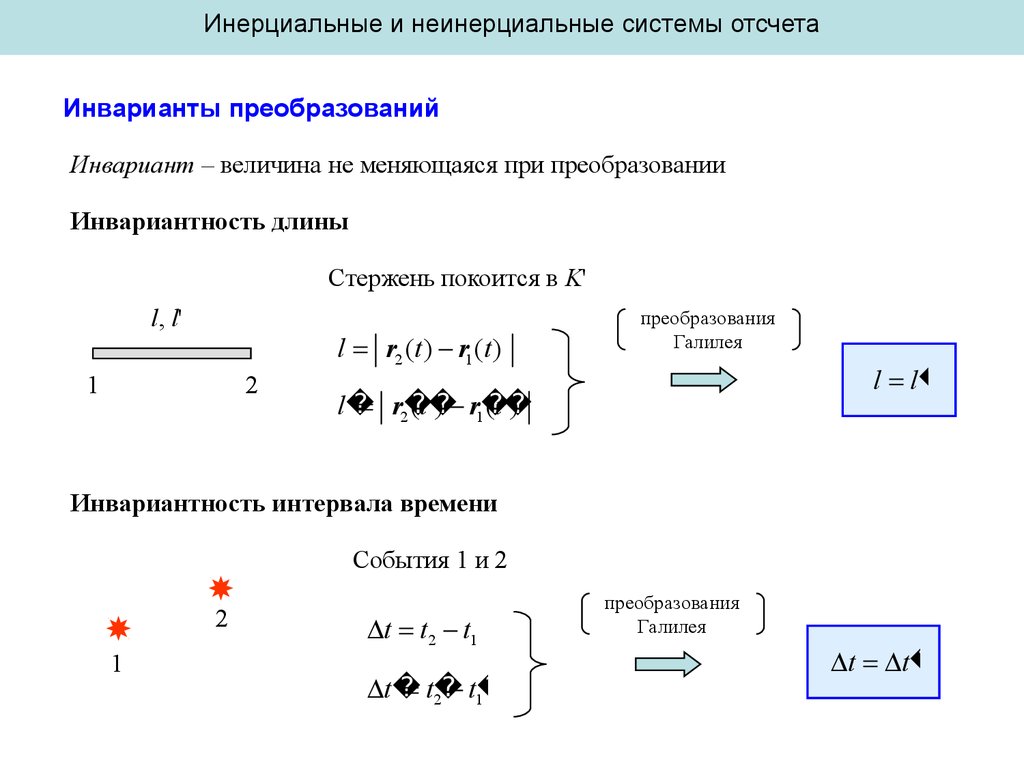
Инерциальные и неинерциальные системы отсчета
Инварианты преобразований
Инвариант – величина не меняющаяся при преобразовании
Инвариантность длины
Стержень покоится в K'
l, l'
l r2 (t ) r1 (t )
1
2
преобразования
Галилея
l l
l
r2
(t ) r1
(t
)
Инвариантность интервала времени
События 1 и 2
2
1
t t2 t1
t
t2 t1
преобразования
Галилея
t t

4.

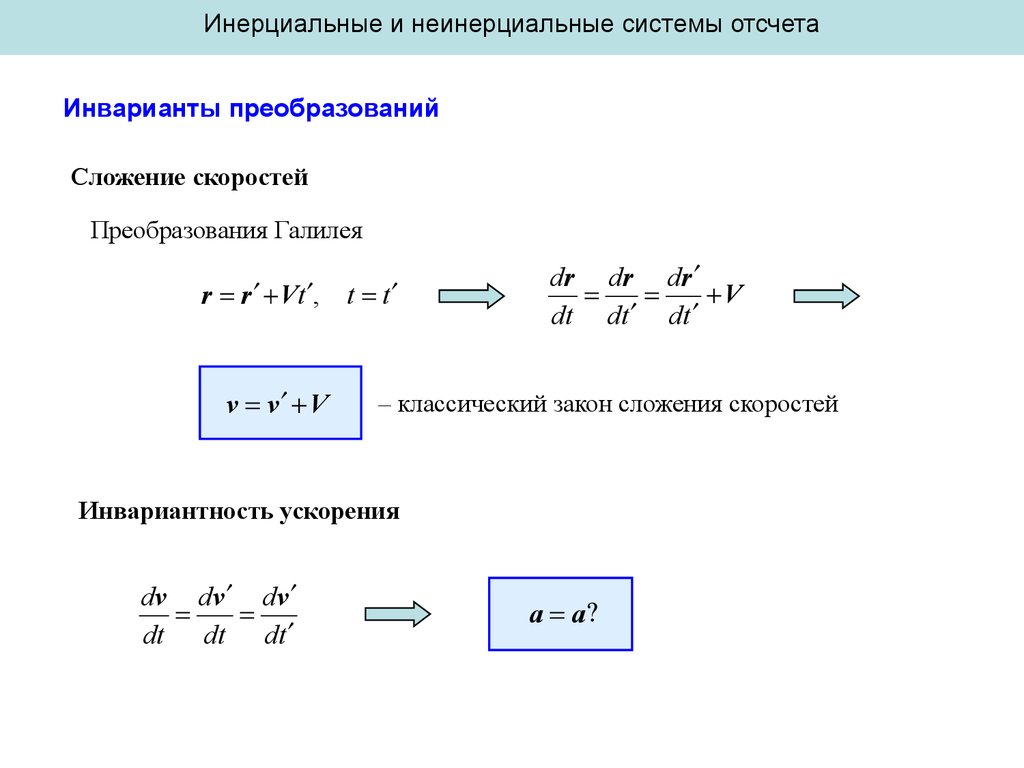
Инерциальные и неинерциальные системы отсчета
Инварианты преобразований
Сложение скоростей
Преобразования Галилея
r r Vt ,
v v V
t t
dr dr dr
V
dt dt dt
– классический закон сложения скоростей
Инвариантность ускорения
dv dv dv
dt dt dt
a a

5.

Инерциальные и неинерциальные системы отсчета
Инварианты преобразований
Инвариантность силы
F, F
Общее выражение для силы
F f ( rij , vij )
преобразования
Галилея
F f ( rij , vij )
F F
F
f ( rij
, vij
)
Инвариантность уравнений движения
ma F
a a
F F
ma
F
механические явления в ИСО протекают одинаково
(в согласии с принципом относительности Галилея)

6.

Инерциальные и неинерциальные системы отсчета
Инварианты преобразований
Закон сохранения массы
На примере неупругого столкновения
m1, v1
m2, v2
m, v
…
в K:
m1v1 m2v2 mv
в K':
m1v1
m2 v2 mv
( m1 m2 )V mV
v1 v1
V
v2 v2 V
v v
V
m m1 m2

7.

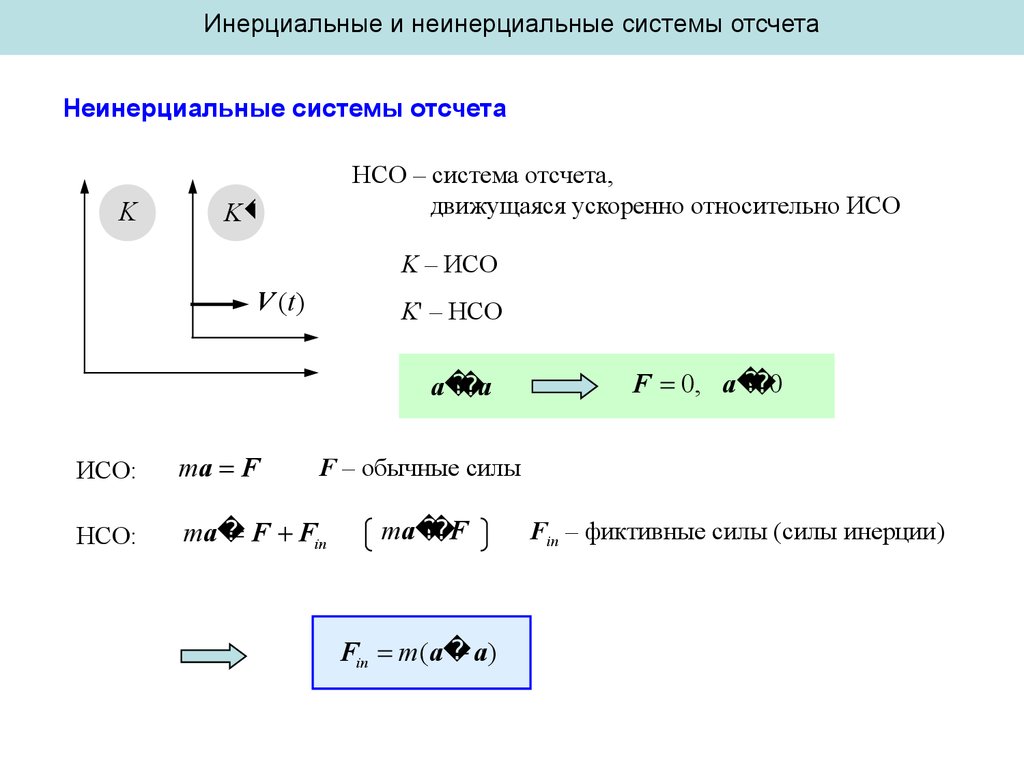
Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
K
НСО – система отсчета,
движущаяся ускоренно относительно ИСО
K
K – ИСО
V (t )
K' – НСО
a
a
ИСО:
ma F
НСО:
ma
F Fin
F 0, a
0
F – обычные силы
ma
F
Fin m( a
a)
Fin – фиктивные силы (силы инерции)

8.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
Поступательные НСО
y
y
x x0 x
y y
z z
t t
K
K
V
x0 (t )
v
dr
dt
x, x
d
dt
в векторном
виде
v v0 v
– абсолютная скорость (скорость в K)
v0
dr0
dt
v
dr
– относительная скорость (скорость в K')
dt
– переносная скорость (скорость в K неподвижной в K' мат. точки)

9.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
Аналогично как для скорости
a a0 a
a
dv
dt
– абсолютное ускорение (ускорение в K)
a0
dv0
dt
– переносное ускорение (ускорение в K неподвижной в K' мат. точки)
a
dv
– относительное ускорение (ускорение в K')
dt
Fin ma0

10.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
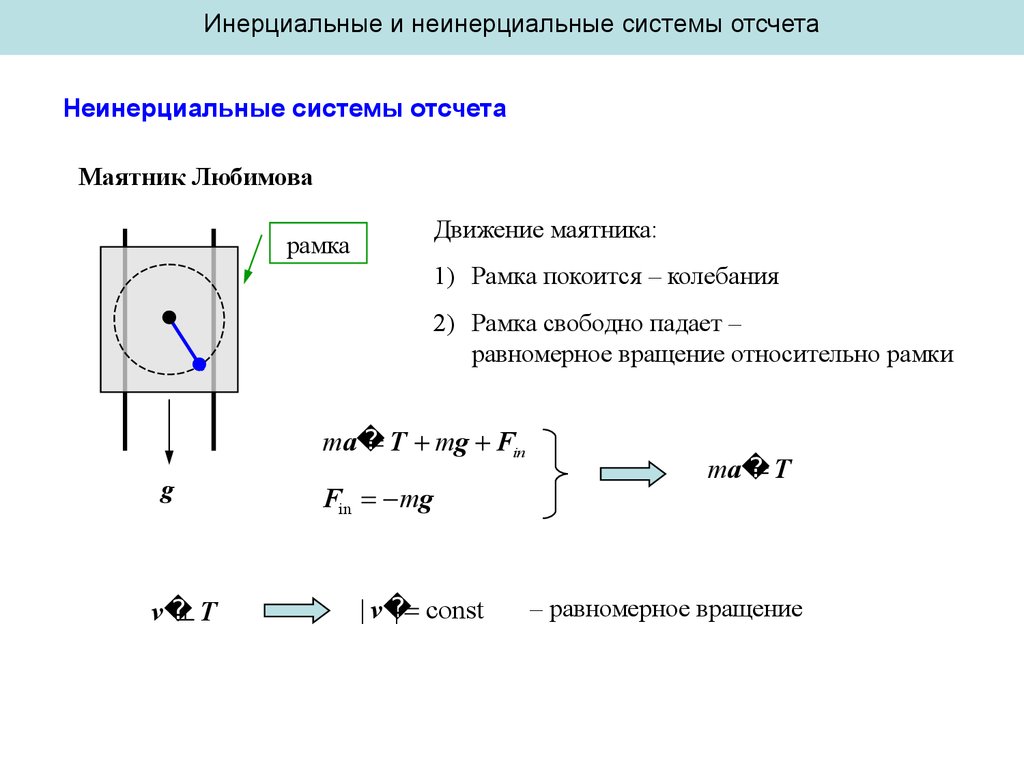
Маятник Любимова
Движение маятника:
рамка
1) Рамка покоится – колебания
2) Рамка свободно падает –
равномерное вращение относительно рамки
m a
T mg Fin
g
v
T
Fin mg
| v
| const
m a
T
– равномерное вращение

11.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
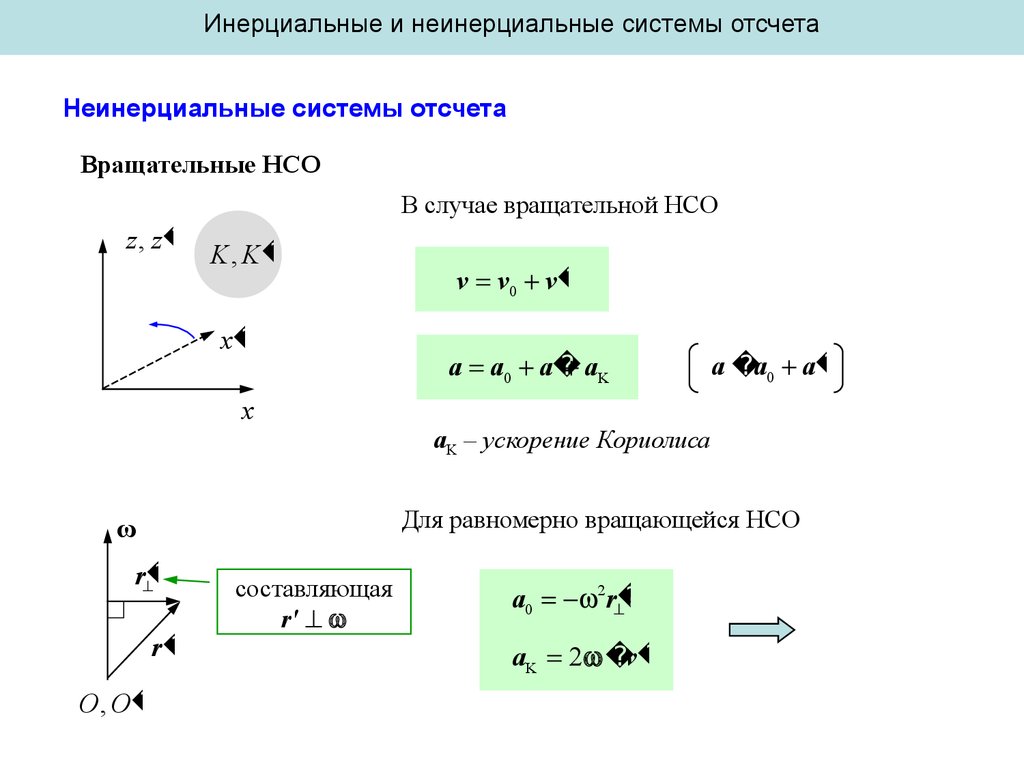
Вращательные НСО
В случае вращательной НСО
z, z
K, K
x
x
v v0 v
a a0 a
aK
a a0 a
aK – ускорение Кориолиса
Для равномерно вращающейся НСО
ω
r
r
O, O
составляющая
r'
a0 2 r
aK 2 v

12.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
Fin m ( a
a) m ( a0ЦБ aK )K F F
FЦБ m 2 r
FK – сила Кориолиса
FK 2m v
ω
FK
v S
FK
v
В северном полушарии FK направлена
вправо по отношению к v',
в южном – влево

13.

Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
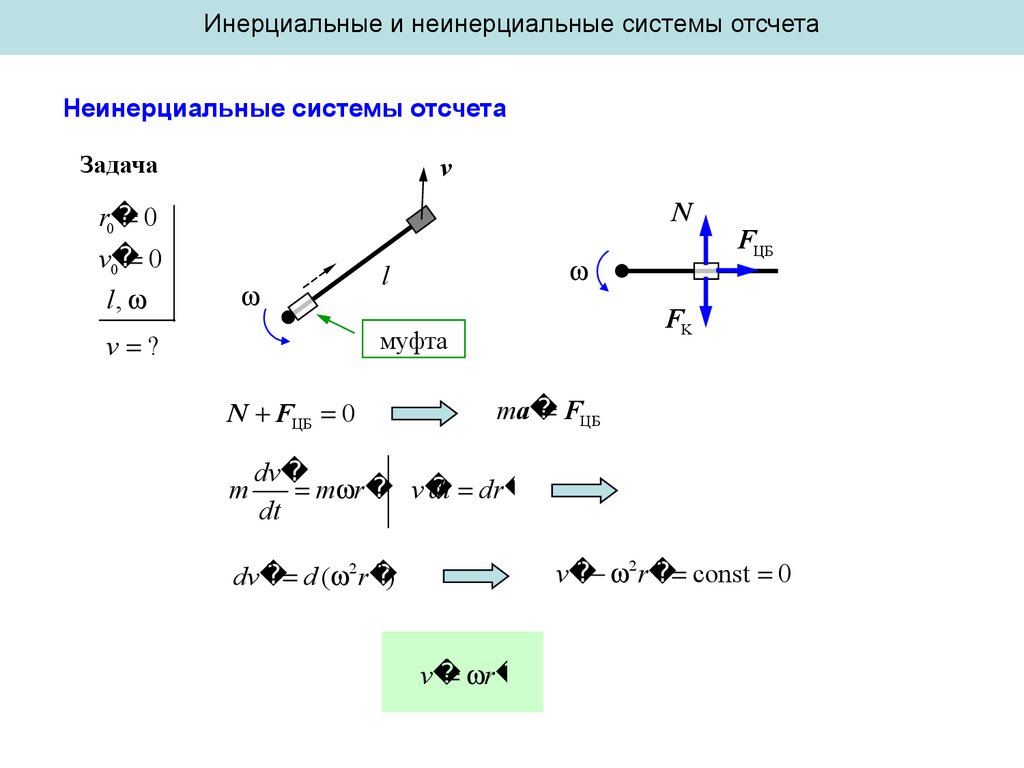
Задача
v
N
r0
0
v0 0
l,
l
FK
муфта
v ?
N FЦБ 0
m
FЦБ
ma
FЦБ
dv
m r v
dt dr
dt
2
2
v
2 r
const 0
2
2
dv
d ( 2 r
)
v
r

14.

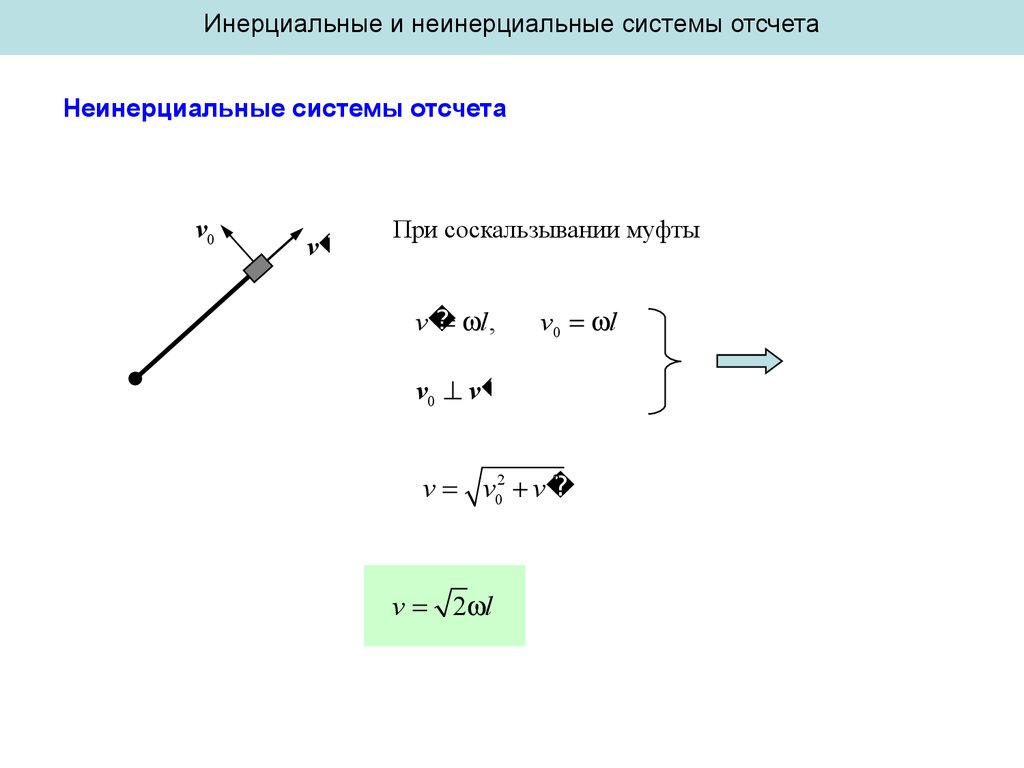
Инерциальные и неинерциальные системы отсчета
Неинерциальные системы отсчета
v0
v
При соскальзывании муфты
v
l ,
v0 l
v0 v
2
v v02 v
v 2 l