Тени в ортогональных проекциях

1.

Тени в ортогональных проекциях

2.

ТЕНИ
Рельефность «происходит от теней и
светов или, другими словами, от
светлого и темного.
Итак, кто избегает теней, избегает
славы искусства»
Леонардо Да Винчи
(Leonardo Da Vinci)
(1452-1519)

3.

Форма предмета воспринимается
точнее, когда предмет освещен и
на его поверхности образуется
светотень
Изображение светотени на проекционных чертежах состоит
из двух графических операций:
- «геометрия теней»;
- «изображение светотени» («отмывка»)
Характер светотени зависит от положения предмета
относительно источника света
и направления лучей к поверхности

4.

«геометрия теней» - это
определение границ (контуров)
собственных и падающих теней,
основанное на построении линии
прикосновения лучевой
поверхности с данной
поверхностью и определение
линии пересечения поверхностей
«изображение светотени» («отмывка»)- графические приемы
выявления светотени на изображении так, чтобы ее
восприятие наиболее близко подходило к восприятию в
натуре. Эта операция основана на физиологии зрительного
восприятия, т.е. на «воздушной перспективе»
4

5.

ВОЗДУШНАЯ ПЕРСПЕКТИВА
Чем освещенное место ближе
к зрителю, тем оно кажется
светлее и ярче, а чем дальше
– тем бледнее и мягче
Светотеневой контраст
(различие между освещенной
и теневой частью
предмета) по мере удаления
от зрителя погашается,
делается менее резким

6. Тени при искусственном освещении

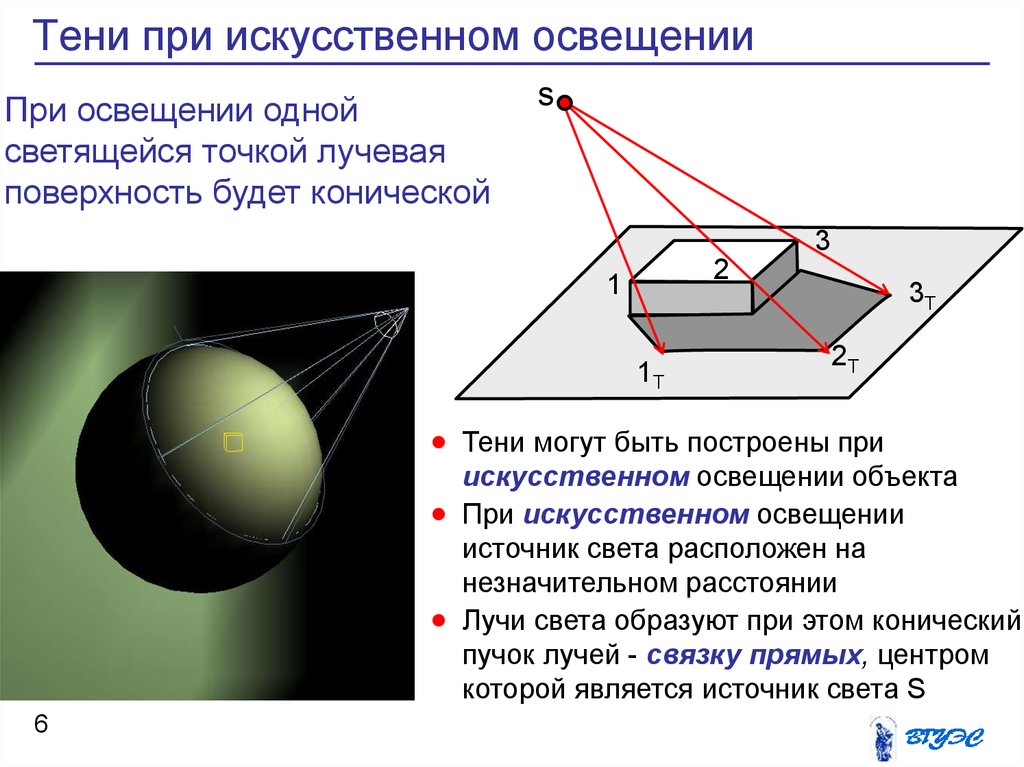
При освещении одной
светящейся точкой лучевая
поверхность будет конической
s
3
2
1
1Т
3Т
2Т
Тени могут быть построены при
искусственном освещении объекта
При искусственном освещении
источник света расположен на
незначительном расстоянии
Лучи света образуют при этом конический
пучок лучей - связку прямых, центром
которой является источник света S
6

7. Тени при естественном освещении

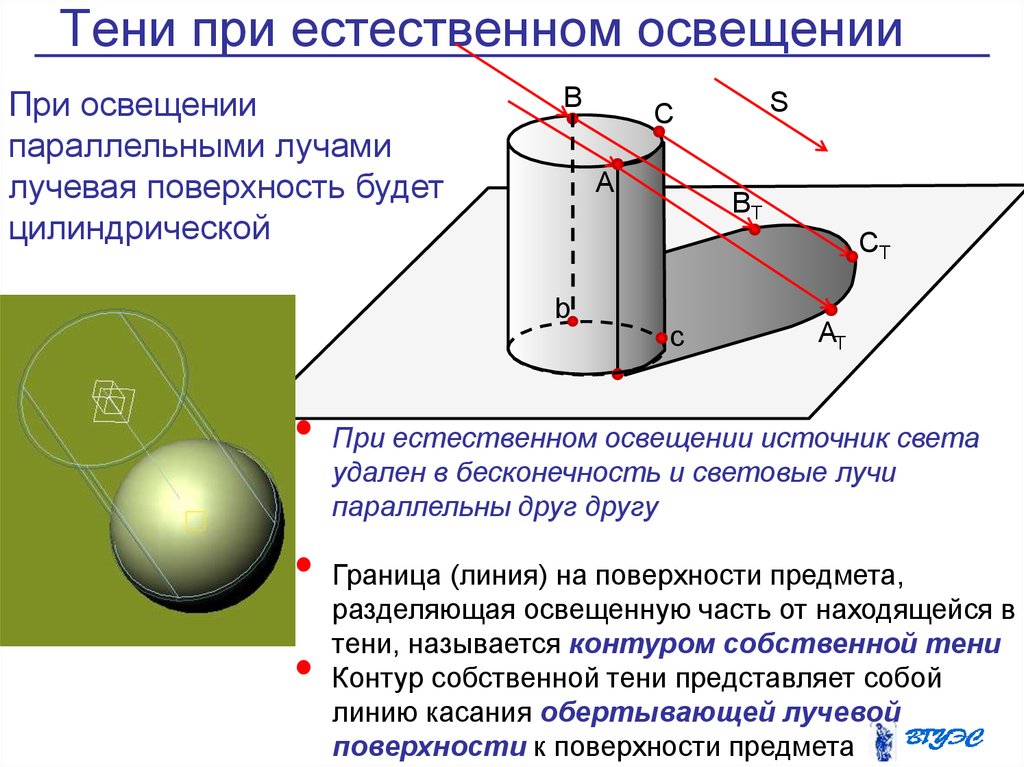
При освещении
параллельными лучами
лучевая поверхность будет
цилиндрической
В
A
BT
CT
b
c
S
C
AT
При естественном освещении источник света
удален в бесконечность и световые лучи
параллельны друг другу
Граница (линия) на поверхности предмета,
разделяющая освещенную часть от находящейся в
тени, называется контуром собственной тени
Контур собственной тени представляет собой
линию касания обертывающей лучевой
поверхности к поверхности предмета

8.

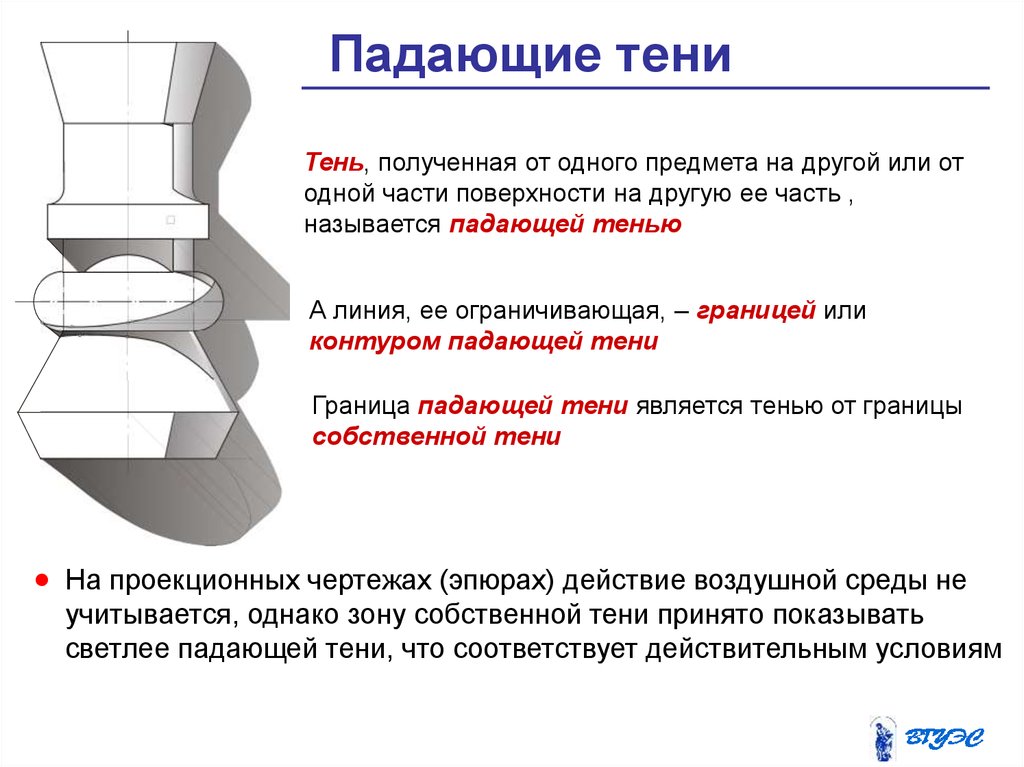
Падающие тени
Тень, полученная от одного предмета на другой или от
одной части поверхности на другую ее часть ,
называется падающей тенью
А линия, ее ограничивающая, – границей или
контуром падающей тени
Граница падающей тени является тенью от границы
собственной тени
На проекционных чертежах (эпюрах) действие воздушной среды не
учитывается, однако зону собственной тени принято показывать
светлее падающей тени, что соответствует действительным условиям

9. Направление световых лучей

a2
A
a3
b3
35о
45о
S3
S2
45о
45о
45о
a1
a2
a3
B b
2
x
b3
b2
b1
45о
b1
S1
a1
При построении теней на комплексных чертежах освещение считают солнечным, с
параллельными лучами
Источник света считают расположенным слева сверху сзади:
направление лучей света принимают параллельным диагонали куба, грани которого
совмещены с плоскостями проекций
Проекциями диагонали куба являются диагонали квадратов,
т. е. горизонтальная и фронтальная проекции светового луча составляют с осью проекции
х угол 45°, истинный угол наклона луча к плоскости проекций ~ 35°
Такое «стандартное» направление световых лучей создает преимущества при построении
теней и выполнении чертежа:
1) достигаются постоянство и простота построения проекций лучей и теней на чертежах
фасада и плана объекта;
2) облегчаются чтение чертежа и понимание форм, пропорций и размеров элементов
изображенного объекта.
9

10.

a2
z
a2
a3
A
a3
b3
B b
2
b3
x
45о
b2
45о
b1
b1
45о
a1
S2
45о
45о
35о
S3
S1
a1
y
3
2
1
35о
45о
4
45о
5
0,7(0,707)
0,3(0,293)
Диагональ квадрата 1-3 совмещается с его стороной 1-4 и полученная точка 5
соединяется с точкой 2.
Линия 2-5 дает истинный угол наклона диагонали куба (35016I16II).
При построении теней часто приходится делить отрезок прямой в отношении
величин стороны квадрата к его диагонали

11. Построение падающей тени от точки

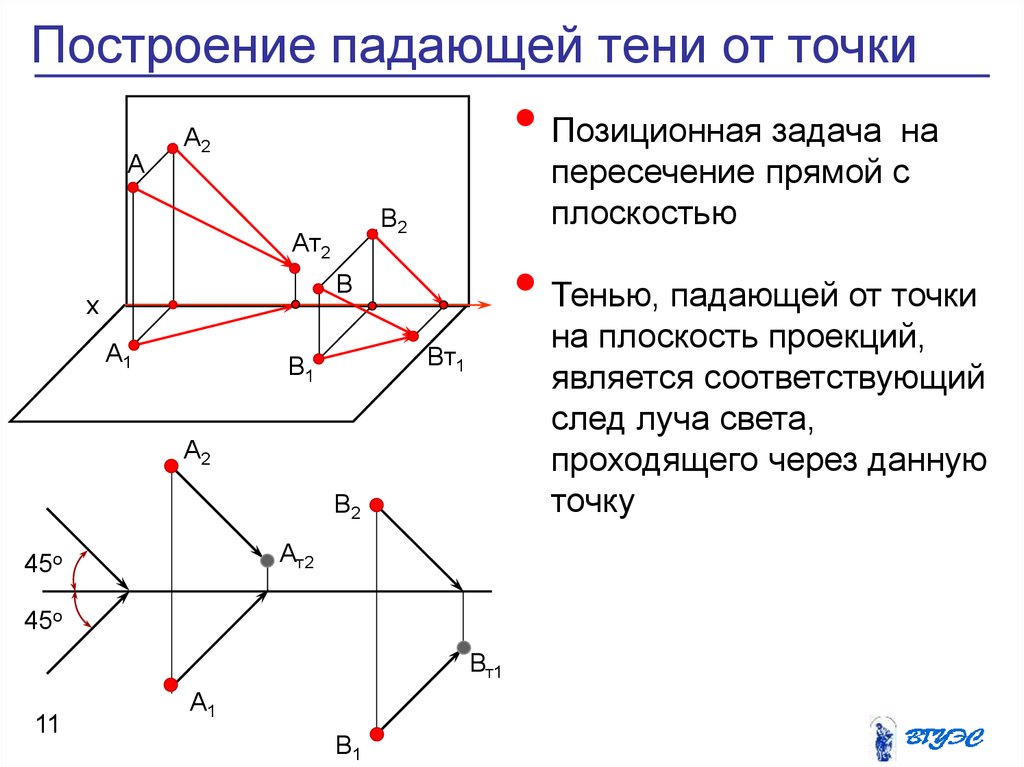
A
• Позиционная задача на
A2
пересечение прямой с
плоскостью
B2
Aт2
• Тенью, падающей от точки
B
x
A1
на плоскость проекций,
является соответствующий
след луча света,
проходящего через данную
точку
Bт1
B1
А2
В2
Ат2
45о
45о
Вт1
11
А1
В1

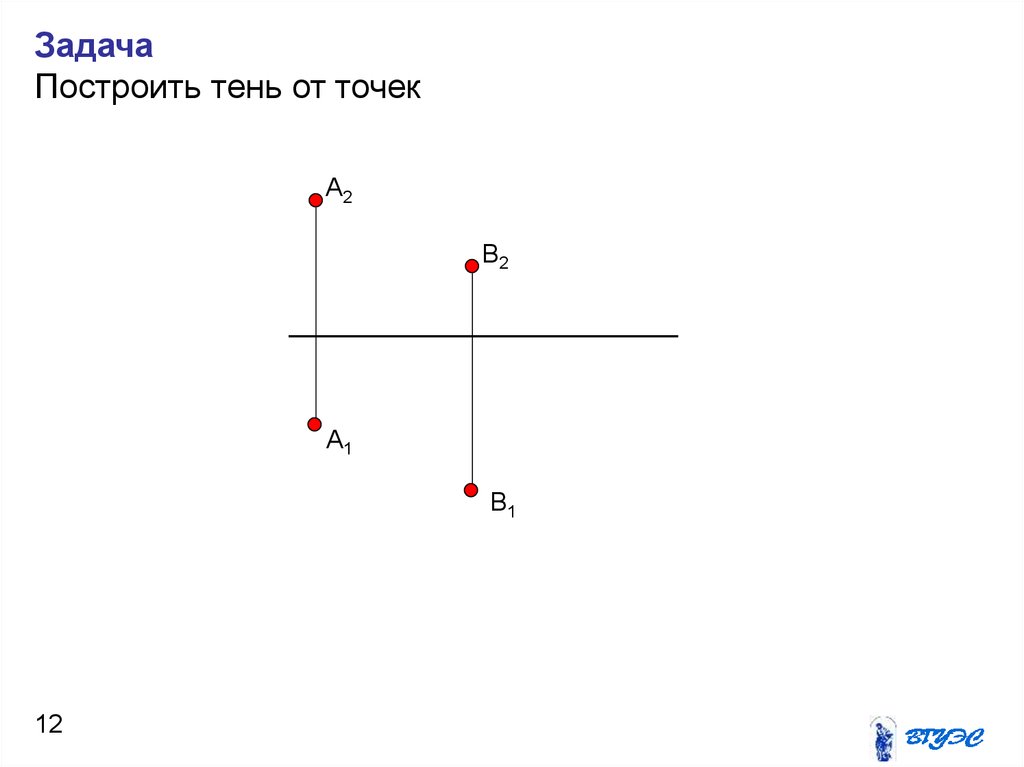
12.

Задача
Построить тень от точек
A2
В2
A1
В1
12

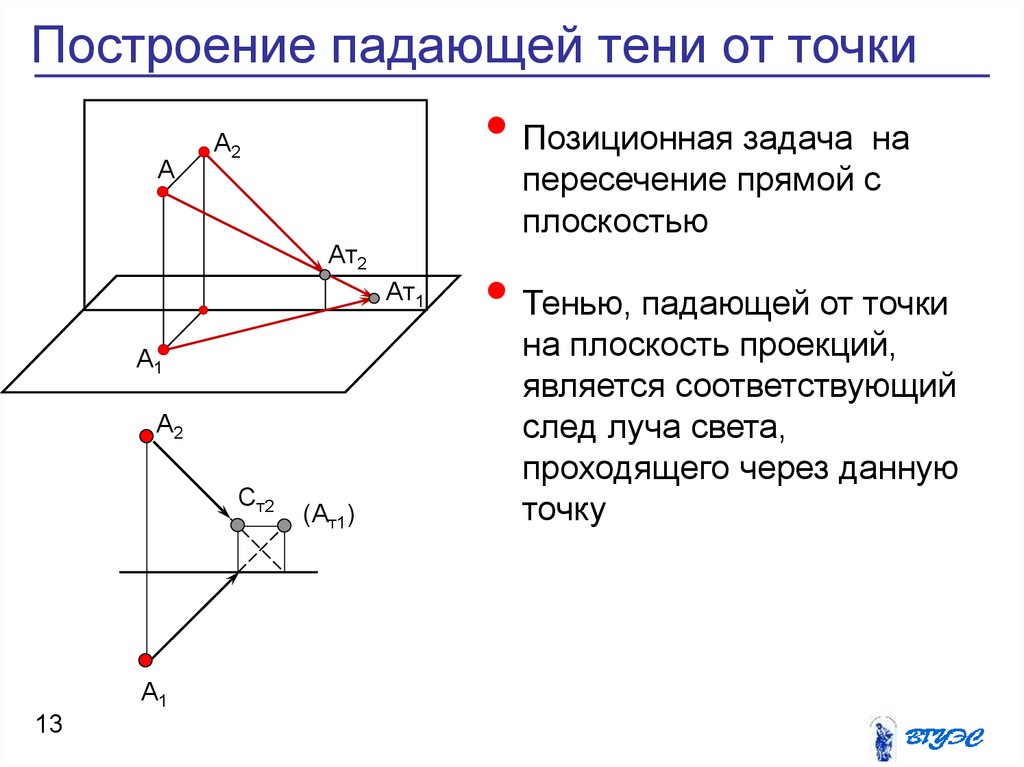
13. Построение падающей тени от точки

A
• Позиционная задача на
A2
пересечение прямой с
плоскостью
Aт2
Aт1
A1
A2
Ст2
A1
13
(Aт1)
• Тенью, падающей от точки
на плоскость проекций,
является соответствующий
след луча света,
проходящего через данную
точку

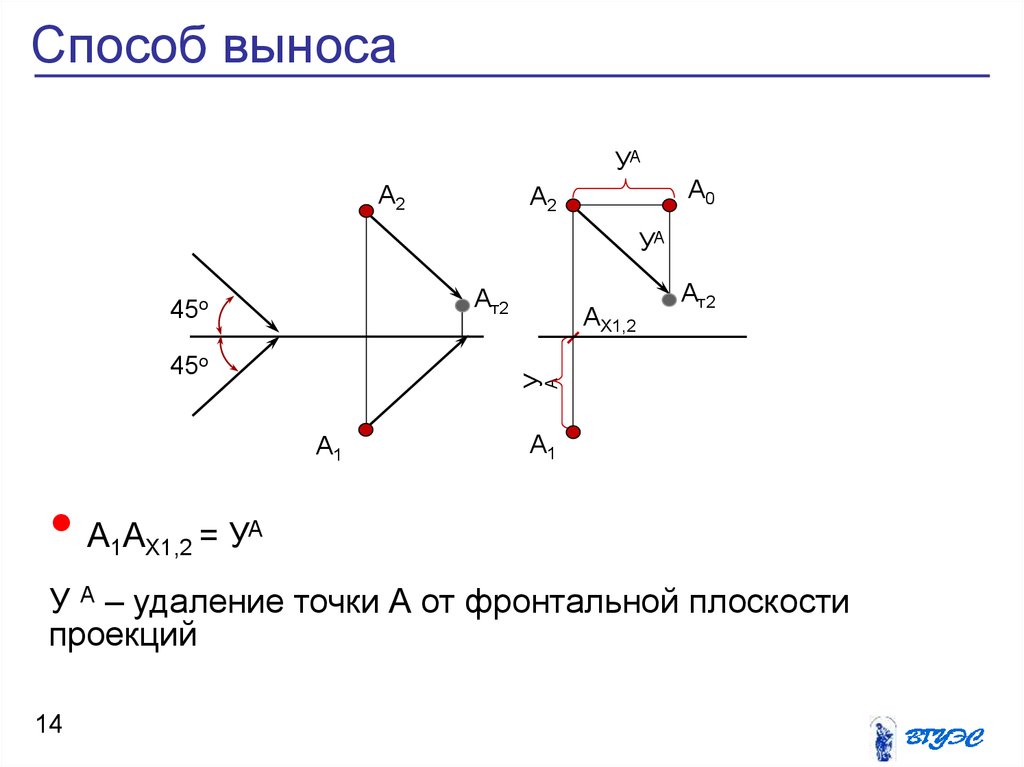
14. Способ выноса

УА
А2
А2
А0
УА
Ат2
45о
А
У
45о
А1
•АА
1
Х1,2 =
АХ1,2
Ат2
А1
УА
У А – удаление точки А от фронтальной плоскости
проекций
14

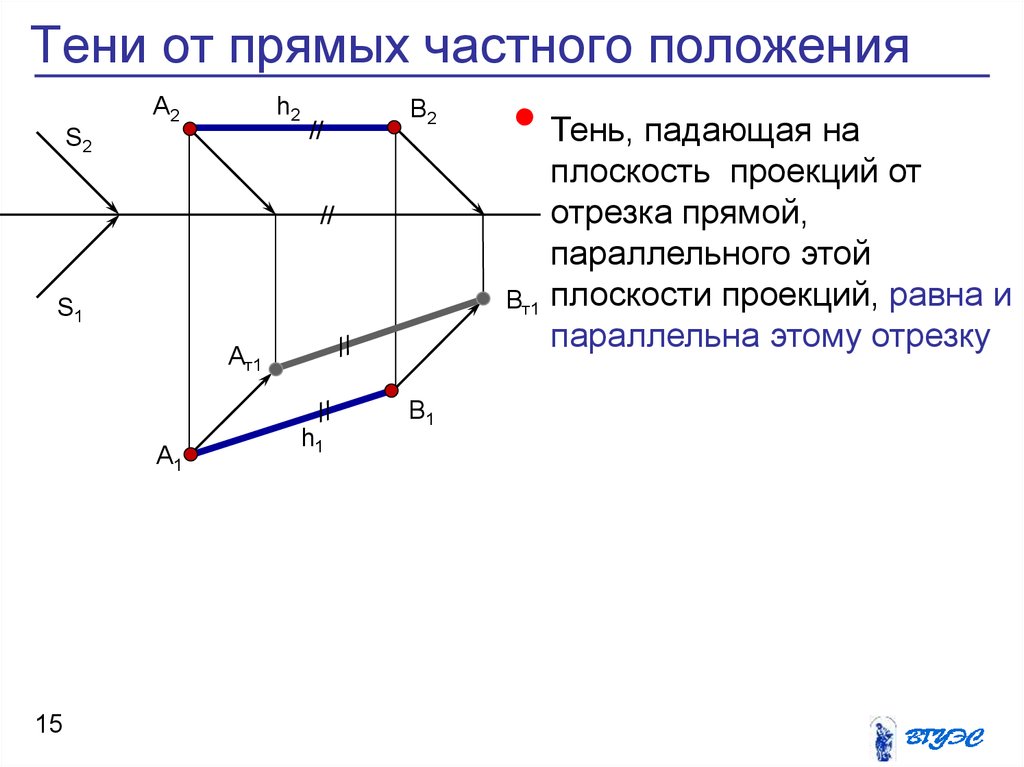
15. Тени от прямых частного положения

А2
h2
S2
//
В2
• Тень, падающая на
//
Вт1
S1
Ат1
А1
15
h1
В1
плоскость проекций от
отрезка прямой,
параллельного этой
плоскости проекций, равна и
параллельна этому отрезку

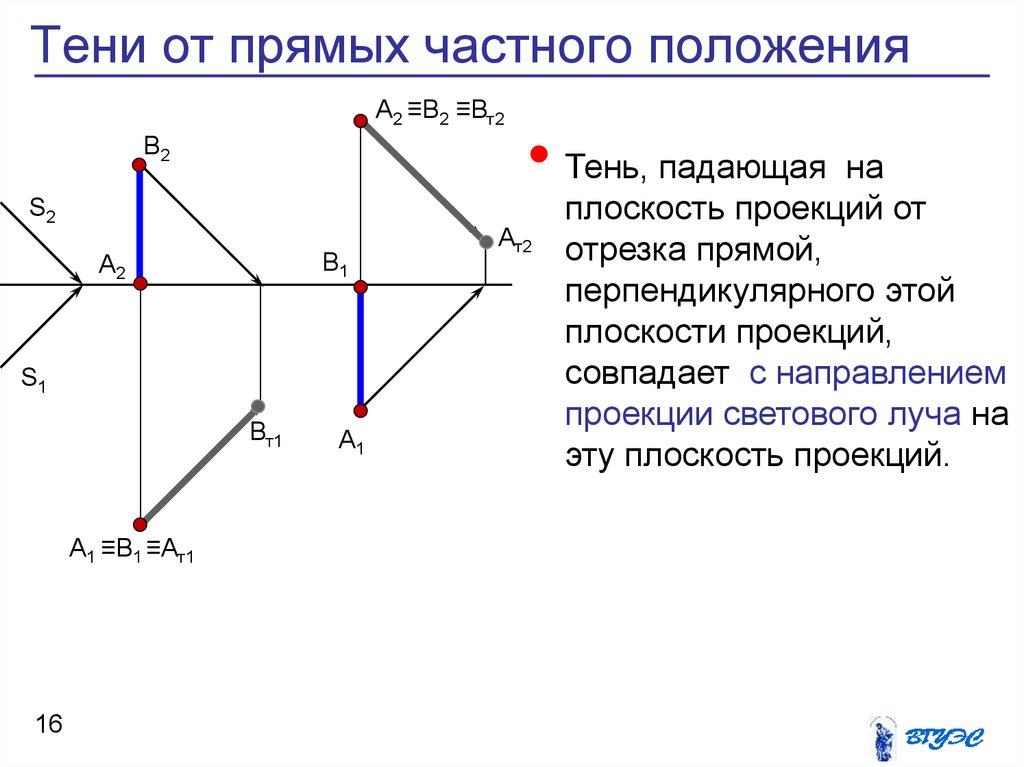
16. Тени от прямых частного положения

А2 ≡В2 ≡Вт2
В2
S2
В1
А2
S1
Вт1
А1 ≡В1 ≡Ат1
16
А1
• Тень, падающая на
Ат2
плоскость проекций от
отрезка прямой,
перпендикулярного этой
плоскости проекций,
совпадает с направлением
проекции светового луча на
эту плоскость проекций.

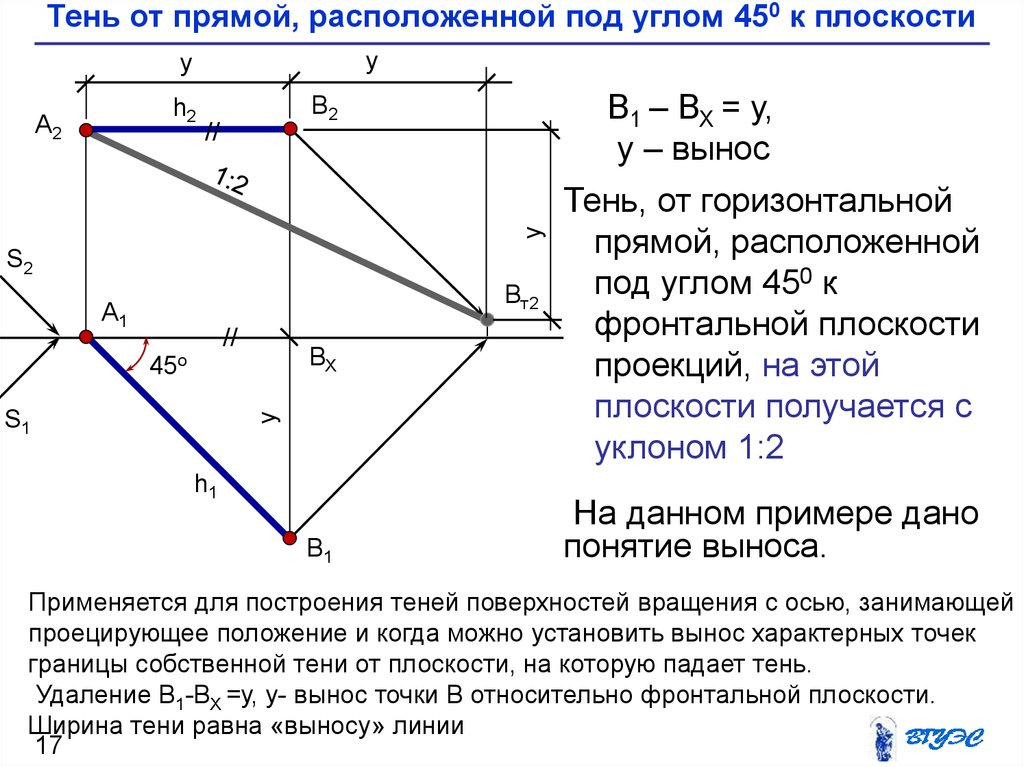
17. Тень от прямой, расположенной под углом 450 к плоскости

y
y
h2
В1 – ВХ = у,
у – вынос
В2
//
y
А2
S2
Вт2
А1
//
45о
y
S1
ВХ
h1
В1
Тень, от горизонтальной
прямой, расположенной
под углом 450 к
фронтальной плоскости
проекций, на этой
плоскости получается с
уклоном 1:2
На данном примере дано
понятие выноса.
Применяется для построения теней поверхностей вращения с осью, занимающей
проецирующее положение и когда можно установить вынос характерных точек
границы собственной тени от плоскости, на которую падает тень.
Удаление В1-ВХ =у, у- вынос точки В относительно фронтальной плоскости.
Ширина тени равна «выносу» линии
17

18. Тени от прямых частного положения

РП2
А2
В2 ≡Вт2
S2
Ат2
45о
S1
А1
РП1
18
В1
Тень от отрезка (общего
положения), лежащего
в вертикальной лучевой
плоскости, совпадает со
следом этой плоскости,
следовательно на фасаде
будет расположена
вертикально.

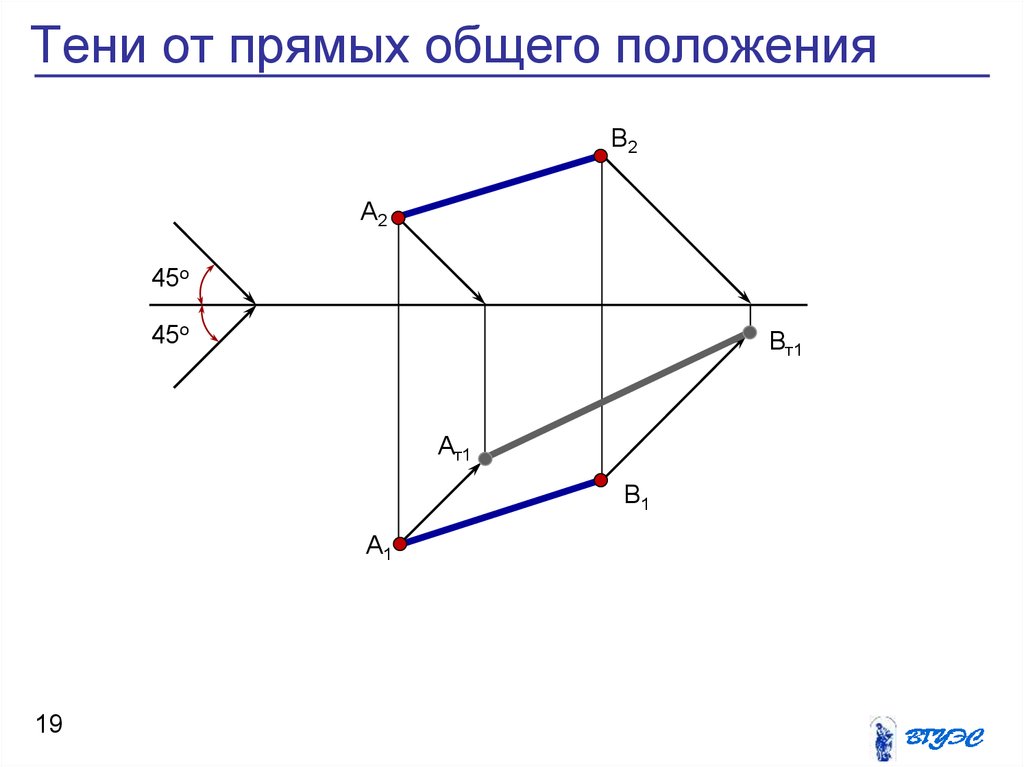
19. Тени от прямых общего положения

В2
А2
45о
45о
Вт1
Ат1
В1
А1
19

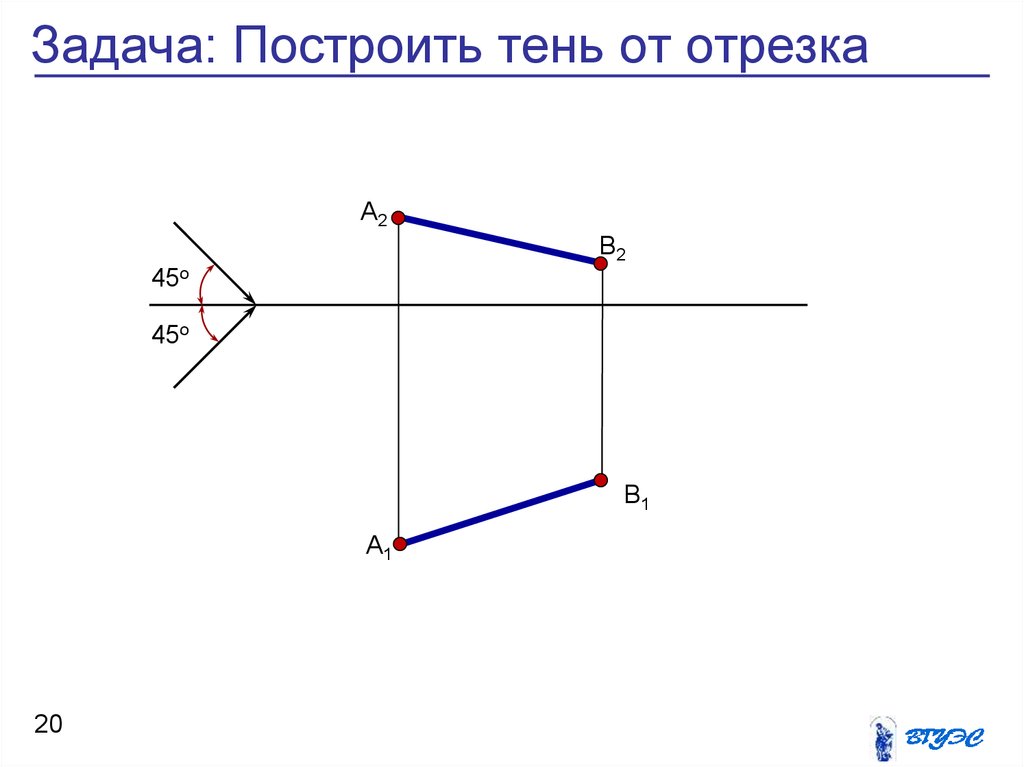
20. Задача: Построить тень от отрезка

А2
В2
45о
45о
В1
А1
20

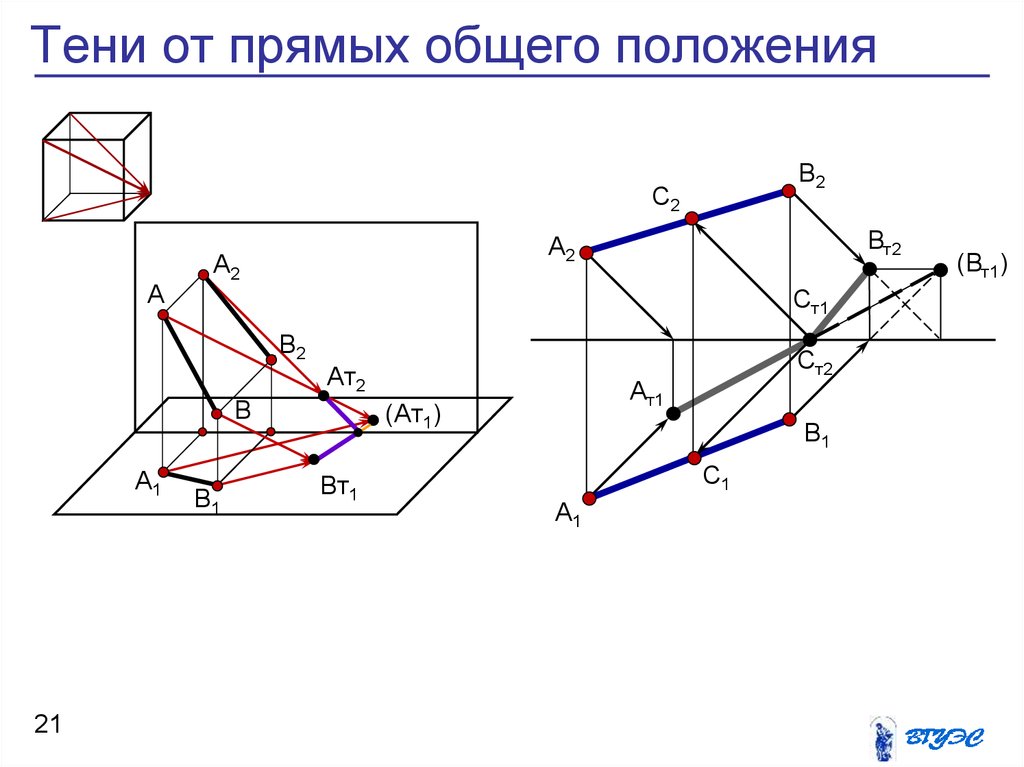
21. Тени от прямых общего положения

В2
С2
Вт2
А2
A2
A
Ст1
B2
Aт2
B
A1
21
B1
Ат1
(Aт1)
Bт1
Ст2
В1
С1
А1
(Вт1)

22. Задача: Построить тень от отрезка

В2
А2
45о
45о
В1
А1
22

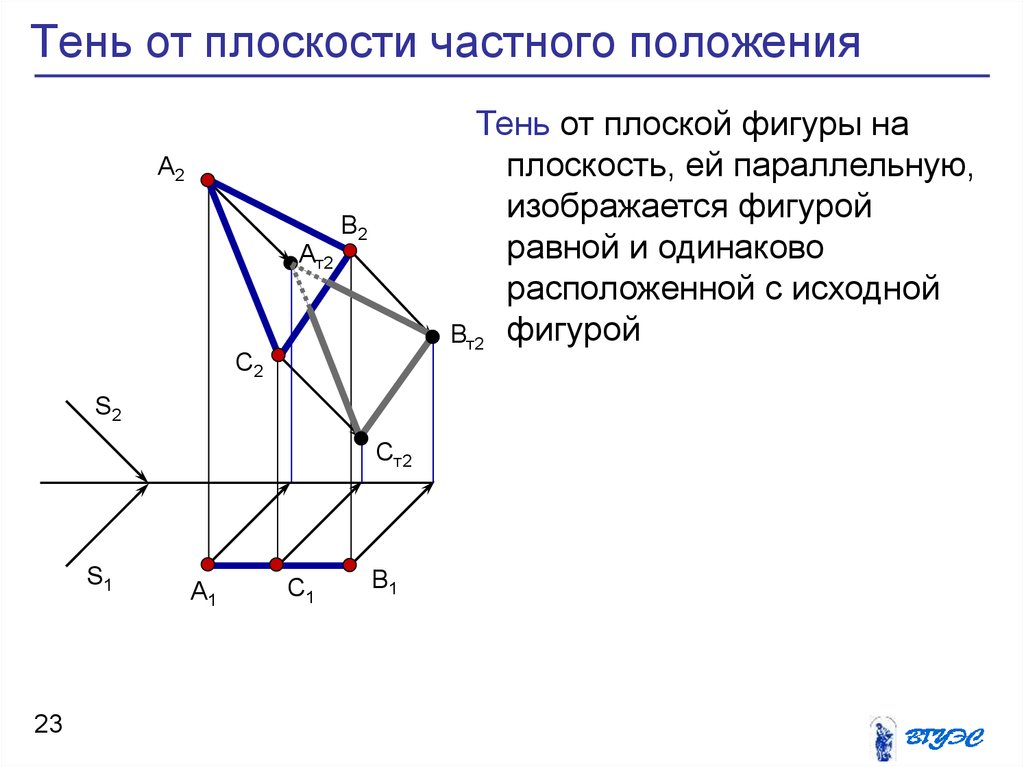
23. Тень от плоскости частного положения

Тень от плоской фигуры на
плоскость, ей параллельную,
изображается фигурой
равной и одинаково
расположенной с исходной
Вт2 фигурой
А2
Ат2
В2
С2
S2
Ст2
S1
23
А1
С1
В1

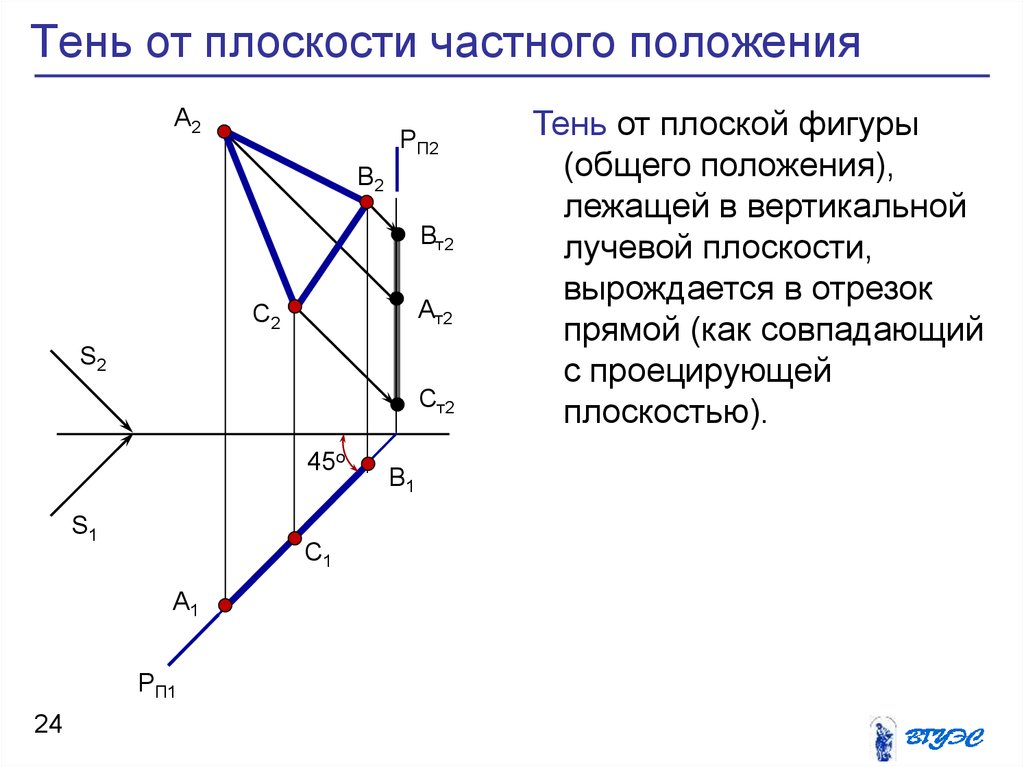
24. Тень от плоскости частного положения

А2
РП2
В2
Вт2
Ат2
С2
S2
Ст2
45о
S1
С1
А1
РП1
24
В1
Тень от плоской фигуры
(общего положения),
лежащей в вертикальной
лучевой плоскости,
вырождается в отрезок
прямой (как совпадающий
с проецирующей
плоскостью).

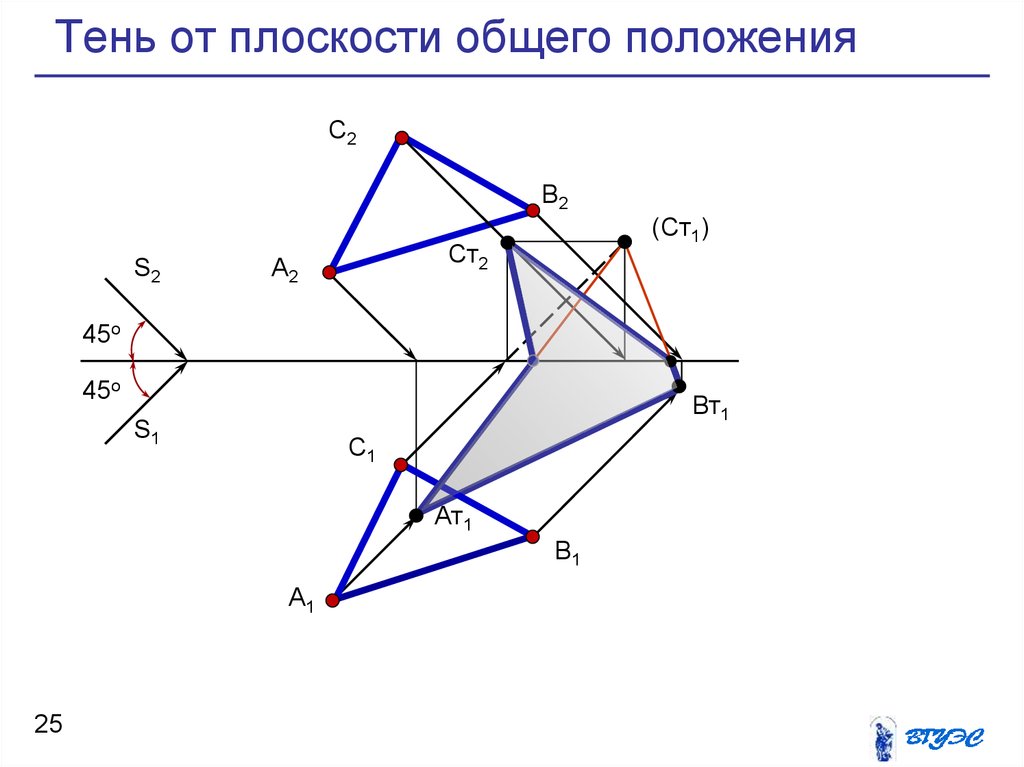
25. Тень от плоскости общего положения

С2
В2
S2
Ст2
А2
(Ст1)
45о
45о
Вт1
S1
С1
Ат1
В1
А1
25

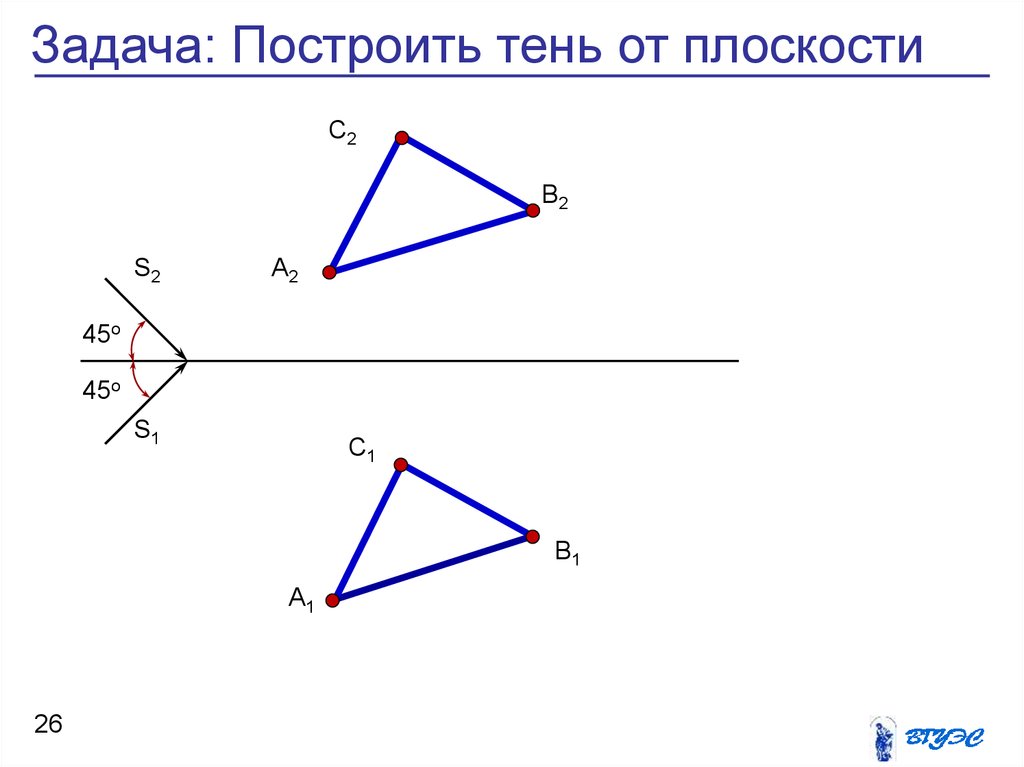
26.

Задача: Построить тень от плоскости
С2
В2
S2
А2
45о
45о
S1
С1
В1
А1
26

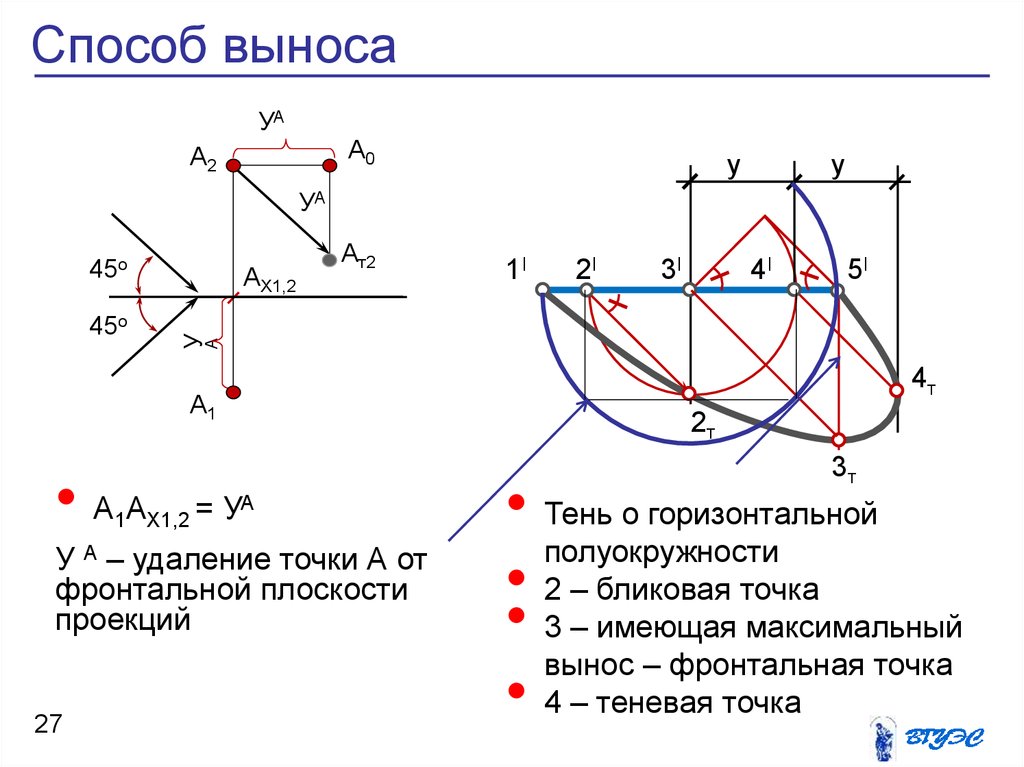
27. Способ выноса

УА
А0
А2
у
у
УА
45о
АХ1,2
3I
4I
5I
А
• АА
Х1,2 =
2т
3т
УА
У А – удаление точки А от
фронтальной плоскости
проекций
27
2I
4т
А1
1
1I
У
45о
Ат2
• Тень о горизонтальной
полуокружности
• 2 – бликовая точка
• 3 – имеющая максимальный
вынос – фронтальная точка
• 4 – теневая точка

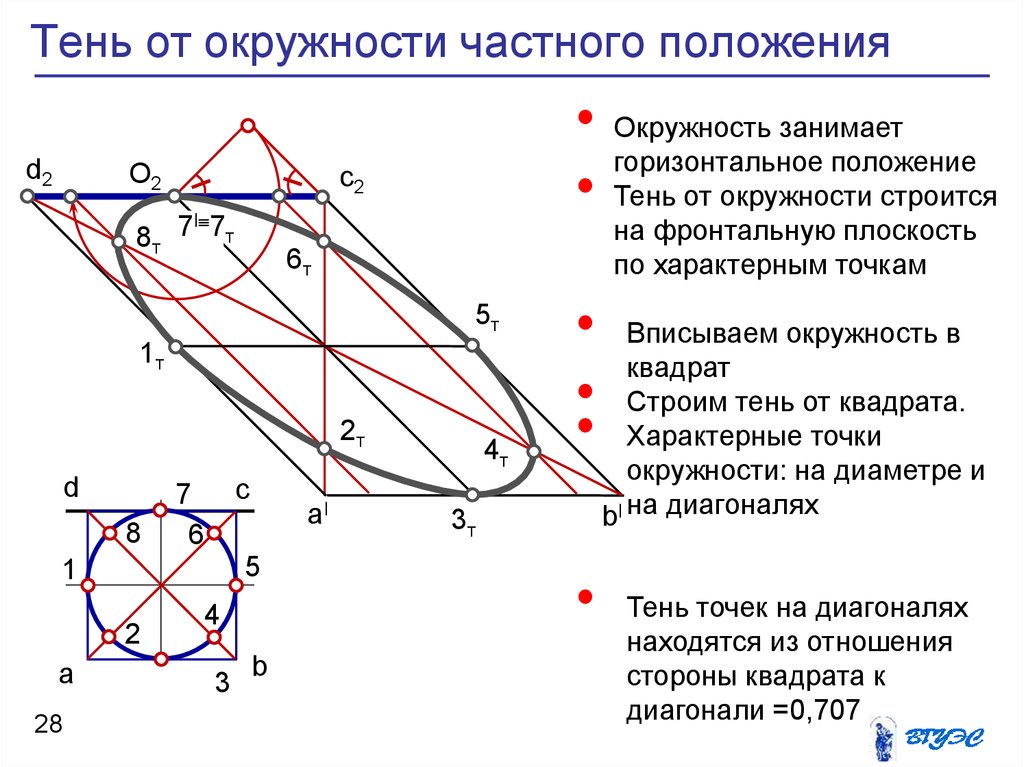
28. Тень от окружности частного положения

О2
d2
c2
I
8т 7 7т
6т
5т
1т
2т
d
8
c
7
6
5
1
2
a
28
aI
4
3
b
4т
3т
Окружность занимает
горизонтальное положение
Тень от окружности строится
на фронтальную плоскость
по характерным точкам
Вписываем окружность в
квадрат
Строим тень от квадрата.
Характерные точки
окружности: на диаметре и
bI на диагоналях
Тень точек на диагоналях
находятся из отношения
стороны квадрата к
диагонали =0,707

29.

Задача: Построить тень от окружности
d2
х
29
О2
c2

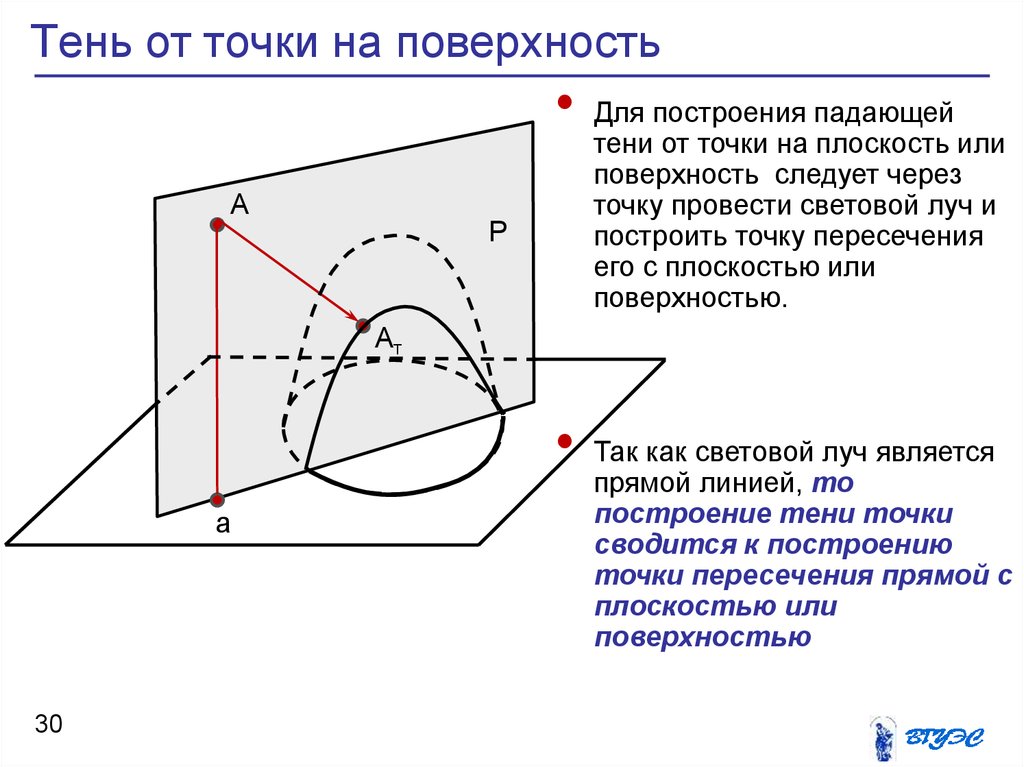
30. Тень от точки на поверхность

А
Р
Для построения падающей
тени от точки на плоскость или
поверхность следует через
точку провести световой луч и
построить точку пересечения
его с плоскостью или
поверхностью.
Ат
а
30
Так как световой луч является
прямой линией, то
построение тени точки
сводится к построению
точки пересечения прямой с
плоскостью или
поверхностью

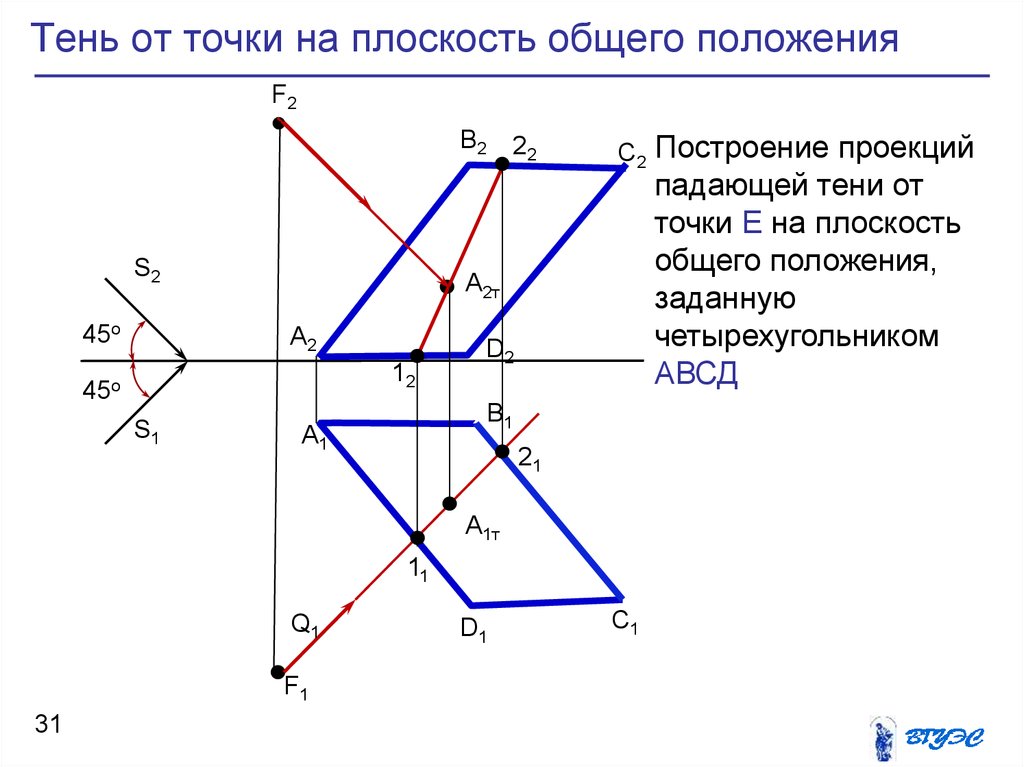
31. Тень от точки на плоскость общего положения

F2
B2
S2
45о
С2
A2т
A2
12
45о
S1
22
D2
B1
A1
21
A1т
11
Q1
F1
31
D1
C1
Построение проекций
падающей тени от
точки Е на плоскость
общего положения,
заданную
четырехугольником
АВСД

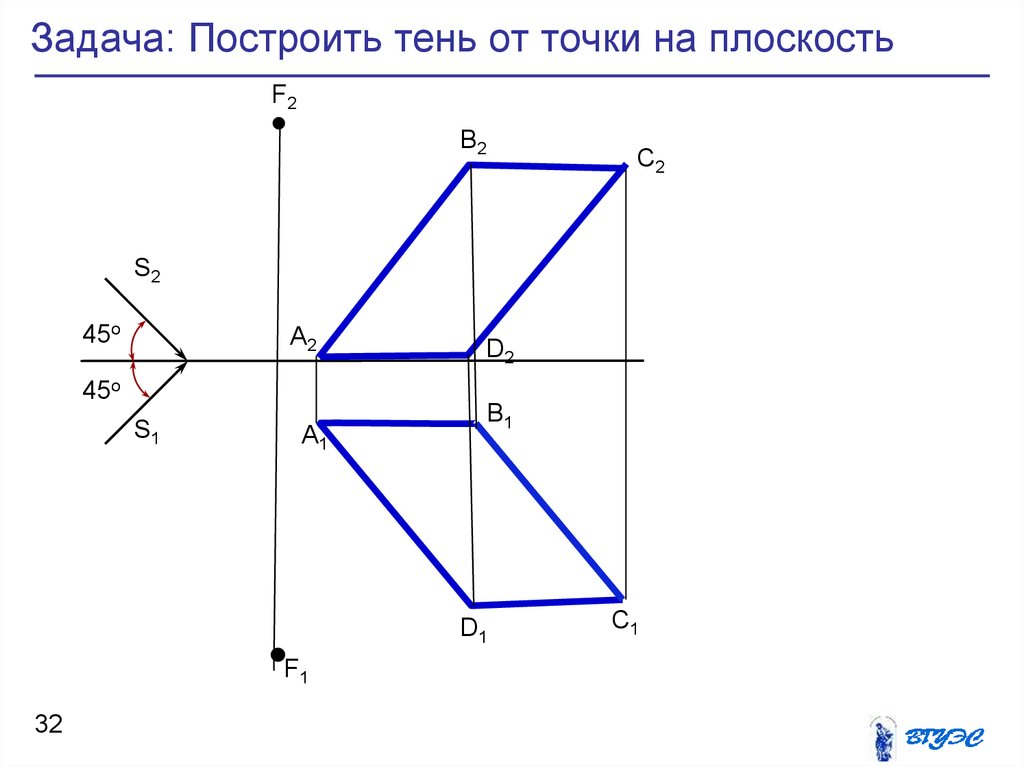
32. Задача: Построить тень от точки на плоскость

F2
B2
С2
S2
45о
A2
45о
S1
A1
D2
B1
D1
F1
32
C1

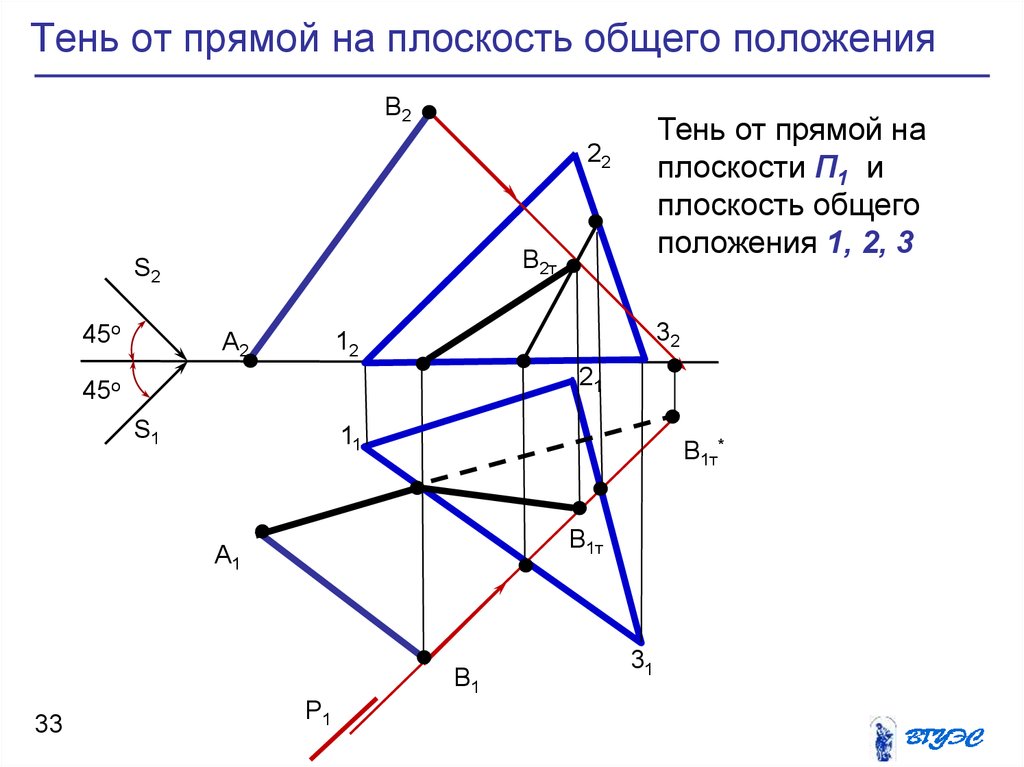
33. Тень от прямой на плоскость общего положения

B2
Тень от прямой на
плоскости П1 и
плоскость общего
положения 1, 2, 3
22
B2т
S2
45о
32
12
A2
21
45о
S1
11
B1т*
B1т
A1
B1
33
P1
31

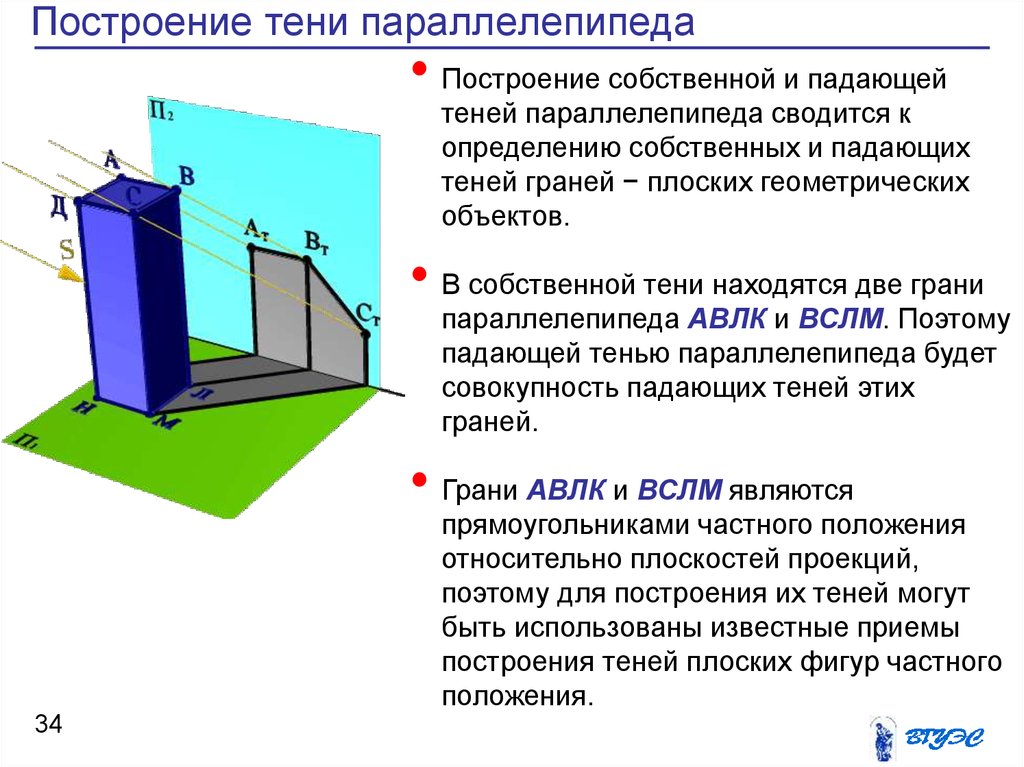
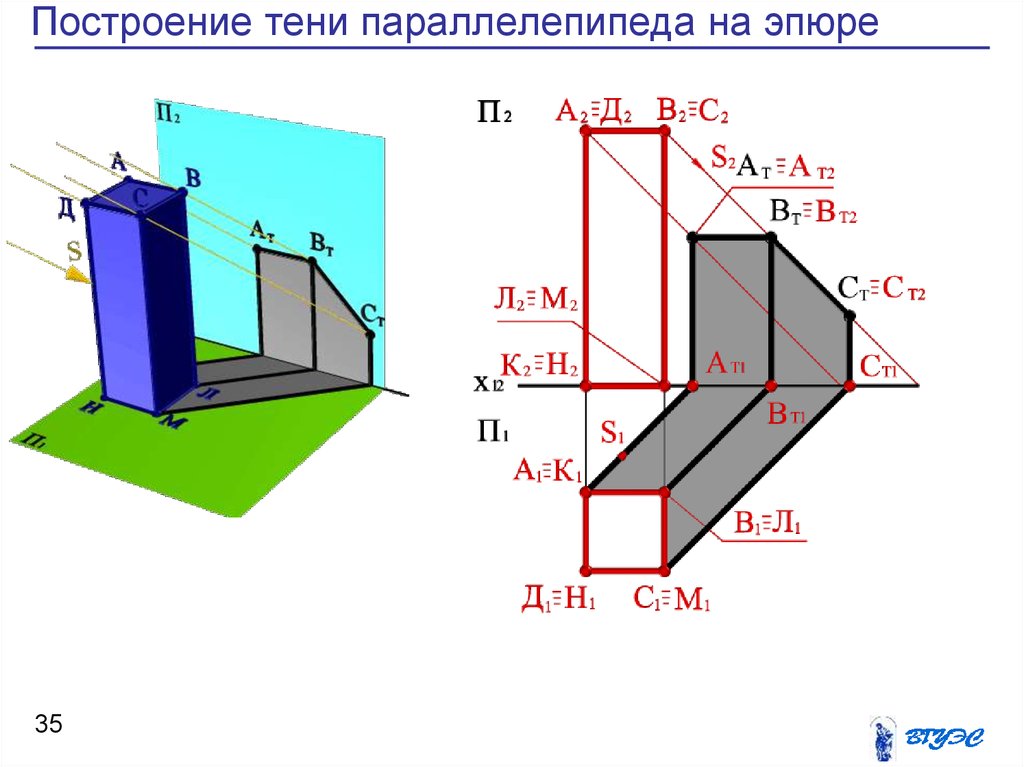
34. Построение тени параллелепипеда

• Построение собственной и падающей
теней параллелепипеда сводится к
определению собственных и падающих
теней граней − плоских геометрических
объектов.
• В собственной тени находятся две грани
параллелепипеда АВЛК и ВСЛМ. Поэтому
падающей тенью параллелепипеда будет
совокупность падающих теней этих
граней.
• Грани АВЛК и ВСЛМ являются
прямоугольниками частного положения
относительно плоскостей проекций,
поэтому для построения их теней могут
быть использованы известные приемы
построения теней плоских фигур частного
положения.
34

35. Построение тени параллелепипеда на эпюре

35

36. Построение тени пирамиды

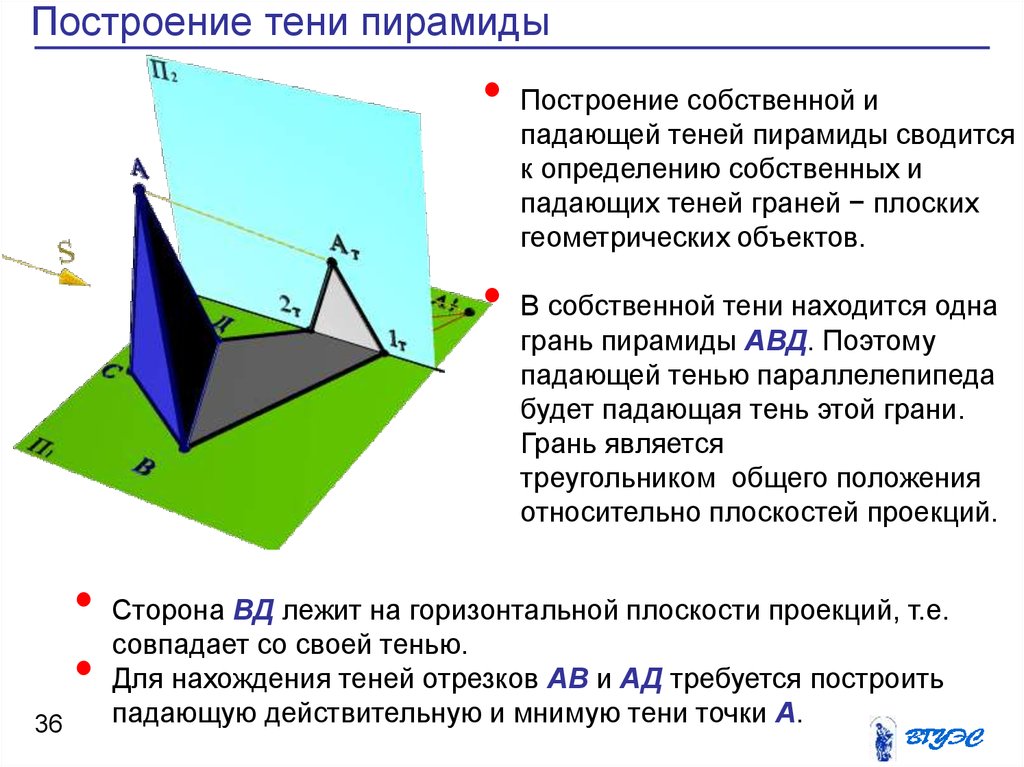
36
Построение собственной и
падающей теней пирамиды сводится
к определению собственных и
падающих теней граней − плоских
геометрических объектов.
В собственной тени находится одна
грань пирамиды АВД. Поэтому
падающей тенью параллелепипеда
будет падающая тень этой грани.
Грань является
треугольником общего положения
относительно плоскостей проекций.
Сторона ВД лежит на горизонтальной плоскости проекций, т.е.
совпадает со своей тенью.
Для нахождения теней отрезков АВ и АД требуется построить
падающую действительную и мнимую тени точки А.

37. Построение тени пирамиды на эпюре

37

38. Построение тени цилиндра

38
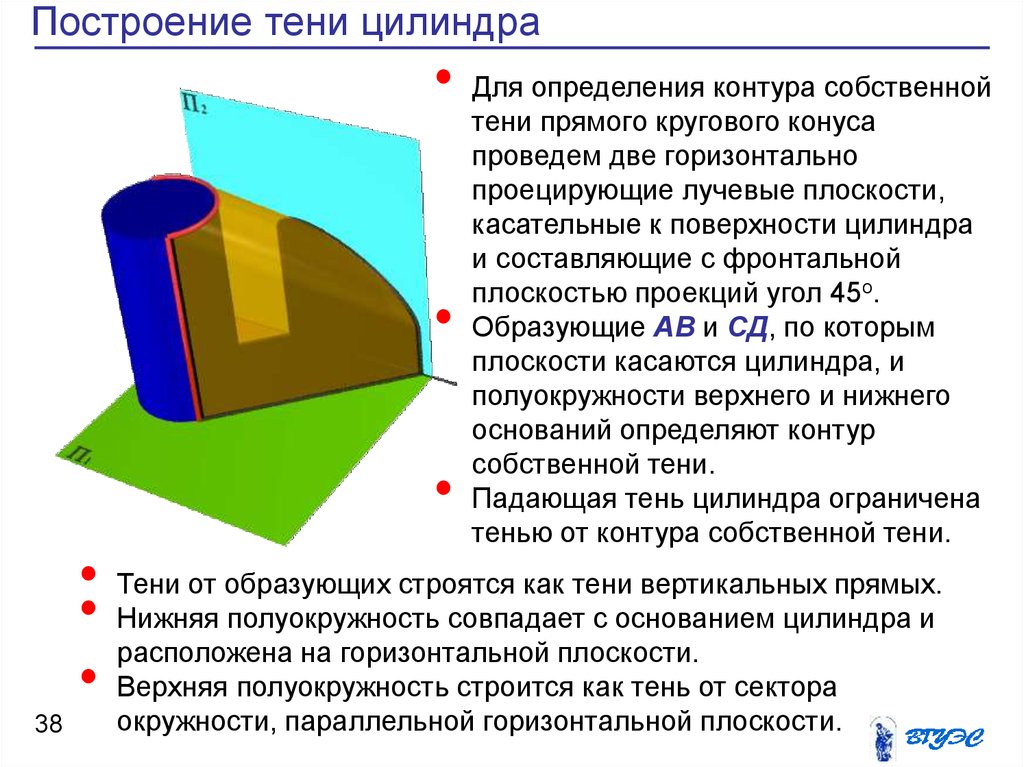
Для определения контура собственной
тени прямого кругового конуса
проведем две горизонтально
проецирующие лучевые плоскости,
касательные к поверхности цилиндра
и составляющие с фронтальной
плоскостью проекций угол 45о.
Образующие АВ и СД, по которым
плоскости касаются цилиндра, и
полуокружности верхнего и нижнего
оснований определяют контур
собственной тени.
Падающая тень цилиндра ограничена
тенью от контура собственной тени.
Тени от образующих строятся как тени вертикальных прямых.
Нижняя полуокружность совпадает с основанием цилиндра и
расположена на горизонтальной плоскости.
Верхняя полуокружность строится как тень от сектора
окружности, параллельной горизонтальной плоскости.

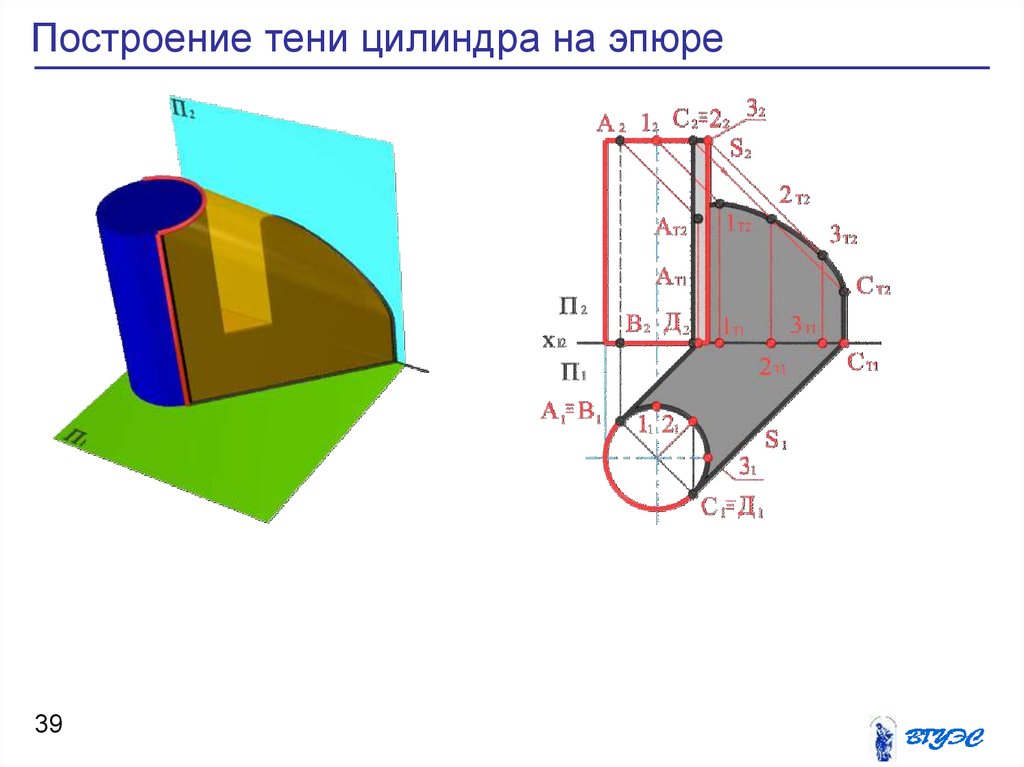
39. Построение тени цилиндра на эпюре

39

40.

Задача: Построить тени цилиндра
S2

41. Построение тени цилиндра на эпюре без второй проекции

41

42.

ТЕНИ ЦИЛИНДРА
12I
Тени строятся на
фронтальную
плоскость, проходящую
через ось цилиндра
ГСТ
ГПТ
ГСТ – граница
собственной тени
22
32
2т2
ГПТ – граница падающей
тени
12
1т2
3т2
Точки 1I и 2I определяют
положение образующих
цилиндра. 2I- невидимая

43.

ТЕНИ КОНУСА

44. Построение тени конуса

44
Построение собственной и
падающей теней прямого
кругового конуса, основание
которого расположено в
горизонтальной плоскости,
выполняется в следующей
последовательности:
1. Определяем действительную
или мнимую тень от вершины А
на горизонтальную плоскость
проекций.
2. Из горизонтальной проекции полученной тени проводим две
прямые, касательные к окружности основания конуса. Точки
касания этих прямых к окружности основания конуса определяют
положение образующих конуса, которые являются контуром
собственной тени конуса.
3. Меньшая дуга окружности основания конуса и построенные
образующие определяют контур падающей тени.

45. Построение тени конуса на эпюре

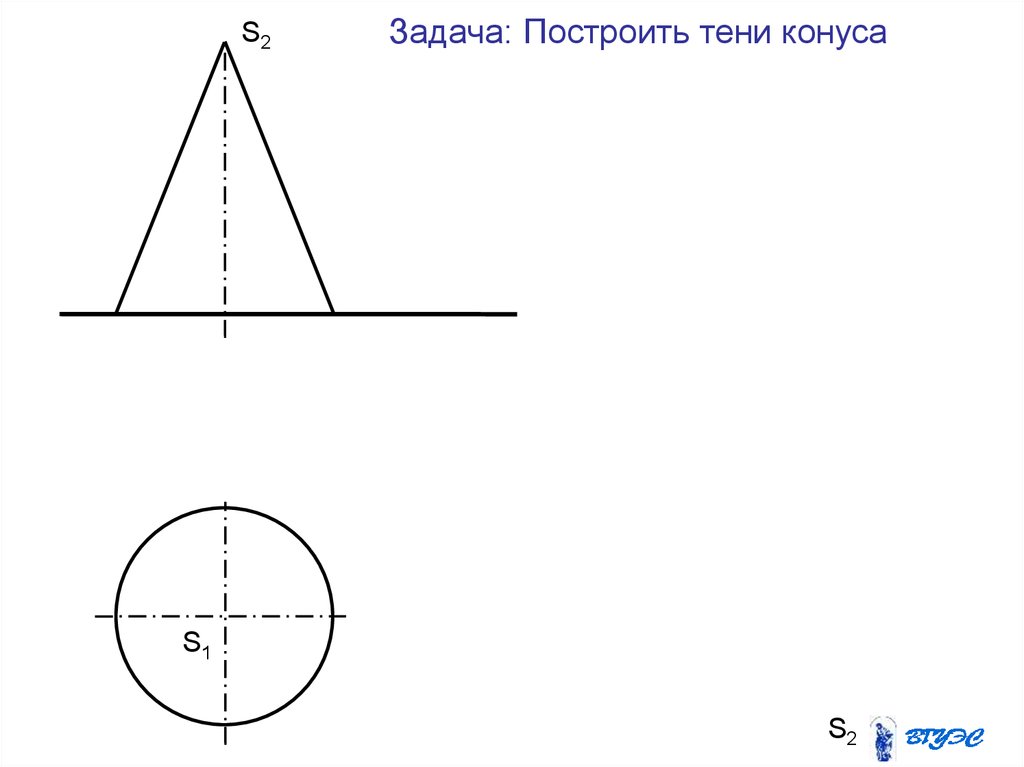
45

46.

S2
Задача: Построить тени конуса
S1
S2

47.

ТЕНЬ КОНУСА
с углом наклона образующей к основанию
равным 45О

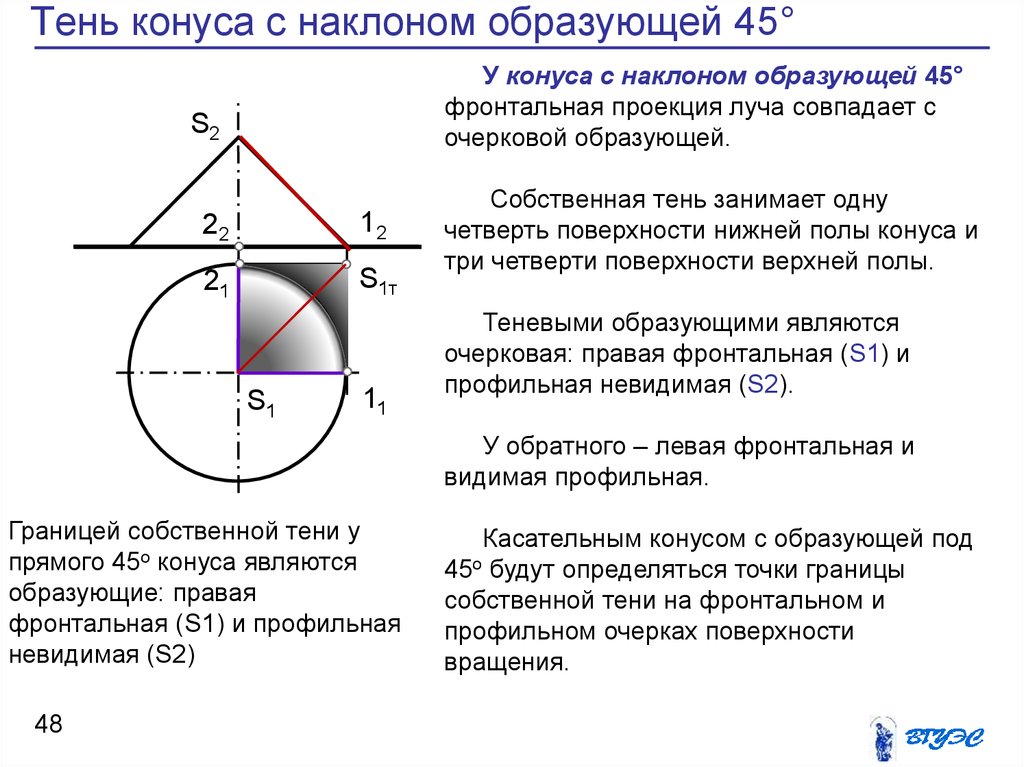
48. Тень конуса с наклоном образующей 45°

У конуса с наклоном образующей 45°
фронтальная проекция луча совпадает с
очерковой образующей.
S2
22
12
21
S1т
S1
11
Собственная тень занимает одну
четверть поверхности нижней полы конуса и
три четверти поверхности верхней полы.
Теневыми образующими являются
очерковая: правая фронтальная (S1) и
профильная невидимая (S2).
У обратного – левая фронтальная и
видимая профильная.
Границей собственной тени у
прямого 45о конуса являются
образующие: правая
фронтальная (S1) и профильная
невидимая (S2)
48
Касательным конусом с образующей под
45о будут определяться точки границы
собственной тени на фронтальном и
профильном очерках поверхности
вращения.

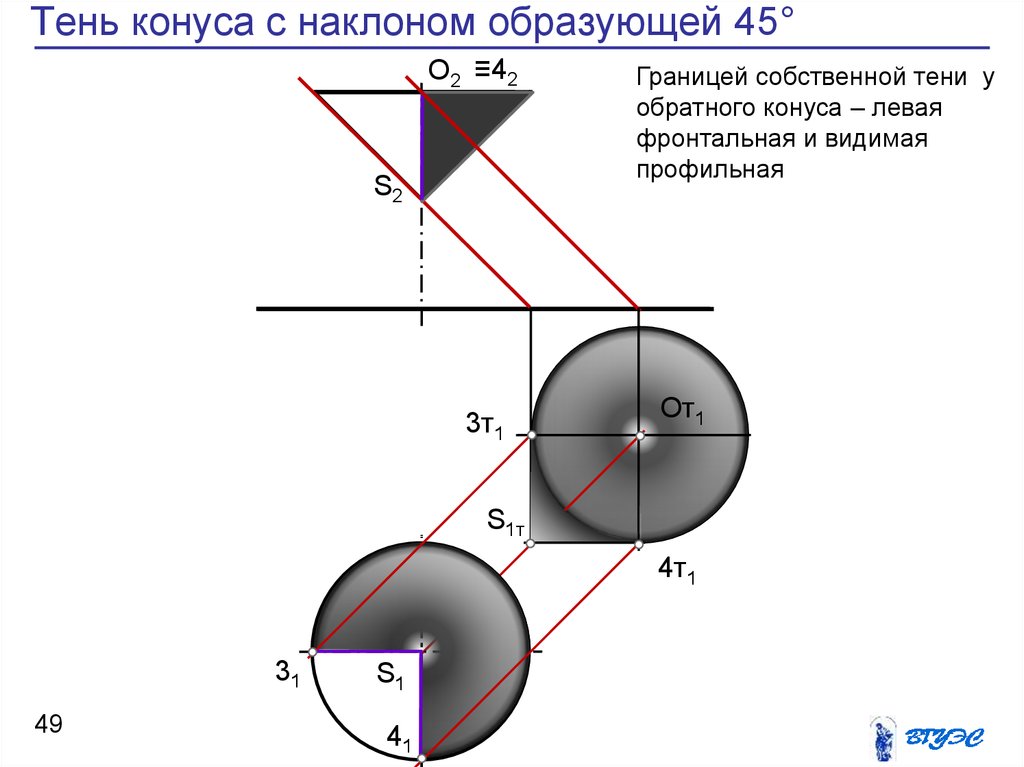
49. Тень конуса с наклоном образующей 45°

О2 ≡42
S2
3т1
Границей собственной тени у
обратного конуса – левая
фронтальная и видимая
профильная
От1
S1т
4т1
31
49
S1
41

50.

Касательным конусом с образующей
под 45о будут определяться точки
границы собственной тени на
фронтальном и профильном
очерках поверхности вращения

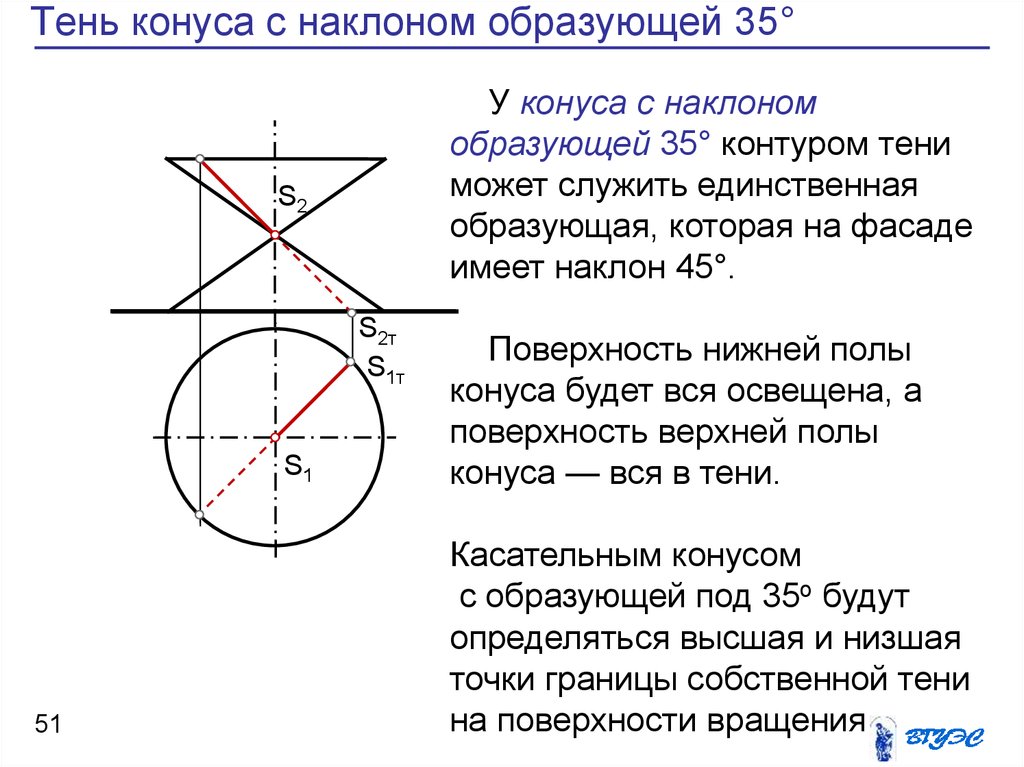
51. Тень конуса с наклоном образующей 35°

У конуса с наклоном
образующей 35° контуром тени
может служить единственная
образующая, которая на фасаде
имеет наклон 45°.
S2
S2т
S1т
S1
51
Поверхность нижней полы
конуса будет вся освещена, а
поверхность верхней полы
конуса — вся в тени.
Касательным конусом
с образующей под 35о будут
определяться высшая и низшая
точки границы собственной тени
на поверхности вращения

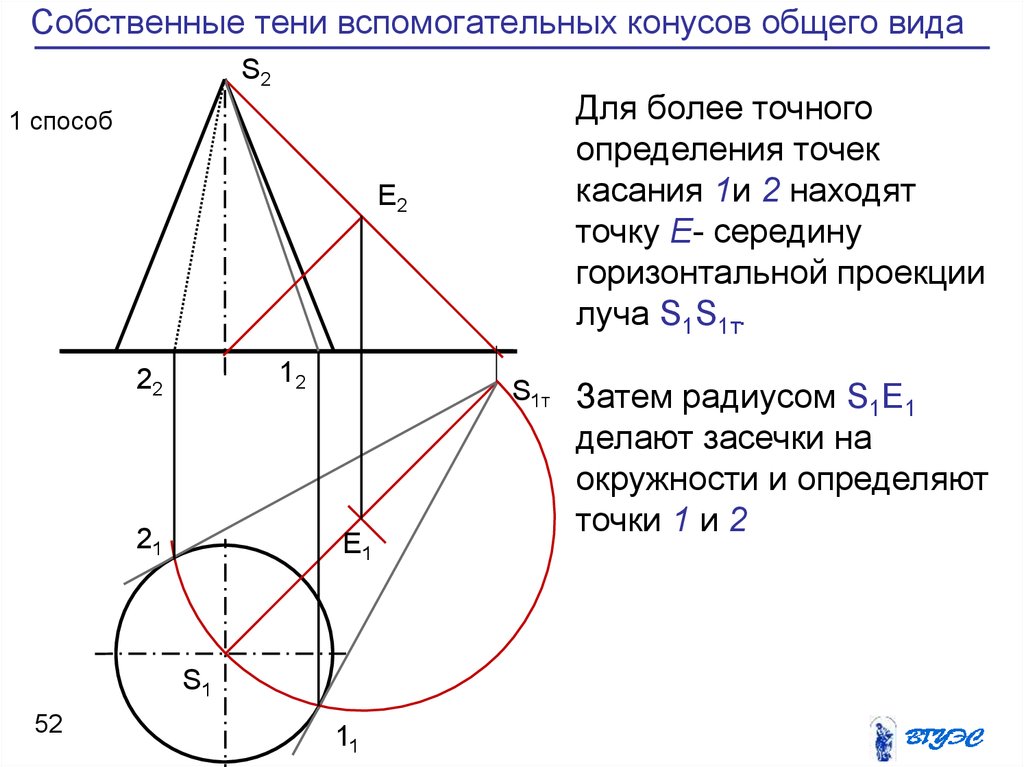
52. Собственные тени вспомогательных конусов общего вида

S2
1 способ
Е2
12
22
S1т Затем радиусом S Е
1 1
Е1
21
S1
52
Для более точного
определения точек
касания 1и 2 находят
точку Е- середину
горизонтальной проекции
луча S1S1т.
11
делают засечки на
окружности и определяют
точки 1 и 2

53. Собственные тени вспомогательных конусов общего вида

S2
2 способ
Е2
22
22
12
12
Е2
S2
53

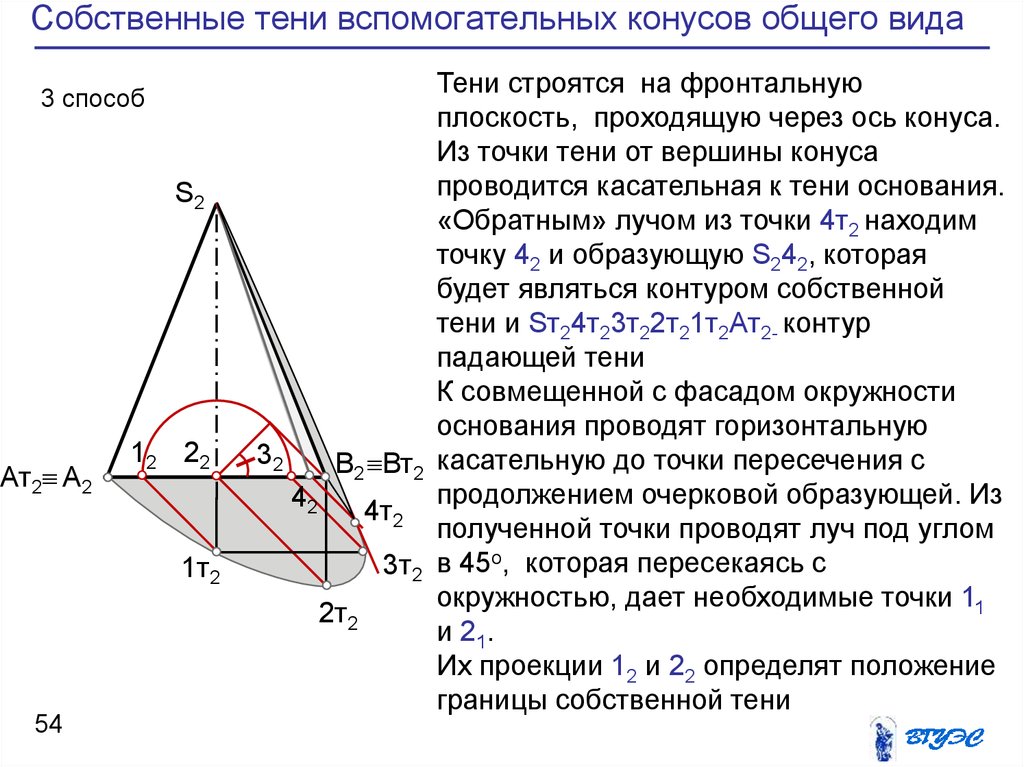
54. Собственные тени вспомогательных конусов общего вида

3 способ
S2
Ат2 А2
12 22
1т2
54
Тени строятся на фронтальную
плоскость, проходящую через ось конуса.
Из точки тени от вершины конуса
проводится касательная к тени основания.
«Обратным» лучом из точки 4т2 находим
точку 42 и образующую S242, которая
будет являться контуром собственной
тени и Sт24т23т22т21т2Aт2- контур
падающей тени
К совмещенной с фасадом окружности
основания проводят горизонтальную
32
В2 Вт2 касательную до точки пересечения с
продолжением очерковой образующей. Из
42
4т2
полученной точки проводят луч под углом
3т2 в 45о, которая пересекаясь с
окружностью, дает необходимые точки 11
2т2
и 21 .
Их проекции 12 и 22 определят положение
границы собственной тени

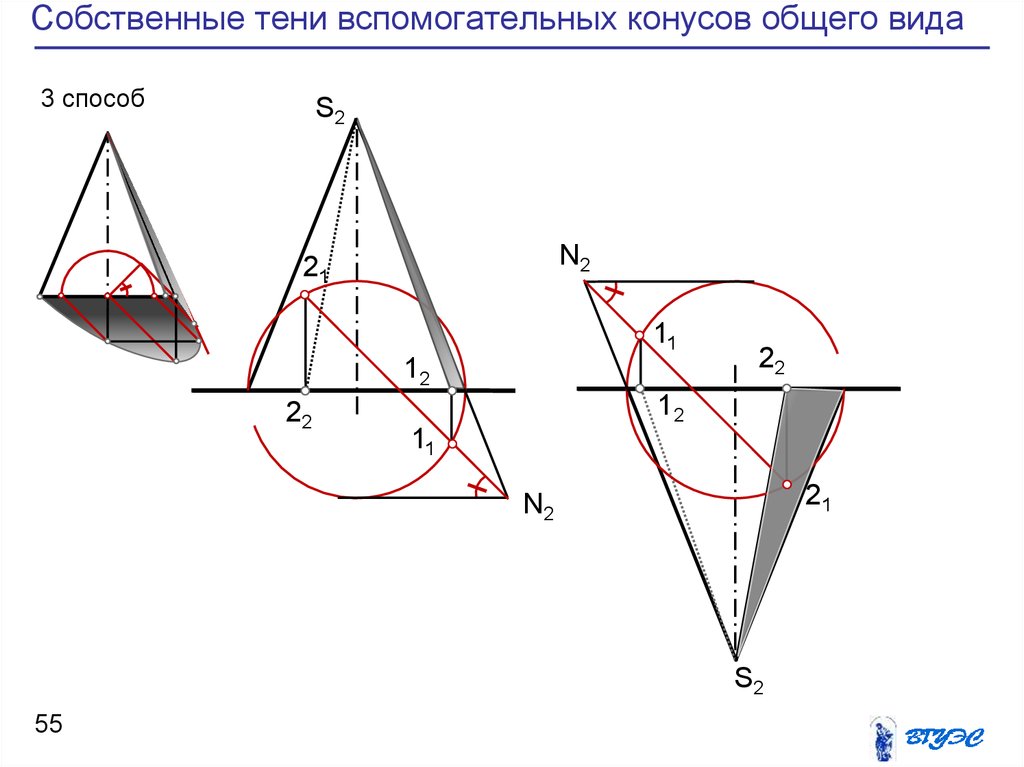
55. Собственные тени вспомогательных конусов общего вида

3 способ
S2
N2
21
11
12
22
22
12
11
21
N2
S2
55

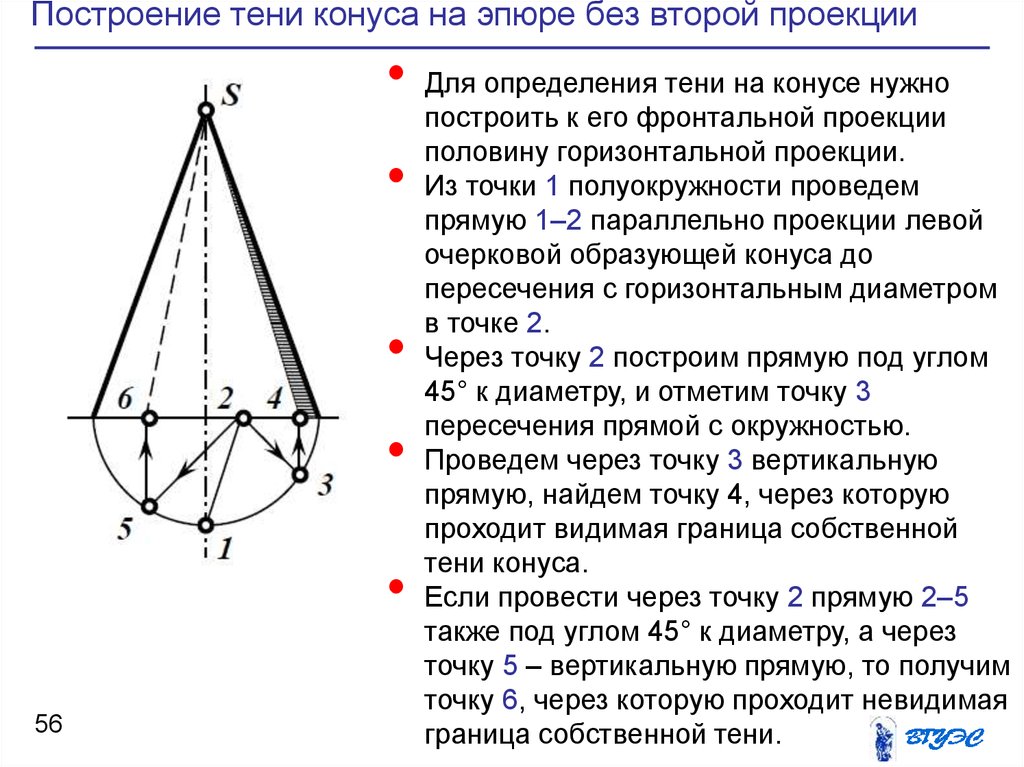
56. Построение тени конуса на эпюре без второй проекции

56
Для определения тени на конусе нужно
построить к его фронтальной проекции
половину горизонтальной проекции.
Из точки 1 полуокружности проведем
прямую 1–2 параллельно проекции левой
очерковой образующей конуса до
пересечения с горизонтальным диаметром
в точке 2.
Через точку 2 построим прямую под углом
45° к диаметру, и отметим точку 3
пересечения прямой с окружностью.
Проведем через точку 3 вертикальную
прямую, найдем точку 4, через которую
проходит видимая граница собственной
тени конуса.
Если провести через точку 2 прямую 2–5
также под углом 45° к диаметру, а через
точку 5 – вертикальную прямую, то получим
точку 6, через которую проходит невидимая
граница собственной тени.

57. Построение собственной тени сферы

• Тень на шаре строится в такой
57
последовательности: проведем
вертикальный, горизонтальный и два
наклонных под углом 45° диаметра
окружности – фронтальной проекции
шара.
Через точку 1 наклонного диаметра 1–2
проведем горизонтальную и
вертикальную прямые, а также прямые,
наклоненные под углом 30° к диаметру
1–2.
В пересечении прямых с
соответствующими диаметрами получим
точки 3, 4, 7, 8.
Точки 5 и 6 получены в результате
проведения вертикальной и
горизонтальной прямых через точку 2.
Соединив плавной кривой построенные
точки, получим эллипс – фронтальную
проекцию границы собственной тени
шара (половина эллипса невидима).

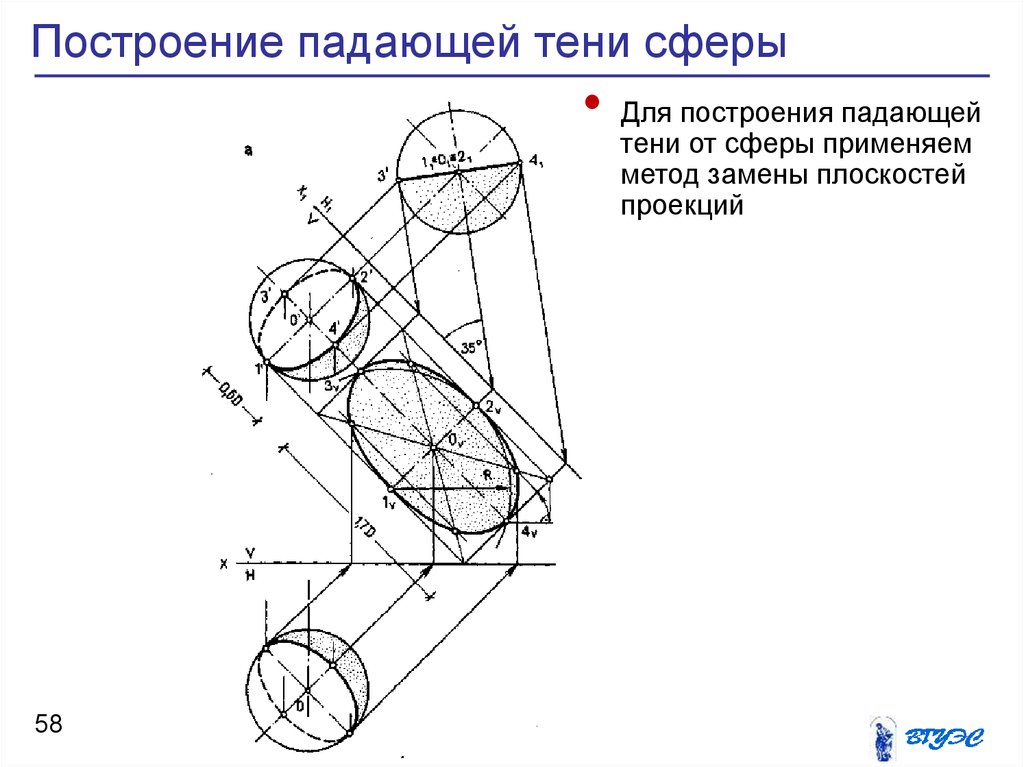
58. Построение падающей тени сферы

58
Для построения падающей
тени от сферы применяем
метод замены плоскостей
проекций

59. Способ обратных лучей

Тени на ступенях лестницы
Тенеобразующими ребрами боковой стенки являются вертикальное,
наклонное и горизонтальное ребра.
Вертикальное ребро повторяет профиль лестницы до точки а0.
Тень от горизонтального ребра совпадает с проекцией луча.
59

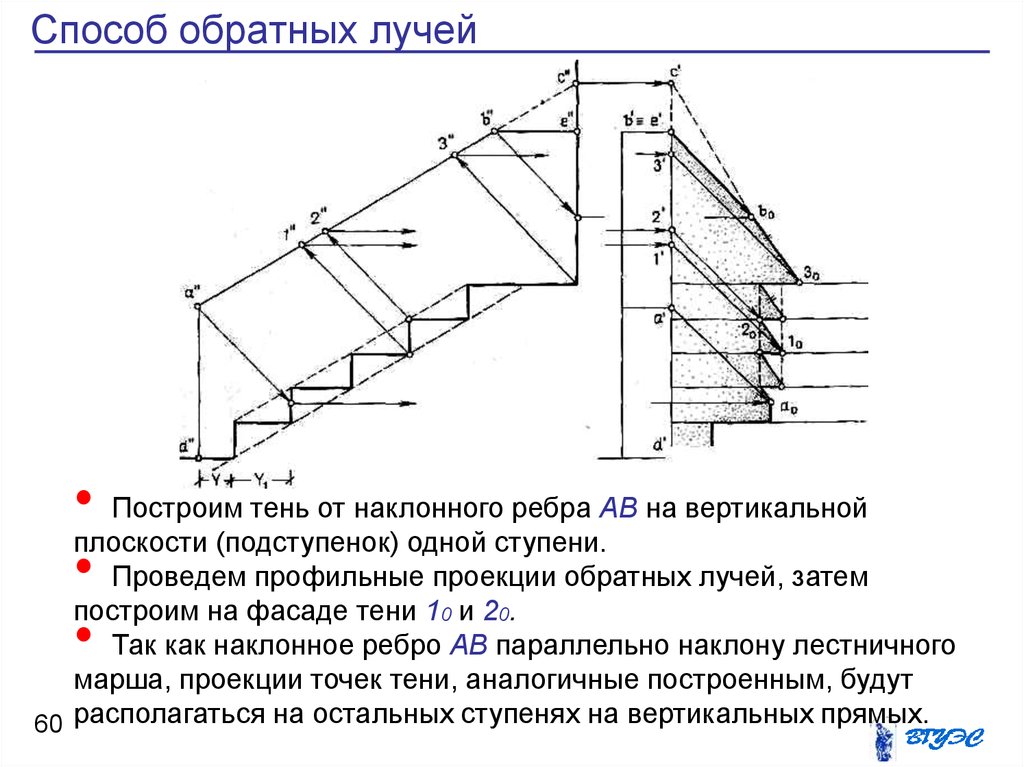
60. Способ обратных лучей

• Построим тень от наклонного ребра АВ на вертикальной
плоскости (подступенок) одной ступени.
• Проведем профильные проекции обратных лучей, затем
построим на фасаде тени 1 и 2 .
• Так как наклонное ребро АВ параллельно наклону лестничного
0
0
марша, проекции точек тени, аналогичные построенным, будут
60 располагаться на остальных ступенях на вертикальных прямых.

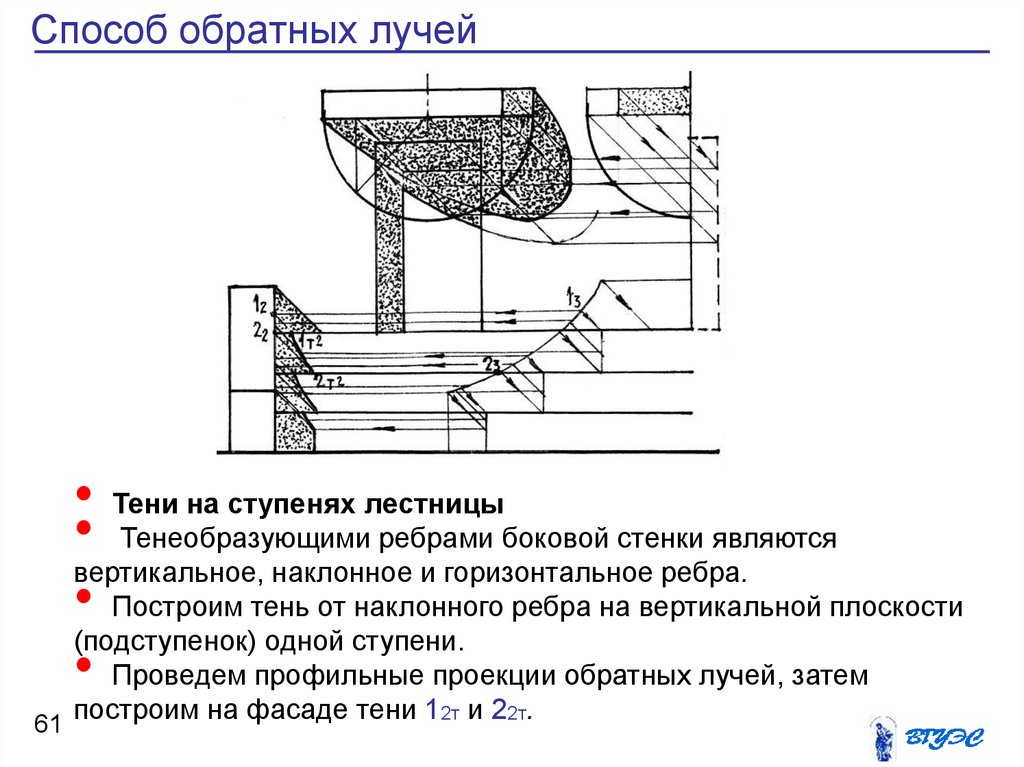
61. Способ обратных лучей

• Тени на ступенях лестницы
• Тенеобразующими ребрами боковой стенки являются
вертикальное, наклонное и горизонтальное ребра.
• Построим тень от наклонного ребра на вертикальной плоскости
(подступенок) одной ступени.
• Проведем профильные проекции обратных лучей, затем
61
построим на фасаде тени 12т и 22т.

62. Способ вспомогательных плоскостей уровня

62

63. Способ лучевых сечений

А
Р
Ат
а
63
Для построения падающей
тени от точки на плоскость
или поверхность следует
через точку провести
световой луч и построить
точку пересечения его с
плоскостью или
поверхностью.
Так как световой луч является
прямой линией, то
построение тени точки
сводится к построению
точки пересечения прямой
с плоскостью или
поверхностью

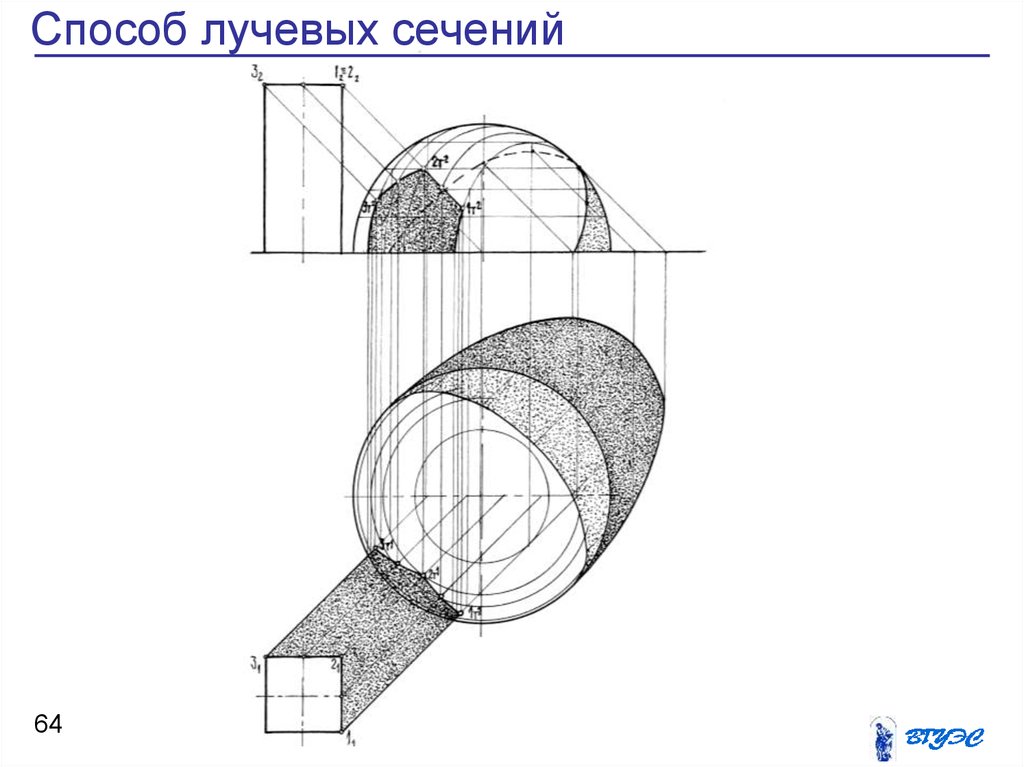
64. Способ лучевых сечений

64

65. Способ конусов и цилиндров

• Способ вспомогательных
касательных поверхностей
• Способ касательных (описанных или
65
вписанных) поверхностей конусов и
цилиндров применяется при
построении на фасаде контуров
собственных теней поверхностей
вращения без второй проекции.
Для построения точек,
принадлежащих контуру
собственной тени, используются
вспомогательные цилиндрические и
конические поверхности, тени
которых определяются просто.
Эти поверхности касаются заданной
поверхности вращения по
окружностям — параллелям.

66. Способ конусов и цилиндров

• Сначала применяют вспомогательные цилиндрические
поверхности, которые касаются поверхности вращения по
экватору или горловине, затем применяют касательные конусы,
соосные с данной поверхностью.
После этого определяют теневые образующие
вспомогательных поверхностей и отмечают точки их
соприкосновения с соответствующими параллелями данной
поверхности. Эти точки принадлежат контуру собственной тени
поверхности вращения. Полученные точки тени соединяют
плавной кривой.
При построении контура собственной тени прежде всего
необходимо построить характерные точки контура — точки
тени, лежащие на фронтальном и профильном очерках
поверхности (точки видимости), а также высшую и низшую
точки контура тени.
Первые две точки определяют с помощью касательных конусов
с углом наклона образующей 45°, а вторые две точки — с
66помощью конусов с углом наклона образующей 35 °

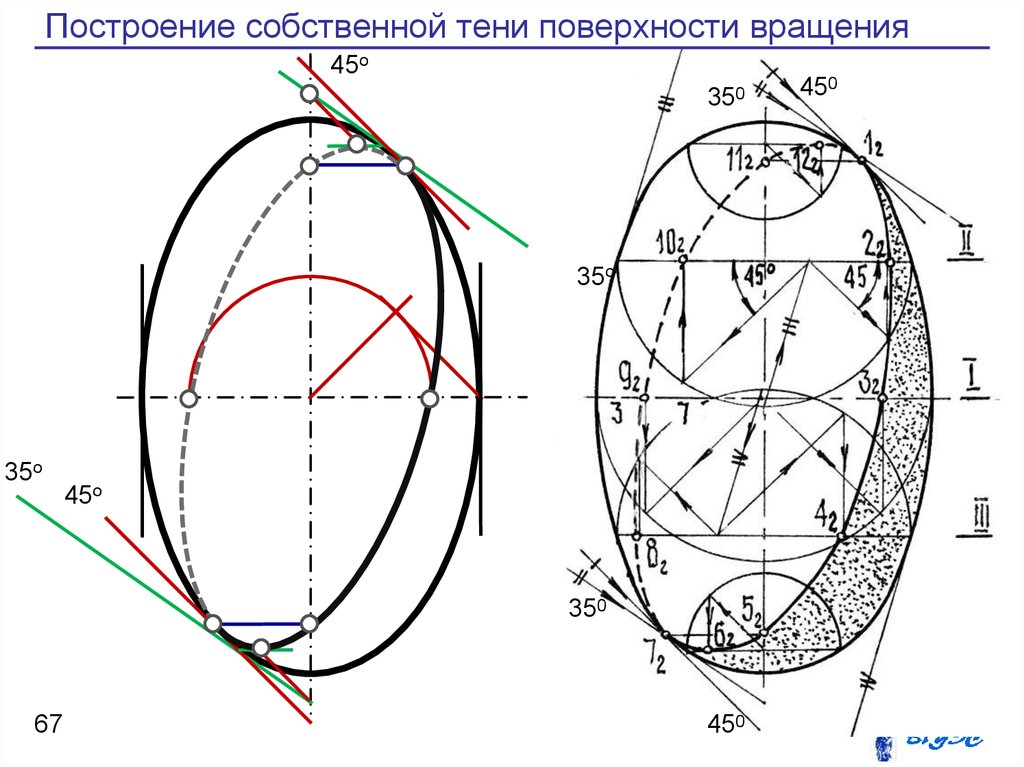
67. Построение собственной тени поверхности вращения

45о
350
35о
35о
45о
350
67
450
450

68. Построение собственной тени поверхности вращения

Применяя перечисленные выше
"стандартные" приемы построения теней
цилиндра и конусов, можно построить
необходимое число точек контура
собственной тени любой поверхности
вращения.
Рассмотрим пример построения контура
собственной тени выпуклой поверхности
вращения — о в о и д а.
Для построения точек тени на экваторе
поверхности опишем вокруг поверхности
соосный цилиндр и на окружности касания
определим общие точки тени 1' и 2'.
Затем построим фронтальные проекции
вспомогательных касательных конусов с
углом наклона образующей 35°, проведя
касательные к очерку овоида до пересечения
с осью, а из этой точки — прямую под углом
45° к линии касания, получим высшую точку 3'
(невидимую) и низшую 4'.
68

69. Построение собственной тени поверхности вращения

• Конусы с углом наклона образующей
69
450 дадут на очерке поверхности
точки 5' и 7' и точки, совпадающие с
проекцией оси, 6' (невидимая) и 8‘.
Если восьми точек окажется
недостаточно, проводят
дополнительную параллель
поверхности и строят касательный
конус произвольного вида (точки 9 и
10). Через полученные точки проводят
плавную кривую, в точках 5' и 7' она
должна коснуться очерка овоида.

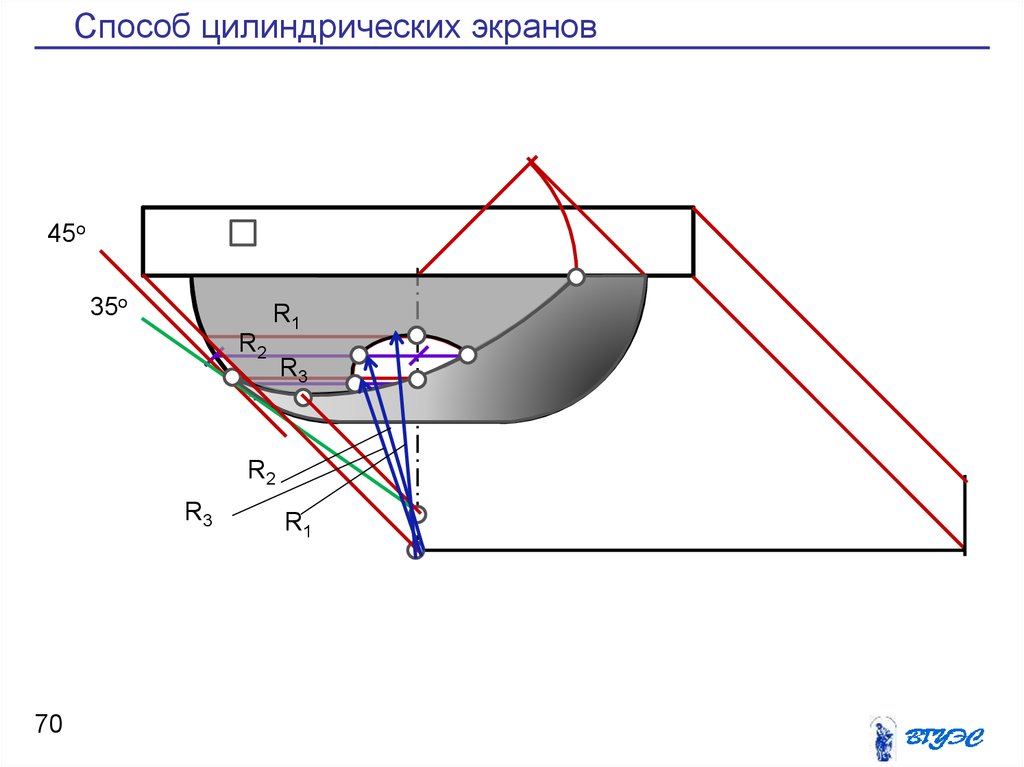
70. Способ цилиндрических экранов

45о
35о
R1
R2
R3
R2
R3
70
R1

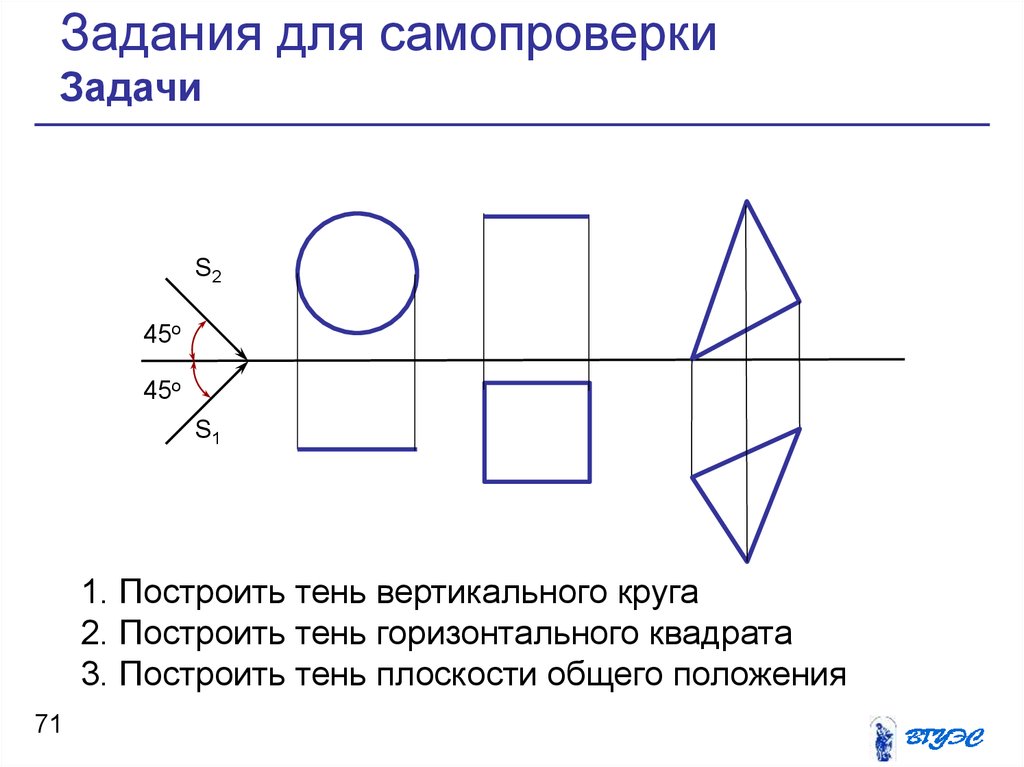
71. Задания для самопроверки Задачи

S2
45о
45о
S1
1. Построить тень вертикального круга
2. Построить тень горизонтального квадрата
3. Построить тень плоскости общего положения
71

72. Задания для самопроверки Задачи

S2
45о
45о
S1
1. Построить тень сферы
2. Построить тень параллелепипеда
3. Построить тень конуса
4. Построить тень пирамиды
72