Наномеханика. Кривизна и неустойчивость тонких пленок

1. Наномеханика Nanomechanics of materials and systems

Lecture 4
Кривизна и неустойчивость тонких
пленок
Curvature and surface instability

2. Деформации и изгиб в пленке и подложке Strain and bending in a film/substrate sandwich

Если деформации зависят только от z: ε = ε(z)
0 (Compatibi lity Relat ions)
t
2
z 2
( ij *ij ) 0;
then
i, j x, y
ij *ij aij zbij
Для подложки *ij 0 ( eigenstrai n in substrate)
Для пленки *ij ( m )ij 0 ( eigenstrai n in film )
Stoney formula
xx 0 z;
0
xx 0 if z
hs
6
M f hf
M s hs
( m ) xx ;
6M f h f
M s hs
2
( m ) xx

3. Упругие деформации в пленке и подложке Strain in film and substrate

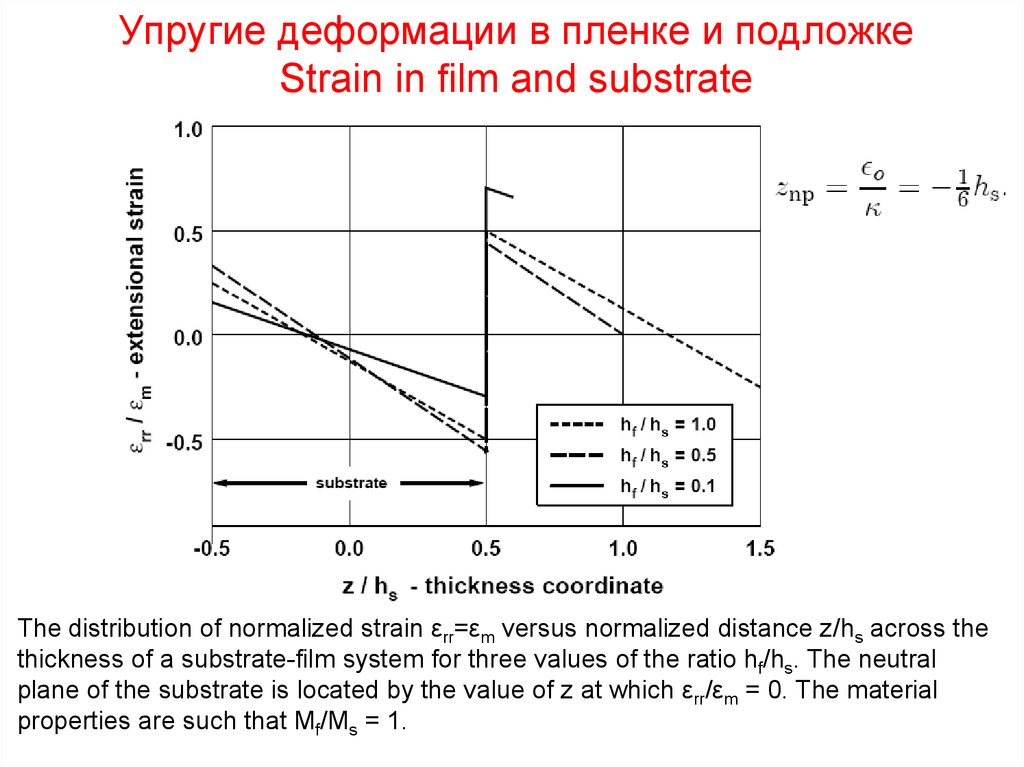
The distribution of normalized strain εrr=εm versus normalized distance z/hs across the
thickness of a substrate-film system for three values of the ratio hf/hs. The neutral
plane of the substrate is located by the value of z at which εrr/εm = 0. The material
properties are such that Mf/Ms = 1.

4. Точность формулы Стони Accuracy of Stoney formula

M s ( 0 z ) for 12 hs z 12 hs
rr
1
1
M
(
z
)
for
h
z
f
0
m
s
2
2 hs h f

5. Экспериментальное определение кривизны структур Experimental study of curvature

• Лазерное сканирование поверхности (Laser scanning)
• Многолучевое оптическое отражение (Multibeam
optical reflection)
• Отражение изображения светлой сетки (Grid
reflection)
• Изменение картины интерференции (Optical
interference fringes)

6. Scanning laser method

2θ
Используется для in-situ мониторинга деформаций при наращивании
пленок, например, при MBE и MOCVD.

7. Многослойные структуры Multilayer structures

To 1-rst order in the small parameters hi/hs, the total curvature
is equal to the simple sum of the curvatures that would be
induced if each individual layer would be deposited by itself
on the substrate. Each individual curvature κSt;i is given by the
Stoney formula.

8. Влияние анизотропии на деформации Anisotropy in curvature

9. Область геометрически-нелинейных деформаций Geometrically nonlinear deformations

2
ds dr ( w dr )
2
Вращения, вызванные изгибом с вертикальным смещением
w(r), могут быть не малы, даже если деформации малы.
Stoney formula: w’(R) = κR and εo = 1/6 κ∙hs
~1
В выражение для деформации надо добавить член второго
порядка малости, связанный с вращениями. Членами второго
порядка малости, связанными с растяжением-сжатием,
пренебрегаем.

10. Изменение кривизны по площади Variation of curvature

Experimentally observed and numerically estimated variation of curvature
as a function of radial position, measured from the center of a Si substrate
with a W film deposit. After Finot et al. (1997).

11. Bifurcation in equilibrium shape

Example:
graphite-polyimide laminate
Требование минимума упругой энергии приводит к (minimum of the elastic energy requires)
R is radius of the wafer

12. Экспериментальное определение упругих деформаций в пленках Experimental determination of strain in films

• Измерения параметра решетки пленок по
рентгеновской дифракции
X-ray diffraction
• Измерения кривизны структур
Optical measurements of curvature
• Микро-Рамановская спектроскопия
Micro-Raman scattering
• Просвечивающая электронная микроскопия
Transmission electron microscopy
• Изменение энергий электронных состояний
Change in electronic states

13. Микро-Рамановская спектроскопия Micro-Raman scattering

Raman intensity (arb. units)
Микро-Рамановская спектроскопия
Micro-Raman scattering
Olympus microscope
Lateral mapping
SiN
GaN buffer
sapphire
Confocal measurements
A1(LO)
1000
E1(TO)
100
A1(TO)
10
0
12
24
36
48
60
Lateral shift across SiN mask (mm)
2.7
DwE2 (cm-1)
SiN
GaN
8mm SiN stripes and 4mm windows
grooves
10000
E2(high)
2.6
2.5
569.7
SiN
GaN
SiN
GaN buffer
sapphire
wE2 (cm-1)
569.6
569.5
569.4
569.3
569.2
0
5
10
15
20
Shift of focal plane (mm)
25
30

14. Просвечивающая электронная микроскопия Transmission electron microscopy

Численный анализ электронномкроскопических изображений
позволяет построить поле
смещений.
Strain mapping into a uniaxial
45 nm strained channel pinched
between Si80Ge20 source and
drain. Simulation is on the left
and experiment on the right.
Courtesy of CEMES-CNRS,
Toulouse, France

15. Изменение энергий электронных состояний Change in energy of electronic states

16. Should a surface of a stressed solid be flat? Does a flat surface provide the lowest energy?

17. Нестабильность механически напряженной пленки Instability of mechanically stressed films

Причина нестабильности – избыточная упругая энергия
Origin of instability is elastic energy
U ( )dV dS
V
S
Механизм развития нестабильности - поверхностная диффузия
Mechanism of instability development is surface diffusion

18. Малые периодические изменения толщины Small periodic variation of thickness

ω=2π/λ
n ( n x , n y ); n x
h
aw sin wx o w 2a 2 ; n y 1 o w 2a 2
x
n 0
Плоская задача. РРешени с помощью функций Айри.
2 A
2 A
2 A
Plane strain. Solving via Airy stress function. σ xx 2 ; σ yy 2 ; σ xy
y
x
x y
1
(1) ( 2 ) ; 4 A 0; A(1) m y 2 xx(1) m ; yy(1) xy(1) 0
2

19. Малые периодические изменения толщины Small periodic variation of thickness

4 A( x, y ) 0; ( 2 ) 0 as y
A( 2 ) ( c0 c1 y )a m exp w ( y h ) cos wx
A( 2 ) a m ( y h ) exp w ( y h ) cos wx
xx( 2 ) 2 A y 2 2w w 2 ( y h ) a m exp w ( y h ) cos wx
yy( 2 ) 2 A x 2 a m ( y h )w 2 exp w ( y h ) cos wx
xy( 2 ) 2 A x y a m w w 2 ( y h ) exp w ( y h ) sin wx
Граничные ууслови (Boundary conditions ) y h :
t x( 2 ) xx( 2 ) n x xy( 2 ) n y a mw sin wx o( a 2w 2 )
(2)
t (y2 ) xy( 2 ) n x yy
n y 0 o( a 2w 2 )
t x(1) xx(1) n x a mw sin wx o( a 2w 2 )
t (y1) 0 o( a 2w 2 )

20. Плотность энергии и химический потенциал Energy and chemical potential

Плоская задача ( plane strain )
1 (2)
(1 ) ( 2 )
xx (1 2 ) yy( 2 ) (1 ) ; xy( 2 )
xy
E
E
Изменение ээнерги деформации вдоль поверхности ( Deformation energy along x )
zz( 2 ) 0; zz( 2 ) ( xx( 2 ) yy( 2 ) ); xx( 2 )
U ( x)
(1)
(2)
m2 (1 v 2 )
Ef
m2 (1 v ) 4 a
2 x
2aw cos wx
cos
Mf
Увеличение площади поверхности квадратично по a / λ (change in surface area)
2
h( x, t )
2 a
2 2 x
1
2
sin
2
2
x
Кривизна поверхности ( curvature of surface)
2
2h ( x, t )
2 x
2 a
4
cos
x 2
2
Химический потенциал (Chemical potential)
a
m2
U U m 4 (1 )
Mf
2 x
cos

21. Критическая длина стабильности Critical length of stability

Пусть a зависит от времени
Изменение свободной энергии, усредненное по периоду λ:
Free energy over a period
vn dx 2 aa (1 )U m
0
Критическая длина периода (Critical period )
с
M
(1 ) m2 (1 ) M m2
Нестабильность Азаро-Тиллера—Гринфельда
Asaro-Tiller-Grinfeld instability

22. Нестабильность напряженной пленки Asaro-Tiller--Grinfeld instability

M = E/(1- ν)
E = 2G(1+ν)
Asaro-Tiller--Grinfeld instability
m
ν = 0.3
G = 0.67 1011 Pa
γ = 1 J/m2
ε = 0.007
200 nm

23. Нестабильность пленки GeSi на Si Asaro-Tiller--Grinfeld instability of GeSi on Si

a
Transmission electron microscopy cross-sectional image of a Si0:81Ge0:19 alloy
film grown epitaxially on a Si substrate (a). The ridges are aligned with a <100>
crystallographic direction. While the TEM image appears to represent a fully twodimensional configuration, the planview images of the film surface (b) shows that
the regular ordering has a relatively short range. The normal distance between
parallel lines in the lower images is the peak-to-peak distance in the upper
image, or about 300nm. Reproduced from Cullis et al. (1992). m=0.66%

24. Возмущения второго порядка Second order disturbation

25. Применимость приближения малых флуктуаций Applicability of small perturbation approach

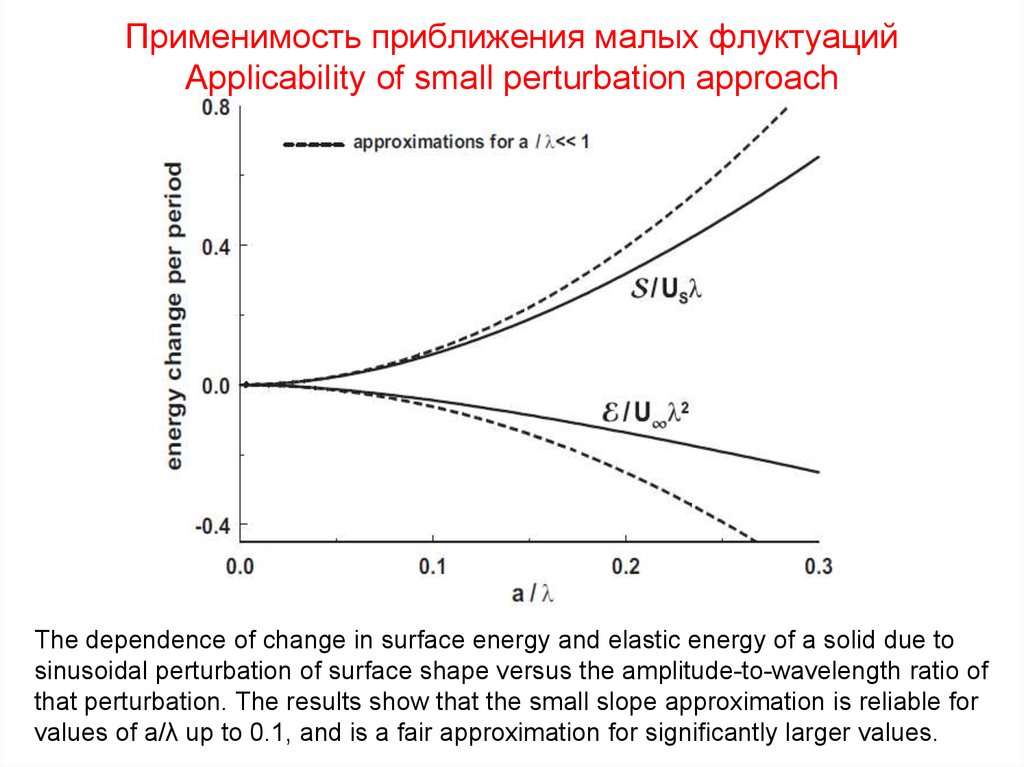
The dependence of change in surface energy and elastic energy of a solid due to
sinusoidal perturbation of surface shape versus the amplitude-to-wavelength ratio of
that perturbation. The results show that the small slope approximation is reliable for
values of a/λ up to 0.1, and is a fair approximation for significantly larger values.

26. Домашнее задание (Homework) 4

Пленка Ge толщиной 4 нм выращена
эпитаксиально на подложке Si с ориентацией (111)
и толщиной 400 мкм.
4-nm-thick Ge epitaxial film was grown over 400-μmthick Si substrate with (111) orientation.
Определить (determine)
1. Анизотропию кривизны структуры по Стони
Anisotropy of Stoney curvature (if any?)
2. Критическую длину Asaro-Tiller-Grinfeld
нестабильности пленки (γ = 1 J/m2).
Asaro-Tiller-Grinfeld critical length (γ = 1 J/m2).