Similar presentations:
Теория и свойства меркаторской проекции
1. Теория и свойства меркаторской проекции.
2. 1. Требования, предъявляемые к морским навигационным картам
При выборе проекции для построения той или иной карты всегда исходят изтребований обеспечения решения задач, для которых она предназначается.
Картографическая проекция морских навигационных карт должна быть наиболее
удобной для их использования в море, т. е. для решения основных задач по
обеспечению безопасности судовождения наиболее простыми способами и
приемами.
Исходя из этого, картографическая проекция морских навигационных карт должна
удовлетворять следующим требованиям:
*линия пути судна, идущего постоянным курсом, т. е. локсодромия, изображалась
прямой линией;
*величина углов, измеряемых с судна между разными ориентирами на местности,
соответствовала величинам углов между теми же ориентирами на карте, т. е.
проекция карты должна быть равноугольной;
*масштаб в пределах карты изменялся в возможно малых пределах т. е. искажения
длин на карте не превышали ошибок графических построений и измерений на карте,
выполняемых с помощью прокладочного инструмента.
3.
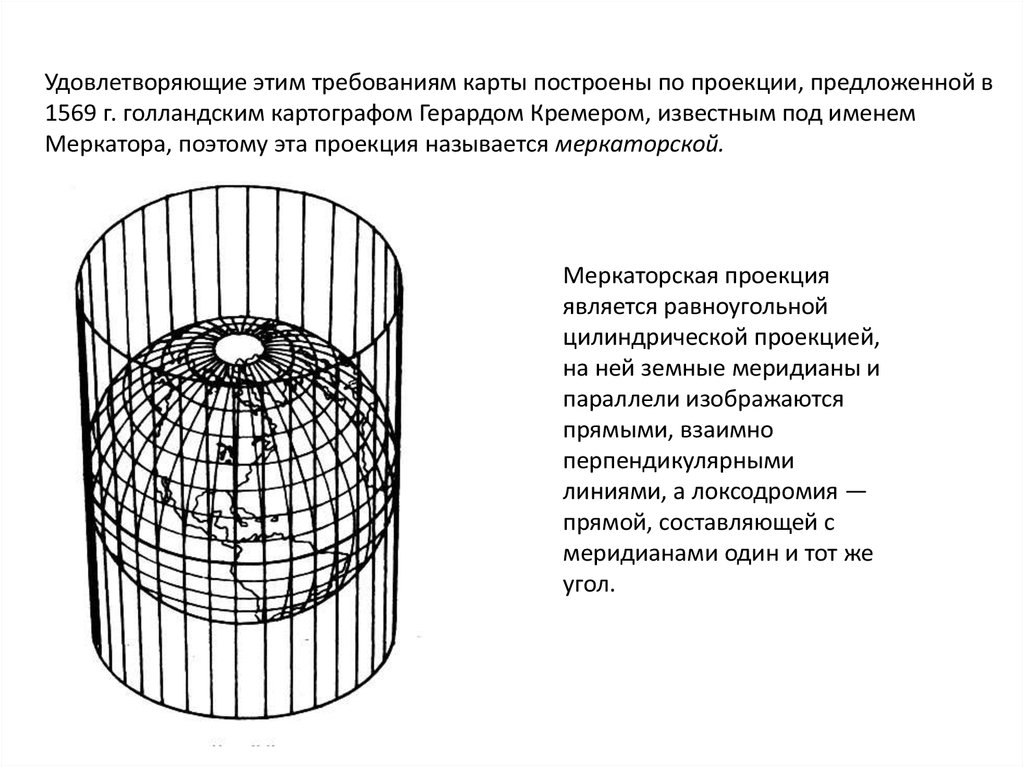
Удовлетворяющие этим требованиям карты построены по проекции, предложенной в1569 г. голландским картографом Герардом Кремером, известным под именем
Меркатора, поэтому эта проекция называется меркаторской.
Меркаторская проекция
является равноугольной
цилиндрической проекцией,
на ней земные меридианы и
параллели изображаются
прямыми, взаимно
перпендикулярными
линиями, а локсодромия —
прямой, составляющей с
меридианами один и тот же
угол.
4. 2. Математическое обоснование принципа меркаторской проекции
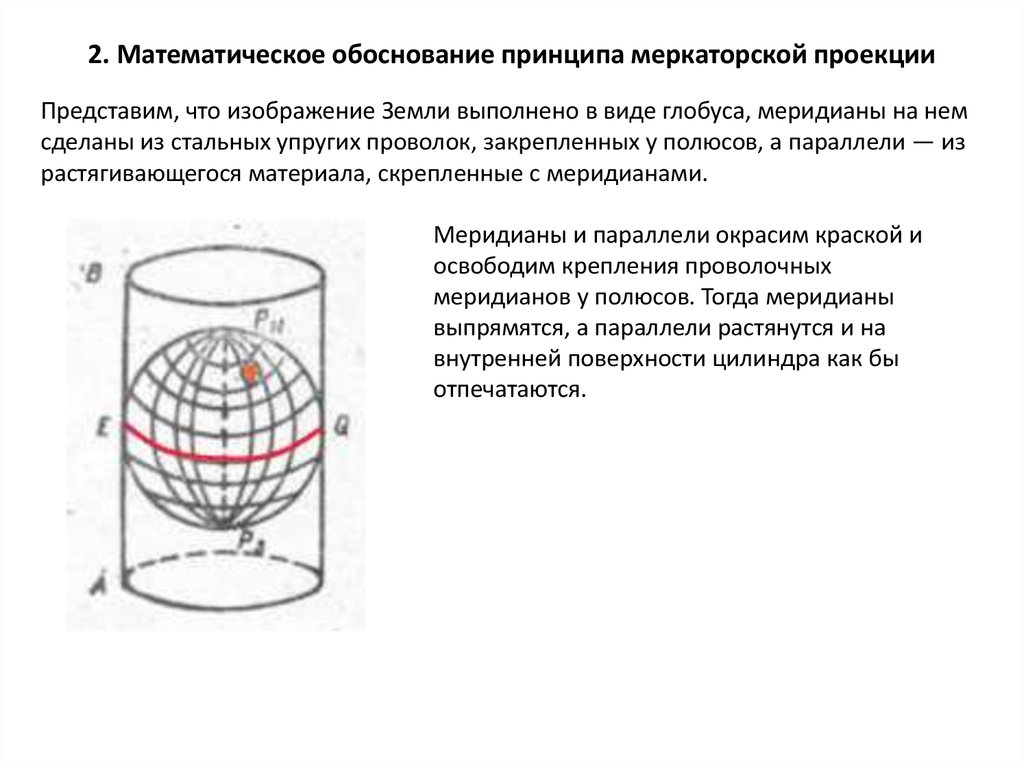
Представим, что изображение Земли выполнено в виде глобуса, меридианы на немсделаны из стальных упругих проволок, закрепленных у полюсов, а параллели — из
растягивающегося материала, скрепленные с меридианами.
Меридианы и параллели окрасим краской и
освободим крепления проволочных
меридианов у полюсов. Тогда меридианы
выпрямятся, а параллели растянутся и на
внутренней поверхности цилиндра как бы
отпечатаются.
5.
Теперь разрежем цилиндр по образующей (по одному из меридианов); на нем будетнанесена прямоугольная сетка (следы параллелей и меридианов), в которой длина
меридианов осталась неизменной, а каждая параллель растянулась до длины экватора. При
этом параллель, близкая к экватору, растянется меньше, а с увеличением широты
растяжение параллелей увеличивается все значительнее. Остров К круглой формы, который
был на глобусе, на развернутой плоскости цилиндра спроектируется в виде овала. Для
сохранения подобия изображения на глобусе и проекции его на плоскости необходимо
соответственно вытянуть по длине и меридианы.
6.
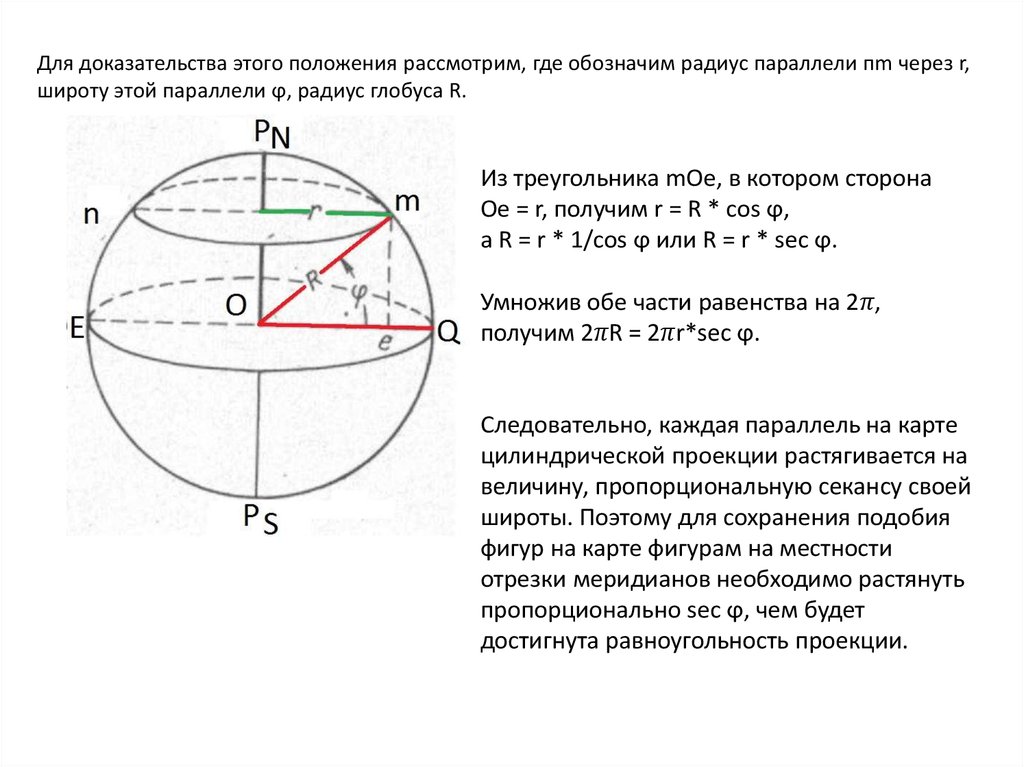
Для доказательства этого положения рассмотрим, где обозначим радиус параллели пm через r,широту этой параллели ϕ, радиус глобуса R.
Из треугольника mОе, в котором сторона
Ое = r, получим r = R * cos ϕ,
a R = r * 1/cos ϕ или R = r * sec ϕ.
Умножив обе части равенства на 2











 geography
geography








