Основы практической навигаци

1.

МОРСКОЙ КОРПУС ПЕТРА ВЕЛИКОГО
САНКТ-ПЕТЕРБУРГСКИЙ ВОЕННО-МОРСКОЙ ИНСТИТУТ
А. П. ЗВЕРЕВ
ОСНОВЫ
ПРАКТИЧЕСКОЙ НАВИГАЦИ
(Сборник слайдов)
Санкт-Петербург
2012 г.

2. Основы практической навигации

Учебно-методическое пособие является
электронной версией издания «Основ
практической навигации» 2001 года и
предназначено для курсантов штурманского факультета, а также
преподавателей кафедры, проводящих занятия
по дисциплине «Морская Навигация».
Учебное пособие разработано
Старшим преподавателем кафедры
Доцентом Зверевым А.П.

3. Раздел 1. Основные понятия в Морской Навигации

4.

Навигация – Наука о выборе
пути, определении
места и
перемещении судна в море с
учетом задач, решаемых судном, и влияния внешней среды
на направление и скорость судна. (ГОСТ 23634-83).

5.

Фигура и модели Земли
Геоид
Земной эллипсоид
Шар

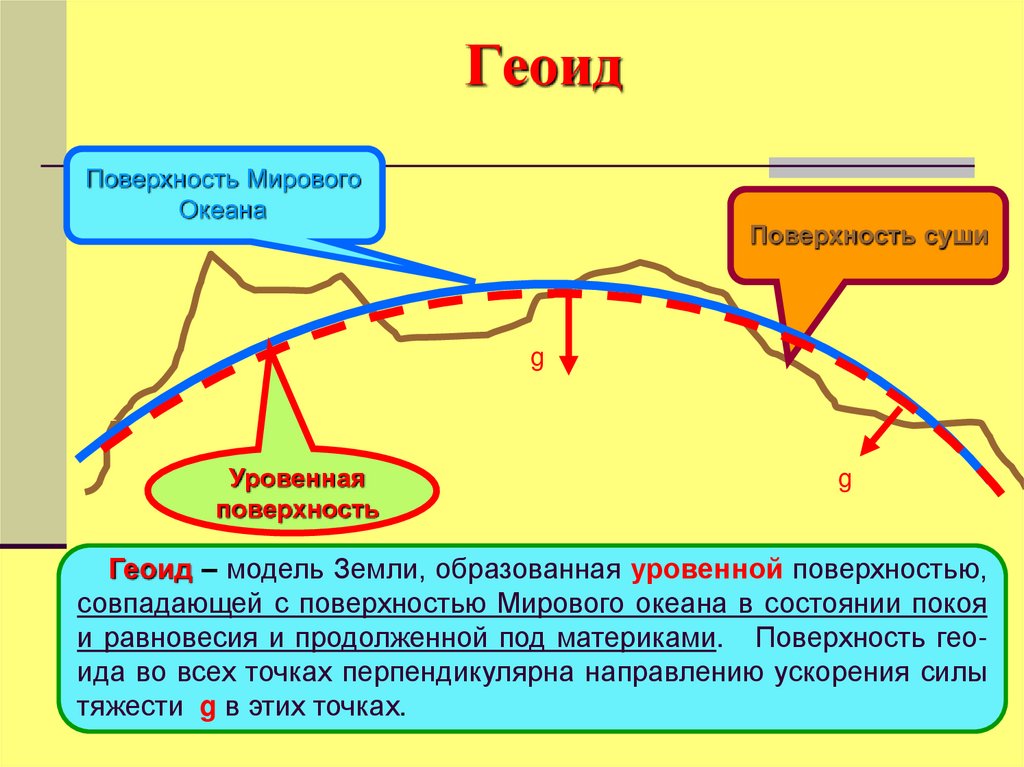
6. Геоид

Поверхность Мирового
Океана
Поверхность суши
g
Уровенная
поверхность
g
Геоид – модель Земли, образованная уровенной поверхностью,
совпадающей с поверхностью Мирового океана в состоянии покоя
и равновесия и продолженной под материками. Поверхность геоида во всех точках перпендикулярна направлению ускорения силы
тяжести g в этих точках.

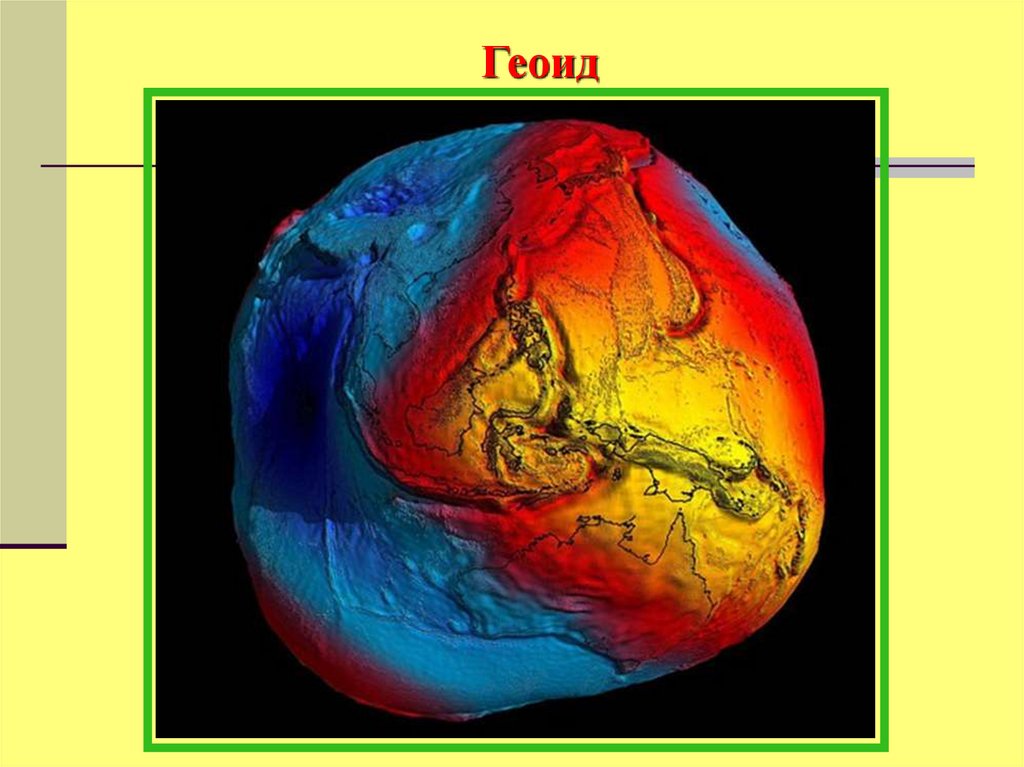
7.

Геоид

8. Земной эллипсоид (сфероид)

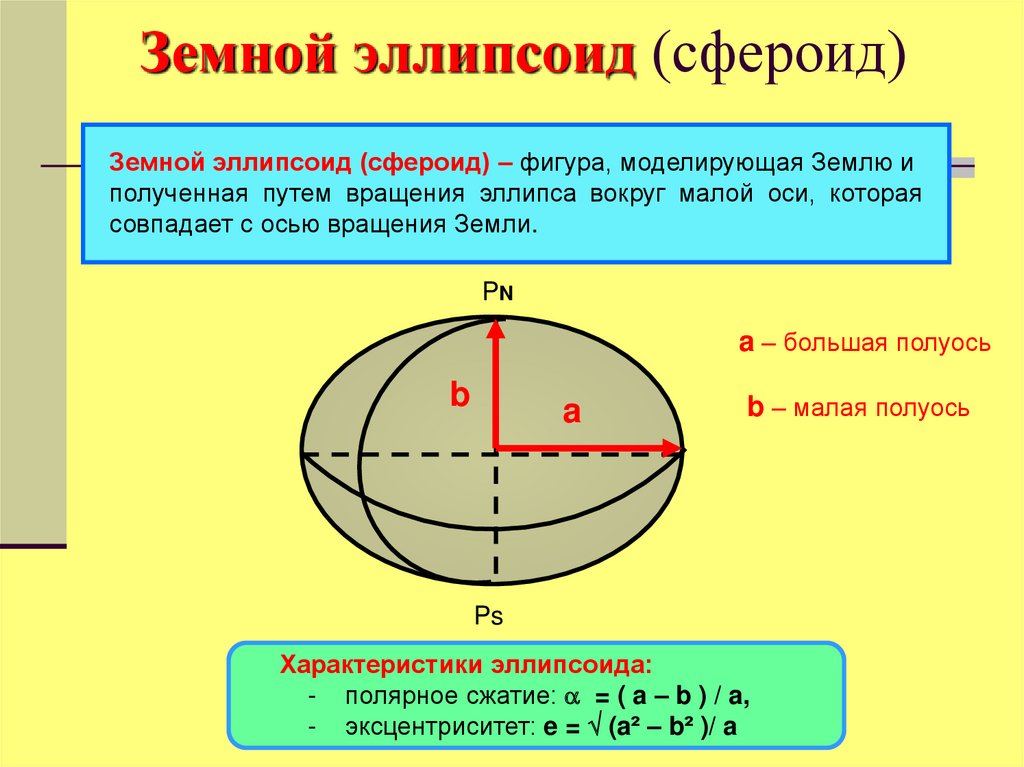
Земной эллипсоид (сфероид) – фигура, моделирующая Землю и
полученная путем вращения эллипса вокруг малой оси, которая
совпадает с осью вращения Земли.
PN
a – большая полуось
b
a
b – малая полуось
Ps
Характеристики эллипсоида:
- полярное сжатие: = ( a – b ) / a,
- эксцентриситет: e = (a² – b² )/ a

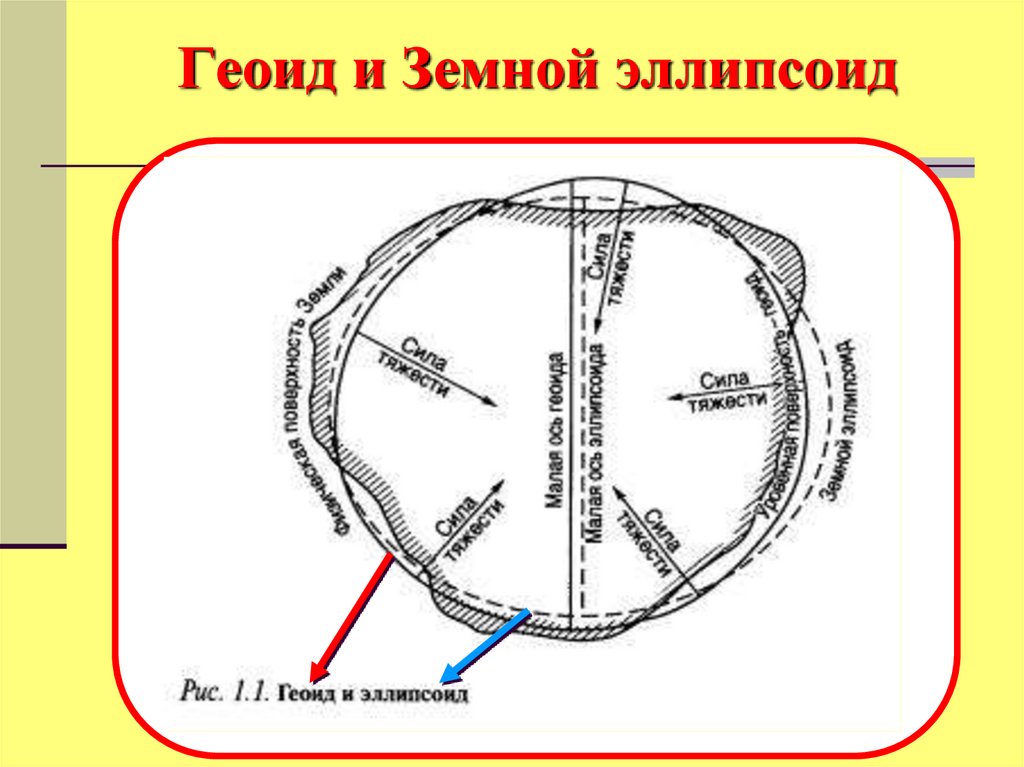
9. Геоид и Земной эллипсоид

10.

Референц-эллипсоид – земной эллипсоид определенных размеров, принятый
в государстве в качестве модели Земли.
В России – референц-эллипсоид
Ф. Н. Красовского, принятый в 1946
году.
Характеристики
референц-эллипсоида:
большая полуось: а = 6378245 м;
малая полуось:
b = 6356863 м;
полярное сжатие = 1 / 298,3.

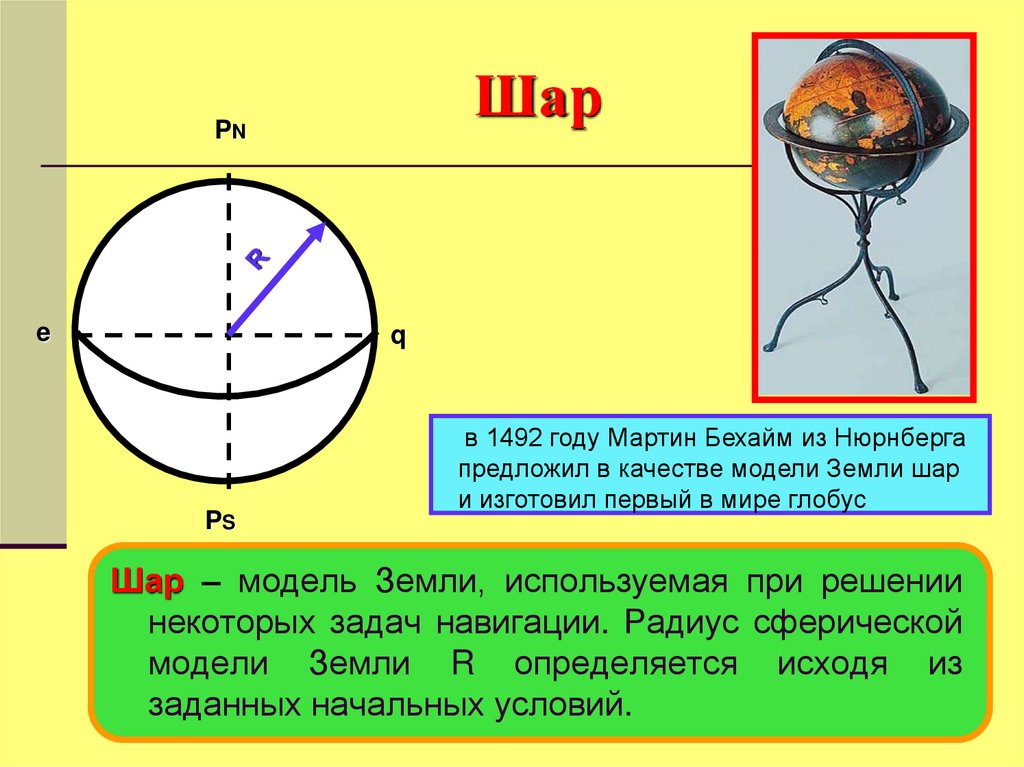
11. Шар

PN
e
q
PS
в 1492 году Мартин Бехайм из Нюрнберга
предложил в качестве модели Земли шар
и изготовил первый в мире глобус
Шар – модель Земли, используемая при решении
некоторых задач навигации. Радиус сферической
модели Земли R определяется исходя из
заданных начальных условий.

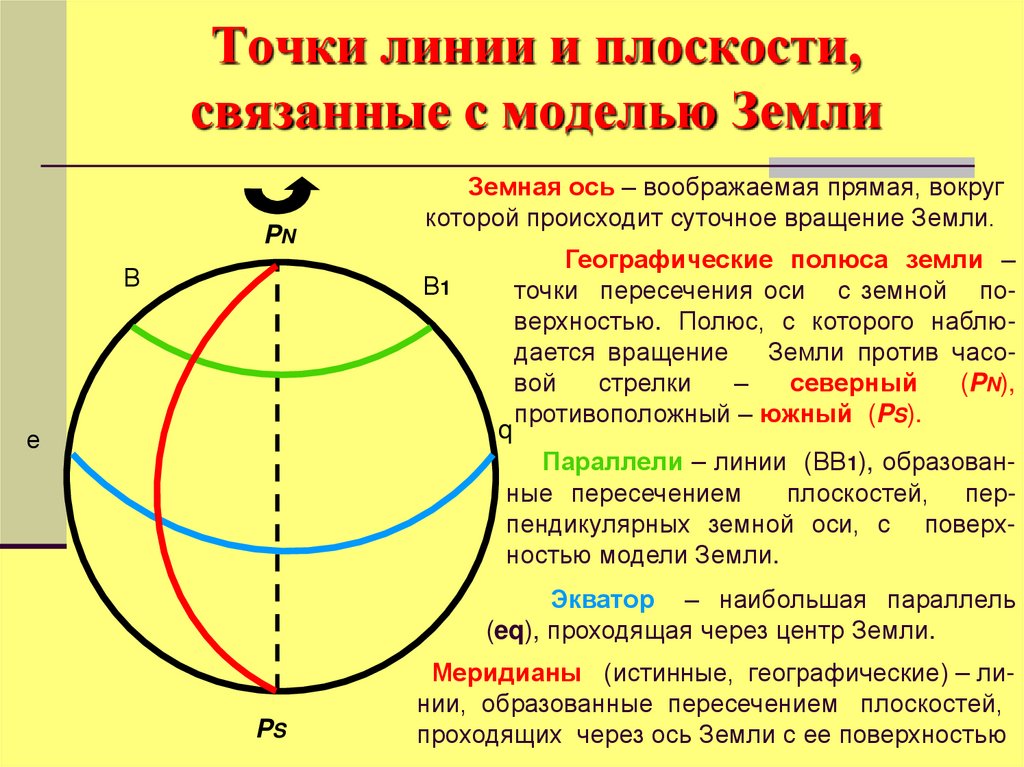
12. Точки линии и плоскости, связанные с моделью Земли

PN
В
Земная ось – воображаемая прямая, вокруг
которой происходит суточное вращение Земли.
В1
q
е
Географические полюса земли –
точки пересечения оси с земной поверхностью. Полюс, с которого наблюдается вращение
Земли против часовой
стрелки
–
северный
(PN),
противоположный – южный (PS).
Параллели – линии (ВВ1), образованные пересечением
плоскостей, перпендикулярных земной оси, с поверхностью модели Земли.
Экватор – наибольшая параллель
(eq), проходящая через центр Земли.
PS
Меридианы (истинные, географические) – линии, образованные пересечением плоскостей,
проходящих через ось Земли с ее поверхностью

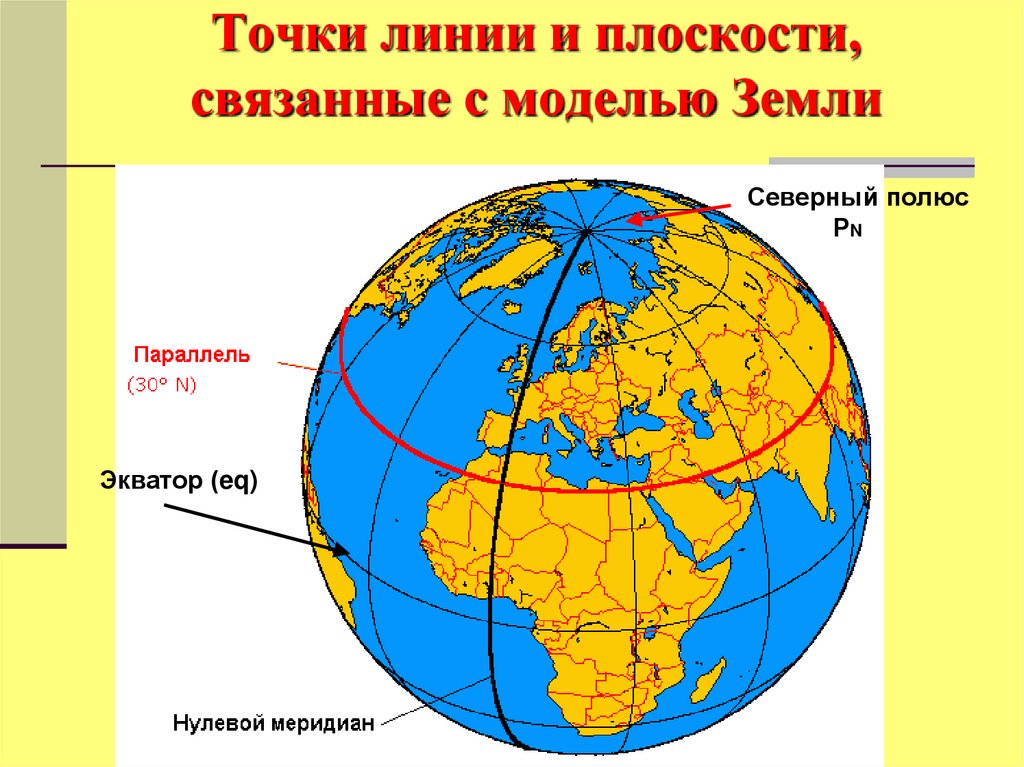
13. Точки линии и плоскости, связанные с моделью Земли

Северный полюс
РN
Экватор (eq)

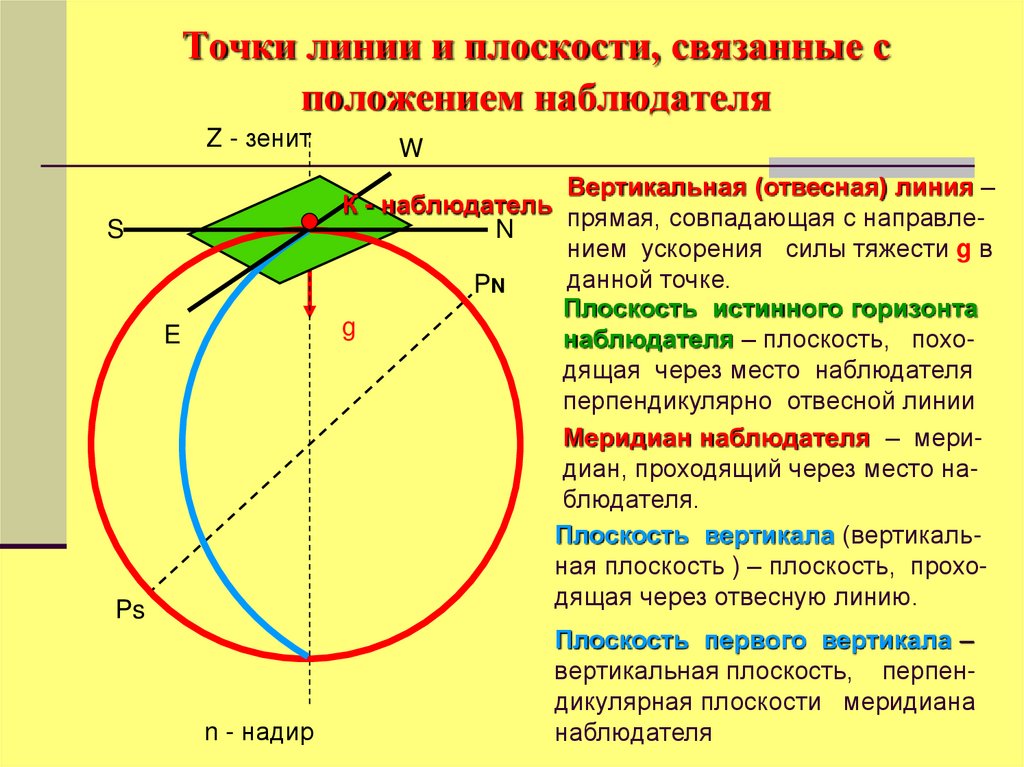
14. Точки линии и плоскости, связанные с положением наблюдателя

Z - зенит
W
Вертикальная (отвесная) линия –
К - наблюдатель прямая, совпадающая с направлеN
нием ускорения силы тяжести g в
данной точке.
PN
Плоскость истинного горизонта
g
наблюдателя – плоскость, походящая через место наблюдателя
перпендикулярно отвесной линии
Меридиан наблюдателя – меридиан, проходящий через место наблюдателя.
Плоскость вертикала (вертикальная плоскость ) – плоскость, проходящая через отвесную линию.
S
E
Ps
n - надир
Плоскость первого вертикала –
вертикальная плоскость, перпендикулярная плоскости меридиана
наблюдателя

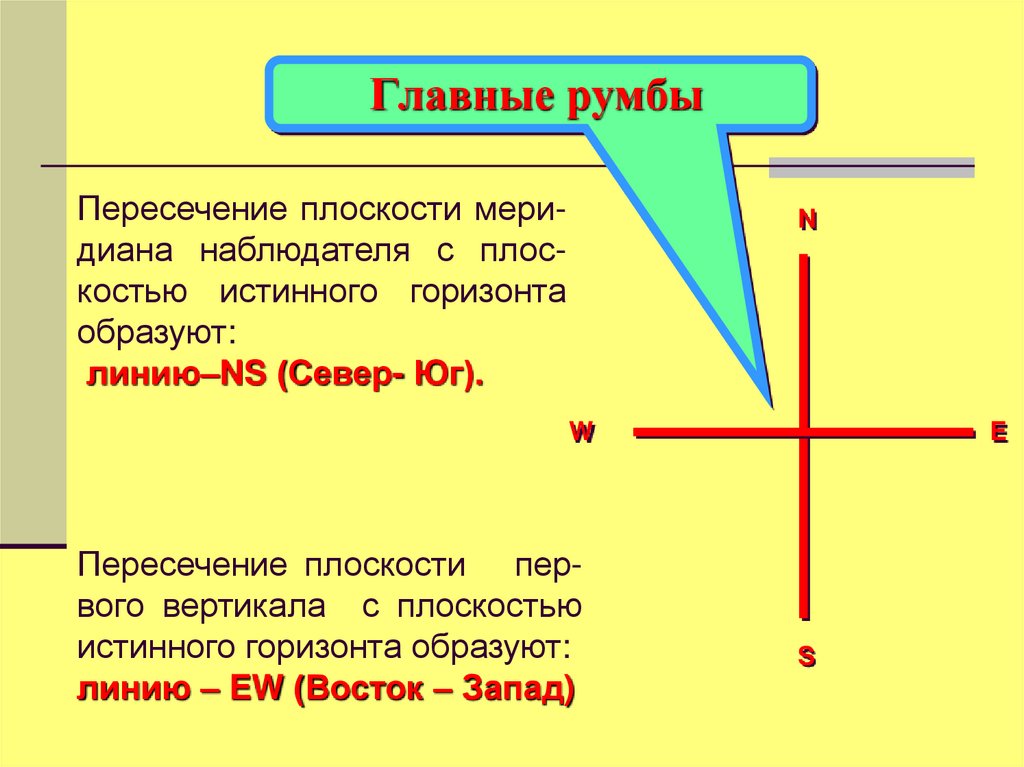
15. Главные румбы

Пересечение плоскости меридиана наблюдателя с плоскостью истинного горизонта
образуют:
линию–NS (Север- Юг).
N
W
Пересечение плоскости первого вертикала с плоскостью
истинного горизонта образуют:
линию – EW (Восток – Запад)
E
S

16.

Координаты, применяемые в
кораблевождении.
При решении задач кораблевождения
применяются следующие системы
координат:
• географическая;
• квазигеографическая;
• прямоугольная;
• полярная.

17.

Географическая система координат
Координатные линии: меридианы и параллели;
Координатные оси: экватор и начальный
(Гринвичский) меридиан.
Географические координаты: широта и долгота.

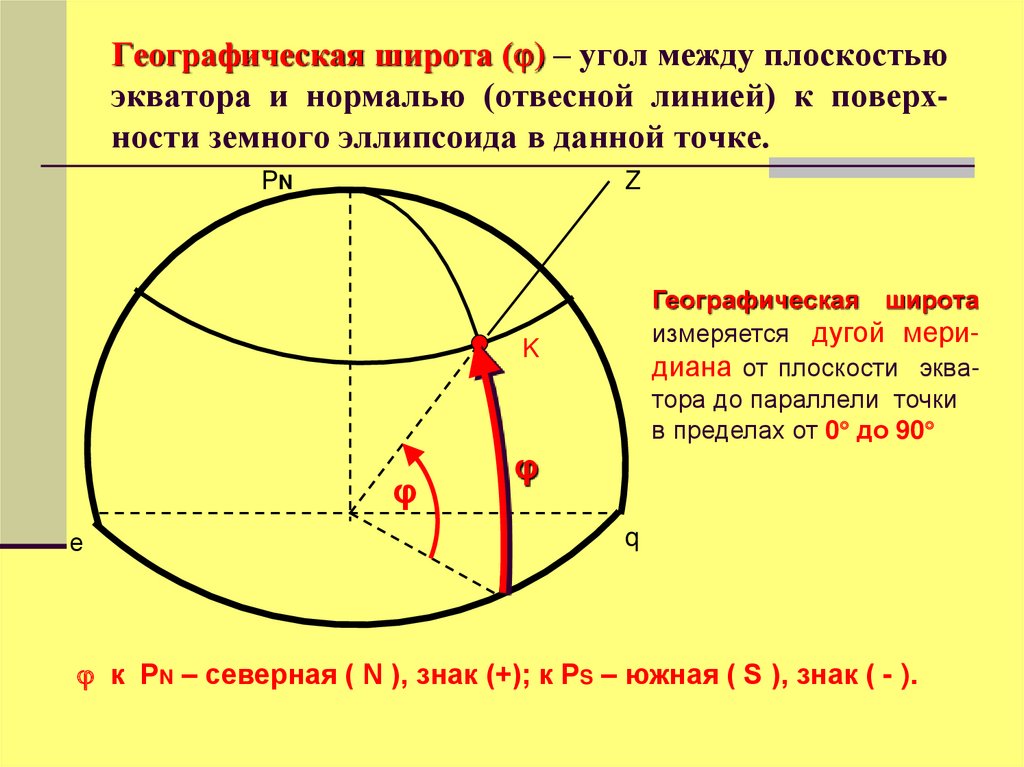
18. Географическая широта () – угол между плоскостью экватора и нормалью (отвесной линией) к поверх-ности земного эллипсоида в

Географическая широта ( ) – угол между плоскостью
экватора и нормалью (отвесной линией) к поверхности земного эллипсоида в данной точке.
PN
Z
Географическая широта
измеряется дугой меридиана от плоскости экватора до параллели точки
в пределах от 0 до 90
K
φ
е
φ
q
к PN – северная ( N ), знак (+); к PS – южная ( S ), знак ( - ).

19. Географическая долгота (  ) – двугранный угол между плоскостью начального ( Гринвичского ) меридиана и плоскостью меридиана

Географическая долгота ( ) – двугранный угол
между плоскостью начального ( Гринвичского )
меридиана и плоскостью меридиана наблюдателя
(данной точки).
PN
Гр
е
Географическая долгота
измеряется дугой экватора от плоскости Гринвичского меридиана до меридиана наблюдателя
в
пределах от 0 до 180 .
λ
q
λ
к востоку от Гринвича – восточная (Е), знак (+); к западу – западная (W), знак (-).

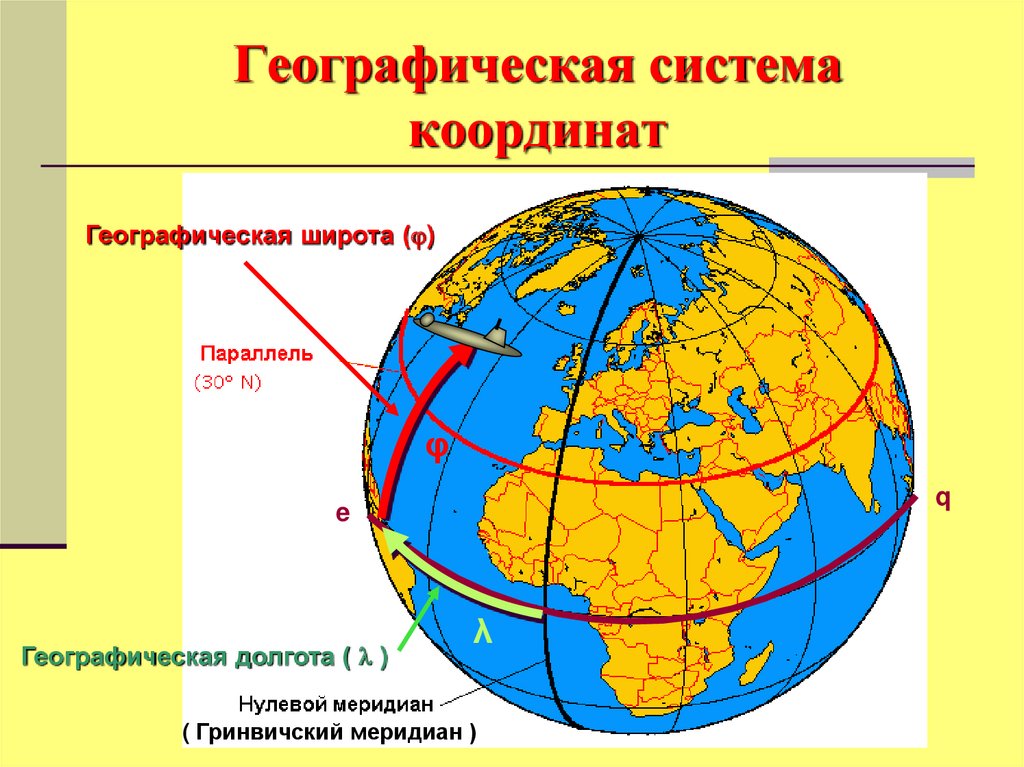
20. Географическая система координат

Географическая широта ( )
φ
q
e
Географическая долгота ( )
λ
( Гринвичский меридиан )

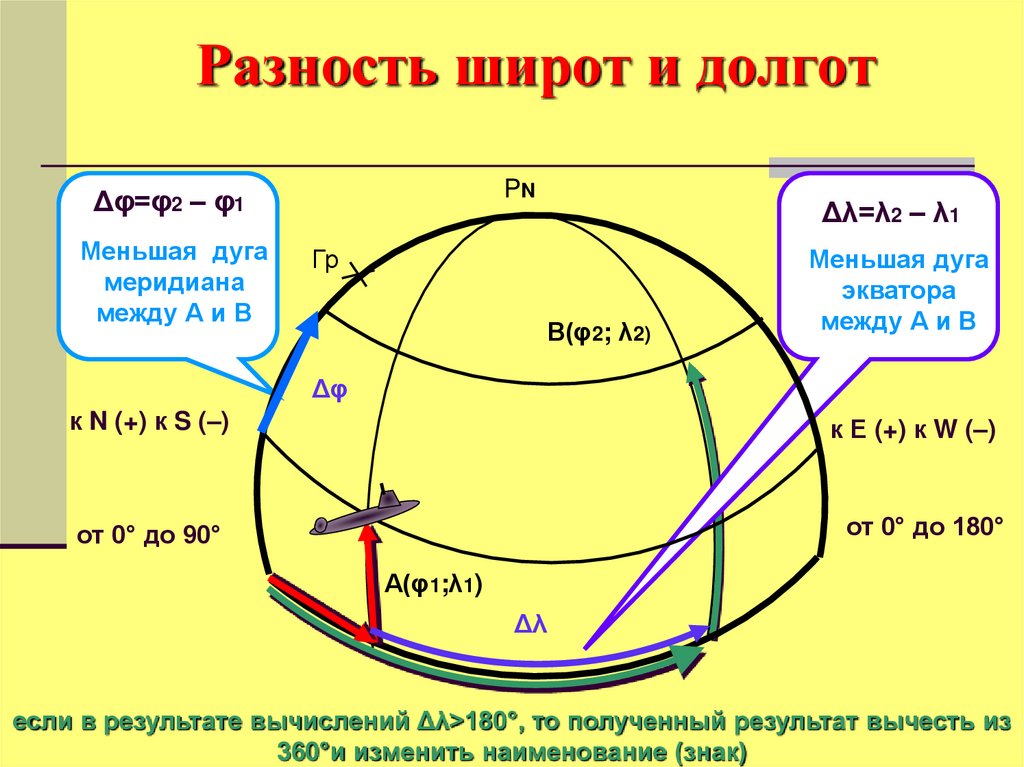
21. Разность широт и долгот

PN
Δφ=φ2 – φ1
Меньшая дуга
меридиана
между А и В
Δλ=λ2 – λ1
Гр
В(φ2; λ2)
Меньшая дуга
экватора
между А и В
Δφ
к N (+) к S (–)
к Е (+) к W (–)
от 0° до 180°
от 0° до 90°
А(φ1;λ1)
Δλ
если в результате вычислений Δλ>180°, то полученный результат вычесть из
360°и изменить наименование (знак)

22.

Квазигеографическая система координат
Квазигеографическая система координат (от лат. quasi –
якобы, как будто, приставка, употребляемая в сочетании с некоторыми
терминами для определения понятий, которые не являясь в точном значении
слова этими терминами, тем не менее заменяют их ) - условная система
координат используемая для кораблевождения в высоких широтах
(более 80 град.) – приполюсных районах Северного Ледовитого океана.
Квазигеографические полюса, смещены относительно географических, на угол 90˚ и имеют следующие координаты:
Северный квазиполюс ( Pnq )
Южный квазиполюс ( Psq )
φ = 0,0˚ λ = 180,0;
φ = 0,0˚ λ = 0,0˚.
Координатные линии системы - квазипараллели и квазимеридианы,
а координаты - квазиширота (φq) и квазидолгота (λq).

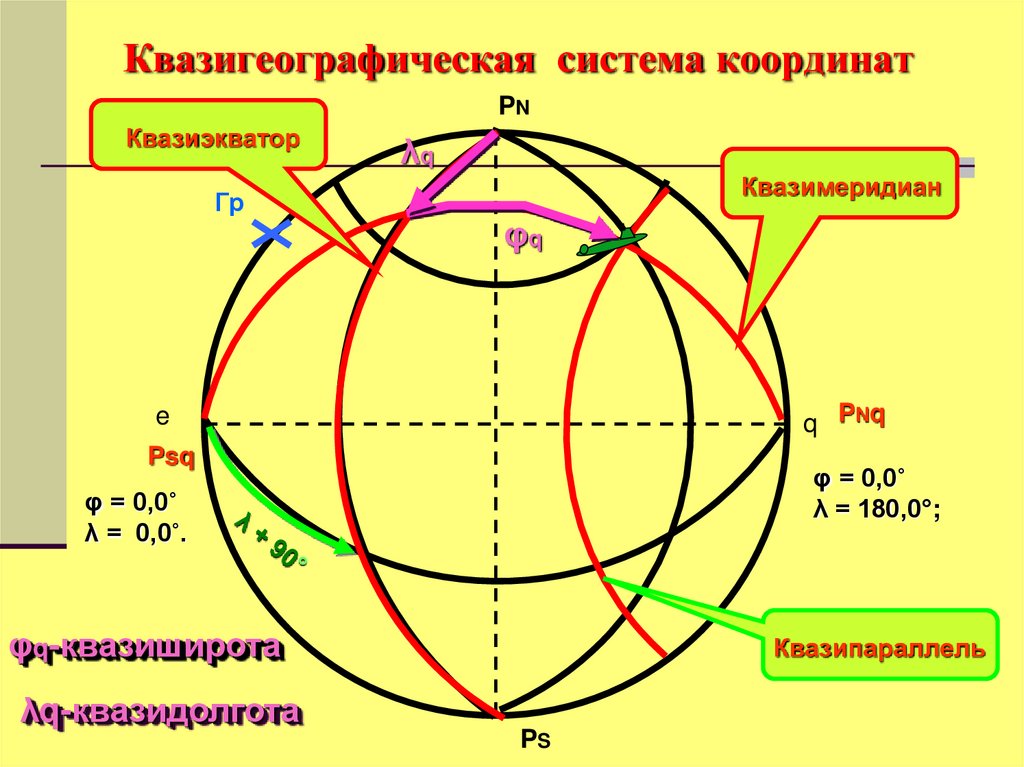
23. Квазигеографическая система координат

PN
Квазиэкватор
Гр
λq
Квазимеридиан
φq
q PNq
e
Psq
φ = 0,0˚
λ = 180,0°;
φ = 0,0˚
λ = 0,0˚.
φq-квазиширота
Квазипараллель
λq-квазидолгота
PS

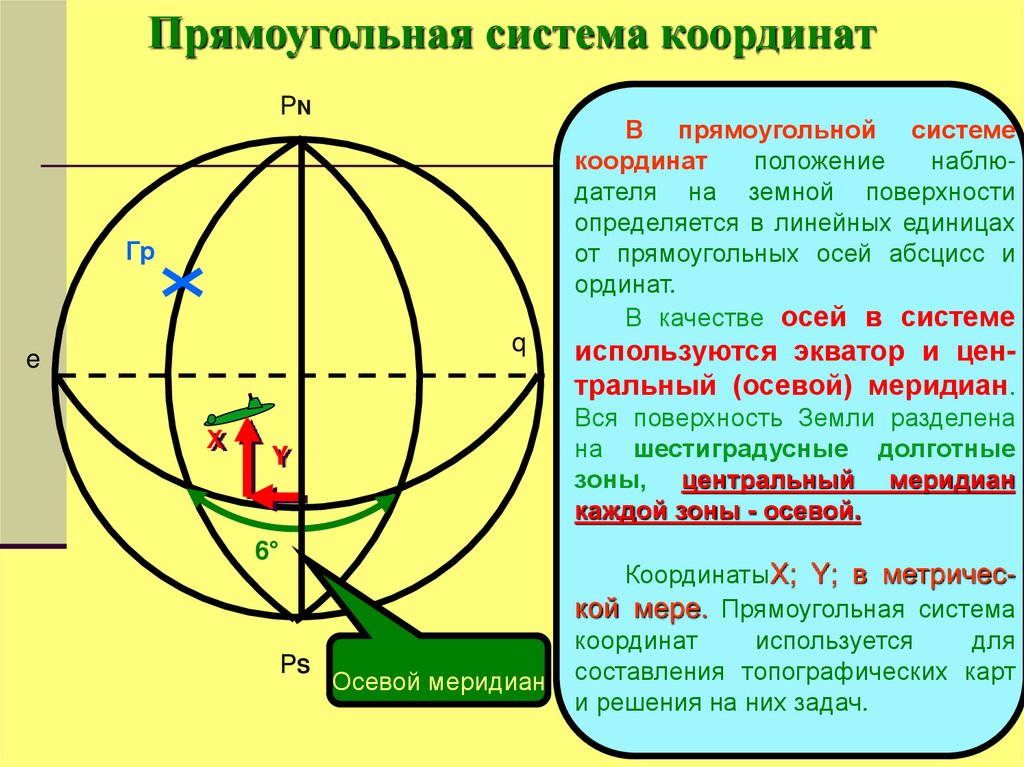
24.

Прямоугольная система координат
PN
В прямоугольной системе
координат
положение
наблюдателя на земной поверхности
определяется в линейных единицах
от прямоугольных осей абсцисс и
ординат.
В качестве осей в системе
Гр
q
e
Х
Вся поверхность Земли разделена
на шестиградусные долготные
зоны, центральный меридиан
каждой зоны - осевой.
Y
6°
PS
используются экватор и центральный (осевой) меридиан.
Осевой меридиан
КоординатыX; Y; в метрической мере. Прямоугольная система
координат
используется
для
составления топографических карт
и решения на них задач.

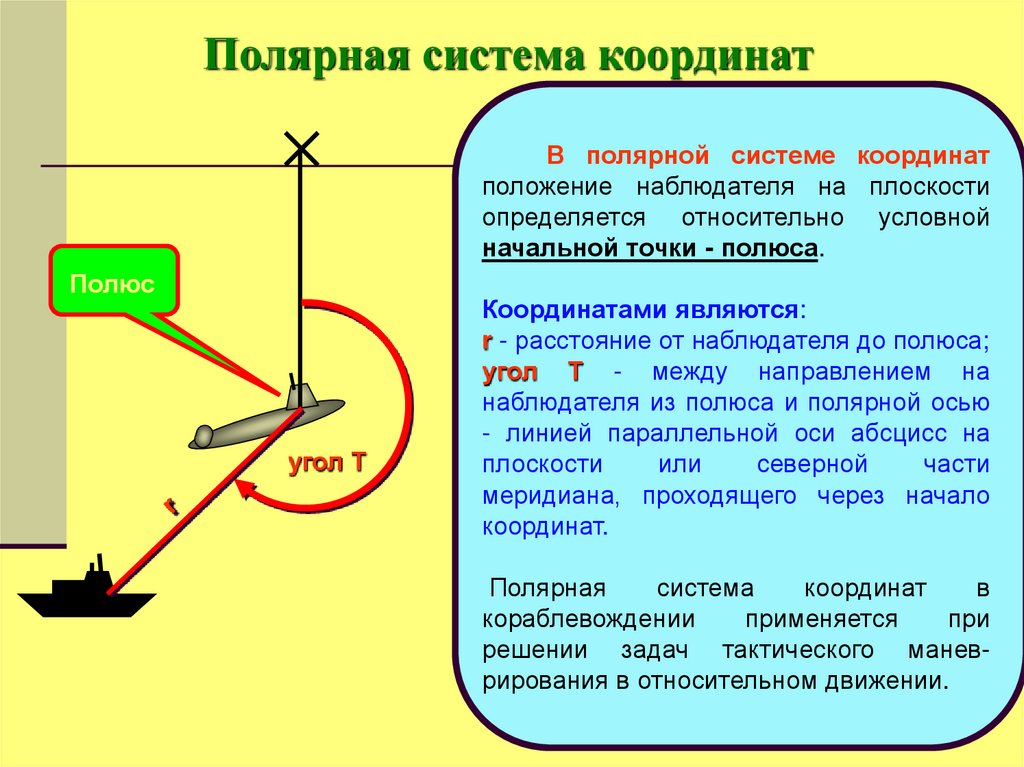
25.

Полярная система координат
В полярной системе координат
положение наблюдателя на плоскости
определяется относительно условной
начальной точки - полюса.
Полюс
угол Т
Координатами являются:
r - расстояние от наблюдателя до полюса;
угол Т - между направлением на
наблюдателя из полюса и полярной осью
- линией параллельной оси абсцисс на
плоскости
или
северной
части
меридиана, проходящего через начало
координат.
Полярная
система
координат
в
кораблевождении
применяется
при
решении задач тактического маневрирования в относительном движении.

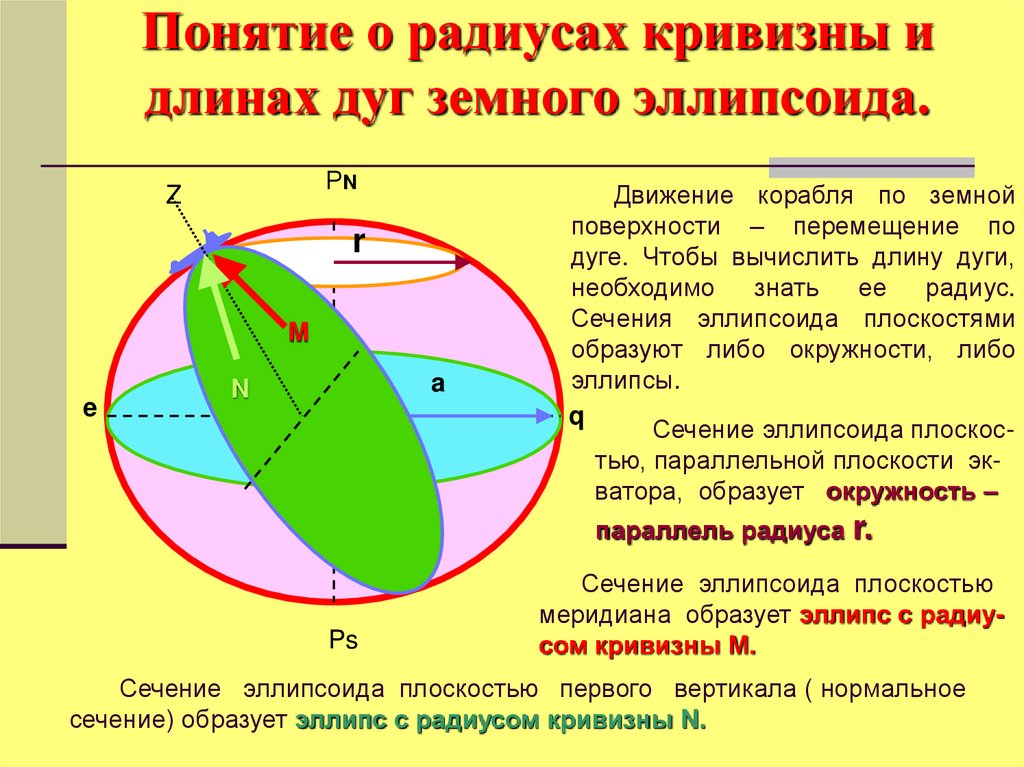
26. Понятие о радиусах кривизны и длинах дуг земного эллипсоида.

РN
Z
r
M
e
a
N
Движение корабля по земной
поверхности – перемещение по
дуге. Чтобы вычислить длину дуги,
необходимо
знать
ее
радиус.
Сечения эллипсоида плоскостями
образуют либо окружности, либо
эллипсы.
q
Сечение эллипсоида плоскостью, параллельной плоскости экватора, образует окружность –
параллель радиуса r.
Ps
Сечение эллипсоида плоскостью
меридиана образует эллипс с радиусом кривизны М.
Сечение эллипсоида плоскостью первого вертикала ( нормальное
сечение) образует эллипс с радиусом кривизны N.

27.

Понятие о радиусах кривизны и длинах дуг
земного эллипсоида.
Зная радиусы кривизны, можно вычислить длины дуг:
длина одной минуты дуги меридиана: 1 м = М · arc 1';
длина одной минуты дуги параллели: 1'r = r · arc 1';
длина одной минуты дуги экватора: 1'r = а · arc 1';
Примечание: 1 рад.=57,3 =3437,75´;
arc 1´= 1 / 3437,75´.

28.

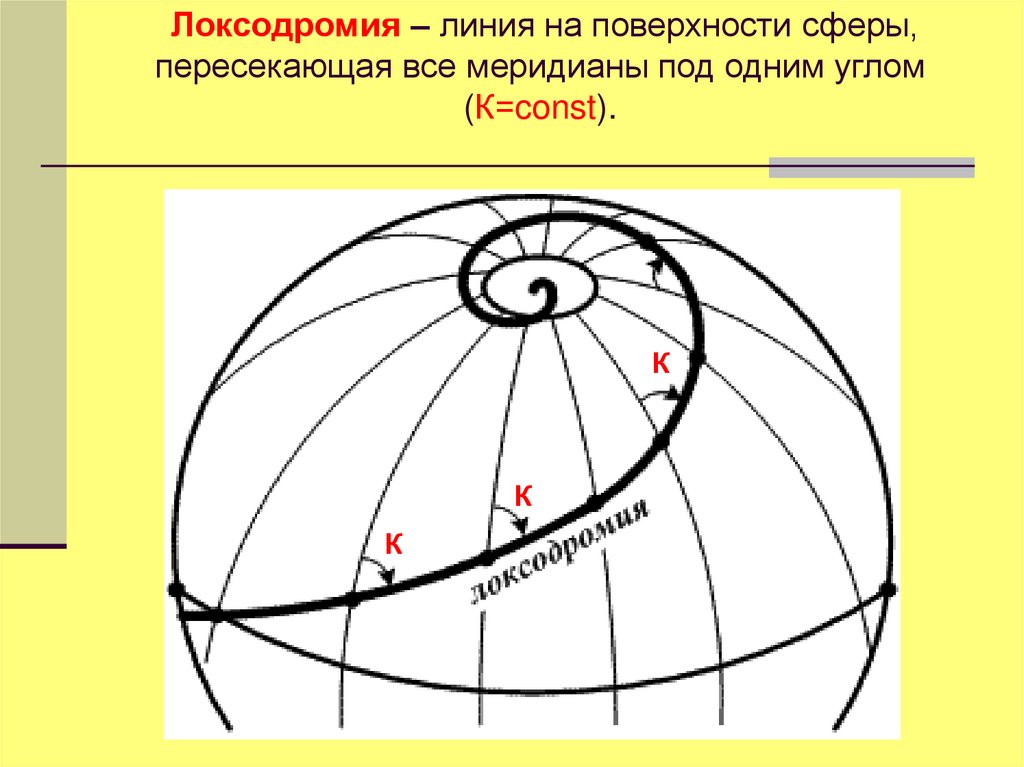
Локсодромия – линия на поверхности сферы,
пересекающая все меридианы под одним углом
(К=const).
К
К
К

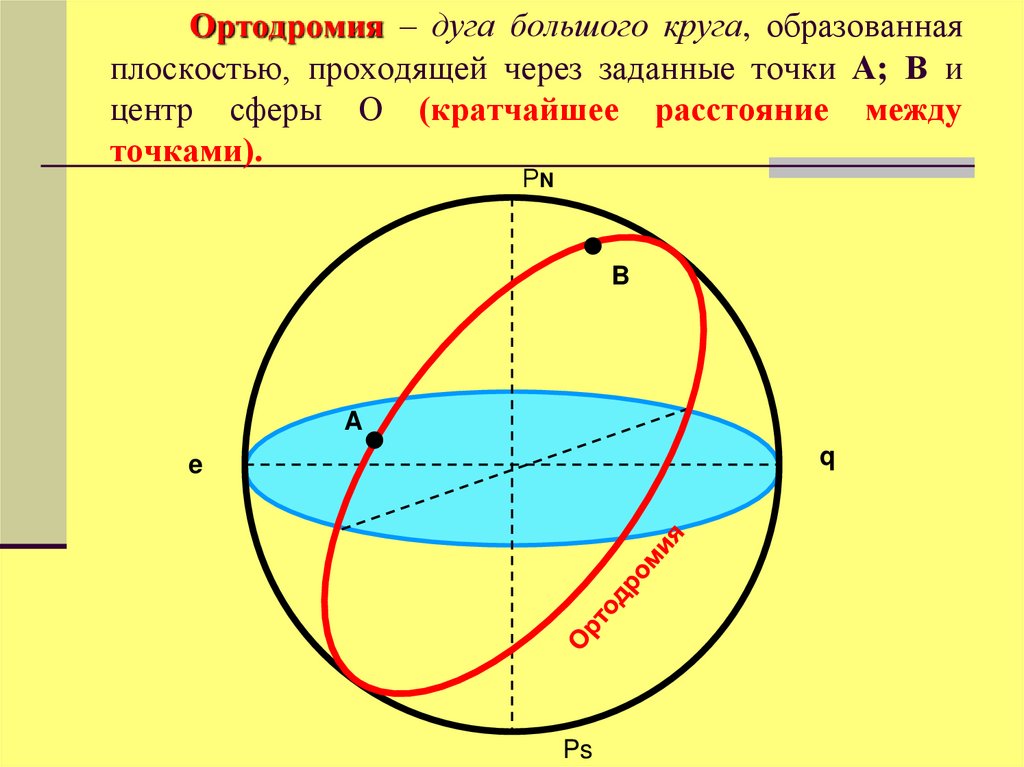
29. Ортодромия – дуга большого круга, образованная плоскостью, проходящей через заданные точки А; В и центр сферы О (кратчайшее

расстояние между
точками).
РN
B
A
q
e
Ps

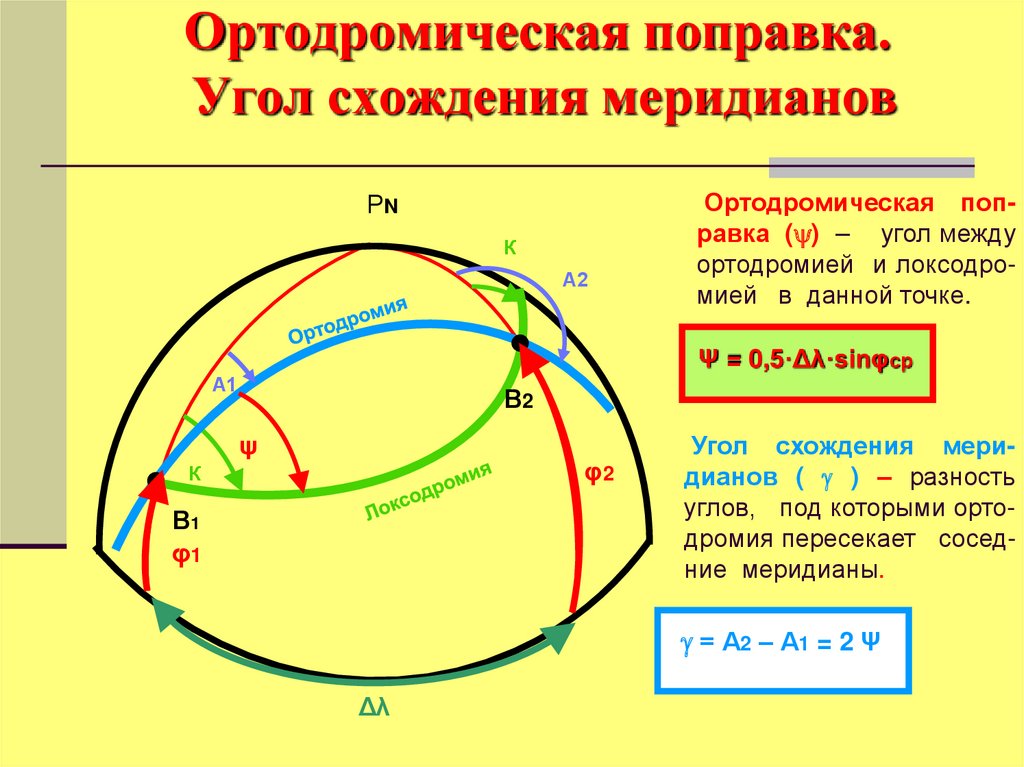
30. Ортодромическая поправка. Угол схождения меридианов

РN
К
А2
Ортодромическая поправка ( ) – угол между
ортодромией и локсодромией в данной точке.
Ψ = 0,5·Δλ·sinφср
А1
В2
ψ
φ2
К
В1
φ1
Угол схождения меридианов ( ) – разность
углов, под которыми ортодромия пересекает соседние меридианы.
= А2 – А1 = 2 Ψ
Δλ

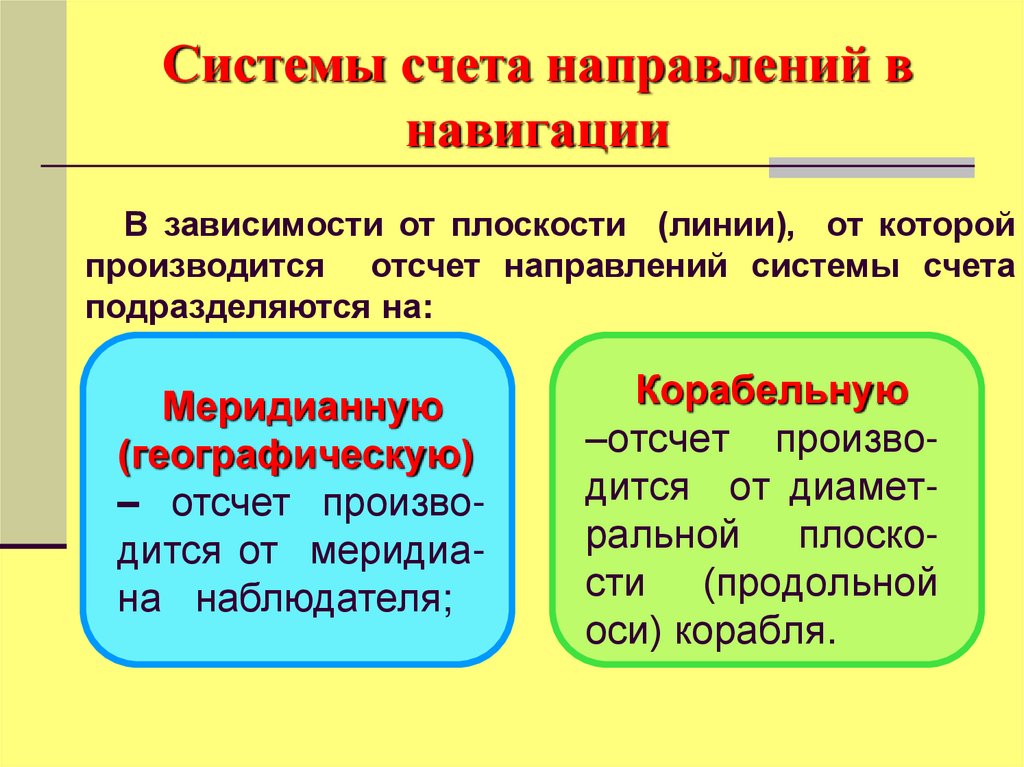
31. Системы счета направлений в навигации

В зависимости от плоскости (линии), от которой
производится отсчет направлений системы счета
подразделяются на:
Меридианную
(географическую)
– отсчет производится от меридиана наблюдателя;
Корабельную
–отсчет производится от диаметральной плоскости (продольной
оси) корабля.

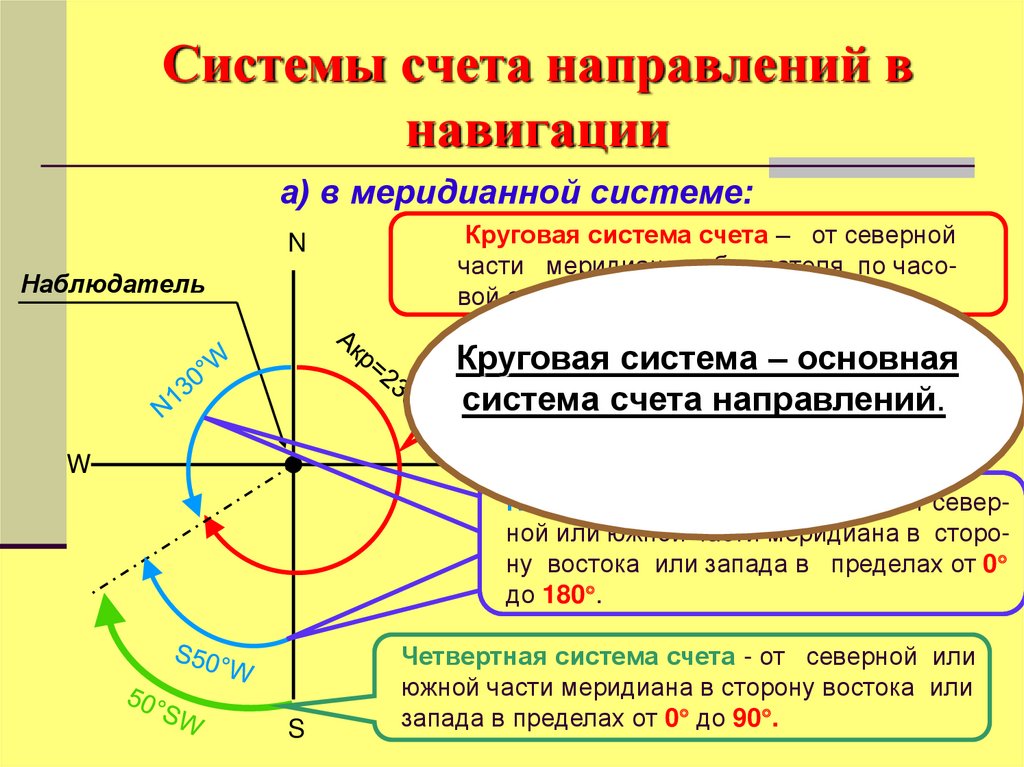
32. Системы счета направлений в навигации

а) в меридианной системе:
N
Наблюдатель
Круговая система счета – от северной
части меридиана наблюдателя, по часовой стрелке от 0 до 360 .
Круговая система – основная
система счета направлений.
E
W
Полукруговая система счета – от северной или южной части меридиана в сторону востока или запада в пределах от 0
до 180 .
S
Четвертная система счета - от северной или
южной части меридиана в сторону востока или
запада в пределах от 0 до 90 .

33. б) в корабельной системе:

Круговая система счета – от носовой части диаметральной плоскости корабля по часовой стрелке в пределах от 0 до 360 Направления в круговой
системе счета называются – отсчет курсового угла.
ДП
КУ л/б
КУ п/б
ОКУ
Полукруговая система счета –
от носовой части диаметральной плоскости корабля в сторону правого или левого борта в
пределах от 0 до 180 .
Направления в полукруговой системе имеют наименования, например: КУ=80 (л/б) левого борта или КУ=40° (п/б)
правого борта и называются курсовые углы.

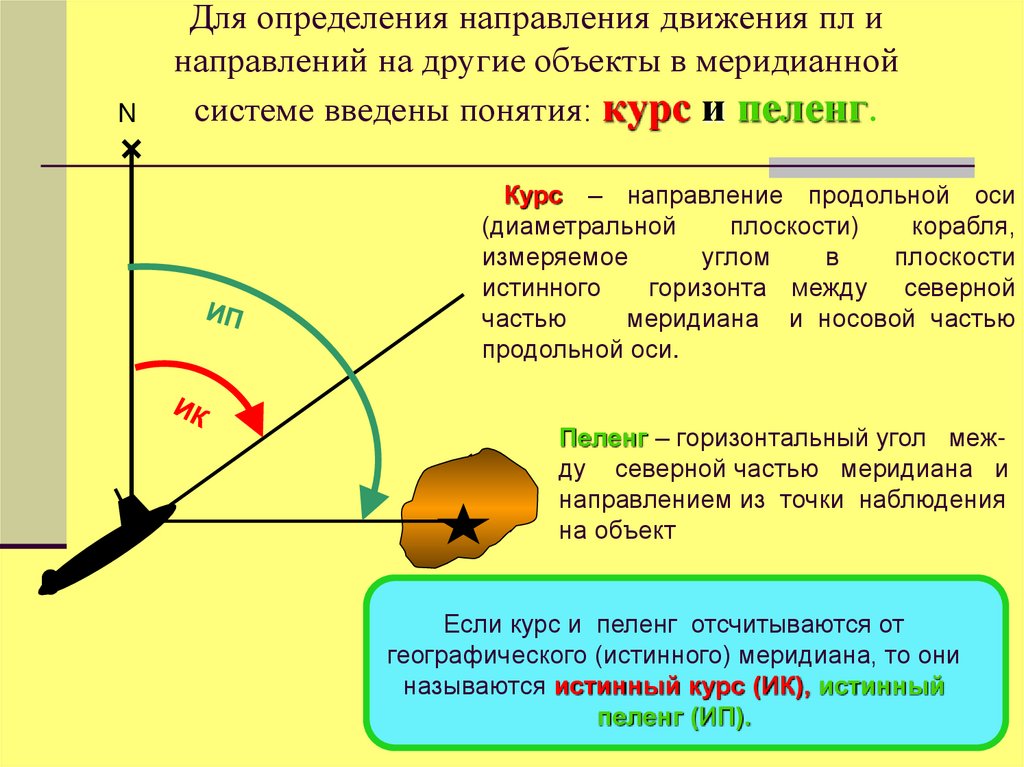
34. Для определения направления движения пл и направлений на другие объекты в меридианной системе введены понятия: курс и пеленг.

N
Для определения направления движения пл и
направлений на другие объекты в меридианной
системе введены понятия: курс и пеленг.
Курс – направление продольной оси
(диаметральной
плоскости)
корабля,
измеряемое
углом
в
плоскости
истинного
горизонта между северной
частью
меридиана и носовой частью
продольной оси.
Пеленг – горизонтальный угол между северной частью меридиана и
направлением из точки наблюдения
на объект
Если курс и пеленг отсчитываются от
географического (истинного) меридиана, то они
называются истинный курс (ИК), истинный
пеленг (ИП).

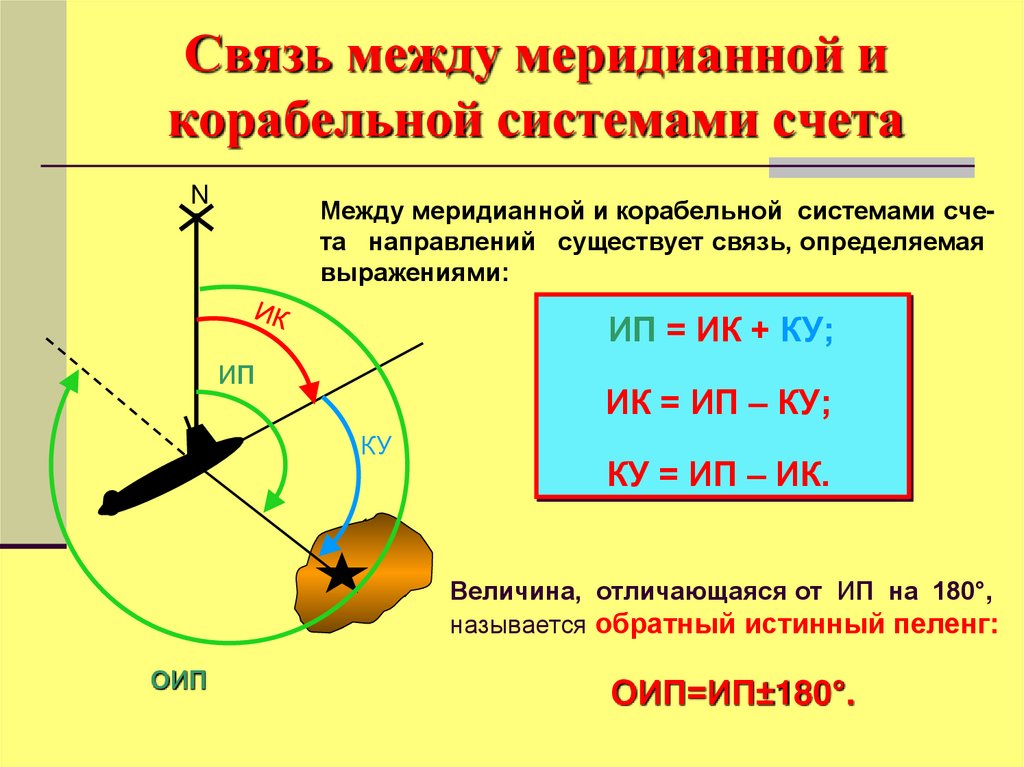
35. Связь между меридианной и корабельной системами счета

N
Между меридианной и корабельной системами счета направлений существует связь, определяемая
выражениями:
ИП = ИК + КУ;
ИП
ИК = ИП – КУ;
КУ
КУ = ИП – ИК.
Величина, отличающаяся от ИП на 180°,
называется обратный истинный пеленг:
ОИП
ОИП=ИП±180°.

36. Компасные направления

Для выработки и хранения направления меридиана на корабле
предназначена:
Корабельная
система
курсоуказания
(курсоуказатели).
Внешний вид гирокомпаса «Курс–3» и
его чувствительного элемента.

37. Компасные направления

Nк
N
Nк
К
+
К
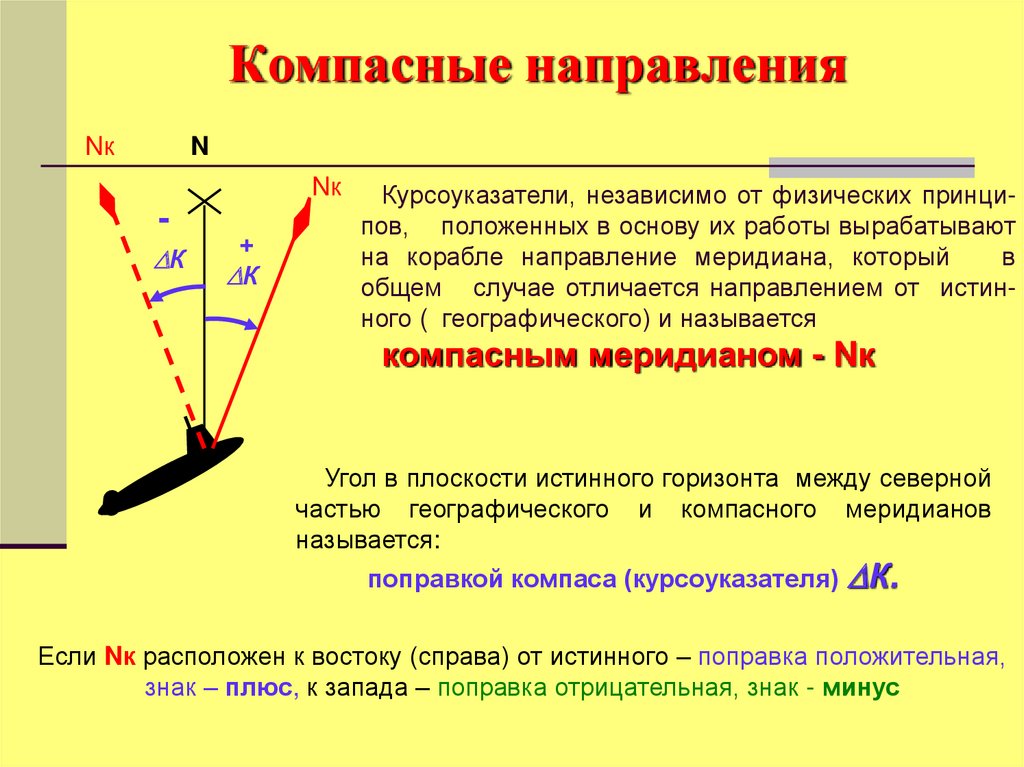
Курсоуказатели, независимо от физических принципов, положенных в основу их работы вырабатывают
на корабле направление меридиана, который
в
общем случае отличается направлением от истинного ( географического) и называется
компасным меридианом - Nк
Угол в плоскости истинного горизонта между северной
частью географического и компасного меридианов
называется:
поправкой компаса (курсоуказателя)
К.
Если Nк расположен к востоку (справа) от истинного – поправка положительная,
знак – плюс, к запада – поправка отрицательная, знак - минус

38. Компасные направления

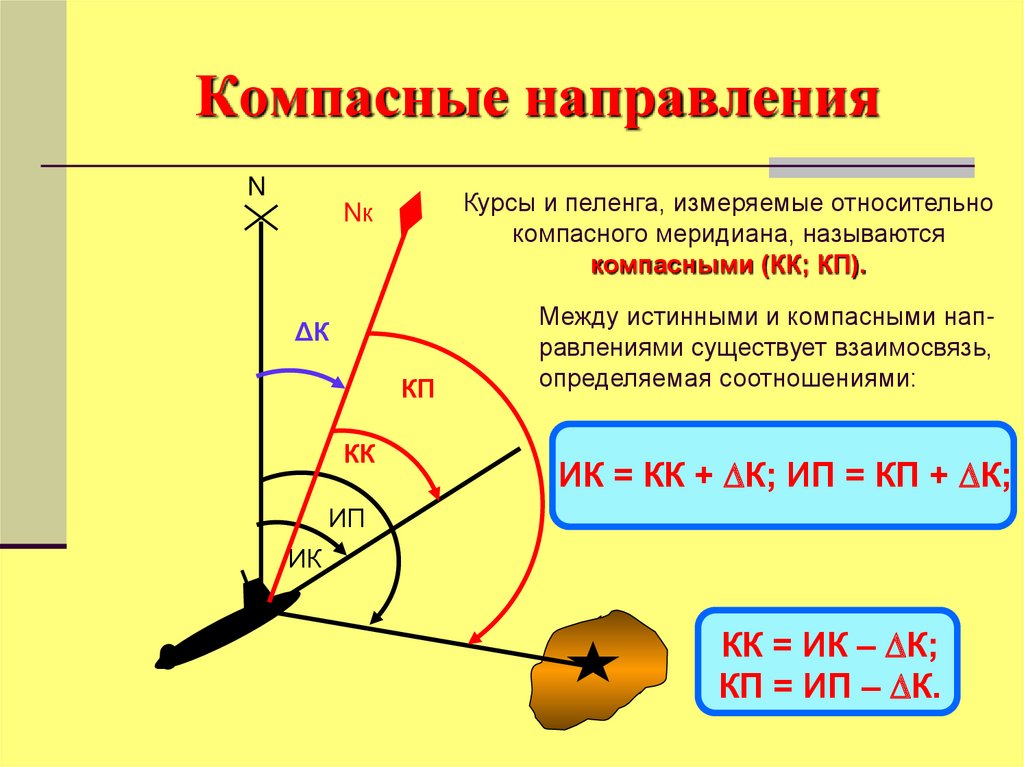
N
Курсы и пеленга, измеряемые относительно
компасного меридиана, называются
компасными (КК; КП).
Nк
ΔК
КП
КК
Между истинными и компасными направлениями существует взаимосвязь,
определяемая соотношениями:
ИК = КК + К; ИП = КП + К;
ИП
ИК
КК = ИК – К;
КП = ИП – К.

39. Определение поправки компаса

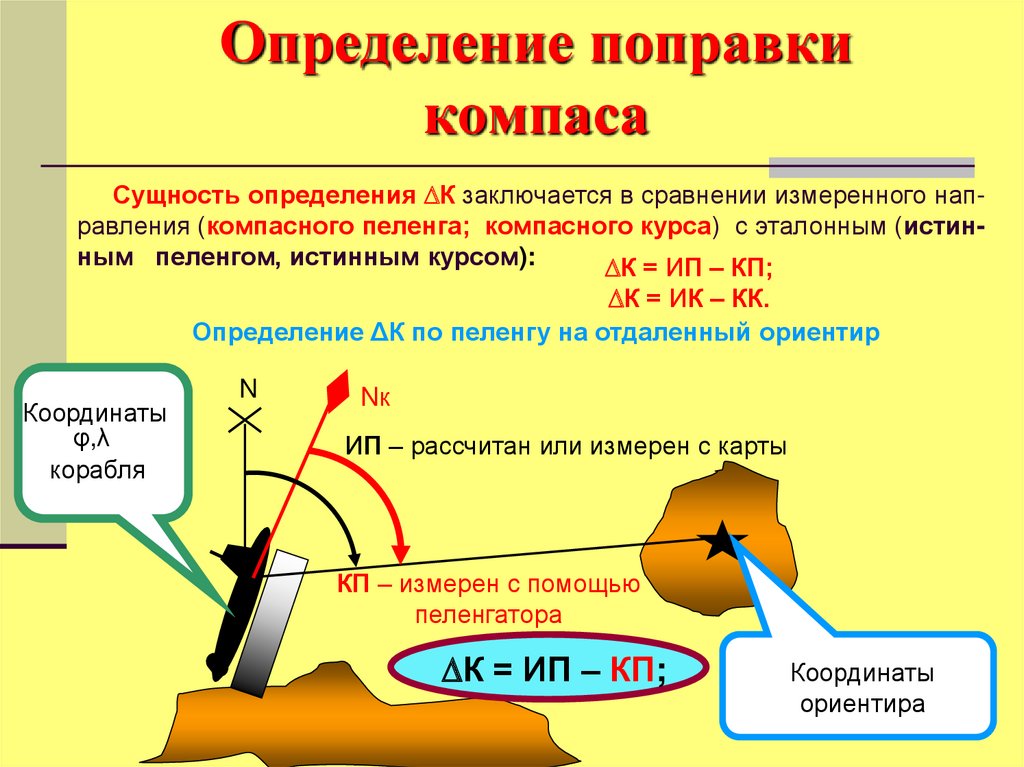
Сущность определения К заключается в сравнении измеренного направления (компасного пеленга; компасного курса) с эталонным (истинным пеленгом, истинным курсом):
К = ИП – КП;
К = ИК – КК.
Определение ΔК по пеленгу на отдаленный ориентир
Координаты
φ,λ
корабля
N
Nк
ИП – рассчитан или измерен с карты
КП – измерен с помощью
пеленгатора
К = ИП – КП;
Координаты
ориентира

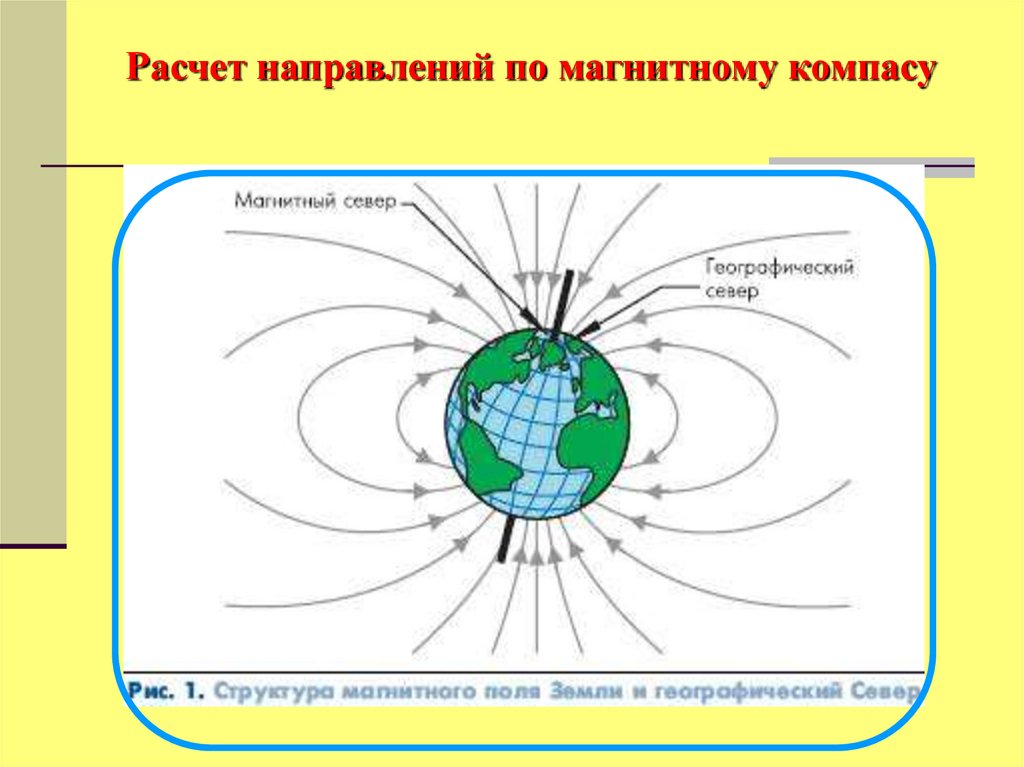
40. Расчет направлений по магнитному компасу

Z
Т
I
Н
Силовая магнитная линия
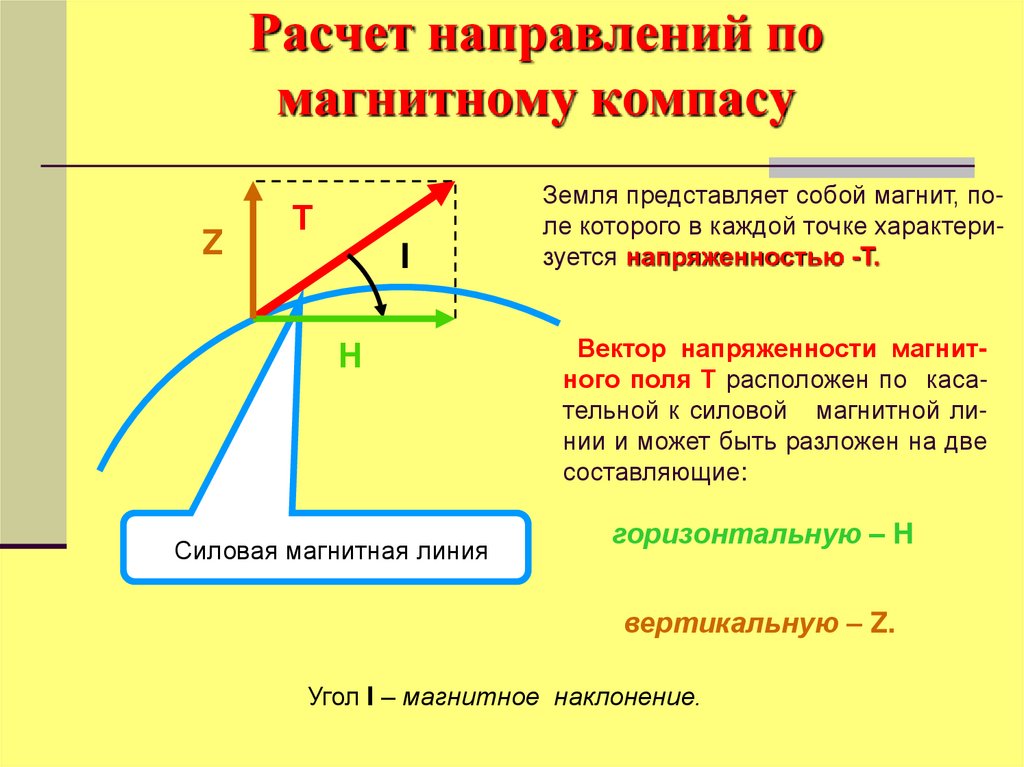
Земля представляет собой магнит, поле которого в каждой точке характеризуется напряженностью -T.
Вектор напряженности магнитного поля Т расположен по касательной к силовой магнитной линии и может быть разложен на две
составляющие:
горизонтальную – H
вертикальную – Z.
Угол I – магнитное наклонение.

41.

Расчет направлений по магнитному компасу

42. Расчет направлений по магнитному компасу

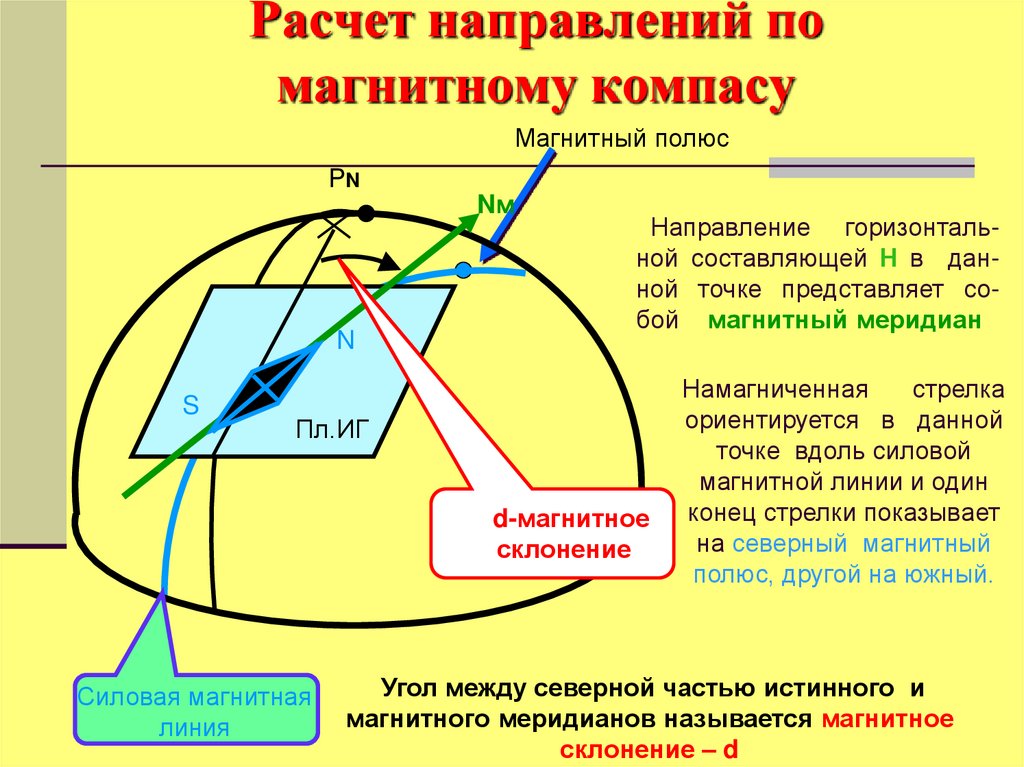
Магнитный полюс
PN
Nм
N
S
Направление горизонтальной составляющей Н в данной точке представляет собой магнитный меридиан
Пл.ИГ
d-магнитное
склонение
Силовая магнитная
линия
Намагниченная
стрелка
ориентируется в данной
точке вдоль силовой
магнитной линии и один
конец стрелки показывает
на северный магнитный
полюс, другой на южный.
Угол между северной частью истинного и
магнитного меридианов называется магнитное
склонение – d

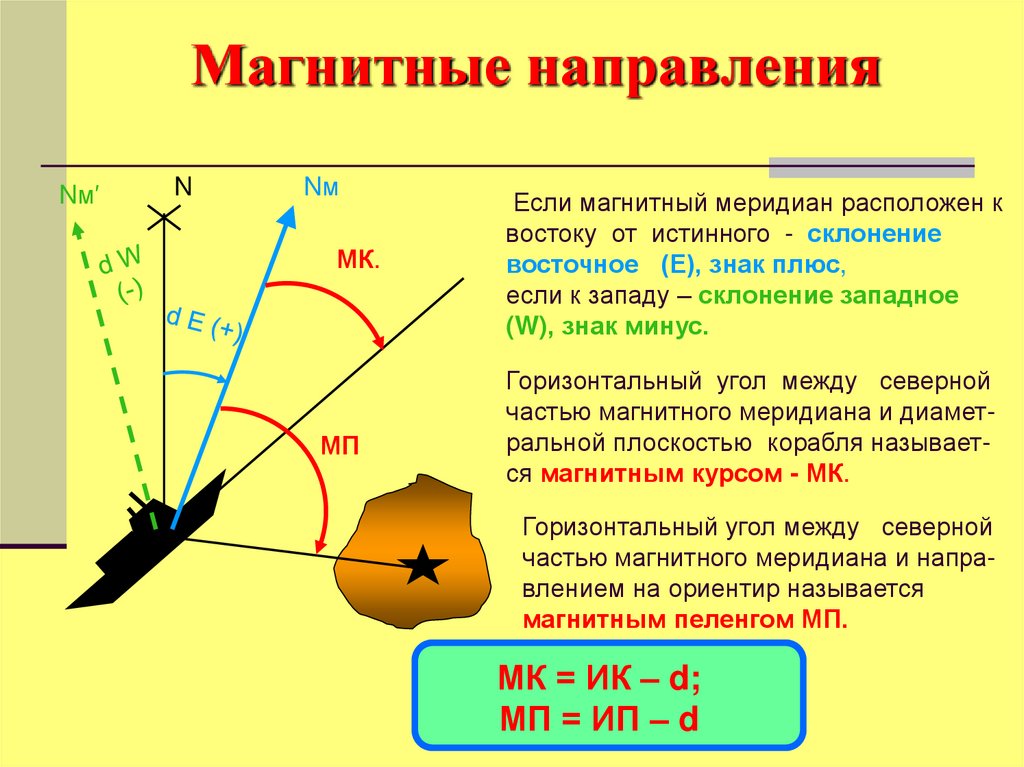
43. Магнитные направления

Nм′
N
Nм
МК.
МП
Если магнитный меридиан расположен к
востоку от истинного - склонение
восточное (Е), знак плюс,
если к западу – склонение западное
(W), знак минус.
Горизонтальный угол между северной
частью магнитного меридиана и диаметральной плоскостью корабля называется магнитным курсом - МК.
Горизонтальный угол между северной
частью магнитного меридиана и направлением на ориентир называется
магнитным пеленгом МП.
МК = ИК – d;
МП = ИП – d

44. Приведение магнитного склонения к году плавания

d = dк + Δd · n
dk - магнитное склонение с карты
Δd- годовое изменение с карты
n- количество лет между годом издания
МНК и годом плавания

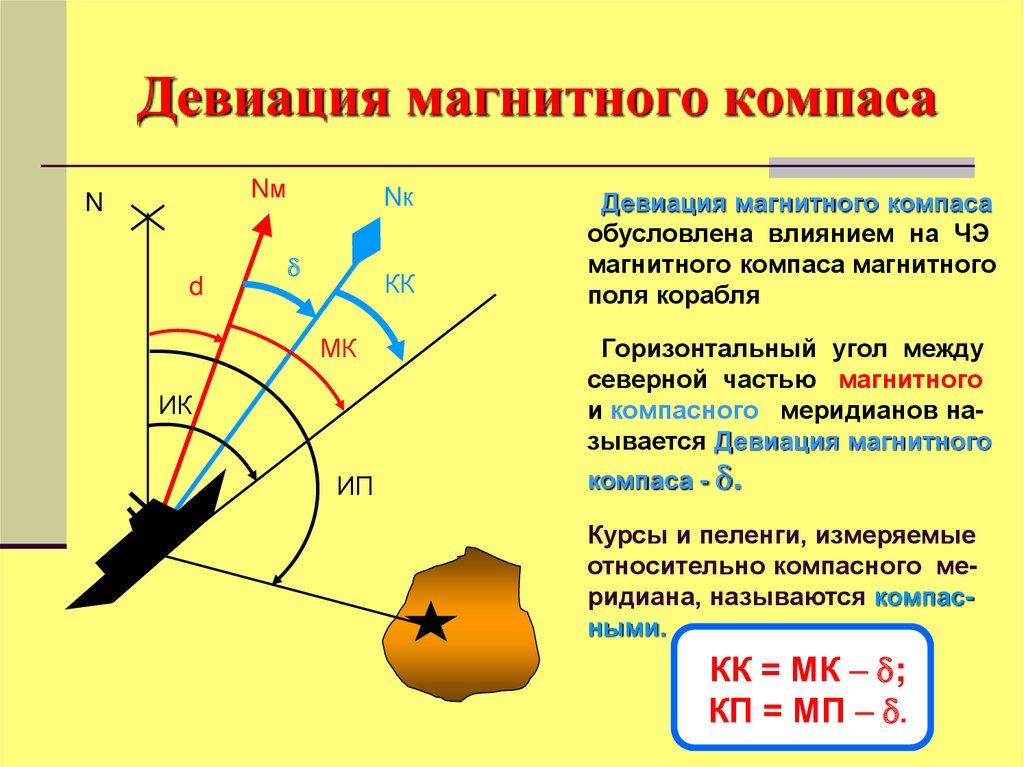
45. Девиация магнитного компаса

Nм
N
d
Nк
КК
МК
ИК
ИП
Девиация магнитного компаса
обусловлена влиянием на ЧЭ
магнитного компаса магнитного
поля корабля
Горизонтальный угол между
северной частью магнитного
и компасного меридианов называется Девиация магнитного
компаса - .
Курсы и пеленги, измеряемые
относительно компасного меридиана, называются компасными.
КК = МК ;
КП = МП .

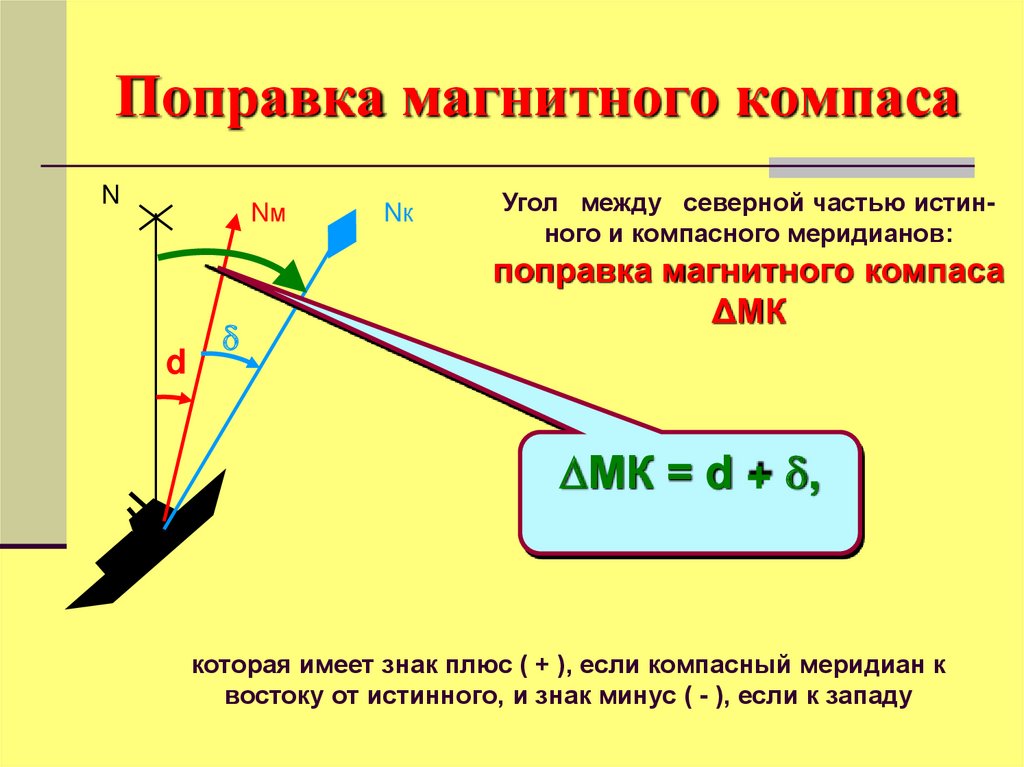
46. Поправка магнитного компаса

N
Nм
d
Nк
Угол между северной частью истинного и компасного меридианов:
поправка магнитного компаса
ΔМК
МК = d + ,
которая имеет знак плюс ( + ), если компасный меридиан к
востоку от истинного, и знак минус ( - ), если к западу

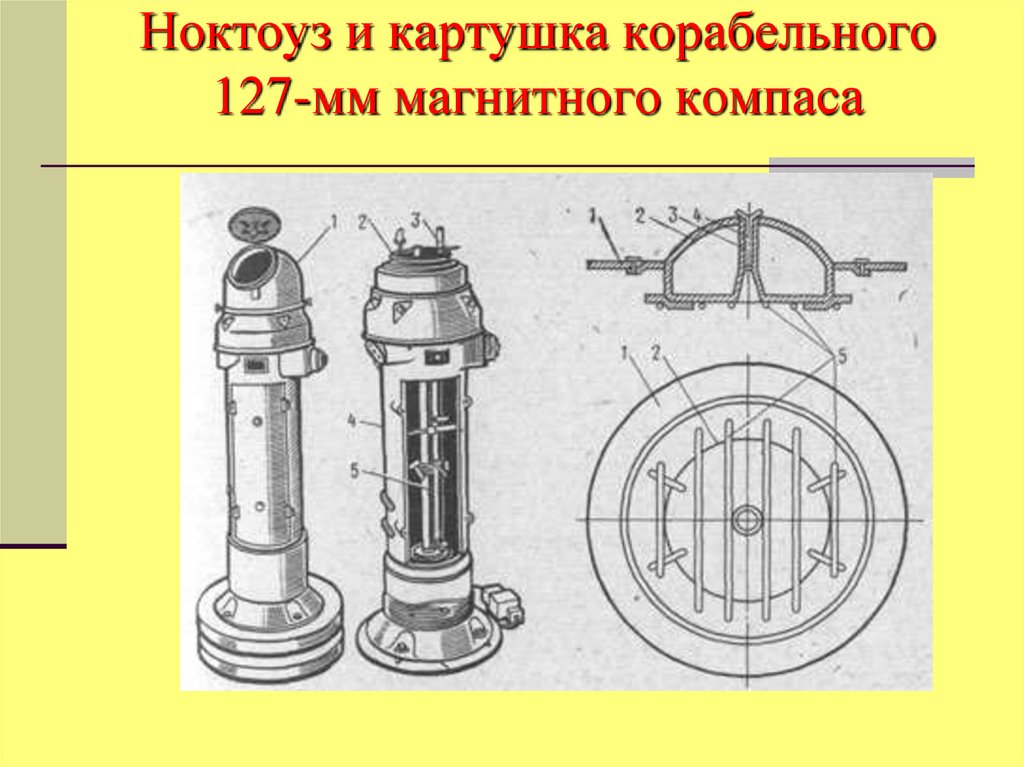
47. Ноктоуз и картушка корабельного 127-мм магнитного компаса

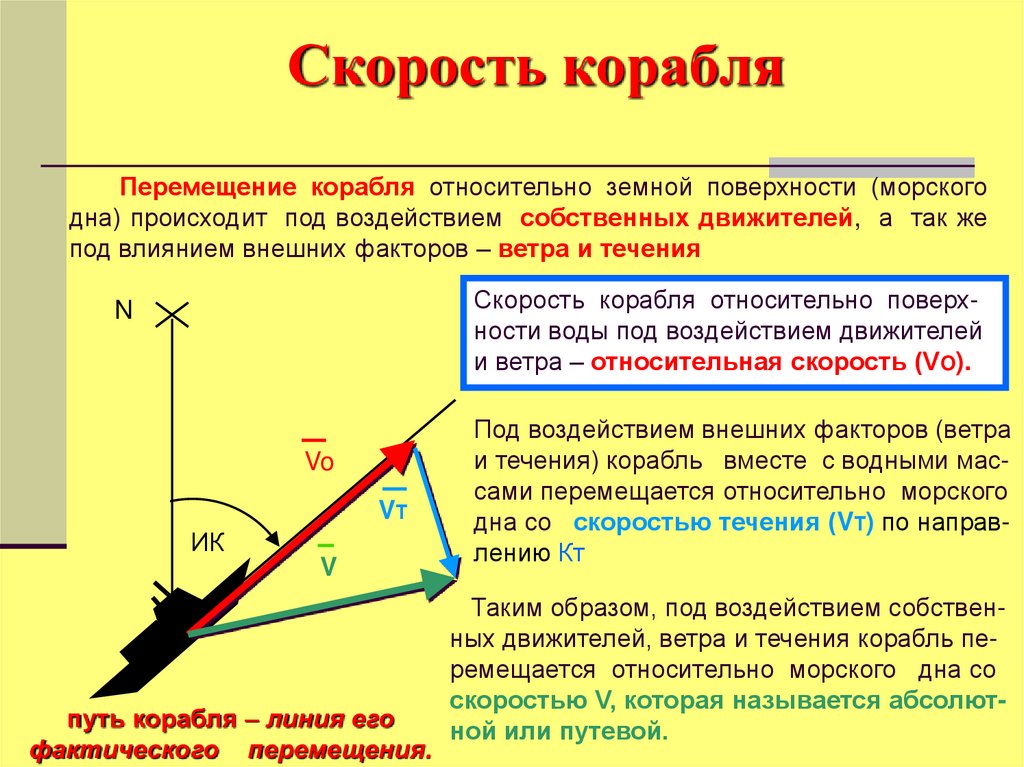
48. Скорость корабля

Перемещение корабля относительно земной поверхности (морского
дна) происходит под воздействием собственных движителей, а так же
под влиянием внешних факторов – ветра и течения
Скорость корабля относительно поверхности воды под воздействием движителей
и ветра – относительная скорость (VO).
N
Vo
VТ
ИК
V
путь корабля – линия его
фактического перемещения.
Под воздействием внешних факторов (ветра
и течения) корабль вместе с водными массами перемещается относительно морского
дна со скоростью течения (VТ) по направлению Кт
Таким образом, под воздействием собственных движителей, ветра и течения корабль перемещается относительно морского дна со
скоростью V, которая называется абсолютной или путевой.

49. Единицы длины и скорости в навигации

Основной единицей длины в навигации является морская миля.
Морская миля – длина одной минуты дуги меридиана
эллипсоида
1 м = М · arc 1 = 1852,3 – 9,3 · cos 2
М – радиус кривизны меридиана эллипсоида.
В 1931 году в качестве единицы длины была принята стандартная
миля, равная длине одной минуты дуги меридиана эллипсоида в широте 44 18 и составляющая
1852 метра.
В настоящее время термин стандартная миля практически вышел из употребления и заменен термином – морская миля.
Кабельтов – одна десятая часть морской мили = 185,2 метра

50. Единицы длины и скорости в навигации

Основной единицей скорости в навигации является узел – скорость, равная одной морской миле в
час.
При решении некоторых задач кораблевождения применяется единица скорости – кабельтов в минуту.
Для перехода от скорости в узлах к скорости в каб/мин используется
соотношение:
Скорость в узлах : 6 = скорость в каб/мин.

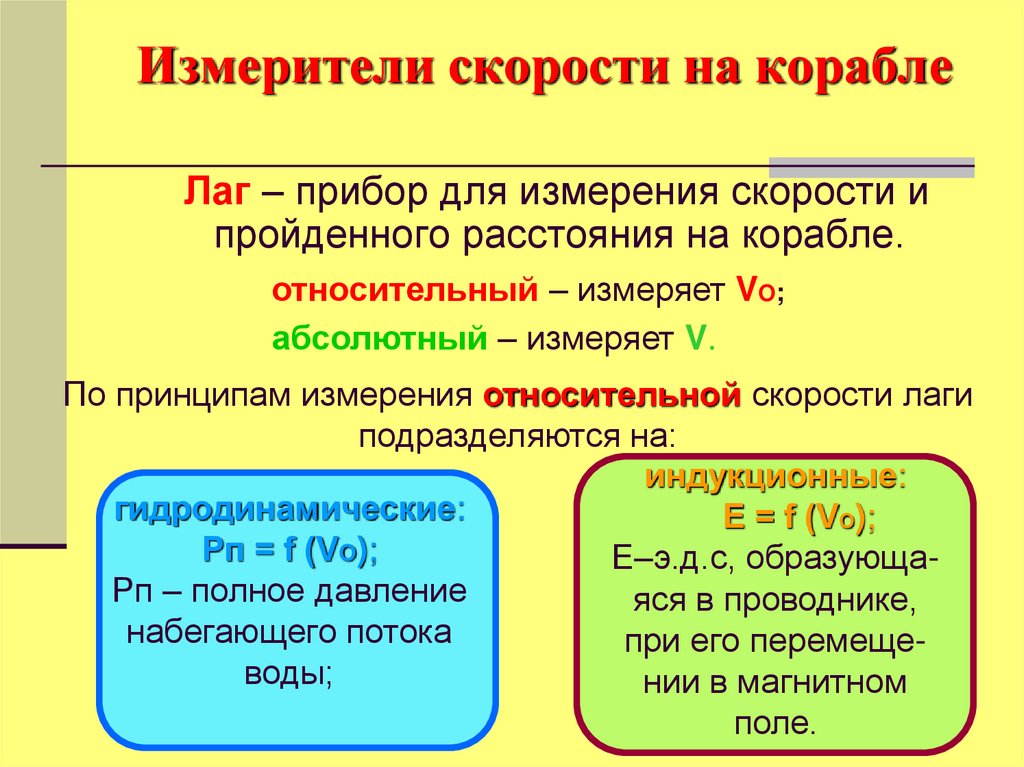
51. Измерители скорости на корабле

Лаг – прибор для измерения скорости и
пройденного расстояния на корабле.
относительный – измеряет VO;
абсолютный – измеряет V.
По принципам измерения относительной скорости лаги
подразделяются на:
индукционные:
гидродинамические:
Е = f (VO);
Рп = f (VO);
Е–э.д.с, образующаРп – полное давление
яся в проводнике,
набегающего потока
при его перемещеводы;
нии в магнитном
поле.

52. Измерители скорости на корабле

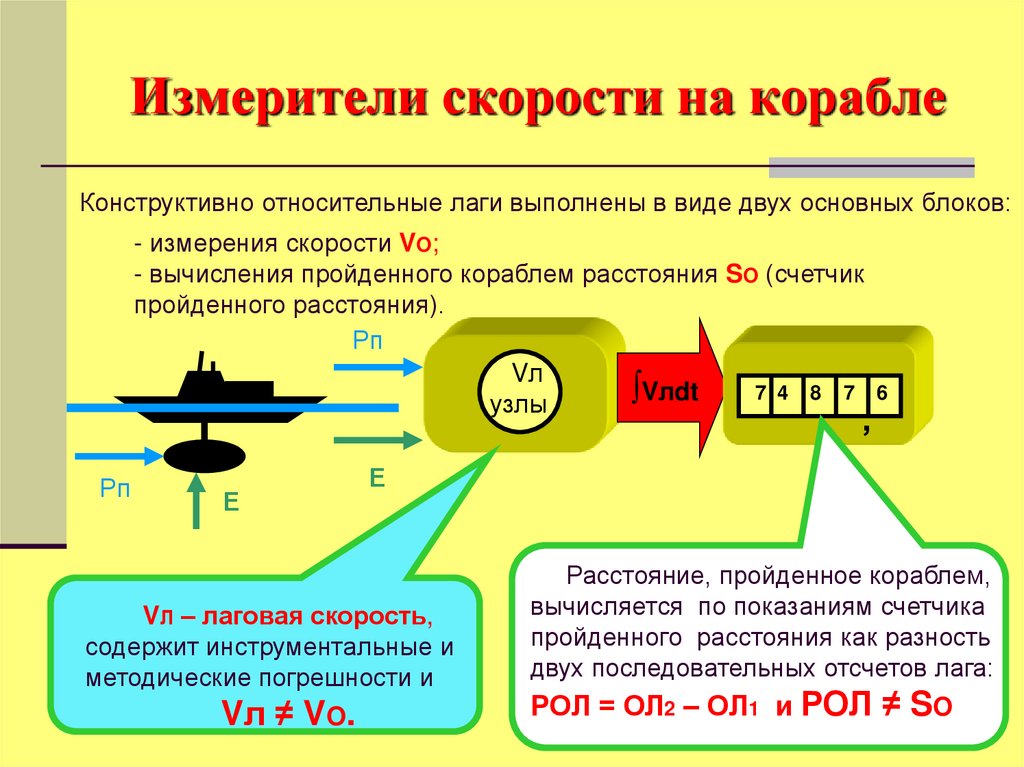
Конструктивно относительные лаги выполнены в виде двух основных блоков:
- измерения скорости VO;
- вычисления пройденного кораблем расстояния SO (счетчик
пройденного расстояния).
Рп
Vл
7 4 8 7
∫Vлdt
узлы
‚
Рп
Е
Е
VЛ – лаговая скорость,
содержит инструментальные и
методические погрешности и
Vл ≠ VO.
6
Расстояние, пройденное кораблем,
вычисляется по показаниям счетчика
пройденного расстояния как разность
двух последовательных отсчетов лага:
РОЛ = ОЛ2 – ОЛ1 и РОЛ ≠ SO

53. Понятие об определении поправок относительного лага

Ежегодно на кораблях ВМФ проводится комплекс мероприятий, называемый определение маневренных элементов. Одной из его составляющих
является:
• определение относительной скорости VO, соответствующей ей частоте работы движителей NO;
• определение поправок относительного лага - л%.
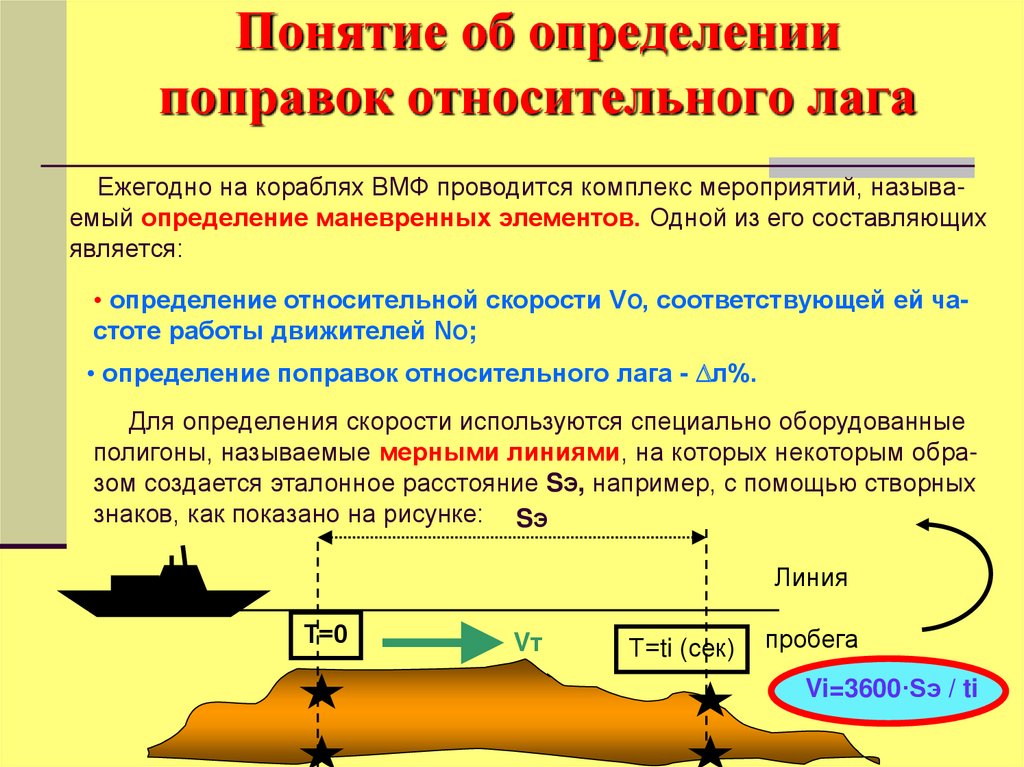
Для определения скорости используются специально оборудованные
полигоны, называемые мерными линиями, на которых некоторым образом создается эталонное расстояние SЭ, например, с помощью створных
знаков, как показано на рисунке: SЭ
Линия
Т=0
Vт
Т=ti (сек)
пробега
Vi=3600·Sэ / ti

54. Понятие об определении поправок относительного лага

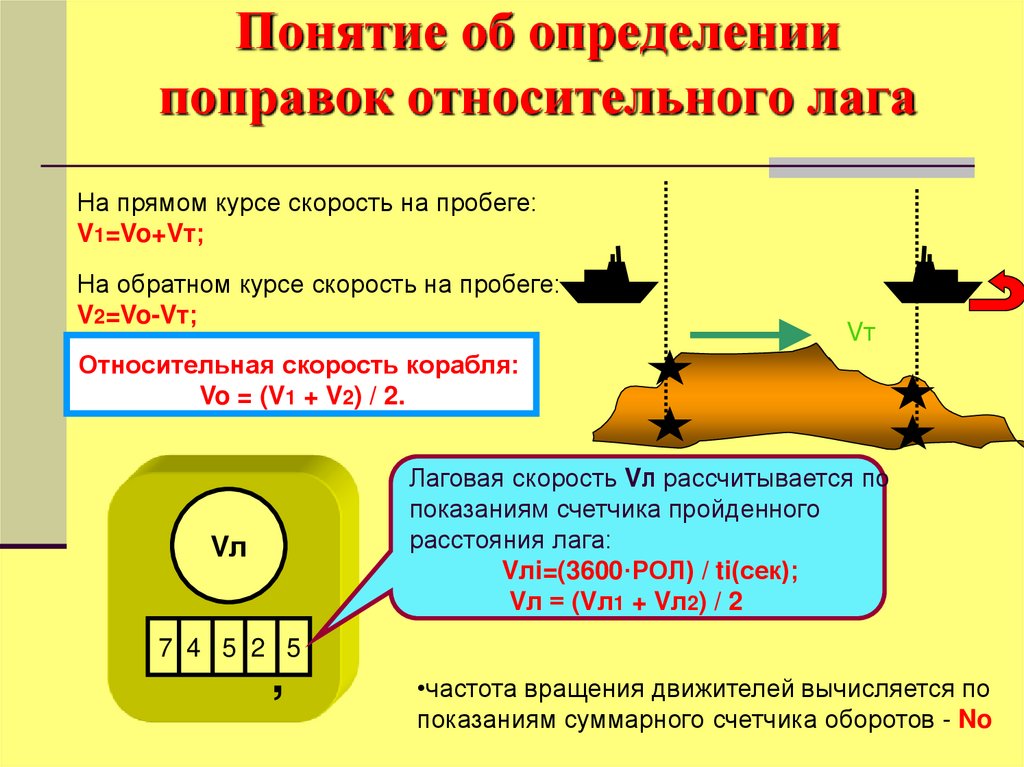
На прямом курсе скорость на пробеге:
V1=Vo+Vт;
На обратном курсе скорость на пробеге:
V2=Vo-Vт;
Vт
Относительная скорость корабля:
Vo = (V1 + V2) / 2.
Лаговая скорость VЛ рассчитывается по
показаниям счетчика пройденного
расстояния лага:
Vлi=(3600·РОЛ) / ti(сек);
Vл = (Vл1 + Vл2) / 2
Vл
7 4 5 2 5
,
•частота вращения движителей вычисляется по
показаниям суммарного счетчика оборотов - No

55. Понятие об определении поправок относительного лага

kЛ = VO / VЛ;
Коэффициент
относительного лага:
Поправка относительного лага л% - относительная суммарная систематическая погрешность лага, взятая с обратным знаком:
л%=[(Vo – Vл) / Vл] ·100%;
л% = 100 · (kЛ – 1).
если kЛ 1 (VO VЛ) – лаг «отстает» – поправка лага л% - положительная;
если kЛ 1 (VO VЛ) – лаг «опережает» – поправка лага л% - отрицательная.

56. Расчет пройденного кораблем расстояния

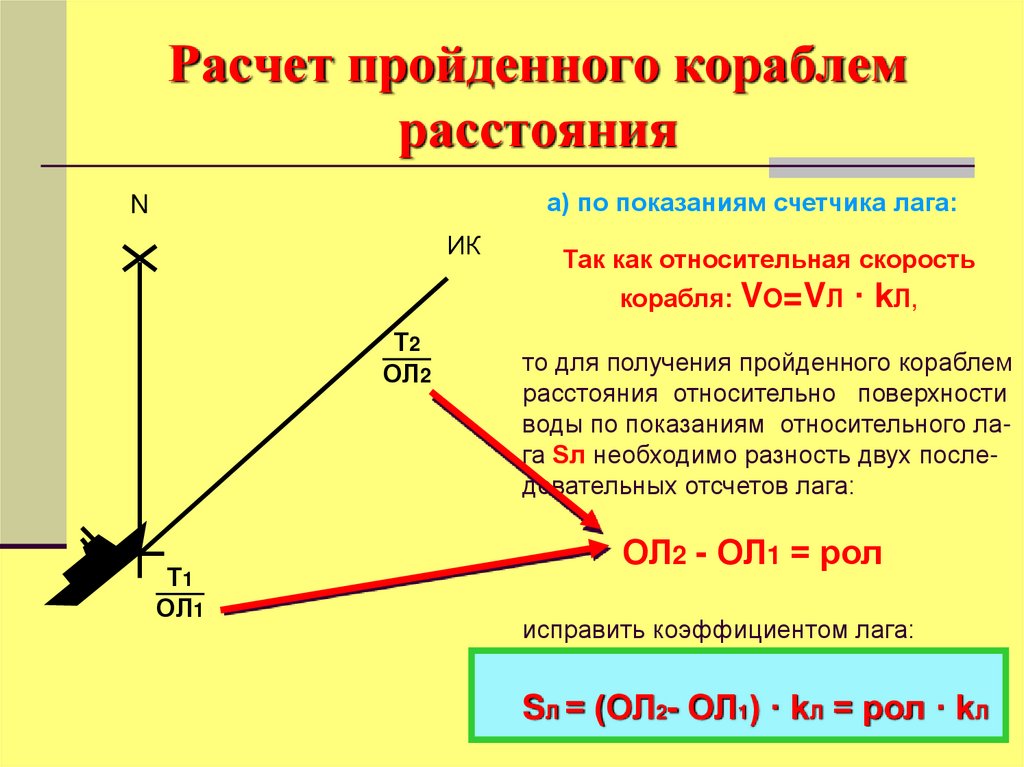
а) по показаниям счетчика лага:
N
ИК
Так как относительная скорость
корабля: VO=VЛ
Т2
ОЛ2
Т1
ОЛ1
· kЛ,
то для получения пройденного кораблем
расстояния относительно поверхности
воды по показаниям относительного лага Sл необходимо разность двух последовательных отсчетов лага:
ОЛ2 - ОЛ1 = рол
исправить коэффициентом лага:
SЛ = (ОЛ2- ОЛ1) · kЛ = рол · kЛ

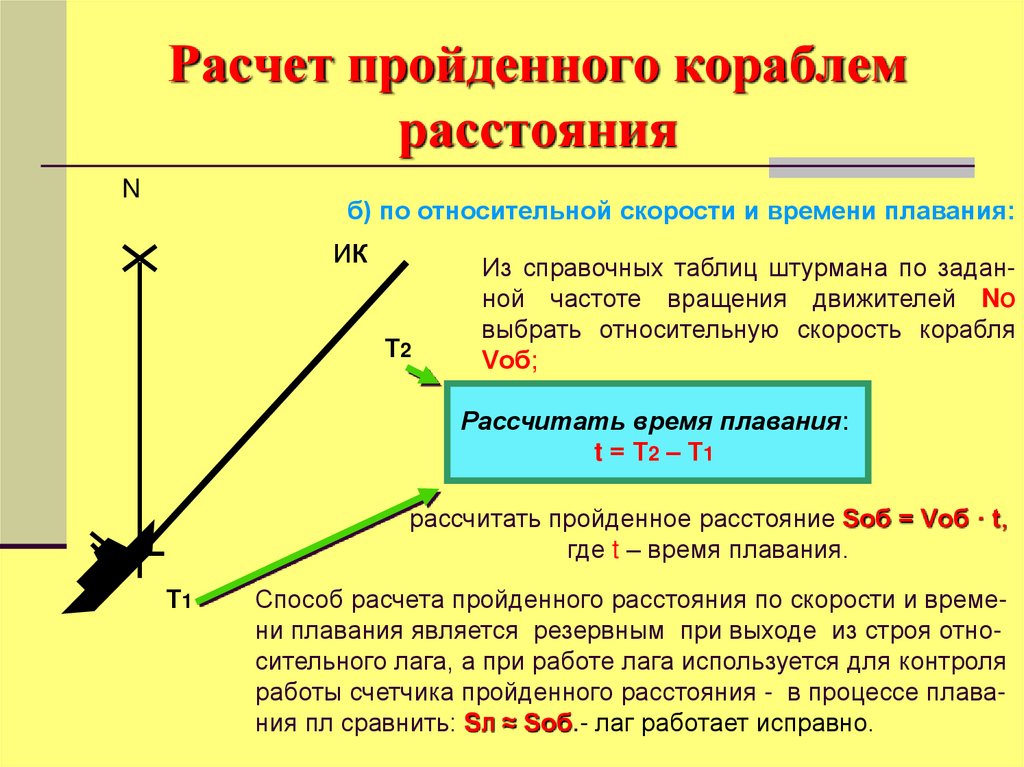
57. Расчет пройденного кораблем расстояния

N
б) по относительной скорости и времени плавания:
ИК
Т2
Из справочных таблиц штурмана по заданной частоте вращения движителей NO
выбрать относительную скорость корабля
Vоб;
Рассчитать время плавания:
t = Т2 – Т 1
рассчитать пройденное расстояние Sоб = Vоб · t,
где t – время плавания.
Т1
Способ расчета пройденного расстояния по скорости и времени плавания является резервным при выходе из строя относительного лага, а при работе лага используется для контроля
работы счетчика пройденного расстояния - в процессе плавания пл сравнить: SЛ ≈ Sоб.- лаг работает исправно.

58. Навигационные опасности. Средства навигационного оборудования

Навигационная опасность – естественный или искусственный подводный или надводный объект, являющийся препятствием для свободного
кораблевождения или ограничивающий возможности маневра корабля.
Навигационная опасность
Естественные
-Мель;
-Отмель;
-Банка;
-Риф;
-Подводная коса;
-Подводная скала
и др.
Искусственные
-Свая;
-Ряж;
-Боно-сетевое заграждение;
-Гидро-технические сооружения;
-Затоновший корабль и др.
Сведения об опасностях – МНК, лоции, руководства для плавания

59. Средства навигационного оборудования

Средства навигационного оборудования (СНО) – специальные сооружения, конструкции или устройства, предназначенные для ориентирования
корабля или для определения его координат в море, а также для ограждения каналов, фарватеров и навигационных опасностей.
Зрительные:
маяки (МК), светящие (несветящие) знаки
(зн) – используются для определения места
корабля:
маяк – сооружение башенного типа с дальностью видимости огня свыше 10 миль;
Маяк Кильдинский - Северный

60. Средства навигационного оборудования

святящий знак – сооружение с дальностью видимости огня менее 10 миль
плавучие
предостерегательные
знаки
(буи, вехи, бакены) – являются средствами
ориентирования и используются для обозначения безопасных путей, навигационных опасностей, мест якорных и карантинных стоянок и т.п
Буй
Веха

61. Средства навигационного оборудования

Звукосигнальные: наутофон (нф),
сирена (с), колокол (к) и др. –
используются для ориентирования в условиях ограниченной видимости и
устанавливаются на маяках, знаках, буях.
Радиотехнические: береговые РЛС, радиомаяки, радионавигационные системы, спутниковые навигационные системы – используются для
определения места корабля.
Гидроакустические:
гидроакустические навигационные системы,
подводные звуковые маяки – используются для определения места пл.
Электромагнитные:
дования фарватеров.
ведущие кабели – используются для обору-

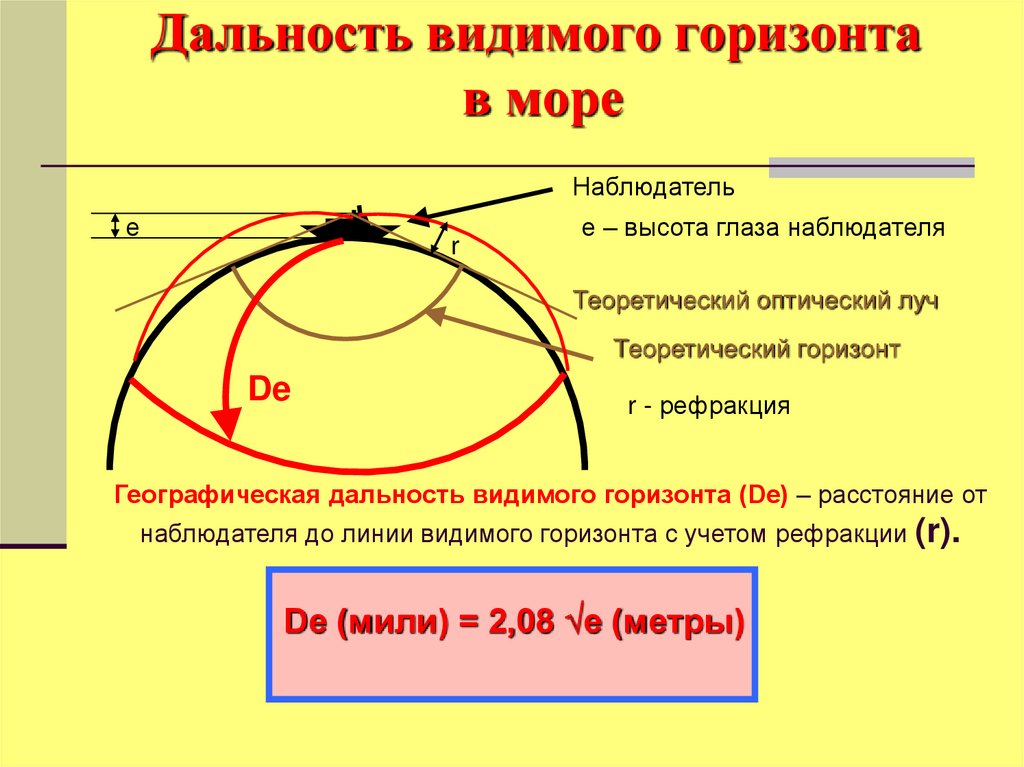
62. Дальность видимого горизонта в море

Наблюдатель
е
r
е – высота глаза наблюдателя
Теоретический оптический луч
Теоретический горизонт
De
r - рефракция
Географическая дальность видимого горизонта (De) – расстояние от
наблюдателя до линии видимого горизонта с учетом рефракции (r).
De (мили) = 2,08 е (метры)

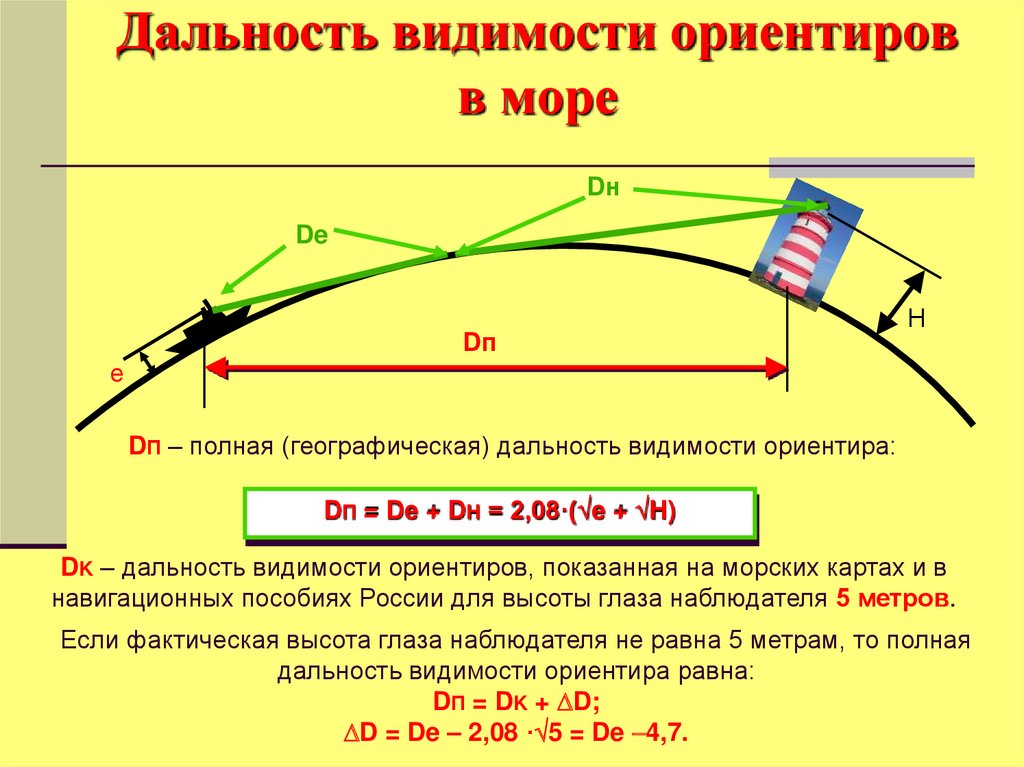
63. Дальность видимости ориентиров в море

Dн
De
Н
Dп
е
DП – полная (географическая) дальность видимости ориентира:
DП = De + DH = 2,08·( e + H)
DK – дальность видимости ориентиров, показанная на морских картах и в
навигационных пособиях России для высоты глаза наблюдателя 5 метров.
Если фактическая высота глаза наблюдателя не равна 5 метрам, то полная
дальность видимости ориентира равна:
DП = DK + D;
D = De – 2,08 · 5 = De 4,7.

64. Общие сведения о картографии

Карта – уменьшенное изображение земной
поверхности на плоскости, выполненное по
определенному математическому закону.
Объемное тело невозможно спроектировать на плоскость без
искажений.
Степень и характер искажений зависит от закона проектирования
Земли на плоскость и
проявляется в непостоянстве масштаба карты.
План – карта ограниченного участка земной
поверхности, полученная без искажений

65. Картографическая проекция

Картографическая проекция – способ проецирования координатных линий (меридианов, параллелей) на
плоскость по определенному математическому закону.
φ
e
Х
q
λ
Y
Картографическая проекция
(математический закон)
X = f1(φ,λ)
Y = f2(φ,λ)

66. Общие сведения о картографии

Картографическая сетка – система координатных линий (меридианов и
параллелей), полученная при данной картографической проекции:
прямая – полюс системы координат совпадает с
географическим полюсом Земли;
поперечная – полюс системы координат отстоит от
географического на угол 90 ;
косая – полюс системы координат отстоит от
географического на угол от 0 до 90 .

67. Общие сведения о картографии Классификация картографических проекций:

а) по характеру искажений:
равноугольные – не искажают углов, сохраняют
подобие фигур на местности и на карте;
равновеликие – не искажают площадей, сохраняют
пропорциональность площадей на местности и на карте;
равнопромежуточные – проекции, сохраняющие
постоянство масштаба по одному из направлений с
экстремальным значением масштаба.
произвольные – проекции, обладающие
специальными свойствами для решения конкретных
задач.

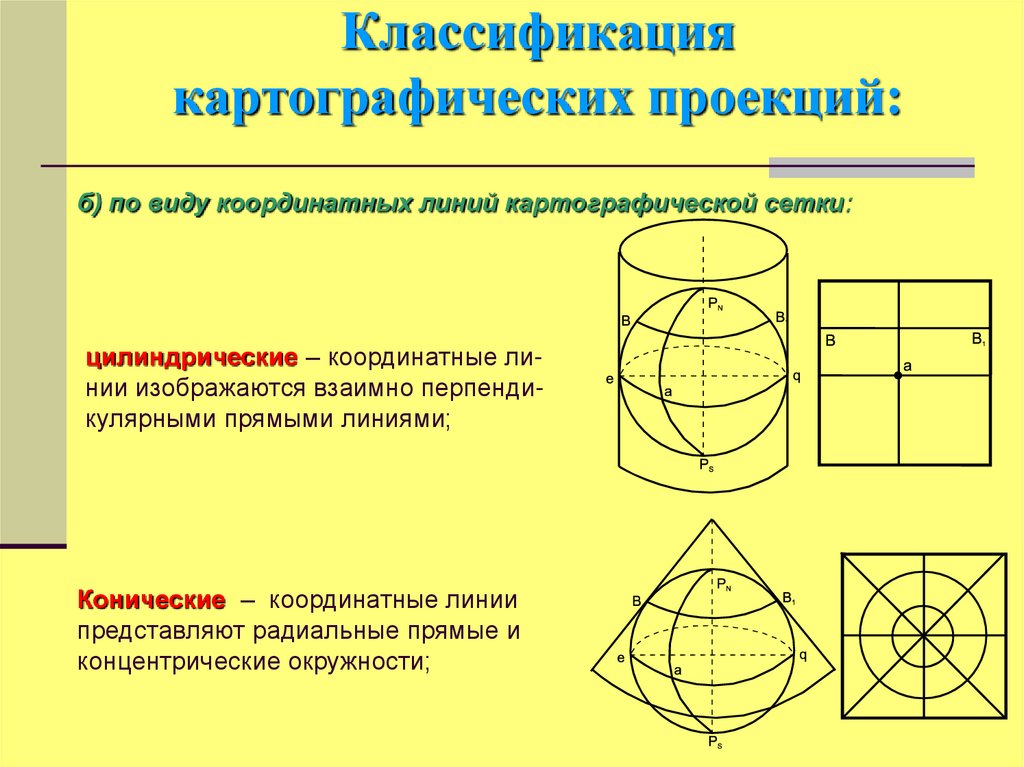
68. Классификация картографических проекций:

б) по виду координатных линий картографической сетки:
цилиндрические – координатные линии изображаются взаимно перпендикулярными прямыми линиями;
Конические – координатные линии
представляют радиальные прямые и
концентрические окружности;

69. Классификация картографических проекций:

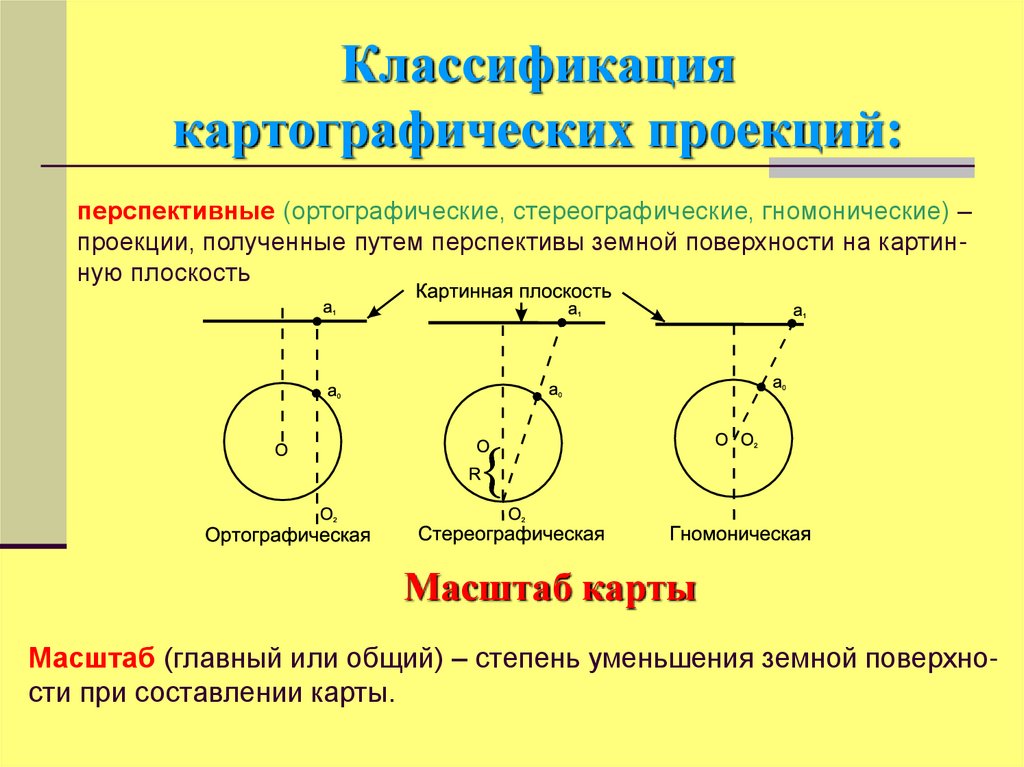
перспективные (ортографические, стереографические, гномонические) –
проекции, полученные путем перспективы земной поверхности на картинную плоскость
Масштаб карты
Масштаб (главный или общий) – степень уменьшения земной поверхности при составлении карты.

70. Масштаб карты

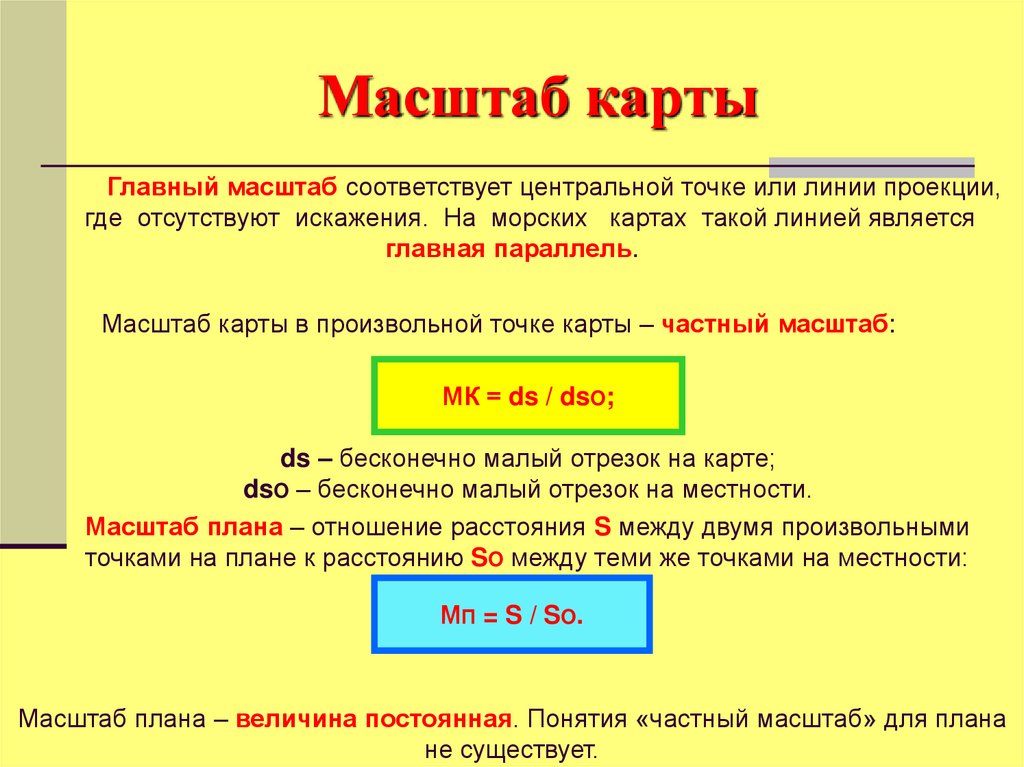
Главный масштаб соответствует центральной точке или линии проекции,
где отсутствуют искажения. На морских картах такой линией является
главная параллель.
Масштаб карты в произвольной точке карты – частный масштаб:
МК = ds / dsO;
ds – бесконечно малый отрезок на карте;
dsO – бесконечно малый отрезок на местности.
Масштаб плана – отношение расстояния S между двумя произвольными
точками на плане к расстоянию SO между теми же точками на местности:
МП = S / SO.
Масштаб плана – величина постоянная. Понятия «частный масштаб» для плана
не существует.

71. Масштаб карты

Числовой масштаб
( 1 / С ) – дробь, числитель которой единица, а
знаменатель (С) – число, показывающее, во
сколько раз уменьшен
участок земной поверхности при отображении
на карте.
Главный
масштаб
соответствует
центральной точке или линии проекции, где отсутствуют искажения.
Линейный
масштаб
показывает, сколько более
крупных единиц длины на
местности содержится в
одной более мелкой единице на карте.
Масштаб карты
Частный масштаб:
Масштаб карты в произвольной точке карты.
Предельная точность масштаба карты (ПТМ) – линейное расстояние на
местности, соответствующее 0,2 мм карты.

72. Прямая равноугольная цилиндрическая проекция Меркатора

При решении задач навигации возникает необходимость отображения на
морской карте линии курса корабля (локсодромии), измерения и прокладки углов и направлений.
Требования к МНК:
1. Локсодромия на карте должна изображаться прямой линией;
2. Углы, измеренные на местности, должны быть равны соответствующим углам, проложенным на карте, т.е. проекция должна быть равноугольной.
Указанным требованиям удовлетворяет прямая
равноугольная цилиндрическая проекция, разработанная в 1569 году голландским картографом
Герардом Кремером (Меркатором).

73. Принцип построения проекции Меркатора

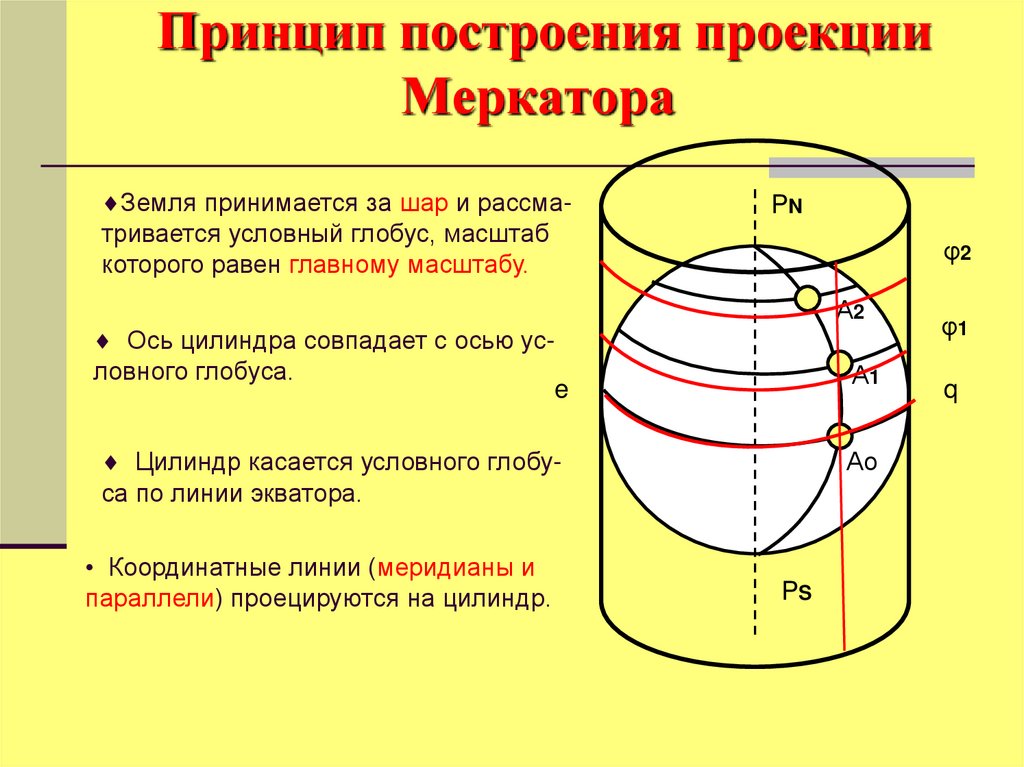
Земля принимается за шар и рассматривается условный глобус, масштаб
которого равен главному масштабу.
PN
φ2
А2
Ось цилиндра совпадает с осью условного глобуса.
e
А1
Цилиндр касается условного глобуса по линии экватора.
• Координатные линии (меридианы и
параллели) проецируются на цилиндр.
Ао
PS
φ1
q

74. Принцип построения проекции Меркатора

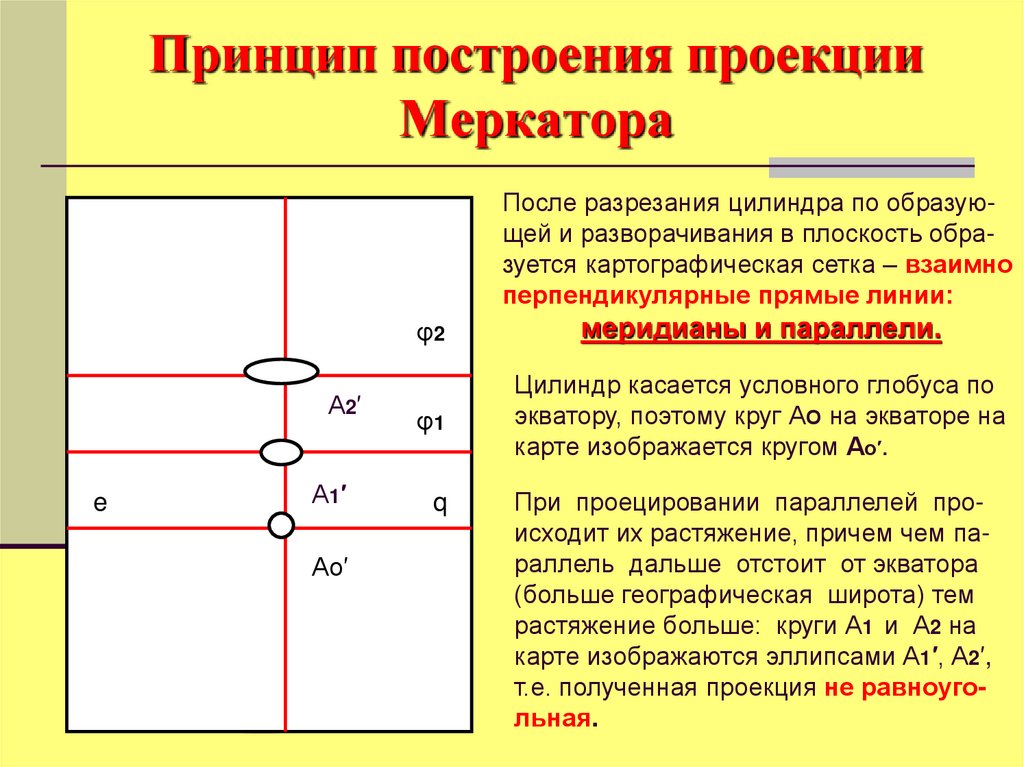
После разрезания цилиндра по образующей и разворачивания в плоскость образуется картографическая сетка – взаимно
перпендикулярные прямые линии:
А2′
e
А1′
Ао′
φ2
меридианы и параллели.
φ1
Цилиндр касается условного глобуса по
экватору, поэтому круг АО на экваторе на
карте изображается кругом Ао′.
q
При проецировании параллелей происходит их растяжение, причем чем параллель дальше отстоит от экватора
(больше географическая широта) тем
растяжение больше: круги А1 и А2 на
карте изображаются эллипсами А1′, А2′,
т.е. полученная проекция не равноугольная.

75. Принцип построения проекции Меркатора

Чтобы эллипсы А1′ и А2′ превратились в круги А1′ , А2′ , необходимо меридиан в каждой точке
вытянуть пропорционально растяжению параллели в данной
точке
φ2
А2′
φ1
e
А1′
Ao
q
Чем больше широта, тем больше
растянута параллель, а следовательно, тем больше должен быть
вытянут меридиан.
В результате одинаковые круги на
глобусе, расположенные на разных
параллелях, на карте изобразятся
кругами разных размеров, увеличивающихся с географической широтой.

76. Принцип построения проекции Меркатора

Полученная таким образом проекция является:
прямой – ось цилиндра совпадает с осью вращения Земли;
равноугольной – элементарный круг на земной поверхности изображается
на карте кругом (сохраняется подобие фигур);
цилиндрической – картографическая сетка (меридианы и параллели) представляет собой взаимно перпендикулярные прямые линии.
Уравнение проекции для шара имеет вид:
x = R ln tg (45 + / 2 ),
y = R .
Графическое изображение на карте одной минуты дуги меридиана (морская миля)
увеличивается с географической широтой.
Следовательно, при измерении и прокладке расстояний необходимо использовать ту часть линейного масштаба карты, в широте которого осуществляется плавание корабля.

77.

Шкала широты
Длина изображения 1′ дуги экватора
в мм – единица карты
Шкала долготы
Единицы длины на меркаторской проекции
W
Длина 1′ дуги меридиана
- Морская миля
Длина дуги параллели
в морских милях –
отшествие (w)
Длина 1′ дуги меридиана
в мм карты – меркаторская
миля
1′ дуги экватора
географическая
или экваториальная миля
Параллель, на которой масштаб
равен главному масштабу, называется главной параллелью.
Широта главной параллели
данной карты указывается в
заголовке карты.