Основные сведения о картографии и картографических проекциях

1.

Основные сведения о картографии и картографических
проекциях.
1. Основные определения. Классификация картографических
проекций.
2. Локсодромия и ортодромия.
3. Меркаторская проекция, меридиональные части, разность
меридианальных частей.
Литература: Ляльков Э.П., Васин А.Г., «Навигация»,
§§ 30 - 36

2.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.
Картография — наука о составлении, производстве и
использовании карт и планов.
Картой называется плоское и искаженное изображение поверхности
Земли или ее частей, на котором искажения подчинены определенному
математическому закону.
Картографической проекцией называется способ, примененный
для условного изображения параллелей и меридианов, подчиненный
определенному математическому закону.
Картографической сеткой называется
изображающих параллели и меридианы на карте.
совокупность
линий,
Планом называется плоское изображение небольшого участка
земной поверхности, на котором искажениями можно пренебречь.

3.

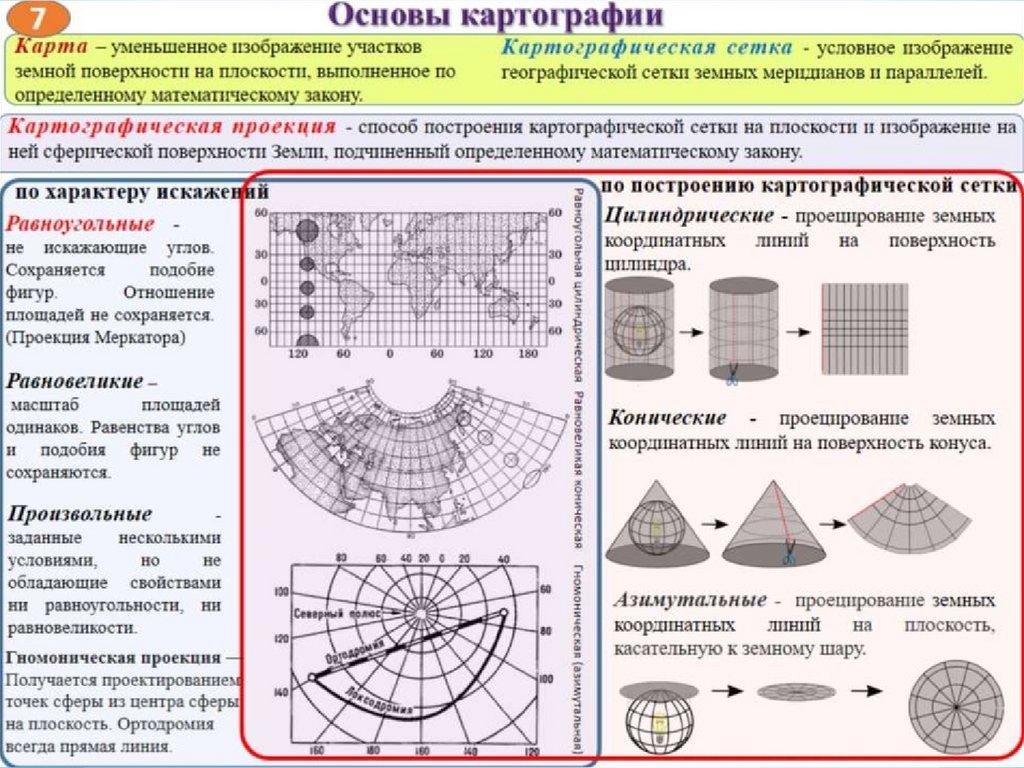
КЛАССИФИКАЦИЯ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ.
По свойству изображений и характеру искажений картографические проекции
бывают равноугольные, равновеликие, или эквивалентные, и произвольные..
Равноугольные проекции сохраняют подобие малых фигур на карте
соответствующим фигурам на поверхности Земли. В таких проекциях углы на карте
между какими-либо направлениями равны углам на местности между теми же
направлениями. Они дают правильное представление о форме участков земной
поверхности, но линейные размеры фигур на них искажены. Так, если взять на
земной поверхности в различных ее местах два одинаковых контура, то на карте
они изобразятся подобными контурами, но с различными размерами.
Равновеликие, или равноплощадные, проекции — это проекции,
сохраняющие пропорциональность площадей фигур на карте и на местности, т. е.
равным площадям на местности будут соответствовать равные площади на карте.
Однако в равновеликой проекции не сохраняется подобие фигур, так как не
сохраняется равенство углов. Остров, имеющий круглую форму на поверхности
Земли, на такой проекции изобразится равновеликим ему эллипсом. Размеры
участков на Земле на сохранение пропорциональности влияния не оказывают. На
картах, составленных в равновеликой проекции, можно измерять площади и
сравнивать их между собой.
Произвольные проекции не сохраняют ни равенство, углов, ни
пропорциональность площадей, но каждая из них обладает особыми свойствами,
необходимыми для выполнения специальных задач.

4.

По
способу
подразделяются
условные.
построения
картографической
сетки
проекции
на азимутальные, конические, цилиндрические и
Цилиндрические проекции — это проекции, в которых картографическую сетку
получают путем проектирования по определенному закону координатных линий земного
сфероида на боковую поверхность касательного или секущего цилиндра с последующей
разверткой этой поверхности в плоскость.
В зависимости от угла, составленного осью цилиндра и осью вращения Земли,
цилиндрические проекции подразделяются на:
● нормальные - ось цилиндра совпадает с осью вращения земного сфероида, а сам
цилиндр касается сфероида по экватору или сечет его по одной из параллелей. В этой
проекции все меридианы - прямые линии, параллельные между собой и
перпендикулярные экватору, а все параллели перпендикулярны меридиану и
параллельны экватору. В зависимости от того, каким выбран закон проектирования,
нормальная цилиндрическая проекция может быть равноугольной, или равновеликой,
или произвольной. Однако на построенной таким образом проекции нельзя изобразить
земные полюсы и чрезвычайно затруднительно изобразить области, расположенные в
широтах свыше 85°. Равноугольная нормальная цилиндрическая проекция
применяется для построения большинства морских карт;
● поперечные - ось цилиндра параллельна плоскости земного экватора;
● косые - ось цилиндра составляет с осью вращения земного сфероида произвольный
угол, отличный от 0 до 90°.

5.

6.

Картографические проекции по способу построения картографической сетки
делятся на:
1.Цилиндрические - проекции, на которых
картографическая сетка меридианов и
параллелей получается путем проецирования
земных координатных линий на поверхность
цилиндра, касающегося условного глобуса (или
секущего его), с последующей разверткой этого
цилиндра на плоскость.
•Прямая цилиндрическая проекция - ось
цилиндра совпадает с осью Земли;
•Поперечная цилиндрическая проекция - ось
цилиндра перпендикулярна оси Земли;
•Косая цилиндрическая проекция - ось
цилиндра расположена к оси Земли под углом
отличным от 0° и 90°.

7.

2.Конические - проекции, на которых
картографическая сетка меридианов и
параллелей получается путем проецирования
земных координатных линий на поверхность
конуса, касающегося условного глобуса (или
секущего его), с последующей разверткой
этого конуса на плоскость. В зависимости от
положения конуса относительно оси Земли
различают:
•Прямую коническую проекцию - ось
конуса совпадает с осью Земли;
•Поперечную коническую проекцию - ось
конуса перпендикулярна оси Земли;
•Косую коническую проекцию - ось конуса
расположена к оси Земли под углом отличным
от 0° и 90°.

8.

3.Азимутальные - проекции, в которых
меридианы - радиальные прямые,
исходящие из одной точки (центральной),
под углами равными соответствующим
углам в натуре, а параллеликонцентрические окружности,
проведенные из точки схождения
меридианов (ортографические, внешние,
стереографические, центральные,
полярные, экваториальные, горизонтные).

9.

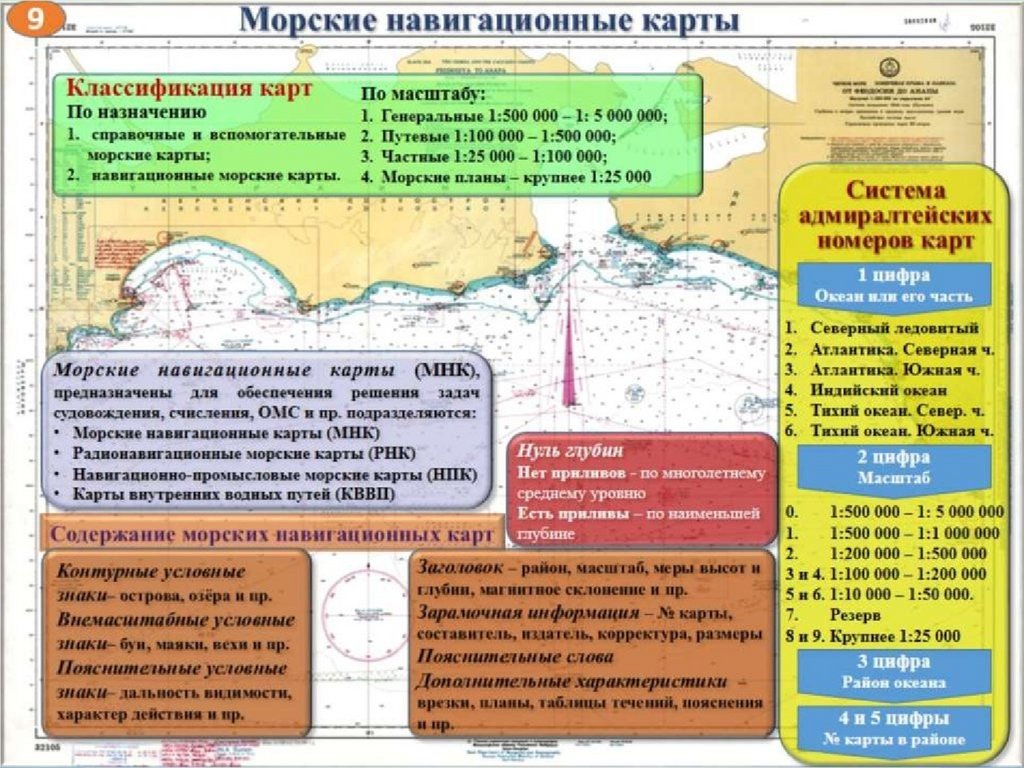
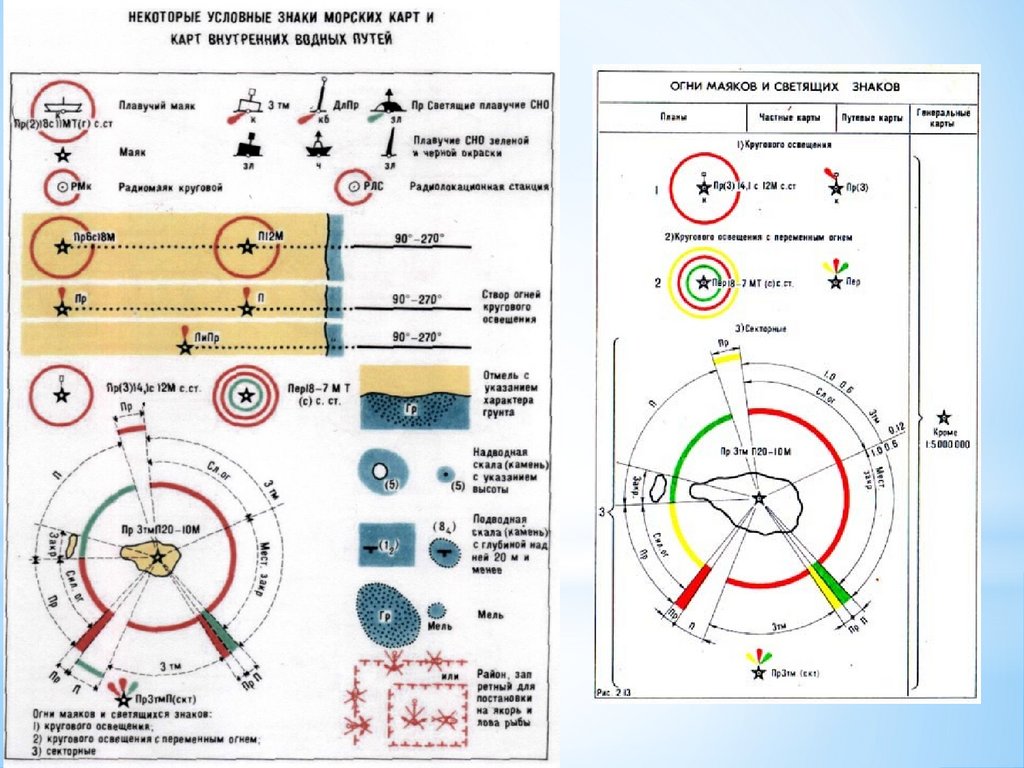
ТРЕБОВАНИЯ
ПРЕДЪЯВЛЯЕМЫЕ К МОРСКОЙ НАВИГАЦИОННОЙ КАРТЕ
Морские навигационные карты предназначаются для ведения на них
графического учета движения судна.
К морским навигационным картам предъявляются следующие требования.
1. Линия пути судна, идущего постоянным курсом, должна изображаться на
морской карте прямой линией, следовательно, все меридианы и параллели на ней
необходимо иметь взаимно параллельными, ибо прямая линия, изображающая
постоянный путь судна, должна пересекать их под одним и тем же углом. Выполнение
условия параллельности меридианов и параллелей можно получить лишь с помощью
цилиндрической проекций.
2. Углы на морской карте должны быть равны соответствующим углам на земной
поверхности, т. е. проекция должна быть равноугольной, при которой форма фигур на
местности соответствует форме фигур на карте. Это же облегчит опознание берега по
его изображению на карте.
3. Масштаб на карте должен изменяться в возможно малых пределах.

10.

Такую проекцию, в достаточной степени удовлетворяющую перечисленным
требованиям, в 1569 г. предложил голландский картограф Герард Кремер, известный
более под именем Меркатора. Поэтому проекция, предложенная им, получила
название меркаторской.
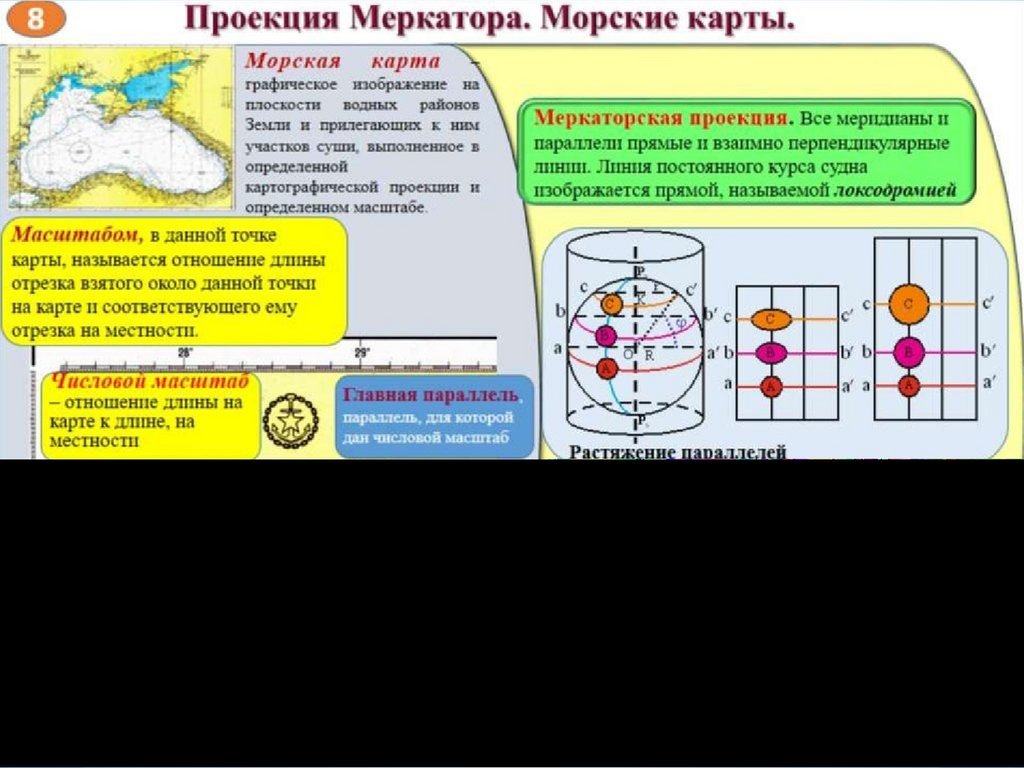
Меркаторская проекция — это нормальная равноугольная цилиндрическая
проекция, в которой все меридианы изображены прямыми параллельными линиями,
а параллели — прямыми, пересекающими меридианы под прямыми углами.
Меркаторская проекция нашла широкое применение в судовождении, и в настоящее
время навигационные карты во всех странах мира строятся в основном в этой
проекции.

11.

12.

ПОСТРОЕНИЕ МЕРКАТОРСКОЙ ПРОЕКЦИИ
Представим себе земной шар или глобус с нанесенными на него
линиями меридианов и параллелей. Обернем его бумажным
цилиндром, ось которого совпадает с земной. Такой цилиндр будет
касаться земного шара только по экватору
Для получения меркаторской проекции необходимо спроектировать меридианы и
параллели земного шара на внутреннюю поверхность этого касательного цилиндра.
Проектирование произведем следующим образом. Разрежем меридианы в полюсах
Рn и Ps и будем выпрямлять их, не выводя из той плоскости, в которой они находятся,
до тех пор, пока по всей своей длине они не расположатся на внутренней поверхности
цилиндра. При этом длина меридианов не изменится и они станут параллельными
друг другу.

13.

В результате таких действий каждая параллель будет тоже доведена до внутренней
поверхности цилиндра, но параллели растянутся и станут по длине равными
экватору и параллельными ему. Параллели, близкие к экватору, растянутся немного,
но с увеличением широты места это растяжение будет все значительнее.

14.

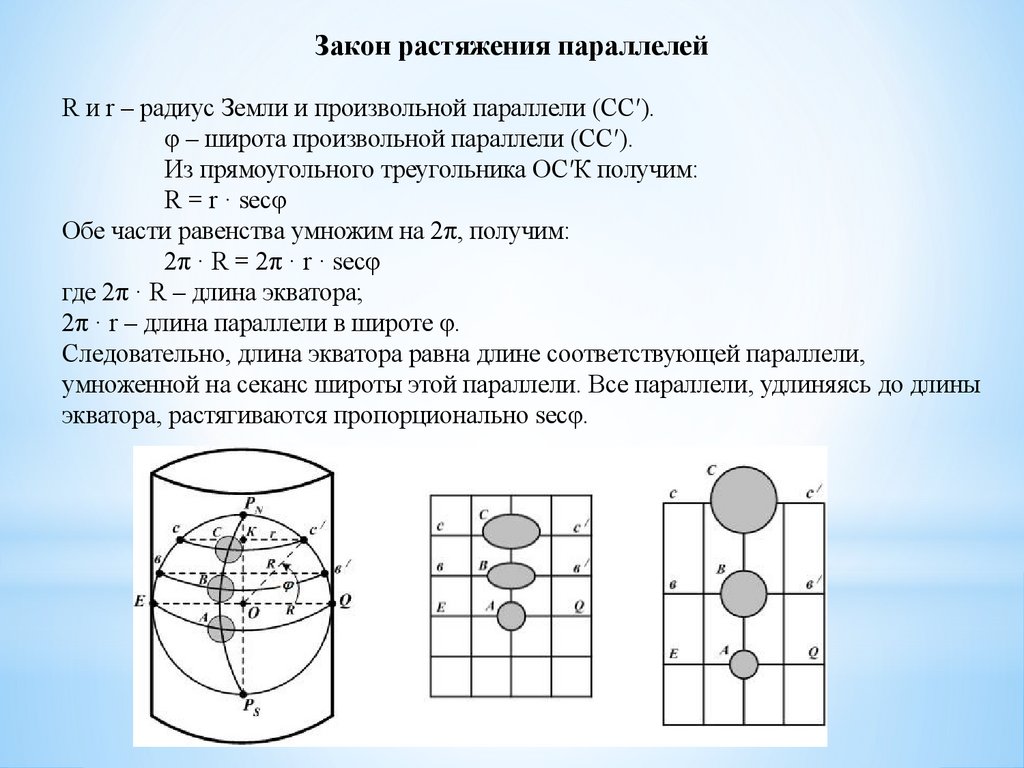
Закон растяжения параллелей

15.

Чтобы она стала равноугольной, надо и малую ось увеличить так, как увеличилась
большая, т. е. пропорционально sec φ. Этим самым будут приравнены масштабы по
меридиану и параллели.
Если произвести подобного рода построения для всей земной поверхности,
ограниченной данной проекцией, то получим достаточно верное изображение Земли
на плоскости, при котором бесконечно малый эллипс, вытянувшись по малой оси,
пропорционально sec φ примет вид круга.
Полученная проекция теперь удовлетворяет всем основным требованиям: она
равноугольна, локсодромия изображается прямой линией, масштаб в границах
карты будет изменяться в малых пределах. Эго и есть меркаторская проекция.

16.

Масштаб на карте не является постоянным – он увеличивается от экватора к
полюсам (как обратный косинус широты). Но масштабы по вертикали и по
горизонтали всегда одинаковы, чем, собственно, и достигается равноугольность
проекции. На картах в данной проекции всегда указывается, к какой параллели
относится основной масштаб карты. НЕДОСТАТОК
Из-за непостоянства масштаба от экватора к полюсам карта не сохраняет площади
объектов. НЕДОСТАТОК
К НЕСОМНЕННЫМ ДОСТОИНСТВАМ НУЖНО ОТНЕСТИ:
• Удобство прокладки курса - путь судна, идущего одним и тем же курсом, т.е.
под одним и тем же углом к меридиану, отображается в виде прямой линии, т.е.
прямая линия, проведенная в произвольном направле­нии, является линией
постоянного курса (пересекает мериди­аны под одинаковым углом и называется
локсодромией - греч. «кривой бег»).Кроме того простота нанесения на нее точек.
• Север на карте всегда вверху, соответственно юг внизу, запад слева, восток
справа.
• Удобство измерения расстояний, поскольку масштабы карты по вертикали и
горизонтали одинаковы.
Именно поэтому меркаторскую проекцию и применяют для
навигационных карт.

17.

ПОНЯТИЕ
О ЛОКСОДРОМИИ И ОРТОДРОМИИ.
Локсодромия в переводе с греческого
означает «косой бег».
Локсодромия – линия постоянного
курса.
На морской навигационной карте в
проекции Меркатора – прямая линия,
пересекающая меридианы под одним и
тем же углом КЛОК = const
При плавании судна на небольшие
расстояния (сотни миль) и ведении
Локсодромия и ее элементы на сфере:
графического счисления пути судна на
при КЛОК = 0°(180°) она совпадает с
карте в проекции Меркатора удобно
меридианом (λ = const);
выполнять это плавание по
при КЛОК = 90°(270°) она совпадает с
локсодромии – линии постоянного
параллелью (φ = const);
курса, несмотря на то, что это и не
при КЛОК = 90°(270°) и φ = 0° – она
кратчайшее расстояние между двумя
совпадает с экватором;
при КЛОК ≠ 0°(180°) и КЛОК ≠ 90°(270°) – заданными точками. Плавание по
она представляет из себя логарифмическую локсодромии, т. е. постоянным курсом,
удобно, так как не требует проведения
спираль, стремящуюся к ближайшему
каких-либо расчетов, связанных с
полюсу и обращенную выпуклостью к
частой переменой курсов
экватору

18.

Ортодромия и ее элементы
• При курсе судна 0°(180°) –
локсодромия и ортодромия
«сливаются» в одну линию,
совпадающую с географическим
меридианом.
• При курсе судна 90°(270°) при φ = 0° –
также «сливаются» в одну линию,
совпадающую с земным экватором.
• При плавании судна на большие
расстояния (тысячи миль) экономно
плыть по ортодромии, так как это –
кратчайшее расстояние между
заданными точками.
ОРТОДРОМИЯ
(Great
Circle)
называется дуга большого круга,
являющаяся кратчайшим расстоянием
между двумя точками на поверхности
земного шара.и пересекает мередианы
под разными углами обращенная (на
МНК
в
проекции
Меркатора)
выпуклостью к ближайшему полюсу
На картах в гномонической проекции –
прямая линия.
Ортодромия в навигации имеет очень
большое значение, поскольку на сфере
она играет такую же роль, как прямая
линия - на плоскости.
Меридианы и экватор являются
частными случаями ортодромии. Через
любые две точки, не лежащие на
противоположных концах одного и того
же диаметра сферы, можно провести
только одну ортодромию.

19.

Меридиональные части.
Разность меридиональных частей.
Меридиональная часть (МЧ) – это расстояние на меркаторской проекции от
экватора до параллели с заданной широтой φ при масштабе на экваторе, равном
единице.
Для навигации МЧ удобнее всего выражать через 1′ дуги экватора, т.е. в
экваториальных милях. в МТ – 75 составлена табл. 26, в которой приведены
значения МЧ для широт от 00 до 89059′ через интервал в 1′ широты. Для нахождения
промежуточных значений МЧ на каждую десятую долю минуты широты достаточно
проинтерполировать их ближайшие табличные значения.
Разность меридиональных частей (РМЧ) – это расстояние по меридиану между
двумя параллелями, выраженное в экваториальных милях. Для расчета РМЧ
необходимо по табл.26 выбрать МЧ для каждой параллели φ и произвести
вычитание:
РМЧ = МЧ2 – МЧ1

20.

МАСШТАБЫ КАРТ
Части земной поверхности изображаются на картах и планах с заранее заданным
уменьшением.
Степень уменьшения изображенных на карте размеров земной поверхности
называется масштабом.
Масштаб карты определяется отношением длины расстояния между двумя
точками на карте к действительному горизонтальному расстоянию между теми же
точками на местности, причем оба расстояния должны быть выражены в одних и
тех же единицах.
Существует несколько видов масштабов, основные из которых численный и
линейный.
Численный масштаб представляет собою дробь, числитель которой единица, а
знаменатель — число, показывающее, скольким единицам длины на местности равна
одна единица длины на карте или плане.
Если указано, что масштаб в данной точке карты равен 1 : 100 000, то это значит,
что 1 см на карте в этом районе соответствует расстояние на местности, равное 100
000 см.
Если знаменатель численного масштаба выражается большим числом, например 1 :
5 000 000, то такой масштаб называется мелким, если знаменатель численного
масштаба выражается небольшим числом, например
1 : 10 000, то такой масштаб называют крупным. В зависимости от величины
знаменателя
масштаба
морские
карты
условно
подразделяются
на
мелкомасштабные и крупномасштабные.

21.

Численный масштаб достаточно просто позволяет решить основную задачу:
зная расстояние на карте, можно вычислить горизонтальное расстояние
между этими же точками на местности

22.

Линейный
масштаб
представляет
собою
графическое
или
числовое
соответствие числа крупных единиц на местности числу мелких на карте.
В первом случае линейный масштаб изображается прямой линией (на морских
картах обычно его наносят на вертикальной рамке карты), разбитой на мелкие
деления выбранной длины. На отметках делений надписывают числа крупных
единиц длины, в которых измеряется расстояние на местности.
Часто мелкие деления на карте в свою очередь делят еще на части для снятия
более точных отсчетов.
При числовом задании линейного масштаба соответствие числа единиц на
местности числу мелких единиц на карте определяется выражением, например, «2
мили в 1 см» или «3 км в 1 см».
Переход от численного масштаба к линейному осуществляется простым
пересчетом мер длины.

23.

Чтобы перейти от численного масштаба к линейному, надо знаменатель
численного масштаба разделить на 185 200 и полученный результат
укажет количество миль и долей мили в 1 см
Чтобы перейти от линейного масштаба к численному, надо число миль
линейного масштаба, содержащихся в 1 см, умножить на 185 200 и
полученный результат даст знаменатель численного масштаба.

24.

Предельная точность масштаба — это наименьшее расстояние на местности,
которое может быть измерено по карте.
Установлено, что люди с нормальным зрением в состоянии различать без
увеличения предельную длину 0,2 мм — это укол ножки циркуля или тонко
очиненного карандаша. Следовательно, эта величина избудет определять предельную
точность масштаба любой карты.
Для определения предельной точности масштаба данной карты надо знаменатель
численного масштаба, выраженный в сантиметрах, умножить на 0,02 см (0,2 мм) и
результат перевести в метры или другие необходимые единицы длины. Однако проще
использовать следующее правило: в знаменателе численного масштаба отделить
запятой последние четыре цифры и удвоить полученное число. Ответ получается в
метрах

25.

При наличии линейного масштаба предельную точность масштаба можно
вычислить, пользуясь правилом: количество миль, соответствующее 1 см карты,
разделить на 50. Ответ получается в милях.

26.

27.

28.

Принцип построения проекции Меркатора:
1. Земля принимается за шар и рассматривается условный глобус, масштаб
которого равен главному масштабу.
2. Координатные линии (меридианы и параллели) проецируются на цилиндр.
3. Ось цилиндра совпадает с осью условного глобуса.
4. Цилиндр касается условного глобуса по линии экватора.
5. Меридианы и параллели условного глобуса проецируются на поверхность
цилиндра таким образом, чтобы их проекции оставались в плоскотях
меридианов и параллелей.
6. После разрезания цилиндра по образующей и разворачивания в плоскость
образуется картографическая сетка — взаимноперпендикулярные прямые
линии: меридианы и параллели.

29.

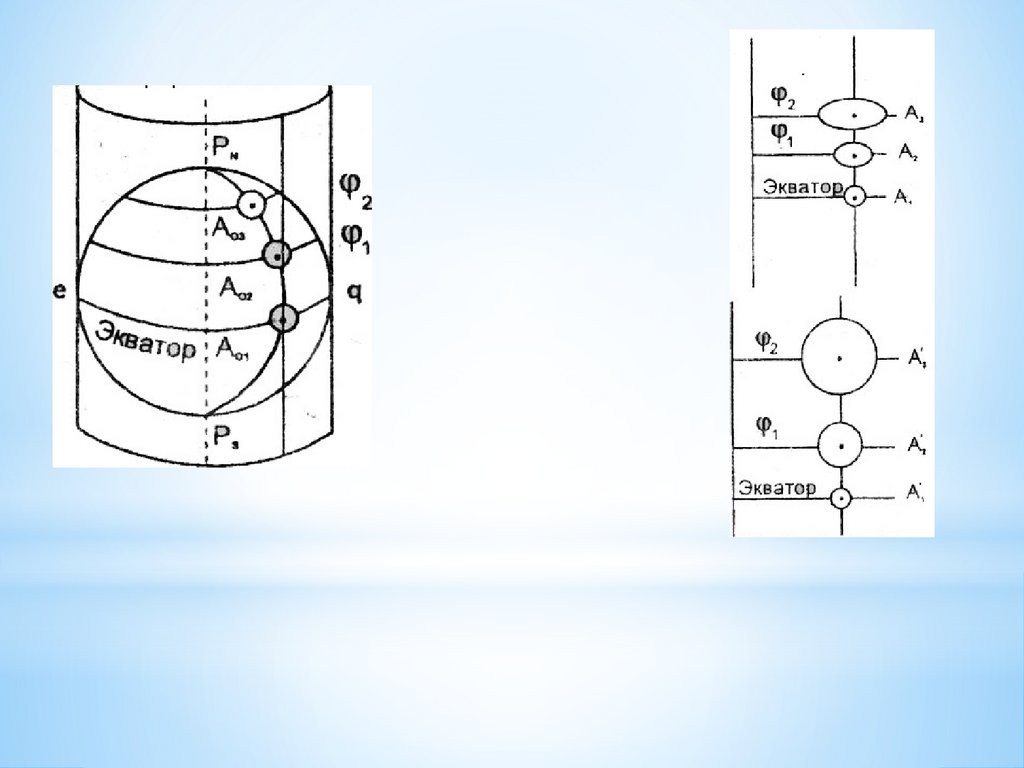
7. Цилиндр касается условного глобуса по экватору, поэтому круг Ao1
на экваторе на карте изображается кругом A1.
8. При проецировании параллелей происходит их растяжение, причем чем
параллель дальше отстоит от экватора (больше географическая широта)
тем растяжение больше: круги Ао2 и Ао3 на карте изображаются эллипсами
А2, А3, т. е. полученная проекция не равноугольная.
9. Чтобы эллипсы А2 и Аз превратились в круги А2' А3' неооходимо
меридиан в каждой точке вытянуть пропорционально растяжению
параллели в данной точке.
Чем больше широта, тем больше растянута параллель, а следовательно,
тем больше должен быть вытянут меридиан
10. В результате одинаковые круги на глобусе, расположенные на разных
параллелях, на карте изобразятся кругами разных размеров,
увеличивающихся с географической широтой.

30.

31.

32.

При получении проекции главный масштаб соответствовал главному
масштабу условного глобуса, т е. при проецировании на цилиндр
искажения отсутствовали на линии, по которой цилиндр касался
глобуса — на экваторе.
При изготовлении карт в данной проекции это оказалось недостаточно
удобным. Поэтому для каждой широтной зоны выбрали линию
проекции, на которой отсутствуют искажения — главную параллель.
Параллель, на которой масштаб равен главному масштабу, называется
главной параллелью. Широта главной параллели данной карты
указывается в заголовке карты.
Единицы измерения на Меркаторской проекции

33.

34.

Закон растяжения параллелей
R и r – радиус Земли и произвольной параллели (СС′).
φ – широта произвольной параллели (СС′).
Из прямоугольного треугольника ОС′К получим:
R = r · secφ
Обе части равенства умножим на 2π, получим:
2π · R = 2π · r · secφ
где 2π · R – длина экватора;
2π · r – длина параллели в широте φ.
Следовательно, длина экватора равна длине соответствующей параллели,
умноженной на секанс широты этой параллели. Все параллели, удлиняясь до длины
экватора, растягиваются пропорционально secφ.

35.

Если разрезать цилиндр по одной из образующих, то получим на плоскости
прямоугольную сетку меридианов и параллелей, расположенных на одинаковых
расстояниях друг от друга.
На такой сетке локсодромия, пересекающая все меридианы под одинаковым углом,
изобразится также прямой линией, так как все меридианы параллельны. Однако
полученная проекция удовлетворяет пока только одному этому условию. Дело в том, что
параллели на ней растянулись пропорционально секансу широты, в то время как
величина меридианов осталась неизменной.
В связи с этим бесконечно малый круг на земной поверхности К изобразится в виде
эллипса на проекции, большая ось которого будет растянута пропорционально sec φ по
сравнению с малой осью. Но это значит, что полученная проекция получилась
неравноугольной.