Позиционные системы счисления, отличные от десятичной

1. Позиционные системы счисления отличные от десятичной

Лекция 4

2.

• Основанием позиционной системы
счисления может быть любое число
p≥2.
• P=2 – двоичная система
• P=3 – троичная система
• P=8 – восьмеричная система

3. Определение

• Записью натурального числа x в
системе счисления с основанием p
называется его представление в виде:
x an p n an 1 p n 1 an 2 p n 2 ... a1 p a0
где коэффициенты a n , a n 1 ,..., a1 , a0
принимают значения 0,1,2,…,p-1 и
an≠ 0

4. Теорема

• Пусть p≥2 – заданное натуральное число.
Тогда любое натуральное число x
представимо, и притом единственным
образом в виде:
n 1
x an p an 1 p an 2 p
n
n 2
... a1 p a0
____________
Краткая запись числа x =
an an 1 ...a1a0 p

5. Доказательство:

n
p
• 1. Разделим число x на
Имеем:
Далее
x an p n x1
x1 an 1 p
n 1
x2
i
Процесс деления остатка на p основание системы – конечен.
Следовательно, число x представимо в виде
суммы разрядных слагаемых.

6.

• 2. Единственность представления
числа х в виде суммы разрядных
слагаемых следует из единственности
деления с остатком.

7. Например:

• В троичной системе (p=3)
x 2 3 0 3 1 3 2
3
2
можно записать в виде:
x 20123
Читать следует так: «два, ноль, один, два
в троичной системе счисления»

8.

• На числовой прямой троичная система
счисления может быть представлена:
100
х
0 1 2 10 1112 20 21 22

9.

• Сравнение чисел и арифметические
действия в любой «p-ичной» системе
счисления выполняются так же как и в
десятичной.
Надо лишь иметь для системы с основанием p
соответствующие таблицы сложения и
умножения однозначных чисел

10. Задание №1

• Сравнить числа x и y, если
x 2110 3
y 20113
Следовательно, x>y
т.к. выполняется 3 условие теоремы о
сравнении чисел в десятичной системе
счисления.

11. Задание №2 Найти сумму чисел в троичной системе.

Запишем числа согласно алгоритму
сложения
1 2 23
2 0 23
_________
Используя таблицу сложения в троичной системе,
имеем:

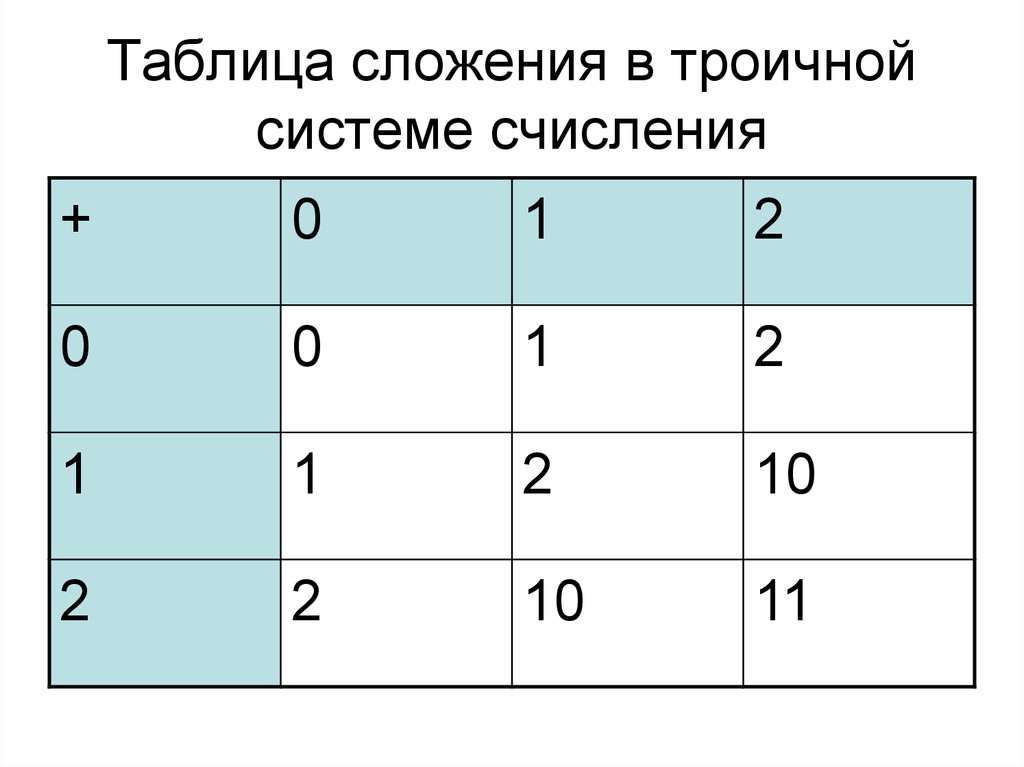
12. Таблица сложения в троичной системе счисления

+
0
1
2
0
0
1
2
1
1
2
10
2
2
10
11

13.

Применив, таблицу сложения, имеем:
1 2 23
2 0 23
___________
1 1 0 13

14. Задание № 3

• Запишите следующие числа в виде
суммы разрядных слагаемых.
• а= 2357
• b = 4302 5
• c= 567038

15. Ответ:

• 1) а= 2 10 5 10 3 10 7
3
2
• 2) b= 4 5 3 5 2
3
2
• 3)c= 5 8 6 8 7 8 3
4
3
2

16. Задание №4. Запишите в десятичной системе числа:

x 2110 3
1.
Число
2.
Число y=
4302 5

17. Ответы:

• Число
x 2 3 1 3 1 3 0
3
2
2 27 1 9 3 66
• Число
y 4 5 3 5 2
3
2
4 125 3 25 2
500 75 2 577

18. Вывод:

Чтобы число, записанное в p-ичной
системе, представить в десятичной,
нужно:
1. Записать число в виде суммы
разрядных слагаемых в p-ичной
системе счисления.
2. Выполнить записанные действия в
десятичной системе счисления.

19. Задание №5. Запишите число в p-ичной системе счисления:

• Число 35 в двоичной системе
счисления;
• Число 124 в пятеричной системе
счисления

20. Ответ :

• Разделим число 35 на 2 – основание системы.
Имеем: 35=2·17+1
• Затем-частное 17разделим на 2-основание системы
Имеем: 17=2·8+1
• Затем частное 8 разделим на 2
Имеем: 8=2·4+0
• Затем частное 4 разделим на2
Имеем: 4=2·2+0
• Затем частное 2 разделим на 2
Имеем: 2=2·1+0.
• Последнее частное 1 меньше делителя 2.
• Процесс деления закончен

21.

Выпишем последнее частное и остатки,
начиная с последнего.
Следовательно: 35=
1000113

22. Ответ:

• Разделим 124 разделим на 5
Имеем: 124=5·24+4
• Разделим частное 24 на 5
Имеем 24=5·4+4
Последнее частное 4 <5.
Деление закончено

23.

• Следовательно: 124=
444 5

24. Вывод: чтобы число, записанное в десятичной системе счисления, представить в p-ичной нужно:

1. Число х разделить (в десятичной
системе счисления) на p- основание
системы счисления с остатком.
Первый остаток – есть последняя
значащая цифра числа х в p-ичной
системе счисления.

25.

2. Первое неполное частное снова делят
на p- основание системы счисления с
остатком.
Второй остаток – есть следующая слева
значащая цифра числа х в p-ичной
системе счисления.
3. Процесс деления продолжаем, пока
Неполное частное не станет меньше p.

26.

4. Первой значащей цифрой числа х
является последнее частное.
5. Второй значащей цифрой числа х
является последний остаток.
Замечание: остатки могут принимать
значения 0, 1,2,…,p-1.

27.

Спасибо за внимание