Similar presentations:
Запись числа в десятичной системе счисления
1.
Запись числа в десятичнойсистеме счисления
Лекция 2
2.
Система счисления – язык длянаименования и записи чисел и
выполнения действий над ними.
3.
• Непозиционные системы счисленияхарактеризуются тем, что каждый знак
всегда обозначает одно и тоже число.
• Например, в римской системе
счисления:
• I – один
• III – один да один, да один равно три
• IV, VIII, IX, XII, CXXI, MMXI
4.
• В России до XVII в. Использоваласьславянская непозиционная нумерация.
• Числа в такой нумерации обозначались
буквами славянского алфавита, над
которыми ставили особый знак – титло.
5.
В России славянская нумерация сохранилась до конца XVII в. ПриПетре I возобладала так называемая арабская нумерация, которой
мы пользуемся и сейчас. Славянская нумерация сохранялась
только в богослужебных книгах.
6.
• В позиционных системах один и тот жезнак может обозначать различные
числа в зависимости от места(позиции)
• Например: 1111,
343434,
2342342
7.
Запись чисел в десятичнойсистеме счисления
Десятичная система счисления
класс миллиардов
разряд
сотен
разряд
десятко
в
разряд
единиц
класс миллионов
разряд
сотен
разряд
десятко
в
разряд
единиц
класс тысяч
разря
д
сотен
разря
д
десятк
ов
разряд
единиц
класс единиц
разря
д
сотен
разря
д
десят
ков
разряд
единиц
1
1
3
5
2
0
4
1
0
1
0
0
8
4
7
8.
Правила нумерации• Правило прочтения чисел:
• 1. Раздели число на классы справа налево. Каждый класс должен содержать
три разряда. Только старший класс
может быть неполным.
• 2. Сначала называем разряды старшего
класса и название класса. Затем
называем разряды и название
следующего класса и т. д.
9.
Правило записи числа• 1. Записываем цифры старшего класса.
• 2. Затем, цифры младших классов,
помня о том, что каждый следующий
класс должен быть полным.
10.
• Например:• Три миллиона двести сорок пять тысяч
шестнадцать.
3___ ___
3 245
016
11.
• Основа записи чисел в десятичнойсистеме
1 1 10
0
10 1 10
1
100 1 10
2
10
...
0 1 10
n
n
12.
Определение.• Десятичной записью натурального
числа х называется представление в
виде:
n
n
1
x
a
10
a
10
...
a
10
a
n
n
1
1
0
где коэффициенты аi принимают значения
0,1,2,3,4,5,6,7,8,9 и аn ≠0
13.
Теорема 1• Любое натуральное число х можно
представить в виде суммы разрядных
слагаемых.
n
1
x
a
10
a
10
...
a
10
a
n
n
1
1
0
n
14.
Доказательство существования записичисла.
• Пусть
n
n
1
x
a
10
a
10
...
a
10
a
n
n
1
1
0
n
n 1
10
x 10
тогда
Разделим число x : 10 n
Имеем
где
n
x 10
a
x
n
1
n
1
n
10
x1 10
15.
• Продолжим деление.где
n
1
x
10
a
x
1
n
1
2
n
2
n
1
10
x
10
2
В результате имеем
n
n
1
x
10
a
10
a
x
n
n
1
2
Процесс деления конечен, так как x x
...
1 x
2
Последний неравный нулю остаток
обозначим a0.
ч.т.д.
16.
Доказательство единственности.• Старшая степень числа x определяется
однозначно.
• Деление с остатком также однозначно.
• Следовательно, представление числа в
виде суммы разрядных слагаемых
также однозначно.
17.
Сравнение натуральныхчисел
• Теорема2: Пусть x и y – натуральные
числа, запись которых дана в
десятичной системе счисления:
n
n
1
n
2
x
a
10
a
10
a
10
...
a
10
a
n
n
1
n
2
1
0
m
m
1
b
2
y
b
10
b
10
b
10
...
b
10
b
m
m
1
m
2
1
0
18.
1.n m
2.
n m
,an bn
3.
n
m
,a
b
...
a
b
n
n
k
k
19.
• Например:• 1. 34 < 341
• 2. 628 < 828
• 3.65734 < 65794
20.
Доказательствоn
1
• 1) Если n
m
,
10
10
n
1
m
x
10
10
y
Следовательно x<y
m;то
21.
• 2) Если n=m,тогда
Значит,
но
a n bn
то
an 1 bn
n
n
a
10
1
b
10
n
n
n
n
x
a
1
10
b
10
y
n
n
Следовательно x<y
22.
Например:• 1) x=54267; y=5426
x= 345; y= 2314
2) a=6789;
a=1245;
b=5789
b=3245
3) m=3456; n=3421
m=1454; n=1458
23.
Алгоритм сложенияx=345; y=598. Найдем сумму чисел х+y:
345+ 598= (300+40+5)+(500+90+8)=
(300+500)+(40+90)+(5+8)=
800+130+13=
800+(100+30)+(10+3)=
(800+100)+(30+10)+3 =900+40+3=943
24.
В основе алгоритма сложения многозначныхчисел лежат следующие теоретические
факты:
1. Способ записи чисел в десятичной
системе счисления;
2. Коммутативный и ассоциативный
законы сложения натуральных чисел;
3. Дистрибутивный закон умножения
относительно сложения;
4. Таблица сложения однозначных чисел.
25.
Рассмотрим алгоритм сложения многозначныхчисел в общем виде (для чисел x и y)
• Пусть числа x и y в общем виде:
x
a
10
a
10
a
2
1
0
2
y
b
10
b
10
b
2
1
0
2
26.
• Сумму чисел x и y можно представить:x
y
(
a
b
)
10
(
a
b
)
10
(
a
b
)
2
2
1
1
0
0
2
27.
• Но ab
10
;
a
b
10
1
1
0
0
a
b
10c
1
1
1
a
b
10
c
0
0
0
2
x
y
(
a
b
)
10
(
10
c
)
10
(
10
c
)
22
1
0
28.
• Применив дистрибутивный закон, имеем:2 2
x
y
(
a
b
)
10
10
c
10
10
c
22
1
0
Применив дистрибутивный закон для 1 и 2 , а так же
для 3 и 4 слагаемых, имеем:
2
x
y
(
a
b
1
)
10
(
c
1
)
10
c
2 2
1
0
29.
• Так каки
то
a
b
1 10
1
1
c1 1 10
2 /
x
y
с
10
c
10
c
1
2
0
Тем самым получена десятичная
запись числа
30.
Алгоритм сложения натуральных чисел, записанных вдесятичной системе счисления
1. Записывают второе слагаемое под
первым так, чтобы соответствующие
разряды находились друг под другом.
2. Складывают единицы первого
разряда. Если сумма меньше 10,
записывают ее в разряде единиц
ответа и переходят к следующему
разряду (десятков)
31.
1. Если сумма единиц больше или равна10, то представляют ее в виде
a
b
1
10
c
0
0
0
где c 0
однозначное число
32.
1. Повторяют те же действия сдесятками, потом с сотнями и т.д.
Процесс этот конечен.
33.
Схема алгоритма сложенияx+y
да
ai bi 10
10 ci
ответ
переход
Сумма ст.
разрядов
конец
нет
ci
-ответ
10 переносим в
старший разряд


























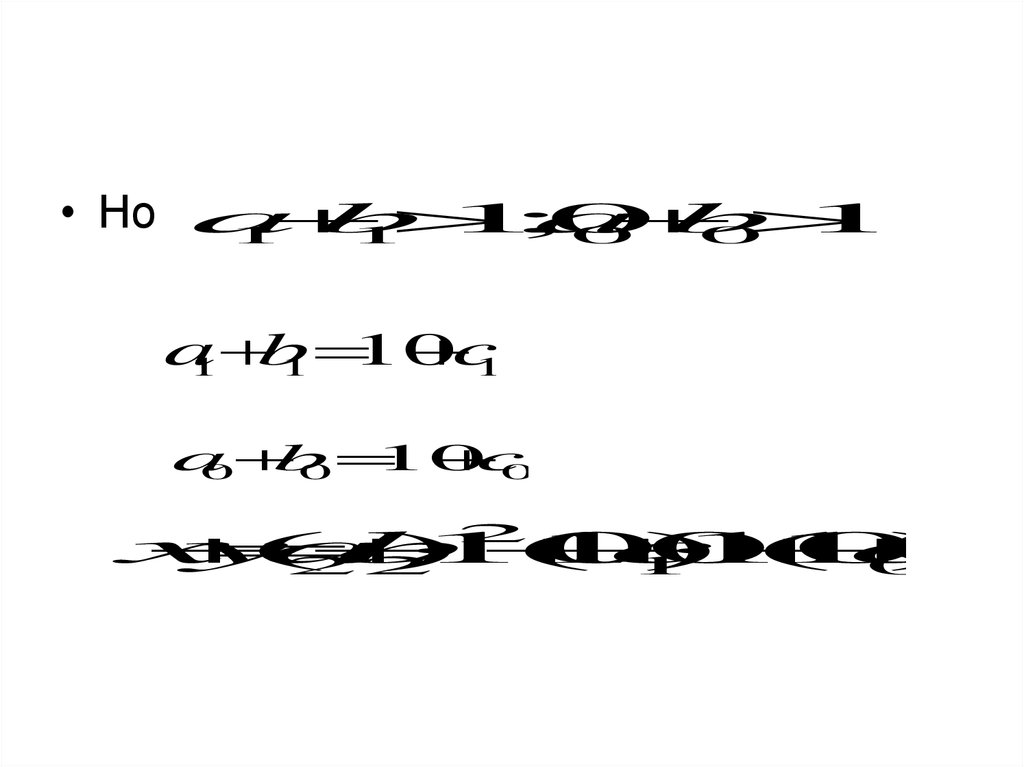







 mathematics
mathematics








