Экстремумы функции

1.

Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action

2.

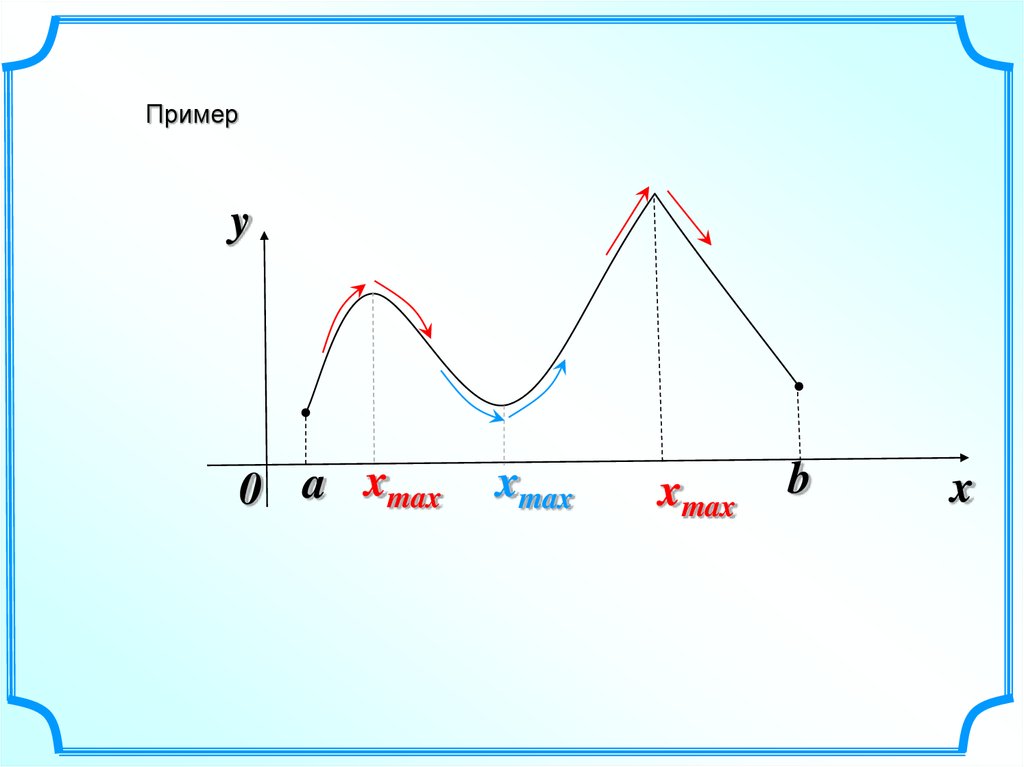
Пример
y
0 a xmax
xmax
xmax
b
x

3.

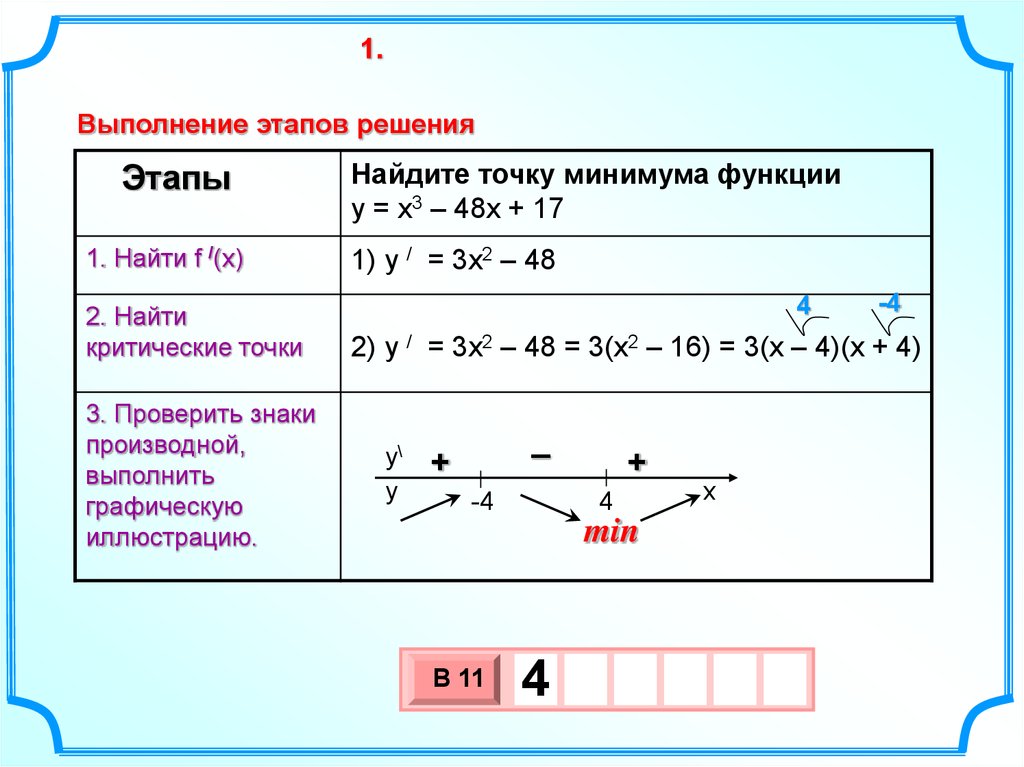
1.
Выполнение этапов решения
Этапы
1. Найти f /(x)
2. Найти
критические точки
3. Проверить знаки
производной,
выполнить
графическую
иллюстрацию.
Найдите точку минимума функции
y = x3 – 48x + 17
1) y / = 3x2 – 48
4
-4
2) y / = 3x2 – 48 = 3(x2 – 16) = 3(x – 4)(x + 4)
y\
y
–
+
-4
+
x
4
min
В 11
4
3
10 х
х

4.

(lnx) =
/
2.
1
x
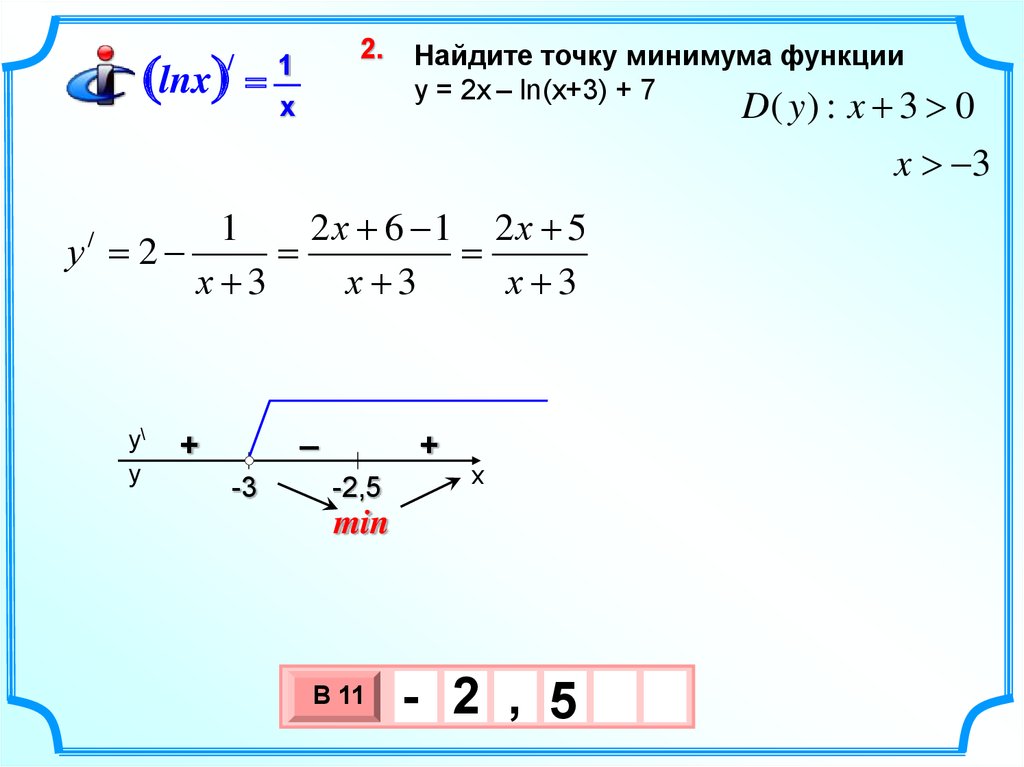
Найдите точку минимума функции
y = 2х – ln(x+3) + 7
D( y ) : x 3 0
x 3
1
2х 6 1 2х 5
у = 2
=
=
х 3
х 3
х 3
/
y\
y
–
+
-3
+
-2,5
x
min
В 11
- 2 , 5
3
10 х
х

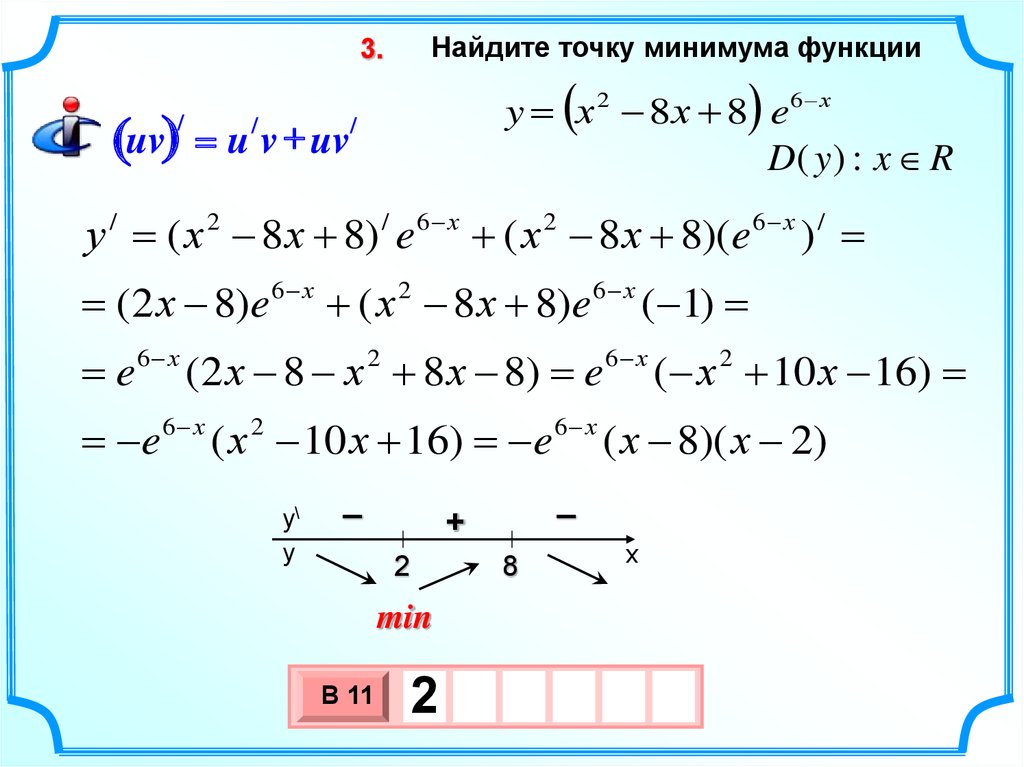
5.

Найдите точку минимума функции
3.
(uv) = u v uv
/
/
(
)
y = х 2 8 х 8 e 6 х
D( y ) : x R
/
у / = ( х 2 8 х 8) / e 6 х ( х 2 8 х 8)(e 6 х ) / =
= (2 х 8)e 6 х ( х 2 8 х 8)e 6 х ( 1) =
= e 6 х (2 х 8 х 2 8 х 8) = e 6 х ( х 2 10 х 16) =
= e 6 х ( х 2 10 х 16) = e 6 х ( х 8)( х 2)
y\
y
–
–
+
2
x
8
min
В 11
2
3
10 х
х

6.

4.
y = (х 16)e x 16
/
(uv) = u v uv
/
/
у = ( х 16) e
/
Найдите точку минимума функции
/
x 16
( х 16)(e
D( y ) : x R
x 16 /
) =
= 1 e x 16 ( х 16)e x 16 = e x 16 (1 х 16) =
= e x 16 ( х 17)
–
y\
y
+
x
-17
min
В 11
- 1 7
3
10 х
х

7.

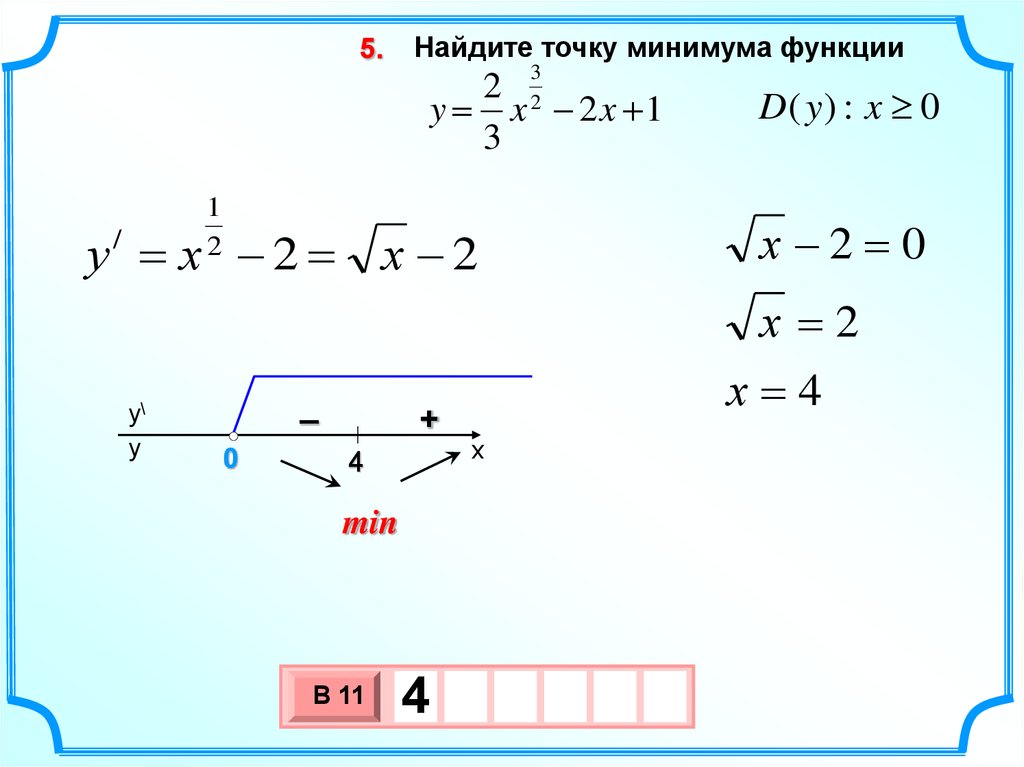
5.
Найдите точку минимума функции
3
2 2
y = x 2x 1
3
1
2
х 2=0
у = х 2 = х 2
/
D( y ) : x 0
х =2
y\
y
–
0
х=4
+
x
4
min
В 11
4
3
10 х
х

8.

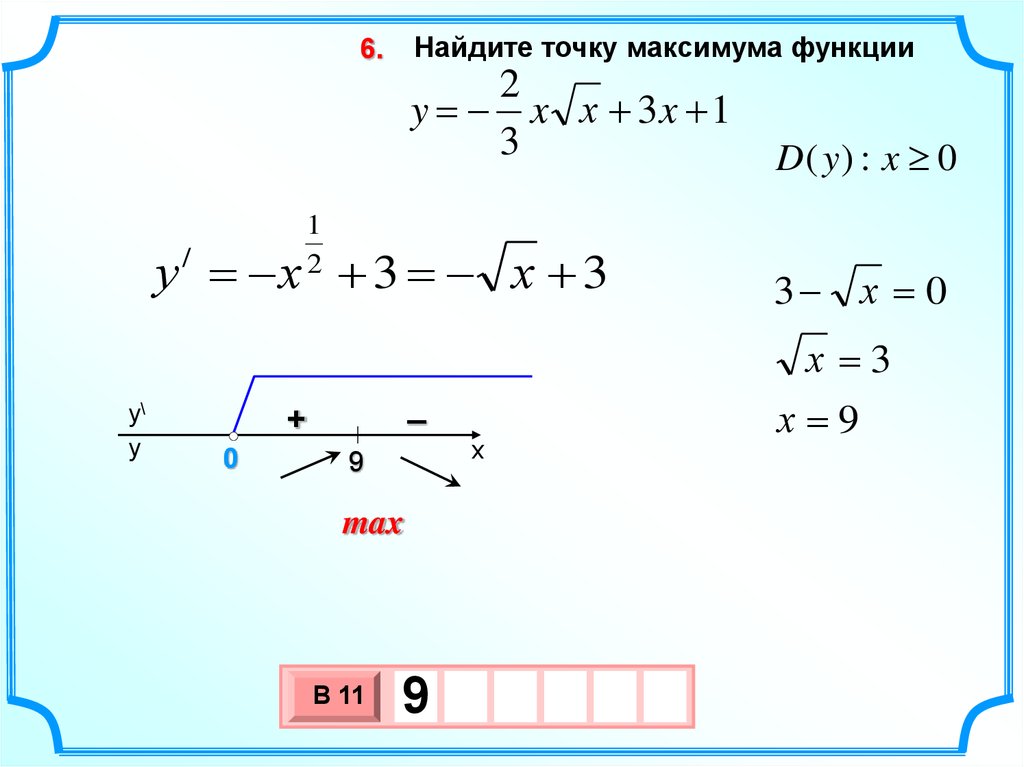
Найдите точку максимума функции
6.
2
y = x х 3x 1
3
1
2
у = х 3 = х 3
/
D( y ) : x 0
3 х = 0
х =3
y\
y
0
х=9
–
+
x
9
max
В 11
9
3
10 х
х

9.

7.
/
1
1
=
2
х
х
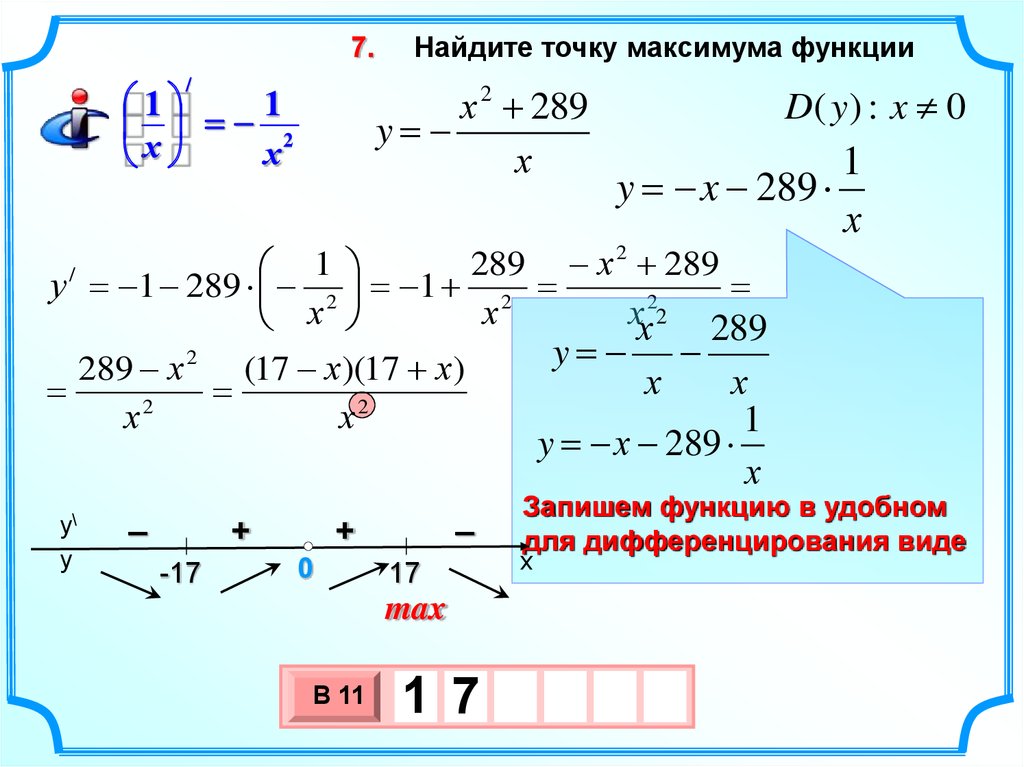
Найдите точку максимума функции
х 2 289
y=
х
D( y ) : x 0
1
y = x 289
х
2
1
289
х
289
/
у = 1 289 2 = 1 2 =
=
2
х
хх 2 289
х
y=
289 х 2 (17 х )(17 х )
х
х
=
=
2
2
х
х
1
y = х 289
y\
y
–
+
-17
–
+
0
17
Запишем функцию в удобном
для дифференцирования виде
x
max
В 11
1 7
х
3
10 х
х

10.

8.
(lnx) =
/
1
x
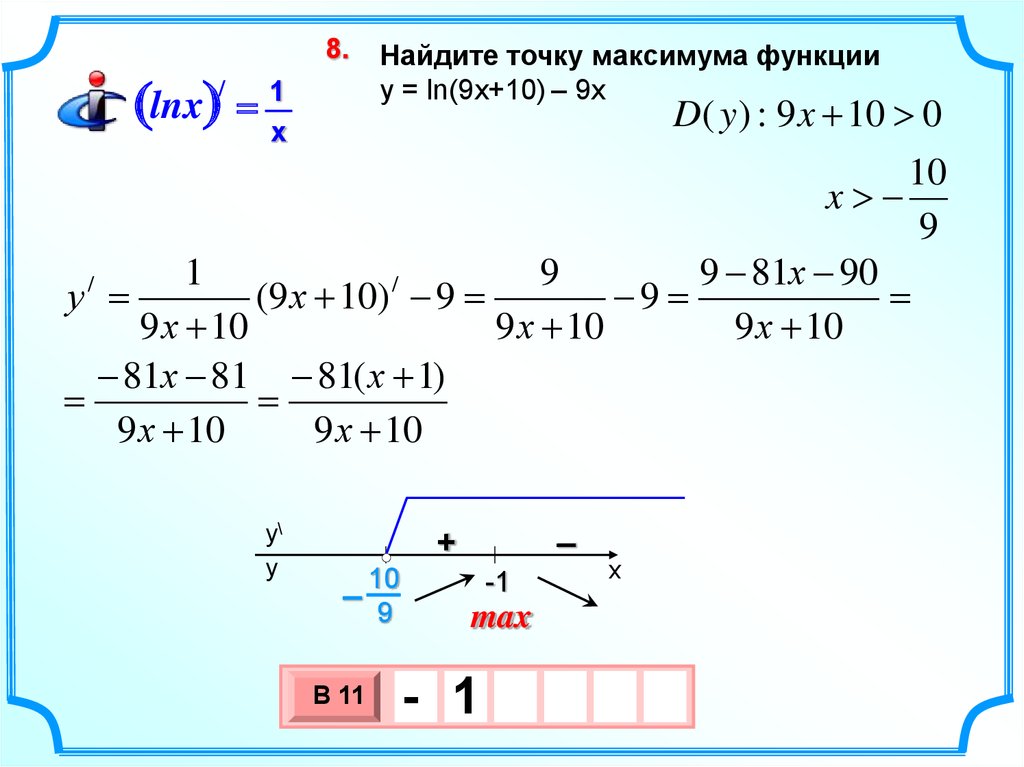
Найдите точку максимума функции
y = ln(9x+10) – 9х
D( y ) : 9 x 10 0
10
x
9
1
9
9 81х 90
/
/
у =
(9 х 10) 9 =
9 =
=
9 х 10
9 х 10
9 х 10
81х 81 81( х 1)
=
=
9 х 10
9 х 10
y\
y
–
+
10
– 9
В 11
-1
x
max
- 1
3
10 х
х

11.

Найдите точку минимума функции
9.
(uv) = u v uv
/
у/ =
/
(
)
2
y = ( х 3) e 2 х= х 2 6 х 9 e 2 х
/
D( y ) : x R
Запишем функцию в удобном
/ 2 х
( х 2 6 х для
9) дифференцирования
e ( х 2 6 х 9виде
)(e 2 х ) /
=
= (2 х 6)e 2 х ( х 2 6 х 9)e 2 х ( 1) =
= e 2 х (2 х 6 х 2 6 х 9) = e 2 х ( х 2 4 х 3) =
= e 6 х ( х 2 4 х 3) = e 6 х ( х 1)( х 3)
y\
y
–
–
+
-3
x
-1
min
В 11
- 3
3
10 х
х