Нахождение наибольших (наименьших) значений, экстремумов функций

1. Нахождение наибольших (наименьших) значений, экстремумов функций. (задача В12 открытого банка задач ЕГЭ).

г. Мурманск МБОУ гимназия №3
Шахова Татьяна Александровна.

2.

Необходимые умения и навыки.
1) Уметь использовать формулы и правила
дифференцирования для нахождения
производных функций.
http://ta-shah.ucoz.ru/load/10_klass/10_klass/formuly_i_pravila_differencirovanija/12-1-0-38
http://ta-shah.ucoz.ru/load/10_klass/10_klass/differencirovanie_slozhnoj_funkcii/12-1-0-41
2) Владеть алгоритмом нахождения
наибольшего (наименьшего) значения функции
на промежутке.
3) Владеть алгоритмом нахождения точек
экстремума.
4) Уметь решать простейшие
тригонометрические и алгебраические
уравнения.
http://ta-shah.ucoz.ru/load/10_klass/10_klass/reshenie_prostejshikh_trigonometricheskikh_uravnenij/12-1-0-15
2

3.

Формулы дифференцирования
С 0
( kx ) k
( x r ) rx r 1
1
1
2
x
x
1
3 x
( x)
(x x)
2
2 x
(sin x ) cos x
(cos x ) sin x
1
( tgx )
cos 2 x
1
( ctgx )
sin2 x
23.06.2022
Правила дифференцирования
( u v ) u v
( ku ) ku
( uv ) u v uv
u
u v uv
v2
v
( u( v )) u ( v ) v
3

4.

Алгоритм нахождения наибольшего (наименьшего)
значения функции на отрезке.
1)Найти стационарные и критические точки,
принадлежащие отрезку.
Для этого – найти производную функции
и решить уравнение у’=0.
2)Найти значение функции в полученных
точках и на краях отрезка.
3)Сравнить полученные значения и записать ответ,
соответствующий вопросу задачи.
23.06.2022
4

5.

Алгоритм нахождения экстремумов функции.
1)Найти стационарные и критические точки.
Для этого – найти производную функции
и решить уравнение у’=0.
2)Определить знаки производной на полученных
Числовых промежутках.
3) Внутренняя точка области определения, в которой
производная меняет знак с «+» на «-» ( с «-» на «+»)
является точкой максимума ( минимума ).
23.06.2022
5

6.

Задачи открытого банка.
Нахождение наибольшего
(наименьшего) значения
тригонометрических функций.
23.06.2022
6

7.

Прототип №1. Найдите наименьшее значение функции 3
;
0
у 5 cos x 6x 4
на отрезке
.
2
1)
у 5 sin x 6
Экстремумов нет.
у 0
Найдем значение функции на краях
отрезка.
5 sin x 6 0
6
sin x
5
2)
у ( 0) 5 cos 0 6 0 4 9
у(
Ø
Формулы
3
3
3
) 5 cos
6
4
2
2
2 9
4
2
Алгоритм
3)Ответ : 9.

8.

Прототип №2. Найдите наибольшее значение функции
5
36
на
отрезке
у 10 sin x x 7
6 ;0 .
1) у 10 cos x
36
Экстремумов нет.
Найдем значение функции на краях
отрезка.
у 0
10 cos x
36
0
18
cos x
1
5
Ø
2)
5
5 36 5
у
10 sin
7
6
6 6
5 30 7 32
36
у ( 0) 10 sin 0
0 7 7
Формулы
Алгоритм
3)Ответ : 32.

9.

Прототип №3. Найдите наибольшее значение функции
у 3tgx 3x 5
на отрезке ;0 .
4
1)
3
3
2
cos x
у 0
у
В указанный отрезок входит число 0 .
Найдем значение функции в этой точке
и на краях отрезка.
3
3 0
2
cos x
cos 2 x 1
2)
cos x 1
у (0) tg 0 3 0 5 5
У
3
у 3tg 3 5
2
4
4
4
4
0
X
Формулы
Алгоритм
3)Ответ : 5.

10.

Прототип №4. Найдите наибольшее значение функции
у
y 14x 7 tgx 3,5 11
на отрезке ; .
3 3
1) у 14
у 0
14
1
2
cos x
2
7
cos 2 x
7
0
2
cos x
В указанный отрезок входят числа и
.
4
4
Найдем значение функции в этих точках
и на краях отрезка.
2)
у 14 tg 3,5 11 10
4
4
4
2
cos x
2 у 4 14 4 tg 4 3,5 11
7 12
У
у
14
tg
3,5 11 7
4
3
3
3
11 3
6
у 14 tg 3,5 11
X
3
3
3
49
11 3
4
6
3)Ответ : 10.
Формулы
Алгоритм

11.

Задачи открытого банка.
Нахождение наибольшего
(наименьшего) значения
алгебраических функций.
23.06.2022
11

12.

Прототип №5. Найдите наибольшее значение функции
у
y x 3 3x 4 на отрезке 2;0 .
В указанный отрезок входит число -1.
Найдем значение функции в этой точке
и на краях отрезка.
1) у 3x 2 3
у 0
2)
у 1 1 3 1 4 6
3x 3 0
3
2
у 2 2 3 2 4 2
3
x 1 0
2
у 0 03 3 0 4 4
x 1
Формулы
Алгоритм
3)Ответ : 6.

13.

Прототип №6. Найдите наименьшее значение функции
у
y x 3 x 2 40х
x 3 на отрезке 0;4 .
1) у 3x 2 2x 40
у 0
В указанный отрезок входит число 4.
Найдем значение функции в этой точке
и на краях отрезка.
2)
3x 2х 40 0
2
у 4 43 42 40 4 3 109
у 0 03 02 40 0 3 3
x 4
10
x
3
Формулы
Алгоритм
3)Ответ : 109.

14.

Прототип №7. Найдите наибольшее
значение функции
3
x
на отрезке 3;3 .
у
y
9x 7
3
Эти числа являются краями отрезка.
Найдем значение функции в этих
точках.
1) у x 2 9
у 0
2)
x2 9 0
33
у 3 9 3 7 25
3
x 3
x 3
( 3) 3
у 3
9 ( 3) 7 11
3
Формулы
Алгоритм
3)Ответ : 11.

15.

Прототип №8. Найдите наименьшее значение функции
у
y x x 3x 1 на отрезке 1;9 .
Это число принадлежит указанному
отрезку.
Найдем значение функции в этой
точке и на краях отрезка.
3 х
3
2
у 0
1) у
2)
3 x
3 0
2
x
1
2
у 4 4 4 3 4 1 3
у 1 1 1 3 1 1 1
у 9 9 9 3 9 1 1
x 2
x 4
Формулы
Алгоритм
3)Ответ : 1.

16.

Прототип №9. Найдите наименьшее значение функции
36
на отрезке 1;9 .
уy x
x
Указанному отрезку принадлежит число 6.
1) у 1
36
x2
Найдем значение функции в этой
точке и на краях отрезка.
у 0
2)
36
1 2 0
x
36
1
2
x
у 6 6
36
12
6
36
у 1 1
37
1
36
у 9 9
13
9
x 2 36
x 6
Формулы
Алгоритм
3)Ответ : 12.

17.

Прототип №10. Найдите наибольшее значение функции
у
y ( x 3)2 ( x 5) на отрезке 4; 1 .
1) у (( x 3)2 ) (x 5) ( x 3)2 ( x 5)
2( x 3) 1 ( x 5) ( x 3)2 1 ( x 3)( 2( x 5) ( x 3))
( x 3)( 3x 13)
Это рациональный способ работы. Но ты можешь, просто,
аккуратно и внимательно раскрыть скобки. Тогда далее
решаешь традиционное квадратное уравнение.
Указанному отрезку принадлежит число -3.
Найдем значение функции в этой
( x 3)( 3x 13) 0 точке и на краях отрезка.
у 0
x 3
13
x
3
4)
у 3 ( 3 3)2 ( 3 5) 0
у 4 ( 4 3)2 ( 4 5) 1
у 1 ( 1 3)2 ( 1 5) 16
Формулы
Алгоритм
3)Ответ : 16.

18.

Прототип №11. Найдите наибольшее значение функции
у
y x5 5x 3 20x на отрезке 6;1 .
1) у 5x4 15x 2 20 Указанному отрезку принадлежит число -2.
Найдем значение функции в этой
у 0
точке и на краях отрезка.
4
2
5x 15x 20 0
t x2
2)
t 2 3t 4 0
t 4
t 1
у 2 ( 2)5 5 ( 2)3 20 ( 2) 48
x 2 4
2
x 1 Ø
у 1 15 5 13 20 1 24
у 6 ( 6)5 5 ( 6)3 20 ( 6) ...
Очевидно, что это значение намного
x 2
меньше двух предыдущих.
Оно не может являться ответом и можно
не выполнять эти неудобные вычисления.
Формулы
Алгоритм
3)Ответ : 48.

19.

Задачи открытого банка.
Нахождение точек экстремумов
функций.
23.06.2022
19

20.

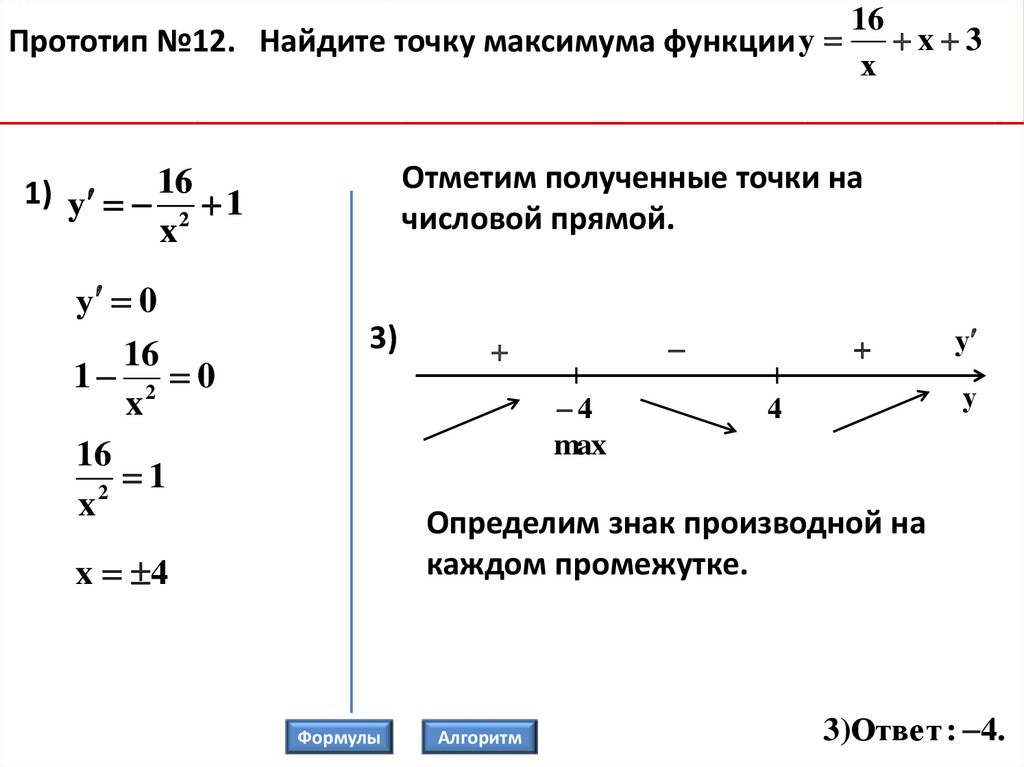
16
Прототип №12. Найдите точку максимума функции у x 3
х
Отметим полученные точки на
числовой прямой.
1) у 16 1
x2
у 0
16
1 2 0
x
16
1
2
x
3)
4
max
у
у
4
Определим знак производной на
каждом промежутке.
x 4
Формулы
Алгоритм
3)Ответ : 4.

21.

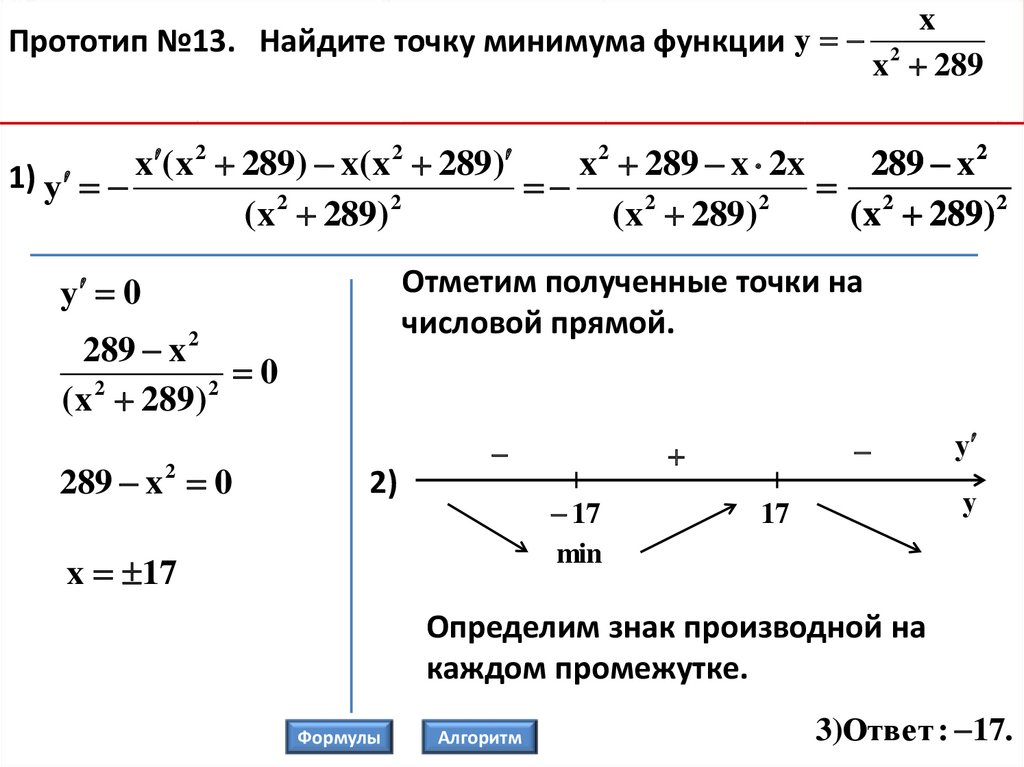
x
Прототип №13. Найдите точку минимума функции у 2
x 289
2
2
2
2
x
(
x
289
)
x
(
x
289
)
x
289
x
2
x
289
x
1) у
2
2
2
2
2
( x 289) 2
( x 289)
( x 289)
у 0
Отметим полученные точки на
числовой прямой.
289 x 2
0
2
2
( x 289)
289 x 2 0
2)
17
min
x 17
у
у
17
Определим знак производной на
каждом промежутке.
Формулы
Алгоритм
3)Ответ : 17.

22.

Прототип №14. Найдите точку максимума функции
у ( x 2)2 (x 4) 5
1) у (( x 2)2 ) ( x 4) (x 2)2 ( x 4)
2( x 2) 1 ( x 4) ( x 2)2 1 ( x 2)( 2( x 4) ( x 2))
( x 2)( 3x 10)
у 0
Отметим полученные точки на
числовой прямой.
( x 2)( 3x 10) 0
x 2
10
x
3
2)
2
max
у
у
10
3
Определим знак производной на
каждом промежутке.
Формулы
Алгоритм
3)Ответ : 2.

23.

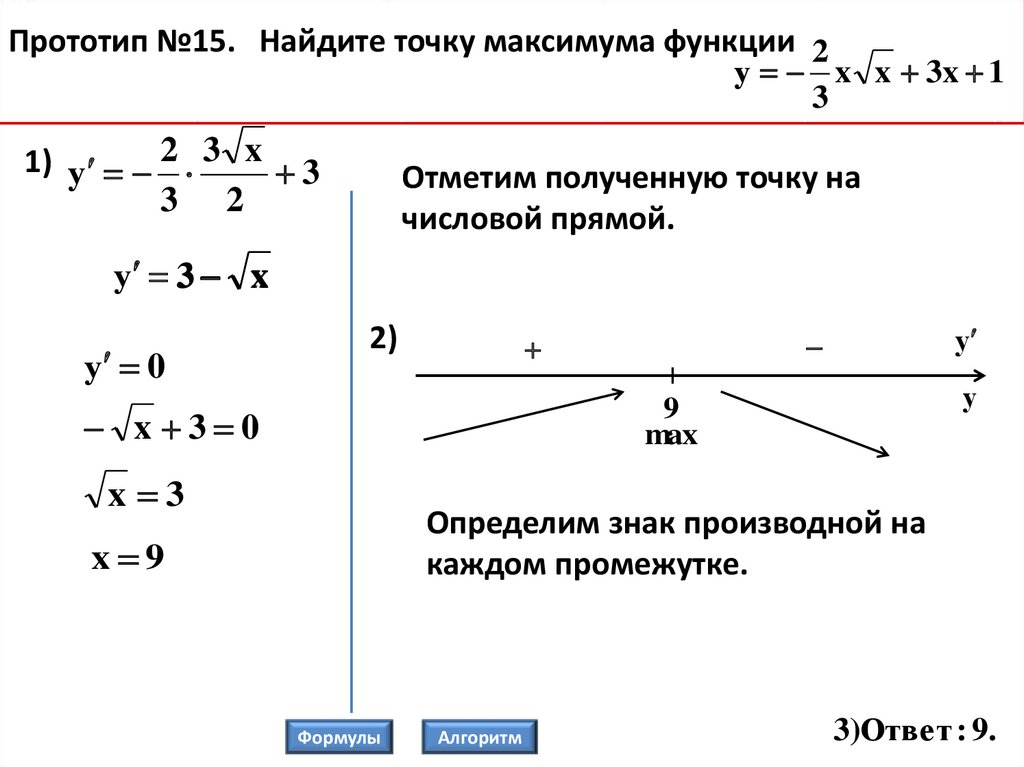
Прототип №15. Найдите точку максимума функции 2
у x x 3x 1
3
1) у 2 3 x 3
3 2
Отметим полученную точку на
числовой прямой.
у 3 x
у 0
2)
у
у
9
max
x 3 0
x 3
Определим знак производной на
каждом промежутке.
x 9
Формулы
Алгоритм
3)Ответ : 9.

24.

Прототип №16. Найдите точку минимума функции
у (0,5 x ) cos x sin x , принадлежащую промежутку 0; .
2
1) у ( 0,5 x ) cos x ( 0,5 x ) cos x sin x
cos x (0,5 x ) sin x cos x ( 0,5 x ) sin x
Указанному промежутку принадлежит
только точка 0,5.
Отметим ее на числовой прямой.
у 0
( 0,5 x ) sin x 0
x 0,5
x n
0
2)
2
у
у
0,5
min
0,5 280
Определим знак производной на
каждом промежутке.
Формулы
Алгоритм
3)Ответ : 0,5.

25.

Задачи открытого банка.
Нахождение наибольшего
(наименьшего) значения
алгебраических функций и
экстремумов без производной.
23.06.2022
25

26.

В случае, если мы имеем дело со сложной
функцией f(g(x)), где f – монотонная функция, то
достаточно исследовать функцию g(x). Точки
экстремума функция f будет иметь такие же, что
и функция g(x) с учетом области определения.
23.06.2022
26

27.

Прототип №17. Найдите точку минимума функции
y x 2 6x 11
Функция y x возрастает на всей области определения,
следовательно ведет себя так же, как подкоренная функция на
области определения.
Подкоренное выражение больше нуля при
любом значении х. D(y):R.
Исследуем функцию, находящуюся
под знаком корня.
Y
f ( x ) x 2 6x 11
График – парабола, ветви направлены
вверх.
b
x0
2a
3
т. min
3
X
Ответ : 3.

28.

Прототип №18. Найдите наибольшее значение функции
y 5 4x x 2
Функция y x возрастает на всей области определения,
следовательно принимает наибольшее значение в той же точке,
что и подкоренная функция с учетом области определения.
Исследуем функцию, находящуюся под знаком корня.
f ( x ) 5 4x x 2 f ( x ) 0 - условие существования корня.
x 5;1
График – парабола, ветви
направлены вниз.
Y
9
f ( x )наиб .
b
x0
2
X
2a
Следовательно y наиб . 9 3
y0 9
Ответ : 3.

29.

Еще полезные ресурсы для тренировки:
http://reshuege.ru/test?theme=78
http://reshuege.ru/test?theme=81
http://reshuege.ru/test?theme=83