Similar presentations:
Вероятностные расчёты НДС конструкций. Постановки задач, методы их решения
1.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ
СТРОИТЕЛЬНАЯ МЕХАНИКА
И НАДЁЖНОСТЬ
СТРОИТЕЛЬНЫХ
КОНСТРУКЦИЙ
Часть 3
ВЕРОЯТНОСТНЫЕ РАСЧЁТЫ НДС КОНСТРУКЦИЙ.
ПОСТАНОВКИ ЗАДАЧ, МЕТОДЫ ИХ РЕШЕНИЯ
2.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Обобщённое условие безотказности
по некоторому критерию работоспособности
~ ~
~ ~ ~
Q R S R Q 0
pQ (Q) , pR (R)
Q
Q, R
R
Pf = P ( R < Q )
pS (S)
0
S
S
Pf = P ( S < 0 ) = PS ( 0 ) β S
β S – характеристика
Sˆ
0
безопасности
(индекс
надёжности,
Pf PS (0) pS (S) d S
~
~ ~
reliability index)
S S (Q, R)
~
~
~ ~
~
Q Q XQ
Q M q~ l 2/8
max
~
~
~
XQ q~ l
XQ ~
xQ1 ~
xQ2 ... ~
xQi ... ~
xQnQ
~
~
~ ~ ~ ~
R R XR
R M0 σ
uW
~
~
~
~
~
~
~
~
X R x R1 x R2 ... x Ri ... x RnR
X R σu W ~ ~2
~ bh
W
~
~
6
u u X
~ u
~ u
~ ...u
~ ...u
~
u
1
2
k
m
3.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Постановки задач вероятностных расчётов
сооружений и конструкций
Принципиальная модель стохастического состояния объекта
Случайные входные
параметры
Стохастическая
система
Случайные выходные
параметры
~
X ~
x1 ~
x2 ... ~
xi ... ~
xn
(объект
с вероятностными
свойствами и
параметрами)
~ u
~1 u
~2 ...u
~k ...u
~m
u
Геометрические,
структурные,
жесткостные
характеристики системы;
свойства материалов;
нагрузки и воздействия
Случайные векторы
(многомерные
случайные величины)
Параметры
напряжённодеформированного
состояния системы
Прямая (поверочная) задача вероятностного расчёта
По известным (заданным) вероятностным характеристикам входных параметров
определить стохастические характеристики выходных параметров.
Обратная (проектная) задача вероятностного расчёта
Определить вероятностные характеристики входных параметров,
обеспечивающие требуемые характеристики случайных выходных параметров.
Оптимизационная задача –
синтез стохастической системы, удовлетворяющей принятому
критерию оптимальности, при выполнении установленных ограничений
на случайные входные и выходные параметры.
4.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Случайные векторы (многомерные случайные величины),
их характеристики и свойства
~
pX (X) = pX (x1 , x2 ,…, xn ) – совместная плотность
X ~
x1 ~
x2 ... ~
xi ... ~
xn
Свойство:
... p
X
распределения элементов
случайного вектора X
(X) dx1 dx2 ... dxn 1
(аналог плотности распределения
px (x) случайной величины )~
x
Схема алгоритма
построения математической модели pX (X)
на примере двумерной случайной величины
~
X ~
x1 ~
x2 ( n = 2 )
( nj /n0 )/(D x1∙D x2)
x
Представление функции pX ( x1 , x2 )
способом горизонталей
pX ( x1 , x2 )
x2
Размерность
x2
x
[ x1∙ x2 ]–1
x2max
x2
D x2
x2 min
0 x1 min
D x1
x1 max x1
0
x1
При произвольном n функция pX (X) описывает поверхность в (n +1)-мерном пространстве
x1
5.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функциональные характеристики случайного вектора
Функция распределения случайного вектора
x1 x2
F(X) F( x1, x2 , ..., xi , ..., xn )
xi
xn
... ... p
X
(X) dx1 dx2 ... dxi ... dxn
P( ~
x1 x1 , ..., ~
xi xi , ..., ~
xn xn )
Плотность распределения i – го элемента
pxi(xi) pi (xi) ... pX (X) dx1 dx2 ... dxi 1 dxi 1... dxn
Числовые
характеристики
i – го элемента
n – 1 раз
математическое ожидание элемента
pi (xi )
xi
~
xi :
xi xi pi (xi) dxi ... xi pX (X) dx1 dx2 ... dxi ... dxn
диcперсия элемента
~
xi :
n раз
xi (xi xi) 2 pi (xi) dxi ... (xi xi) 2 pX (X) dx1 dx2 ... dxi ... dxn
n раз
xi
6.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функциональные характеристики случайного вектора
Совместная плотность распределения группы элементов Xk = { x1 x2 … xk }
pX k (X k) pX k (x1, x2 ,..., xk) ... pX (X) dxk 1 dxk 2 ... dxk
Для i – го и j – го элементов ( k = 2 ):
n – k раз
xj
p ij (xi , x j ) ... pX (X) dx1 dx2 ... dxi 1 dxi 1... dx j 1 dx j 1... dxk
xj
n – 2 раза
Математические ожидания элементов:
Числовые
характеристики
i – го и j – го элементов
xi
x p (x , x ) dx dx ;
i
ij
i
j
i
j
Диcперсии элементов:
xi0
xi
xi
x j x j pij (xi , x j) dxi dx j
xi
x0j
2
2
(
x
x
)
p
(
x
,
x
)
dx
dx
;
x
(
x
x
)
pij (xi , x j) dxi dx j
i
i
ij
i
j
i
j
j
j
j
Ковариация (смешанная дисперсия) элементов:
корреляционный момент
xi x j (xi xi) (x j x j) pij (xi , xi ) dxi dx j
xj
x i xj > 0
xi
xj
xi xj < 0
xi
7.
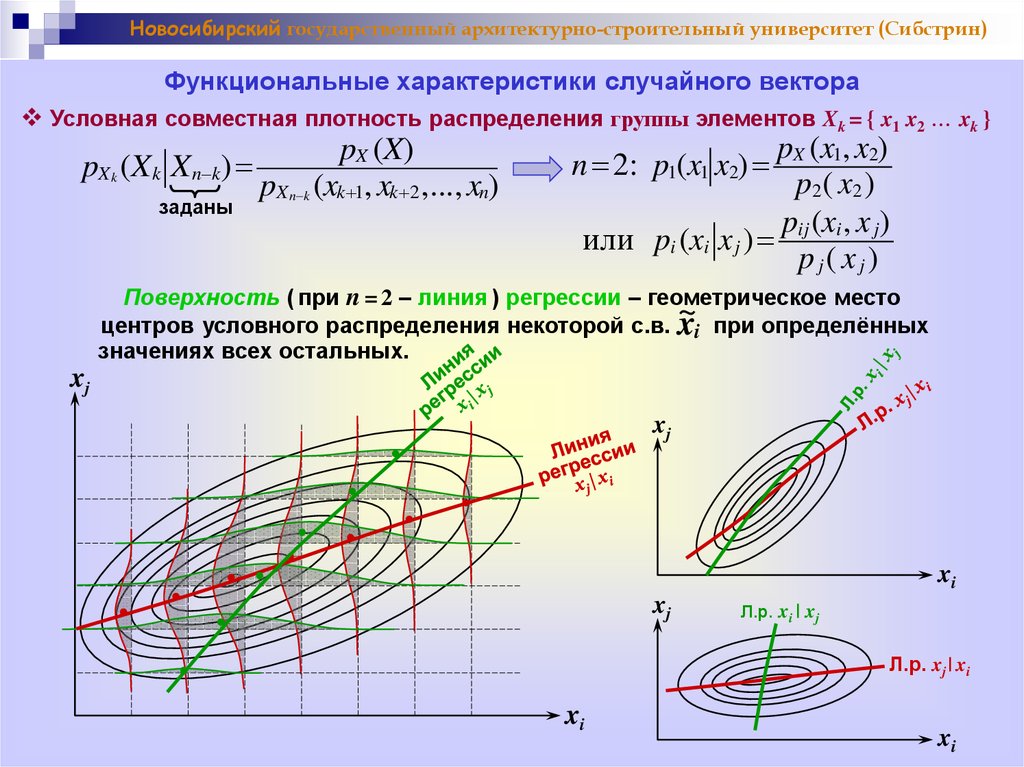
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функциональные характеристики случайного вектора
Условная совместная плотность распределения группы элементов Xk = { x1 x2 … xk }
pX (X)
pX k (X k X n k)
pX n k (xk 1, xk 2 ,..., xn)
заданы
pX (x1, x2)
n 2: p1(x1 x2)
p 2 ( x2 )
pij (xi , x j)
или pi (xi x j )
p j( x j )
Поверхность ( при n = 2 – линия ) регрессии – геометрическое место
центров условного распределения некоторой с.в. ~
xi при определённых
значениях всех остальных.
xj
xj
xi
xj
Л.р. xi | xj
Л.р. xj | xi
xi
xi
8.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Числовые характеристики случайного вектора
Вектор математических ожиданий координат центра распределения
x
...
x
p
(
X
)
dx
dx
...
dx
...
dx
i
i
X
1
2
i
n
1 2
i
n
X x x ... x ... x
Матрица ковариаций ( ≡ матрица дисперсий )
(ковариационная матрица, корреляционная матрица)
x1
x 2 x1
x i x1
X
x x
j 1
x n x 1
x1 x 2
x2
xi x2
x j x2
xnx2
x1 x i
x2xi
xi
x j xi
xnxi
x1 x j
x2x j
xi x j
xj
xnx j
x1 x n
x 2 x n
x i x n
x j x n
xn
xi x j (xi xi) (x j x j) pij (xi , xi ) dxi dx j x j xi x j xi x j xi
Если два элемента
~
x j независимые, то xi xj = xj xi = 0.
xi и ~
Если независимыми являются все элементы случайного вектора
то матрица дисперсий – диагональная:
xj
~
X,
X diag ~
x1 ~
x2 ... ~
xi ... ~
xn ;
n
при этом совместная плотность распределения
pX (X) pi (xi)
i 1
Л.р. xi | xj
Л.р. xj | xi
xi
9.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Числовые характеристики случайного вектора
Индексы и коэффициенты корреляции
μi j μj i
Коэффициент корреляции
Индекс корреляции
(при линейной зависимости между
(корреляционное отношение)
0 μi j 1
xi xj
( ri j r j i )
xi xj
1 μi j , ri j 1
0 ri j 1
xj
0 μ i j 0,2 – слабая стохастическая зависимость между ~xi и ~x j
0,8 μ i j
1 – зависимость между ~xi и ~
x j, близкая к функциональной
xi
xj
Л.р. xj | xi
Матрица коэффициентов (индексов) корреляции
r11
r21
r
ri1
rn1
r12 r1i
r22 r2i
ri2 rii
rn2 rni
r1n
r2n
rin
rnn
~
xj )
xi и ~
В случае стохастически независимых
(некоррелированных) всех элементов
~
случайного вектора X матрица r –
единичная диагональная:
r = E = diag [ 1 1 … 1 ]
Л.р. xi | xj
xi
10.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Задача : требуется определить функциональные и / или числовые
вероятностные характеристики многомерной случайной величины –
~ u
~1 u
~2 ...u
~k ...u
~m , элементы которого являются функциями
вектора u
~
x1 ~
x2 ... ~
xi ... ~
xn с известной совместной плотслучайного вектора X ~
ностью распределения pX (X).
~ ~ ~
~ u
~1 ; X
При m = 1 и n = 1: u
x1 ; u1 u1(~
x1) ; для краткости u = u (x).
px (x)
px (x)
x
x
pu (u)
Условие равновероятности:
~ u Du)
P (x ~
x x Dx) P (u u
Задана
При Dx → dx Du → du
px (x) ∙ dx = pu (u) ∙ du
Dx
Найти
pu (u)
u (x) u (x +D x) =
= u+Du
u
pu (u) dx px (x)
du
Здесь x = x (u) –
обращением зависимости u = u (x)
11.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Аналитическое определение плотности распределения функции
случайных аргументов
При произвольных n и m < n , аналогично выводу при n = 1 и m = 1:
pu (u)
... pX ( f1 , f2 , , fm , , xm 1 , xm 2 , , xn )
f
dx m 1 dx m 2 ...dx n
u
n – m раз
f1
u1
f2
f
u1
u
fm
u1
f1
u2
f2
u2
fm
u2
f1
um
f
2 ; f x u , u , , u , x , x , , x
um
j
j
1
2
m
m 1
m 2
n
f
m
um
f
При произвольных n и m ≥ n: pu (u) pX ( f1 , f2 , , fn )
u
dx (u)
Для получения используются
Частный случай:
pu (u) px(u) x[(u)]
любые n из m зависимостей u = u ( X )
m=n=1
du
12.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Пример 1
px (x)
~ a ~
u
x2
0,5
pu (u)
0
1
2
3
4
5
6
x
dx (u)
x (u) u ;
1
a
du 2 a u
1 px(u) x (u)
2 au
Пример 2
pu (u)
~ a ~
u
x b
1
12a
x (u) u - b ;
a
a
25a
9a
Дисперсия
pu (u) 1 px(u) x(u)
a
u
Математическое ожидание
dx (u) 1
du a
-
-
u u pu (u)du u px (x)dx ax b
2
2
2
u (u - u ) pu (u)du (u - u ) px (x)dx a x
-
-
13.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Пример 2
~ ~
u
x1 ~
x2 , например, q~ q~const q~temp
~ ~ ~
~ u
~ ; X
(u
x1 x2 ; m 1, n 2 )
1
Применение общей формулы в случае m = 1 <
где
n = 2 даёт pu (u)
df1
f1 x1 u x2 ;
1
du
При независимых нормально распределенных
pX (X) p1(x1) p2 (x2)
тогда
1
2πx1
x1 x1
2
x
1
e
pu (u)
2
1
2πx
x2 x2
2
x
2
e
1
2πxˆ1 xˆ2
2
2
1
2πxˆ1 xˆ2
u x2 x1 x2 x2
2x
2
e 2x1
df1
dx ,
du 2
~
x1 и ~
x2 :
2
2
pX ( f1 , x2 )
x1 x1 x2 x2
2
x
2
x
1
2
e
2
2
dx2
В результате преобразований и интегрирования:
pu (u)
1
2πu
u u
2
u
e
2
– н о р м а л ь н о е распределение
с математическим ожиданием
u x1 x2
и дисперсией u x1 x2
14.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
px (x)
0
при x x b
b - x x при x b x x
2
px( x) b
b x - x при x x x b
b2
x
x -b x x b
0
при x x b
0
b - x
1
pu(u) 2 u
b x
2b a
u
0
px (x)
px(x)
x
x
1 e
2πxˆ
при x x b
1 при x b x x
a
1 при x b x x
a
при x x b
x x 2
2x
pu (u)
1
2e
x 2
2x
1
e
2πax u
u x u
2a a
x
15.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Пример 3
Линейная функция конечного числа случайных аргументов
n
~
u a0 ai ~
xi ; m 1 n
i 1
n
df1 1
1
f1 x1 u a0 ai ~
xi ;
a
du
a1
i 2
1
pu (u) pX ( f1 , x2 , x3 , , xn ) 1 dx2 dx3 dxn
a1
Математическое ожидание
n
u a0 ai xi
i 1
Дисперсия
n n
u ai a j xi x j
i 1 j 1
Важное свойство: если все элементы вектора X = { x1 x2 … xn } – нормально
~ (x~) – также нормально распределённая.
распределённые с.в., то линейная функция u
В других случаях плотность pu (u) определяется в результате интегрирования.
16.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Пример 4
Требуется: найти функцию плотности распределения нормального напряжения
в поперечном сечении стержня при его осевом растяжении
~
A Нагрузка и площадь сечения – независимые случайные величины с нормальным распределением
~ ~ 1
~ F
σ
А
u~ ~x1 ~x2 1
~
F
pX (X) pF (F) pA (A )
pu (u) p ( )
x F
2F
1 e
2πF
2
A A
2A
1 e
2πA
2
2
F F
A A
2F
1 e
2πFˆ Aˆ
2
2A
df 1
pX ( f1, x2 )dx2 dF pX ( F, A)dA
du
d
f1 F u x2 σ A;
df1 dF d (σ A)
A
du dσ
dσ
( A F)2 (A A )2
2A
2F
p ( ) A pX ( F, A) dA 1 A e
2 FˆAˆ
1
p ( )
2 AA
s 1 2
s 2 e 2A 2A s2 2
s2 2 3
dA
s σ/σ
α AF /AA
AF , AA –
коэффициенты
вариации
17.
Новосибирский государственный архитектурно-строительный университет (Сибстрин)Функции случайных аргументов,
определение их вероятностных характеристик
Пример 4
Требуется: найти функцию плотности распределения нормального напряжения
в поперечном сечении стержня при его осевом растяжении
~
A
2
~
F
pσ(σ ) ( σ 1
1
p ( )
2 AA
)
8
s 1
2A 2A
s 2 2
7,4082
7
=10
6
5
AF = 0,1
AA = 0,01
= 10
AF = 0,05
AA = 0,02
= 2,5
4,7799
4,8504
3,9696
4
3,5104
3,5043
3
2
1,3026
1,3035
1,2943
1
0,1782
0,6
0,5459
0,7
0,8
=2,5
2,4170
2,4218
0
s e
s2 2 3
2
0,1362
0,9
1,3318
0,1727
1,0
1,1
0,5502
1,2
0,1819
1,3
1,4
1,5
s σ
σ
















 Construction
Construction








