Вероятностные методы строительной механики и теория надёжности строительных конструкций (ВМСМ и ТНСК)

1.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ
ВЕРОЯТНОСТНЫЕ МЕТОДЫ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
И ТЕОРИЯ НАДЁЖНОСТИ
СТРОИТЕЛЬНЫХ
КОНСТРУКЦИЙ
ПРЯМЫЕ И ОБРАТНЫЕ ЗАДАЧИ
ВЕРОЯТНОСТНЫХ РАСЧЁТОВ КОНСТРУКЦИЙ

2.

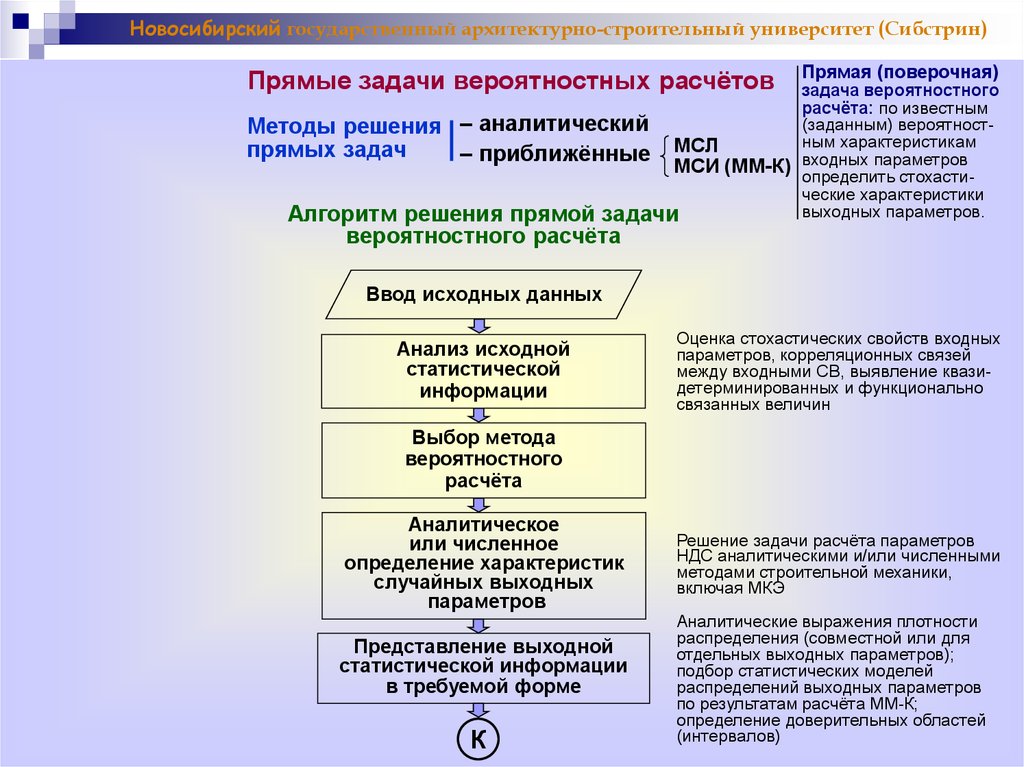
Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Прямая (поверочная)
задача вероятностного
расчёта: по известным
(заданным) вероятностМетоды решения – аналитический
ным характеристикам
МСЛ
прямых задач
– приближённые МСИ (ММ-К) входных параметров
определить стохастические характеристики
выходных параметров.
Алгоритм решения прямой задачи
вероятностного расчёта
Ввод исходных данных
Анализ исходной
статистической
информации
Оценка стохастических свойств входных
параметров, корреляционных связей
между входными СВ, выявление квазидетерминированных и функционально
связанных величин
Выбор метода
вероятностного
расчёта
Аналитическое
или численное
определение характеристик
случайных выходных
параметров
Представление выходной
статистической информации
в требуемой форме
К
Решение задачи расчёта параметров
НДС аналитическими и/или численными
методами строительной механики,
включая МКЭ
Аналитические выражения плотности
распределения (совместной или для
отдельных выходных параметров);
подбор статистических моделей
распределений выходных параметров
по результатам расчёта ММ-К;
определение доверительных областей
(интервалов)

3.

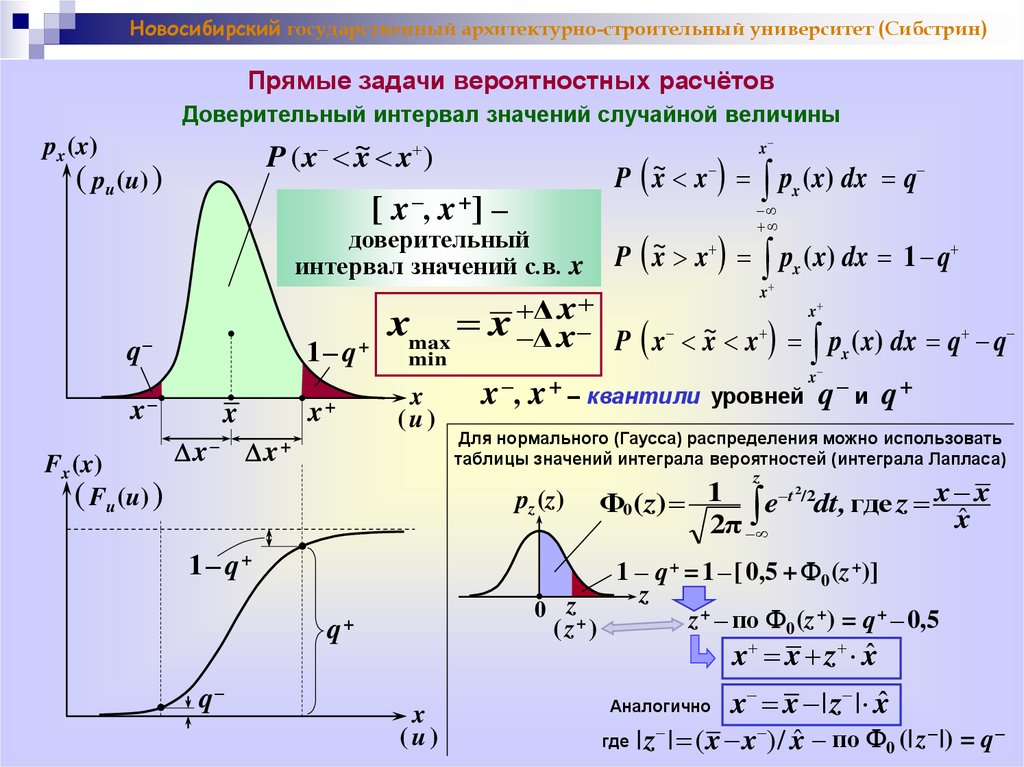
Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Доверительный интервал значений случайной величины
Fx (x)
( Fu (u) )
P ~x x px ( x) dx q
[ x – , x +] –
доверительный
~x x p ( x) dx 1 q
P
интервал значений с.в. x
x
x
x
Δ x
xmax x Δ x – P x ~x x p ( x) dx q q
+
x
1– q
q–
x–
x
P (x ~
x x )
px (x)
( pu (u) )
min
x
x+
x
(u)
D x– D x+
x –,
x
+
x – квантили уровней q – и
q+
Для нормального (Гаусса) распределения можно использовать
таблицы значений интеграла вероятностей (интеграла Лапласа)
z
pz (z)
1 – q+
1 – q + = 1 – [ 0,5 + F0 (z +)]
z
0 z
z + – по F0 (z +) = q + – 0,5
( z+ )
q+
q–
2
Φ0 (z) 1 e t /2dt, где z x x
xˆ
2π
x x z xˆ
x
(u)
Аналогично
где
x x | z | xˆ
| z | ( x x ) / xˆ – по F0 (| z – |) = q –

4.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
ТАБЛИЦА ЗНАЧЕНИЙ ИНТЕГРАЛА ВЕРОЯТНОСТЕЙ (ИНТЕГРАЛА ЛАПЛАСА)
Функция распределения
x
Ф0(х)= (t )dt =
0
1
x
t / 2
e dt
2
0
нормированного
и центрированного
нормального распределения
X
0
1
2
3
4
5
6
7
8
9
0,0
0,0000
040
080
120
160
199
239
279
319
359
0,1
398
438
478
517
557
596
636
675
714
753
0,2
793
832
871
910
948
987
0,1026
064
103
141
0,3
0,1179
217
255
293
331
368
406
443
480
517
0,4
554
591
628
664
700
736
772
808
844
879
0,5
915
950
985
0,2019
054
088
123
157
190
224
0,6
0,2257
291
324
357
389
422
454
486
517
549
0,7
580
611
642
673
708
734
764
794
823
852
0,8
881
910
939
967
995
0,3023
051
078
106
133
0,9
0,3159
186
212
238
264
289
315
340
365
389
1,0
413
437
461
485
508
531
554
577
599
621
1,1
643
655
686
708
729
749
770
790
810
830
1,2
849
869
888
907
925
944
962
980
997
0,4015
1,3
0,4032
049
066
082
099
115
131
147
162
177
1,4
192
207
222
236
251
265
279
292
306
319
1,5
332
345
357
370
382
394
406
418
429
441
1,6
452
463
474
484
495
505
515
525
535
545
1,7
554
564
573
582
591
599
608
616
625
633
1,8
641
649
656
664
671
678
686
693
699
706
1,9
713
719
726
732
738
744
750
756
761
767
2,0
772
778
783
788
793
798
803
808
812
817
2,1
821
826
830
834
838
842
846
850
854
857
860
864
867
871
874
877
880
883
886
889
966
474
906
263
545
755
894
962
962
893
892
895
898
900
903
906
908
911
913
915
759
559
296
969
581
133
625
060
437
758
2,2
*)
2,3
*)
2,3
Начиная с этого места, значение Ф0(x) приведено с семью знаками после запятой. Например, запись
892
759
означает Фо (2,30) =
0,4892759.

5.

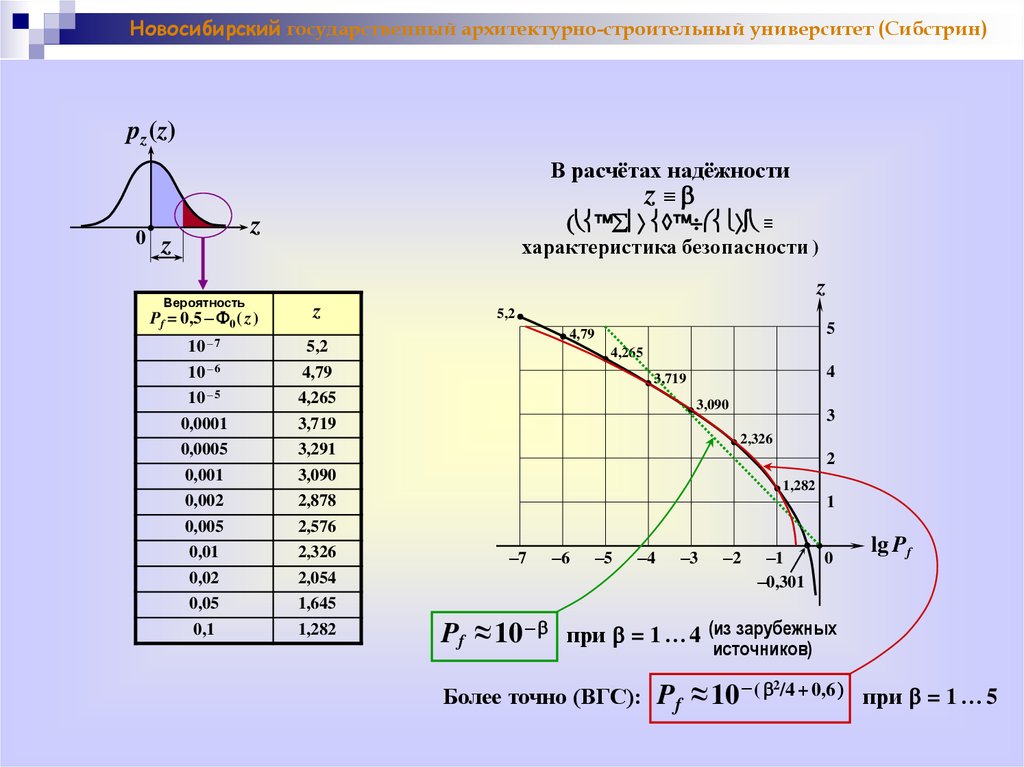
Новосибирский государственный архитектурно-строительный университет (Сибстрин)
pz (z)
В расчётах надёжности
z≡b
0
≡
z
z
Вероятность
характеристика безопасности )
z
Pf = 0,5 – F0 ( z )
z
10 – 7
10 – 6
10 – 5
0,0001
0,0005
5,2
4,79
4,265
3,719
3,291
0,001
0,002
0,005
0,01
0,02
0,05
3,090
2,878
2,576
2,326
2,054
1,645
0,1
1,282
5,2
5
4,79
4,265
4
3,719
3,090
3
2,326
2
1,282
1
–7
Pf ≈ 10 –b
–6
–5
–4
–3
–2
–1
–0,301
0
lg Pf
при b = 1 … 4 (из зарубежных
Более точно (ВГС):
источников)
Pf ≈ 10 – ( b /4 + 0,6
2
при b = 1 … 5

6.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Коэффициенты Стьюдента ta, n
a
0,10
0, 05
0,02
0,01
0,005
0,002
0,001
1
6,314
12,706
31,821
63,657
127,3
318,3
636,6
2
2,920
4,303
6,965
9,925
14,089
22,327
31,598
3
2,353
3,182
4,541
5,841
7,453
10,214
12,941
4
2,132
2,776
3,747
4,604
5,597
7,173
8,610
5
2,015
2,571
3,365
4,032
4,773
5,893
6,859
6
1,943
2,447
3,143
3,707
4,317
5,208
5,959
7
1,895
2,365
2,998
3,499
4,029
4,785
5,405
8
1,860
2,306
2,896
3,355
3,833
4,501
5,041
9
1,833
2,262
2,821
3,250
3,690
4,291
4,781
10
1,812
2,298
2,764
3,169
3,581
4,144
4,587
12
1,782
2,179
2,681
3,055
3,428
3,930
4,318
14
1,761
2,145
2,624
2,977
3,326
3,787
4,140
16
1,746
2,120
2,583
2,921
3,252
3,686
4,015
18
1,734
2,101
2,552
2,878
3,193
3,610
3,922
20
1,725
2,086
2,528
2,845
3,153
3,552
3,849
22
1,717
2,074
2,508
2,819
3,119
3,505
3,792
24
1,711
2,064
2,492
2,797
3,092
3,467
3,745
26
1,706
2,056
2,479
2,779
3,067
3,435
3,707
28
1,701
2,048
2,467
2,763
3,047
3,408
3,674
30
1,697
2,042
2,457
2,750
3,030
3,386
3,646
1,645
1,960
2,326
2,576
2,807
3,090
3,291
n –1
tα , u P u 1 α
u1 P u α
1
2
2
P (x ~
x x ) = 1 – a
px (x)
α
2
α
2
x–
x
x+
x
Dx Dx
[ x –, x +] –
доверительный интервал
значений с.в. x
x Δ x ~
x x Δ x
xmax x Δ x
min
Δ x xˆ tα ,

7.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
F
Пример 1
b
F
h
a
Для балки, схема которой в случае детерминистического расчёта
показана на рисунке, определить с требуемой вероятностью Ps
доверительный интервал значений наибольшего нормального
напряжения в поперечных сечениях.
a
l
Решение
M
Fa
1. Детерминистический расчёт
Fa
Наибольшее нормальное напряжение в балке
σ
2. Вероятностный расчёт
max
σM M
W
max
M max
Fa
W
bh2 / 6
Формирование вероятностной расчётной схемы
~
F1
x
~γ
~ i
~
F2
а)
Fi
~ ~
F1 b
y
i = 1, 2
~
h (x)
c~1
a~1
j( ~
y j, ~
z j)
~
β1
~
β2
a~2
~
l
~
σ
c~2
~
M
~
σM ~
max
W
z
e~i
~
M max
~
W
max
~
h
~
F2
~
l
~ ~
~
~ ~ ~
X F1 F2 l a~1 a~2 b h
~ a~1 ~ a~1 a~2
6
~
σM ~ ~ 2 F1 a~1 1 ~ F2 ~
l
bh
l
F1 F2 , Fˆ1 Fˆ2 ,
a1 a2 , aˆ1 aˆ2
a~2
a~1
~
M1
n 7
~
M
~
M2
~ ~ a~1 ~ a~1 a~2
~
~
M max M 1 F1 a1 1 ~ F2 ~
l
l

8.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Математическое ожидание напряжения
6F0 a0
a1
a
a
1
2
6
σM σM ( X ) 2 F1 a1 1 F2
2 σ M , теор ,
l b0h0
bh
l
где
F0 , a0 , b0 и h0 – теоретические (проектные) значения величин
Стандарт напряжения (по МСЛ):
σM
F1
X X
a
6 2 a1 1 1
bh l
X X
σ
σˆ M M
i 1 xi
n
σM
F2
6a
a
02 (1 α) 1 α σM , где α 0
F0
l0
b0h0
σM
a1
2a
a
6 2 F1 1 1 F2 2
l
l
bh
X X
σM
l
a
aa
6 2 F1a1 21 F2 12 2
bh
l
l
X X
X X
0
X X
(симметрия)
σM
a2
6F0 (1 α) 1 α
σ
a0 M
b0h02l
X X
6a a
12 2
bh l
X X
xˆi
X X
X X
X X
a
aa
123 F1a1 1 1 F2 1 2
l
bh
l
6a02
α σ
M
2
b0h0 l F0
6F0α α
6F2 a1
σM
bh2 l X X b0h02 a0
σM
26 2 F1a1 1 a1 F2 a1a2
b X X
l
bh l
σ M
h
2
X X
X X
6F20a20 1 σM
b0
b0 h0
12F0a0
2 σM
3
h0
b0 h0

9.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
2
σˆ M σM
2
2
2
2
2
1 α ˆ α ˆ 1 α α 1 ˆ 2 ˆ
F F1 F F2 a aˆ1 a aˆ2 b b h h
0
0 0
0 0 0
ˆ M σM
σ
(1 α) 2 AF21 α2 AF22 (1 α) 2 Aa21 α2 Aa22 Ab2 4 Ah2
σM
(1 2α 2α2 )( AF2 Aa2) Ab2 4 Ah2 ,
AF AF1 AF2 Fˆ1 / F0 Fˆ2 / F0 ; Aa .Aa1 Aa2 aˆ1 / a0 aˆ2 / a0; Ab bˆ / b0; Ah hˆ / h0
коэффициенты вариации входных параметров
Коэффициент вариации напряжения
AσM
при AF = 0,06;
AσM
σˆ M
σM
γ ( AF2 Aa2) Ab2 4 Ah2 , g = 1 – 2a + 2a2
(1 γ 1/ 2 при 0 α 1/ 2 )
aˆ = 0,005 l0 ( Aa = 0,005/a ); Ab = Ah = 0,01:
0,0052
γ (0,06 2 ) 0,012 4 0,012 10 2 (1 2α 2α2 )(36 1 2) 5
α
4α
2

10.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
A
, 10 – 2
σ
M
AσM (F )
a
Aσ M
0
6,000
0,1
7,418
5,433
7
0,2
5,808
4,948
6
0,25
5,477
4,743
0,3
5,243
4,569
0,4
4,953
4,327
0,5
4,848
4,243
8
AσM
5
4
AσM (F )
0
0,1
0,2
0,3
0,4
0,5
a
Определение доверительного интервала значений напряжения в балке
Dσ M
ДИ σM σM
Dσ M
Для симметричного
распределения:
ДИ σM σM DσM
DσM σˆ M u
ДИ σM σM ( 1 Aσ u P ) .
M
При
при
Ps = 0,95: u
при Ps = 0,99: u
Pσ
σ
a = 0,25: Aσ M = 5,477∙10 –2 ;
2
=
1,960;
ДИ
σ
σ
(
1
5
,
477
10
1,96 ) σM (1 0,107 );
M
M
0,95
= 2,576; ДИ σ σ ( 1 0,141 ).
0,99
M
M

11.

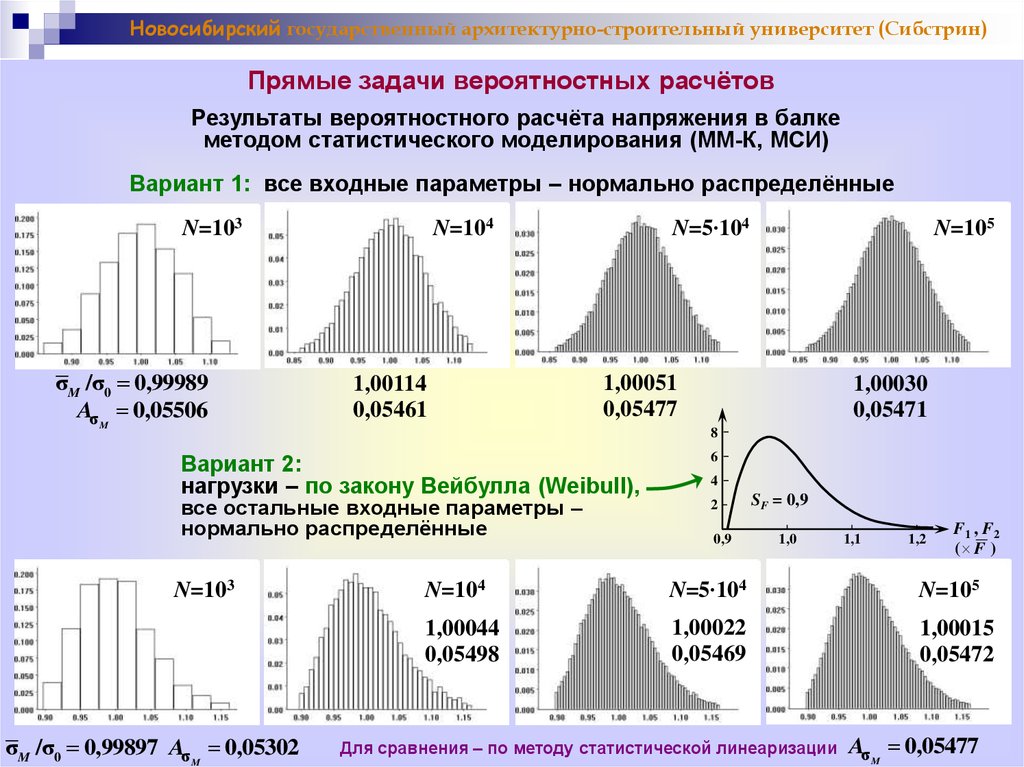
Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Результаты вероятностного расчёта напряжения в балке
методом статистического моделирования (ММ-К, МСИ)
Вариант 1: все входные параметры – нормально распределённые
N=103
σM /σ0 0,99989
AσM 0,05506
N=104
1,00114
0,05461
N=5∙104
1,00051
0,05477
все остальные входные параметры –
нормально распределённые
σM /σ0 0,99897 AσM 0,05302
1,00030
0,05471
8
Вариант 2:
нагрузки – по закону Вейбулла (Weibull),
N=103
N=105
6
4
2
0,9
SF = 0,9
1,0
1,1
1,2
F1 , F2
( F )
N=104
N=5∙104
N=105
1,00044
0,05498
1,00022
0,05469
1,00015
0,05472
Для сравнения – по методу статистической линеаризации
AσM 0,05477

12.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 1
учетом функциональной зависимости
(вариант с учётом
между входными параметрами)
а) зависимые нагрузки
~
F1
a~1
~
~F
b
~
h
Решение
~ ~ ~
F 2 F F1
a~2
~
l
~1 ~ ~ a
~1 a
~2
~~ a
~
M max F1 a1 1 ~ (F F1) ~
σM
F1
σM
F
Условие : F1 F2 F / 2
l
l
6 2 a1 1 a1 a2
6a02 (1 2α) 1 2α σM ;
F0
l l X X b0 h0
X X bh
6a
aa
62 1 2
02 α α σM ;
l X X b0h0
F0
bh
X X
Вклад нагрузок в коэффициент вариации напряжения:
2
AσM (F )
2
ˆ
ˆ
( 1 2α )2 F1 α2 F
F0
F0
AF
2
2
ˆ
ˆ
( 1 2α )2 F1 α2 2F1
F0
F0
В исходном решении:
( 1 2α )2 ( 2α )2 AF 1 4α 8α 2 A
σ
ˆ
M (F )
AF
1 2α 2α2
Коэффициент вариации напряжения:
AσM
(1 4α 8α2) AF2 γ Aa2 Ab2 4Ah2 10 2 411 ( 1 2α) 1 2 144α .
2
4α

13.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 1
(вариант с учётом функциональной зависимости
между входными параметрами)
a
Aσ M
AσM (F )
0
6,000
8
0,1
7,070
4,948
7
0,2
5,289
4,327
0,25
5,050
4,243
0,3
5,033
4,327
0,4
5,504
4,948
0,5
6,442
6,000
AσM , 10 – 2
AσM
6
5
4
AσM (F )
0
0,1
0,2
0,3
0,4
0,5
a

14.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 1
(вариант с учётом функциональной зависимости
между входными параметрами)
б) зависимые нагрузки и размеры
c~
~
F1
~ ~
b F
~
h
a~1
~
l
Решение
~
~ ~ a~1 ~ ~ a~1 ( l a~1 c~ )
~
M max F1 a1 1 ~ (F F1)
;
~
l
~ ~ ~
F 2 F F1 σM
a1c
62
6a02 (1 2α) 1 2α σM ;
F1 X X bh l X X b0h0
F0
σM
F
a~2
Условие : F1 F2 F / 2
~1 a~2 c~ ~
Дополнител ьно : a
l
σM
a1
σM
c
σM
l
Коэффициент
вариации
напряжения: AσM
l
2
1 2α Fˆ1
F0
X X
6a1 a1 c
1
bh2 l l
X X
6a0
α σ ;
2α
F0 M
b0h0
2a
2a
6 2 F1 1 1 (F F1) 1 1 c
bh
l
l l
X X
X X
X X
2
α Fˆ
F0
6(F F1) a1 1
l
bh2
X X
X X
X X
1 2α aˆ1
a0
(1 2α)
σM ;
a0
1 σM ;
l
a1 c
6a1 a1
F
(
F
F
)
2
1
1
bh2
l2
l
2
2
1 cˆ
l
1 σM ;
l
2
1 lˆ
l
2
1 bˆ
b0
(1 4α 8α2) AF2 (1 2α)2( Aa2 Aс2) Al2 Ab2 4Ah2 .
2
2 hˆ
h0

15.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 1
(вариант с учётом функциональной зависимости
между входными параметрами)
При Ac = Al = 0,001:
AσM 10 2 36(1 4α 8α2) (1 2α)2 1 2 0,01 5,01 .
4α
AσM , 10 – 2
a
Aσ M
0
8
0,1
6,745
6,362
7
0,2
5,097
4,579
0,25
4,900
4,359
0,3
4,917
4,378
5
0,4
5,436
4,954
4
0,5
6,404
Aσ
M
(F , a)
6,000
6
AσM
Aσ
0
M
(F , a)
0,1
0,2
0,3
0,4
0,5
a

16.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 2
a~
1
~
M 01
Учёт стохастической зависимости (корреляции)
между входными параметрами
~
b
~
F
~
h
Т р е б у е т с я: определить предельную (разрушающую)
нагрузку * ), учитывая корреляцию пределов текучести
материала и пластических моментов сопротивления
сечений с пластическими шарнирами
~
l
Решение
~
Fu
~
V
2
~
M 02
~
h2
~
h1
~
b1
~
b2
Эпюра
~
M 01
изгибающих моментов
в предельном состоянии
~
M 02 ~
l a~
a~
* ) Условно прямая задача
Из условий равновесия балки в предельном состоянии
~ ~ ~
~
m1 V l Fu a~ M 01 0,
~ ~
~
m2прав V l a~ M 02 0
~
после исключения
Vполучается
s < ss
s = ss
s
ss
M0=ssWp
~
~ W~ s
~ b~ h~2 / 4 ;
M 01 s
s1 p1
s1 1 1
где ~
~
~ W s
~ b~ h~2 / 4
M 02 s
s2
p2
s2 2 2
e
~
M 02
~ 1 ~
Fu ~ M 01
,
~
~
a
1 a / l
~~~~~ ~ ~ ~
~
~
~
{
X
}
{
l a b1 h1 b2 h2 ss1 ss2 } (n 8)
Fu u ({ X})
Математическое ожидание предельной нагрузки:
a
2
Fu M0 2 a , где M0 ss b h / 4; α
l
l a a

17.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Дисперсия предельной нагрузки (по МСЛ):
8
8
Fu u u
xi x j
i 1 j 1 xi x j X X
Учитываемые ковариации:
h1h2 = h2h1 = kh hˆ1hˆ 2 kh h ; b1b2 = b2b1 = kb bˆ1bˆ 2 kb b; ss1ss2 = ss2ss1 = kσs σˆ s1σˆ s2 kσs σ
s
Fu
l
Fu
b1
Fu
b2
X X
X X
X X
M0
Fu
1
2
;
a
l
(1 a) 2
M0 1
Fu
;
h1
l ab
M0
Fu
1
;
h2
l a(1 a)b
X X
X X
X X
M 0 (2 a) 2 2
2
;
l
a (1 a) 2
M0 2
Fu
;
s s1
l ah
X X
M0
Fu
2
;
s s 2
l a(1 a)h
M0 1
;
l ass
X X
M0
1
.
l a(1 a) s s
2
2
2
2
2
M0
A
2 a 2 Aa2 Ab 2 Ah Ass
Fu
l
2
1
a
l
a
1
a
a a a
2
2
2
As s
Ab 2 Ah
2
2
2
2
a 1 a a 1 a a 1 a kb Ab 4kh Ah ks s As s .
a
1
a
2
2

18.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
После преобразований:
2 a 2
2
Fu Fu a Al
Aa Ab2 4 Ah2 As2 s
2 a a 1 a
2 1 a
2
2
2
2 kb A b 4 kh Ah kss A ss .
2 a
2
2
2
Учет смешанных дисперсий (парной корреляции)
величин
~ ~~
b , h, σ
s
для сечений 1 и 2.
l = 4 м; Al = 0,001; a = 2 м; Aа = 0,003; h = 20 см; Ah = 0,005;
b = 10 см; Ab = 0,005; σ s = 300 МПа; Ass = 0,08; kb = kh = 0,5; kss = 0,7.
Исходные данные:
Математическое ожидание:
M0 a
6M 0 3 s s b h 2 3 300 МПа 0,1 м (0,2 м)2
Fu
0,45 МН
2
4
м
a
a
2
l
l
l
2
4kb Ab2 4 1 4kh Ah2 1 4ks As2
Дисперсия: Fu Fu 1 Al2 Aa2
1
9
9
9 s s
9
Fu 0,1111 Al2 Aa2 1,2222 Ab2 4 Ah2 1,3111 As2s
2
= (0,45 МН)2*10 –4 * [0,1111*(0,12 +0,32 ) + 1,2222*(0,52 + 4*0,52 ) + 1,3111*82 ] =
= 0,17303*10–2 МН2
0,0111
1,5278
83,9104

19.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
Требуетс
я:
Получить статистические оценки наибольшего
F
по абсолютной величине напряжения в жёсткой ( короткой ) стойке,
в детерминистическом представлении испытывающей в упругой стадии
осевое сжатие c напряжением s0 = | s |max = F / A = F / (bh).
h
b
Формирование
стохастической расчётной модели
~
~0
~
αxz
x v
α xy
e~0 y ~
F
e~0 z ~
0
~
F
F
x
x
Решение
Стержень испытывает сжатие с изгибом в двух
главных плоскостях. Для плоскости x0y:
e~
~
f
~
b
~
l
~
~ h( x)
v
*
y
z
y
0
~ (x) –
Замечание: v
*
начальное несовершенство
(погибь), не прогиб!
Математическое
ожидание
напряжения:
~
~
F | M | max ,
~σ | ~σ | | ~σ |
~
~
~ ~2
0
N
M max
bh / 6
~
~ ~ ~ b~h
| M | max F | e0 v0 v (x) | max
~
~ ~ ~ ~
~ *~
~
F | e0 v0 f | F | D | F e~ ; e~ | D |;
~ ~ ~ ~
~ ~
~
~
~
F e
6 e D e0 v0 f .
F
F
~
σ0 ~ ~ ~ ~2 ~ ~ 1 ~ .
b h b h /6 b h
h
~ ~
~
~
~
~
σ0 ~
σ0 ( X ), где X { F e~ b h } ( n 4 ).
6e
6e
σ0 F 1 | σN | 1 , | σN | F /(b h ).
bh
h
h

20.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Стандарт ( по методу статистической линеаризации ):
2
σ
0
σˆ 0
xˆi ,
i 1 xi
X
X
где σ0
1 1 6e | σN | 1 1 6e ; σ0
F 6 | σN | 6 ;
F X X b h h
F h
e X X b h h
h
σ0
F2 1 6e | σN | 1 1 6e ;
b X X
b h
b h h
σ0
F 2 1 12e | σN | 1 1 12e ;
h X X
h
h
h
bh
4
2
σˆ 0 | σN |
2
2
6e 2
eˆ 6e 2 12e 2
1
A
36
F
1 Ab 1
Ah
h
h
h h
2
| σN |
2
2
2
6e 2
eˆ 12e 2
2
1
(
A
A
)
36
F b
1
Ah .
h
h
h

21.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Коэффициент вариации напряжения:
Aσ0 σˆ 0
σ0
2
6e
2
2
AF Ab 1
h
2 12 e 2
36 eˆ 1 Ah2 .
h h
Исходные данные
Ab = Ah = 0,007; AF – в двух вариантах: 0 и 0,08; e0 v0 f 0 ; vˆ0 fˆ l /400
( по СНиП, допустимое отклонение кирпичной стены от вертикали – 3 см на этаж );
~
~~
ρ W/A – ядровое расстояние; для прямоугольного сечения ~
ρ h /6,
eˆ0 ρ /10 ( ~
тогда
eˆ0 h /60).
Математическое ожидание и дисперсия эксцентриситета
~
e~ | Δ |
через вероятностные характеристики случайной величины
жение):
2
2
e Δ pΔ (Δ ) dΔ
e
Δ
2
2
π
~
~0 ~
Δ e~0 v
f (см. Прило-
ˆ 0,8Δ
ˆ ; Δˆ eˆ20 vˆ 20 fˆ 2
Δ
2
pΔ (Δ ) dΔ e 1 Δ 0,3634Δ
π
Вычислив
2
ˆ 5 10 2 h 1 0,045β2
Δ
3
~
Δ 2 определяются
, где
eˆ 0,6 Δˆ
β l/h, находим
σ0 α1σN ; σˆ 0 σN α12( AF2 0,0072) (0,0603k)2 (0,007α2)2
( здесь k 1 0,045 β2 ; α1 1 0,08k ; α2 1 0,16k )

22.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Коэффициент вариации напряжения:
2
Aσ0 10
AF
36,0125k 2 0,1568k 0,49
( 100AF ) 0,49
( 1 0,08k) 2
σ0
α
1
Aσ0
σN
2
b
0,20
0
4
8
12
16
0,15
0,08
0,0979
0,1076
0,1301
0,1570
0,1841
0,10
0
0,0565
0,0720
0,1026
0,1351
0,1658
0,05
a1
1,080
1,105
1,158
1,219
1,283
1,4
Aσ0
1,3
AF = 0,08
1,2
AF = 0
В ы в о д ы:
0
a1
4
8
1,1
12
1,0
16
β l
h
1. Основное влияние на вариативность напряжений в стойке имеют начальные
несовершенства геометрии оси стержня и эксцентричность приложения нагрузки.
2. Для очень массивных колонн ( 0 β 4) в бόльшей степени сказывается влияние
случайного эксцентриситета нагрузки, а с увеличением гибкости преобладающим
становится влияние начальных искривлений стержня.
Доверительный интервал значений наибольшего напряжения в стойке
При b = 8, AF = 0,08
и доверительной
вероятности
Pσ0 = 0,99 : σ0 σ0
( | u |Pσ0 2,576)
σ0 σ0 ( 1 Aσ0 | u |Pσ0 )
0,711
0,546 При b = 12:
( 1 0,335) | σN | 1 0,230 σ0 σ0( 1 0,404) | σN | 1 0,273

23.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
П р и л о ж е н и е к примеру 3
Вероятностные характеристики абсолютной величины функции случайного аргумента
~
~ ~
~
~
~ ~
f ), используем
Рассматривая e как функцию от Δ ( e~ | Δ | Δ 2 , Δ e~0 v
0
формулы для определения математического ожидания и дисперсии функции
одного аргумента:
e
Δ pΔ (Δ ) dΔ ; e
2
Δ
2
2
pΔ (Δ ) dΔ e 2
~
~
~
Если распределения e0 , v0 и f – нормальные, то и распределение их суммы
получается также нормальным:
pΔ (Δ ) 1
2πΔ
pe (e)
e
тогда e
Δ
2
2
Δ
2
e
e
2
Δ
e 2Δ ,
2
πΔ
t=
t
e Δ dt
0
Δ2
1 e 2Δ dΔ 2
2πΔ
2πΔ
t 2
2 Δ e Δ
πΔ
2
Δ
Δe 2Δ dΔ
0
2Δ ( 0 1)
π
0
D2/2
2 Δˆ
π
ˆ 0,8 Δ
ˆ;
0,798Δ
2
2
pΔ (Δ ) dΔ e Δ pΔ (Δ ) dΔ e Δ e Δ 1 0,3634Δ
π
2
2
Коэффициент вариации величины
2
eˆ 0,603Δˆ 0,6 Δˆ
0,603
0,756.
e~ : Ae eˆ/e
0,798

24.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
1. Учёт пространственного изгиба
~
~
~ |M
|
M
|
y |
F
~
~
~
~
z
σ0 | σN | | σM z | | σMy | max ~ ~ ~ ~2 ~2 ~
bh bh / 6 b h / 6
max
~
~
~ ~
~ ~
~
6
F
|
D
|
e
6
F
|
D
|
ez
y
~
z
~F~ ~1~ ~ y
|
σ
|
1
6
~ ~ ;
N
b
bh bh h
h b max
max
~
~
~
~ w
~ (x) |
F
~
| σN | ~ ~ ; e~y | D y | | e~0 y ~v0 ~v*(x) |; e~z | D z | | e~0z w
0
*
bh
Математическое ожидание напряжения:
ey e
σ0 |σN | 1 6 z ; |σN | F ;
bh
h b max
Стандарт:
2
eˆy 2 eˆ 2 6ey 12e 2
ey ez 2
12
e
y 6ez
2
2
z
z
1
6
A
36
1
A
1
A
F
b
h
h b
h b
h
b
h
b
2
σˆ 0 | σN |

25.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
1. Учёт пространственного изгиба
Коэффициент вариации напряжения:
2
Aσ0 10
72 1,62 αс β2 { 2,064 14,4 10 4αс β2 0,48 (ky kz) 0,0512 ky kz } (100 Ab)2
(100 AF )
[1 0,08 (ky kz)]2
2
2
2
αс 1 h ;
b
β l ; ky 1 0,045 β ; kz 1 0,045 h β
h
b
h = 0,5
h =2
Значения Aσ при
Значения Aσ при
0
0
b
b
b
b
8
12
8
12
AF
AF
0,1130
0,1418
0,1690
0,2157
0
0
0,08
0,1389
0,1629
0,08
0,1870
0,2301
Доверительный интервал
при AF = 0,08 и Pso = 0,99
для b =8 :
σ0 σ0( 1 0,482)
1,135
| σN | 1 0,254
2
Для сравнения – при учёте изгиба только в плоскости x0y
b
AF
0
0,08
8
12
0,1026
0,1301
0, 1351
0,1570
Доверительный интервал :
σ0 σ0( 1 0,335)
0,546
| σN | 1 0,230

26.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
2. Учёт эффекта продольно-поперечного изгиба
~~
~
2 ~ ~ ~3
6 e~
1
~ π2E
I
π
Eb h
F
~
Приближённо: σ0 ~ ~ 1 ~
, где Feil ~ 2
~
~
~
b h
h 1 F / Feil
(2l )
48l 2
2
3
π
E
b
h
эйлерова сила с математическим ожиданием Feil
и стандартом
2
48l
2
2
2
2
Fˆeil π b h2 Eˆ π E h2 bˆ π E b 2h hˆ 2π E h3 lˆ
48 l
48 l
16 l
48 l
2
π E b2h
48l
2
3
3
2
3
2
2
2
3
2
2
2
2
ˆ
ˆ
ˆ
ˆ
E b 3h 2l ; A A2 A2 9 A2 4 A2 .
E
b
h
l
Feil
E b h l
Математическое ожидание напряжения
6e
6e
1
σ0 F 1
| σN | 1 1 α1* | σN |,
bh
h 1 F / Feil
h 1 ξ
6e 1
*
где α1 1
; ξ F .
h 1 ξ
Feil

27.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
2. Учёт эффекта продольно-поперечного изгиба
Рассматривая эйлерову силу как дополнительный входной параметр, имеем
6e 1
α1* ξ
σ0
1
1
1
;
2 | σN |
F X X b h h (1 ξ )
F 1 ξ
| σN | F ;
bh
*
α
σ0
F
6
1
1 1
| σN |
;
e X X b h h 1 ξ
e
*
6e 1
α
σ0
F
2 1
| σN | 1 ;
b X X
b
b h h 1 ξ
*
12e 1
2α
σ0
F
2 1
| σN | 1 1 ;
h X X
h 1 ξ
h
bh
2
ξ2 α1* 1
ξ α1* 1
ξ
σ0
6
e
2
| σN |
| σN |
.
Feil X X
F 1 ξ
Feil 1 ξ
b h 1 ξ

28.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
2. Учёт эффекта продольно-поперечного изгиба
Стандарт и коэффициент вариации напряжения
2
*
α1 ξ
2
2
2
α1* 1
AF2 α1* 1 Ae2 (α1*)2 Ab2 2α1* 1 Ah2 ξ
σˆ 0 | σN |
AF2eil ;
1 ξ
1 ξ
2
*
α1 ξ
2
2 2
2 2
2
1
2
*
* 2 2
*
AF α1 1 Ae (α1) Ab 2α1 1 Ah ξ
Aσ0 *
AFeil .
α1 1 ξ
1 ξ
α1* 1
Для вычисления значений Aσ0 используем те же исходные данные, что и в расчёте
жёсткой стойки: Ab = Ah = 0,007; Ae = 0,756; AF – в двух вариантах: 0 и 0,08.
Дополнительно вводим коэффициенты вариации модуля упругости AE = 0,015 ,
длины Al = 0,001 и находим
AFeil AE2 Ab2 9 Ah2 4 Al2 10 2 1,52 0,7 2 9 0,7 2 4 0,12 0,0268 .
Задан
kF F / Feil0 0,25; Feil0 эйлерова сила для стойки с l / h = 6
x = F / Feil b2/144 ; α 1* 1
11,52 k
144 β 2
k 1 0,045 β 2

29.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Прямые задачи вероятностных расчётов
Пример 3
( дополнения )
2. Учёт эффекта продольно-поперечного изгиба
2
Aσ0 1*
α1
AF
0,08
0
b
4
8
10
0,0982
0,1142
0,1921
0,3401
1,080
0,0804
1,118
0,1675
1,284
α*1 σ0
| σN |
Aσ0
0
0,0569
α1*
2
α1* ξ 2
α1* 1
* 2
*
AF 0,57178 (α1 ) 1,14327 α1 0,57158 0,000718 ξ
.
1
ξ
1
ξ
0,3038
1,668
12
16
Не
определяется
0,30
2,0
0,25
AF = 0,08
0,20
AF = 0
Aσ0
1,6
0,15
При AF = 0,08 и Pσ0 = 0,99 :
для b = 8
для b = 10
σ0 σ0 (1 0,495 ) σ0 σ0 (1 0,876 )
0,919
2,128
σ0 | σN | 1 0,352 σ0 | σN | 1 0,793
1,8
0,10
1,4
α1*
1,2
0,05
0
4
8
12
1,0
16
b= l
h

30.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)

31.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Контрольные вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*) ;
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 18» )