Similar presentations:
Расчет эквивалентных сопротивлений линейных бесконечных цепей
1. Подготовка к региону. День первый.
Эквивалентные схемы.2.
3.
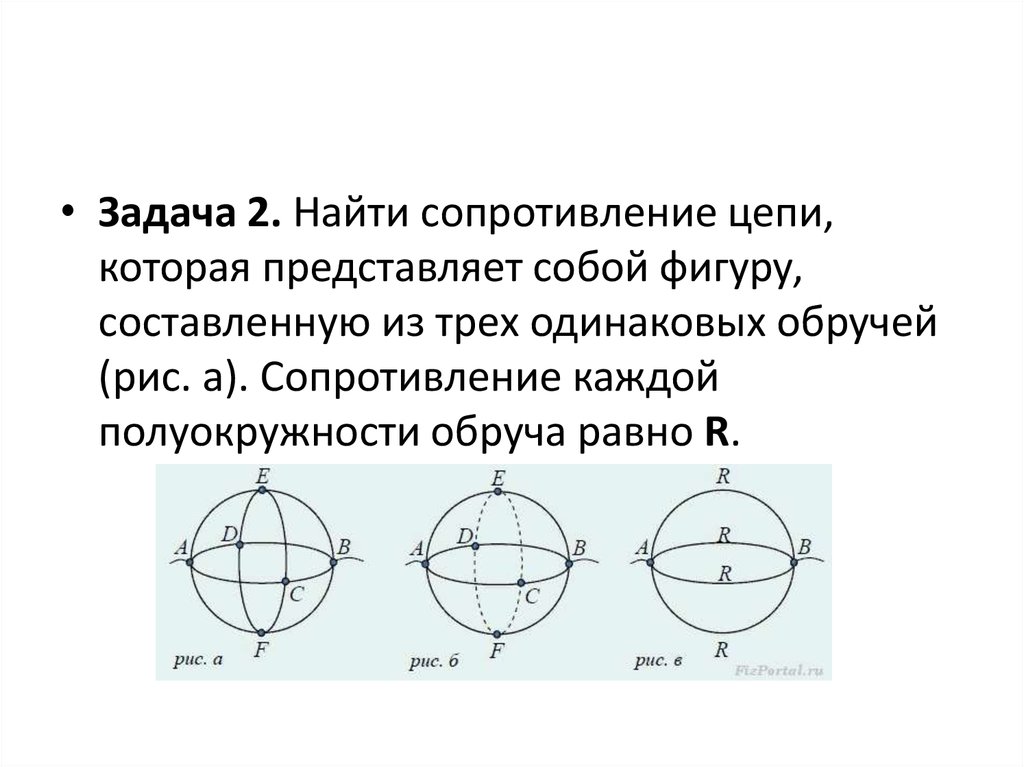
• Задача 2. Найти сопротивление цепи,которая представляет собой фигуру,
составленную из трех одинаковых обручей
(рис. а). Сопротивление каждой
полуокружности обруча равно R.
4.
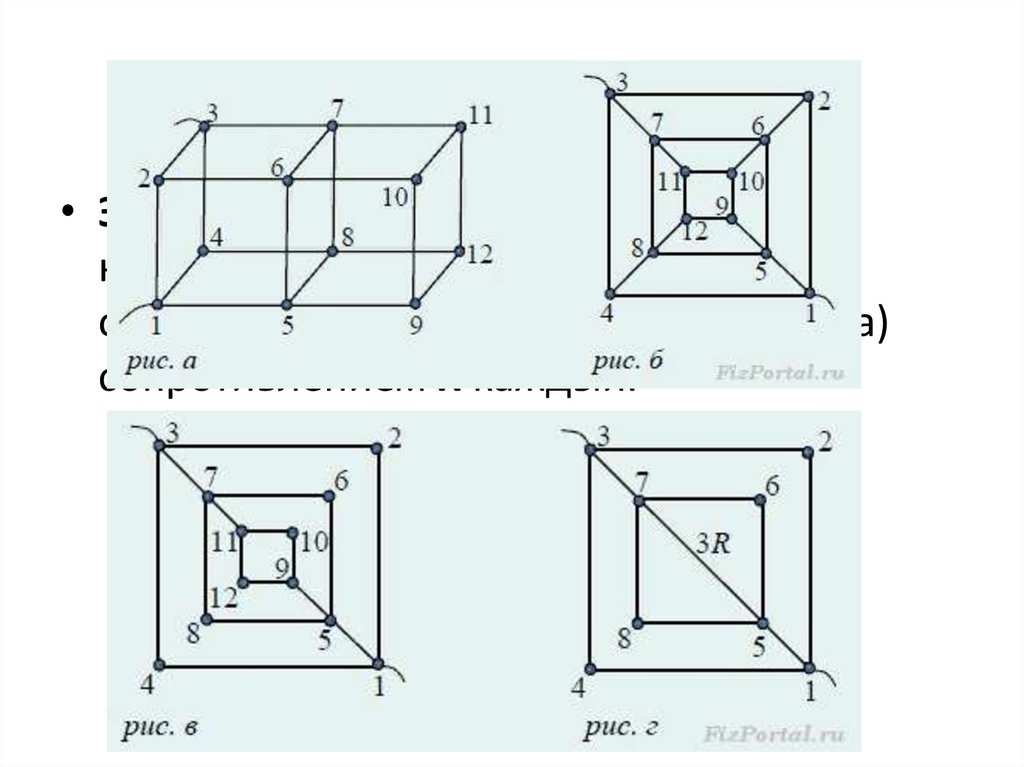
• Задача 3. Найти сопротивление цепи,которая представляет собой каркас из
одинаковых отрезков проволоки (рис. а)
сопротивлением R каждый.
5.
6.
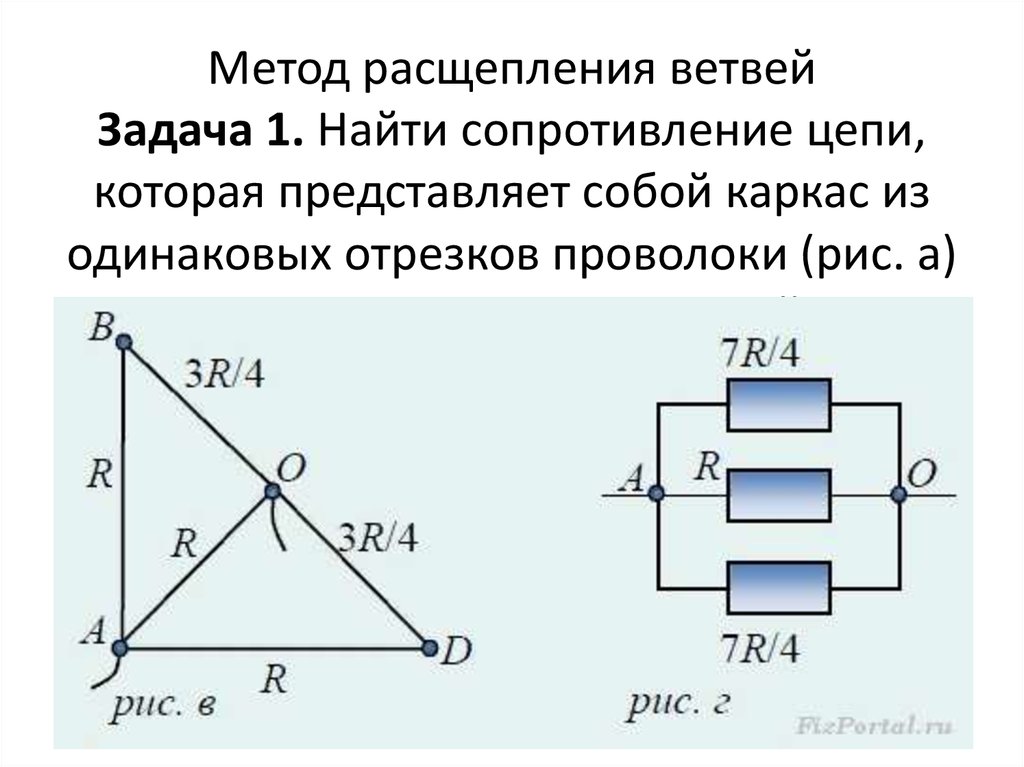
Метод расщепления ветвейЗадача 1. Найти сопротивление цепи,
которая представляет собой каркас из
одинаковых отрезков проволоки (рис. а)
сопротивлением R каждый.
7. Метод расщепления ветвей Задача 1. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки
8.
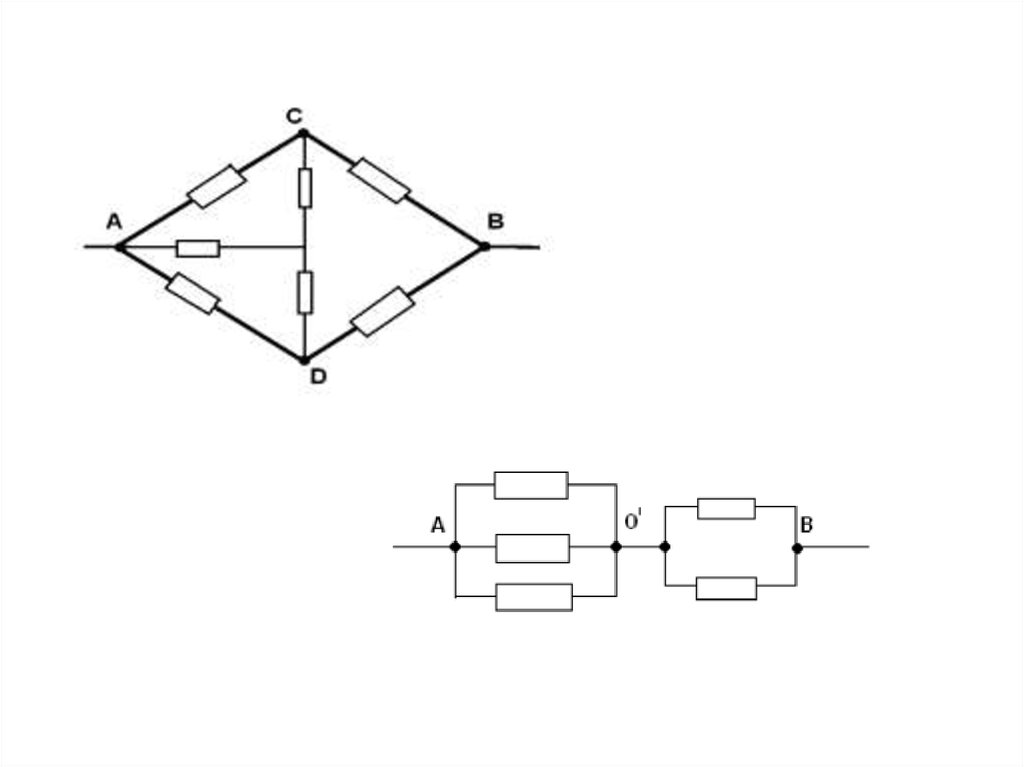
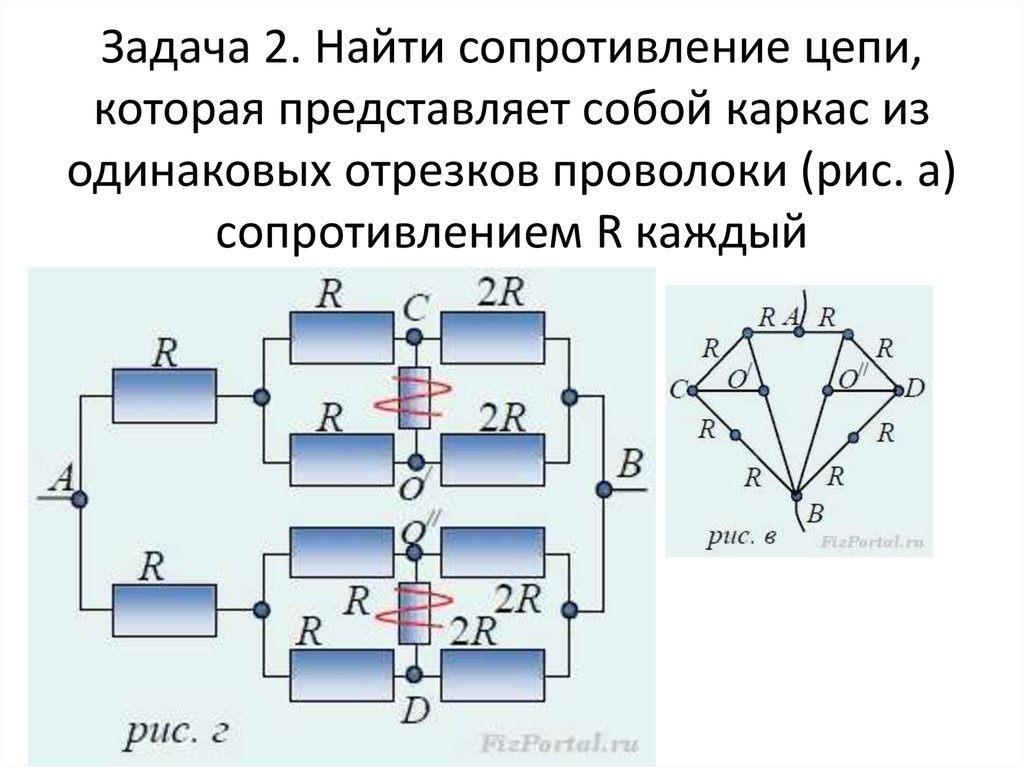
Задача 2. Найти сопротивление цепи,которая представляет собой каркас из
одинаковых отрезков проволоки (рис. а)
сопротивлением R каждый
9. Задача 2. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. а) сопротивлением
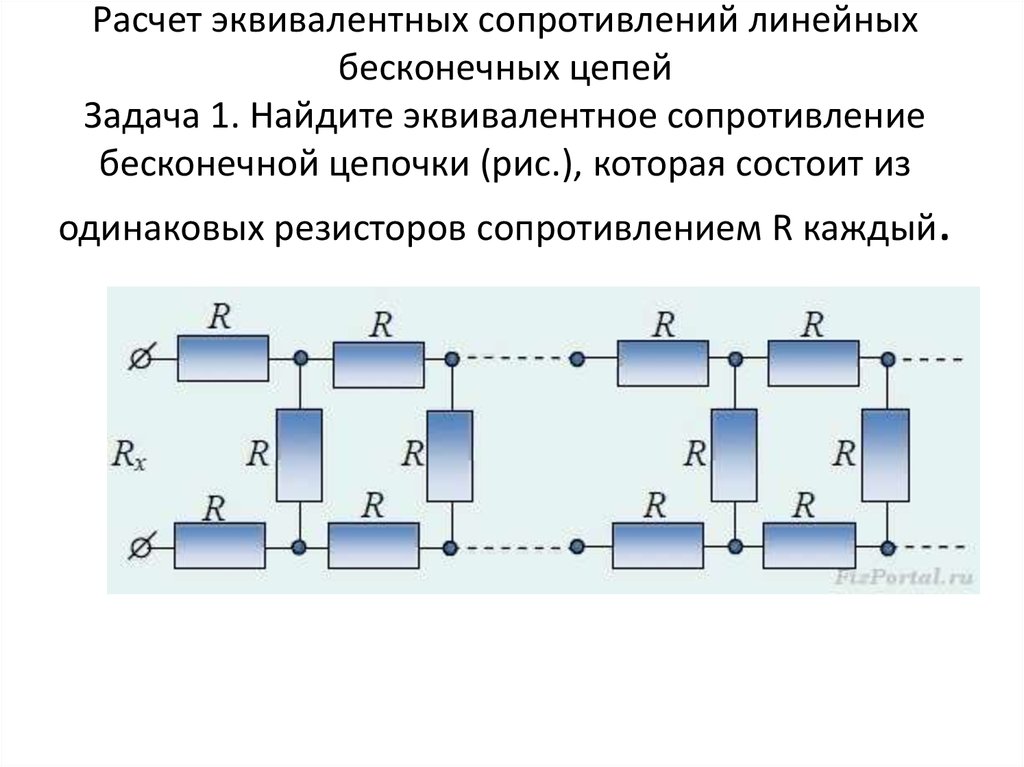
Расчет эквивалентных сопротивлений линейныхбесконечных цепей
Задача 1. Найдите эквивалентное сопротивление
бесконечной цепочки (рис.), которая состоит из
одинаковых резисторов сопротивлением R каждый.
10. Расчет эквивалентных сопротивлений линейных бесконечных цепей Задача 1. Найдите эквивалентное сопротивление бесконечной цепочки
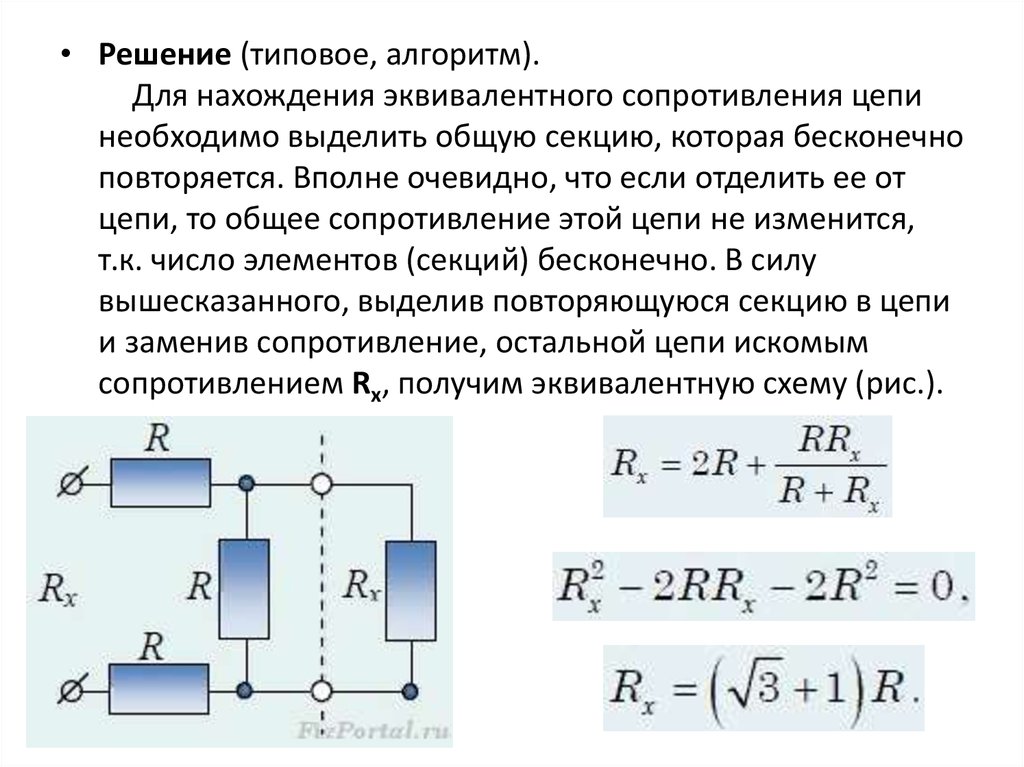
• Решение (типовое, алгоритм).Для нахождения эквивалентного сопротивления цепи
необходимо выделить общую секцию, которая бесконечно
повторяется. Вполне очевидно, что если отделить ее от
цепи, то общее сопротивление этой цепи не изменится,
т.к. число элементов (секций) бесконечно. В силу
вышесказанного, выделив повторяющуюся секцию в цепи
и заменив сопротивление, остальной цепи искомым
сопротивлением Rх, получим эквивалентную схему (рис.).
11.
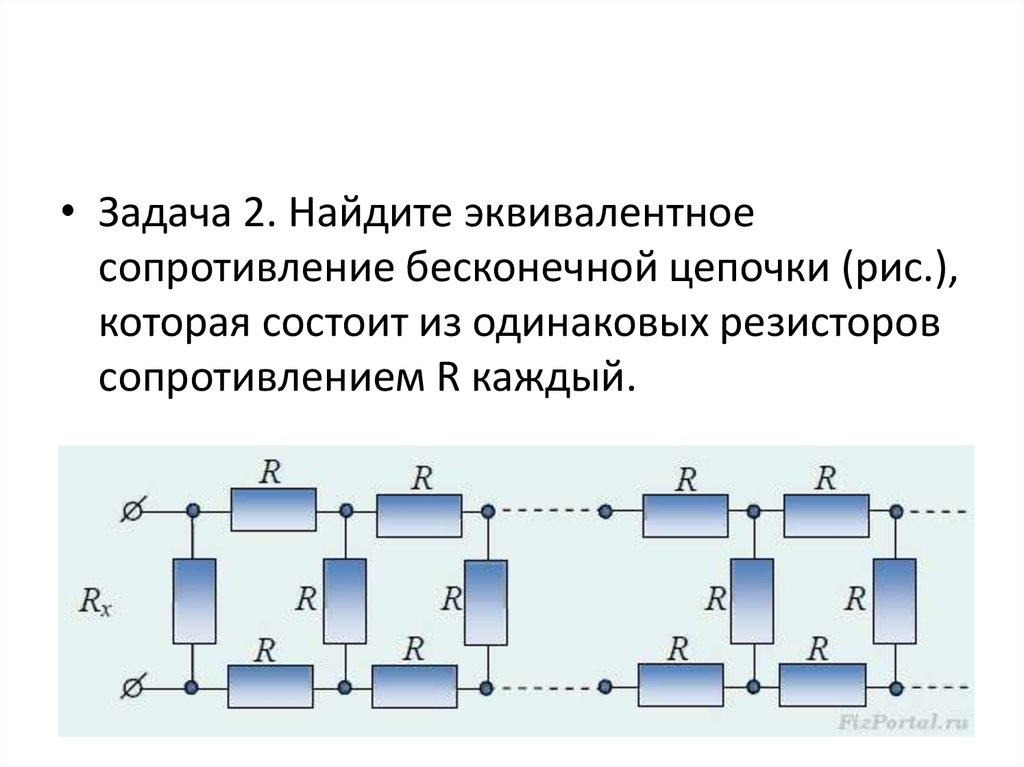
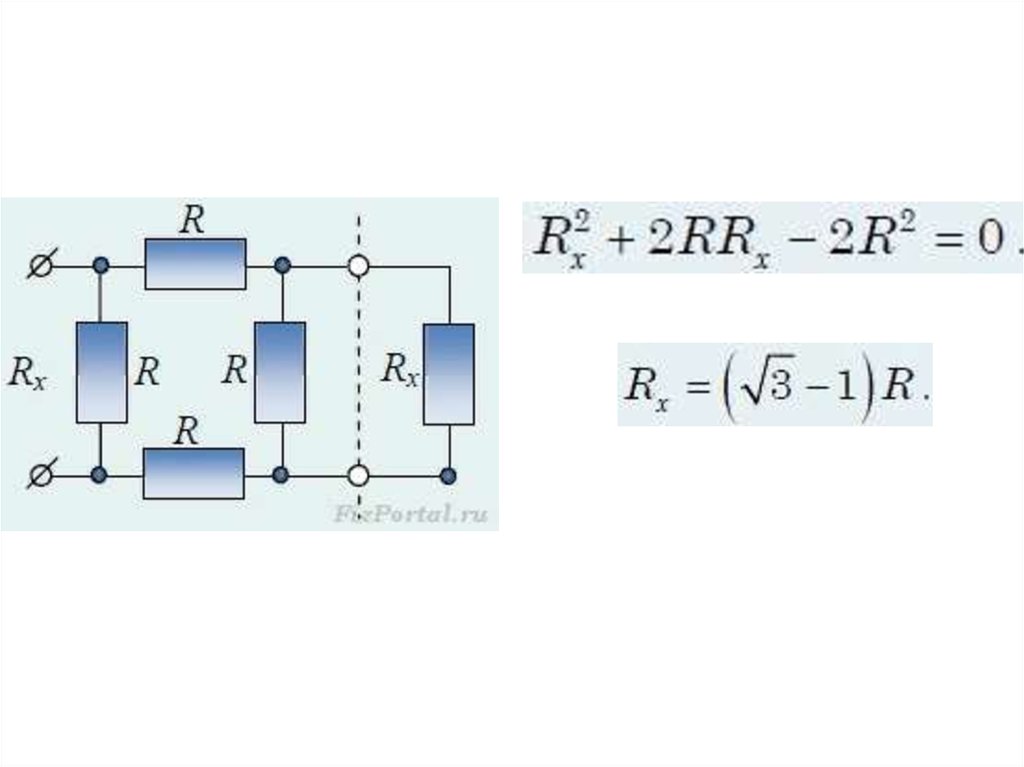
• Задача 2. Найдите эквивалентноесопротивление бесконечной цепочки (рис.),
которая состоит из одинаковых резисторов
сопротивлением R каждый.
12.
13.
14.
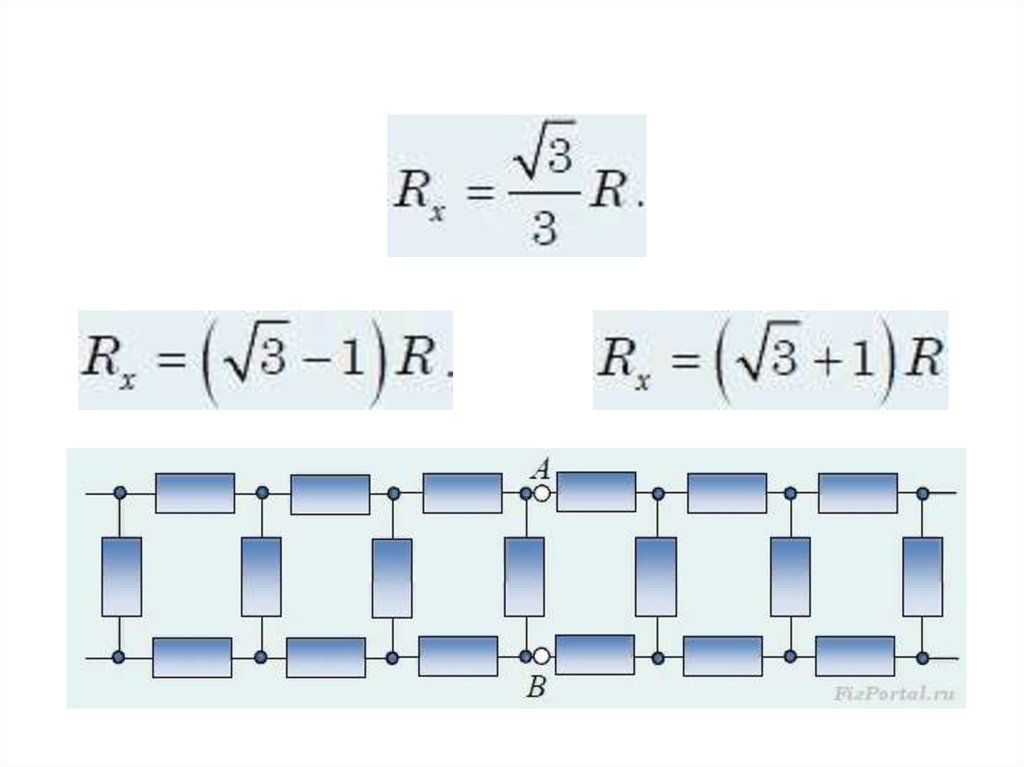
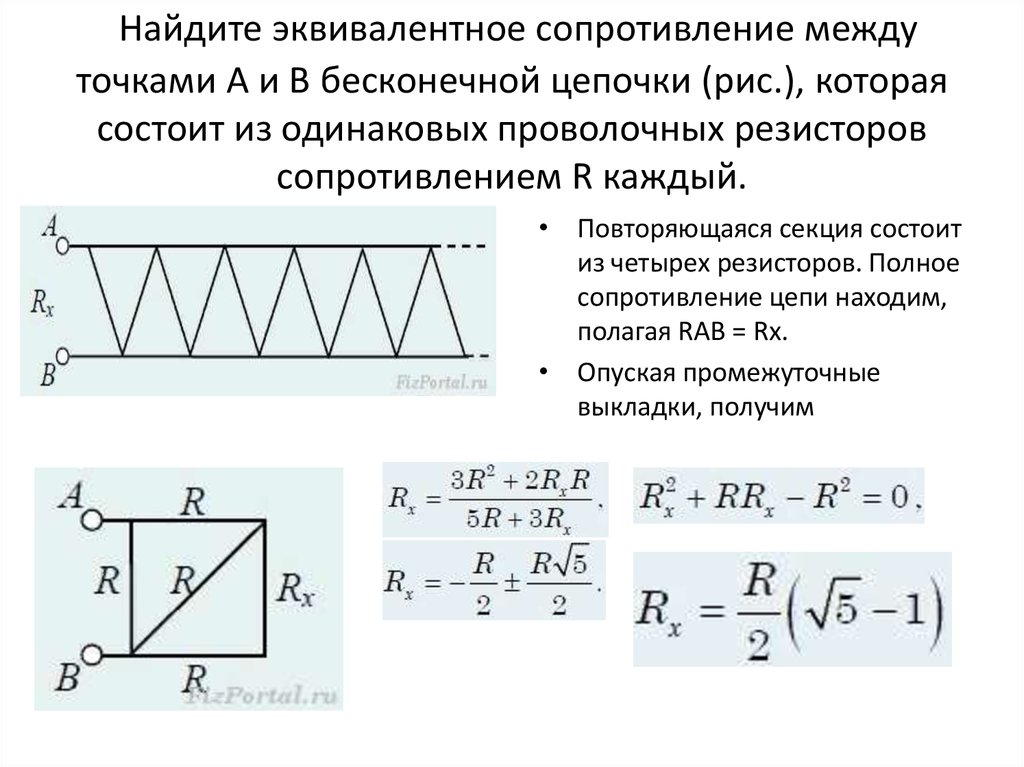
Найдите эквивалентное сопротивление междуточками А и В бесконечной цепочки (рис.), которая
состоит из одинаковых проволочных резисторов
сопротивлением R каждый.
• Повторяющаяся секция состоит
из четырех резисторов. Полное
сопротивление цепи находим,
полагая RAB = Rх.
• Опуская промежуточные
выкладки, получим
15. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых проволочных
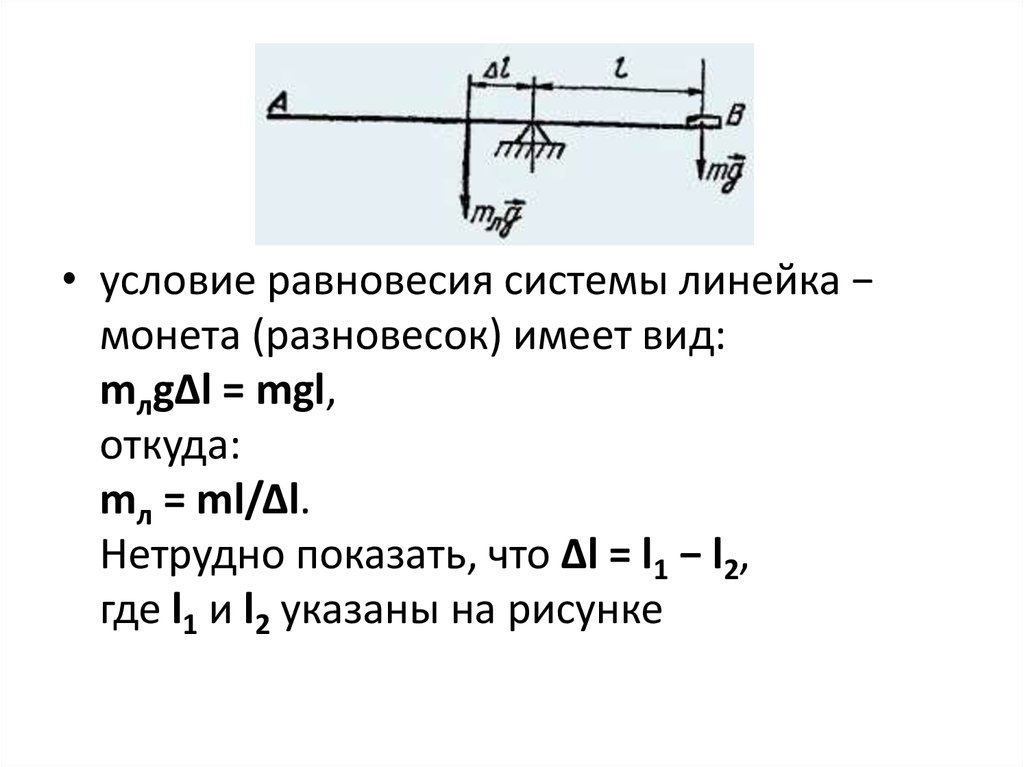
• Определить массу линейки.• Оборудование: ученическая линейка,
пятикопечная монета или линейка и
разновес.
16.
• условие равновесия системы линейка −монета (разновесок) имеет вид:
mлgΔl = mgl,
откуда:
mл = ml/Δl.
Нетрудно показать, что Δl = l1 − l2,
где l1 и l2 указаны на рисунке
17.
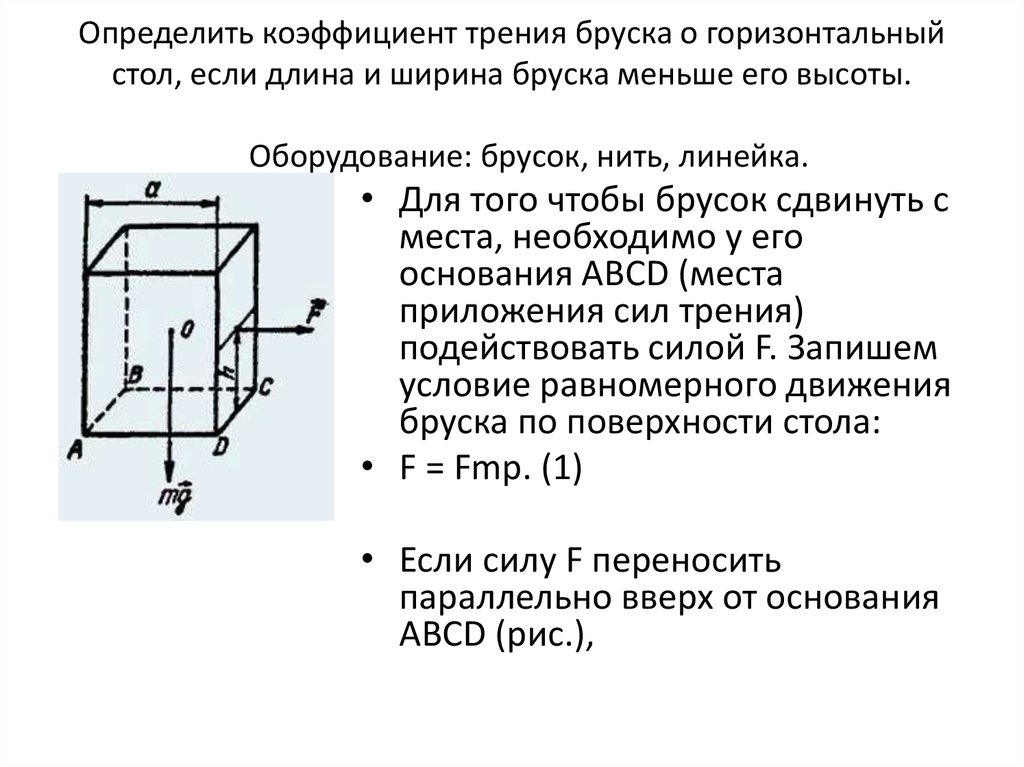
Определить коэффициент трения бруска о горизонтальныйстол, если длина и ширина бруска меньше его высоты.
Оборудование: брусок, нить, линейка.
• Для того чтобы брусок сдвинуть с
места, необходимо у его
основания ABCD (места
приложения сил трения)
подействовать силой F. Запишем
условие равномерного движения
бруска по поверхности стола:
• F = Fmp. (1)
• Если силу F переносить
параллельно вверх от основания
АВСD (рис.),
18. Определить коэффициент трения бруска о горизонтальный стол, если длина и ширина бруска меньше его высоты. Оборудование:
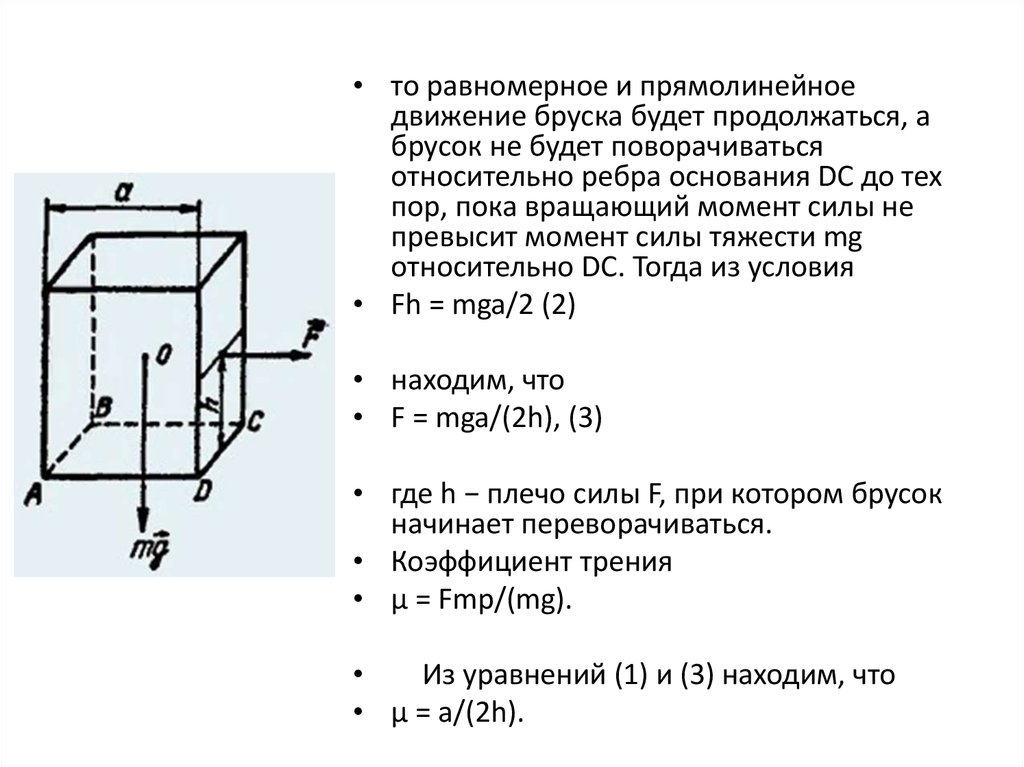
• то равномерное и прямолинейноедвижение бруска будет продолжаться, а
брусок не будет поворачиваться
относительно ребра основания DC до тех
пор, пока вращающий момент силы не
превысит момент силы тяжести mg
относительно DC. Тогда из условия
• Fh = mga/2 (2)
• находим, что
• F = mga/(2h), (3)
• где h − плечо силы F, при котором брусок
начинает переворачиваться.
• Коэффициент трения
• μ = Fmp/(mg).
Из уравнений (1) и (3) находим, что
• μ = a/(2h).
19.
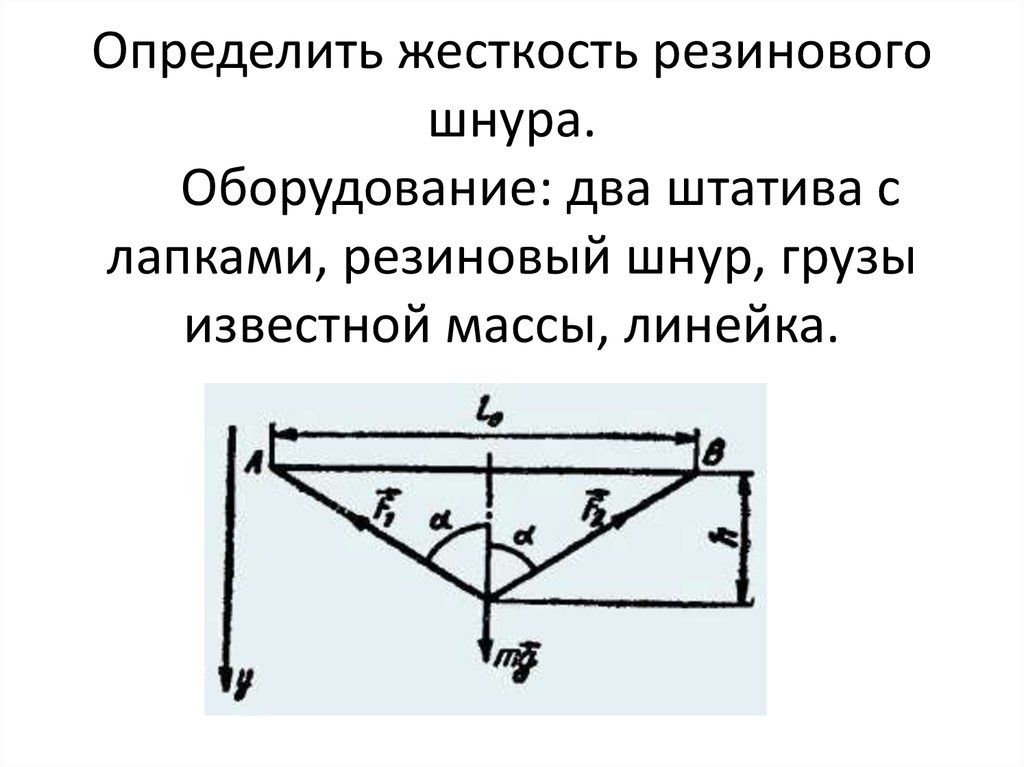
Определить жесткость резиновогошнура.
Оборудование: два штатива с
лапками, резиновый шнур, грузы
известной массы, линейка.
20. Определить жесткость резинового шнура. Оборудование: два штатива с лапками, резиновый шнур, грузы известной массы, линейка.
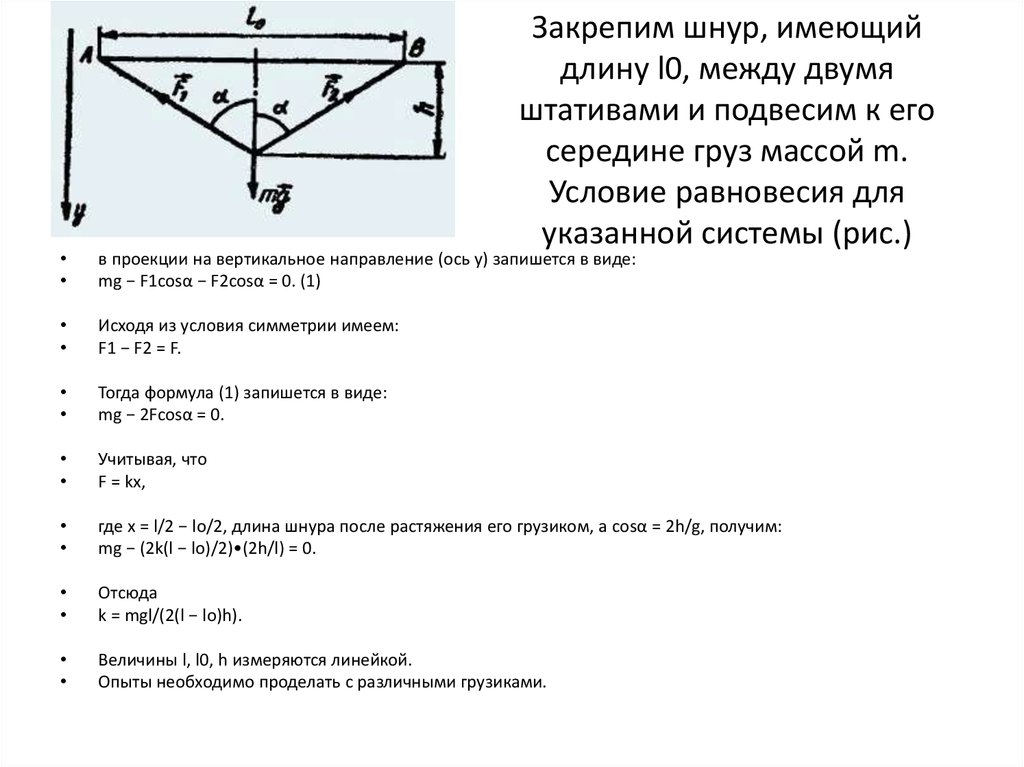
Закрепим шнур, имеющийдлину l0, между двумя
штативами и подвесим к его
середине груз массой m.
Условие равновесия для
указанной системы (рис.)
в проекции на вертикальное направление (ось y) запишется в виде:
mg − F1cosα − F2cosα = 0. (1)
Исходя из условия симметрии имеем:
F1 − F2 = F.
Тогда формула (1) запишется в виде:
mg − 2Fcosα = 0.
Учитывая, что
F = kx,
где x = l/2 − lo/2, длина шнура после растяжения его грузиком, а cosα = 2h/g, получим:
mg − (2k(l − lo)/2)•(2h/l) = 0.
Отсюда
k = mgl/(2(l − lo)h).
Величины l, l0, h измеряются линейкой.
Опыты необходимо проделать с различными грузиками.
21. Закрепим шнур, имеющий длину l0, между двумя штативами и подвесим к его середине груз массой m. Условие равновесия для
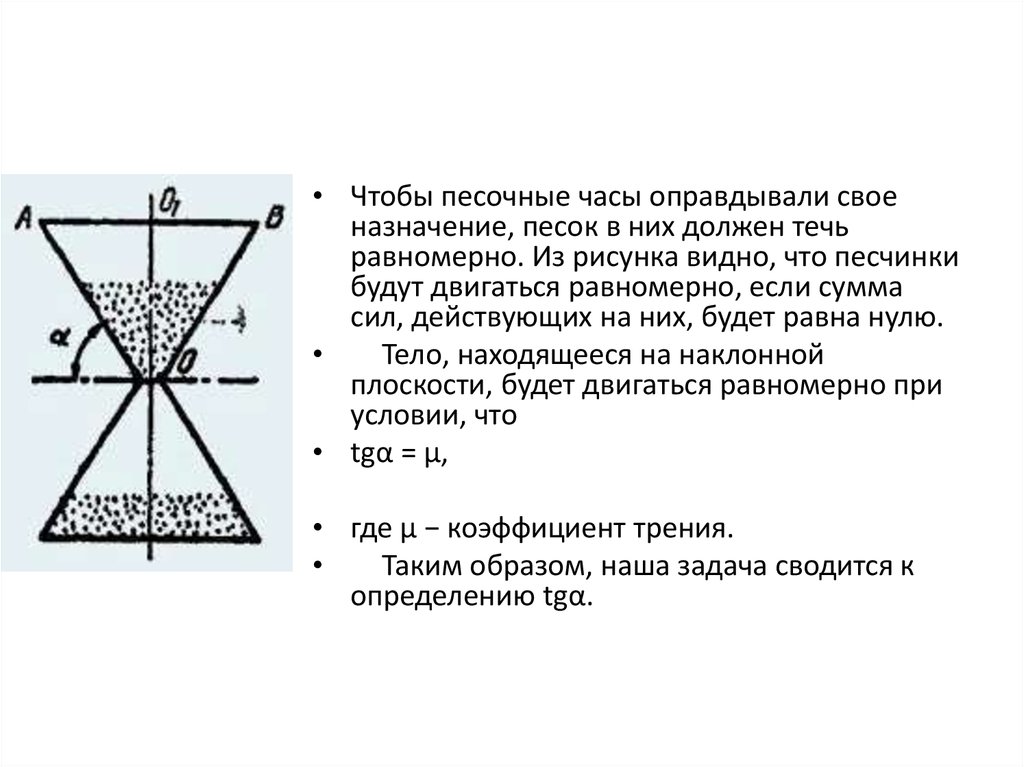
• Определить приближенное значениекоэффициента трения песка о стекло.
Оборудование: песочные часы, линейка.
22.
• Чтобы песочные часы оправдывали своеназначение, песок в них должен течь
равномерно. Из рисунка видно, что песчинки
будут двигаться равномерно, если сумма
сил, действующих на них, будет равна нулю.
Тело, находящееся на наклонной
плоскости, будет двигаться равномерно при
условии, что
• tgα = μ,
• где μ − коэффициент трения.
Таким образом, наша задача сводится к
определению tgα.
23.
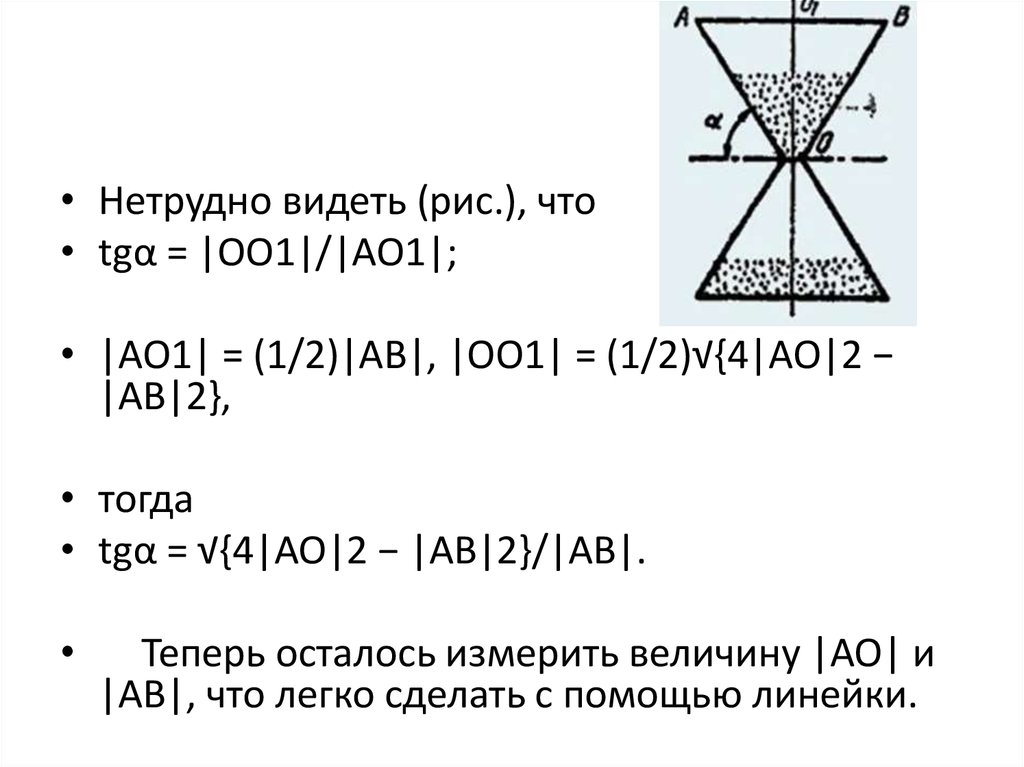
• Нетрудно видеть (рис.), что• tgα = |OO1|/|AO1|;
• |AO1| = (1/2)|AB|, |OO1| = (1/2)√{4|AO|2 −
|AB|2},
• тогда
• tgα = √{4|AO|2 − |AB|2}/|AB|.
Теперь осталось измерить величину |AO| и
|AB|, что легко сделать с помощью линейки.




 physics
physics