Similar presentations:
Задачи на построения с помощью циркуля и линейки
1. Задачи на построения с помощью циркуля и линейки
7 класс2.
Основныеэтапы
решения задачи на
построение
1 АНАЛИЗ
2. ПОСТРОЕНИЕ
3. ДОКАЗАТЕЛЬСТВО
4. ИССЛЕДОВАНИЕ
В том случае, когда при построении получаются равные фигуры,
будем считать, что задача имеет единственное решение.
3.
Условные обозначенияокр(О;г) - окружность с центром в точке О и
радиусом г
- знак угла
- знак принадлежности
- знак перпендикулярности
-
знак пересечения
- в скобках указано множество точек
пересечения
: - заменяет слова ”такой что”
4.
Задача 1Отложить от данного луча угол, равный данному
Дано:
К
луч ОМ
А
С
А
Построить:
KOM= А
О
В
Е
М
К1
Построение:
1. окр(А,г); г-любой
2. окр(А;г) А= В;С
3. окр(О,г)
4. окр(О,г) ОМ=
Е
5. окр(Е,ВC)
6. окр(Е,BС) окр(О,г)= К;К1
7. луч ОК; луч ОК1
8. КОМ -искомый
5.
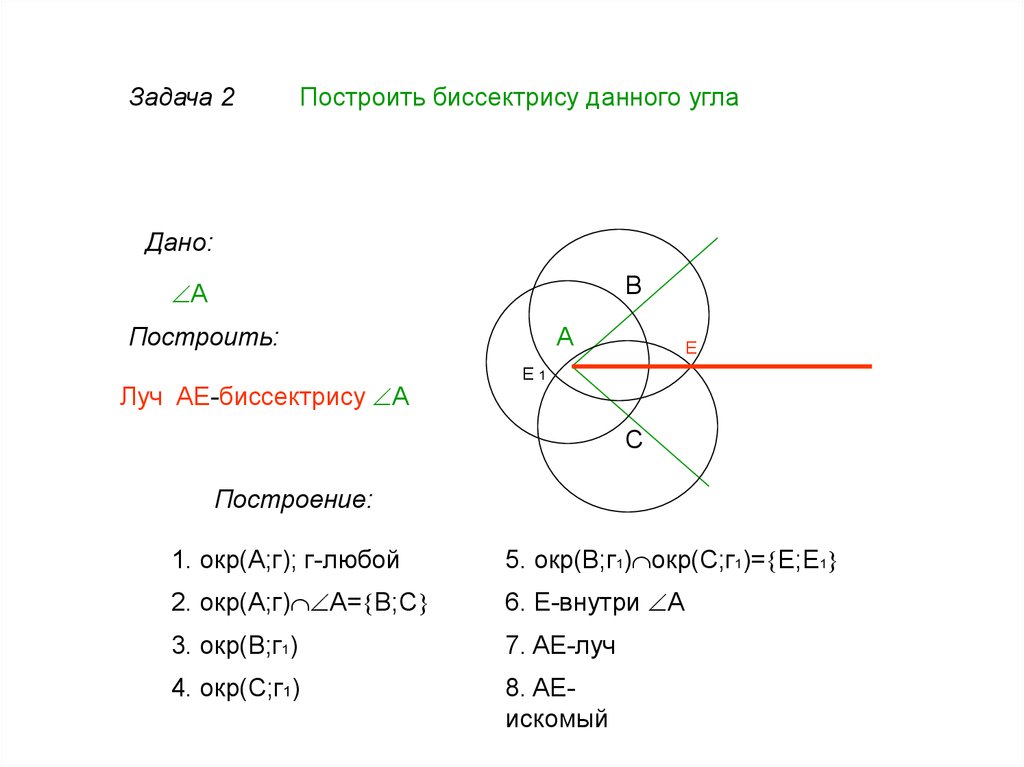
Задача 2Построить биссектрису данного угла
Дано:
B
А
Построить:
Луч AE-биссектрису А
А
E
Е
E1
C
Построение:
1. окр(А;г); г-любой
5. окр(В;г1) окр(С;г1)= Е;E1
2. окр(А;г) А= В;С
6. Е-внутри A
3. окр(В;г1)
7. AE-луч
4. окр(С;г1)
8. AEискомый
6.
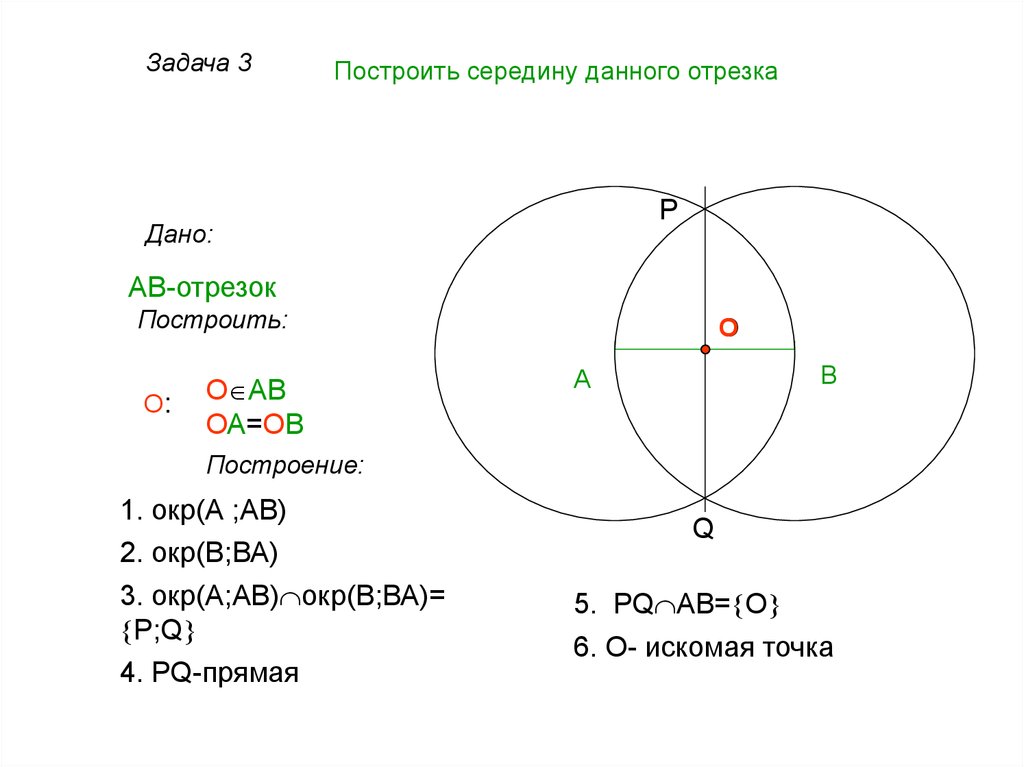
Задача 3Построить середину данного отрезка
P
Дано:
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
О
O
А
B
Построение:
1. окр(А ;АВ)
2. окр(В;ВА)
3. окр(А;АВ) окр(В;ВА)=
P;Q
4. PQ-прямая
Q
5. PQ AB= O
6. O- искомая точка




 mathematics
mathematics