25.30M

Category:

physics

Закономерности переноса носителей заряда в низкоразмерных структурах и приборы на их основе

1.

3. ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА
В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ
И ПРИБОРЫ НА ИХ ОСНОВЕ
3.1.
Транспорт носителей
заряда вдоль
потенциальных
барьеров
3.1.1. Интерференция электронных волн
3.1.2. Вольт-амперные характеристики низкоразмерных структур
3.1.3. Квантовый эффект Холла
3.1.4. Электронные приборы на интерференционном и баллистическом
эффектах
3.2.
3.3.
Транспорт носителей
заряда через
потенциальные
барьеры
3.2.1. Одноэлектронное туннелирование и электронные приборы на этом
эффекте
Спинтроника
3.3.1. Гигантское магнитосопротивление
3.2.2. Резонансное туннелирование и электронные приборы на этом
эффекте
3.3.2. Спин-контролируемое туннелирование
3.3.3. Управление спинами электронов в полупроводниках
3.3.4. Эффект Кондо
3.3.5. Электронные приборы на спиновых эффектах

2.

3.1. Транспорт носителей заряда вдоль потенциальных
барьеров
3.1.1. Интерференция электронных волн
Фазовая интерференция (phase interference of electron waves)
1 = A1exp(i 1)
2 = A2exp(i 2)
W = 1 + 2 2 = A12 + A22 + 2A1*A2cos( 1 - 2)
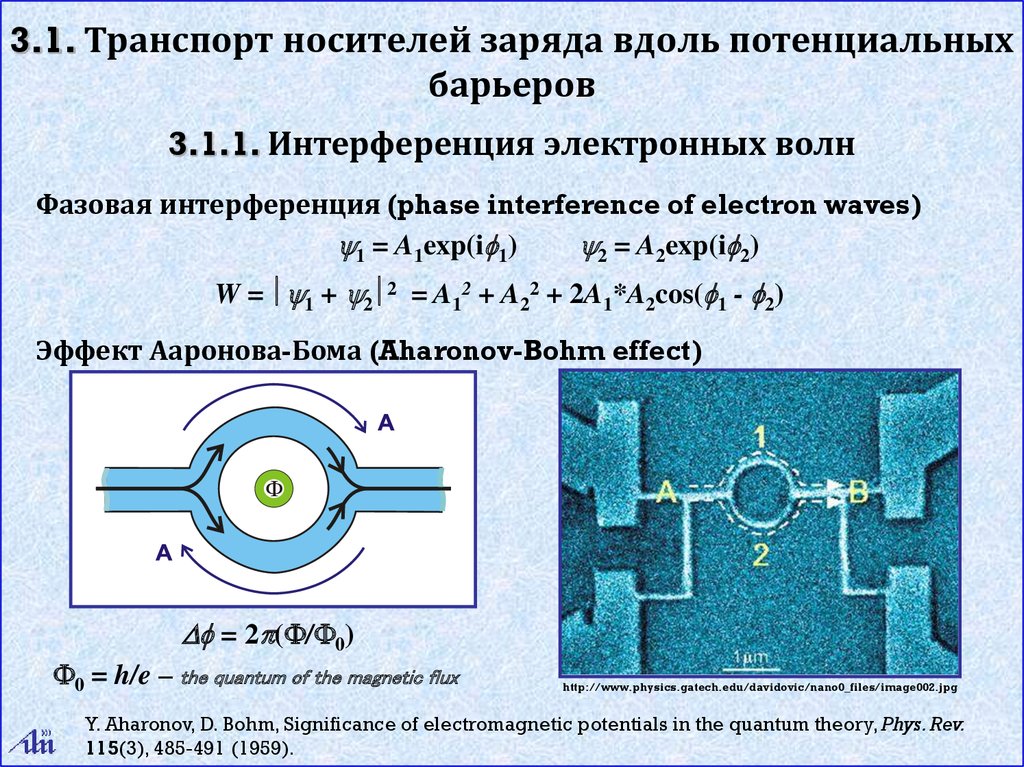
Эффект Ааронова-Бома (Aharonov-Bohm effect)
= 2 ( / 0)
0 = h/e – the quantum of the magnetic flux
http://www.physics.gatech.edu/davidovic/nano0_files/image002.jpg
Y. Aharonov, D. Bohm, Significance of electromagnetic potentials in the quantum theory, Phys. Rev.
115(3), 485-491 (1959).

3.

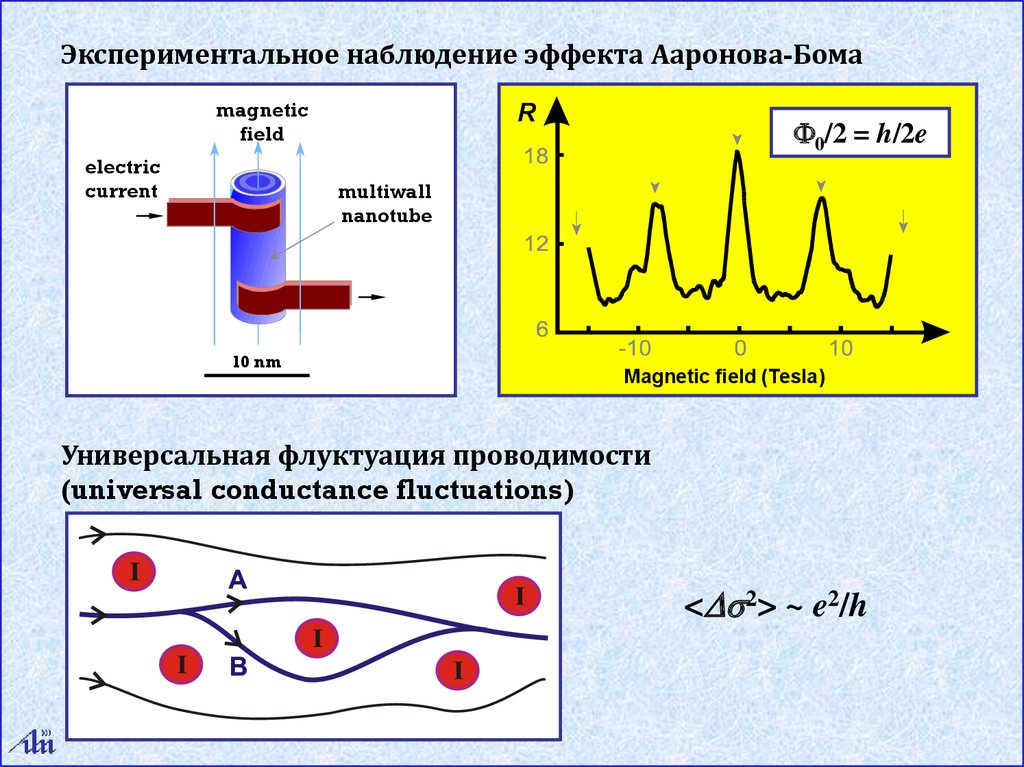
Экспериментальное наблюдение эффекта Ааронова-Бома
magnetic
field
electric
current
R
0/2 = h/2e
multiwall
nanotube
10 nm
Magnetic field (Tesla)
Универсальная флуктуация проводимости
(universal conductance fluctuations)
< s2> ~ e2/h

4.

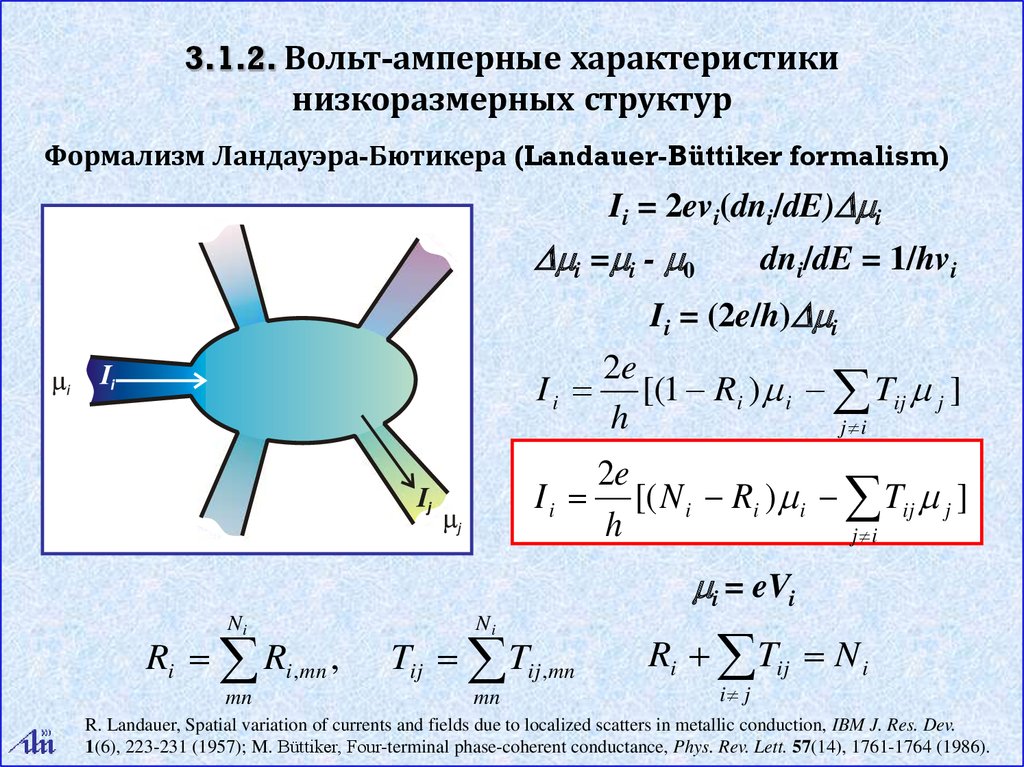
3.1.2. Вольт-амперные характеристики
низкоразмерных структур
Формализм Ландауэра-Бютикера (Landauer-Büttiker formalism)
Ii = 2evi(dni/dE) i
i = i - 0
dni/dE = 1/hvi
Ii = (2e/h) i
2e
I i [(1 Ri ) i Tij j ]
h
j i
2e
I i [( N i Ri ) i Tij j ]
h
j i
i = eVi
Ni
Ni
Ri Ri ,mn ,
Tij Tij,mn
mn
mn
Ri Tij N i
i j
R. Landauer, Spatial variation of currents and fields due to localized scatters in metallic conduction, IBM J. Res. Dev.
1(6), 223-231 (1957); M. Büttiker, Four-terminal phase-coherent conductance, Phys. Rev. Lett. 57(14), 1761-1764 (1986).

5.

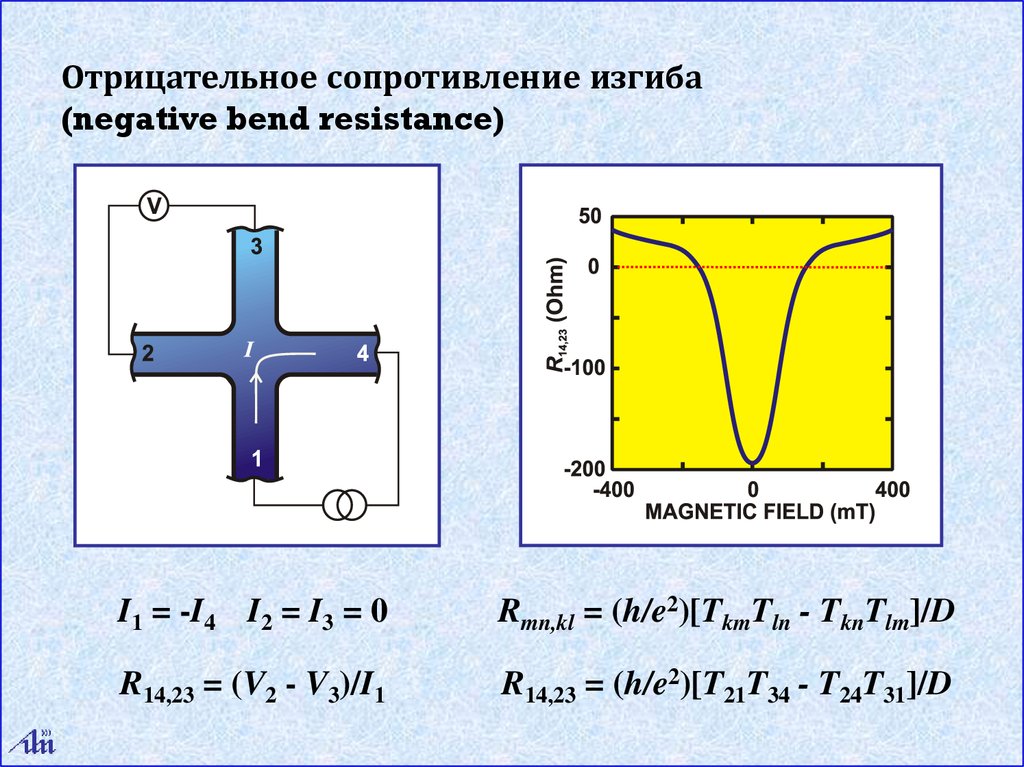
Отрицательное сопротивление изгиба
(negative bend resistance)
I1 = -I4 I2 = I3 = 0
Rmn,kl = (h/e2)[TkmTln - TknTlm]/D
R14,23 = (V2 - V3)/I1
R14,23 = (h/e2)[T21T34 - T24T31]/D

6.

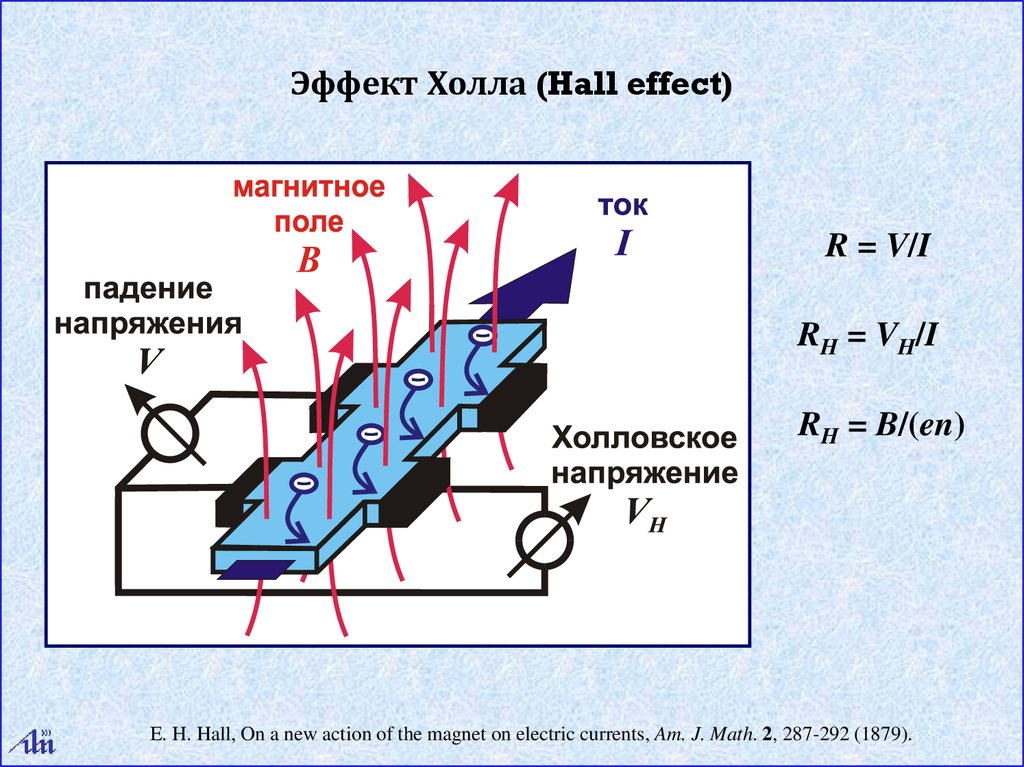
Эффект Холла (Hall effect)
R = V/I
RH = VH/I
RH = B/(en)
E. H. Hall, On a new action of the magnet on electric currents, Am. J. Math. 2, 287-292 (1879).

7.

3.1.3. Квантовый эффект Холла (quantum Hall effect )
RH = h/(ie2)
i = 1, 2, 3, …
integer quantum Hall effect
i = p/q p = 1, 2, … q = 3, 5, 7, …
fractional quantum Hall effect

8.

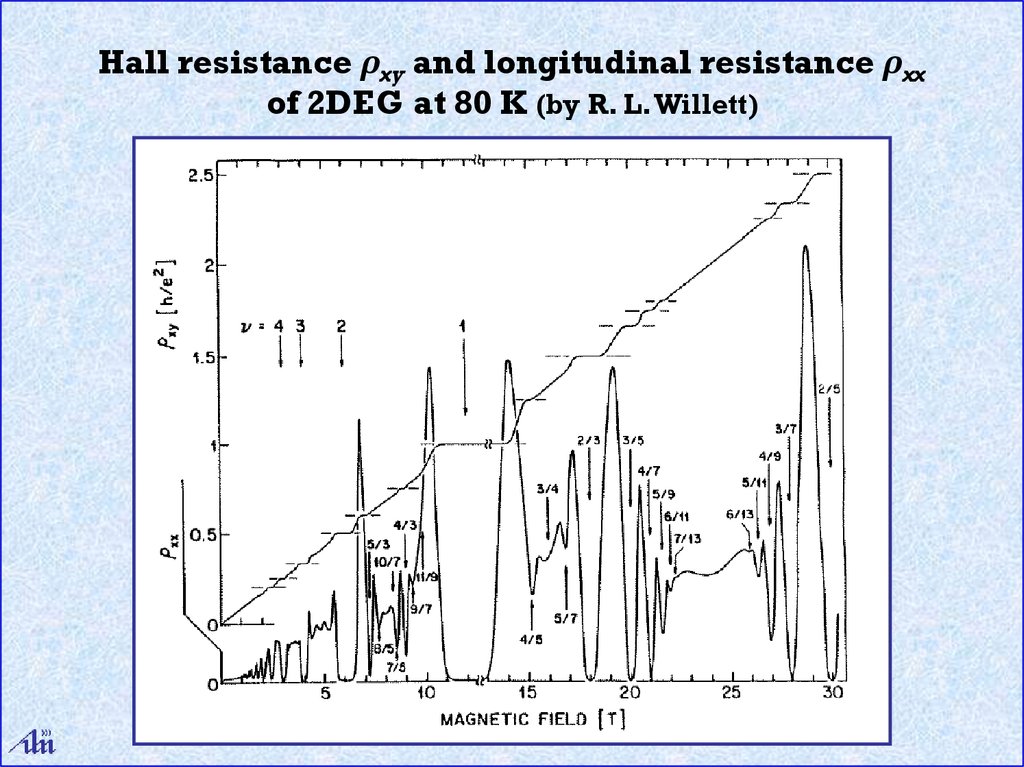
Hall resistance ρxy and longitudinal resistance ρxx
of 2DEG at 80 K (by R. L. Willett)

9.

Объяснение квантового эффекта Холла
идеальная структура
The cyclotron frequency
ωc = eB/m
Landau levels
Ei = (i + ½)ħωc i = 1, 2, ….
разупорядоченная структура
kBT << ħωc
EF

10.

From the History of the Quantum Hall Effect
Klaus von Klitzing
(1943)
Max-Planck-Institut für Festkörperforschung
Stuttgart, Germany
The Nobel Prize in Physics, 1985
for the discovery of the quantized Hall effect
K. von Klitzing, G. Dorda, M. Pepper, New method for high-accuracy determination of the fine-structure constant based
on quantized Hall resistance, Phys. Rev. Lett. 45(6), 494-497 (1980) – the integer quantum Hall effect

11.

From the History of the Quantum Hall Effect
Robert B. Laughlin
(1950)
Stanford University
Stanford, CA, USA
Horst L. Störmer
(1943)
Columbia University
New York, NY, USA
Daniel C. Tsui
(1939)
Princeton University
Princeton, NJ, USA
The Nobel Prize in Physics, 1998
for their discovery of a new form of quantum fluid with
fractionally charged excitations
D. C. Tsui, H. L. Störmer, A. C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett.
48(22), 1559-1562 (1982) and R. B. Laughlin, Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally
charged excitations, Phys. Rev. Lett. 50(18), 1395-1398 (1983) – the fractional quantum Hall effect

12.

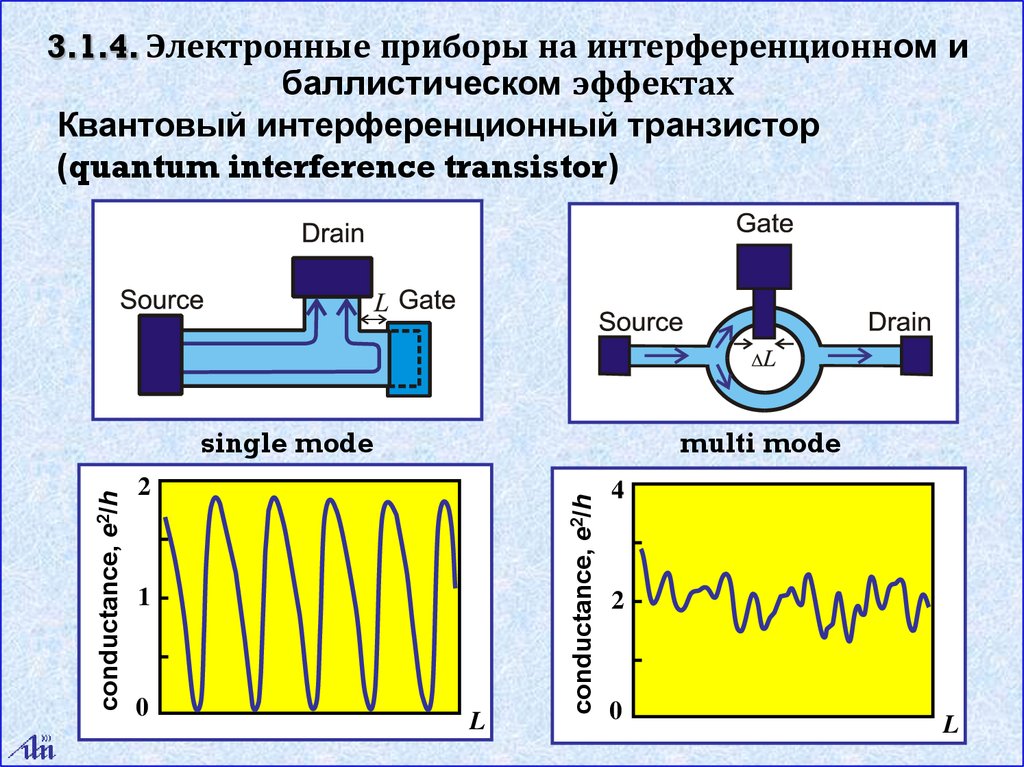
3.1.4. Электронные приборы на интерференционном и
баллистическом эффектах
Квантовый интерференционный транзистор
(quantum interference transistor)
multi mode
2
1
0
L
conductance, e2/h
conductance, e2/h
single mode
4
2
0
L

13.

Молекулярный квантовый интерференционный
транзистор
D. M. Cardamone, C. A. Stafford, S. Mazumdar, Controlling quantum transport through a single
molecule, NanoLett. 6(11) 2422-2426 (2006); C. A. Stafford, D. M. Cardamone, S. Mazumdar,
Quantum interference effect transistor (QUIET), United States Patent Application 2007/0215861
(09/20/2007).

14.

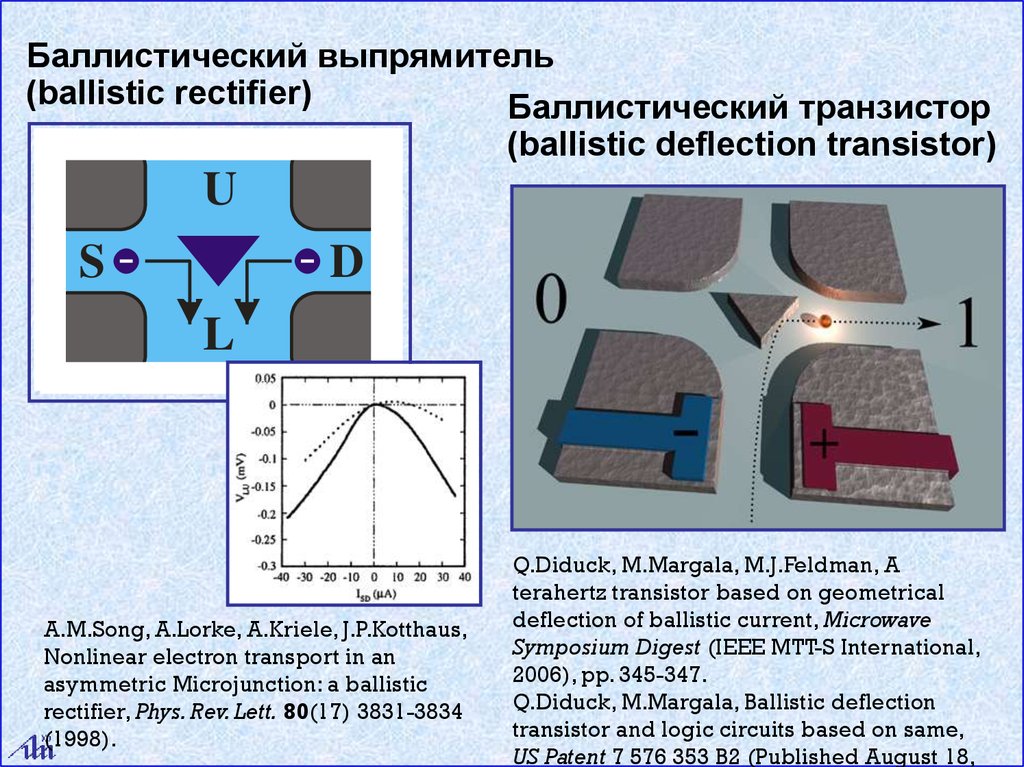
Баллистический выпрямитель
(ballistic rectifier)
Баллистический транзистор
(ballistic deflection transistor)
U
S
D
L
A.M.Song, A.Lorke, A.Kriele, J.P.Kotthaus,
Nonlinear electron transport in an
asymmetric Microjunction: a ballistic
rectifier, Phys. Rev. Lett. 80(17) 3831-3834
(1998).
Q.Diduck, M.Margala, M.J.Feldman, A
terahertz transistor based on geometrical
deflection of ballistic current, Microwave
Symposium Digest (IEEE MTT-S International,
2006), pp. 345-347.
Q.Diduck, M.Margala, Ballistic deflection
transistor and logic circuits based on same,
US Patent 7 576 353 B2 (Published August 18,

15.

16.

3.2. Транспорт носителей заряда через потенциальные
барьеры
3.2.1.Одноэлектронное туннелирование
и электронные приборы на этом эффекте
c onductor
dielec tric
conductor
single electron tunneling
First theory:
K. K. Likharev, A. B. Zorin, Theory of Bloch-wave oscillations in small
Josephson junctions, J. Low Temp. Phys. 59(3/4), 347-382 (1985)
D. V. Averin, K. K. Likharev, Coulomb blockade of tunneling and coherent
oscillations in small tunnel junctions, J. Low. Temp. Phys. 62(2), 345-372
(1986)
Q = e/2
tunneling
elec tron
First experiment:
T. A. Fulton, G. J. Dolan, Observation of single-electron charging effects in
small tunneling junctions, Phys. Rev. Lett. 59(1), 109-112 (1987)

17.

Однобарьерная структура (single barrier structure)
I
Rt=∂I/∂V
-e/2C
C = Ct + Ce
E = e2/2C – eV
E 0
Vt = e/2C
e/2C
f = I/e
kBT << e2/2C
e2/2C - Coulomb gap
Rt > h/e2
V

18.

Двухбарьерная структура (double barrier structure)
I
V0
-e/2C
e/2C
C = CL + CR
V
C CR >> CL
E = 1/2[(e/C + Vo)2C – Vo2C]
V C(e/2C + Vo)/CR
I
-2<N<2
-1<N<1
Coulomb staircase
N=0
1
3
5
VC/e

19.

Сотуннелирование (co-tunneling)
упругое (elastic)
неупругое (inelastic)
hs 1s 2 1
1
I
(
)V
2 2
E1 E 2
8 e
hs 1s 2 1
1 2
eV 2
2
I
(
) [(k B T ) ( ) ]V
2
E1 E 2
2
6e

20.

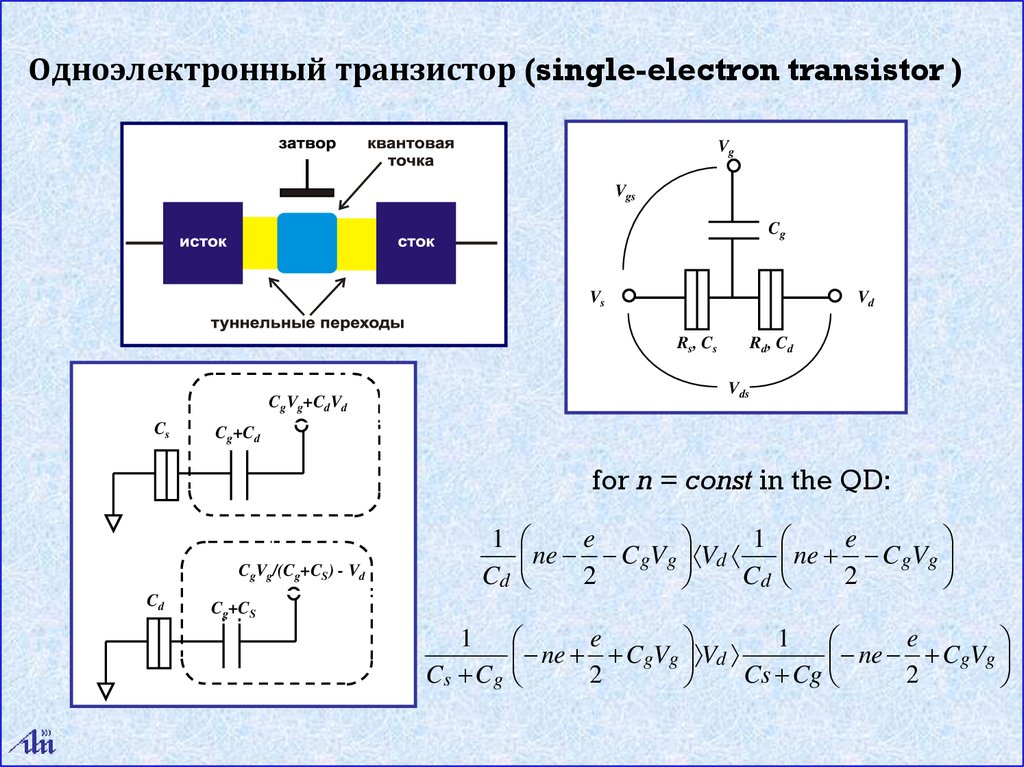
Одноэлектронный транзистор (single-electron transistor )
Vg
Vgs
Cg
Vs
Vd
Rs, Cs
Vds
CgVg+CdVd
Cs
Rd , Cd
Cg+Cd
for n = const in the QD:
CgVg/(Cg+CS) - Vd
Cd
1
Cd
e
1
ne C gVg Vd
2
Cd
e
ne C gVg
2
Cg+CS
1
e
1
e
ne CgVg Vd
ne CgVg
Cs C g
2
Cs Cg
2

21.

Характеристики одноэлектронного транзистора
Vd
0
2
1
2,1,0
1,0,1
0
-1
1,0
0
Ids
1
0
2,1
1
2
-e/2Cg
Vg
e/2Cg 3e/2Cg 5e/2Cg
Ids
Vg=0
Vds
Vg=
/C g
e
2
Vg

22.

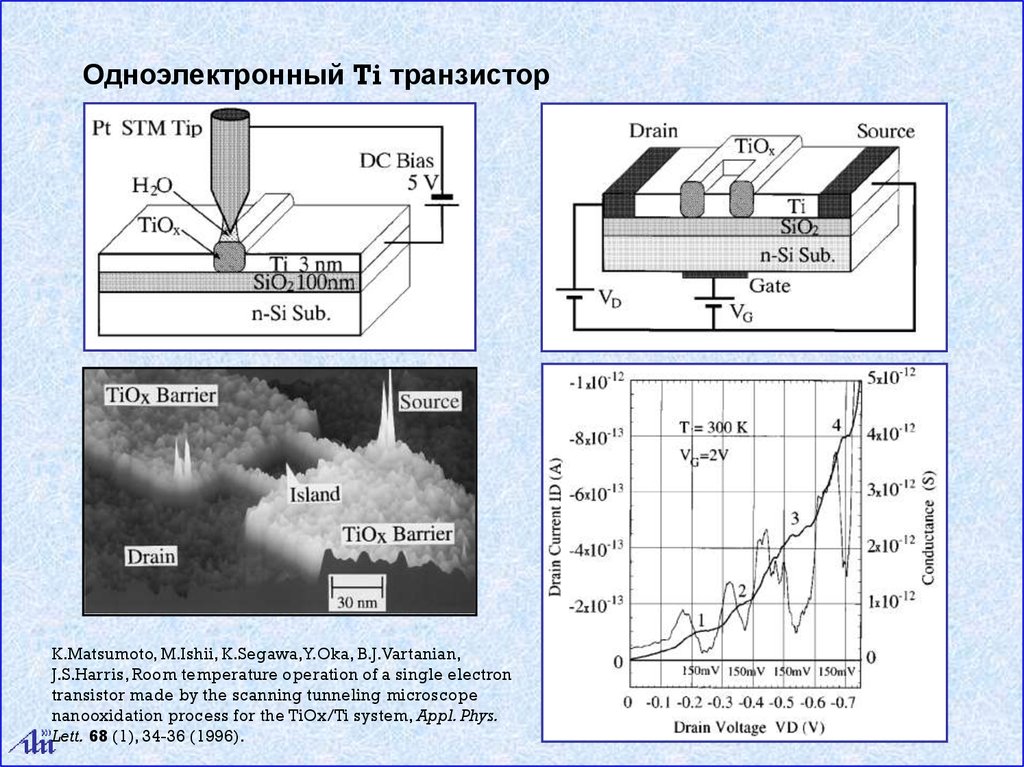
Одноэлектронный Ti транзистор
K.Matsumoto, M.Ishii, K.Segawa,Y.Oka, B.J.Vartanian,
J.S.Harris, Room temperature operation of a single electron
transistor made by the scanning tunneling microscope
nanooxidation process for the TiOx/Ti system, Appl. Phys.
Lett. 68 (1), 34-36 (1996).

23.

Одноэлектронный InAs транзистор
Первый Ge транзистор
1948
www.ece.umd.edu/labs/ebl/

24.

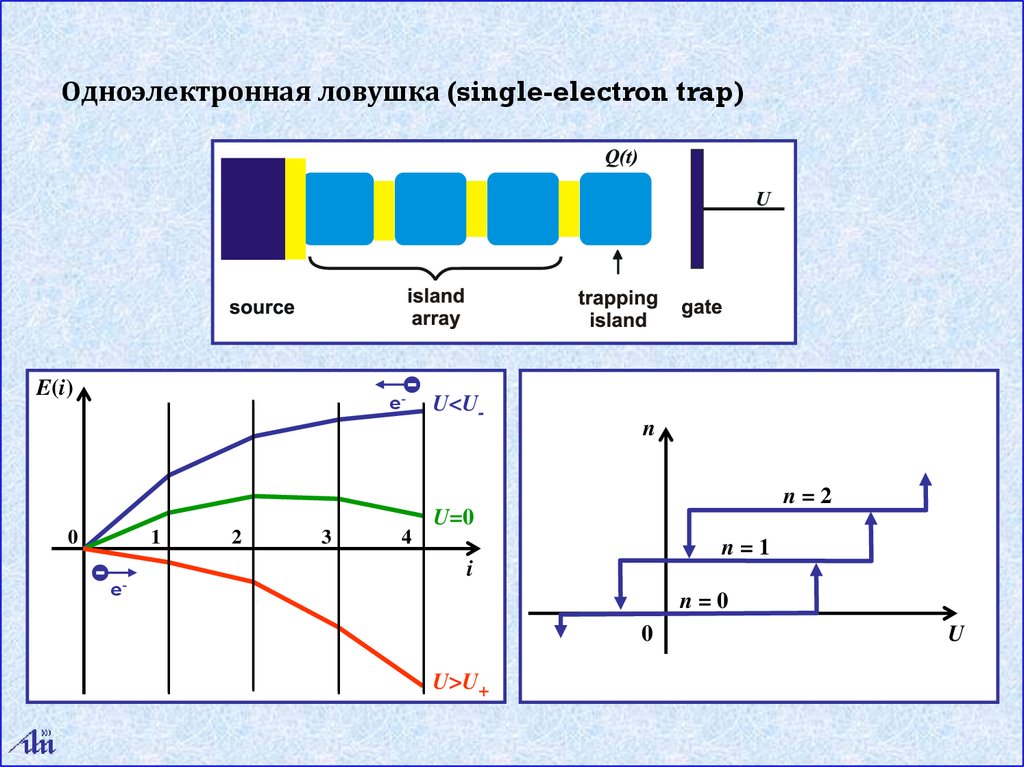
Одноэлектронная ловушка (single-electron trap)
E(i)
e-
U<U-
n
n=2
U=0
0
1
e-
2
3
4
n=1
i
n=0
0
U>U+
U

25.

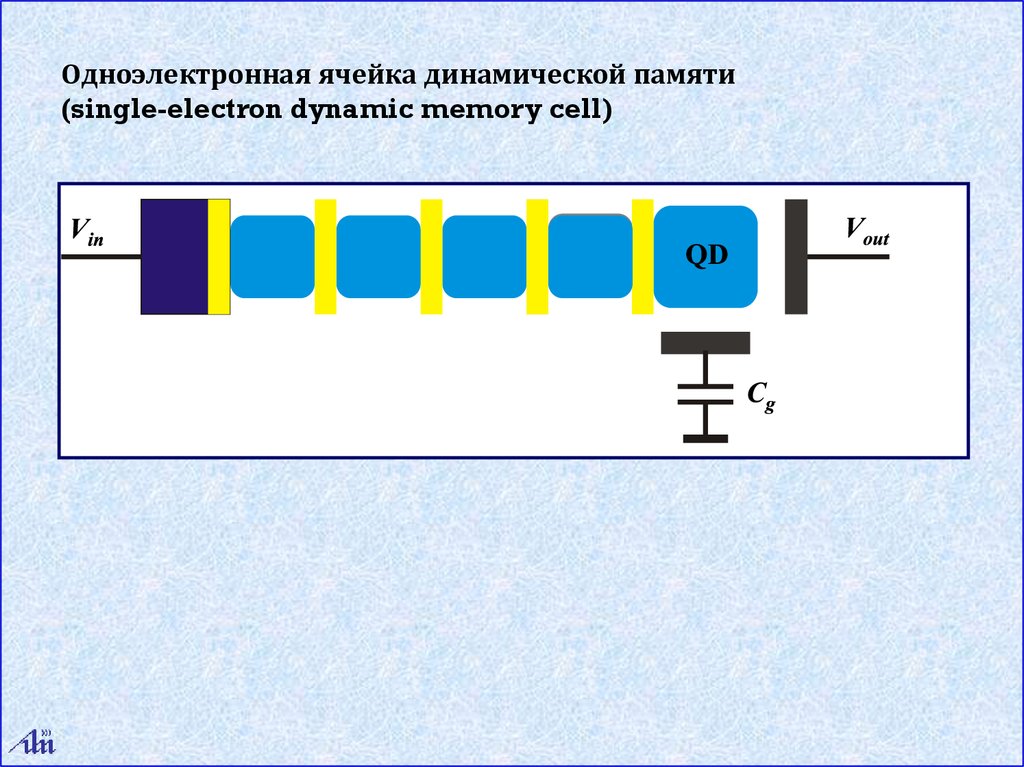
Одноэлектронная ячейка динамической памяти
(single-electron dynamic memory cell)

26.

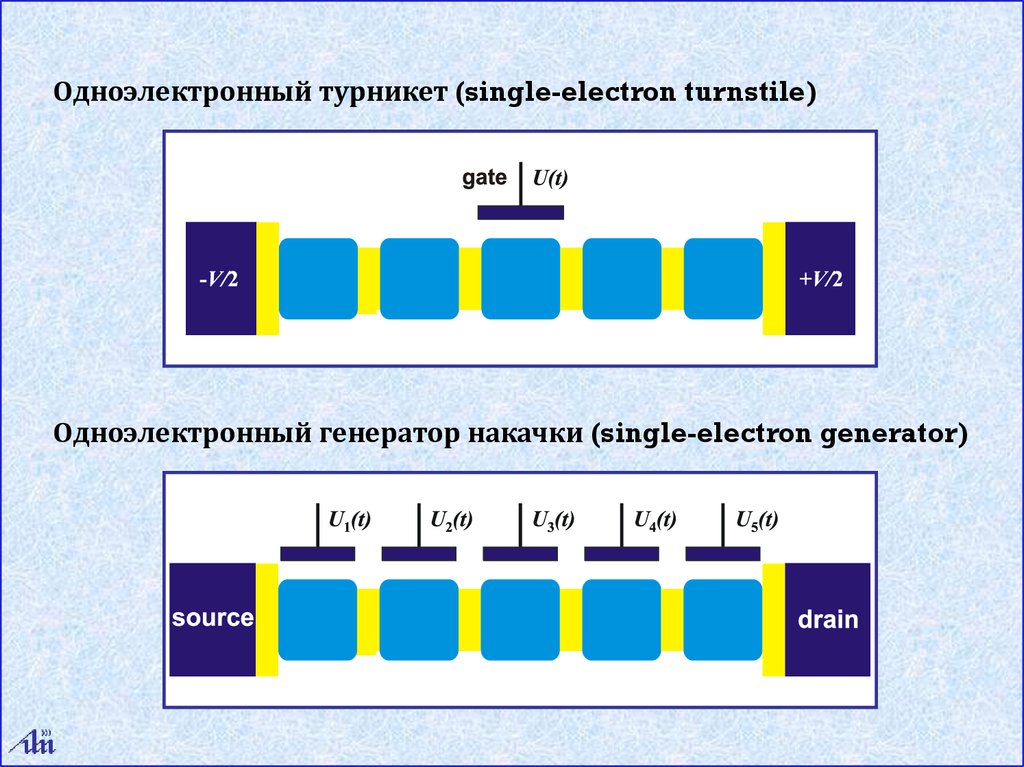
Одноэлектронный турникет (single-electron turnstile)
Одноэлектронный генератор накачки (single-electron generator)

27.

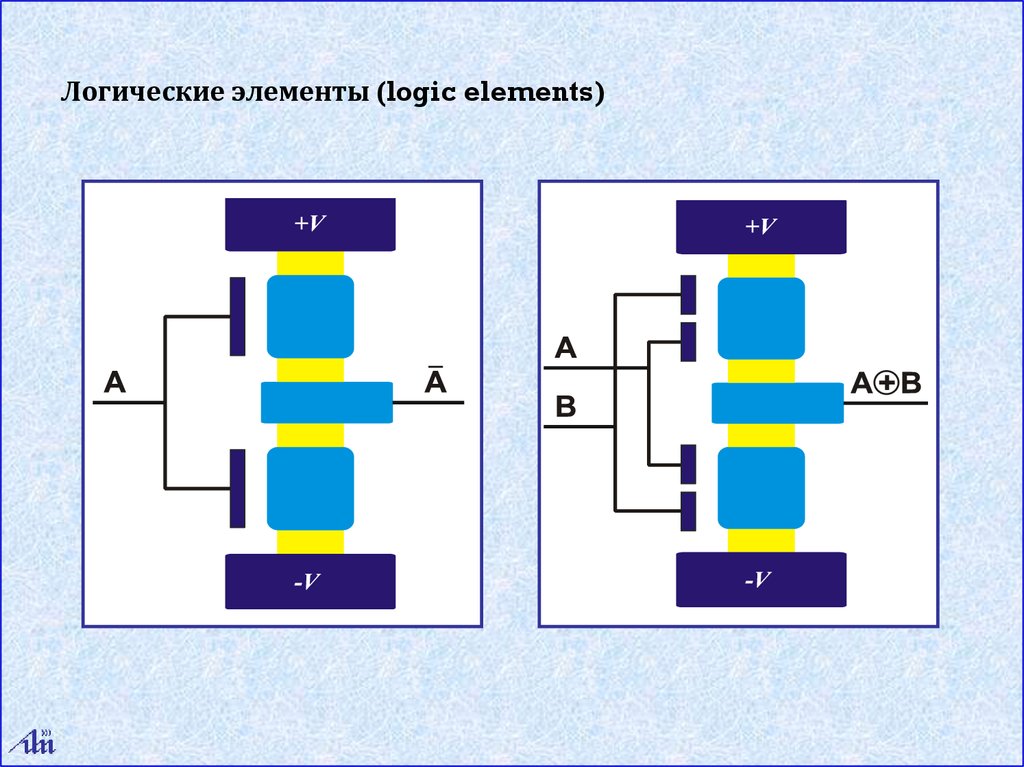
Логические элементы (logic elements)

28.

3.2.2. Резонансное туннелирование
и электронные приборы на этом эффекте
(resonant tunneling)
2 2
E1
2m * a 2
E1
EF
1
EF
eV
EF
eV
2E1/e
E
J 3 dk x dk y dk zT ( Ez )[ f ( E ) f ( E ' )](
)
4 0
k z
0
e
E' = E + eV

29.

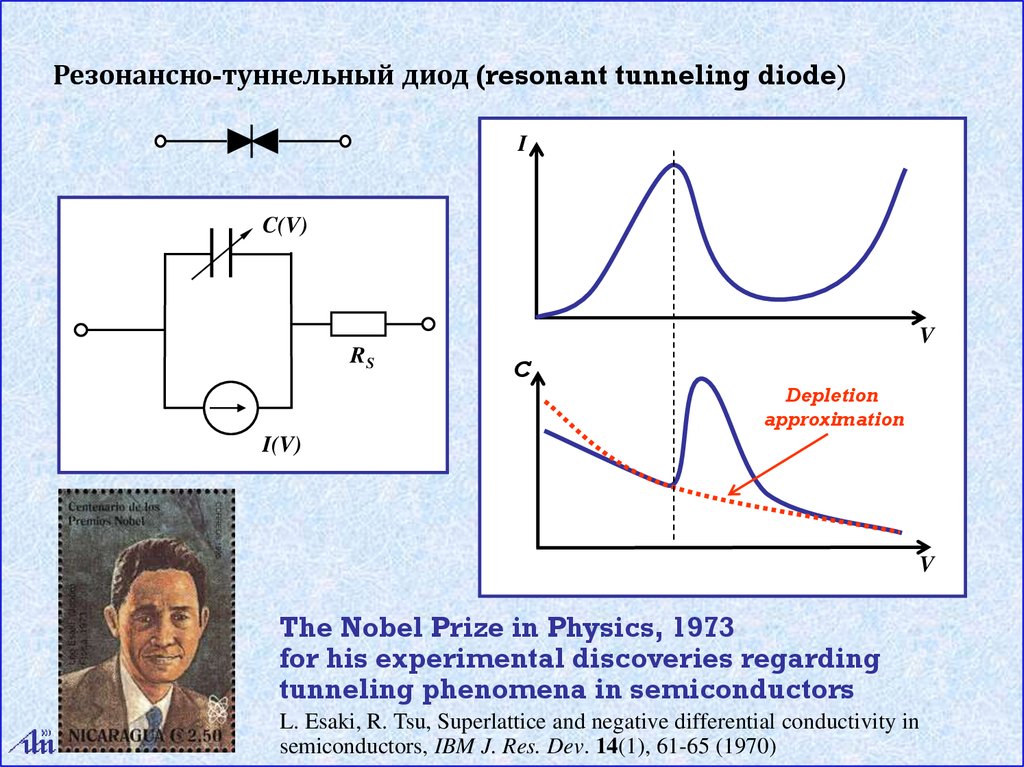
Резонансно-туннельный диод (resonant tunneling diode)
I
C(V)
RS
V
C
Depletion
approximation
I(V)
V
The Nobel Prize in Physics, 1973
for his experimental discoveries regarding
tunneling phenomena in semiconductors
L. Esaki, R. Tsu, Superlattice and negative differential conductivity in
semiconductors, IBM J. Res. Dev. 14(1), 61-65 (1970)

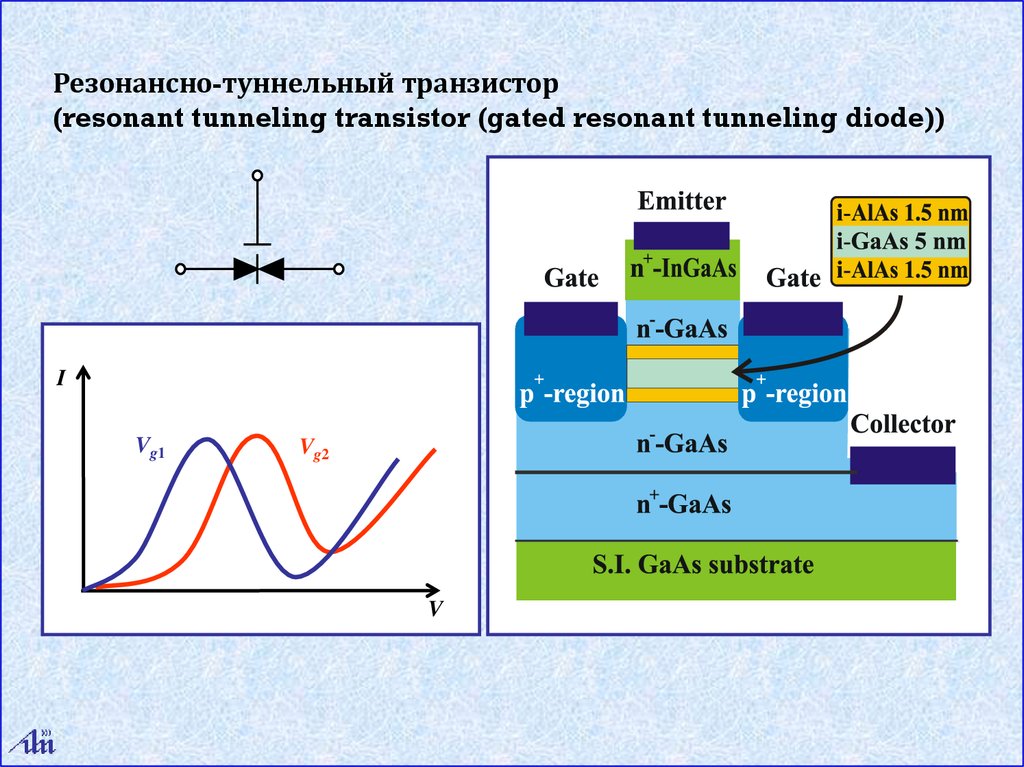
30.

Резонансно-туннельный транзистор
(resonant tunneling transistor (gated resonant tunneling diode))
I
Vg1
Vg2
V

31.

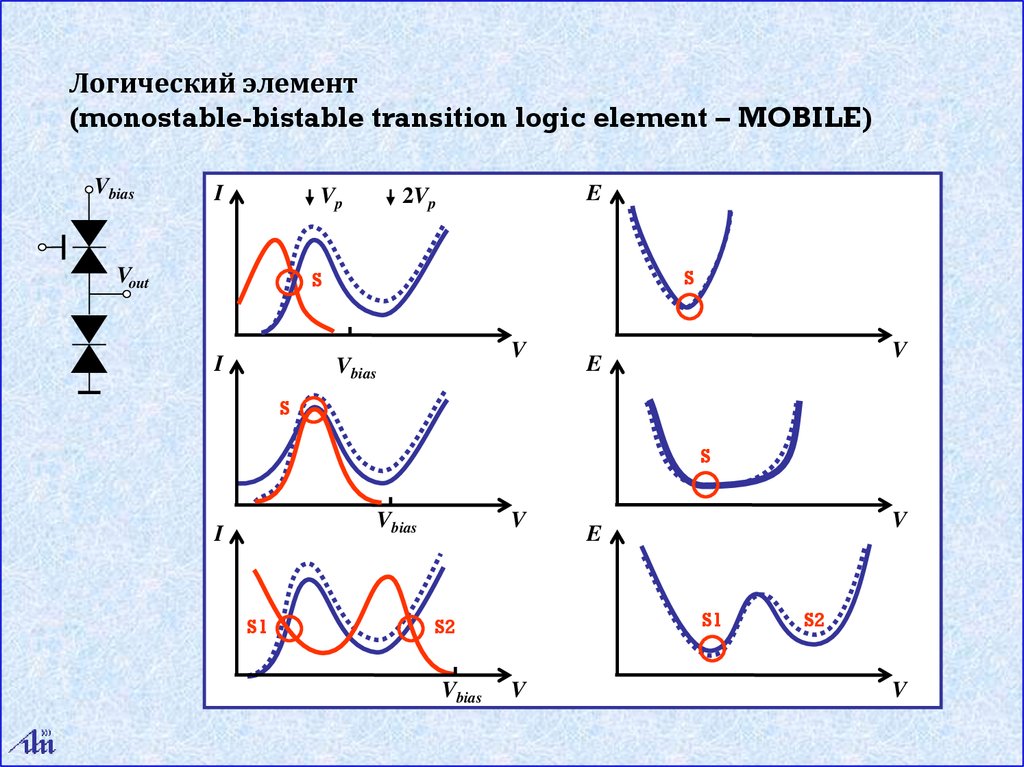
Логический элемент
(monostable-bistable transition logic element – MOBILE)
Vbias
I
Vp
Vout
E
2Vp
S
S
I
V
Vbias
V
E
S
S
Vbias
I
S1
V
S1
S2
Vbias
V
E
V
S2
V

32.

33.

3.3. Спинтроника (spintronics)
область науки и техники, занимающаяся
созданием, исследованием и применением
электронных приборов, в которых спин
электрона наравне с его зарядом
используется для обработки информации

34.

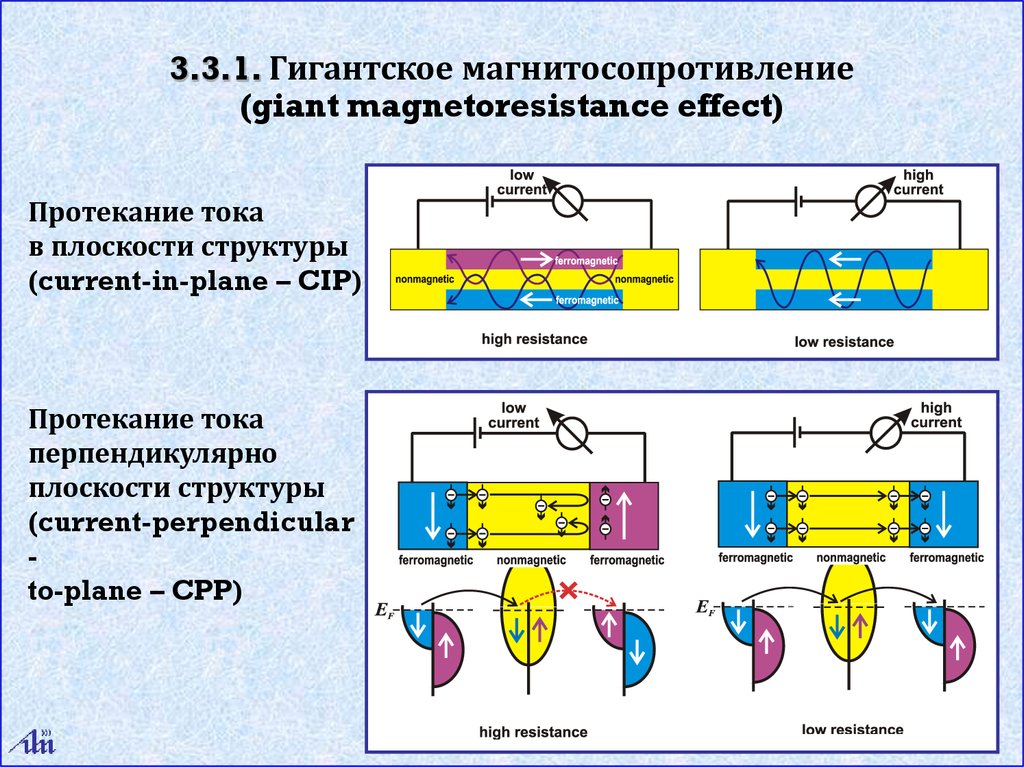
3.3.1. Гигантское магнитосопротивление
(giant magnetoresistance effect)
Протекание тока
в плоскости структуры
(current-in-plane – CIP)
Протекание тока
перпендикулярно
плоскости структуры
(current-perpendicular
to-plane – CPP)

35.

From the History of the Giant Magnetoresistance Effect
Albert Fert
(1938)
Université Paris-Sud
Orsay, France
Peter Grünberg
(1939)
Forschungszentrum Jülich
Jülich, Germany
The Nobel Prize in Physics, 2007
for the discovery of Giant Magnetoresistance
M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, Giant magnetoresistance of (001)Fe/(001)Cr
magnetic superlattices, Phys. Rev. Lett. 61(21), 2472-2475 (1988).
G. Binasch, P. Grünberg, F. Saurenbach, W. Zinn, Enhanced magnetoresistance in layered magnetic
structures with antiferromagnetic interlayer exchange, Phys. Rev. B 39(7), 4828-4830 (1989).

36.

3.3.2. Спин-контролируемое туннелирование
(tunneling magnetoresistance effect )
2 P1 P2
R Rap R p
R
Rap
1 P1 P2
Magnetoresistance (%)
0
-0.25
Co film
-0.50
0.12
CoFe film
0.06
0
CoFe/Al2O3/Co
junction
10.0
7.5
5.0
2.5
0
-600
-300
0
300
Magnetic field (Oe)
600

37.

расщепление
состояний
носителей заряда
по спинам
инжекция
носителей заряда
с определенным спином
3.3.3. Управление спинами электронов в полупроводниках
перенос
спин-поляризованных
носителей заряда
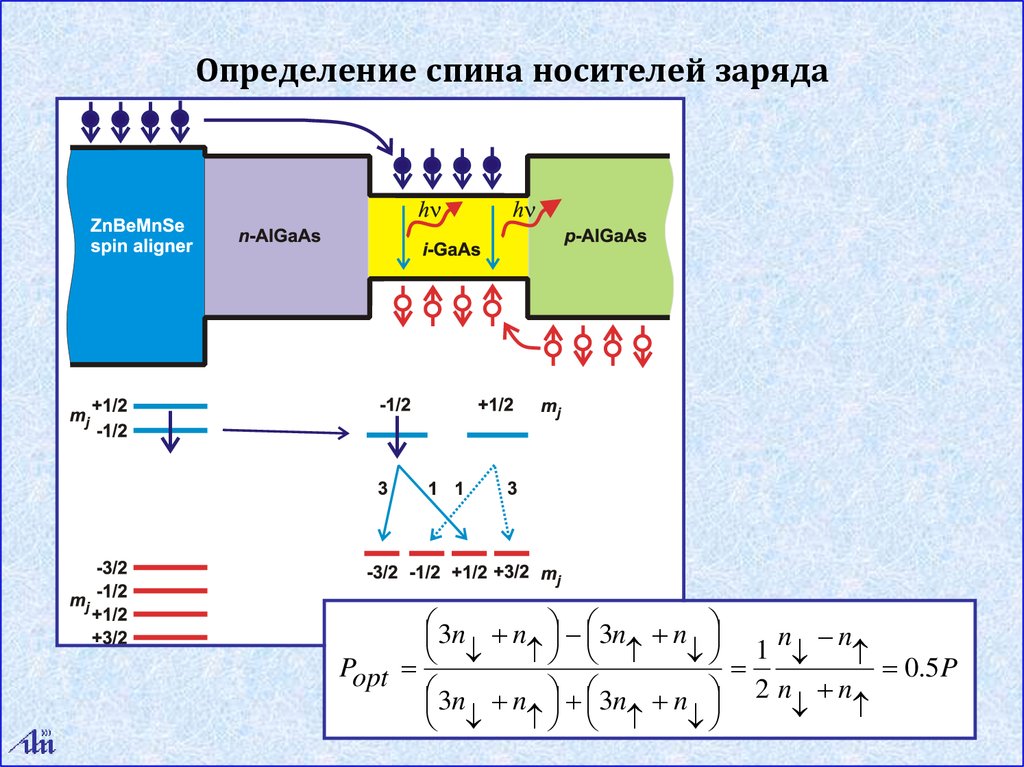
определение спина
носителей заряда

38.

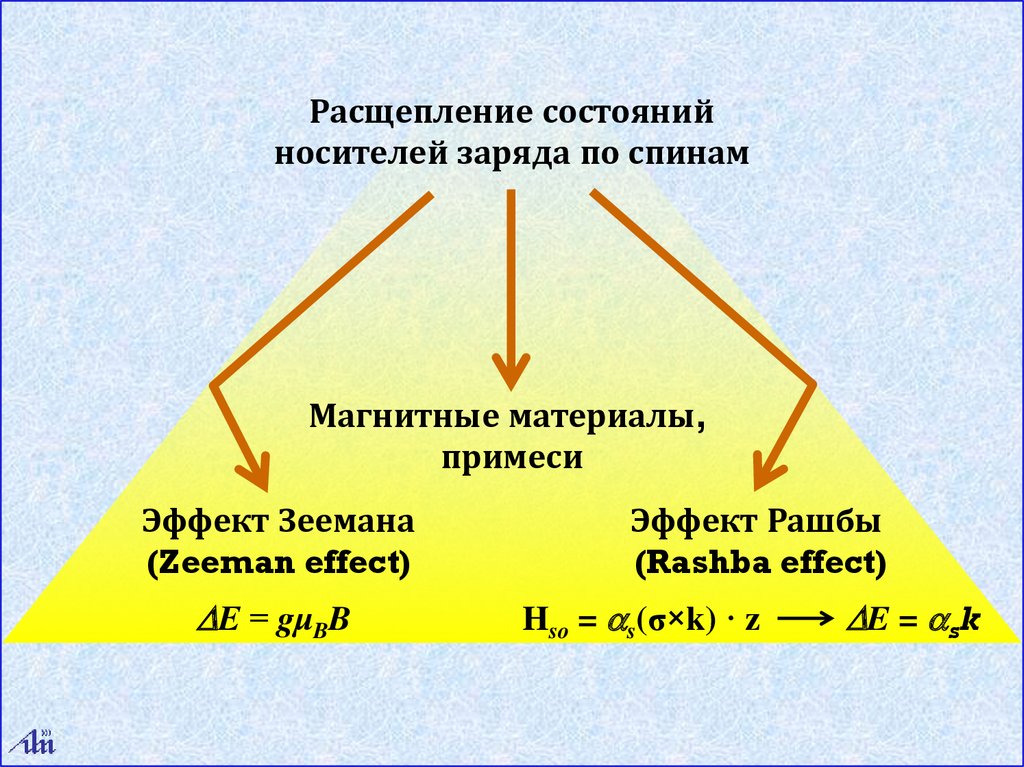
Расщепление состояний
носителей заряда по спинам
Магнитные материалы,
примеси
Эффект Зеемана
(Zeeman effect)
E = gμBB
Эффект Рашбы
(Rashba effect)
Hso = as(σ×k) · z
E = ask

39.

Инжекция носителей заряда
с определенным спином

40.

Перенос спин-поляризованных носителей заряда
(механизмы спин-релаксации в полупроводниках)
Механизм Бира-Аронова-Пикуса
(Bir-Aronov-Pikus mechanism)
1
s
2
0
N a aB3
vk p
5 N a p
4
0
vB N a
3N a
Механизм Эллиота-Яфета
(Elliot-Yafet mechanism)
1
s Ek
so
A
E
so
g
2
Ek
E
g
2
1
E
p k
Механизм Дьяконова-Перела
(D’yakonov-Perel mechanism)
a2
A 2
E
s
g
1
pT 3
a 2 p2 2
z
2 2
s 2 m E g
1
Следствие обменного
взаимодействия и рекомбинации
электронов и дырок. Низкие Т,
р-полупроводники.
Следствие спин-орбитального
рассеивания, при столкновении
электронов с фононами или
примесями. Низкие и умеренные Т.
Следствие спин-расщепления зоны
проводимости. Повышенные Т.
pT
сверхтонкое взаимодействие спинов электронов и спинов
ядер (hyperfine interaction of the electron spins and nuclear
spins)

41.

Определение спина носителей заряда
3n n 3n n
n n
1
0.5 P
Popt
3n n 3n n 2 n n

42.

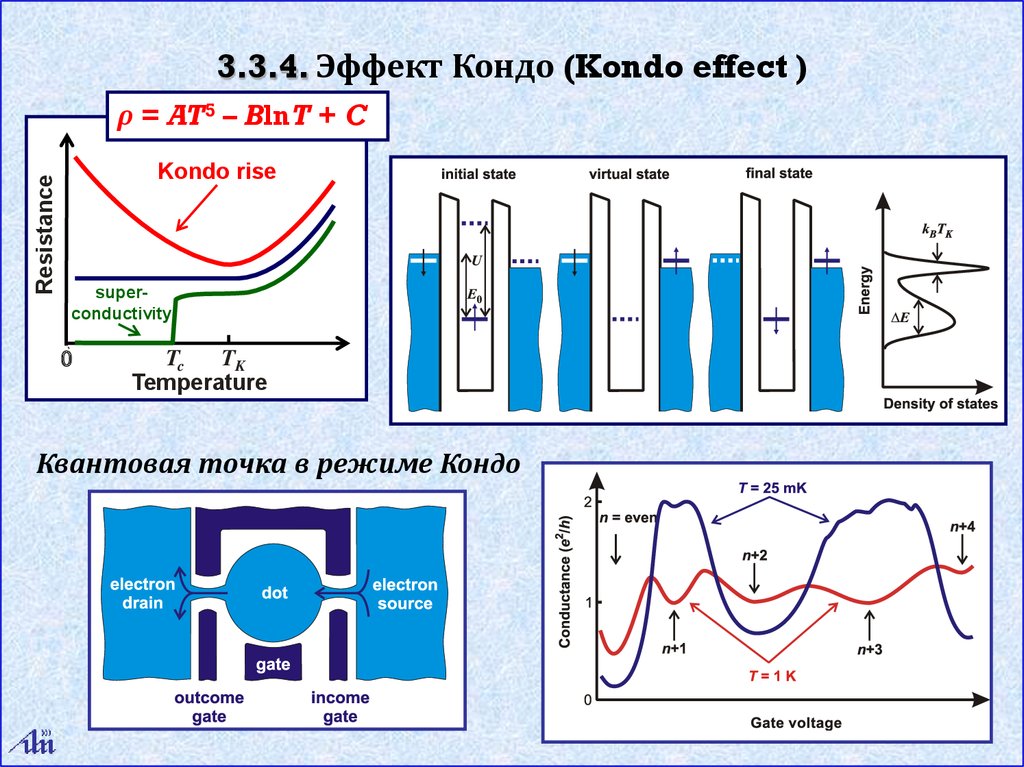
3.3.4. Эффект Кондо (Kondo effect )
Resistance
ρ = AT5 – BlnT + C
Kondo rise
superconductivity
0
Tc
TK
Temperature
Квантовая точка в режиме Кондо

43.

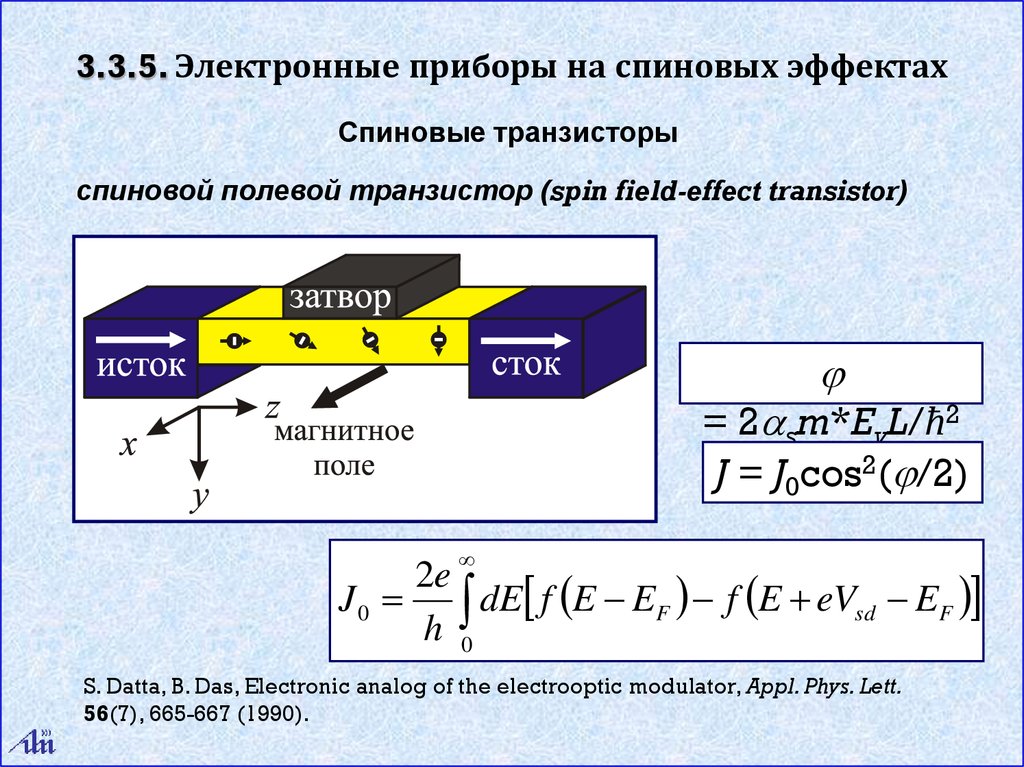
3.3.5. Электронные приборы на спиновых эффектах
Спиновые транзисторы
спиновой полевой транзистор (spin field-effect transistor)
= 2asm*EyL/ħ2
J = J0cos2( /2)
2e
J 0 dE f E EF f E eVsd EF
h 0
S. Datta, B. Das, Electronic analog of the electrooptic modulator, Appl. Phys. Lett.
56(7), 665-667 (1990).

44.

время-пролетный спиновой транзистор
(transit time spin transistor)
g B B L
v
I. Appelbaum, D. J. Monsma, Transit-time spin field-effect transistor, Appl. Phys. Lett.
90, 262501 (2007).

45.

Collector current (arb. units)
спин-вентильный транзистор (spin-valve transistor)
12
8
4
0
-40
-20
0
20
Magnetic field (Oe)
40
D. J. Monsma, J. C. Lodder, T. J. A. Popma, B. Dieny, Perpendicular hot electron spin-valve
effect in a new magnetic field sensor: the spin-valve transistor, Phys. Rev. Lett. 74(26),
5260-5263 (1995).

46.

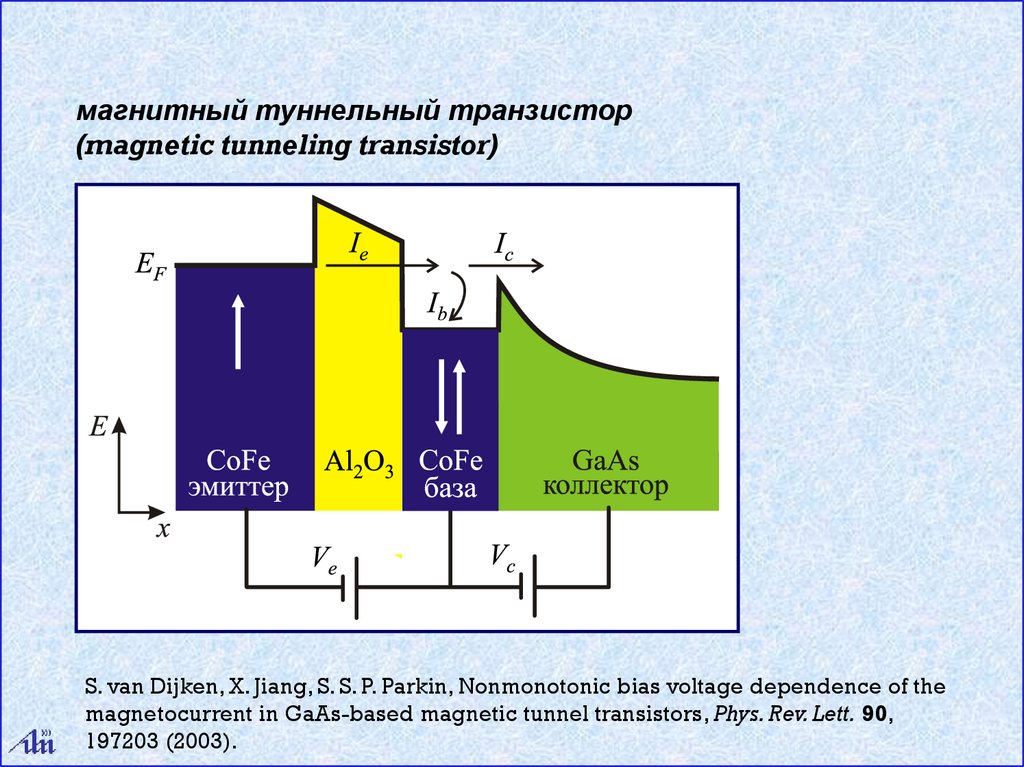
магнитный туннельный транзистор
(magnetic tunneling transistor)
S. van Dijken, X. Jiang, S. S. P. Parkin, Nonmonotonic bias voltage dependence of the
magnetocurrent in GaAs-based magnetic tunnel transistors, Phys. Rev. Lett. 90,
197203 (2003).

47.

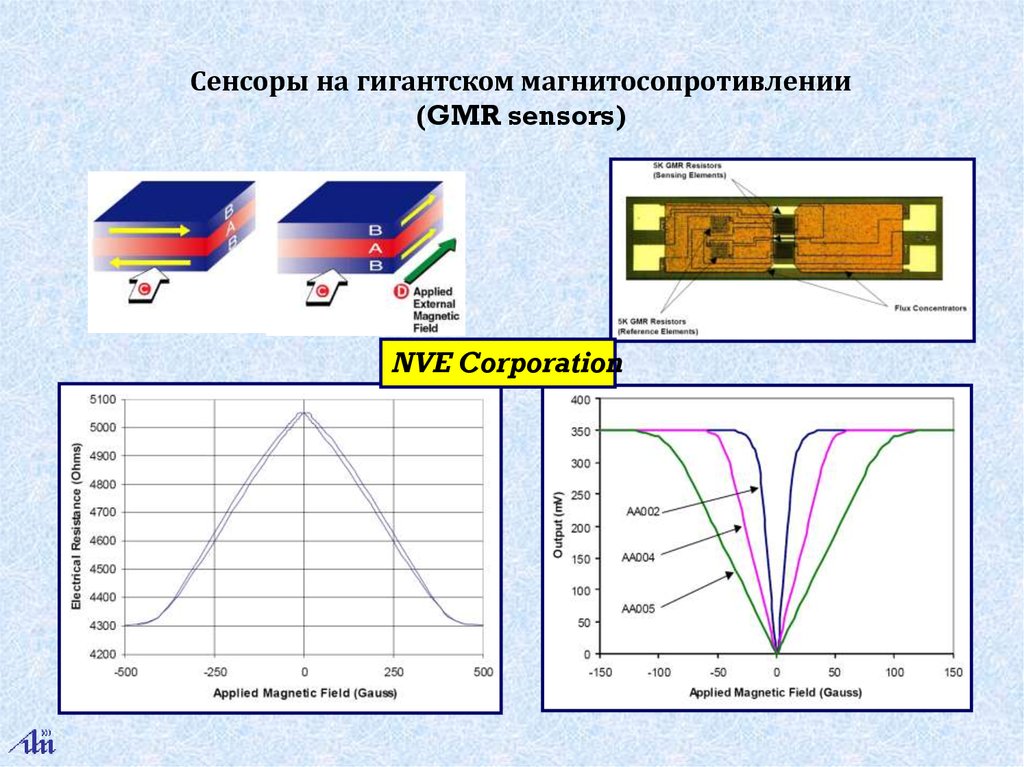
Сенсоры на гигантском магнитосопротивлении
(GMR sensors)
NVE Corporation

48.

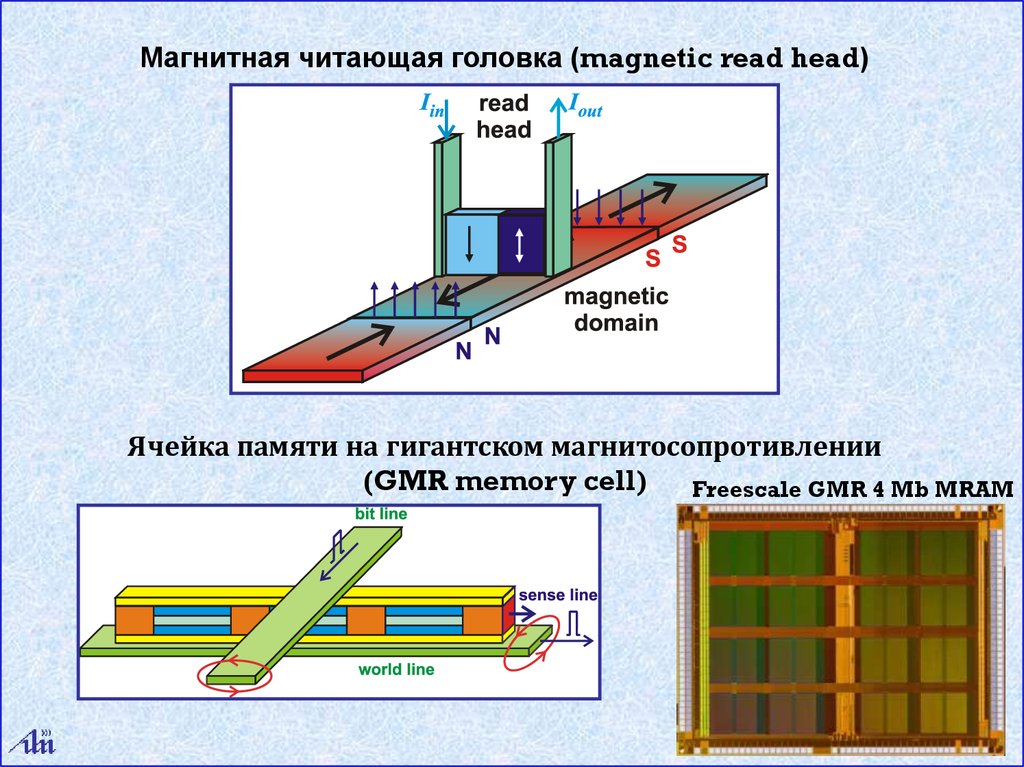
Магнитная читающая головка (magnetic read head)
Ячейка памяти на гигантском магнитосопротивлении
(GMR memory cell)
Freescale GMR 4 Mb MRAM

49.

Ячейки памяти на туннельном магнитосопротивлении
(TMR memory cells)
структуры металл/диэлектрик/метал
IBM

50.

51.

структуры металл/диэлектрик/полупроводник

52.

53.

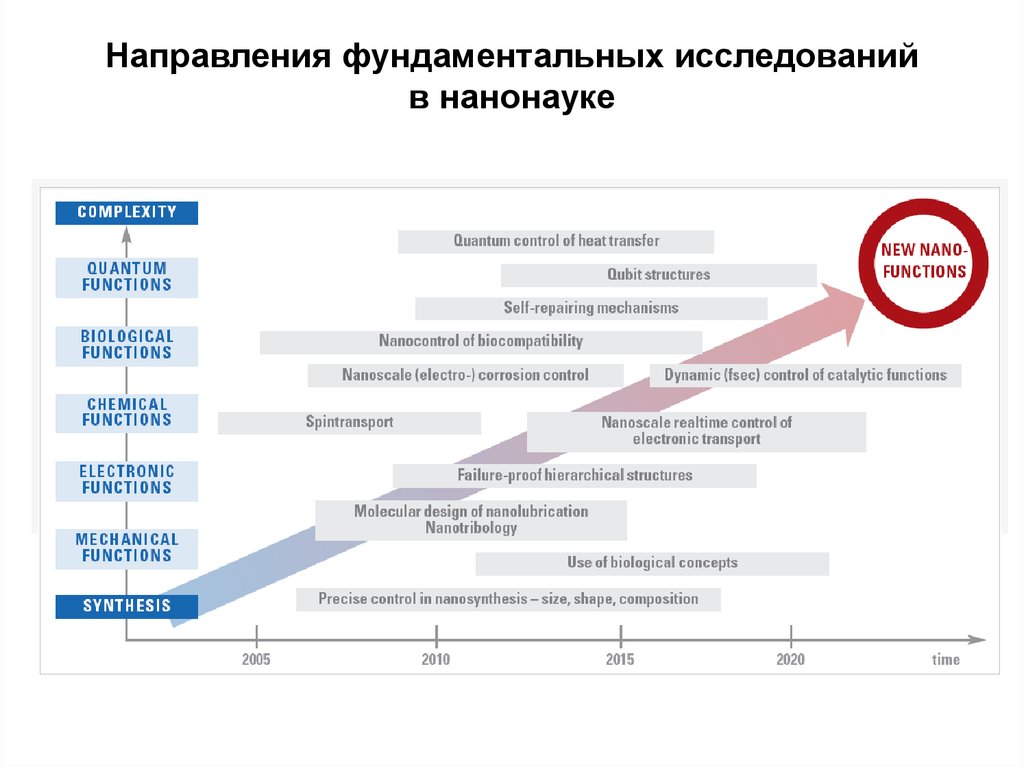
Направления фундаментальных исследований
в нанонауке

54.

NANOELECTRONICS
лекционный курс
“Наноэлектроника”
завершен
C В. Е. Борисенко, 2016

55.

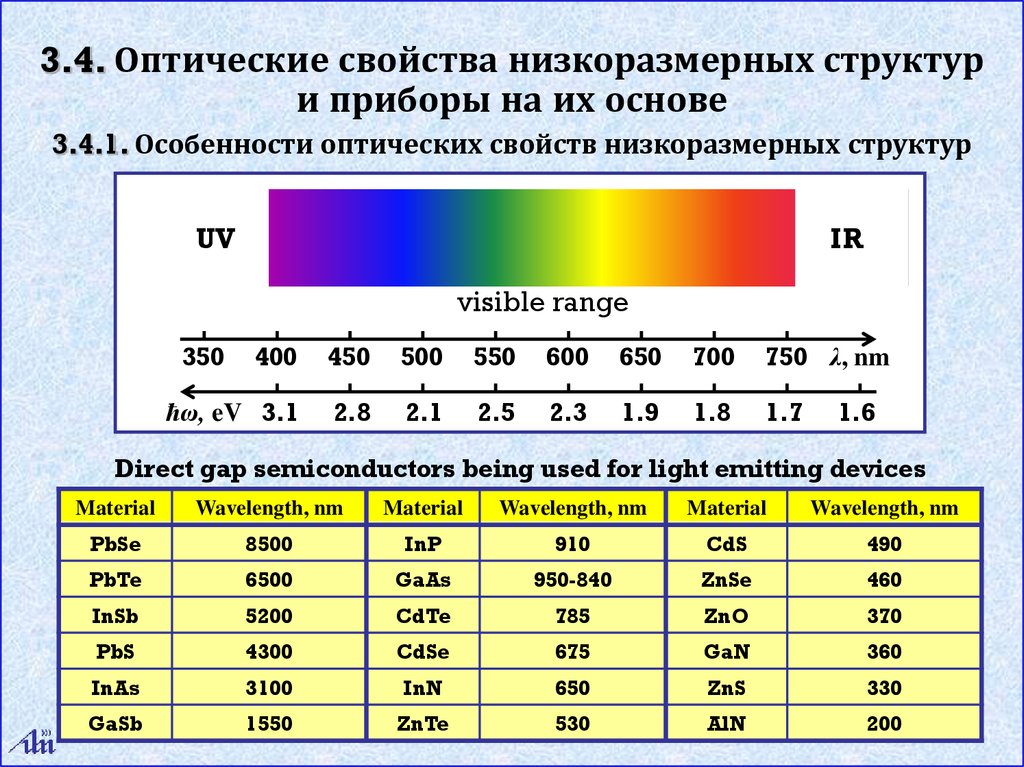
3.4. Оптические свойства низкоразмерных структур
и приборы на их основе
3.4.1. Особенности оптических свойств низкоразмерных структур
UV
IR
visible range
350
400
450
500
550
600
650
700
750 λ, nm
ħω, eV 3.1
2.8
2.1
2.5
2.3
1.9
1.8
1.7
1.6
Direct gap semiconductors being used for light emitting devices
Material
Wavelength, nm
Material
Wavelength, nm
Material
Wavelength, nm
PbSe
8500
InP
910
CdS
490
PbTe
6500
GaAs
950-840
ZnSe
460
InSb
5200
CdTe
785
ZnO
370
PbS
4300
CdSe
675
GaN
360
InAs
3100
InN
650
ZnS
330
GaSb
1550
ZnTe
530
AlN
200

56.

Light Emitted by Semiconductors

57.

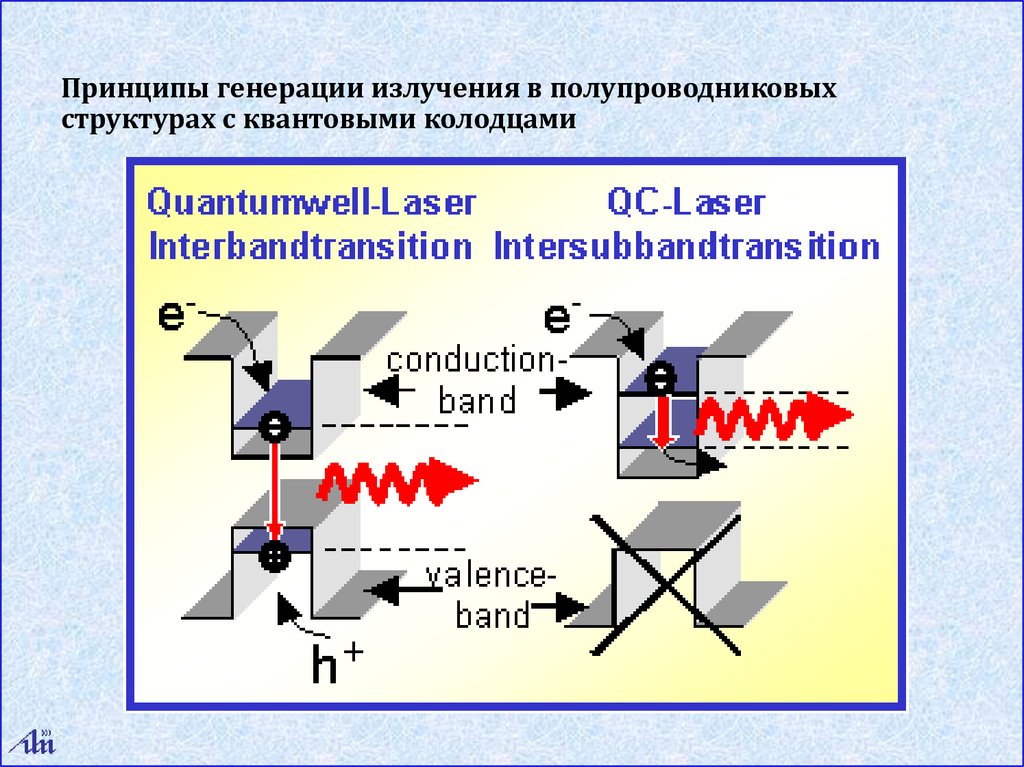
Принципы генерации излучения в полупроводниковых
структурах с квантовыми колодцами

58.

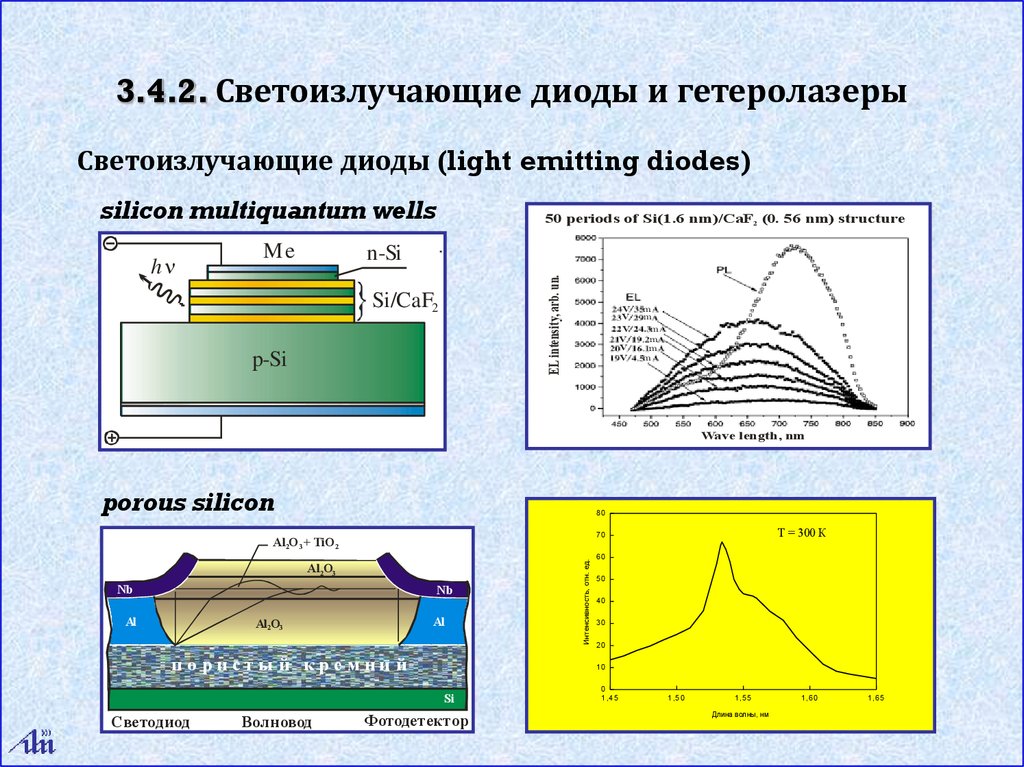
3.4.2. Светоизлучающие диоды и гетеролазеры
Светоизлучающие диоды (light emitting diodes)
silicon multiquantum wells
Me
n-Si
EL intensity, arb. un.
h
50 periods of Si(1.6 nm)/CaF2 (0. 56 nm) structure
Si/CaF2
p-Si
V
V
V
V
V
V
m
m
m
m
m
m
Wave length, nm
porous silicon
80
3
Nb
Nb
Al
Al
Al2Оксид
O3 алюми ния
п о ри ст ы й кр е м ни й
Волновод
60
50
40
30
20
10
Si
Светодиод
Интенсивность, отн. ед.
Оксид алюми
Al ния
O
2
Т = 300 К
70
Al2O 3 + TiO 2
Фотодетектор
0
1 ,4 5
1 ,5 0
1 ,5 5
Длина волны, нм
1 ,6 0
1 ,6 5

59.

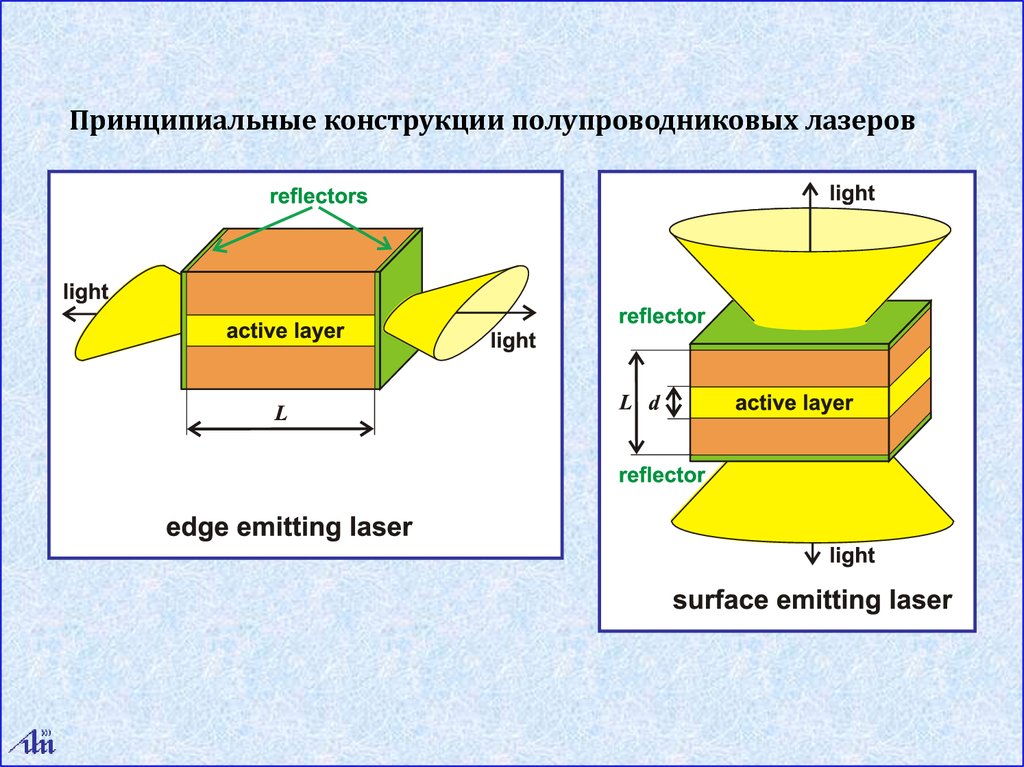
Принципиальные конструкции полупроводниковых лазеров

60.

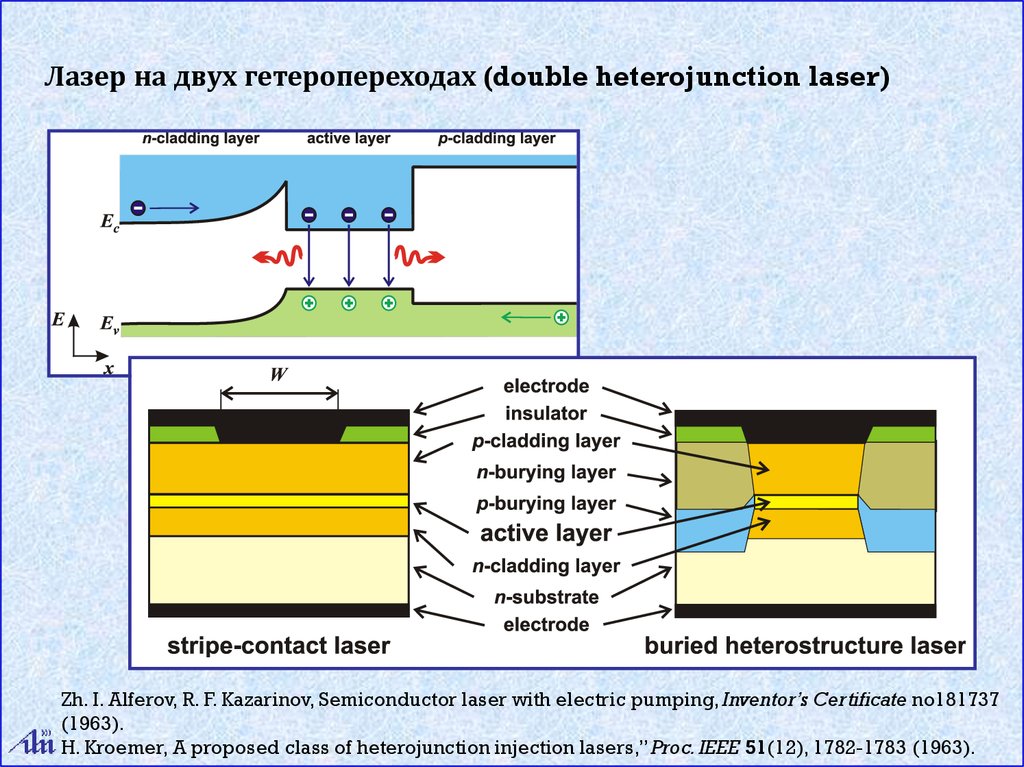
Лазер на двух гетеропереходах (double heterojunction laser)
Zh. I. Alferov, R. F. Kazarinov, Semiconductor laser with electric pumping, Inventor’s Certificate no181737
(1963).
H. Kroemer, A proposed class of heterojunction injection lasers,” Proc. IEEE 51(12), 1782-1783 (1963).

61.

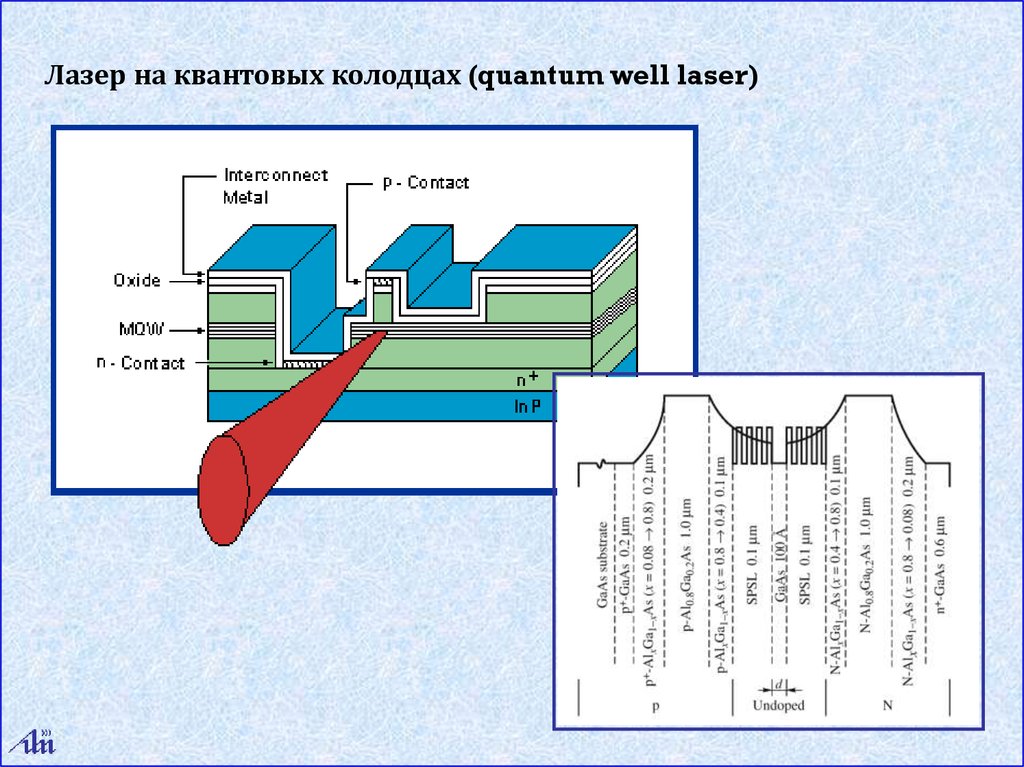
Лазер на квантовых колодцах (quantum well laser)

62.

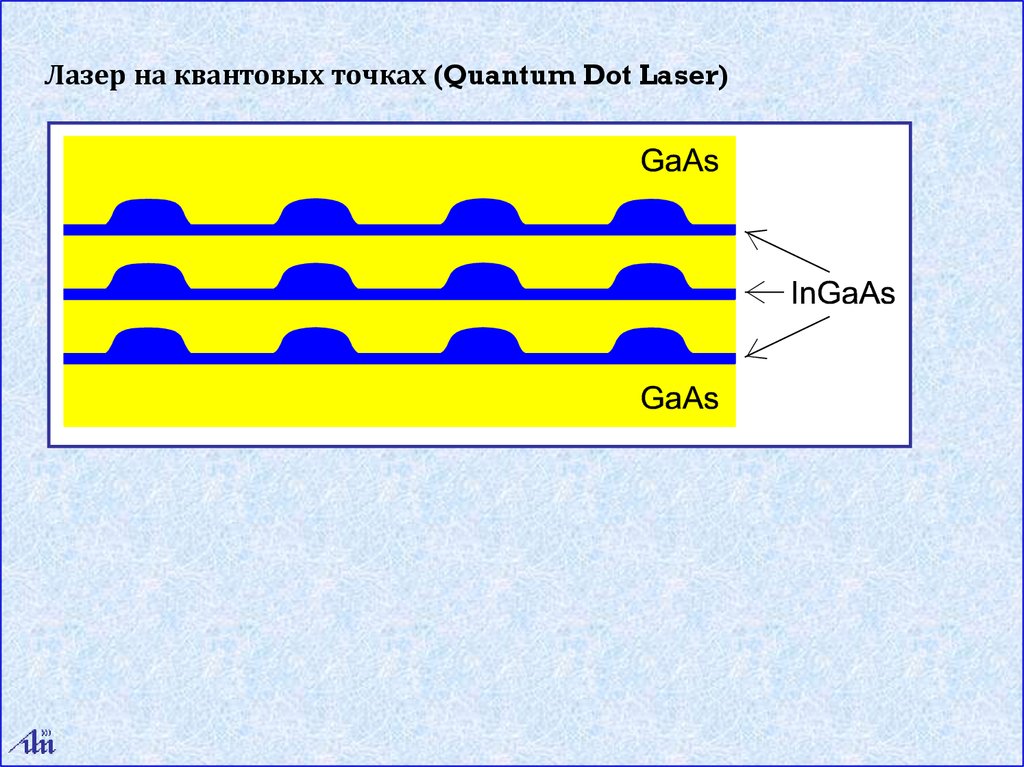
Лазер на квантовых точках (Quantum Dot Laser)

63.

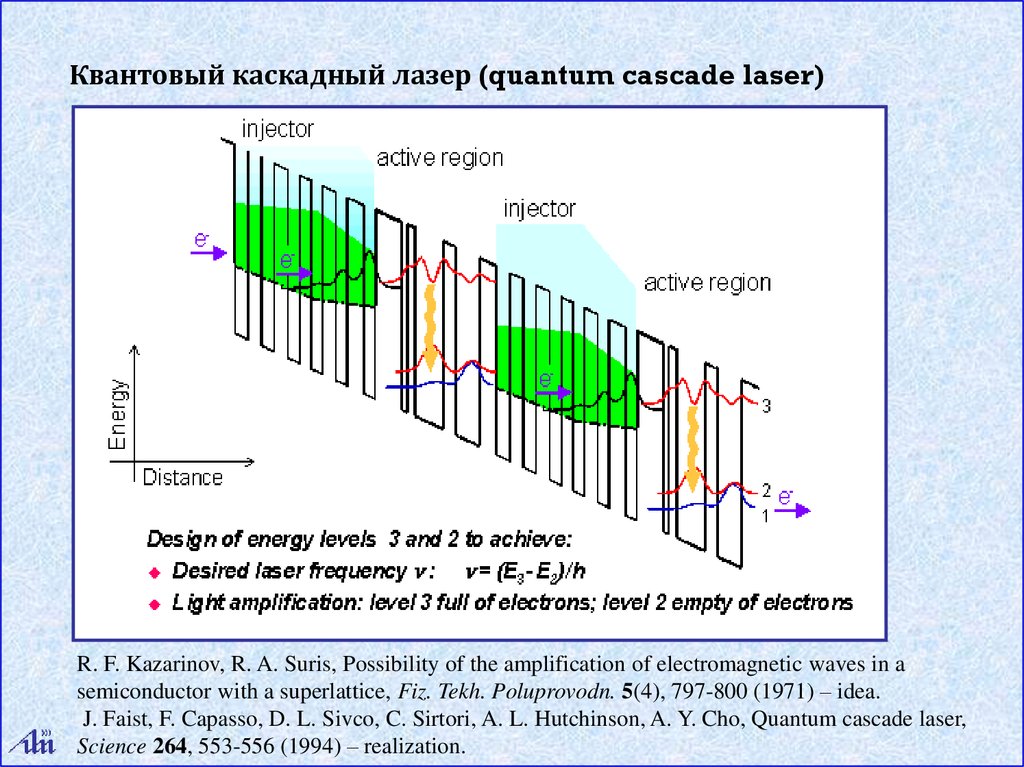
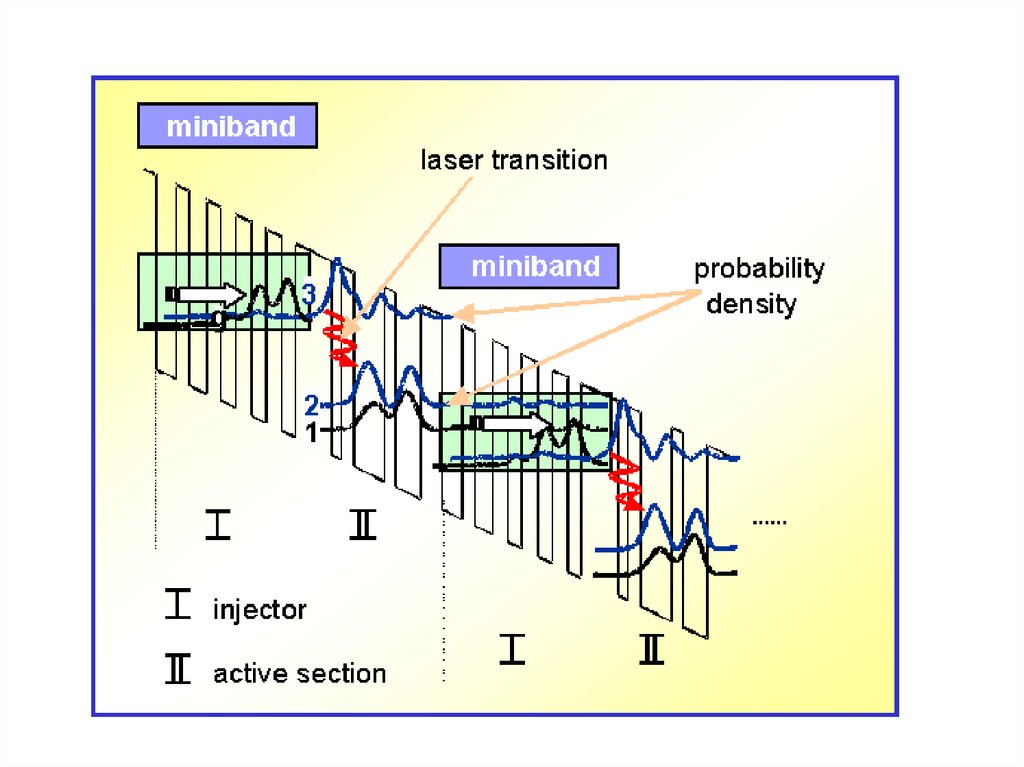
Квантовый каскадный лазер (quantum cascade laser)
R. F. Kazarinov, R. A. Suris, Possibility of the amplification of electromagnetic waves in a
semiconductor with a superlattice, Fiz. Tekh. Poluprovodn. 5(4), 797-800 (1971) – idea.
J. Faist, F. Capasso, D. L. Sivco, C. Sirtori, A. L. Hutchinson, A. Y. Cho, Quantum cascade laser,
Science 264, 553-556 (1994) – realization.

64.

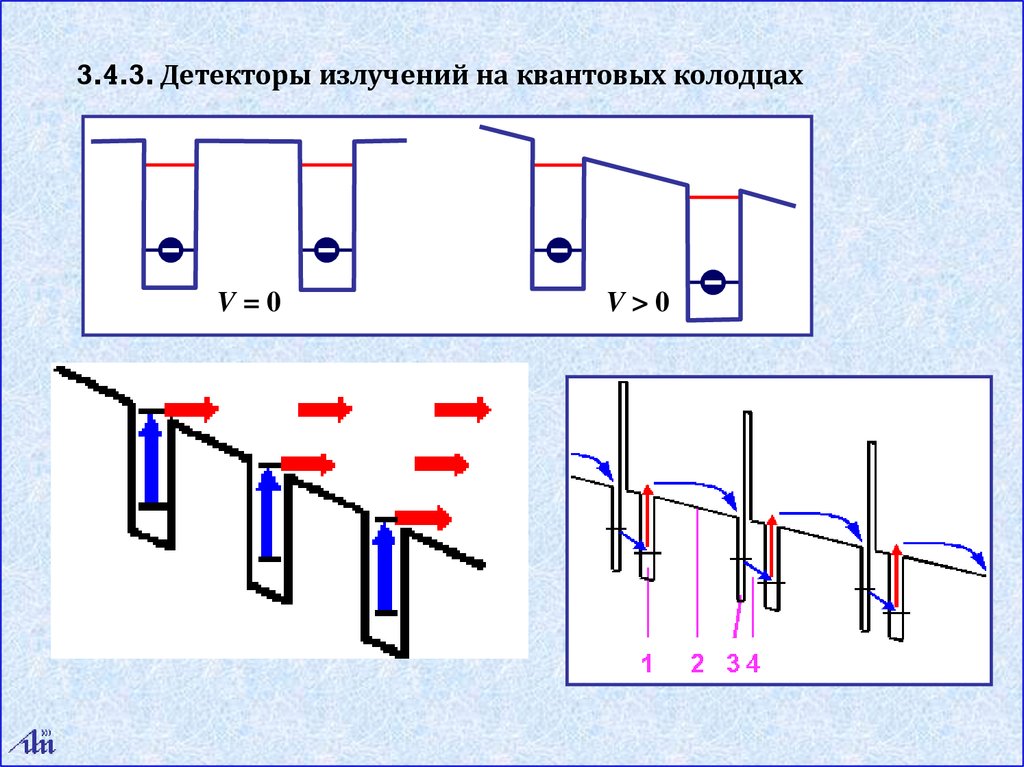
3.4.3. Детекторы излучений на квантовых колодцах
V=0
V>0

65.

From the History of Heterostructures and Information
Technology
Zhores I. Alferov
(1930)
A.F. Ioffe PhysicoTechnical Institute
St.Petersburg, Russia
Herbert Kroemer
(1928)
University of
California
Santa Barbara, USA
Jack S. Kilby
(1923 - 2005)
Texas Instruments
Dallas, USA
The Nobel Prize in Physics, 2000
for basic work on information and communication technology
for developing semiconductor
heterostructures used in high-speed- and
optoelectronics
for his part in the
invention of the
integrated circuit

66.

67.

68.

Fig. 1: Interband- vs. intersubbandtransitions
C
с
Fig. 2: Principle of
cascading

69.

70.

71.

transistor laser
R. Chan, M. Feng, N. Holonyak, Jr., and G. Walter,
Microwave operation and modulation of a transistor
laser, Appl. Phys. Lett. 86, 131114 (2005).

72.

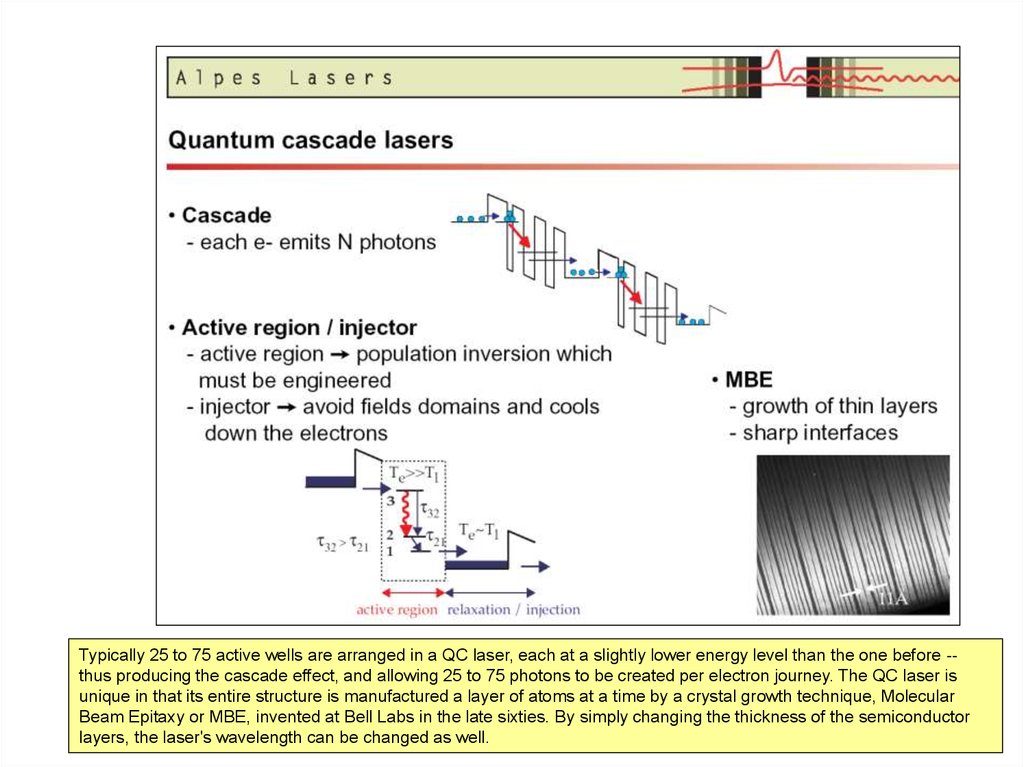
Typically 25 to 75 active wells are arranged in a QC laser, each at a slightly lower energy level than the one before -thus producing the cascade effect, and allowing 25 to 75 photons to be created per electron journey. The QC laser is
unique in that its entire structure is manufactured a layer of atoms at a time by a crystal growth technique, Molecular
Beam Epitaxy or MBE, invented at Bell Labs in the late sixties. By simply changing the thickness of the semiconductor
layers, the laser's wavelength can be changed as well.

73.

74.

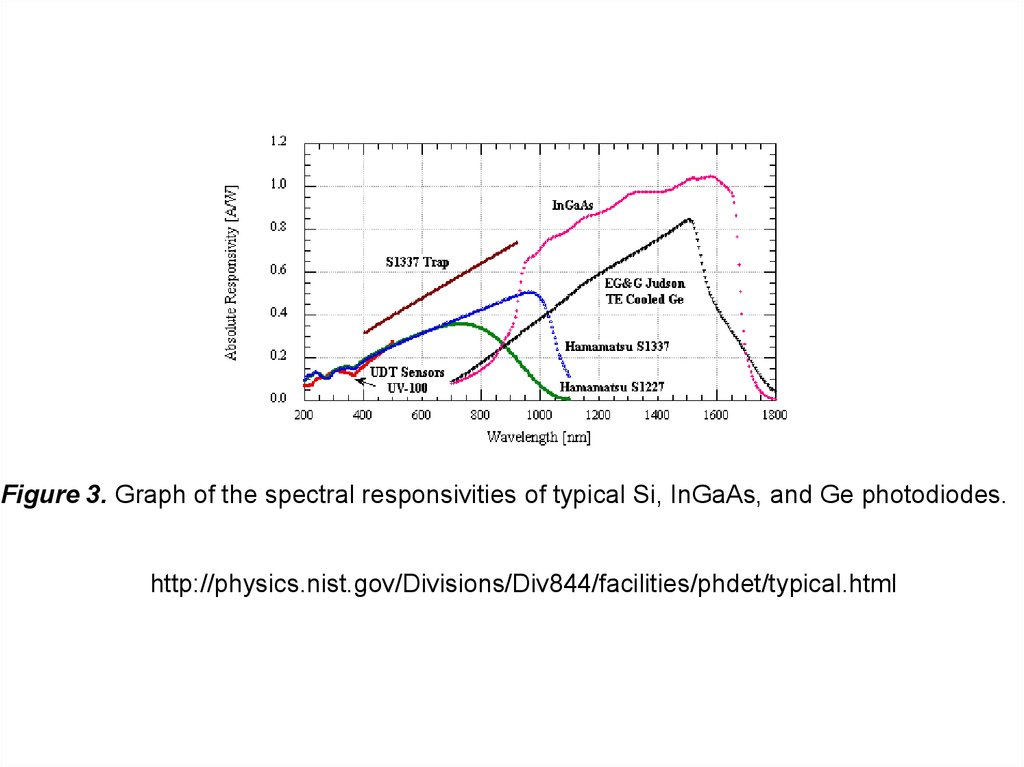
Figure 3. Graph of the spectral responsivities of typical Si, InGaAs, and Ge photodiodes.
http://physics.nist.gov/Divisions/Div844/facilities/phdet/typical.html

English Русский Rules