Диэлектрофорез: движение клеток или частиц в неоднородном переменном электрическом поле

1.

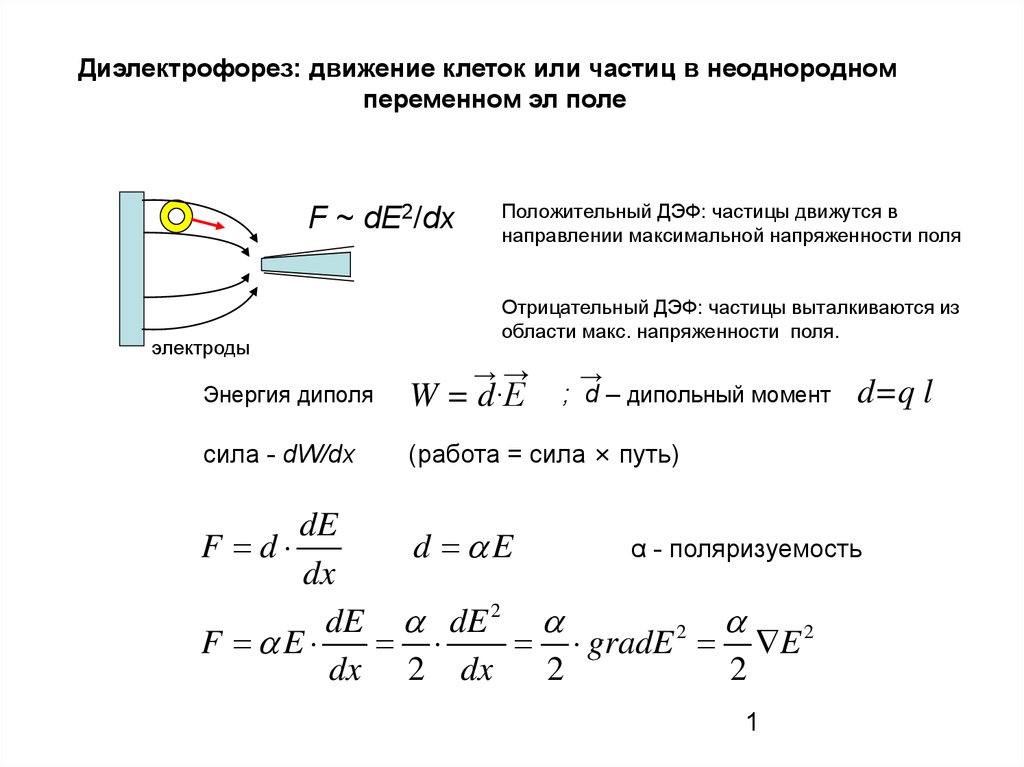
Диэлектрофорез: движение клеток или частиц в неоднородном
переменном эл поле
F ~ dE2/dx
электроды
Положительный ДЭФ: частицы движутся в
направлении максимальной напряженности поля
Отрицательный ДЭФ: частицы выталкиваются из
области макс. напряженности поля.
→→
→
; d – дипольный момент
Энергия диполя
W = d∙E
сила - dW/dx
(работа = сила × путь)
d=q l
dE
α - поляризуемость
d E
dx
dE dE 2
2
F E
gradE E 2
dx 2 dx
2
2
F d
1

2.

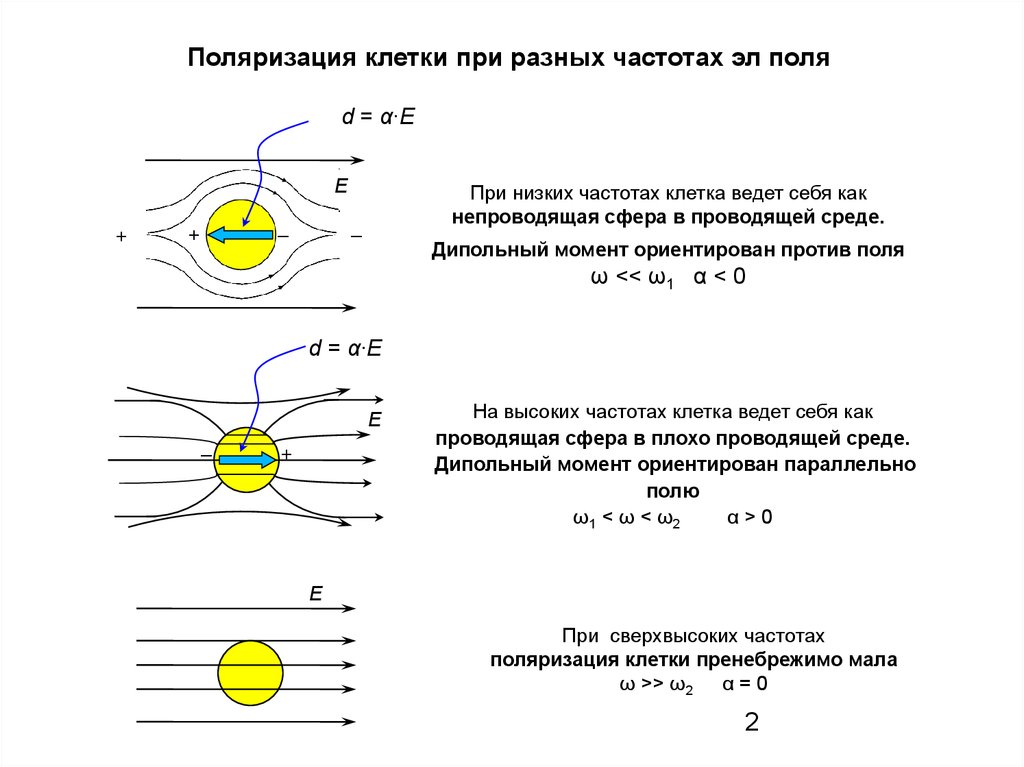
Поляризация клетки при разных частотах эл поля
d = α∙E
E
+
–
+
При низких частотах клетка ведет себя как
непроводящая сфера в проводящей среде.
–
Дипольный момент ориентирован против поля
ω << ω1 α < 0
d = α∙E
E
–
+
На высоких частотах клетка ведет себя как
проводящая сфера в плохо проводящей среде.
Дипольный момент ориентирован параллельно
полю
ω1 < ω < ω2
α>0
E
При сверхвысоких частотах
поляризация клетки пренебрежимо мала
ω >> ω2 α = 0
2

3.

Зависимость диэлектрофореза от частоты эл поля
α
При частоте ω1 токи, текущие
через клетку и в обход нее равны
ω1 ~ 105 Hz
ω2 ~ 109 Hz
В грубом приближении
1
Cm r 2
ω1
0
ω2
α<0,
отриц.
ДЭФ
R =XC = (ω С)–1
lg ω
α>0,
положит.
ДЭФ
Скорость движения ( v ) при ДЭФ
определяется балансом между силой ДЭФ и
силой вязкого трения
F=6πrvη
FDEP = k grad E2
η – вязкость; r – радиус
1 r
r2
1
r
Cm
Cm
10 3 S / m
См/м
C m 10 2 F / m 2
Ф/м2
r 1 m 10 6 m
м
1
,
Cmr
1 10 Hz
5
Сm – емкость мембраны;
σ – проводимость среды
3
Гц
r

4.

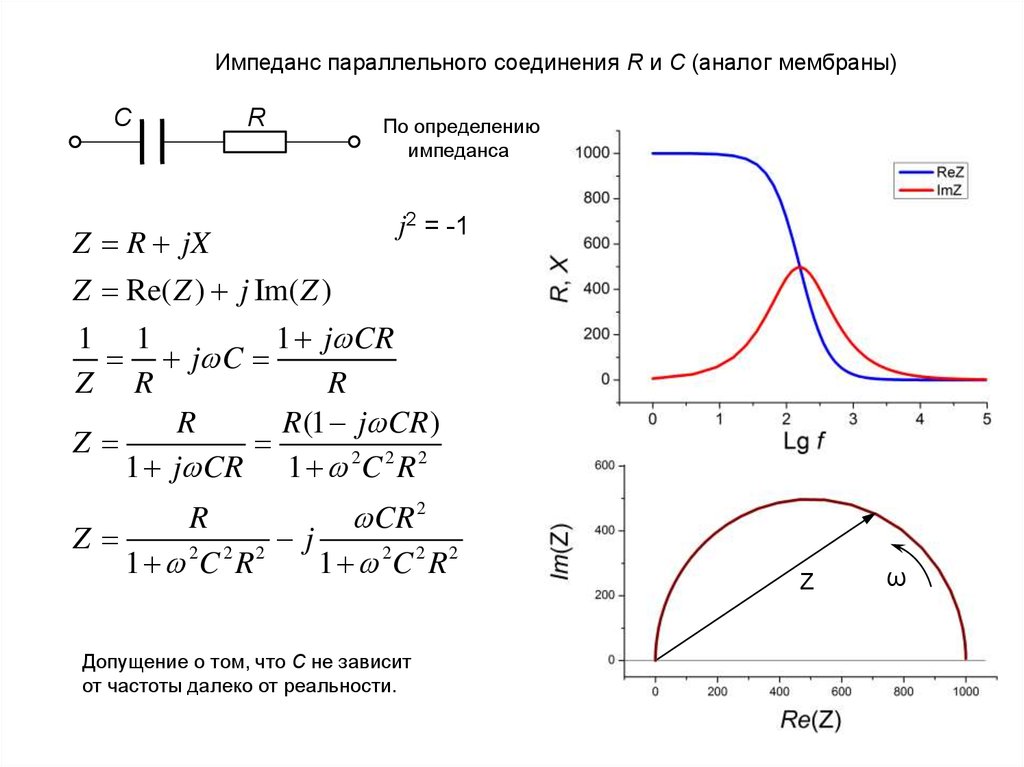
Импеданс параллельного соединения R и C (аналог мембраны)
C
R
Z R jX
По определению
импеданса
j2 = -1
Z Re( Z ) j Im( Z )
1 1
1 j CR
j C
Z R
R
R
R (1 j CR )
Z
1 j CR 1 2C 2 R 2
R
CR 2
Z
j
2 2 2
1 C R
1 2C 2 R 2
Z
Допущение о том, что С не зависит
от частоты далеко от реальности.
4
ω

5.

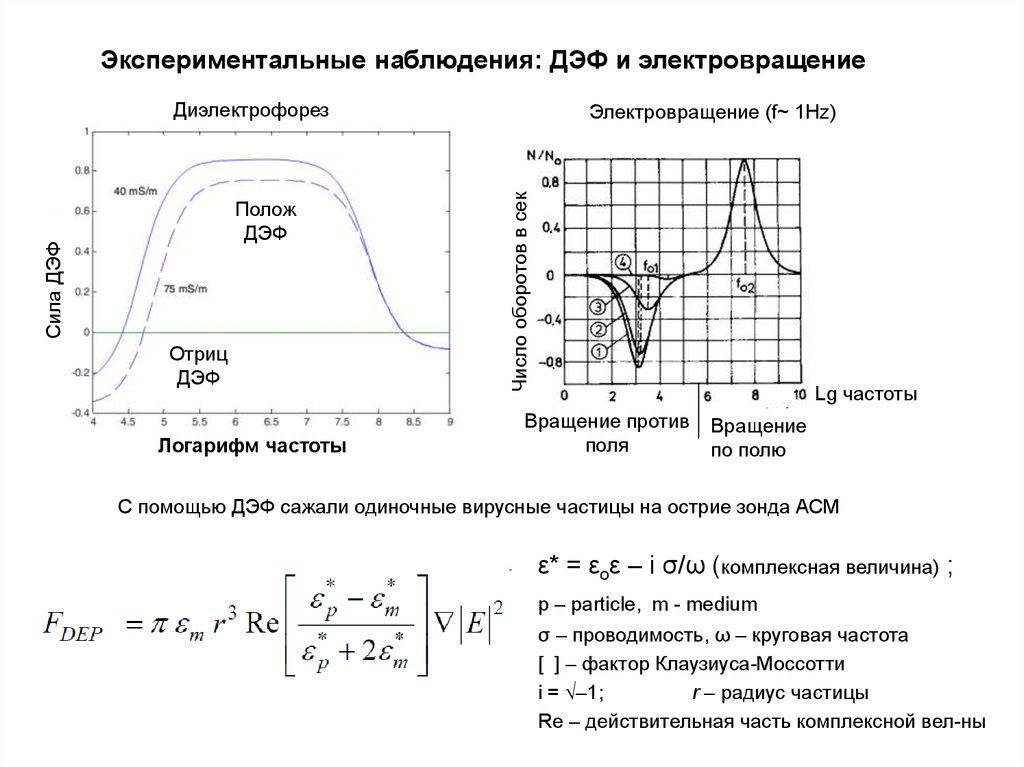
Экспериментальные наблюдения: ДЭФ и электровращение
Диэлектрофорез
Отриц
ДЭФ
Логарифм частоты
Число оборотов в сек
Сила ДЭФ
Полож
ДЭФ
Электровращение (f~ 1Hz)
Lg частоты
Вращение против
поля
Вращение
по полю
С помощью ДЭФ сажали одиночные вирусные частицы на острие зонда АСМ
ε* = εoε – i σ/ω (комплексная величина) ;
p – particle, m - medium
σ – проводимость, ω – круговая частота
[ ] – фактор Клаузиуса-Моссотти
i = √–1;
r – радиус частицы
Re – действительная часть
5 комплексной вел-ны

6.

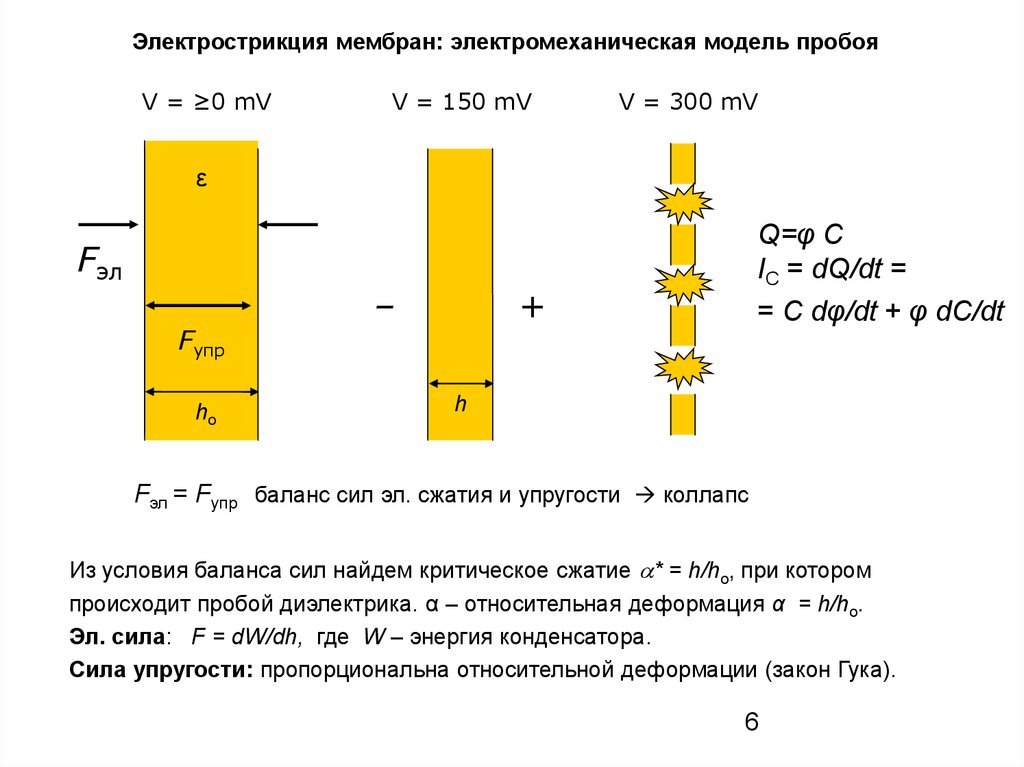
Электрострикция мембран: электромеханическая модель пробоя
V = ≥0 mV
V = 150 mV
V = 300 mV
ε
Fэл
Fупр
ho
–
Q=φ C
IC = dQ/dt =
= C dφ/dt + φ dC/dt
+
h
Fэл = Fупр баланс сил эл. сжатия и упругости коллапс
Из условия баланса сил найдем критическое сжатие * = h/ho, при котором
происходит пробой диэлектрика. α – относительная деформация α = h/ho.
Эл. сила: F = dW/dh, где W – энергия конденсатора.
Сила упругости: пропорциональна относительной деформации (закон Гука).
6

7.

Сила эл сжатия мембран и сила упругости
dh
dF E ;
h
Fmech
h
E ln E ln
ho
α = h/ho.
o 2
o 2
d o 2
Fel
2 2;
2
dh 2h
2h
2 ho
2 ln
o 2
2 E ho 2
Закон Гука: изменение упругой силы пропорционально относительной деформации,
E - модуль упругости.
Эл силу находят как производную эл энергии заряженного конденсатора
по толщине диэл. слоя (по толщине мембраны).
Эти силы сбалансированы; получим ур-ие, к-рое можно решить графически,
построив графики зависимости правой и левой части от отн. деформации.
Точки пересечения являются решениями ур-ия.
7

8.

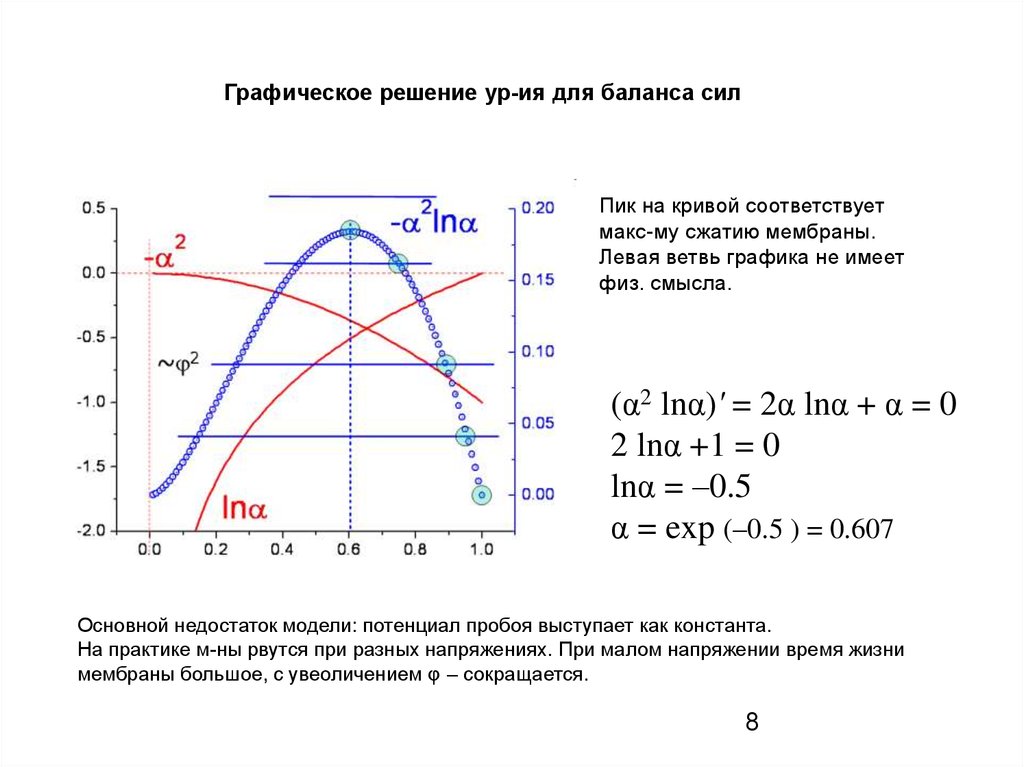
Графическое решение ур-ия для баланса сил
Пик на кривой соответствует
макс-му сжатию мембраны.
Левая ветвь графика не имеет
физ. смысла.
(α2 lnα)' = 2α lnα + α = 0
2 lnα +1 = 0
lnα = –0.5
α = exp (–0.5 ) = 0.607
Основной недостаток модели: потенциал пробоя выступает как константа.
На практике м-ны рвутся при разных напряжениях. При малом напряжении время жизни
мембраны большое, с увеоличением φ – сокращается.
8

9.

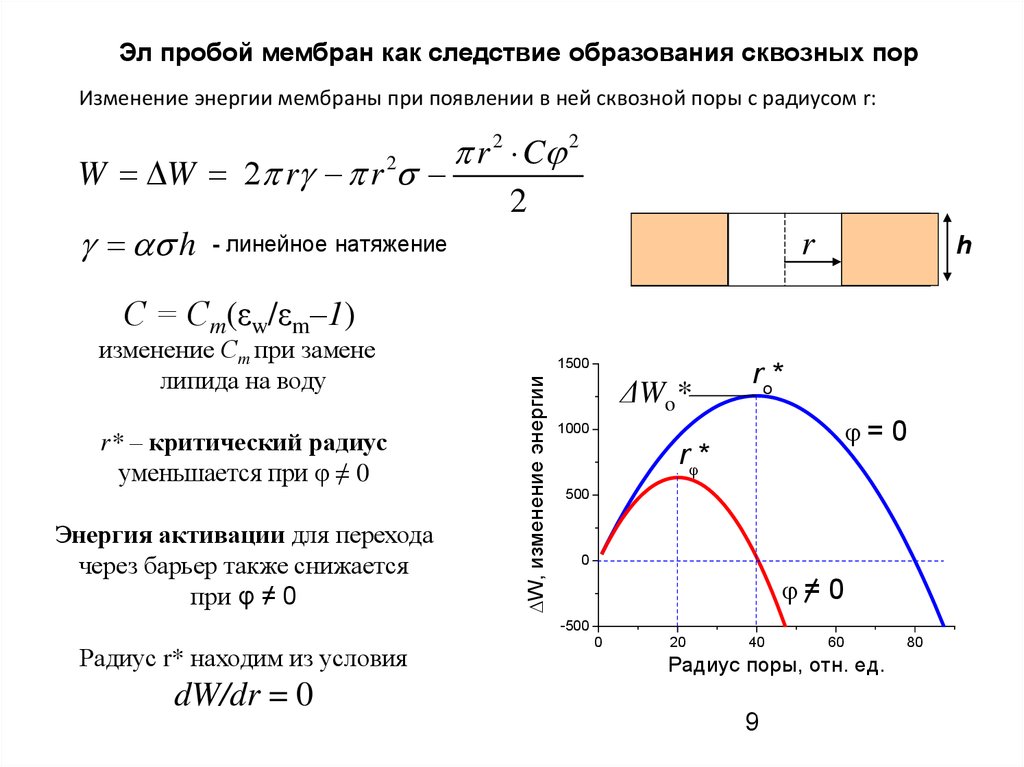
Эл пробой мембран как следствие образования сквозных пор
Изменение энергии мембраны при появлении в ней сквозной поры с радиусом r:
W W 2 r r –
2
2
r
- линейное натяжение
dWС = С (ε /ε –1) 2 rC 2
2 m w2 mr
изменение Сm при замене
dr
2
dW липида на воду
0
r*
2
r* – критический радиусC
dr
уменьшается при φ ≠
0
2
Conclusion:
the life 2time
of перехода
BLM
Энергия активации
для
in the
depends
Welectric
*барьер
fieldтакже
j A exp
через
снижается
2
primarily on linear tension
C≠ 0 of the
при
φ
pore γ, which depends
on the
shape of phospholipid2molecules.
Радиус r* находим из условия
W
=0
t 1/ jdW/dr
A exp
RT
1500
W, изменение энергии
h
r 2 C 2
ΔWo*
h
ro*
= 0
1000
r *
500
W
0
RT
= 0
-500
0
20
40
60
Радиус поры, отн. ед.
9
R-
80

10.

Влияние мембр. потенциала φ на время жизни БЛМ в эл. поле
dW
2 rC 2
2 2 r
dr
2
dW
0
dr
W *
r*
C 2
2
2
C 2
j A exp
W
RT
2
W
t 1/ j A exp
RT
Логарифм времени жизни БЛМ, с
h
PE
PC+LPC
Напряжение на БЛМ, В
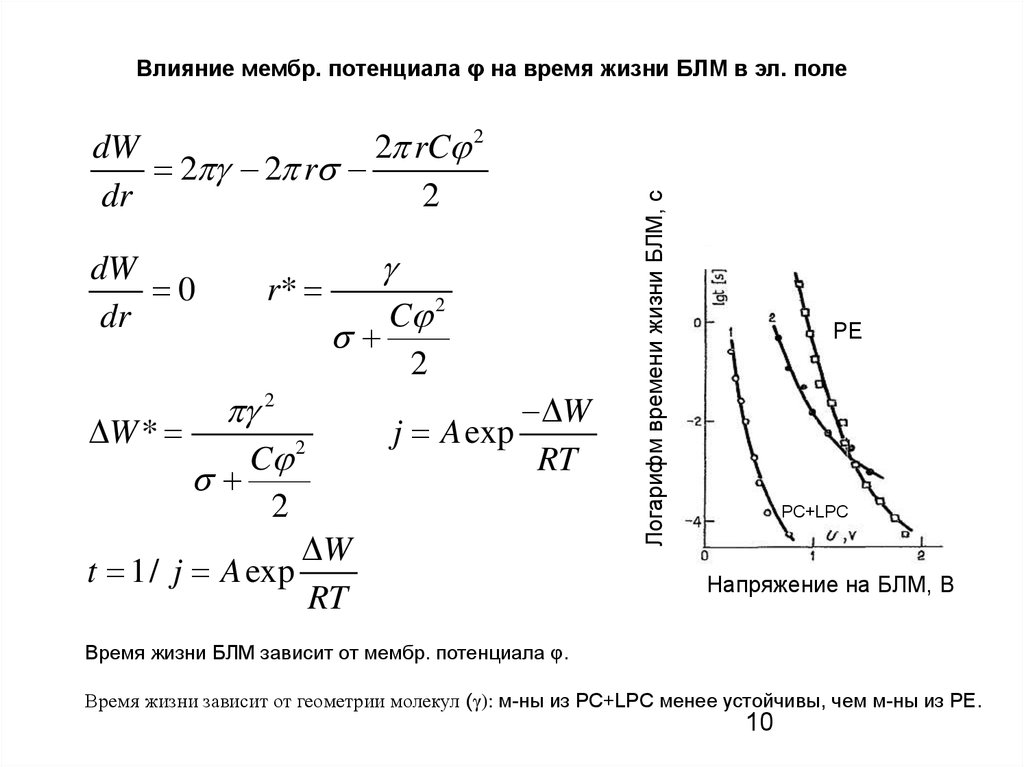
Время жизни БЛМ зависит от мембр. потенциала φ.
Время жизни зависит от геометрии молекул (γ): м-ны из PC+LPC менее устойчивы, чем м-ны из PE.
10

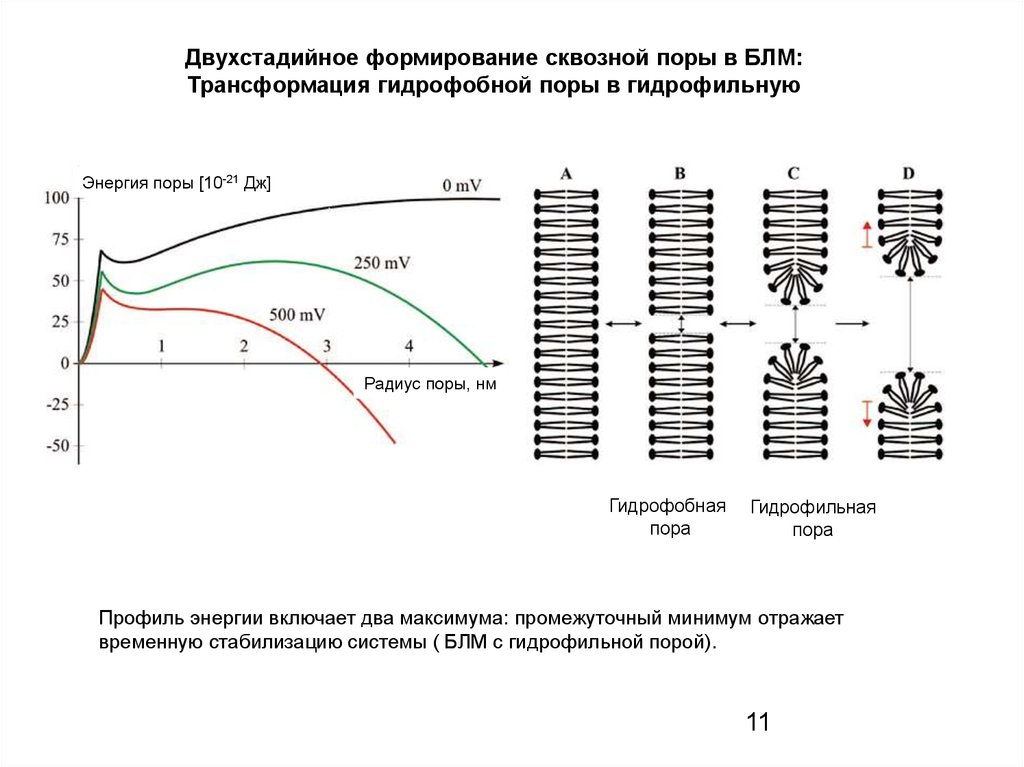
11.

Двухстадийное формирование сквозной поры в БЛМ:
Трансформация гидрофобной поры в гидрофильную
Энергия поры [10-21 Дж]
Радиус поры, нм
Гидрофобная
пора
Гидрофильная
пора
Профиль энергии включает два максимума: промежуточный минимум отражает
временную стабилизацию системы ( БЛМ с гидрофильной порой).
11

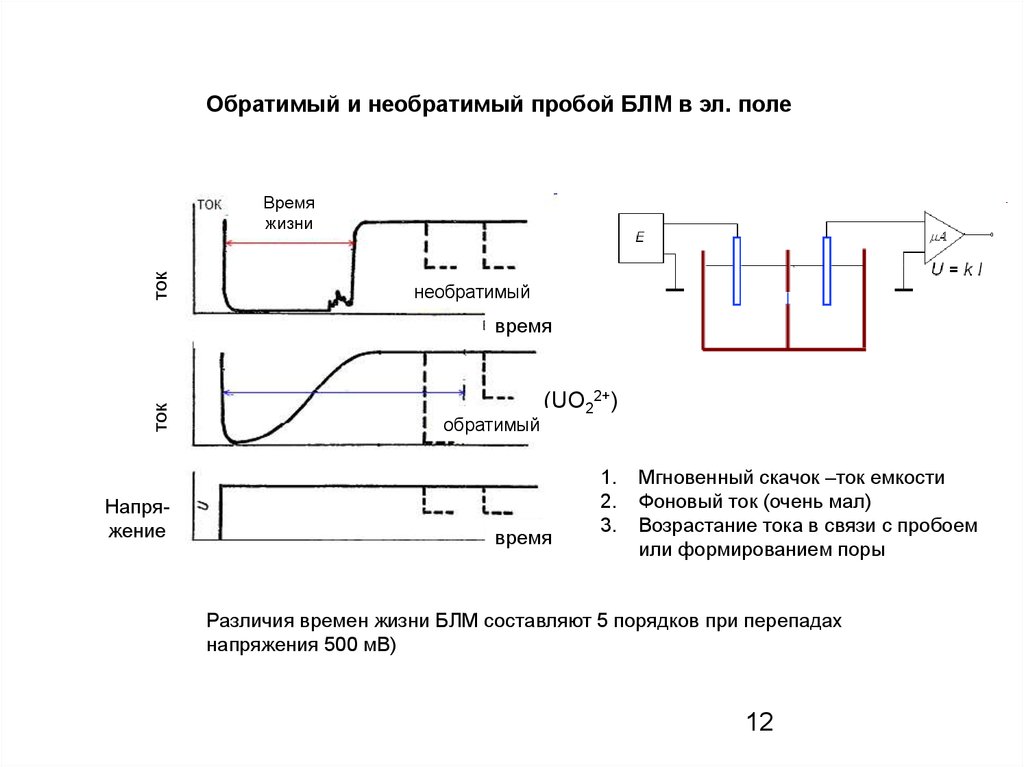
12.

Обратимый и необратимый пробой БЛМ в эл. поле
ток
Время
жизни
необратимый
ток
время
Напряжение
обратимый
(UO22+)
время
1.
2.
3.
Мгновенный скачок –ток емкости
Фоновый ток (очень мал)
Возрастание тока в связи с пробоем
или формированием поры
Различия времен жизни БЛМ составляют 5 порядков при перепадах
напряжения 500 мВ)
12

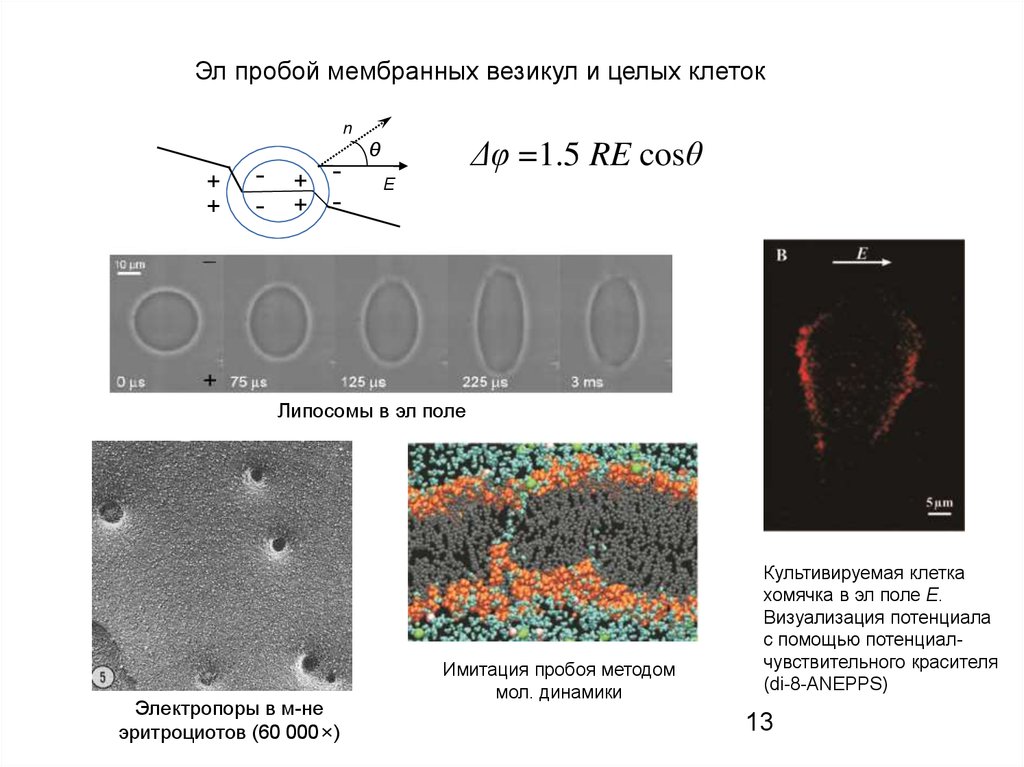
13.

Эл пробой мембранных везикул и целых клеток
n
+
+
-
+ + -
Δφ =1.5 RE cosθ
θ
E
Липосомы в эл поле
Электропоры в м-не
эритроциотов (60 000×)
Имитация пробоя методом
мол. динамики
Культивируемая клетка
хомячка в эл поле Е.
Визуализация потенциала
с помощью потенциалчувствительного красителя
(di-8-ANEPPS)
13

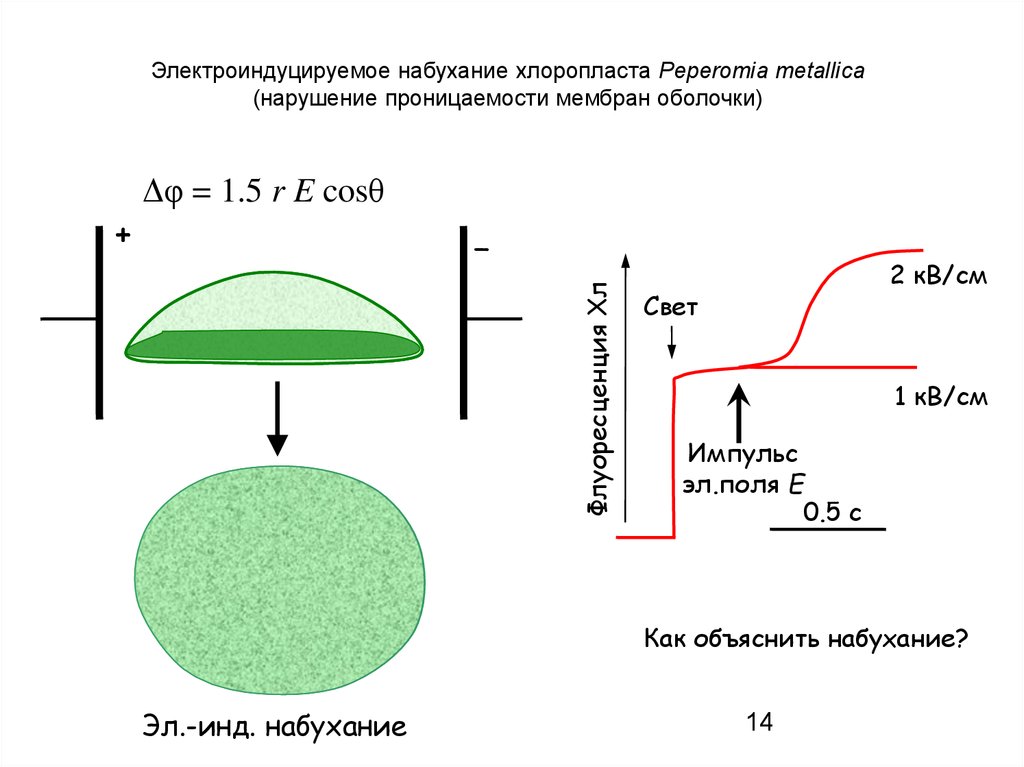
14.

Электроиндуцируемое набухание хлоропласта Peperomia metallica
(нарушение проницаемости мембран оболочки)
−
Флуоресценция Хл
+
Δφ = 1.5 r E cosθ
2 кВ/см
Свет
1 кВ/см
Импульс
эл.поля Е
0.5 c
Как объяснить набухание?
Эл.-инд. набухание
14

15.

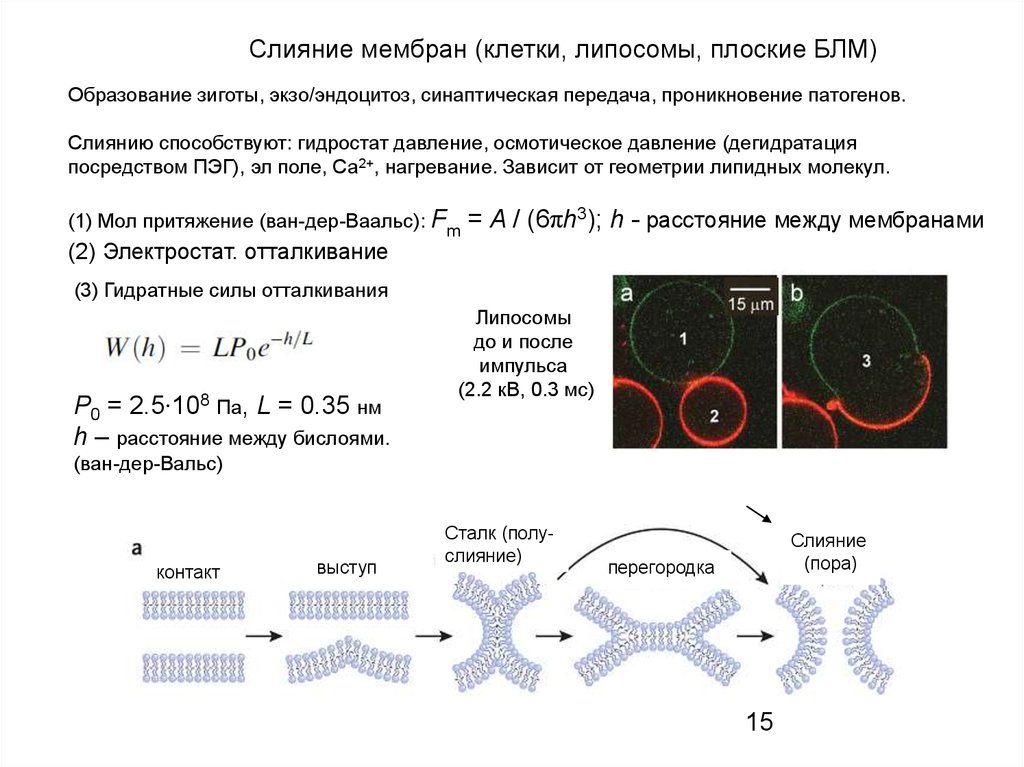
Слияние мембран (клетки, липосомы, плоские БЛМ)
Образование зиготы, экзо/эндоцитоз, синаптическая передача, проникновение патогенов.
Слиянию способствуют: гидростат давление, осмотическое давление (дегидратация
посредством ПЭГ), эл поле, Са2+, нагревание. Зависит от геометрии липидных молекул.
(1) Мол притяжение (ван-дер-Ваальс): Fm
= A / (6πh3); h - расстояние между мембранами
(2) Электростат. отталкивание
(3) Гидратные силы отталкивания
P0 = 2.5∙108 Па, L = 0.35 нм
h – расстояние между бислоями.
Липосомы
до и после
импульса
(2.2 кВ, 0.3 мс)
(ван-дер-Вальс)
контакт
выступ
Сталк (полуслияние)
Слияние
(пора)
перегородка
15

16.

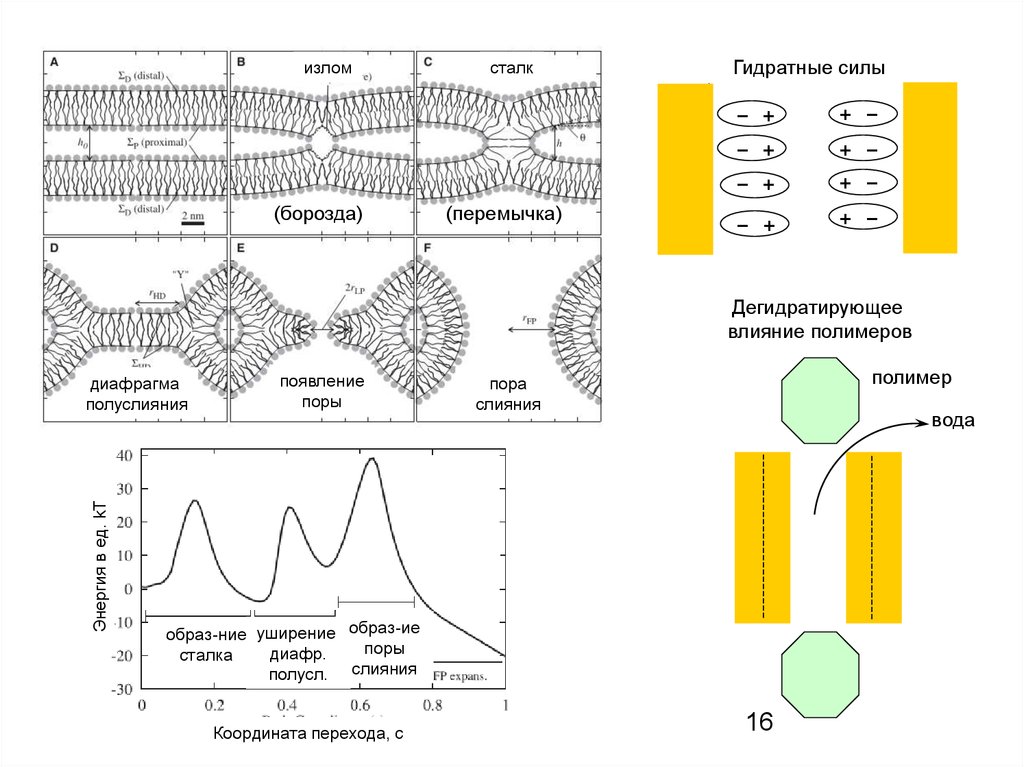
излом
(борозда)
сталк
(перемычка)
Гидратные силы
− +
+ −
− +
− +
+ −
+ −
− +
+ −
Дегидратирующее
влияние полимеров
Энергия в ед. kT
диафрагма
полуслияния
появление
поры
полимер
пора
слияния
вода
образ-ние уширение образ-ие
поры
диафр.
сталка
полусл. слияния
Координата перехода, с
16