Механические свойства твердых полимеров, малые деформации. (Лекция 9)

1.

Лекция № 9
Механические свойства твердых полимеров
(малые деформации)
Термин механические свойства обычно используют для характеристики соотношения напряжение деформация. Характерная особенность механических свойств полимеров - сильная зависимость от
температуры и времени воздействия.
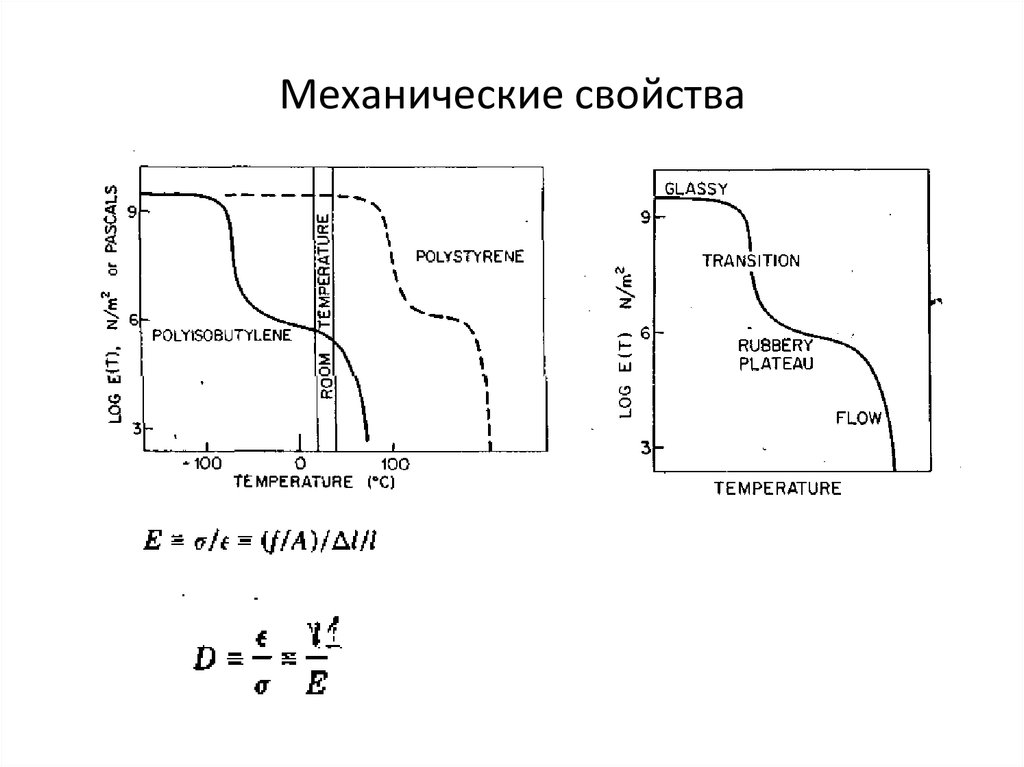
Зависимость модуля от температуры.
lgE(t)
9
ПИБ
ПСт
6
3
-100
0 комн.
темп-ра
100
Тс
Т
Полиизобутилен (ПИБ) - стекло до температуры -75 oС, при которой он переходит в высокоэластическое состояние
и модуль изменяется на 3 порядка.
В области tком наблюдается сильное падение модуля, т.к. полимер переходит в вязко-текучее состояние.
Полистирол имеет тот же модуль (3·109) и переходит в каучукоподобное состояние при 100 ˚С. Оба полимера
являются несшитыми.

2. Механические свойства

3.

Эту зависимость можно обобщить:
lgE(T)
стеклообразное состояние
переход от стеклообразного состояния к высокоэластическому
высокоэластическое плато
- большая сшивка
- меньшая сшивка
- большая молекулярная масса
- меньшая молекулярная масса
T
Имеем 4 области:
1) стеклообразное состояние - модуль слабо зависит от температуры.
2) переходное состояние (переход от стеклообразного состояния к высокоэластическому)
3) плато высокоэластичности - модуль слабо зависит от температуры. Чем больше число
узлов в сетке, тем выше находится плато. Это плато для сшитых полимеров простирается до
области деструкции. Чем больше молекулярная масса, тем при большей температуре образец
начинает течь.
4) вязко-текучее состояние

4.

w

5.

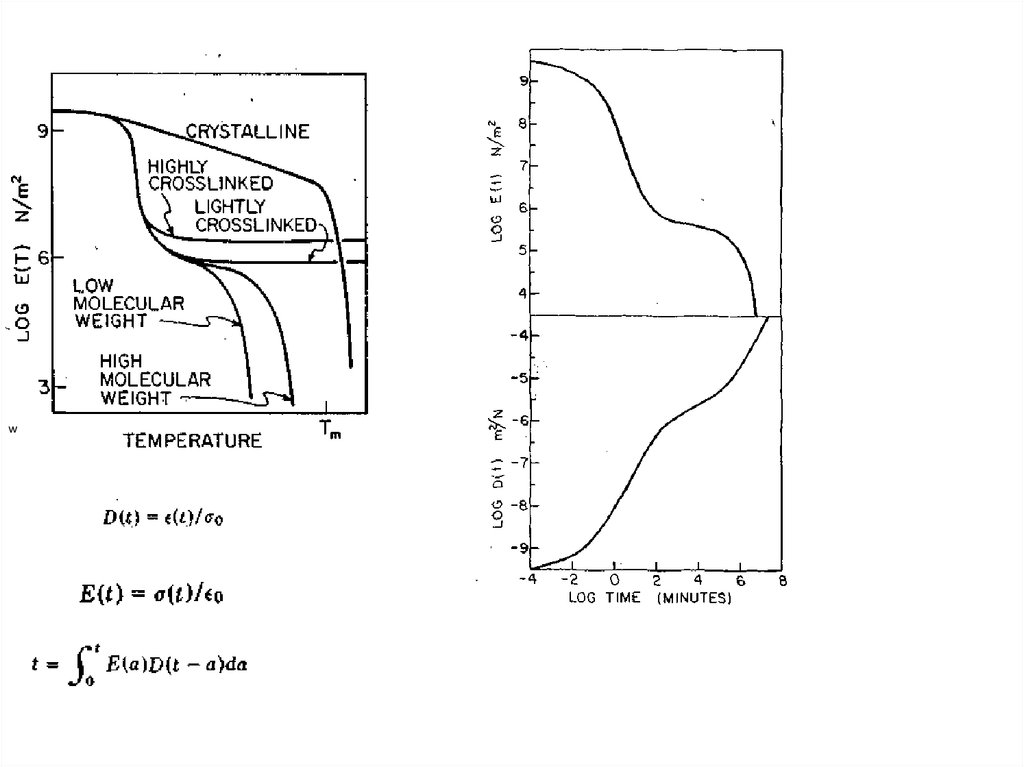
Для кристаллических полимеров эта зависимость иная. В кристаллическом полимере есть аморфные
области, которые ведут себя как аморфные стеклообразные полимеры, есть и кристаллические области
(макромолекулы полимеров обычно входят в состав кристаллической части не целиком, а лишь частью, т.
е. тем или иным числом сегментов; другая же часть макромолекулы может оставаться в аморфной
области полимера или входить в состав другой кристаллической области). Поэтому в отличие от
кристаллов низкомолекулярных веществ кристаллические образования в полимерах не имеют четких
граней, из-за чего их называют кристаллитами (т. е. несовершенными кристаллами).
lgE(T)
стеклообразный
полимер
- кристаллический полимер
Tc Tc
Tпл
Т
При нагревании образца, содержащего 50% кристаллитов наблюдается резкое изменение модуля (либо изменяется
наклон кривой), а затем резкое падение модуля.

6.

Виды деформаций:
1) Растяжение (сжатие):
f
f
L0 L / L0 - относительная деформация
f / S 0 - условное напряжение,
S0 – исходное поперечное сечение
ε
L L0
- относительная деформация
L0
E - закон Гука, Е - модуль Юнга
2)Простой сдвиг (изменение формы):
f
α
tg - деформация сдвига, α – угол
сдвига
G - напряжение сдвига, G модуль сдвига

7.

3)Всестороннее сжатие (растяжение):
p
p
p
p
p - сжимающее напряжение (давление)
К - модуль всестороннего сжатия
K p
δV/V ;
δV
V
V V0
- относительное изменение объема; изменяется только объем
V0
Податливость: величина, обратная модулю
(J = 1/G, B = 1/K, D = 1/E )
Соотношение модулей: E 3K 1 2μ 2 1 μ G ,
- коэффициент Пуассона (отношение поперечного сдвига к продольному растяжению при односторонн
растяжении)
при = 0.5 - нет изменения объема при растяжении,
= 0.4996 – для каучука,
= 0.2 - 0.4 – для твердых полимеров
= 0.5 Е = 3G - для эластомеров

8.

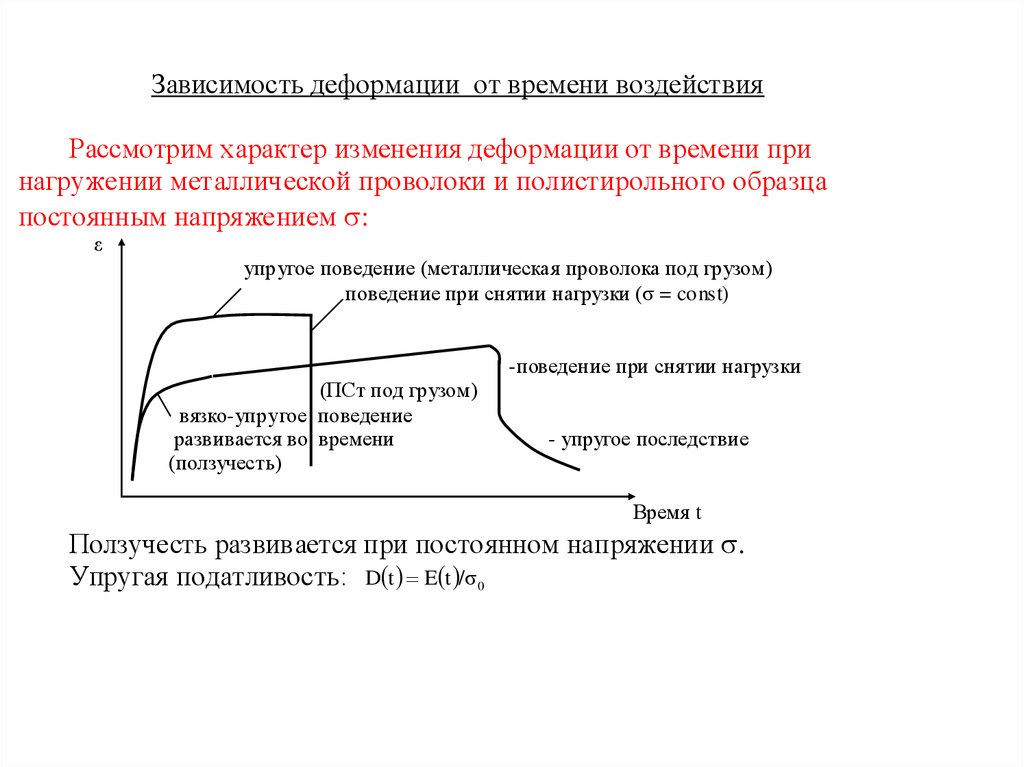
Зависимость деформации от времени воздействия
Рассмотрим характер изменения деформации от времени при
нагружении металлической проволоки и полистирольного образца
постоянным напряжением :
ε
упругое поведение (металлическая проволока под грузом)
поведение при снятии нагрузки (σ = const)
-поведение при снятии нагрузки
(ПСт под грузом)
вязко-упругое поведение
развивается во времени
(ползучесть)
- упругое последствие
Время t
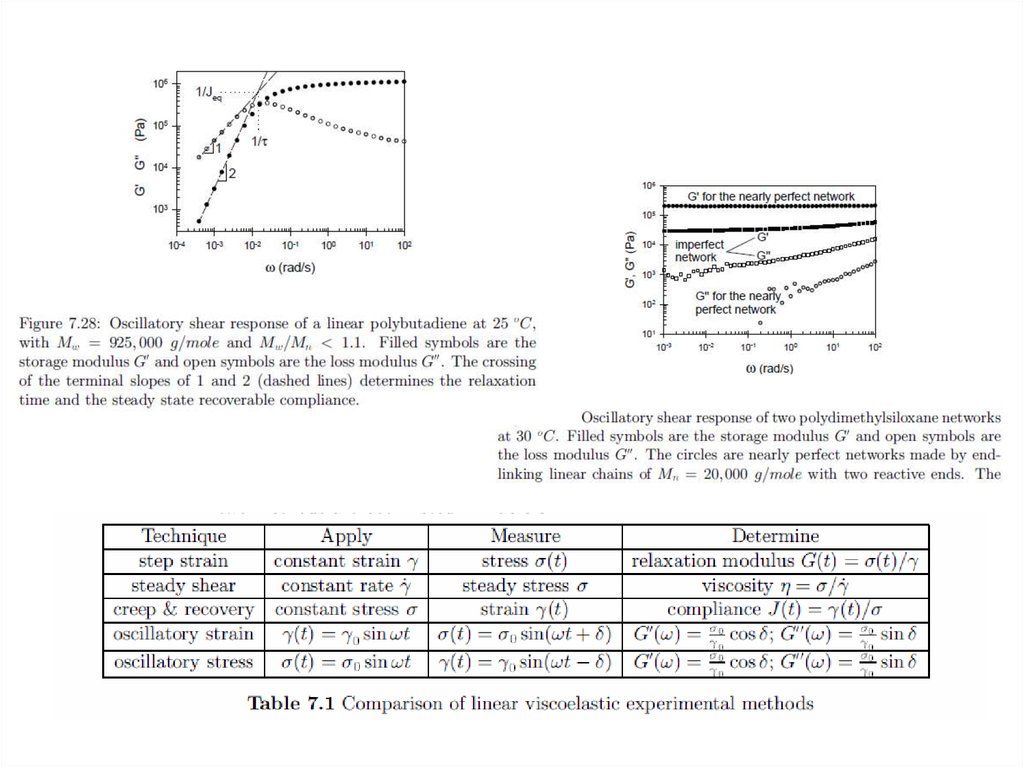
Ползучесть развивается при постоянном напряжении .
Упругая податливость: D t E t /σ 0

9.

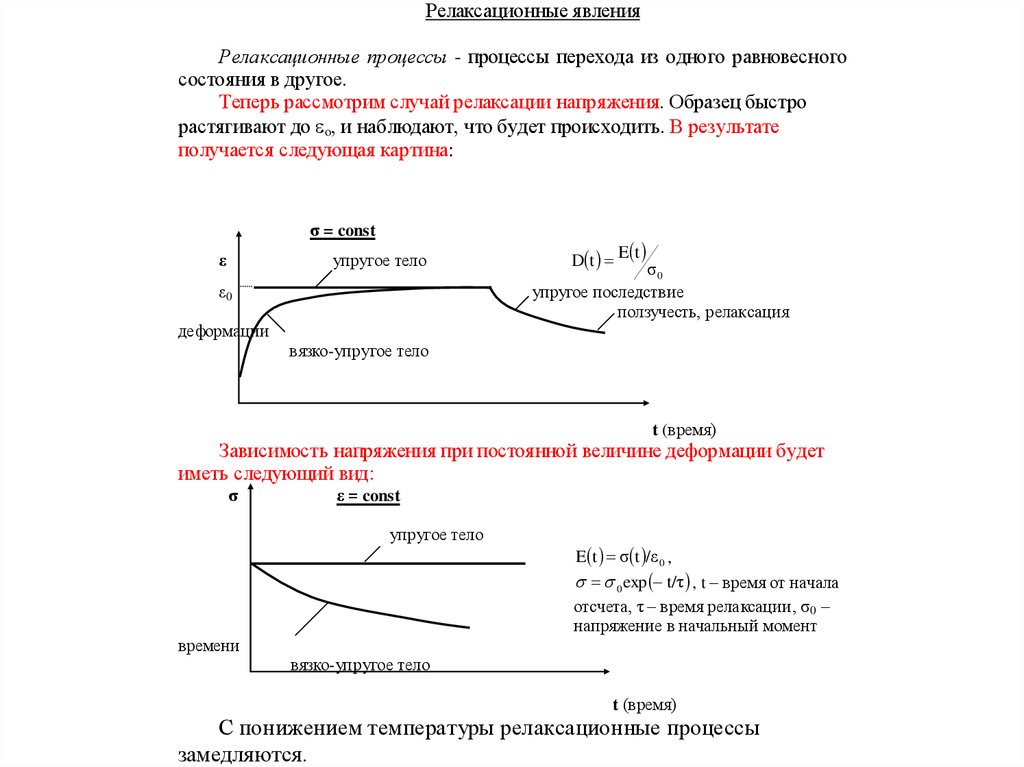
Релаксационные явления
Релаксационные процессы - процессы перехода из одного равновесного
состояния в другое.
Теперь рассмотрим случай релаксации напряжения. Образец быстро
растягивают до o, и наблюдают, что будет происходить. В результате
получается следующая картина:
σ = const
ε
упругое тело
ε0
D t E t
σ0
упругое последствие
ползучесть, релаксация
деформации
вязко-упругое тело
t (время)
Зависимость напряжения при постоянной величине деформации будет
иметь следующий вид:
σ
ε = const
упругое тело
E t σ t /ε 0 ,
0 exp t/τ , t – время от начала
отсчета, τ – время релаксации, σ0 –
напряжение в начальный момент
времени
вязко-упругое тело
t (время)
С понижением температуры релаксационные процессы
замедляются.

10.

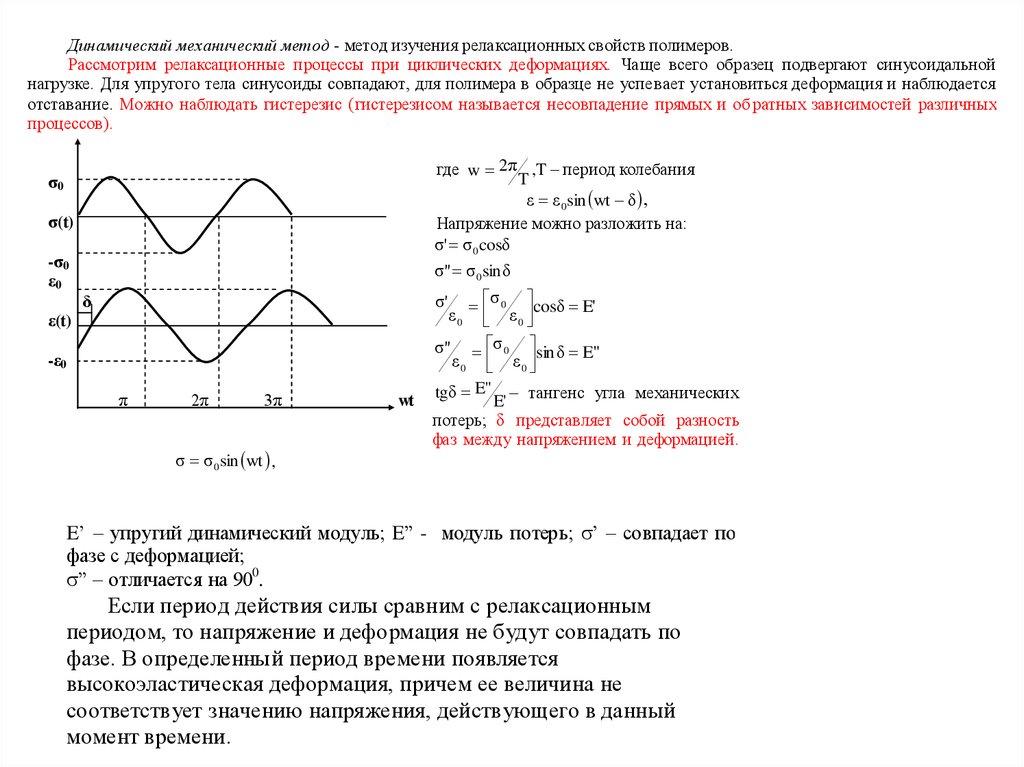
Динамический механический метод - метод изучения релаксационных свойств полимеров.
Рассмотрим релаксационные процессы при циклических деформациях. Чаще всего образец подвергают синусоидальной
нагрузке. Для упругого тела синусоиды совпадают, для полимера в образце не успевает установиться деформация и наблюдается
отставание. Можно наблюдать гистерезис (гистерезисом называется несовпадение прямых и об ратных зависимостей различных
процессов).
где w 2π ,T – период колебания
T
ε ε 0 sin wt δ
Напряжение можно разложить на:
σ' σ 0 cosδ
σ" σ 0 sinδ
σ0
σ(t)
-σ0
ε0
δ
σ
0 cosδ E'
ε 0
σ" σ 0 sinδ E"
ε 0 ε 0
tgδ E" – тангенс угла механических
E'
потерь; δ представляет собой разность
фаз между напряжением и деформацией.
σ'
ε(t)
-ε0
π
2π
3π
σ σ 0 sin wt ,
wt
ε0
E’ – упругий динамический модуль; E” - модуль потерь; ’ – совпадает по
фазе с деформацией;
” – отличается на 900.
Если период действия силы сравним с релаксационным
периодом, то напряжение и деформация не будут совпадать по
фазе. В определенный период времени появляется
высокоэластическая деформация, причем ее величина не
соответствует значению напряжения, действующего в данный
момент времени.

11.

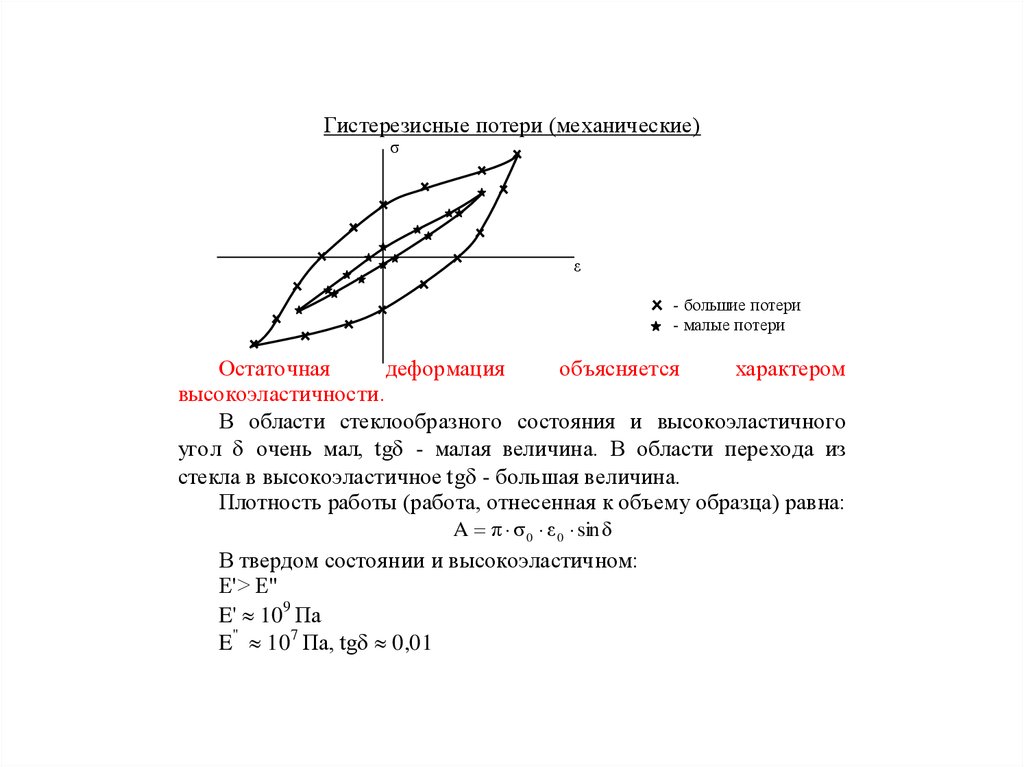
Гистерезисные потери (механические)
σ
ε
- большие потери
- малые потери
Остаточная
деформация
объясняется
характером
высокоэластичности.
В области стеклообразного состояния и высокоэластичного
угол очень мал, tg - малая величина. В области перехода из
стекла в высокоэластичное tg - большая величина.
Плотность работы (работа, отнесенная к объему образца) равна:
A π σ 0 ε 0 sinδ
В твердом состоянии и высокоэластичном:
Е'> E"
E' 109 Па
E" 107 Па, tg 0,01

12.

Угол сдвига фаз зависит от частоты и температуры. Изучая за висимость tg - T,
можно выявить области релаксационных переходов в полимере.
Е'
ω1 ω2 ω3
ω=const ,
ω 1 <ω 2 <ω 3
Увеличение
частоты
воздействия
приводит
к
повышению
температуры
размораживания молекулярной
подвижности.
tgδ
ω3
ω1
T
ω2
T
На рисунках приведена зависимость тангенса угла сдвига фаз от частоты
воздействия силы и температуры. Очевидно, что угол сдвига фаз отсутств ует при очень
малых и очень больши х значениях частоты и температуры : при малой частоте или
большей температуре потому, что релаксационные процессы успевают пройти полностью
за время действия силы, а при большей частоте или очень низкой температуре потому, что
релаксационные процессы не успевают пройти до конца и материал ведет себя как
упругое стеклообразное тело.
tgδ
Т2
Т1
Т1 >T2
w
δ – отсутств ует при очень малых и очень больших значениях w и T. При малой w и
большой T потому, что релаксационные процессы не успевают пройти полностью за
время действия силы, а при большой w и малой Т - из-за того, что релаксационные
процессы не успевают пройти до конца, и материал ведет себя как упругое стеклообразное
тело.

13.

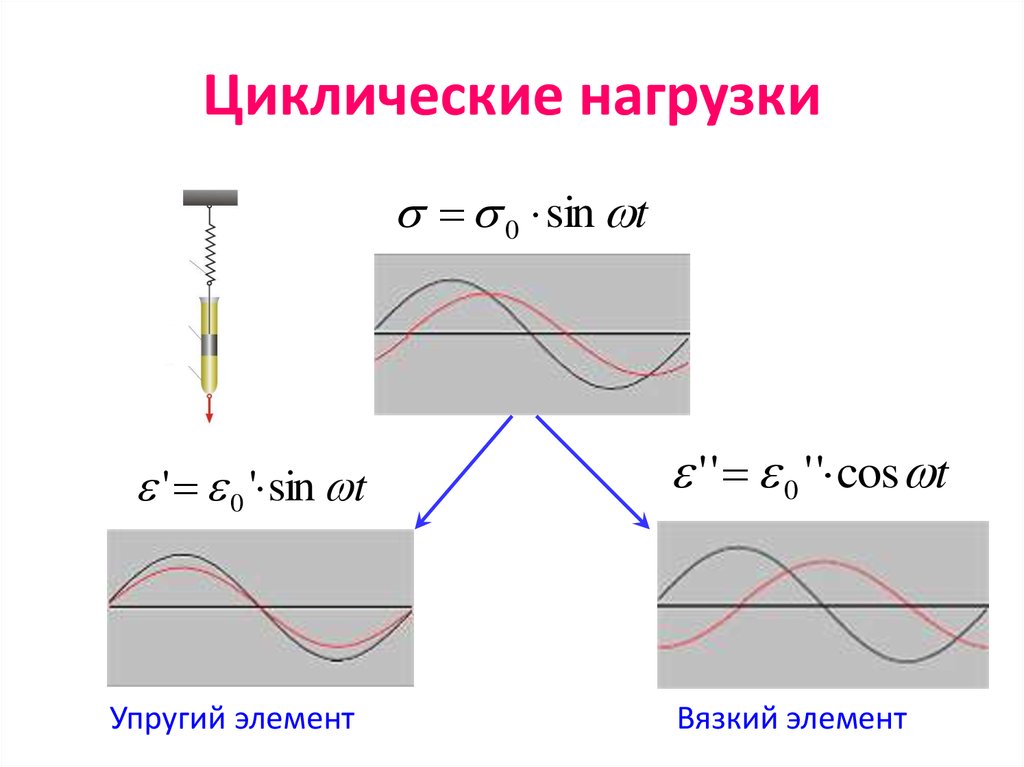
14. Циклические нагрузки

0 sin t
' 0 ' sin t
Упругий элемент
' ' 0 ' ' cos t
Вязкий элемент

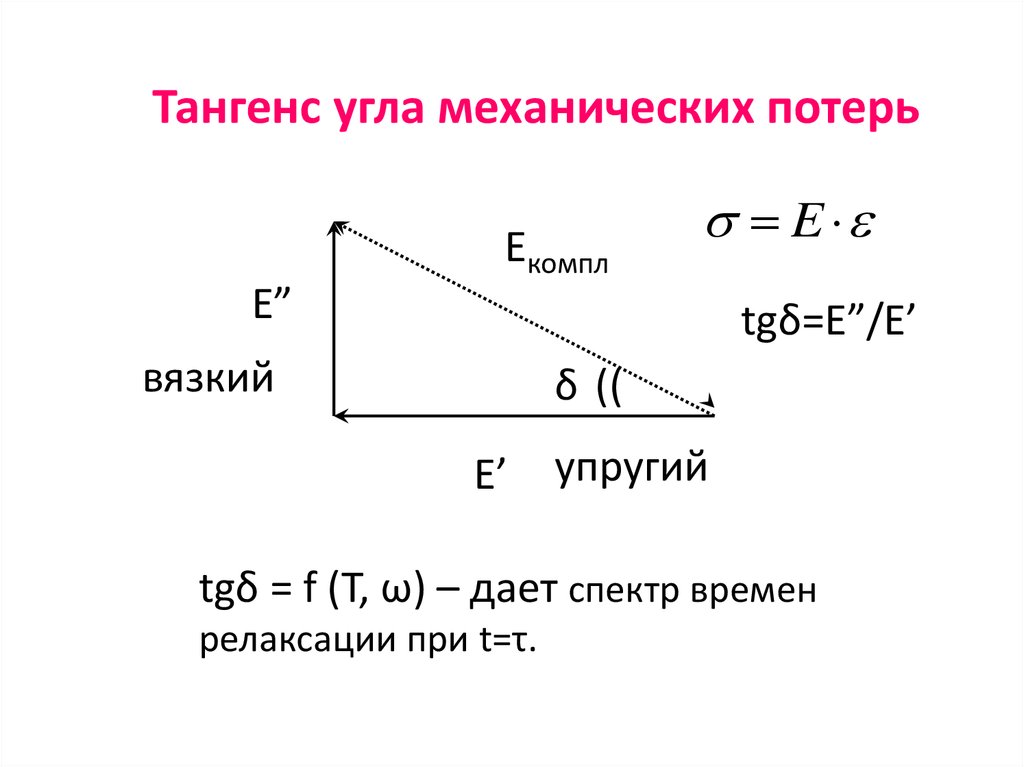
15. Тангенс угла механических потерь

Eкомпл
E
E”
tgδ=E”/E’
вязкий
δ ((
E’
упругий
tgδ = f (T, ω) – дает спектр времен
релаксации при t=τ.

16.

17.

Влияния температуры и времени воздействия на полимер тесно
взаимосвязаны и выражаются принципом температурно-временной
эквивалентности, или температурно-временной суперпозиции.
Этот принцип устанавливает эквивалентность влияния
температуры и продолжительности воздействия на релаксационные
свойства полимеров.
Уменьшение частоты (увеличение времени воздействия)
эквивалентно повышению температуры, и наоборот, повышение
температуры эквивалентно понижению частоты (увеличению
времени воздействия).
Зависимость модуля от времени воздействия представлена на
рисунке:
lgE(t), H/м2
9
8
Податливость в этом случае выглядит следущим образом:
lgD(t), м2 /Н
7
6
-4
5
-5
4
-6
-4
-2
0
2
4
6
8
lg t,мин
-7
-8
-9
lg t, ми
-4
-2
0
2
4
6
8

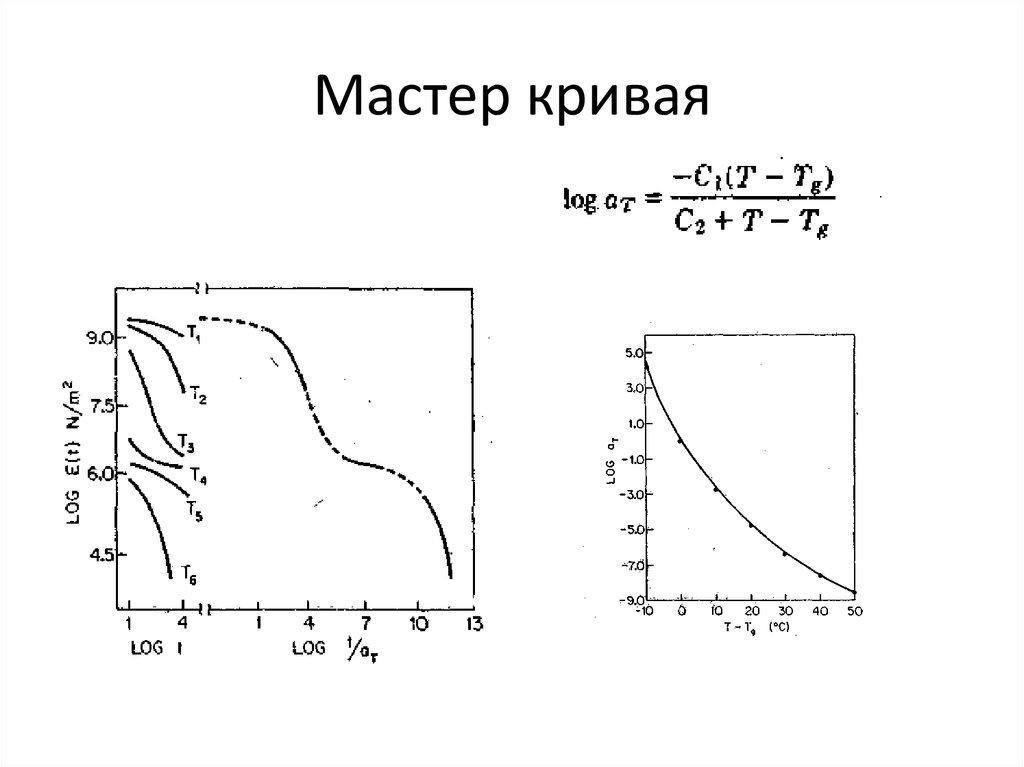
18. Мастер кривая

19.

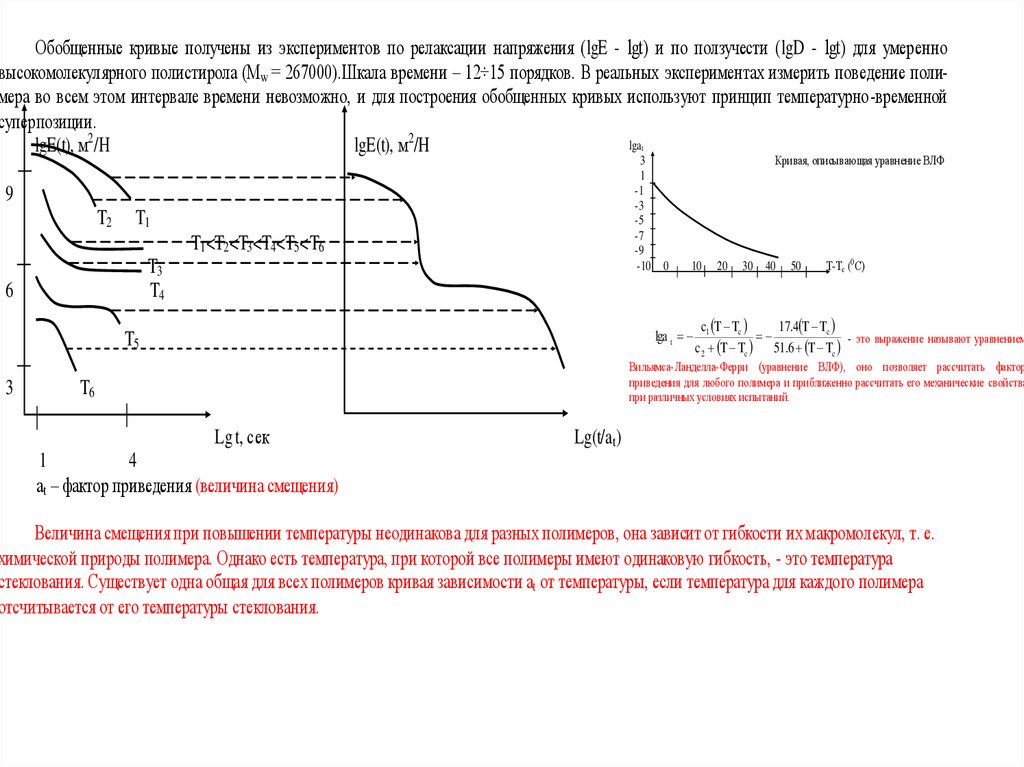
Обобщенные кривые получены из экспериментов по релаксации напряжения (lgE - lgt) и по ползучести (lgD - lgt) для умеренно
высокомолекулярного полистирола (Мw = 267000).Шкала времени – 12÷15 порядков. В реальных экспериментах измерить поведение полимера во всем этом интервале времени невозможно, и для построения обобщенных кривых используют принцип температурно-временной
суперпозиции.
lgat
lgE(t), м2/H
lgE(t), м2/H
3
1
-1
-3
-5
-7
-9
-10 0
9
T2
T1
T1<T2<T3<T4<T5<T6
T3
T4
6
10
lga t
T5
3
Кривая, описывающая уравнение ВЛФ
20
30 40
50
Т-Тс (0С)
c1 T Tc
17.4 T Tc
- это выражение называют уравнением
c 2 T Tc 51.6 T Tc
Вильямса-Ланделла-Ферри (уравнение ВЛФ), оно позволяет рассчитать фактор
приведения для любого полимера и приближенно рассчитать его механические свойства
при различных условиях испытаний.
T6
Lg t, сек
Lg(t/at )
1
4
аt – фактор приведения (величина смещения)
Величина смещения при повышении температуры неодинакова для разных полимеров, она зависит от гибкости их макромолекул, т. е.
химической природы полимера. Однако есть температура, при которой все полимеры имеют одинаковую гибкость, - это температура
стеклования. Существует одна общая для всех полимеров кривая зависимости аt от температуры, если температура для каждого полимера
отсчитывается от его температуры стеклования.

20.

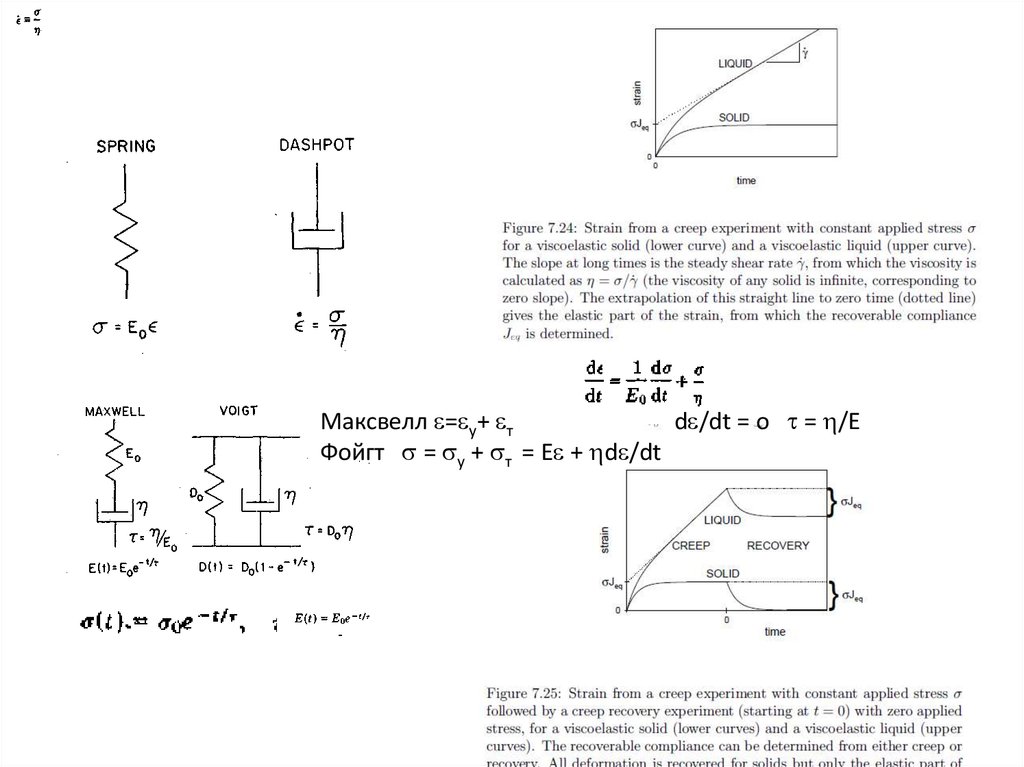
Механические модели для описания вязко-упругого поведения полимеров
Пружина моделирует "упругое поведение"; поршень в сосуде с вязкой жидкостью
моделирует "неупругое поведение". Из этих элемен тов собираются модели. Модель Кельвина – Фойгта
σ
Модель
Максвелла:
- пружина
E0
σ
- демпфер
η - вязкость
η
E0
σ
σ1
σ
ε ε упр ε тек ε упр σ/Е 0
dε упр/dt 1/E 0 d / dt
σ2
- пружина
σ σ1 σ 2 , - одинаково для всех элемент
σ E ε η dε , σ ε η dε
dt
E
E
dt
dy
σ ε y,
dε , y τ dy ,
E
dt
dt
dt
dt τ dy ,
y
dt dy
t
y
dε тек /dt σ/η - демпфер
dε
dt
1/E 0 dσ
dt
σ/η
(1)
Релаксация напряжения
0 при t=0, (t) – t
d /dt = 0, т.е. напряжение в конце концов упадет до 0
dσ E dt
σ
η
σ t σ 0 e t/τ
E t E 0 e t/τ
- время релаксации, = /E0
t = = 0 / , т.е. - время релаксации, за которое 0 уменьшится в раз.
1) при t >> / 0, что подтверждает опыт;
2) при t << t/ 0, 0. т.е. релаксация не успевает пройти, и начальное o сохраняется в течение
всего кратковременного опыта.
Модель Максвелла наглядна для релаксации напряжения.
Ползучесть
= const, d /dt = 0
Из (1) d /dt = / - одна из форм выражения закона Ньютона.
Под действием постоянного напряжения происходит вязкое течение во все время действия силы.
Et
t
ε σ 1 e η σ 1 e τ , после
E
E
снятия нагрузки
E ε η dε , dε dt , lnε t ,
dt
ε
τ
τ
ε ε0 e
t
τ

21.

Максвелл = у+ т
d /dt = o = /E
Фойгт = у + т = Е + d /dt

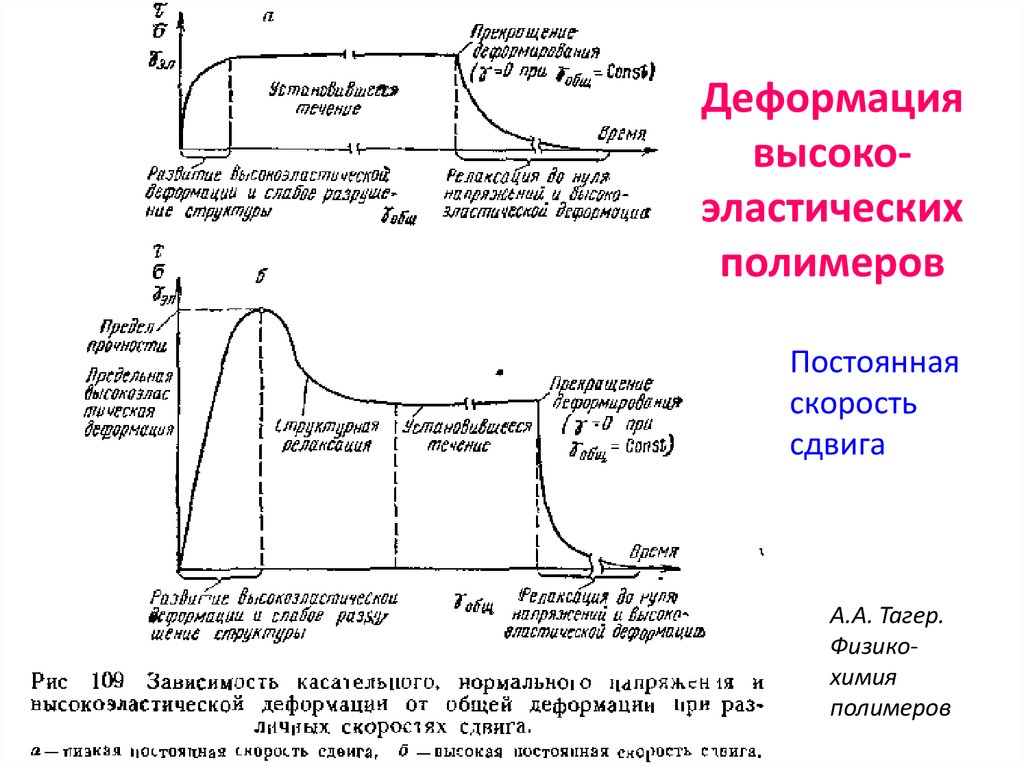
22. Деформация высоко-эластических полимеров

Деформация
высокоэластических
полимеров
Постоянная
скорость
сдвига
А.А. Тагер.
Физикохимия
полимеров

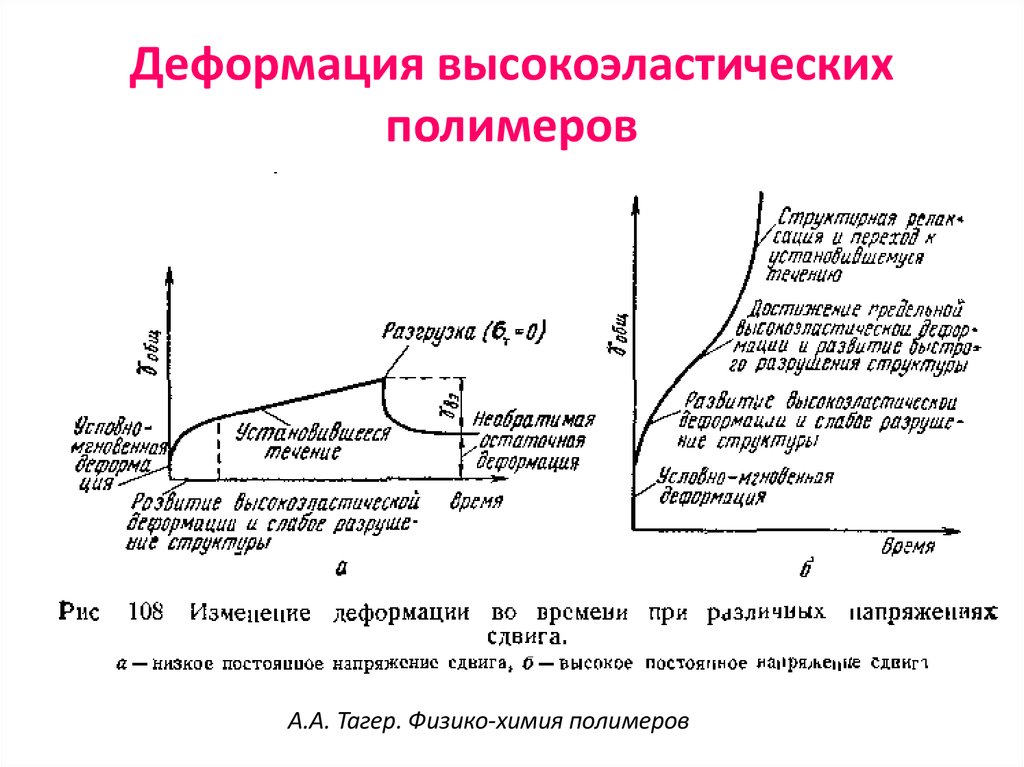
23. Деформация высокоэластических полимеров

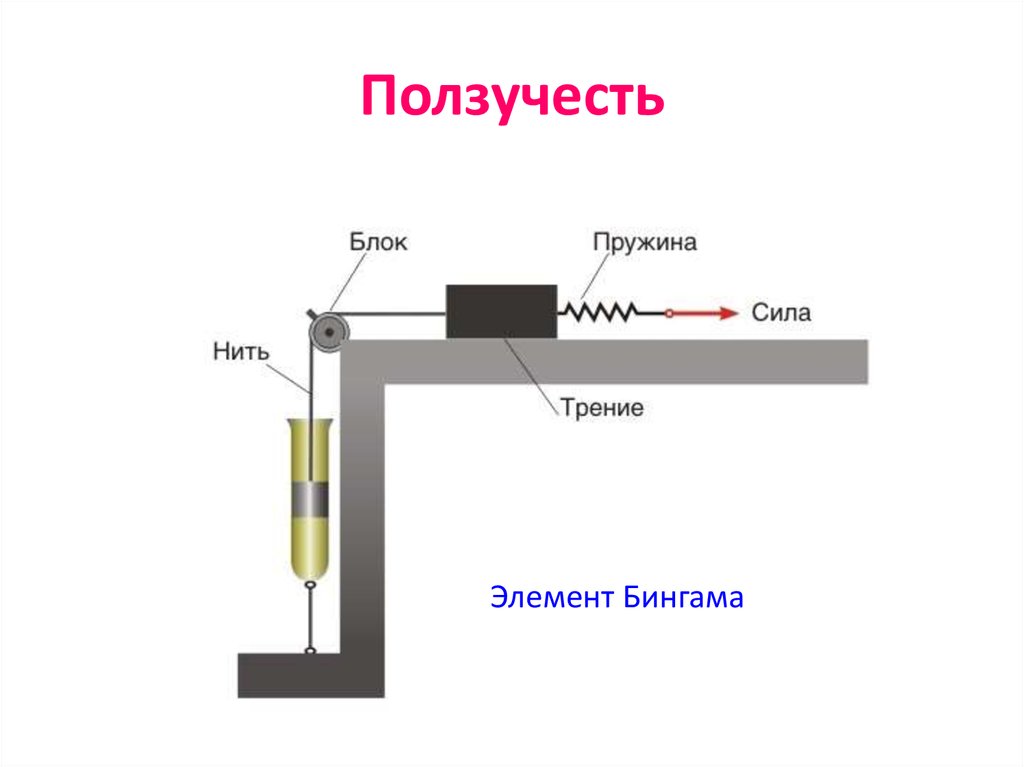
А.А. Тагер. Физико-химия полимеров

24. Ползучесть

Элемент Бингама

25. Высокоэластичность вязкотекучего состояния

При определенных значениях напряжения сдвига вязкая жидкость
проявляет высокоэластические свойства

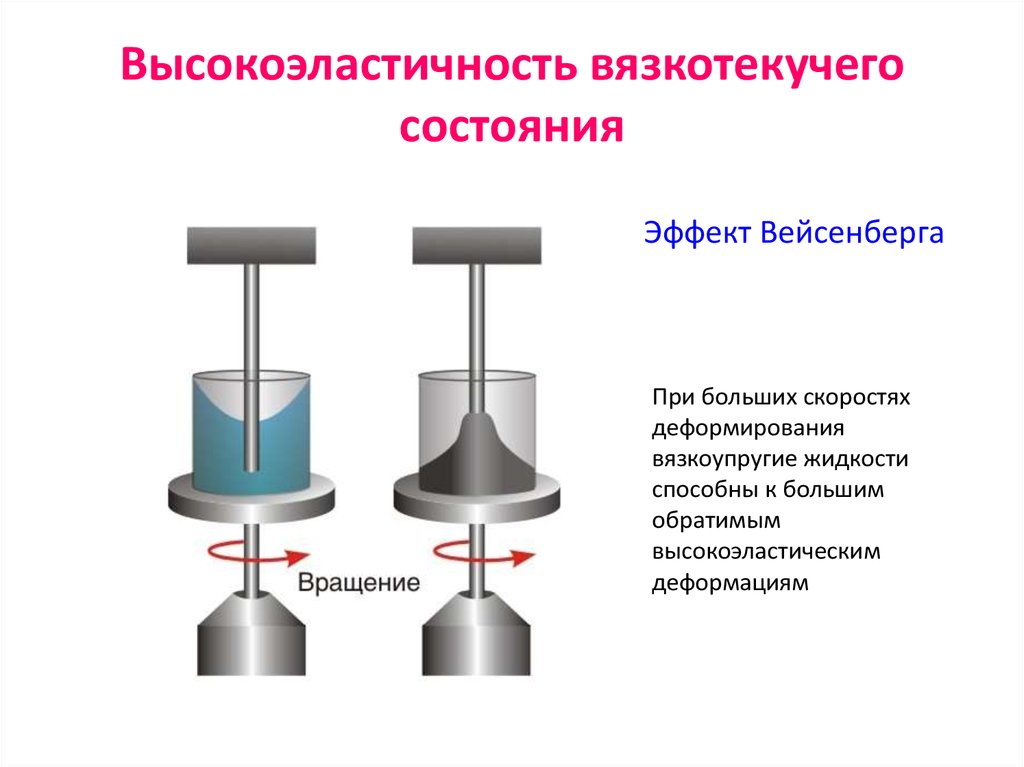
26. Высокоэластичность вязкотекучего состояния

Эффект Вейсенберга
При больших скоростях
деформирования
вязкоупругие жидкости
способны к большим
обратимым
высокоэластическим
деформациям

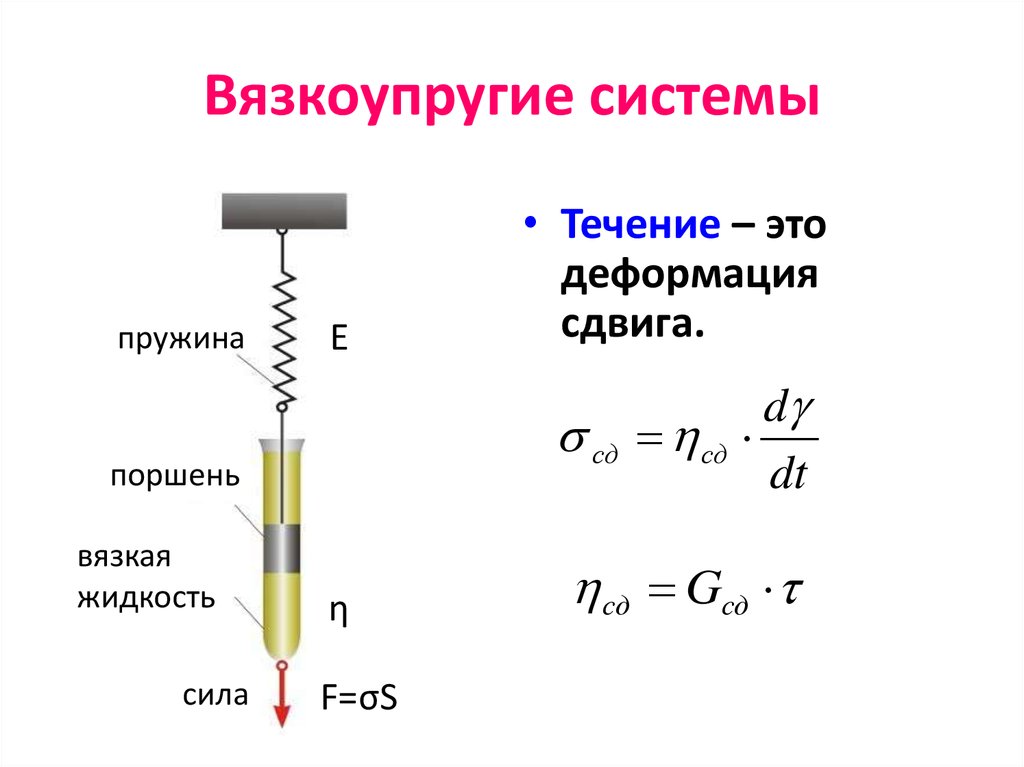
27. Вязкоупругие системы

пружина
E
сд
поршень
вязкая
жидкость
сила
• Течение – это
деформация
сдвига.
η
F=σS
d
сд
dt
сд Gсд

28. Связь вязкости и скорости сдвига

сд
const
d
f
dt
d
k
dt
d
сд
dt
Ньютоновская жидкость
Неньютоновская жидкость
1 d
k dt
1
1

29. Наибольшая ньютоновская вязкость

0
Вязкость, при которой жидкость ЕЩЕ ведет себя как
ньютоновская
vw
ln 0 a b Уравнение Дулитла
vf
vh Уравнение Коэна - Тарнбалла
ln 0 a
vf
NA
0
e
V
Gвязк
RT
NA
0
e
V
S вязк
R
e
H вязк
RT

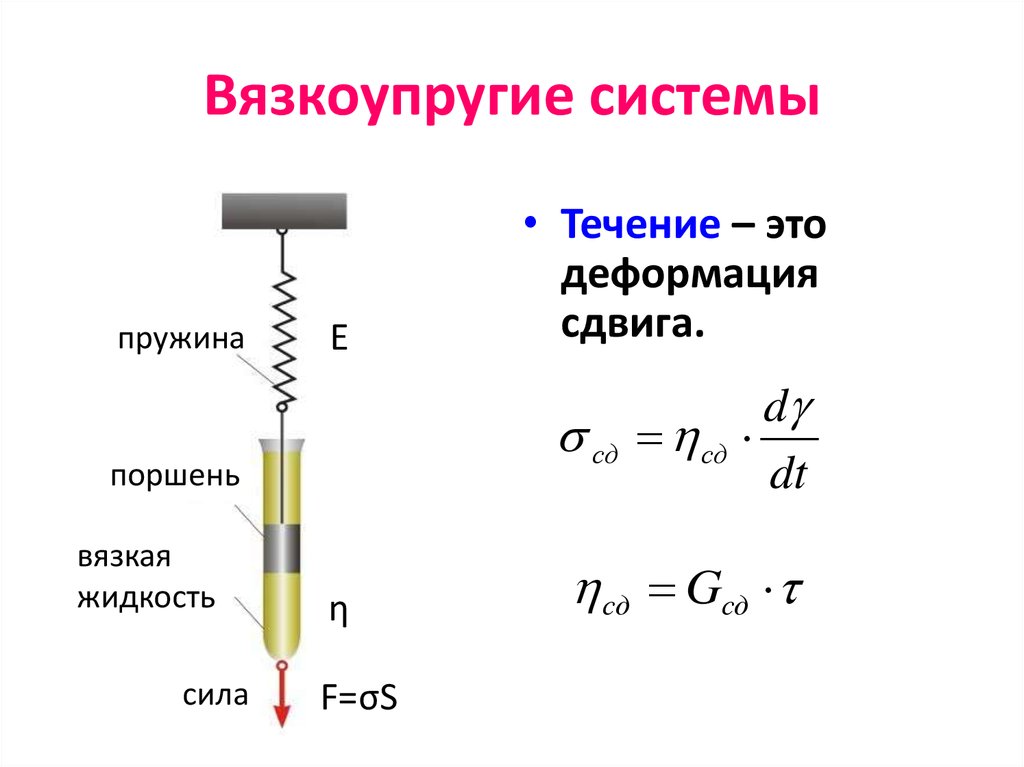
30. Вязкоупругие системы

пружина
E
сд
поршень
вязкая
жидкость
сила
• Течение – это
деформация
сдвига.
η
F=σS
d
сд
dt
сд Gсд

31. Связь вязкости и скорости сдвига

сд
const
d
f
dt
d
k
dt
d
сд
dt
Ньютоновская жидкость
Неньютоновская жидкость
1 d
k dt
1
1

32. Наибольшая ньютоновская вязкость

0
Вязкость, при которой жидкость ЕЩЕ ведет себя как
ньютоновская
vw
ln 0 a b Уравнение Дулитла
vf
vh Уравнение Коэна - Тарнбалла
ln 0 a
vf
NA
0
e
V
Gвязк
RT
NA
0
e
V
S вязк
R
e
H вязк
RT