Уравнение Г-Х-К для мембранного потенциала

1.

Уравнение Г-Х-К для мембранного потенциала
z 2 F 2 co ci exp( zF / RT )
Ij
Pj
RT
1 exp( zF / RT )
Отдельные виды ионов j:
Na+, K+, Cl–.
В стац. состоянии сумма всех токов равна нулю: INa + IK + ICl = 0.
Протекание тока означало бы перенос заряда и изменение φ (нестац. состояние).
Потенциал φ ≠ 0. Для суммы INa + IK вывод легче, чем с учетом ICl. Для ионов Cl:
ci
co
exp( F / RT ) ci co exp( F / RT )
1
1 exp( F / RT )
1
exp( F / RT )
Суммируем токи и приравниваем к 0
RT PK [ K o ] PNa [ Na o ] PCl [Cl i ]
m
ln
zF PK [ K i ] PNa [ Na i ] PCl [Cl o ]
В покое PK >> PNa, φm ~ φK; при возбуждении
PNa >> PK, φm ~ φNa.
1

2.

Токи в режиме короткого замыкания (фиксация напряжения) и
в разомкнутой цепи (физиол. состояние и измерения потенциала)
out
0
gNa
Сm
φNa
in
gK
φK
gleak
φleak
A
V
g Na
gK
m
K
Na
gi
gi
φ=0
В режиме фиксации напряжения трансмембр. ток выводится во внешнюю цепь,
эл. сопротивление к-рой (R амперметра) предельно мало (→0).
В физиол. условиях внешней цепи нет: цепь разомкнута. При внутриклет измерениях
потенциала φ цепь также разомкнута, т.к. R вольтметра очень велико (→∞).
В стац. режиме ток емкоcти равен нулю (dφ/dt=0) и сумма ионных токов равна 0.
При изменениях φ во время потенциала действия (при разомкнутой цепи)
сумма ионных токов равна емкостному току.
2

3.

Описание транспорта ионов на основе теории скоростей реакций
Критика электродиффузионной теории
• Мембрана неоднородна (каналы, липидная часть)
• Каналы – узкие; ионы движутся однорядно:
взаимодействия неизбежны
• Коэф-ты распределения на разных сторонах м-ны
могут отличаться из-за различий поверхн. заряда.
• Линейность профиля φ в мембране допускают
с оговорками.
Трехбарьерная модель
1.
2.
3.
Ea
kT
j ~
exp
h
kT
Константа преодоления энерг. барьера
4.
Потеря гидратной оболочки компенсируется
связями с полярными группами канала.
Свойства канала определяются профилем
энергии иона. Одна «яма» вмещает один ион.
Ион долго сидит в потенциальной яме и
совершает мгновенный перескок в свободную яму
за счет тепловых флуктуаций.
Эл поле служит не только движущей силой, но
может влиять на высоту активационного барьера.
3

4.

Описание ионных потоков на основе теории скоростей реакций
cm c
Конц-ия иона в участке связывания (при низких конц-иях в р-ре с)
Константа скорости р-ций включает потенциалозависимую и независимую части
Ea
E
zF
zF
A exp
A exp
exp
exp
RT
RT
2 RT
2 RT
ν – константа преодоления центр. барьера при φ=0; конц-ия в м-не γ∙с (заполнение)
J= (ci-co)
zψ
zψ
Пот-л Нернста
2
2
J = γν ci e
co e
;
При
сi = co = c и 0
J = γν
z F
c;
RT
J
ВАХ
Pi = γν
4

5.

Односторонние потоки
Соотношение Уссинга соблюдается
(вывод из ф-лы для общего потока ионов)
Профиль энергии Na+ в канале:
уровни энергии выражены в ед. RT
(по Хилле 2001)
Интерпретация профиля энергии:
Взаимодействие с СОО- создает “яму”
основной пик – сужение канала.
5

6.

Взаимодействия ионов в каналах: насыщение и блокировка
с
k1
1-θ
k2
Концентр. насыщение: такого эффекта нет в эл.-диф. теории
θ – заполненные участки
1-θ – свободные
6
участки
θ

7.

Функции состояния «двухместного» канала
Оба участка заполнены
пустой
Состояния канала F( 1,1); F(0,0), F(1,0); F(0,1) описывают системой диф ур-ний
с учетом зависимости констант k и ν от мембр. потенциала φ. Сдвиг φ (ψ)
нарушает (в разной мере) константы переходов и состояние канала.
3
1
dF (1,1)
F (1, 0) k2 c exp F (0,1) k1c exp
dt
2
2
3
F (1,1) k 1 exp
F (1,1) k 2 exp 1
7
2
2

8.

Влияние эл. полей на клеточные и липидные мембраны
1. Движения
электрофорез
диэлектрофорез
электровращение
2. Деформации и образование
клеточных цепочек
Эритроциты в эл. поле
3. Электропорация и эл. пробой мембран
4. Слияние мембран (получение гигантских липосом, клеточные гибриды)
5. Влияние эл поля на фотосинтетические мембраны
8

9.

Силы, действующие на клетки в эл. поле: Максвеллово напряжение
T – сила (tension), действующая на частицы и клет мембраны:
T = εεo [E (E∙n)
(E∙n) – (E2/2)∙n]
А
E – напряженность поля (вектор),
n – вектор нормали к поверхности
εεo – абсолютная диэлектрическая
проницаемость
En En cos
E
n
Б
B
Эритроциты в эл. поле:
E1 – 250 В/см (А) , Е2 – 5500 В/см (Б)
На низких частотах ω
поле – тангенциально.
cosφ = 0. Сила направлена
внутрь – сжимает клетку
T
T
o 2→
E n
2
Б
n
E
На высоких частотах ω: cos φ = 1.
Поле – по нормали к поверхности.
Сила направлена по полю,
тащит мембрану, вытягивает клетку
T
o 2→
E n
2
9

10.

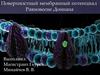
Влияние эл полей на мембраны: деформации и слияние
Две близко лежащие клетки с дефектами
типа сквозной поры
Здесь поле - тангенциально
Края бислоев сливаются. Теперь поле
направлено тангенциально и расширяет пору
Здесь поля нет
Мембраны сближаются
1 V, 1 MHz
Электропорация
100 μm
Поле расширяет пору в бислое
Локальные деформации клетки: Образование
клеточных отростков в эритроцитах.
Макс. напряженность поля вблизи краев электродов.
Поле направлено параллельно вектору нормали к
поверхности; оно вытягивает отростки (псевдоподии)
(без контакта с электродами).
10

11.

Электрофорез
Клетки или частицы, несущие поверхностный заряд, движутся в постоянном однородном эл поле
Сила, действующая на поверхностный заряд σ при напряженности поля E равна E·σ
Сила вязкого трения действует на клетки, движущиеся в жидкой среде; она пропорциональна
η и градиенту скорости движения v/δ,
v скорость движения частицы, а δ – расстояние от поверхности клетки до неподвижного
вязкости жидкости
где
слоя воды.
Эти силы уравновешены:
v
E
Одно из предсказаний состоит в том, что электрофоретическая подвижность возрастает с
увеличением толщины δ.
Это означает, что длинные нитевидные цепочки гликокаликса, прикрепленные к мембране
и несущие остатки органич к-т должны повышать электрофоретическю подвижность:
E
v
-
δ
v
E
Скорость
v
x
δ
Гликокаликс − глоикопротеин-полисахаридный покров животных клеток
11
Расстояние до
поверхности клетки