Similar presentations:
Расчёт неизотермического течения вязкоупругой полимерной жидкости между двумя соосными цилиндрами с контролем погрешности
1. Расчёт неизотермического течения вязкоупругой полимерной жидкости между двумя соосными цилиндрами с контролем погрешности
Докладчик: Круглова Е.А, 4й курс ММФ НГУНаучный руководитель: к.ф. – м.н. с.н.с ИВТ СО РАН Семисалов Б.В
2.
По оценкамWohlers Report 2015
к 2020 г. международный
рынок аддитивных
технологий достигнет
21,2 млрд долларов США.
2/21
3.
Наиболее востребованные направленияприменения аддитивных технологий
▪ автомобилестроение
▪ авиастроение
▪ военная и космическая отрасли
▪ медицина
▪ производство потребительских товаров и
электроники
▪ производство средств производства
3/21
4. Модели течения растворов и расплавов полимеров
1) Феноменологические моделиучитывают свойства течений жидкости, наблюдаемые в эксперименте на
макроуровне
2) Микроструктурные модели
учитывают свойства макромолекул и их взаимодействие в полимере
3) Мезоскопические модели
задают динамику макромолекул с параметрами, определяемыми в
эксперименте на макроуровне
Pokrovskii V. N. The Mesoscopic Theory of Polymer Dynamics. 2nd ed. Berlin: Springer, 2010.
4/21
5.
Постановка задачи{(y, z) | r y z 1}
2
0
2
2
1) Алтухов Ю. А., Гусев А. С., Пышнограй Г. В. Введение в
мезоскопическую теорию текучести полимерных систем.
Барнаул: изд-во АлтГПА, 2012.
2) Блохин А. М., Семисалов Б. В. Стационарное
течение несжимаемой вязкоупругой полимерной
жидкости в канале с эллиптическим сечением //
Сибирский журнал индустриальной
математики. 2014. Т. XVII. №4 (60). С. 38–47.
5/21
6.
Уравнение моделиβ – феноменологический
параметр реологической
модели, учитывающий
ориентацию
макромолекулярного клубка
Re – число Рейнольдса
W – число Вейсенберга
Ra – число Релея
Pr – число Прандтля
Ậ - перепад давления вдоль
Ох
ЕА – энергия активации
θ – относительная разность
температур между
цилиндрами
Ф - температурный фактор
Ga – число Грасгофа
6/21
(1)
y r cos z r sin
Блохин А. М., Круглова Е. А., Семисалов Б. В. Стационарные неизотермические течения несжимаемой вязкоупругой полимерной
жидкости между двумя соосными цилиндрами // /Журн. выч. мат. и мат. физ. 2017. Т. 57. № 7, C. 99-112
7. Численное решение
Используем итерационный метод установления.Временную переменную t для итерации
Вводим
Регуляризующий
операторB(регуляризацию)
)
Оператор
Соболева
t u ( k1 k 2
2
r t
Bt u urr f (r, u)
7/21
2
t
8. Численное решение
Введём сетку по временной переменной t с шагом и узлами tn = n , n NПриблизим
ut
конечной разностью
(u
[n]
u
Bt u urr f (r, u)
[ n 1]
) /
=
[ n 1]
[ n 1]
[ n 1]
k1u (k2 )urr = (k1 k2 2 )u
f (r , ur ) = f (r , u ).
r
Критерий остановки: Bt /u S , S - невязка установления
2
[n]
8/21
[n]
(2)
9. Алгоритм численного решения
1 ri 2pN (r , u )
2
|r r
( ( 1)i j
i
r
1 r0 j 1, j i
(ri rj ) 1 rj2
N
3 ri
uj
ui )
2
2 1 ri
Для приближения решения
vj
aij , i j используем
интерполяционный полином в форме Лагранжа с
2
N
2(1
r
многочленов
4узлами в нулях
1 2
i ) 3ri ( ri rj )Чебышёва
i j
2 pN (r , u )
|x x
( ( 1)
2
2
j
r
(1 r0 ) j 1, i j
(ri rj ) 2 1 rj2
3ri 2
u
( N 5)
u
)
j
2
2
i
1 ri
1 ri
1 ri 2
b ij , i j
( 2 j 1)
pN ( r , u)
u( rj ), rj cos
'
2N
j 1 ( r r j )Tn ( r j )
N
9/21
w ( r , rj )TN ( r )
(4)
i
1 r2
w(r , rj )
1 rj2
(3)
10. Сведение к задаче линейной алгебры
1a21
С=
aN 1
a12
2
aN 2
1 b12
... a1N
Спектральное
разложение
... a2 N
b21 2
,
A=
1
...
A = RA DA RA .
... N
bN 1 bN 2
... b1N
... b2 N
...
... N
Для аппроксимации первой и второй производной получаем
Ux = С U
10/21
Uxx = AU.
11. Численные результаты
urr f ( r , ur )Конечно-разностными методами решения найдены для r0 не меньше 0.15!
А.М Блохин, Р.Е Семенко. Течение несжимаемой полимерной жидкости между двумя соосными
цилиндрами
11/21
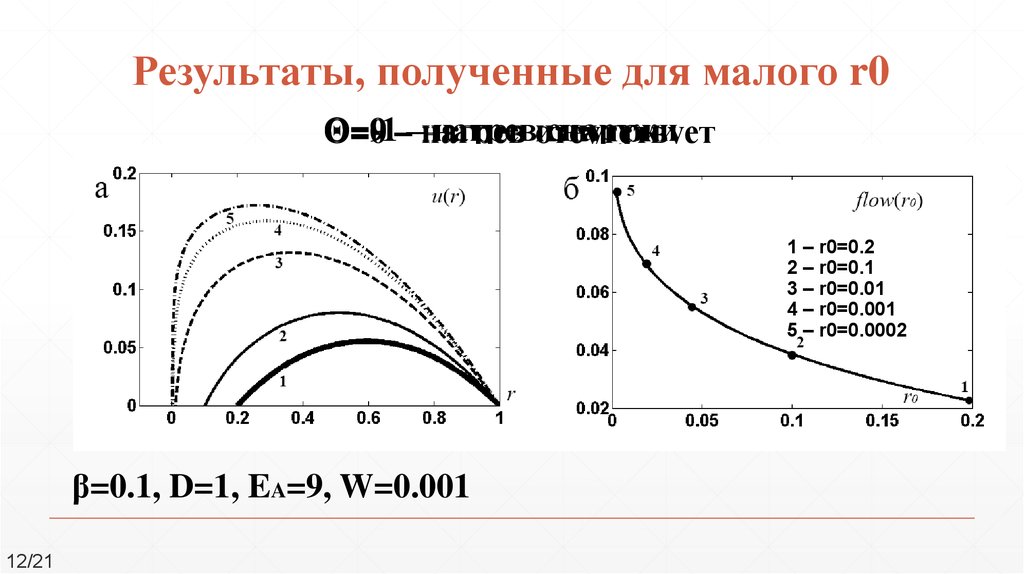
12. Результаты, полученные для малого r0
Θ=-1нагревизнутри
снаружи
Θ=9
Θ=0 ––нагрев
отсутствует
1 – r0=0.2
2 – r0=0.1
3 – r0=0.01
4 – r0=0.001
5 – r0=0.0002
β=0.1, D=1, EA=9, W=0.001
12/21
13. Контроль погрешности
Погрешность численного решения:R
M
- Вычислительная погрешность, связанная с округлением
действительных чисел в памяти ЭВМ
- Погрешность использования метода приближения
Число
a
записывается в память ЭВМ так:
10
13/21
R M
l 1
a a a
Для типа double l = 16
, где
a a
14. Верхняя оценка
R[ n 1]
u
[ k 1]
R
u
( I A) F ( u ) u
1
[n]
[ n 1]
S (u )
[ n]
u
1 q
[k ]
(5)
//А.М. Мацокин, С.Б.Сорокин «Численные методы» гл.4, пар.3, стр.78
14/21
15. Погрешность метода
M(6)
,
,
Пусть
N
(7)
– нечетное количество узлов. Тогда 0 – узел интерполяции
PN
, (8)
Наблюдая за поведением величины N можем сделать вывод о характере
сходимости метода
15/21
(9)
16. Погрешность метода
1) Bernstein S.N. "On the Best Approximation of Continuous Functions by Polynomials of a Given Degree",Soobshch. Khar'kov Mat.Obshch 13, 49--144 (1912)
2) Jackson D.} On Approximation by Trigonometric Sums and Polynomials
// Trans. Amer. Math. Soc. 1912. Vol. 13. 491 -- 515
16/21
17. Определение величины
r0 0.1qˆ
r0 0.0002
,
(6)
(8)
17/21
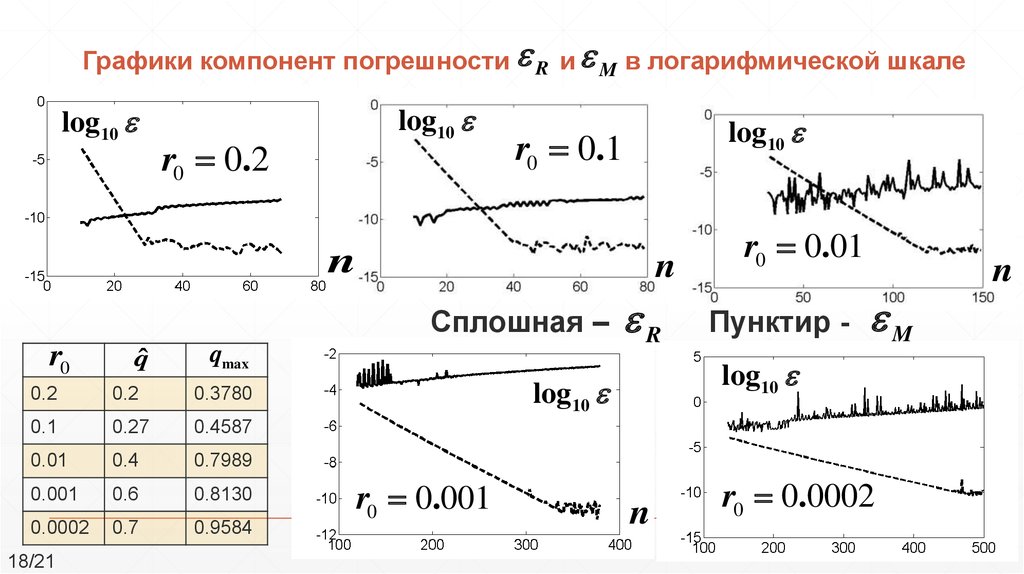
18. Графики компонент погрешности и в логарифмической шкале
Графики компонент погрешности R и M в логарифмической шкалеlog10
log10
r0 0.2
log10
r0 0.1
n
n
Сплошная –
r0
qˆ
qmax
0.2
0.2
0.3780
0.1
0.27
0.4587
0.01
0.4
0.7989
0.001
0.6
0.8130
0.0002
0.7
0.9584
18/21
R
Пунктир -
M
log10
log10
r0 0.001
r0 0.01
n
r0 0.0002
n
19. Основные результаты
1. Для мезоскопической модели Покровского-Виноградова дана постановказадачи о стационарном неизотермическом течении вязкоупругой
полимерной жидкости между двумя соосными цилиндрами
2. Разработан вариант численного алгоритма без насыщения, позволяющий
решать задачу с малым параметром
3. Проведён анализ зависимости численных решений от параметров задачи.
4. Получены решения для предельно малого радиуса сечения нагревательного
элемента (r0=0.0001)
5. Получена оценка вычислительной погрешности и погрешности метода
19/21
20. Список публикаций
20/21Блохин А.М., Круглова Е.А., Семисалов Б.В. Стационарные неизотермические течения несжимаемой
вязкоупругой полимерной жидкости между двумя соосными цилиндрами // Журн. выч. мат. и мат. физ.
2017. Т. 57. № 7, C. 99-112
Блохин А.М., Круглова Е.А., Семисалов Б.В. Численное моделирование неизотермического течения
полимерной жидкости между двумя соосными цилиндрами с контролем погрешности // Тез. док. XVII
Всерос. конф. мол. учёных по мат. мод. и информац. тех. Новосибирск, 30 октября–3 ноября 2016 г. С. 46.
Блохин А.М., Круглова Е.А., Семисалов Б.В. Расчёт неизотермического течения полимерной жидкости
между двумя соосными цилиндрами // Тез. док. VIII Всероссийской конф. «Актуальные проблемы
прикладной математики и механики», посвящ. памяти акад. А.Ф. Сидорова, и Всероссийской молодёжной
школы-конференции. Абрау-Дюрсо, 5–10 сентября 2016 г. С. 16–17.
Круглова Е.А. Численный анализ свойств неизотермического течения полимерной жидкости в
цилиндрическом канале с тонким нагревательным элементом // Материалы 54-й Международной научной
студенческой конференций (ISSC). Россия. Новосибирск, 16.04 – 20.04.2016. С. 50.
Круглова Е.А. Численное моделирование неизотермического течения полимерной жидкости между двумя
соосными цилиндрами с контролем погрешности // Материалы 55-й Международной научной
студенческой конференций (ISSC). Россия. Новосибирск, 16.04 – 20.04.2017. С. 153.
21.
Спасибо за внимание!Круглова Е.А гр. 13111
Научный руководитель: Семисалов Б.В
22.
Выступления наспецсеминарах:
1) «Проекционные методы
решения PDE»
(руководитель: Шапеев В.П)
2) «Вычислительная
топология»
(руководитель: Базайкин Я.В)
23. Модель Покровского - Виноградова
divu = 0,1
Ra 1 0
ut P =
div ( )
0 ,
Re
Pr 1
(a11 )t 2 A1u x 2a12u y 2a13u z L11 = 0,
(a22 )t 2a12vx 2 A2v y 2a23vz L22 = 0,
(a33 )t 2a13 wx 2a23 wy 2 A3 wz L33 = 0,
(a12 )t wz a12 A1vx A2u y vz a13 u z a23 L12 = 0,
(a13 )t wy a12 A1wx A3u z v y a13 u y a23 L13 = 0,
(a23 )t u x a23 A2 wy A3vz wx a12 vx a13 L23 = 0,
t = x , y , z / Pr.
Здесь t – время; u,v,w – компоненты вектора скорости в декартовой с.к. x,y,z;
P – давление; aij , i, j = 1, 2,3 – компоненты тензора анизотропии = (aij ) = (a1 , a2 , a3 ) ранга 2
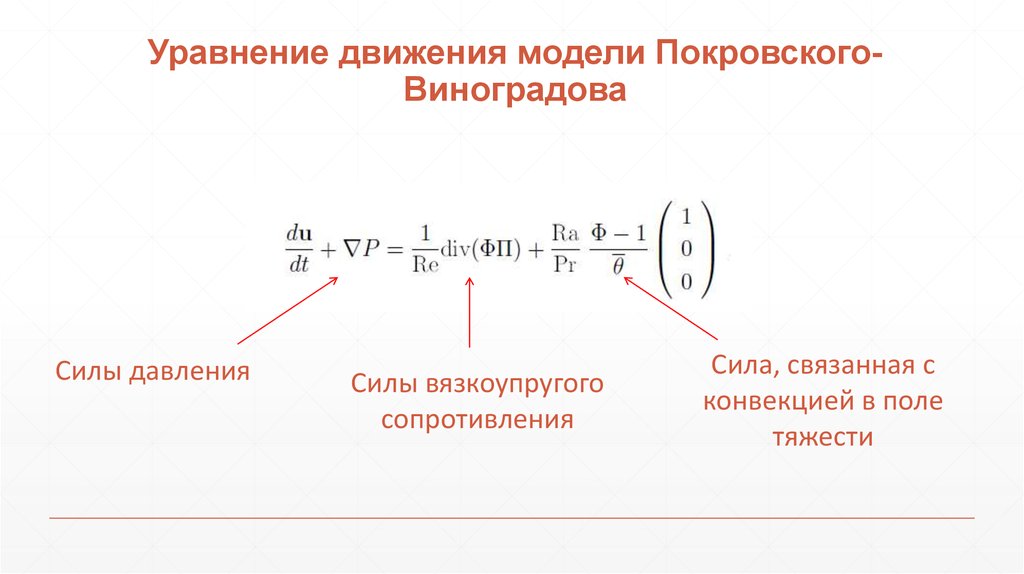
24. Уравнение движения модели Покровского-Виноградова
Уравнение движения модели ПокровскогоВиноградоваСилы давления
Силы вязкоупругого
сопротивления
Сила, связанная с
конвекцией в поле
тяжести
25.
Пример устанавливающегося течения дляуравнений Навье-Стокса
y
-1
g
1
x
v v ( u, v )
v
1
(v )v v p g ,
t
( v ) 0. - уравнение неразрывности
(1)
В координатном виде.
u
u
u
2 u 2 u 1 p
( u v ) ( 2 2 )
,
t
x
y
x
y
x
v
v
v
2v 2v
1 p
( u v ) ( 2 2 )
g,
t
x
y
x
y
y
u v
0.
x y
(2)
26.
Пример устанавливающегося течения дляуравнений Навье-Стокса
Ищем стационарное решение Пуазейля
p
0,
x
v
2v 2v
1 p
v ( 2 2 )
g 0,
y
x
y
y
p p( y ),
v
g , const
2
x
1 p
.
y
v 1 p
2
g 0,
x
y
2
(3)
v
0.
y
u
v
( 0, 0)
t
t
(4)
v v ( x ).
g 2
v( x )
x C1 x C 2
2
2
(5)
Добавим условия прилипания
v ( 1) v (1) 0
g 2
v( x )
( x 1)
2
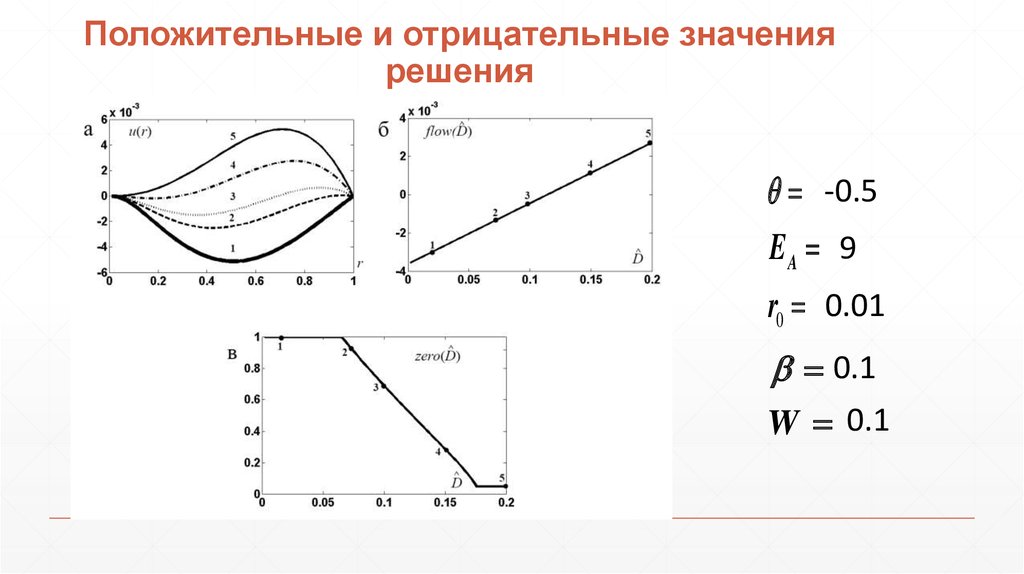
27. Положительные и отрицательные значения решения
-0.5EA 9
r0 0.01
0.1
W 0.1
28.
Методы без насыщенияК. И. Бабенко Основы
численного анализа, 2002
Метод, обладающий асимптотикой погрешности наилучшего
приближения для любой степени гладкости решений
Основная идея – использовать информацию о гладкости
решения
Обоснование содержится в работах по теории приближений
Фурье, Чебышёва, Лебега, Джексона, Бернштейна, Бабенко
29.
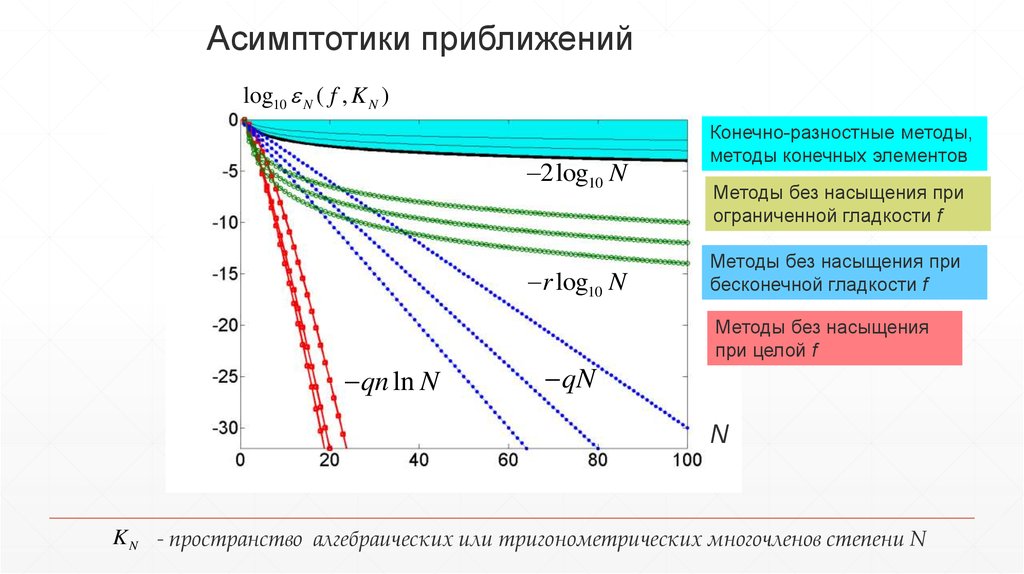
Асимптотики приближенийlog10 N ( f , K N )
2log10 N
r log10 N
qn ln N
qN
Конечно-разностные методы,
методы конечных элементов
Методы без насыщения при
ограниченной гладкости f
Методы без насыщения при
бесконечной гладкости f
Методы без насыщения
при целой f
N
K N - пространство алгебраических или тригонометрических многочленов степени N
30.
Уравнение моделиβ – феноменологический
параметр реологической
модели, учитывающий
ориентацию
макромолекулярного клубка
Re – число Рейнольдса
W – число Вейсенберга
Ra – число Релея
Pr – число Прандтля
Ậ - перепад давления вдоль
Ох
ЕА – энергия активации
θ – относительная разность
температур между
цилиндрами
Ф - температурный фактор
Ga – число Грасгофа
А. М. Блохин, Б. В. Семисалов, А. С. Шевченко Стационарные решения уравнений, описывающих неизотермические течения
несжимаемой вязкоупругой полимерной жидкости// Матем. моделирование, 28:10 (2016), 3–22
31. Сведение к задаче линейной алгебры
Домножим на1
A
R * | k1 U
Обозначим
Тогда
[ n]
V
( k2 ) AU
n
k1V
U
n
= F( U
n
1
A
[ n 1]
R U , G R F (U
n
vj
Ответ получим из
1
A
[ n]
( k2 ) DAV
gj
k1 ( k2 )d
RAV
n
j
A
n
.
G,
n 1
),
),
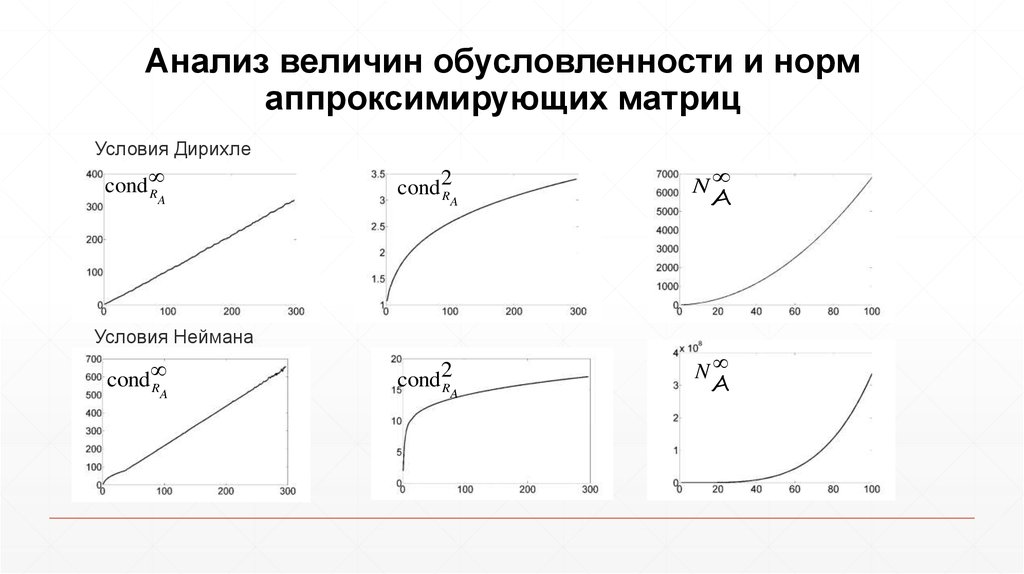
32. Анализ величин обусловленности и норм аппроксимирующих матриц
Условия Дирихлеcond
R
A
cond 2R
N
A
cond2
N
A
A
Условия Неймана
cond
RA
RA
33. Основные оценки
1) Элементы массива решения U имеют погрешности U U U , U UU - массив, элементы которого суть возмущения элементов;
U - максимальное из этих возмущений
2) При поиске значений производных
U погрешность возрастает:
AU ( A A )( U U ) AU AU , AU A U A U A U ,
N
N
A U max | ( A )ij u j | max | a ij | max | u j | N A U , N A A
i 1,..., N
i 1,..., N
j 1,..., N
j 1
N
j 1
N
A U max | aij ( U ) j | max | a ij | max | ( U ) j | N A U .
i 1,..., N
j 1
i 1,..., N
j 1
j 1,..., N
AU N A ( U U )
,
34. Основные оценки
k1 U[n]
( k2 ) AU
n
[n]
= F( U
n
k1V k ( k2 ) DAV
V
1
A
) | *R слева
= Gk
G k1 U k1 U
N 1 G
RA
min ( k1 ( k2 )d )
j 1,..., N
[ n 1]
j
A
( k2 )( AU AU ) [ S (N A , , U )]
k1 U k1 U ( k2 )( AU AU ) [ S (N , , U )]
R U N R V +cond R
j
A
A
min (k1 ( k2 )d A )
A
j 1,..., N




























 mathematics
mathematics








