Similar presentations:
Небесная механика. Лекции 3 - 4
1.
3-4 лекция2.
басы белгіленеді.Жазықтықта m нүктесі қозғалады, бірақ X ,Y , Z координат жүйесінде
2.1.3
Екі
дене орбиты
есебіндегі
және қозғалыс
жазықтық
қозғалыссыз
болады.
Уравнение
иорбита
законтеңдеуі
движения
в задачезаңы
двух тел
Жазықтықтың теңдеулерін векторлық және координаттық түрінде жазуға
m, М – екі материалдық нүкте.
болады:
, - c тікбұрышты
Сонда қозғалыс
жазықтығына
r , - полярлы
m нүктенің
жылдамдығы
c - момент
r - радиус-векторы
rжәне
0 , r - оныңжәне
векторына
перпендикуляр
болғандықтан, кеңістікте осы векторларымен
рдинат
жүйелерін
енгізуге болады.
анықталған жазықтықтың бағыттауы
тұрақты
c1 x c2 yбағытталған,
c3 z 0болады.
,
векторының бойымен
- осі -Лаплас
- полярлы бұрыш
r векторы
жазықтықта болғандықтан, осы жазықтықта M 0 - координат
Сонда
ын аномалиясы)
векторының
бағытынан
есептеледі.
қозғалыс
жазықтығына
Прямоугольная
система
координат
– , - тікбұрышты және r , - поляр
cбасы
, c2 , белгіленеді.
c3 - c
вектордың
компоненттері.
1
- осьті енгізген
c момент
,система
векторының
сЕгер
жазықтығына
- тікбұрышты
және
- полярлы
rбірақ
,
бойымен
Полярная
координат
– бағытталған
Жазықтықта
m жүйелерін
нүктесі
қозғалады,
жүйесінде
X ,Y , Z координат
енгізуге
болады.
-координат
Лаплас векторы
қозғалыс
жазықтықтың
нормаль векторына
c
әне енгізуге
полярлы
r ,жазықтық
-- истинная
нде,
орбиталдық
координат
жүйесі
пайда болады.
аномалия
ерін
болады.
қозғалыссыз
болады.
-Лаплас
осі
векторының
бойымен
бағытталған, - полярлы бұры
-болғандықтан,
перпендикуляр
осы
жазықтықта
орналасады.
система
, ,Жазықтықтың
-- орбитальная
координат
жүйесі
қозғалыс
жызықтығымен
байланыста
теңдеулерін
векторлық
және координаттық
түрінде жазуға
асОсы
векторының
бойымен
бағытталған,
- полярлы
бұрыш есептеледі.
координат
(шын
аномалиясы)
векторының
бағытынан
болады:бұрыш
есептеледі.
ады.
- полярлы
векторының
бағытынан
Егер c момент
векторының
бойымен бағытталған - осьті енгіз
r 0,
Көбінесе бастапқы координат cжүйесі
ретінде гелиоцентрлік
нт векторының
бойымен
бағытталған
енгізген
- осьті
кезінде,
орбиталдық
координат
жүйесі
пайда
болады.
иптикалық
немесе
геоцентрлік
экваториалды
жүйелер
қарастырылады.
- осьті енгізген
ық координат
жүйесі пайда
c1 x c2 y cжүйесі
z 0 , қозғалыс жызықтығымен байланы
, , болады.
- координат
жетті жағдайлардаОсы
селеноцентрлік
немесе 3 планетоцентрлік
координат
координат жүйесі
қозғалыс
жызықтығымен
байланыста
болады.
елерін таңдайды.
Егер қос жұлдыз жүйесі қозғалысын қарастырғанда,
ғыменc1 ,байланыста
c2 , c3 - c вектордың
компоненттері.
Көбінесе
бастапқы
координат
жүйесі бастапқы
ретінде гелиоцентр
інесе аспан сферасына
жанама
болатын бейнелік
жазықтығын
стапқы
координат
жүйесі
гелиоцентрлік
немесе
геоцентрлік
экваториалды
жүйелер
қарастырыла
-эклиптикалық
Лаплас
векторы
- қозғалыс
жазықтықтың
нормаль
векторына
c ретінде
рдинат жүйесінің
негізгі
жазықтығы
ретінде
алады.
де геоцентрлік
гелиоцентрлік
есе
экваториалды
жүйелер
қарастырылады.
перпендикуляр
болғандықтан,
осыселеноцентрлік
жазықтықта
орналасады.
Қажетті
жағдайларда
немесе планетоцентрлік коорди
ер қарастырылады.
рда
селеноцентрлік
немесе
планетоцентрлік
координат
жүйелерін
таңдайды.
Егер қос жұлдыз
жүйесі қозғалысын қарастырған
ентрлік
координат
ы.
Егер қос
жұлдыз жүйесі
қозғалысынжанама
қарастырғанда,
көбінесе
аспан сферасына
болатын бейнелік жазықтығын бастап
ын қарастырғанда,
расына
жанама
болатынжүйесінің
бейнелік негізгі
жазықтығын
бастапқы
координат
жазықтығы
ретінде алады.
бастапқы ретінде алады.
ңықтығын
негізгі жазықтығы
3.
4.
cos2 c 2 c 2
r .r .
r rcos
r r r r c c r
2
r
r
r cos r r c 2 c r .
rr
Осыдан
Осыдан
r cos r r c 2 2 c 2 r .
Осыдан
c cr
2
c
Осыдан
r
r c 2
r 1 1 cos
cos
r 1 cos
немесе
немесе
1 cos2
немесе
c2c
p
p
p2 , e, e . .
r p
, c
(2.13)
p
r
,
(2.13)
немесе
1
e
cos
r 1 e cos, p 2 , e .
(2.13)
c
1 e pcos
r
, p , e .
(2.13)
- фокальный
қисықтыңфокалды
фокалды
параметрі
- фокус
арқылыөтетін
өтетінэллипстің
эллипстіңүлкен
үлкен
- фокус
1 e cos
кривой
арқылы
р р- -қисықтың
параметрі
параметр
р -осіне,
қисықтың
фокалды нақты
параметрі
- фокус
арқылы
өтетін эллипстің
үлкен
осіне,гиперболаның
гиперболаның
нақтыосіне
осіне
немесе
параболаның
симметрия
осіне
немесе
параболаның
симметрия
осіне
- круг, фокалды
осіне,
гиперболаның
нақты
осіне
параболаның
симметрия
осіне
перпендикуляр
орналасқан
фокалды
жартылай
хорданың
ұзындығына
тең
р -перпендикуляр
қисықтың
параметрі
-немесе
фокус
арқылы
өтетін
эллипстің
үлкен
орналасқан
фокалды
жартылай
хорданың
ұзындығына
тең
перпендикуляр
орналасқан
жартылай
хорданың симметрия
ұзындығынаосіне
тең
болады.
осіне,
гиперболаның
нақтыфокалды
осіне немесе
параболаның
болады.
болады.
перпендикуляр орналасқан фокалды жартылай хорданың ұзындығына тең
болады.
- парабола
5.
Эллипс немесе гипербола центрінен фокустарына дейін арақашықтығы с –фокустық арақашықтық деп аталады. Сонда
c
a 22 b22
(2.17)
e бойымен, материалдық нүктенің
6 сурет – Эллипстік орбита
қозғалысы
a
a
с – фокусное расстояние, «-» элиппс, «+» гипербола
«-» таңбасы эллипсқа, «+» - гиперболаға байланысты. Орбитаның фокалды
для
эллипса
параметрі:
эллипс
(2.18)
p a 1 e22 .
және гипербола
үшін
для гиперболы
(2.19)
p a e 22 1 .
Перицентр, апоцентр - апсиды
6.
Басқаша айтқанда - шын аномалияның немесе r - радиустың t - уақытқажәне
орбиталдық координаталар
Радиус-векторына
перпендикуляр
орналасқан жылдамдықтың
құраушысы
және
орбиталдық
координаталар
тәуелділігін
анықтау
керек. Момент интегралының
модулін қарастырайық
Радиус-векторына
перпендикуляр
немесе
шеңберлік жылдамдық
Радиус-векторына
перпендикуляр орналасқан
орналасқан жылдамдықтың
жылдамдықтың құраушысы
құраушысы
r cos
, шеңберлік жылдамдық r cos ,
немесе
r cos
,r , r c .
немесе шеңберлік жылдамдық rV
sin
r sin ,
(2.23)
r sinr , ,r r ,
(2.23)
(2.20)
Vrsin
sin ,
(2.23)
(2.20)
sin
r , rr , r
r r, ,
0. Радиус-векторына
v - бұрыштық жылдамдық,
V V
0.sin
(2.20)
перпендикуляр
орналасқан
жылдамдықтың құраушысы
0
.
жылдамдық,
немесе
жылдамдық,
v v - -бұрыштық
-бұрыштық
угловая жылдамдық
скорость
шеңберлік
2
ат жүйесінде,
екі денеX есебінің
шешімінrжүйесінде,
табу
Бастапқы
координат
екі дене есебінің шешімін
,
Y
,
Z
.
mc нүктенің
табу
, табу
, (2.21)
Орбиталдық
жүйесінде
радиус-векторы
Бастапқы
жүйесінде,
екі
дене
есебінің
шешімін
X ,Yкоординат
, Z координат
2
2
.c .
(2.21)
нықтаунемесе
үшін, rжүйеге
салыстырмалы
rV, r sin
, c үшін,
радиус-векторын
анықтау
жүйеге
салыстырмалы
,
,
(2.21)
r , r жүйеге
r ,
және орбиталдық
координаталар
немесе
салыстырмалы
, , (2.20)
анықтау үшін,
r радиус-векторын
Қозғалыс теңдеуін
(2.21)-ші
интегралдау
арқылы анықтаймыз
векторына
формуланы
ған косинустар
матрицаларын
векторына
координат
жүйесінің
бағытталған
косинустар
матрицаларын
бұрыштық
жылдамдық,
v
координат
жүйесінің
бағытталған
косинустар
матрицаларын
векторына
Қозғалыс
теңдеуін
(2.21)-ші
формуланы
интегралдау
арқылы
анықтаймыз
Қозғалыс
теңдеуін
(2.21)-ші
формуланы
интегралдау
арқылы
анықтаймыз
P
,
Q
,
R
ің бірлік
векторлары
.
Бағытталған
r
cos
,
көбейту керек. , , өстерінің
бірлік векторлары - P, Q, R . Бағытталған
көбейту керек. , , өстерінің
векторлары
- P, Q, R . Бағытталған
бірлік
dv
2
.
r
c
r sin
R векторлардың
тұрады.
(2.23)
r 2 ,
(2.21)
.
(2.22)
, R dv
косинустарқұраушыларынан
матрицалары P, Q
векторлардың
құраушыларынан
тұрады.
r
3 t
косинустар матрицалары P, Q 0 , 1R eвекторлардың
құраушыларынан
тұрады.
r
dvv p 2
cos
t . .
(2.22)
2
3 t
радиус-вектордың
теңдеуі
0
.
(2.22)
2
3
2
e
cos
v
Қозғалыс теңдеуін
радиус-вектордың
теңдеуі
0 1
p
2
1
e
cos
v
(2.21)-ші
формуланы
интегралдау
арқылы
анықтаймыз
0
p
P
P
, Pшын
0 болғанда,
тәуелсіз тұрақтысы.
Егер t жүйесінде,
мәні
аномалияның
- Бастапқы
координат
екі дене есебінің
шешімін
табу X
,
Y
,
Z
r Qm
,
(2.24)
аномалияның
,
(2.24) - орбита
t r tr өту
0 0болғанда,
тәуелсіз
тұрақтысы.
Егер
мәні
-нүктенің
перицентрін
, Qшын
dv
тұрақтысы.
Егер
,Q моменті.
шын
мәні
болғанда,
үшін,
, аномалияның
(2.24)
анықтау
жүйеге
салыстырмалы
, , (2.22)
r радиус-векторын
немесе
- тәуелсіз
2
3 t .
Rm m
нүктенің
орбита
перицентрін
өту
моменті.
2
орбита перицентрін
0 1 e cos
координат
нүктенің
p матрицаларын векторына
өту
жүйесінің
бағытталған
косинустар
RR v моменті.
осында
P
, Q, R . Бағытталған
көбейту
керек.
өстерінің
бірлік
векторлары
,
,
осында
t , шын
c
cтұрақтысы. Егер
c аномалияның
мәні 0 болғанда,
c - тәуелсіз
PP, Q
,
R
векторлардың
құраушыларынан
тұрады.
, Q косинустар
, R матрицалары
.
(2.25)
r
c
c
, Q
, R .
(2.25)
m cнүктенің
орбита
перицентрін
P , өту
Q моменті.
, R c.
(2.25)
c
c
радиус-вектордың теңдеуі
c
c
P
P, Q,дене
R, e, есебінің
p, -тұрақты
шімін Екі
шамаларымен
элементы
,Q
, R, e, p, тұрақты шамаларымен
жалпы орбиты
шешімін
PP
, Q , R, e, p, тұрақты шамаларымен
Екі дене есебінің жалпы шешімін
r Q ,
(2.24)
анықтауға болады.
анықтауға болады.
R
осында
р
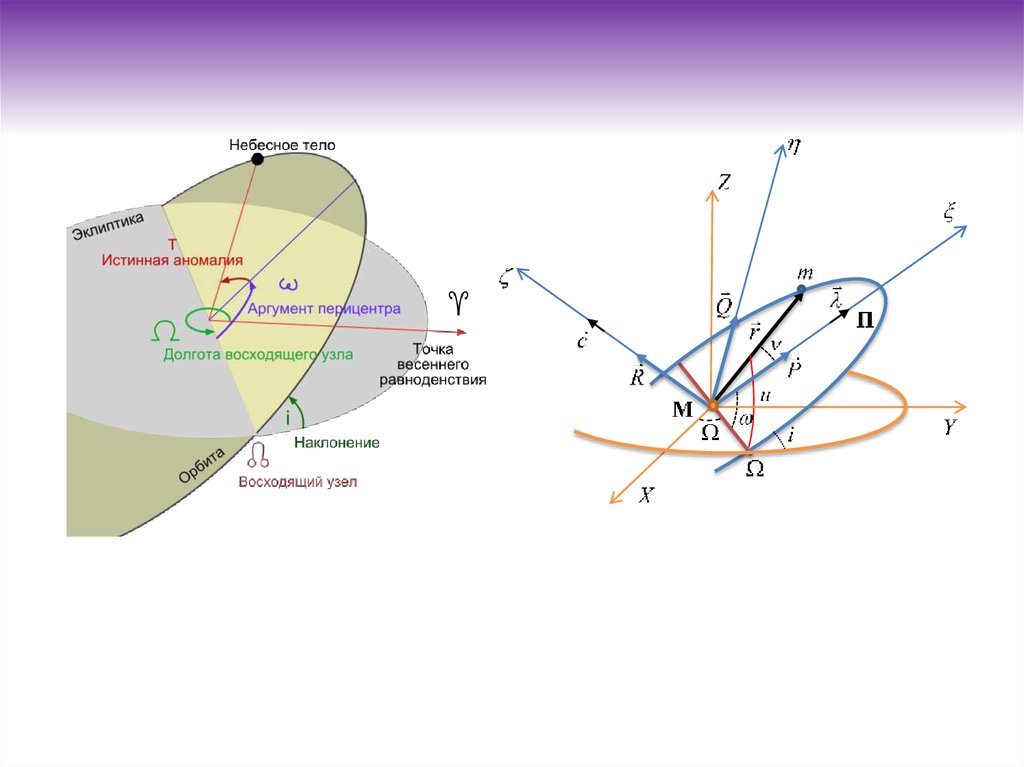
7.
Орбитаның Кеплер элементтерОрбитаның
үш топқа
бөлуге бол
1. Векторные элементы – P, Q, R, e, p, - орбита
элементтері
Орбитаның
P, Q,Кеплер
R–
, элементтері
e, p,элементтері
- орбита- элементтері
2. Элементы определяющие
параметры
орбиты
P, Q, R ) Бірінші
топ (векторлық
P, Q, R, e, –
p, - орбита элементтері
үш топқа
болады.элемен
3.Динамический элемент
Бірінші
топ бөлуге
кеңістіктегі орналасуын және
орбитаның
бағыттауын
көрсете
(векторлық
, және
R )өлшемін
Бірінші топ
(векторлық
- P, Qмен
-орбитаның
орбита
орналасуын
Екінші
топ ( e, кеңістіктегі
- орбитаның
пішіні
анықж
p )элементтері
Углы Эйлера кеңістіктегі орналасуын
Екінші
топнүктенің
( e, pкөрсетеді.
) - орбитаның
піші
бағыттауын
Үшінші және
топ - орбитаның
орбита бойымен
- материалдық
Кеплероские элементы
орбиты
Екіншісондықтан
топ
( e, p осы
) - орбитаның
пішіні мен
анықтайды. нүкт
Үшінші
топөлшемін
-деп
материалдық
элемент динамикалық
-аталады.
сондықтан
осыорбита
элемент
динамикалық
де
Үшінші топ - - материалдық
нүктенің
бойымен
қозғалуын
Қазіргі динамикалық
уақытта орбитаның
сондықтан осы элемент
деп аталады.орналасуын Эйлер
қарастырады.
Қазіргі уақытта орбитаның о
қарастырады.
Қазіргі уақытта орбитаның
орналасуын Эйлер бұрышта
қарастырады. Негізгі xy координат жазықтығын орбита жазықты
Негізгі xy
координат
жазықтығы
орналасқан бір түзу сызығымен
кесіп
өтеді. Бұл
нүктелер
Негізгісызық
орбита
xy координат
– түйіндержазықтығын
сызығы
деп аталады.
орналасқан
бір түзужазықтығы
сызығымен қиылыс
кесіп ө
сызық
деп аталады.
орналасқан бір түзу сызығымен
кесіп– түйіндер
өтеді. Бұлсызығы
нүктелер
орбита т
Қозғалыс
жағдайда
сызық – түйіндер
сызығы деп
аталады.m дененің z-координатасының
таңбасынан «+» таңбасына
ауысу кезіндегі
немесе
Қозғалыс
жағдайда
m солтүстік
дененің
нүктесін
- жоғары
Ω немесе
«+»
та
таңбасынан
«+»солтүстік
таңбасынатүйіні,
ауысу
кезінд
Қозғалыс
жағдайда
m түйіні
дененің
z-координатасының
(апплика
кезіндегі немесе
оңтүстік
бағытындағы
нүк
нүктесін
- жоғары
түйіні
Ωқиылысу
немесе
солт
таңбасынанауысу
«+» таңбасына
ауысу
кезіндегі
немесе
солтүстік
бағытында
немесе
оңтүстік
тұйінітүйіні,
деп атайды.
ауысу
кезіндегі
немесе
оңтүстік
бағыты
нүктесін - жоғары түйіні
Ω немесе
солтүстік
«+»
таңбасынан
«
немесе
оңтүстік
тұйіні
деп
ауысу кезіндегі немесе оңтүстік бағытындағы
қиылысу
нүктесін
– төм
немесе оңтүстік тұйіні деп атайды.
8.
анықтаймыз. Радиус-вектордың бағыттау косинустары:x Аспан
, mсферасына
u, xорбитаның
m 180 iпроекциясын
.
(2.29)
қарастырған
кезінде x m
r мен бұрышы:
сфералық үшбұрышының қабырғалары
, , .
ргументі (түйін сызықтарымен m нүктенің
радиус-векторы
r
рақашықтық), ω – перицентрдің
x аргументі.
, m u, x m 180 i .
(2.29)
Аспан сферасына орбитаның проекциясын қарастырған кезінде x m
xm
) аргументі
cos cos u (түйін
sin sin
u cosмен
i, бұрышы:
сфералық
үшбұрышының
қабырғалары
u - cos(
еңдік
сызықтарымен
m нүктенің
радиус-векторы
m нүктенің
Бастапқы координат
жүйесінде
координаттары
m
Бастапқы
координат
жүйесінде
нүктенің
координаттары
m
Бастапқы
координат
жүйесінде
нүктенің
координаттары
(2.30)
cos(ym)координат
sin cosжүйесінде
u cos
uнүктенің
cos i, координаттары
арасындағы
арақашықтық),
ω
– sin
перицентрдің
аргументі.
m
Бастапқы
Бастапқы
координат
нүктенің
координаттары
mcos(
Бастапқы
координат
x
, жүйесінде
xmжүйесінде
r
нүктенің
um,xm
x
mrкоординаттары
180
i . u sin sin u cos(2.29)
r
)
cos
cos
i ,
cos(
zm
)
sin
u
sin
i
.
апқы координат жүйесінде m нүктенің координаттары
x
r
r
cos(
xm
)
r
cos
cos
u
sin
sin
u
cos
i i, ,
x
r
r
cos(
xm
)
r
cos
cos
u
sin
sin
u
cos
xmy )xm
cos
cos
u
sin
sin
u
cos
i
,
x r cos(
rxcos(
)
r
cos
cos
u
sin
sin
u
cos
i
,
r r cos(
r)cos(
cos
r sin
cos
usin
cos
usin
i ,
(2.31)
xm
) ym
ym
r)ym
cos
u cos
sin
cos
icos
,ucos
x r r
r
cos(
xm
cos(
rcos(
cos
cos
usin
sin
sin
u cos
cos
i
, usin
y
r
r
)
r
u
sin
u
i
,
y
r
r
)
r
sin
cos
u
cos
cos
i
,
(2.3
(2
u - xеңдік
(түйін
сызықтарымен
m
нүктенің
радиус-векторы
(2.30)
cos(
ym
)
sin
cos
u
cos
sin
u
cos
i
,
r аргументі
r cos(xm
) r r
cos
cos
u
sin
sin
u
cos
i
,
y
rycos(
ym
)
r
sin
cos
u
cos
sin
u
cos
i
,
(2.31)
r r cos(
r )cos(
)r
sin
r sin
u sin
i .
zm
(2.31)
sin
, i , (2.31)
y r ω –zrr zперицентрдің
cos(
cos(
r)zm
cosuicos
арасындағы арақашықтық),
аргументі.
rym
)
. isin
z
r rym
r cos(
zm
)cos
r sin
rucos
sinucos
uusin
sinicos
. usin
cos(
zm
)zm
)usin
usin
sin
. uir. sin
sin
y r r cos(ym
cos
cos i ,
(2.31)
z )r r
r cos(
rcos
uisin
r cos(
zm
z rz rr cos(
zm)
r)sin
u sin ui.sin i.
0
тең болады
r
z r r cos(
zm
)
r
sin
u
sin
i
.
Q iвекторлары
Егер u
және
болса
және
90
cos(
xm
) u u cos
cos
u
sin
u
cos
,
0 0 sinP
r
r тең
r
Q
Егер
және
болса
және
векторлары
Q
u
Егер
және
болса
және
векторлары
теңболад
бола
P
u 0 , тогда
u векторы
90 90
P и r
Если
r
r
Q
Егер u Сонда
және
болса
және
векторлары
тең
болады.
u
90
P
0
0
r тең
(2.30)
және
cos(
ym
sin
cosPu және
Pcos
sin
i, r r тең
Qu cos
және
векторлары
болады.
u және
u
) 90
90 болса
Q
ЕгерЕгер
болса
векторлары
болады.
u
u
r
Сонда
Сонда
0
r
r тең
Q векторлары
және u 90 болса P жәнебудут
болады.
u
P
cos cos
sin
sin cosi,
Сонда
xsin i.
равны
r
cos(
zm
)
sin
u
Сонда
PxP
cos
cos
sin
i, i,
Сонда
cos
cos
sin sin
sin cos
cos
x
Px cos Pcos
sin
sin
cos
i
,
(2.32)
sin
cos
sin
cos
sin
icos
i,
P
cos
cos
sin
, cos
y cos
Px cos
cos
sin
sin
cos
cos
i
,cos
x
(2.3
PyP
sin
sin
i
,
(2
sin
cos
cos
sin
cos
i
,
y
Px cos cos P y
sinsin
sincos
cos
i
,
(2.32)
cos
sin
cos
i
,
Psin
sin
sin
,cos
(2.32)
cos
sin
i
sin
i,cosi,
(2.32)
Py P
sin
cos
sin
cos
z cos
y
P
sin
i
,
P
sin
sin
i
,
(2.32)
Py sin cos P z cos
icos
sin sin
sin
,sinz i ,z sin i,
P
Pz sin
z sin i ,
Qx cos sin sin cos cosi,
Pz sin sin i,
cos sin sin cos cosi,
x x cos sin sin cos cosi ,
Qx cosQ
sin
cos
i,cos
sin
sin
sin
cos
sin
sin
cos
cos icos
i,
(2.33)
Q yQ
sin
Qx xcos
cos
sin
cos
cos
sin sin cos
i,cos
cos , cosi,
(2.3
Q
(2
y
y sin sin cos cos cosi ,
Qx cos sinQ
y sin
Q
cos
cos
i
,
sin
sin
cos
cos
cos
i
,
(2.33)
cos
sin
i . cos
Q z
sin
sin
sin
cos
i,cosi,
(2.33)
Qy ysin
sin
cos
cos
(2.33)
z cos
i. icos
cos
sin
.
z
Qy sin sin Q
z cos
cos
cosi,
(2.33)
cos
Q
sin
i.cos
sin
i
.
Qz cos
z sin i.
Q cos sin i.
9.
Rz cosi.x, y, z осьтеріне R вектордың проекциясы
Rx sin sin i,
Сонда екі дене есебінің жалпы
(2.34)
Ry шешімі
cos sin i,
Rx sin sin i,
Rz x cos i.P
(2.34)
Ry cos
sin i, Qx
x
y cos
i.Py Qy .
(2.35)
Rz
Сонда екі дене есебінің жалпы
шешімі
z P
Q
z
z
Сонда екі дене есебінің жалпы
x шешімі
Px
Qx
дифференциалдау арқылы
(2.31) және (2.35) теңдеулерді
t бойынша
y
P
(2.35)
y
Qy .
x
P
Q
x
r x x , y , z анықтауға болады.
жылдамдық векторының компонентерін
z Pz
Qz
r y - радиалды
r .
Жылдамдық векторының құраушылары:
және V(2.35)
y Py V
Q
r
n
z P
Q
нормалды
(тангенциалды):
t zбойынша
z дифференциалдау арқылы
(2.31) және
(2.35) теңдеулерді
жылдамдық векторының компонентерін
Vr
e sin r , x , y , z анықтауға болады.
(2.31) және
(2.35) теңдеулерді
t p бойынша
Vr r - дифференциалдау
r Жылдамдық
векторының
құраушылары:
радиалды және Vарқылы
n
r x , y , z анықтауға болады.
жылдамдық
векторының компонентерін
нормалды (тангенциалды):
(2.36)
Vn
(1 e cos ),
Жылдамдық векторының құраушылары:
p Vr r - радиалды және Vn r Vr
e sin ,
нормалды (тангенциалды):
p
1 2e cos e 2 .
V
Vr epsin ,
(2.36)
Vn p (1 e cos ),
p
(2.36)
Vn (1 e cos ), 2
p
V
1 2e cos e .
p
V
1 2e cos e 2 .
p








 physics
physics








