Similar presentations:
Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора
1. 1.8 Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора .
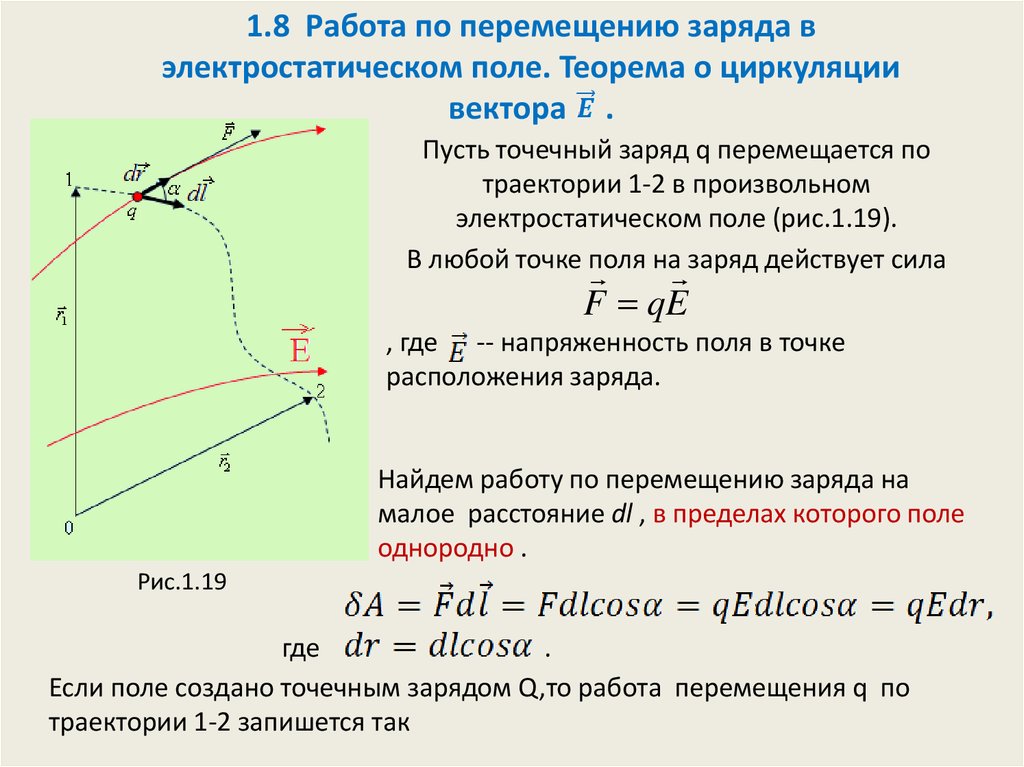
Пусть точечный заряд q перемещается потраектории 1-2 в произвольном
электростатическом поле (рис.1.19).
В любой точке поля на заряд действует сила
F qE
, где -- напряженность поля в точке
расположения заряда.
Найдем работу по перемещению заряда на
малое расстояние dl , в пределах которого поле
однородно .
Рис.1.19
где
.
Если поле создано точечным зарядом Q,то работа перемещения q по
траектории 1-2 запишется так
2.
r2A12
r
r2
2
F dr Eqdr
r1
r1
4 0r
r1
Q
q dr
2
r2
dr
r 2 4 0
4 0
r1
1 1
r1 r2
(1.11)
Т.о. работа перемещения заряда q в поле точечного заряда Q не зависит от
траектории, а лишь от начального и конечного положений q.
Из (1.11) следует, что работа сил электростатического поля по
перемещению заряда вдоль любой замкнутой траектории в поле
точечного заряда тождественно равна нулю. Этот вывод справедлив для
любых эл.– ст. полей.
3. Работа, совершаемая силами электростатического поля при перемещении заряда по замкнутому пути, равна нулю
Отсюда следует, что электростатические силы консервативны, а ихполе потенциально.
Последнее выражение можно записать иначе:
(1.13)
Криволинейный интеграл от вектора
вдоль кривой L в поле вектора
, взятый
(1.14)
называется циркуляцией
контуру L.
по замкнутому
4. Т.о. из (1.13) следует ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА : циркуляция вектора напряженности электростатического поля вдоль
замкнутого контура, проведенного в этом поле, тождественноравна нулю и выражает потенциальный характер этого поля.
1.9 Потенциал электростатического поля.
Поскольку электростатическое поле потенциально, работа сил поля в
Qq 1 1
формуле (1.11)
A
12
4 0 r1
r2
может быть представлена как убыль потенциальной энергии Wp заряда q
при его перемещении:
(1.14) ; здесь
-- потенциальная
энергия заряда q в поле точечного заряда Q, определенная с точностью до
произвольной постоянной С.
5.
В поле точечного заряда С выбирается так, чтобы при r→∞→0.
Следовательно С=0, и потенциальная энергия q в поле точечного заряда Q
(1.15)
Введем понятие потенциала
:
(1.16)
Потенциал
– энергетическая характеристика поля в данной точке,
подобно тому как -- силовая характеристика поля в этой точке .
Потенциал – энергетическая характеристика поля в данной точке,
численно равная потенциальной энергии единичного
положительного заряда, помещенного в данную точку.
Потенциал поля точечного заряда
Потенциал – скалярная алгебраическая величина.
(1.17)
6. Тогда в (1.11) потенциальная энергия заряда q в т.1 , в т.2 -- , а работа (1.14) может быть записана как
Тогда в (1.11) потенциальная энергия заряда q в т.1, а работа (1.14) может быть записана как
(1.18)
--разность потенциалов двух точек поля численно равна работе сил поля при перемещении единичного положительного заряда между этими точками.
, в т.2 -
7.
Принцип суперпозиции электростатического поля применительно кпотенциалу:
потенциал любой точки поля, созданного системой точечных
зарядов, равен алгебраической сумме потенциалов, созданных в
данной точке каждым из зарядов в отдельности.
(1.19)
При графическом изображении электростатического поля часто используют
понятие эквипотенциальной поверхности.
Эквипотенциальной поверхностью называется геометрическое место
точек, потенциал которых одинаков: const
Необходимо выполнять два условия при построении этих поверхностей:
1) Силовые линии ( линии напряженности) и эквипотенциальные
поверхности всегда взаимно перпендикулярны.
8.
2) Условились проводить эквипотенциальныеповерхности так, чтобы разность потенциалов
двух
соседних
поверхностей
оставалась
постоянной
n n 1 const
Тогда в тех областях пространства, где напряженность поля возрастает,
эквипотенциальные поверхности сгущаются, т.е. по густоте их
расположения можно судить о неоднородности поля.
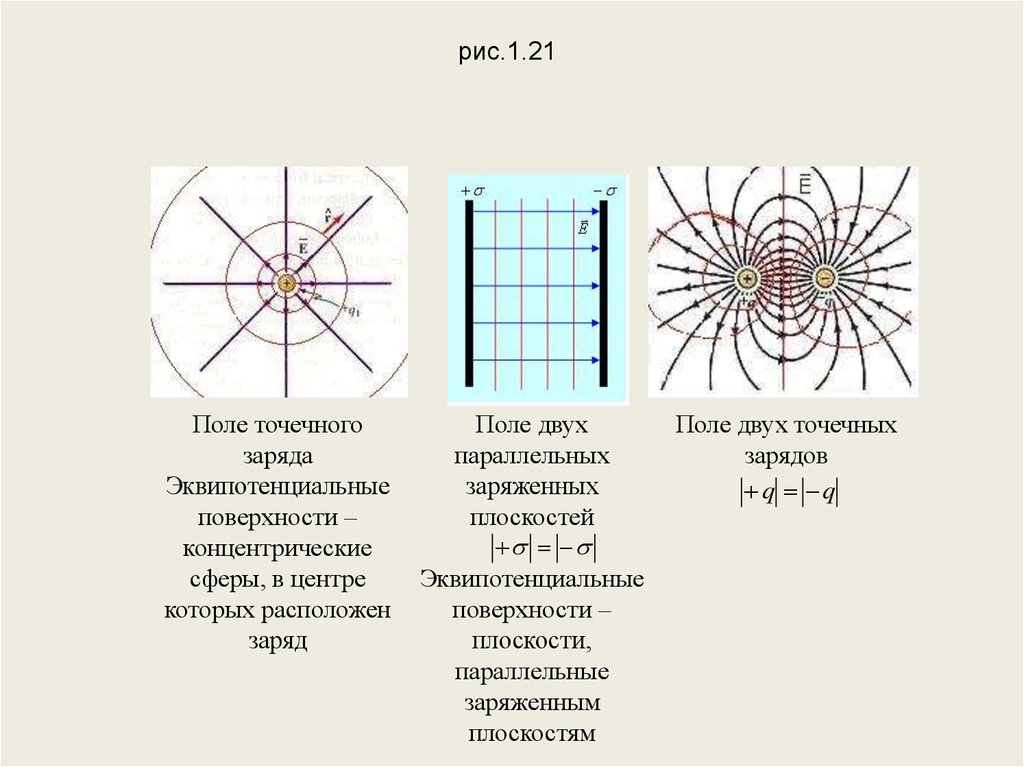
На рис.1.21 даны графические карты полей простейших конфигураций;
эквипотенциальные поверхности изображены коричневым цветом .
9.
рис.1.21Поле точечного
заряда
Эквипотенциальные
поверхности –
концентрические
сферы, в центре
которых расположен
заряд
Поле двух
параллельных
заряженных
плоскостей
Эквипотенциальные
поверхности –
плоскости,
параллельные
заряженным
плоскостям
Поле двух точечных
зарядов
q q
10. 1.10 Связь между напряженностью и потенциалом электростатического поля
В механике для потенциального силового поля уже найдено соотношениемежду силой, действующей на частицу со стороны поля, и потенциальной
энергией этой частицы в данной точке поля, которое является общим для
потенциальных полей:
F gradWp .
В случае электростатических полей F qE. W q .
p
Подставляя последние два выражения в первое,
получим
E grad .
(1.23)
Вектор напряженности электростатического поля
в данной
точке равен градиенту потенциала в этой точке, взятому с
противоположным знаком .
11.
Из (1.23) и смысла градиента непосредственно следует, что векторнапряженности направлен в сторону наискорейшего убывания потенциала
и по величине равен максимальной скорости убывания потенциала.
В декартовой системе координат равенство (1.23) имеет вид
E
i
j
k,
x
y
z
Ex;
Ey;
E z . (1.24)
где
x
y
z
В одномерном случае:
d
E
, d Edx, 2 1 Edx
dx
x1
x2
12. 1.11 Расчет потенциалов в полях высокой симметрии
1. Бесконечная, заряженная поповерхности плоскость ( σ > 0).
Напряженность поля плоскости
2 , x 0
0
E
, x 0
2 0
E
(*)
Поле плоскости
однородно. Связь
напряженности с
потенциалом в этом
случае:
d
dx
Положим потенциал самой плоскости
Тогда для произвольной точки поля получим
0 E x,
или 0 Ex.
рис.1.23
13. Учитывая выражение для напряженности (*), для потенциала окончательно имеем
o 2 x п ри x 0,(1.25)
o
o
x п ри x 0.
2 o
Зависимости E(x) и (x ) для случая
0
изображены на рис.1.23 б,в соответственно.
Вывод
При переходе через заряженную поверхность потенциал поля меняется непрерывно, в
отличие от напряженности поля, которая при этом меняется скачком.
14. 2. Поле двух бесконечных параллельных равномерно заряженных плоскостей
=Поле существует только между
плоскостями и оно однородно.
(0 x d )
E
,
o
Принято отсчитывать потенциал от (–)
заряженной пластины, т.е. считать d 0 .
Поэтому разность потенциалов между
плоскостями
, или
рис.1.24
Между плоскостями потенциал поля линейно
зависит от координаты.
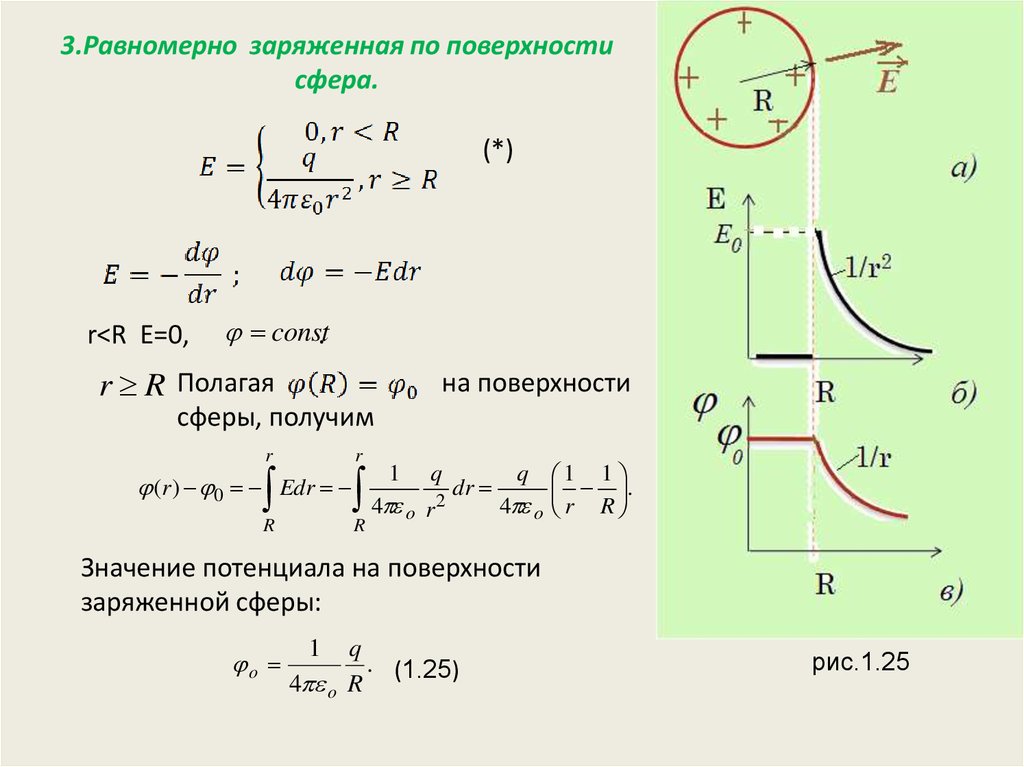
15. 3.Равномерно заряженная по поверхности сфера.
(*)r<R E=0,
const.
r R Полагая
на поверхности
сферы, получим
r
r
R
R
( r ) 0 Edr
q 1 1
dr
.
4 o r 2
4 o r R
1
q
Значение потенциала на поверхности
заряженной сферы:
o
1
q
. (1.25)
4 o R
рис.1.25
16. Выражение (1.25) в силу непрерывности потенциала определяет его величину и внутри сферы.
Итак, потенциал равномерно заряженной по поверхности сферыописывается равенствами:
q
, 0 r R,
4 o R
1 q
, r R.
4 o r
o
1
(1.26)
вывод:
Вне равномерно заряженной по поверхности сферы ее поле
полностью совпадает с полем точечного заряда q , помещенного в
центр этой сферы. Другими словами, при стягивании заряда сферы к
ее центру без нарушения равномерности его распределения, в
области r R никаких изменений поля не происходит.
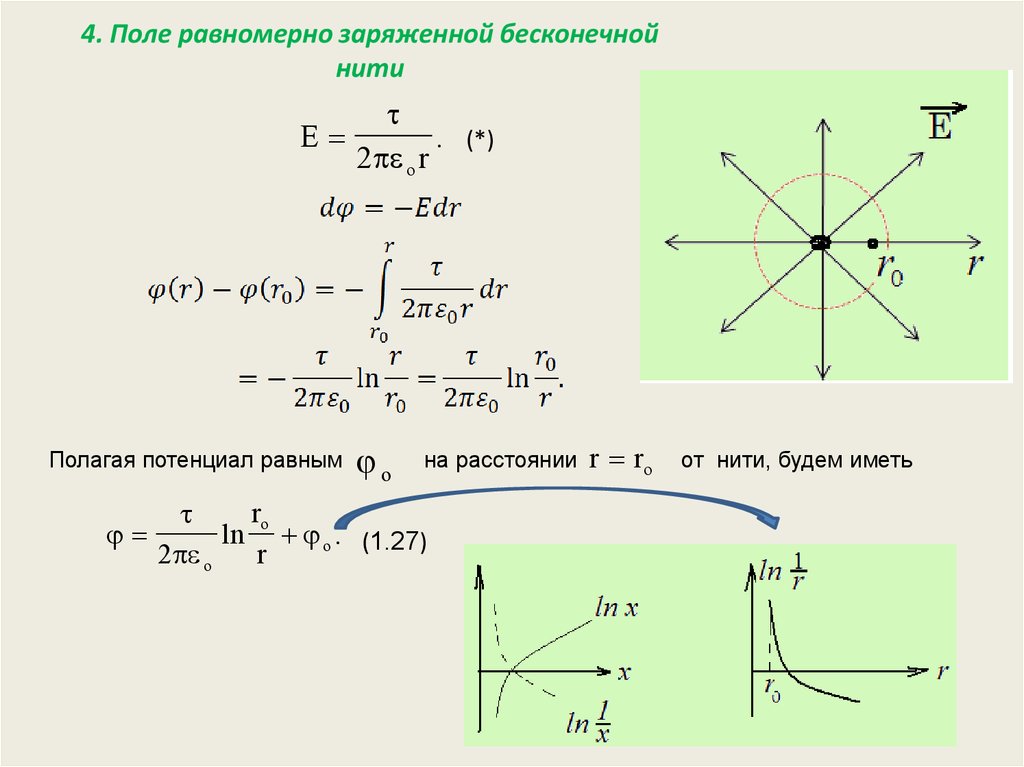
17. 4. Поле равномерно заряженной бесконечной нити
EПолагая потенциал равным
. (*)
2 o r
o
на расстоянии
ro
ln o . (1.27)
2 o
r
r ro
от нити, будем иметь













 physics
physics








