Правило Лопиталя

1.

Лекция N13
Лектор: доц. Лаптева Надежда Александровна
Тема: Правило Лопиталя

2.

Правило Лопиталя используется для
раскрытия неопределенностей
0
0
или
.

3.

Теорема. Пусть f ( x) и ( x ) функции, дифференцируемые в
некотором полуинтервале ( a, b],
причем ( x ) 0.
Пусть при x a обе эти функции
стремятся к нулю, или обе стремятся
к бесконечности.
В таком случае
f ( x)
f ( x)
lim
lim
.
x a ( x )
x a ( x)

4.

Примеры.
sin5x
sin5 x
1) lim
lim
x 0
x 0
x
x
lim5cos5 x 5.
x 0
1 cos x
sin x
2) lim
lim
2
x 0
x 0 2 x
x
cos x 1
lim
.
x 0
2
2

5.

Неопределенность вида
3)
lim
sec
x
tg
x
x 0
2
sin x
1
lim
cos x
x 0 cos x
2
1 sin x
cos x
lim
lim
0.
cos
x
x 0
x 0 sin x
2
2

6.

Неопределенность вида
0
ln x
4) lim x ln x lim 1
x 0
x 0 x
1
x
lim 2 lim ( x) 0.
x 0 x
x 0

7.

1 , 0 ,
.
Неопределенности вида
5)
lim 1 x
x
1
2 x
0
1 x ;
2
1
0.
x
Обозначим
y 1 x
1
2 x
.
0
0

8.

Логарифмируя, находим
ln
1
x
1
2
ln y ln 1 x
.
x
x
Так как при x числитель и
2
знаменатель стремятся к бесконечности,
то получаем неопределенность
.

9.

Применяем правило Лопиталя:
2
x
2
ln 1 x
2
1
x
lim ln y lim
lim
0.
x
x
x
x
1
Т.к.
lim ln y ln lim y
x
x
, то
ln lim y 0. Следовательно, lim y 1.
x
Итак,
lim 1 x
x
1
2 x
x
1.

10.

Отыскание наибольшего и
наименьшего значений функции
Правило нахождения наибольшего
и наименьшего значения функции
на отрезке [a, b].
1. Находим все критические точки
функции в интервале ( a, b) и
вычисляем в них значения функции.
2. Вычисляем значения функции на
концах отрезка [a, b].
3. Из всех значений выбираем
наибольшее и наименьшее.

11.

Пример. Найти наибольшее и наименьшее
значение функции f ( x) x3 3x на
отрезке [ 3,2].
Находим критические точки функции в
интервале ( 3,2) :
f ( x) 3x 3; 3x 3 0;
x1 1, x2 1.
2
2
Находим значения функции в этих точках:
f ( 1) 2,
f (1) 2.

12.

Вычисляем значения на концах отрезка:
f ( 3) 27 9 18,
f (2) 8 6 2.
yнаиб 2;
yнаим 18.

13.

Пример. Построить график функции
ln x
y ( x)
.
x
1) Область определения: x 0.
ln x
lim
.
x 0 x
2) Так как в точке x 0 функция имеет
бесконечный разрыв, то прямая x 0
(ось Oy ) является асимптотой.

14.

Найдем наклонную асимптоту.
1
ln x
1
x
k lim 2 lim
lim 2 0,
x x
x 2 x
x 2 x
1
ln x
ln x
x
b lim
0 x lim
lim 0.
x
x 1
x
x x
(при нахождении пределов мы
воспользовались правилом Лопиталя)
Итак, k b 0 и y 0 горизонтальная асимптота.

15.

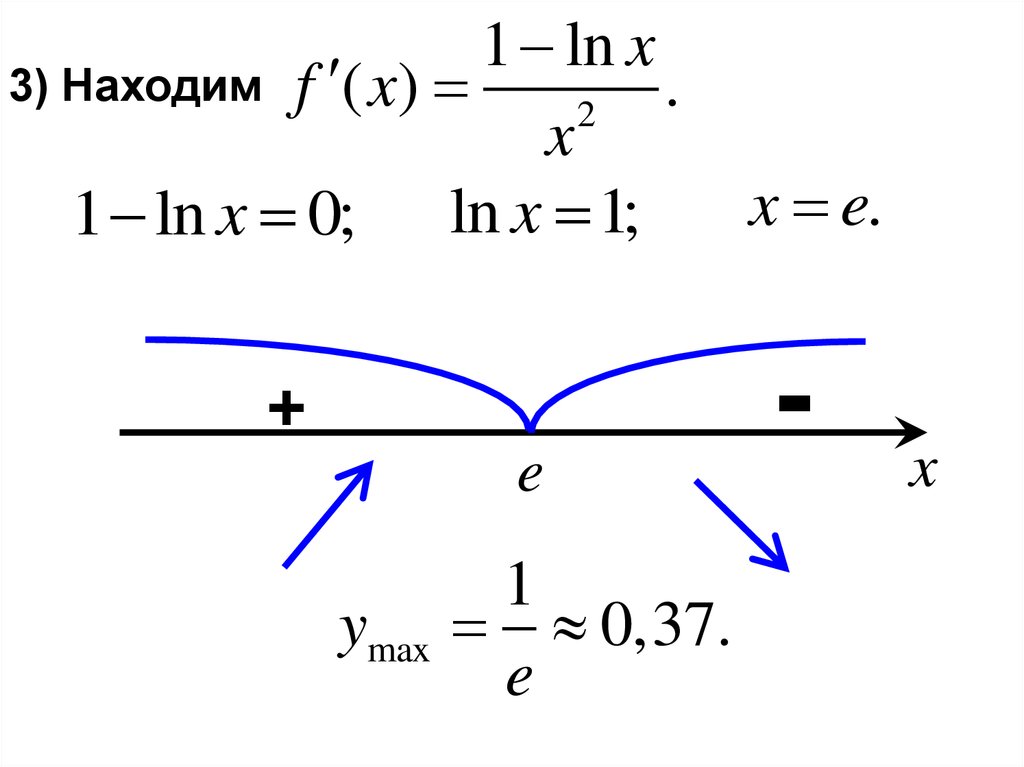
1 ln x
3) Находим f ( x)
.
2
x
1 ln x 0; ln x 1;
+
e
ymax
1
0,37.
e
x e.
-
x

16.

4) Находим
1 2
x 2 x (1 ln x)
x
f ( x)
4
x
x 2 x(1 ln x) 1 2(1 ln x)
4
3
x
x
2ln x 3
.
3
x

17.

f ( x) 0; 2ln x 3 0;
3
32
ln x ; x e .
2
Определяем знак f ( x ).
Точка перегиба
+
e
32
+
3
y 3 2 0,33.
2e
x

18.

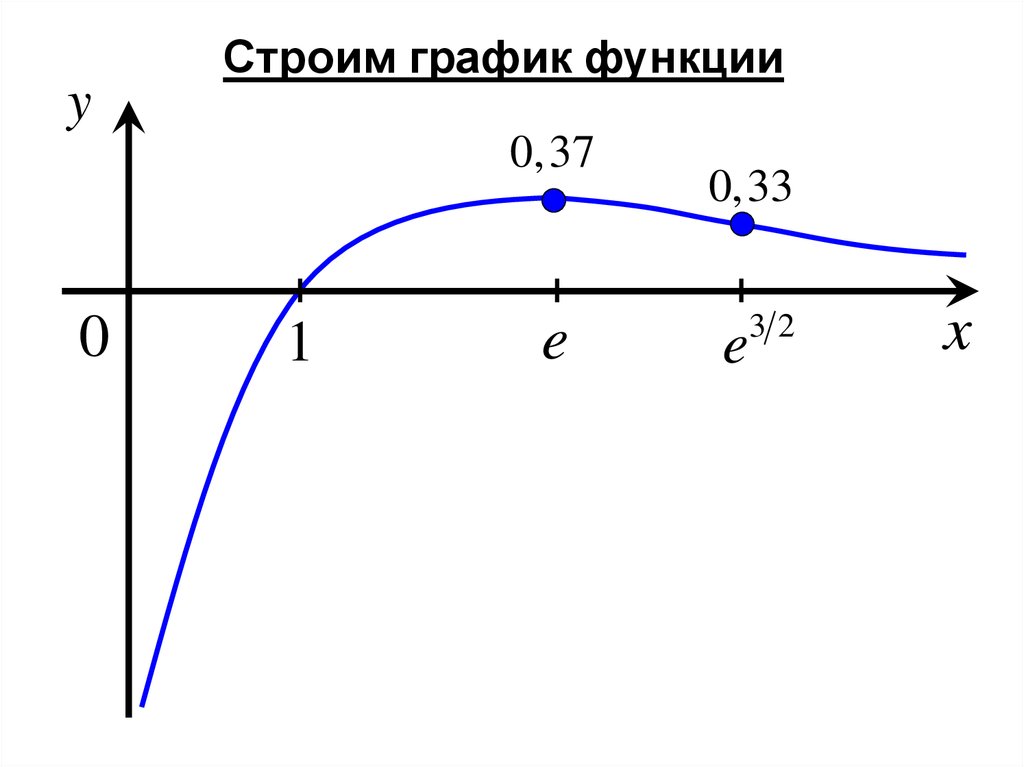
y
Строим график функции
0, 37
0
1
e
0,33
e
32
x