Приложения производной. Правило Лопиталя

1. Приложения производной. Правило Лопиталя.

Теорема. Предел отношения двух бесконечно
малых или бесконечно больших величин
равен пределу отношения их производных,
если этот предел существует.
0
Если имеется неопределенность
0
то
f ( x)
f ( x)
lim
lim
x a g ( x )
x a g ( x )
( x )
( x )
или
,

2. Возрастание и убывание функции.

Теорема (достаточные условия возрастания и
убывания функции).
Если x (a, b)
f ( x) 0 то f(x) возрастает на (a,b).
Если x (a, b)
f ( x) 0 то f(x) убывает на (a,b).

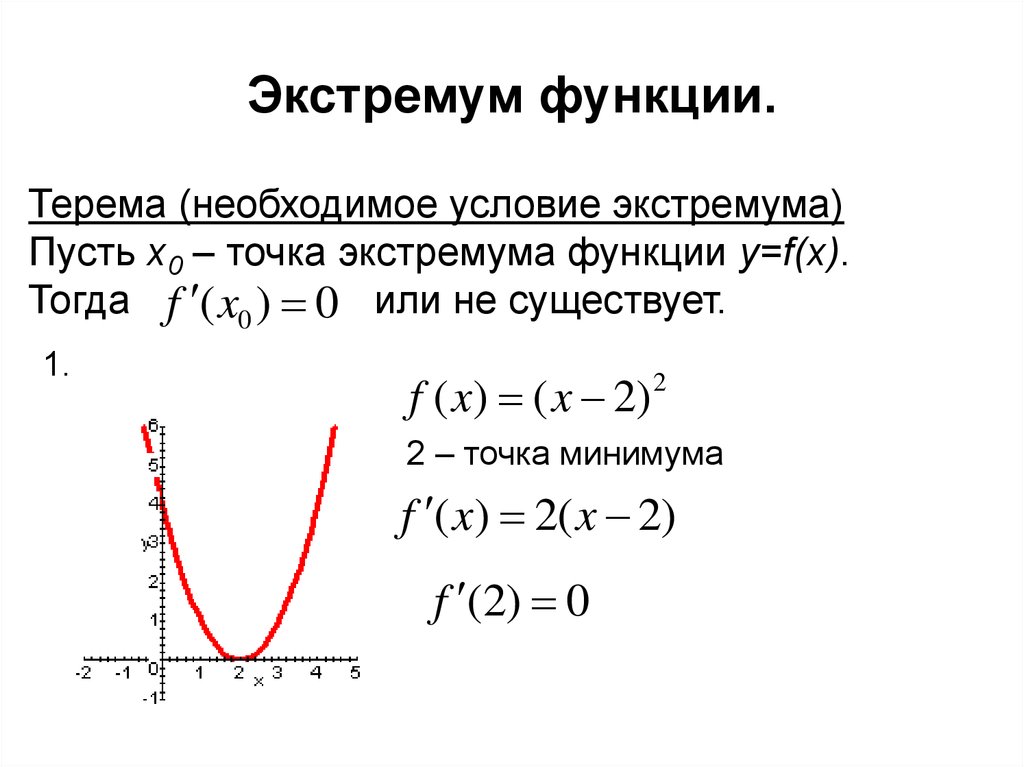
3. Экстремум функции.

Терема (необходимое условие экстремума)
Пусть x0 – точка экстремума функции y=f(x).
Тогда f ( x0 ) 0 или не существует.
1.
f ( x) ( x 2)
2
2 – точка минимума
f ( x) 2( x 2)
f (2) 0

4. Экстремум функции.

3.
f ( x) x
3
2
0 – точка минимума
2
f ( x) x
3
f (0)
1
3
2
33 x
не существует

5. Экстремум функции.

Замечание Из того, что f ( x0 ) 0 не следует, что
x0 – точка экстремума функции y=f(x).
Т.е. условие f ( x0 ) 0 является необходимым,
но не достаточным условием экстремума.
f ( x) x
2
f ( x) 3 x
f (0) 0
3
0 не является т. экстремума

6. Экстремум функции.

Опр. Точки, в которых производная равна 0 или не
существует, называются критическими точками.

7. Экстремум функции.

1-е достаточное условие экстремума.
Пусть x0 - критическая точка функции y=f(x). Если
при переходе через
x0
производная этой функции
меняет свой знак с “+” на “-”, то
x0
- точка
максимума функции y=f(x), а если с “-” на “+”, то
- точка минимума.
x0

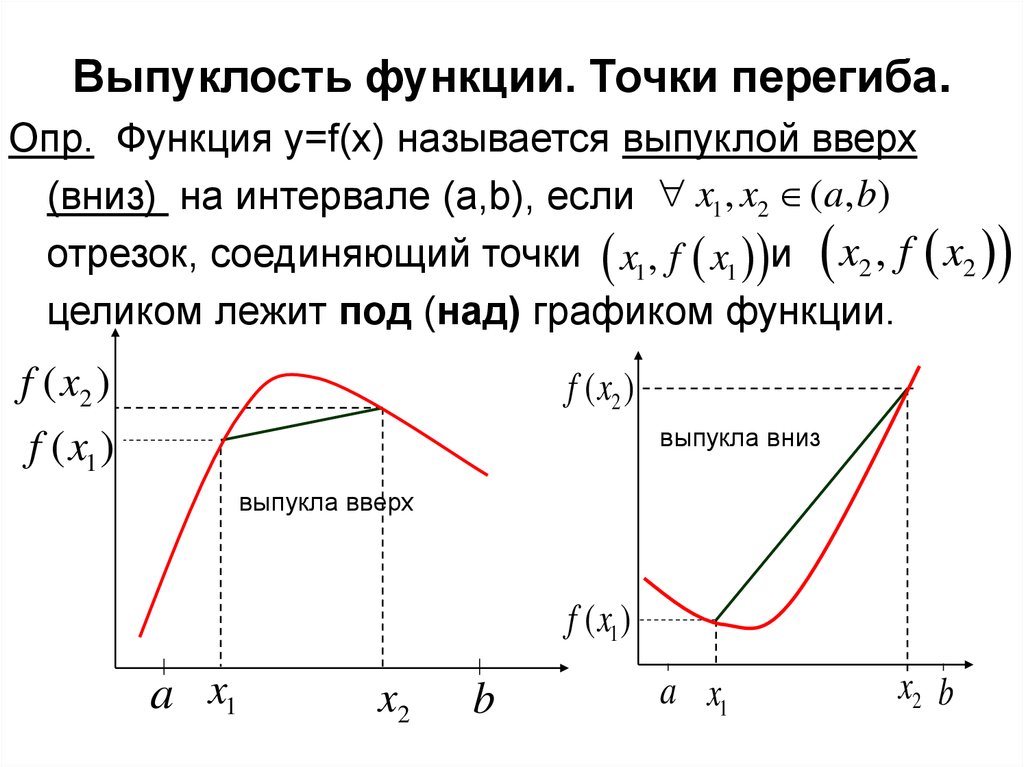
8. Выпуклость функции. Точки перегиба.

Опр. Функция y=f(x) называется выпуклой вверх
(вниз) на интервале (a,b), если x1 , x2 (a, b)
отрезок, соединяющий точки x1 , f x1 и x2 , f x2
целиком лежит под (над) графиком функции.
f ( x2 )
f ( x2 )
выпукла вниз
f ( x1 )
выпукла вверх
f ( x1 )
a x1
x2
b
a x1
x2 b

9. Выпуклость функции. Точки перегиба.

Теорема.
Если x (a, b)
f ( x) 0 то f(x) выпукла вниз на
(a,b).
Если x (a, b)
(a,b).
f ( x) 0 то f(x) выпукла вверх на

10. Выпуклость функции. Точки перегиба.

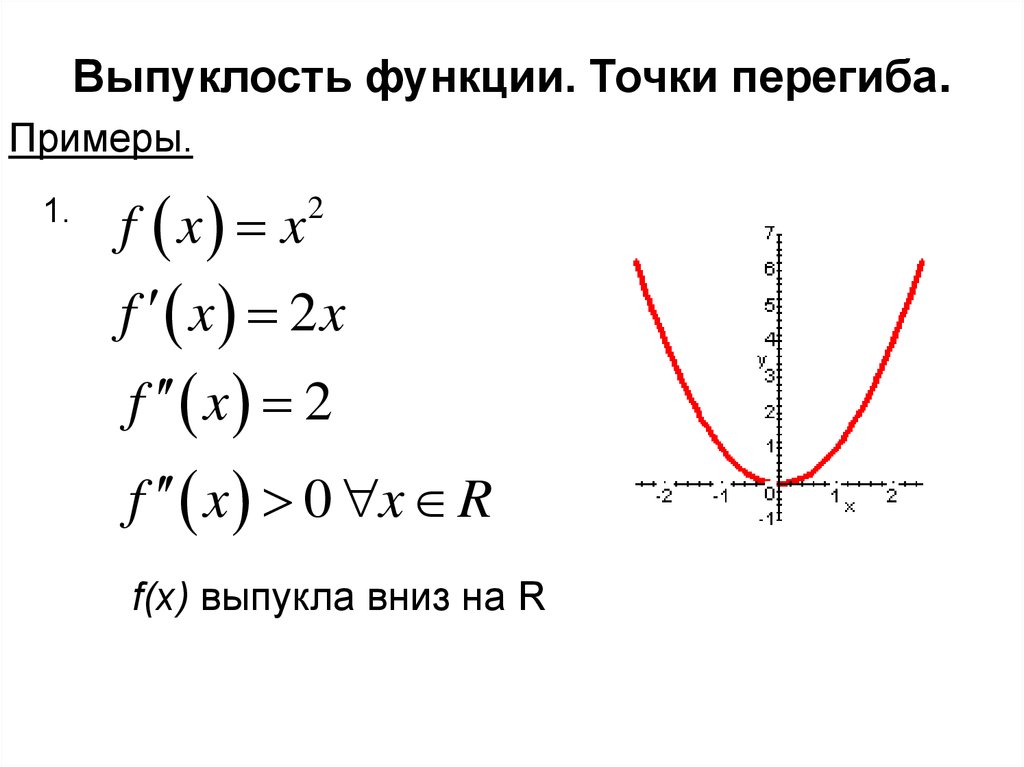
Примеры.
1.
f x x
2
f x 2x
f x 2
f x 0 x R
f(x) выпукла вниз на R

11. Выпуклость функции. Точки перегиба.

Примеры.
2.
f x x
2
f x 2 x
f x 2
f x 0 x R
f(x) выпукла вверх на R

12. Выпуклость функции. Точки перегиба.

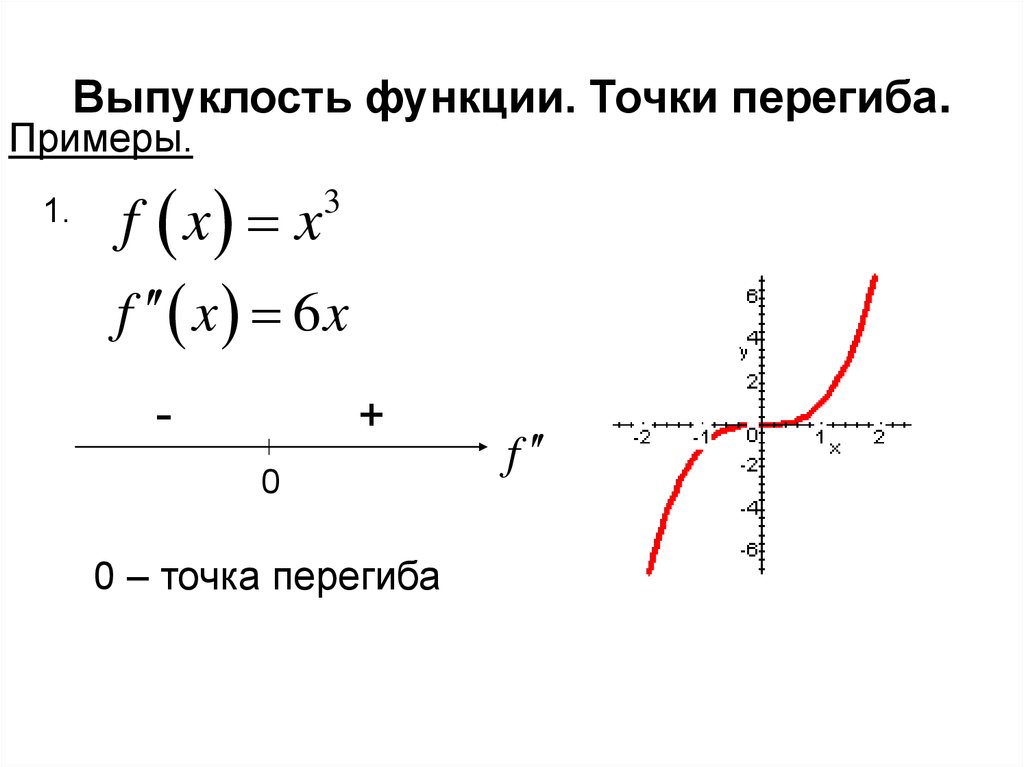
Примеры.
3.
f x x
3
f x 3x
2
f x 6 x
-
+
0
f
f(x) выпукла вверх на (-∞;0)
f(x) выпукла вниз на (0;+∞)

13. Выпуклость функции. Точки перегиба.

Опр. Точкой перегиба графика непрерывной
функции называется точка, разделяющая
интервалы, на которых функция выпукла вниз и
вверх.
f x x
3
0 – точка перегиба

14. Выпуклость функции. Точки перегиба.

Теорема (необходимое условие перегиба) Если x0 –
точка перегиба функции y=f(x), то f x0 0 .
Теорема (достаточное условие перегиба) Если
вторая производная функции y=f(x) при переходе
через некоторую точку x0 меняет свой знак, то x0 точка перегиба.

15. Выпуклость функции. Точки перегиба.

Примеры.
1.
f x x
3
f x 6 x
-
+
0
0 – точка перегиба
f

16. Выпуклость функции. Точки перегиба.

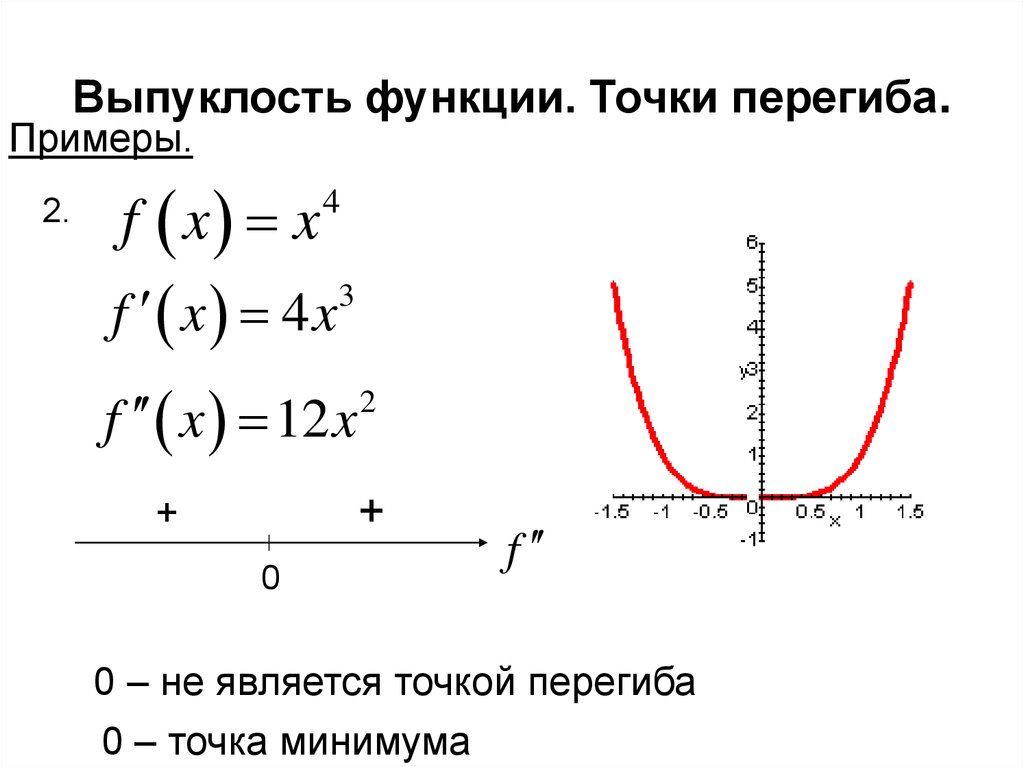
Примеры.
2.
f x x
4
f x 4x
3
f x 12 x
2
+
+
0
f
0 – не является точкой перегиба
0 – точка минимума