Окружность. (Задача 18. Вариант 105)

1. Задача 18. Вариант 105

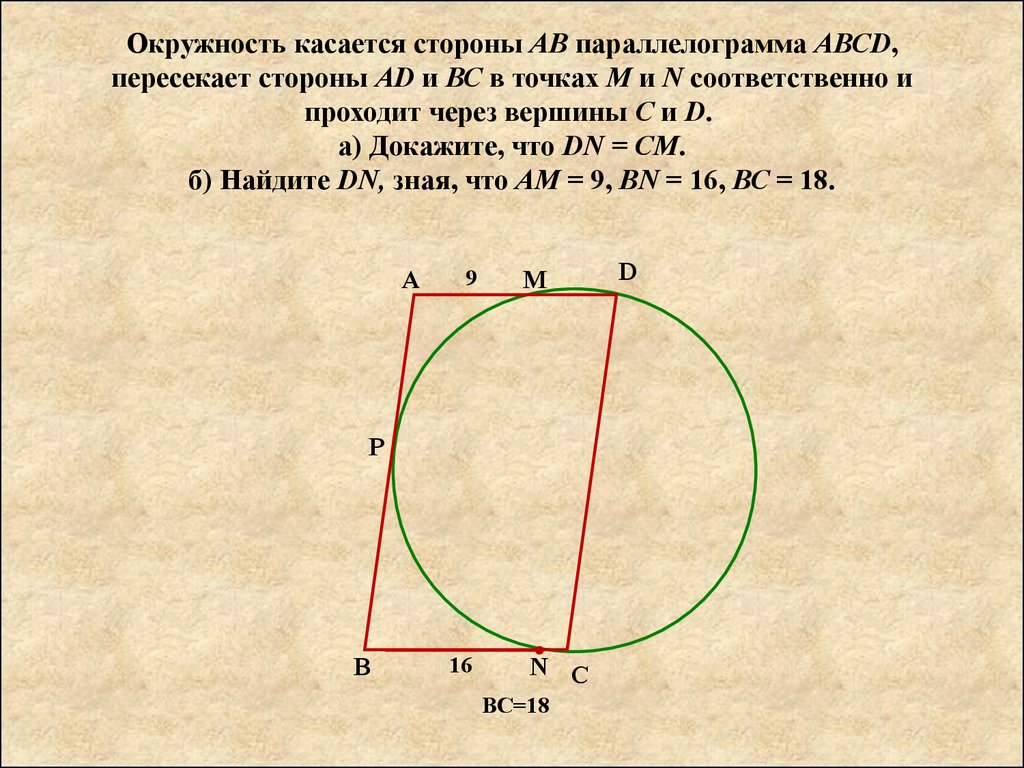
2. Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через

вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
А
9
M
P
В
16
N С
ВС=18
D

3.

Окружность касается стороны АВ параллелограмма АВСD,
пересекает стороны AD и ВС в точках М и N соответственно и
проходит через вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
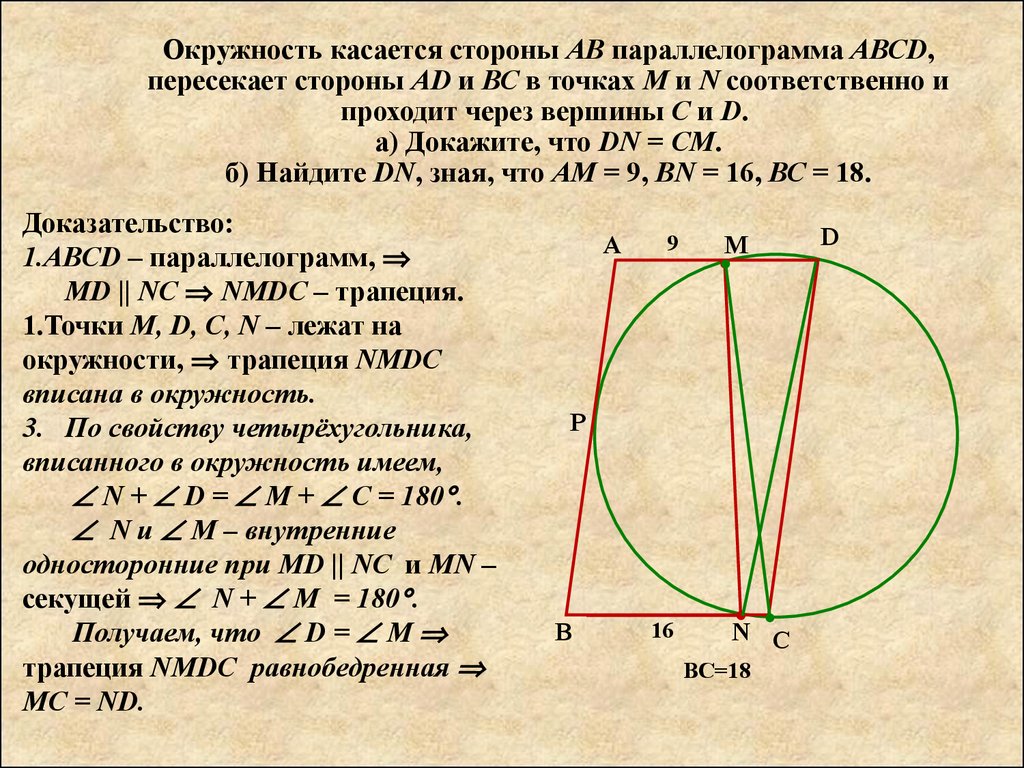
Доказательство:
1.ABCD – параллелограмм,
MD || NC NMDC – трапеция.
1.Точки M, D, C, N – лежат на
окружности, трапеция NMDC
вписана в окружность.
3. По свойству четырёхугольника,
вписанного в окружность имеем,
N + D = M + C = 180 .
N и M – внутренние
односторонние при MD || NC и MN –
секущей N + M = 180 .
Получаем, что D = M
трапеция NMDC равнобедренная
МС = ND.
А
9
M
P
В
16
N С
ВС=18
D

4. Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через

вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
А
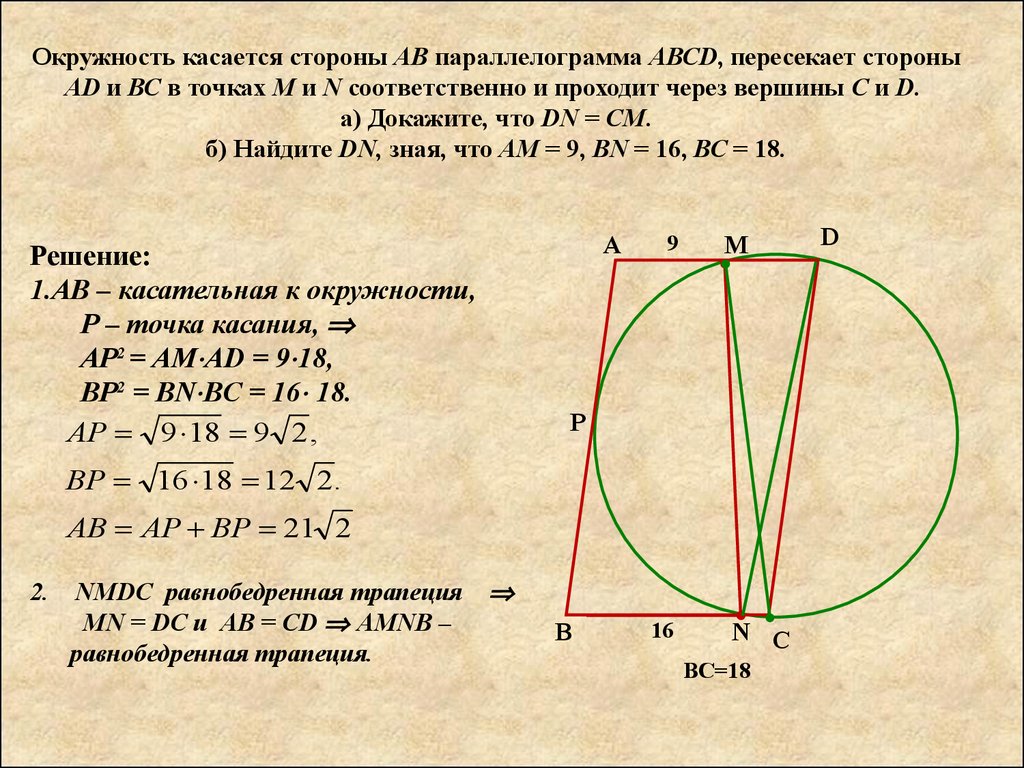
Решение:
1.АВ – касательная к окружности,
Р – точка касания,
AР2 = АМ AD = 9 18,
ВР2 = BN BC = 16 18.
AP 9 18 9 2 ,
9
M
P
BP 16 18 12 2 .
AB AP BP 21 2
2.
NMDC равнобедренная трапеция
MN = DC и AB = CD AMNB –
равнобедренная трапеция.
В
16
N С
ВС=18
D

5. Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через

вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
Решение:
1.NMDC равнобедренная трапеция
MN = DC и AB = CD AMNB –
равнобедренная трапеция.
MK 441 2 12,25 869,75
Ответ: ND = 30.
M
9
Н 16
3,5
21 2
2. МКС – прямоугольный.
MC 869,75 30,25 900 30
9
А
В
3,5
2
К N
С