Similar presentations:
Преобразование графиков функций
1.
Преобразование графиковфункций
2. Основные приёмы преобразования графиков
1. Параллельный перенос вдоль оси абсцисс2. Параллельный перенос вдоль оси ординат
3. Растяжение и сжатие вдоль оси абсцисс
4. Растяжение и сжатие вдоль оси ординат
5. Преобразование симметрии относительно оси
абсцисс
6. Преобразование симметрии относительно оси
ординат
7. Построение графика функции у =│f(x)│
8. Построение графика функции у = f(│x│)
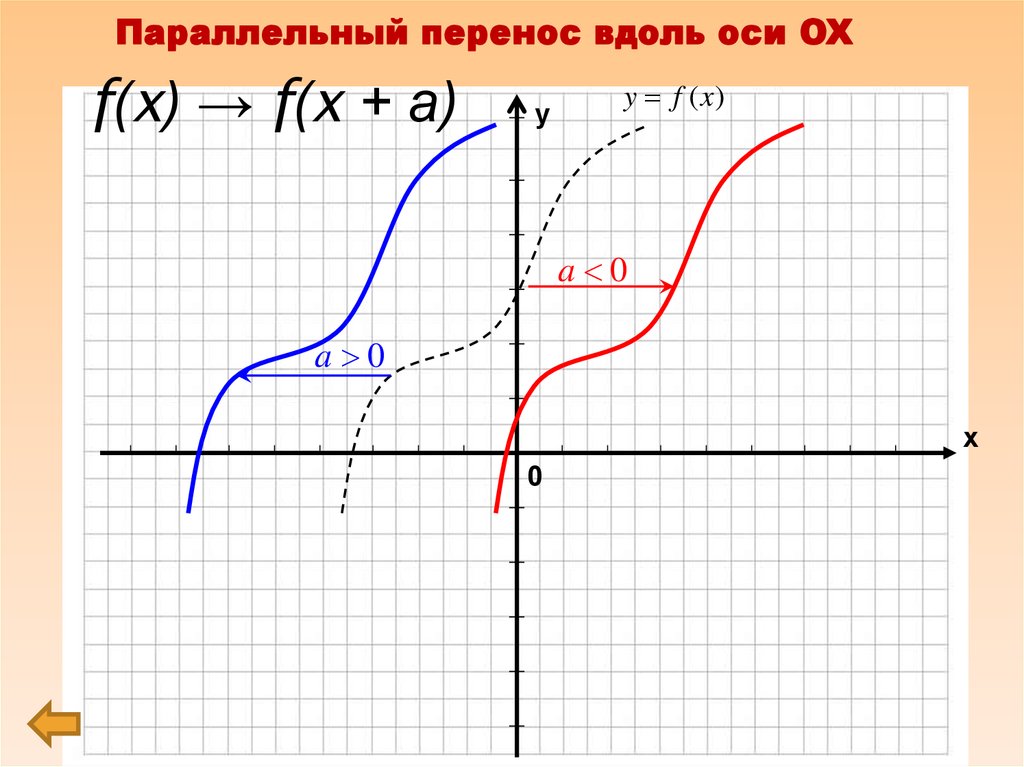
3. f(x) → f(x + а)
Параллельный перенос вдоль оси OXf(x) → f(x + а)
у
y f (x)
a 0
a 0
х
0
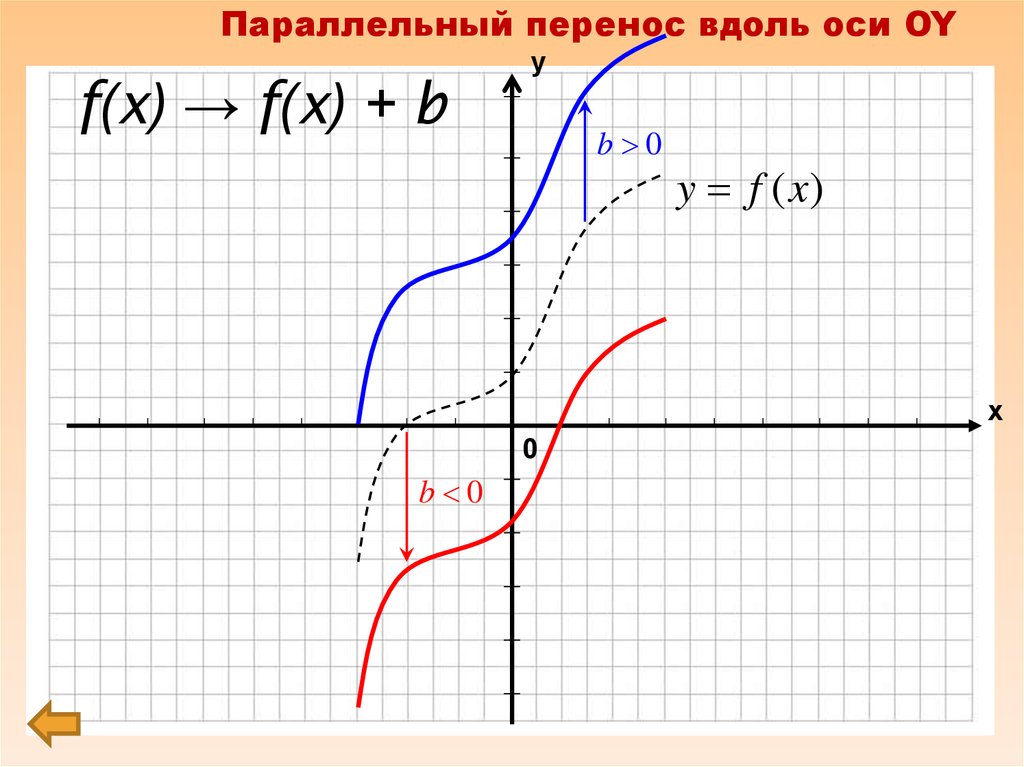
4. f(x) → f(x) + b
Параллельный перенос вдоль оси OYf(x) → f(x) + b
у
b 0
y f (x)
х
0
b 0
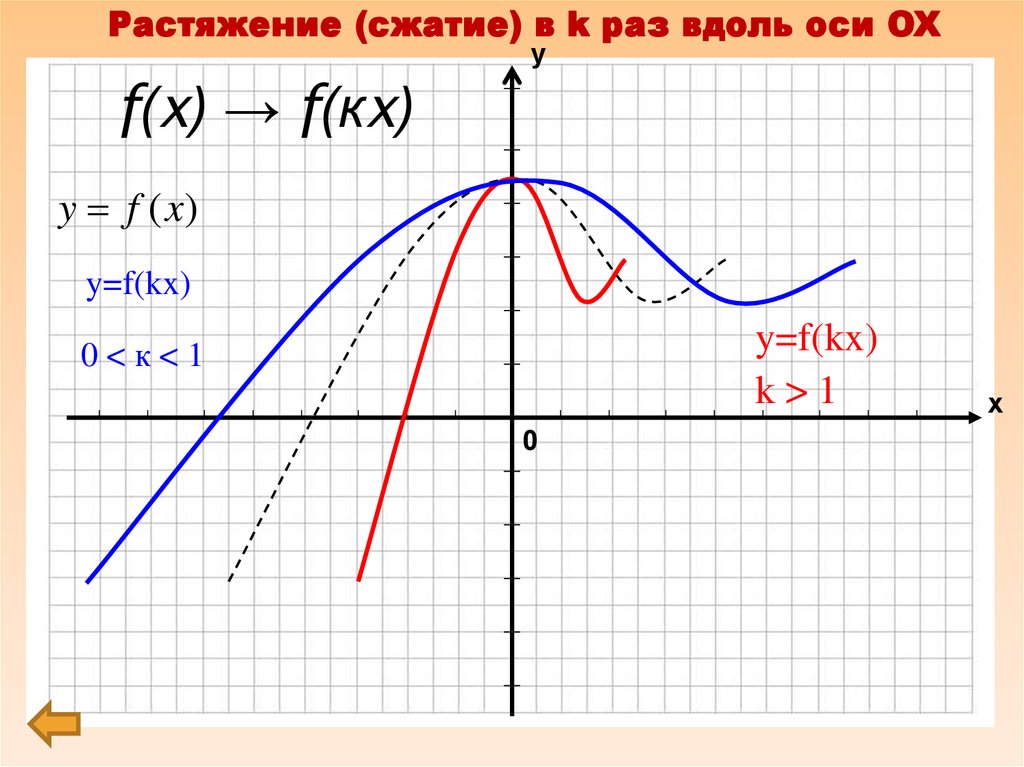
5. f(x) → f(кx)
Растяжение (сжатие) в k раз вдоль оси OXу
f(x) → f(кx)
y f (x)
y=f(kx)
y=f(kx)
k>1
0<к<1
0
х
6. 0 < k < 1
Растяжение (сжатие) в k раз вдоль оси OYf(x) → к f(x)
у
y=f(kx)
k>1
y=f(kx)
0<k<1
х
0
y f (x)
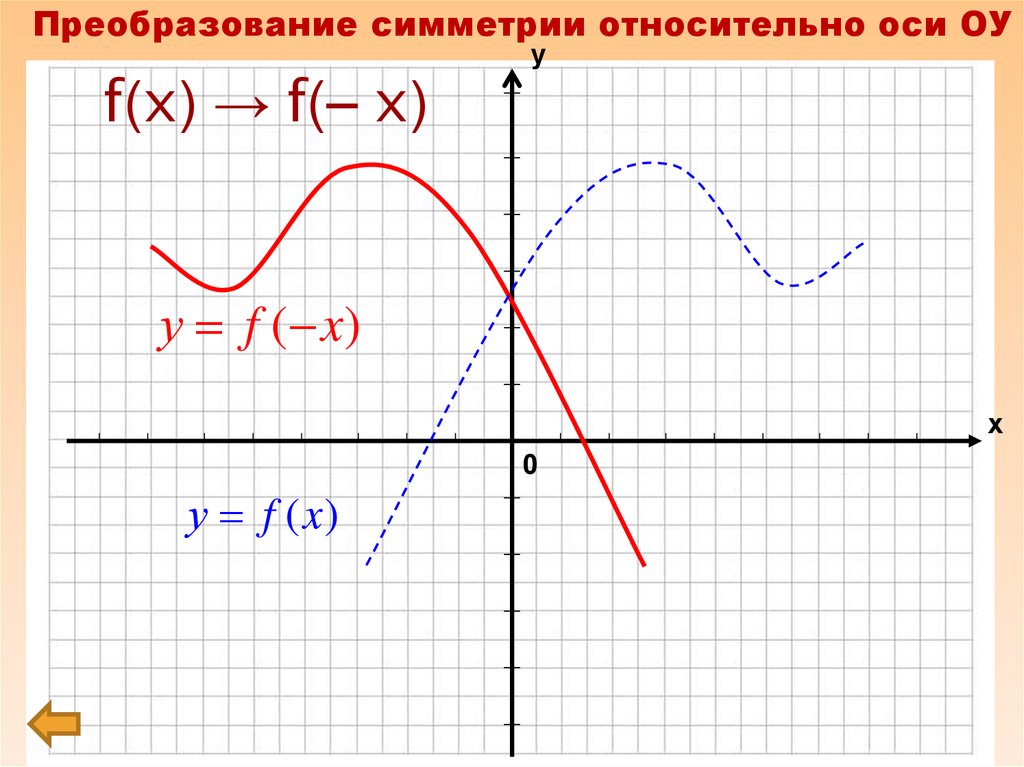
7. f(x) → f(– x)
Преобразование симметрии относительно оси ОУf(x) → f(– x)
у
у f ( x)
х
0
у f (x)
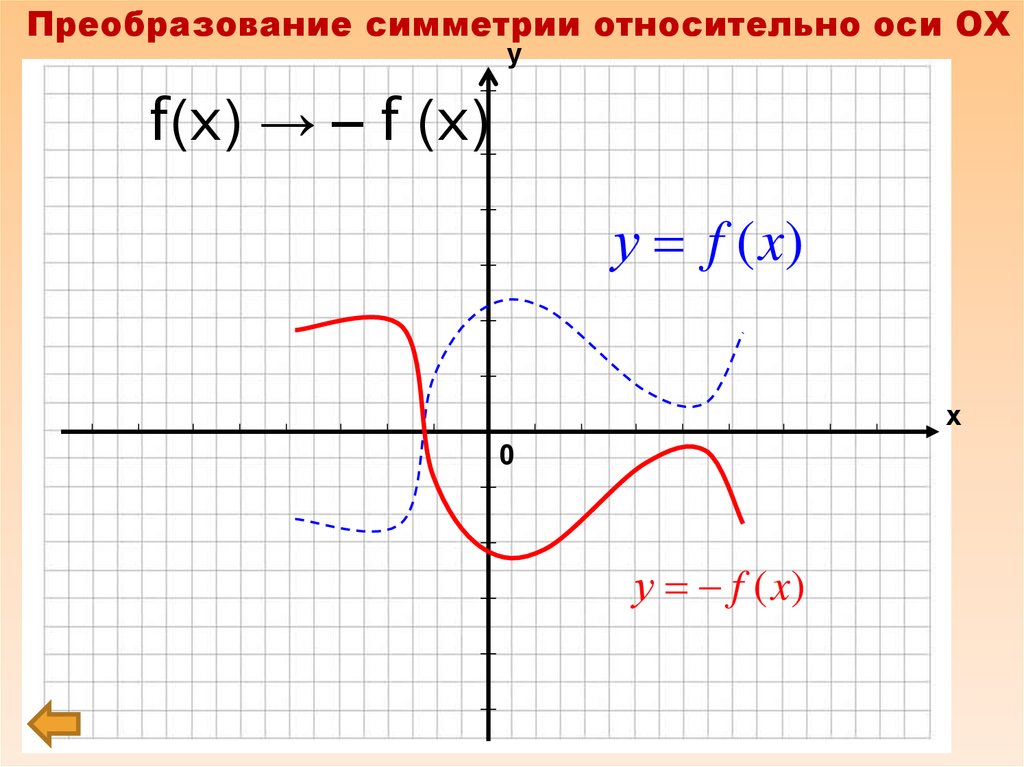
8. f(x) → – f (x)
Преобразование симметрии относительно оси ОХу
f(x) → – f (x)
у f (x)
х
0
у f (x)
9.
Преобразованиеу
f(x) → │f(x)│
f(x) → │f(x)│
у f (x)
х
0
у f (x)




 mathematics
mathematics








