Similar presentations:
Условные и разделительные силлогизмы. (Тема 8)
1. Основы формальной логики
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТМЕЖДУНАРОДНЫХ ОТНОШЕНИЙ
Кафедра философии
Основы формальной
логики
Тема 8
Условные и разделительные,
силлогизмы
2. Условные и разделительные силлогизмы
Условные силлогизмы• Чисто условный силлогизм
• Условно-категорический силлогизм
• Эквивалентно-категорический силлогизм
Разделительные силлогизмы
• Чисто разделительный силлогизм
• Разделительно-категорический силлогизм
Условно-разделительные (лемматические)
силлогизмы
• Дилеммы, трилеммы, тетралеммы
• Простые и сложные условно-разделительные силлогизмы
• Конструктивные и деструктивные условно-разделительные
силлогизмы
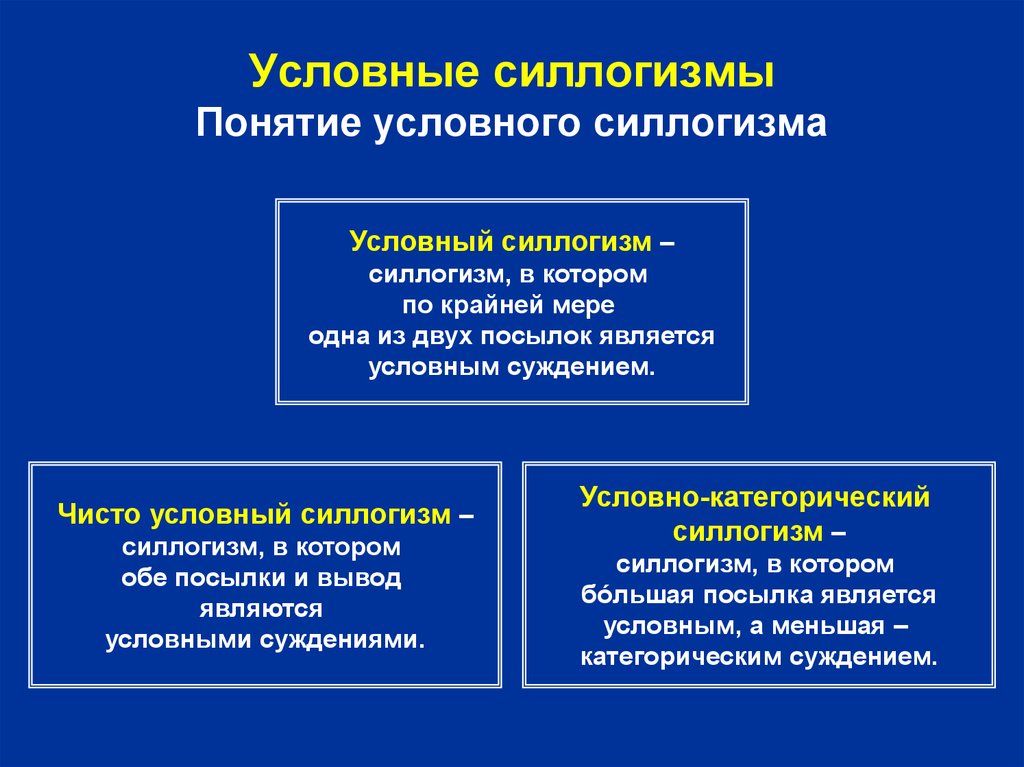
3. Условные силлогизмы Понятие условного силлогизма
Условный силлогизм –силлогизм, в котором
по крайней мере
одна из двух посылок является
условным суждением.
Чисто условный силлогизм –
силлогизм, в котором
обе посылки и вывод
являются
условными суждениями.
Условно-категорический
силлогизм –
силлогизм, в котором
бóльшая посылка является
условным, а меньшая –
категорическим суждением.
4. Условные силлогизмы Чисто условный силлогизм
Если A, то BЕсли B, то C
Аксиома
чисто условного силлогизма
Следовательно,
если A, то C
Следствие следствия
есть следствие основания.
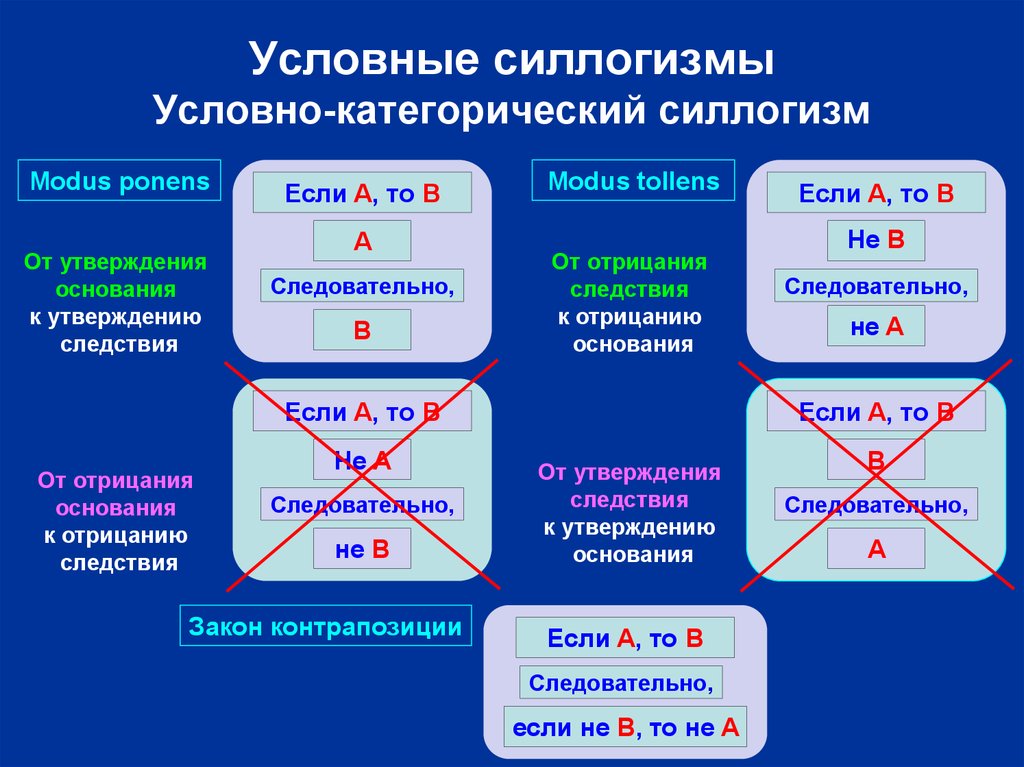
5. Условные силлогизмы Условно-категорический силлогизм
Modus ponensОт утверждения
основания
к утверждению
следствия
Если A, то B
A
Следовательно,
B
Modus tollens
От отрицания
следствия
к отрицанию
основания
Если A, то B
От отрицания
основания
к отрицанию
следствия
Не A
Следовательно,
не B
Закон контрапозиции
Если A, то B
Не B
Следовательно,
не A
Если A, то B
От утверждения
следствия
к утверждению
основания
Если A, то B
Следовательно,
если не B, то не A
B
Следовательно,
A
6. Условные силлогизмы Условно-категорический силлогизм
Если идёт дождь, то крыши мокрые.Если идёт дождь, то крыши мокрые.
Идёт дождь.
Крыши не мокрые.
Следовательно,
Следовательно,
крыши мокрые.
дождя нет.
Если идёт дождь, то крыши мокрые.
Если идёт дождь, то крыши мокрые.
Дождя нет.
Крыши мокрые.
Следовательно,
Следовательно,
крыши не мокрые.
идёт дождь.
Закон контрапозиции
Если идёт дождь, то крыши мокрые.
Следовательно,
если крыши не мокрые, то дождя нет.
7. Условные силлогизмы Условно-категорический силлогизм
Если число делится на 6,то оно делится на 2.
Если число делится на 6,
то оно делится на 2.
Это число делится на 6.
Это число не делится на 2.
Следовательно,
Следовательно,
оно делится на 2.
оно не делится на 6.
Если число делится на 6,
то оно делится на 2.
Если число делится на 6,
то оно делится на 2.
Это число не делится на 6.
Это число делится на 2.
Следовательно,
Следовательно,
оно не делится на 2.
оно делится на 6.
Закон контрапозиции
Если число делится на 6, то оно делится на 2.
Следовательно,
если число не делится на 2, то оно не делится на 6.
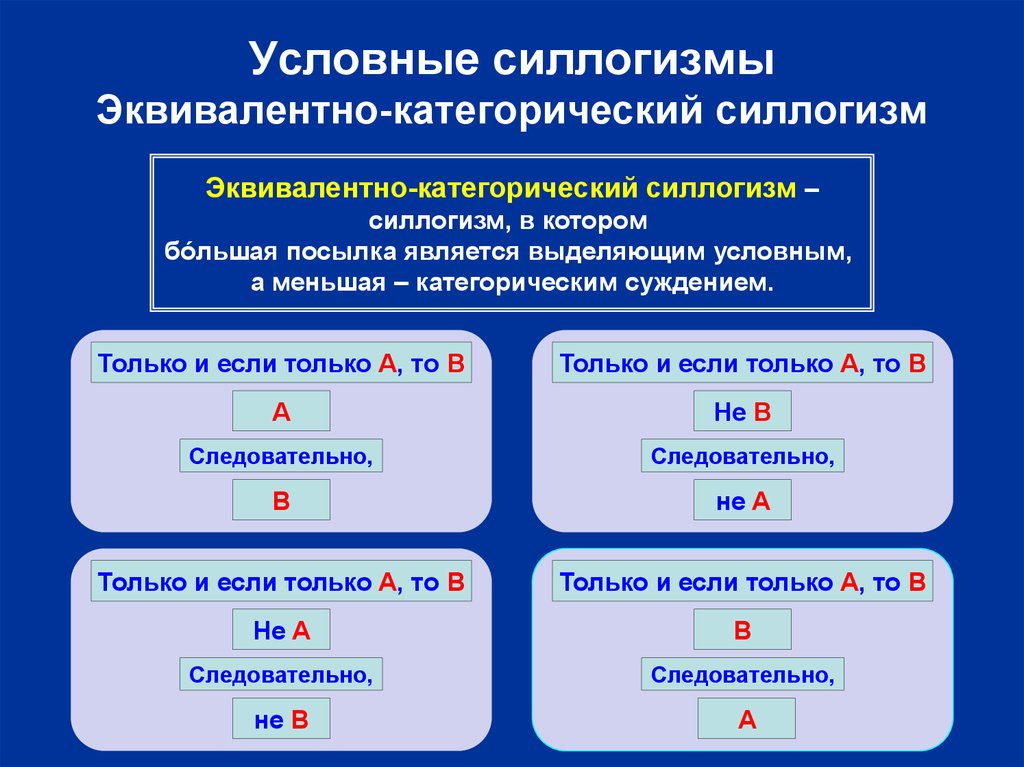
8. Условные силлогизмы Эквивалентно-категорический силлогизм
Эквивалентно-категорический силлогизм –силлогизм, в котором
бóльшая посылка является выделяющим условным,
а меньшая – категорическим суждением.
Только и если только A, то B
Только и если только A, то B
A
Не B
Следовательно,
Следовательно,
B
не A
Только и если только A, то B
Только и если только A, то B
Не A
B
Следовательно,
Следовательно,
не B
A
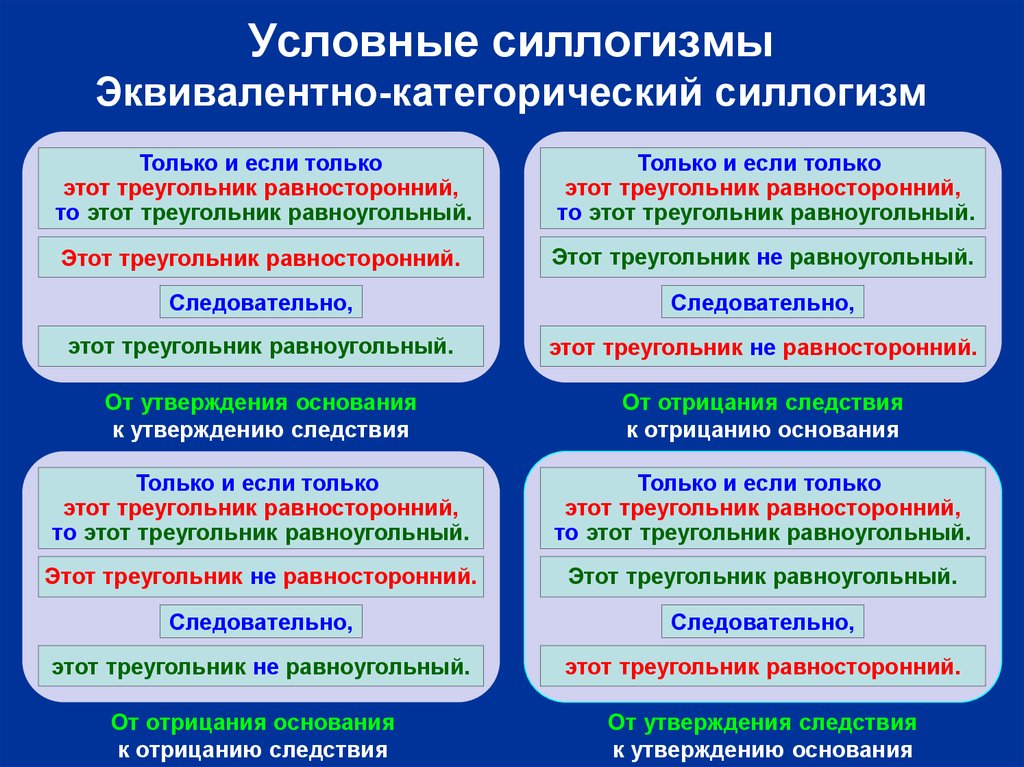
9. Условные силлогизмы Эквивалентно-категорический силлогизм
Только и если толькоэтот треугольник равносторонний,
то этот треугольник равноугольный.
Только и если только
этот треугольник равносторонний,
то этот треугольник равноугольный.
Этот треугольник равносторонний.
Этот треугольник не равноугольный.
Следовательно,
Следовательно,
этот треугольник равноугольный.
этот треугольник не равносторонний.
От утверждения основания
к утверждению следствия
От отрицания следствия
к отрицанию основания
Только и если только
этот треугольник равносторонний,
то этот треугольник равноугольный.
Только и если только
этот треугольник равносторонний,
то этот треугольник равноугольный.
Этот треугольник не равносторонний.
Этот треугольник равноугольный.
Следовательно,
Следовательно,
этот треугольник не равноугольный.
этот треугольник равносторонний.
От отрицания основания
к отрицанию следствия
От утверждения следствия
к утверждению основания
10. Условные силлогизмы Эквивалентно-категорический силлогизм
Только и если толькочисло делится на 6,
то оно делится и на 2, и на 3.
Только и если только
число делится на 6,
то оно делится и на 2, и на 3.
Это число делится на 6.
Это число не делится и на 2, и на 3.
Следовательно,
Следовательно,
оно делится и на 2, и на 3.
оно не делится на 6.
От утверждения основания
к утверждению следствия
От отрицания следствия
к отрицанию основания
Только и если только
число делится на 6,
то оно делится и на 2, и на 3.
Только и если только
число делится на 6,
то оно делится и на 2, и на 3.
Это число не делится на 6.
Это число делится и на 2, и на 3.
Следовательно,
Следовательно,
оно не делится и на 2, и на 3.
оно делится на 6.
От отрицания основания
к отрицанию следствия
От утверждения следствия
к утверждению основания
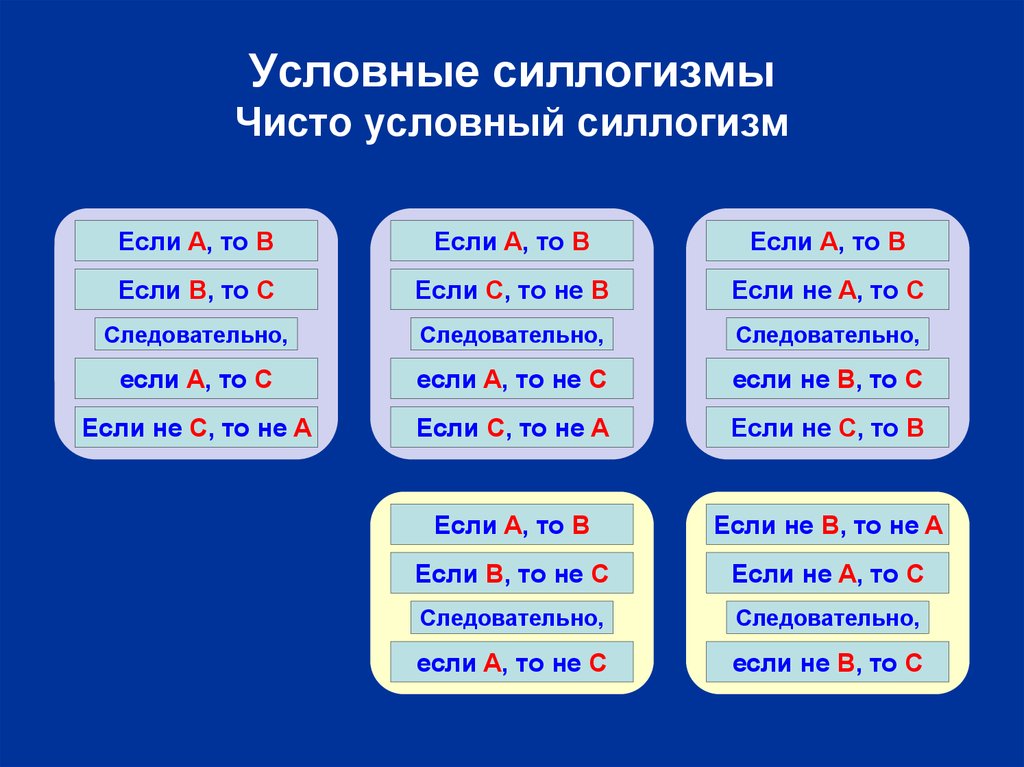
11. Условные силлогизмы Чисто условный силлогизм
Если A, то BЕсли A, то B
Если A, то B
Если B, то C
Если С, то не B
Если не A, то C
Следовательно,
Следовательно,
Следовательно,
если A, то C
если A, то не C
если не B, то C
Если не C, то не A
Если С, то не A
Если не С, то B
Если A, то B
Если не B, то не A
Если B, то не C
Если не A, то C
Следовательно,
Следовательно,
если A, то не C
если не B, то C
12. Условные силлогизмы Чисто условный силлогизм
Если A, то BЕсли лодку перегрузить, то она перевернётся.
Если B, то C
Если лодка перевернётся, то груз потонет.
Следовательно,
Следовательно,
если A, то C
если лодку перегрузить, то груз потонет.
Если не C, то не A
Если груз не потонул, значит лодку не перегрузили.
13. Условные силлогизмы Чисто условный силлогизм
Если A, то BЕсли число делится на 8, то оно делится на 4.
Если B, то C
Если число делится на 4, то оно делится на 2.
Следовательно,
Следовательно,
если A, то C
если число делится на 8, то оно делится на 2.
Если не C, то не A
Если число не делится на 2, то оно не делится на 8.
14. Условные силлогизмы Чисто условный силлогизм
Если A, то BКогда (если) приходит весна, морозы прекращаются.
Если С, то не B
Если лежит снег, значит морозы не прекратились.
Следовательно,
Следовательно,
если A, то не C
когда (если) приходит весна, снег тает (не лежит).
Если С, то не A
Пока (если) лежит снег, весна не наступила.
Если A, то B
Когда (если) приходит весна, морозы прекращаются.
Если B, то не C
Если морозы прекращаются, снег тает (не лежит).
Следовательно,
Следовательно,
если A, то не C
когда (если) приходит весна, снег тает (не лежит).
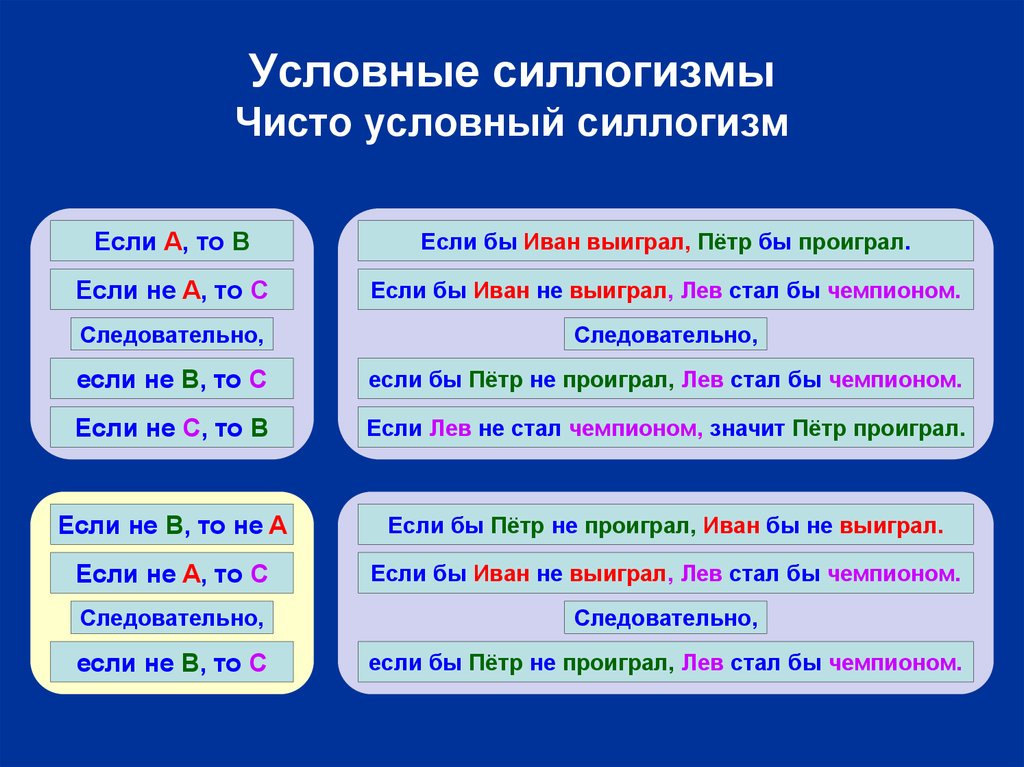
15. Условные силлогизмы Чисто условный силлогизм
Если A, то BЕсли бы Иван выиграл, Пётр бы проиграл.
Если не A, то C
Если бы Иван не выиграл, Лев стал бы чемпионом.
Следовательно,
Следовательно,
если не B, то C
если бы Пётр не проиграл, Лев стал бы чемпионом.
Если не С, то B
Если Лев не стал чемпионом, значит Пётр проиграл.
Если не B, то не A
Если бы Пётр не проиграл, Иван бы не выиграл.
Если не A, то C
Если бы Иван не выиграл, Лев стал бы чемпионом.
Следовательно,
Следовательно,
если не B, то C
если бы Пётр не проиграл, Лев стал бы чемпионом.
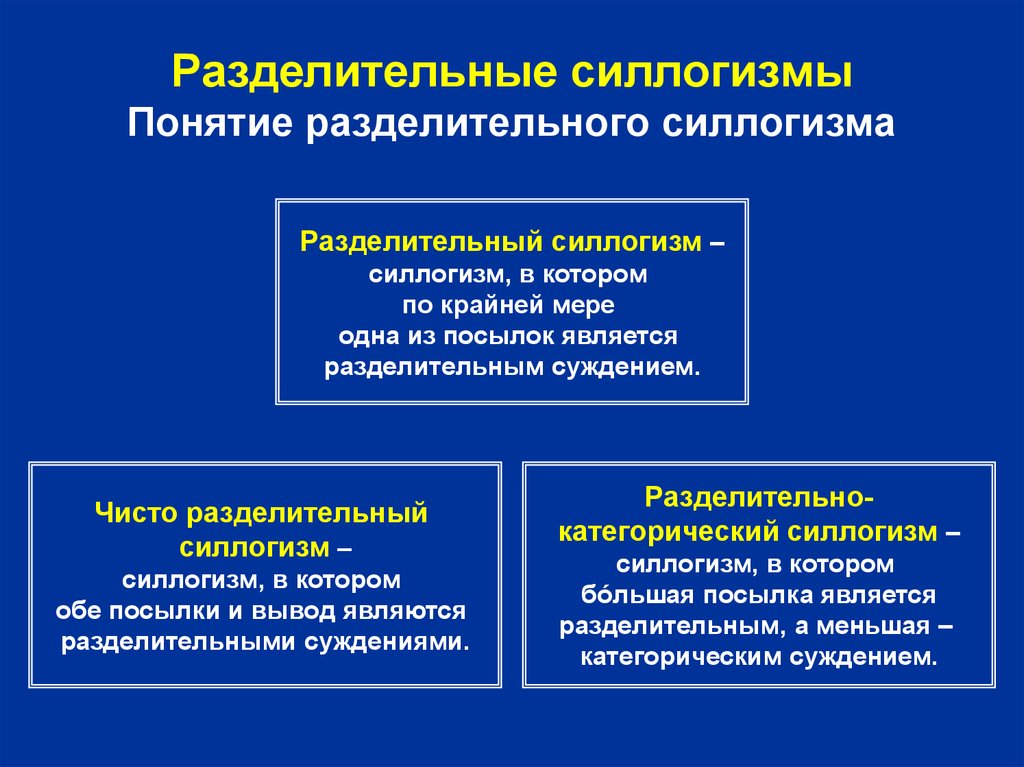
16. Разделительные силлогизмы Понятие разделительного силлогизма
Разделительный силлогизм –силлогизм, в котором
по крайней мере
одна из посылок является
разделительным суждением.
Чисто разделительный
силлогизм –
силлогизм, в котором
обе посылки и вывод являются
разделительными суждениями.
Разделительнокатегорический силлогизм –
силлогизм, в котором
бóльшая посылка является
разделительным, а меньшая –
категорическим суждением.
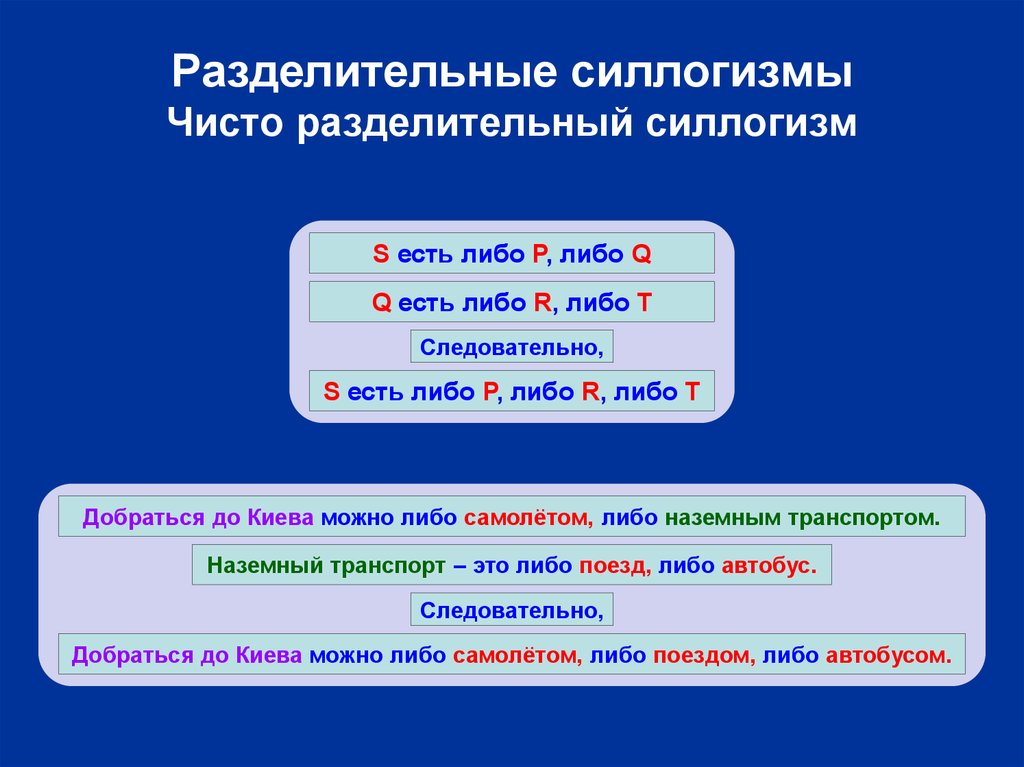
17. Разделительные силлогизмы Чисто разделительный силлогизм
S есть либо P, либо QQ есть либо R, либо T
Следовательно,
S есть либо P, либо R, либо T
Добраться до Киева можно либо самолётом, либо наземным транспортом.
Наземный транспорт – это либо поезд, либо автобус.
Следовательно,
Добраться до Киева можно либо самолётом, либо поездом, либо автобусом.
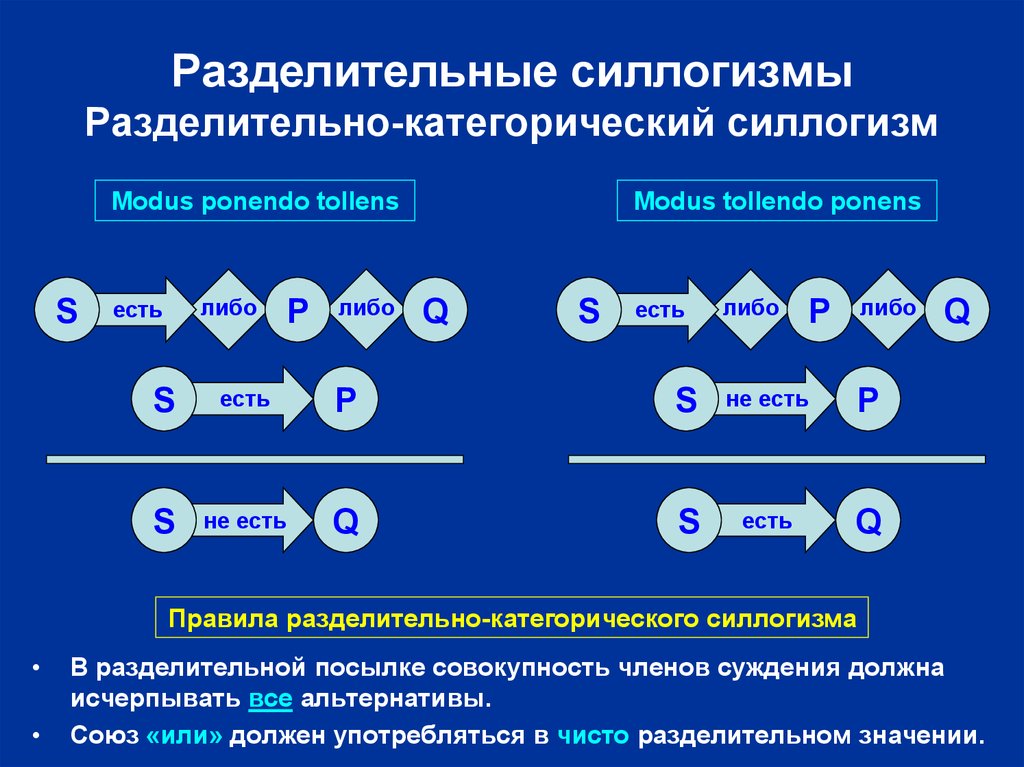
18. Разделительные силлогизмы Разделительно-категорический силлогизм
Modus ponendo tollensS
либо
есть
P
либо
Modus tollendo ponens
Q
S
есть
либо
либо
P
S
есть
P
S
не есть
P
S
не есть
Q
S
есть
Q
Q
Правила разделительно-категорического силлогизма
В разделительной посылке совокупность членов суждения должна
исчерпывать все альтернативы.
Союз «или» должен употребляться в чисто разделительном значении.
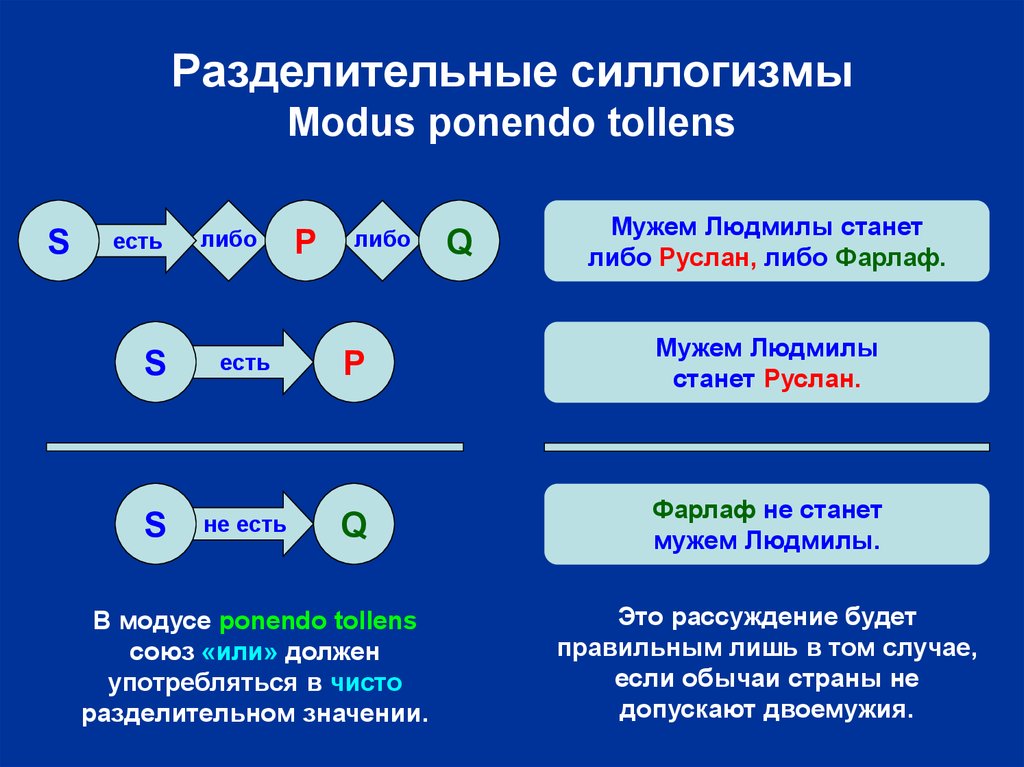
19. Разделительные силлогизмы Modus ponendo tollens
Sесть
либо
P
либо
Q
Мужем Людмилы станет
либо Руслан, либо Фарлаф.
S
есть
P
Мужем Людмилы
станет Руслан.
S
не есть
Q
Фарлаф не станет
мужем Людмилы.
В модусе ponendo tollens
союз «или» должен
употребляться в чисто
разделительном значении.
Это рассуждение будет
правильным лишь в том случае,
если обычаи страны не
допускают двоемужия.
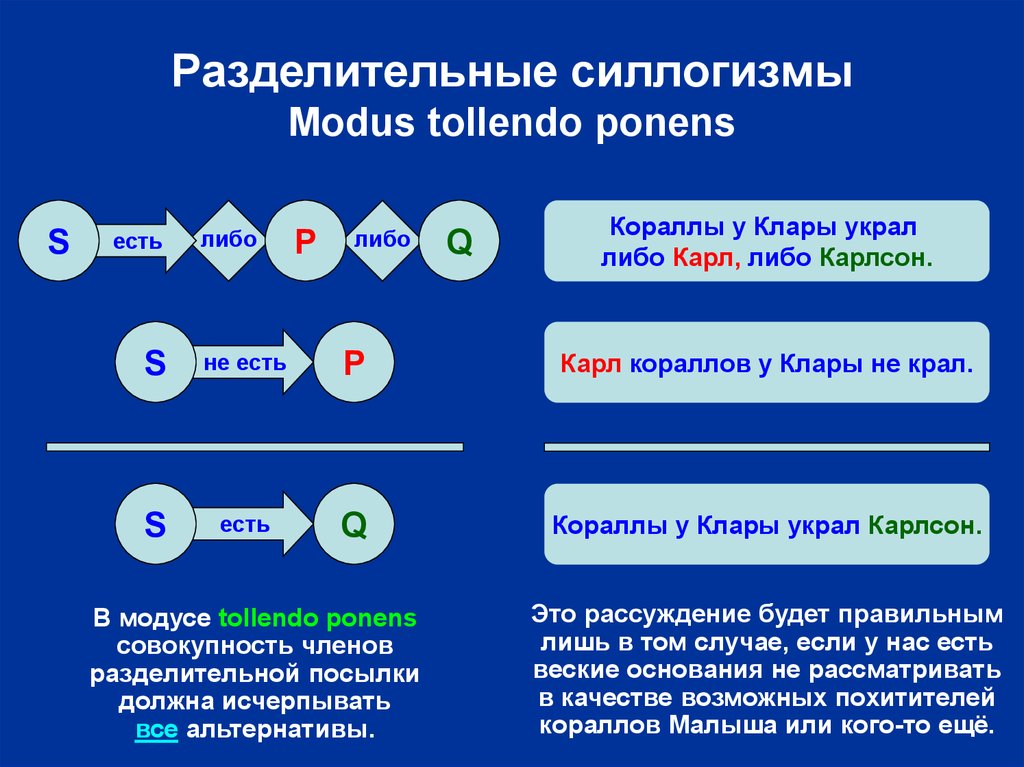
20. Разделительные силлогизмы Modus tollendo ponens
Sесть
либо
P
либо
Q
Кораллы у Клары украл
либо Карл, либо Карлсон.
S
не есть
P
Карл кораллов у Клары не крал.
S
есть
Q
Кораллы у Клары украл Карлсон.
В модусе tollendo ponens
совокупность членов
разделительной посылки
должна исчерпывать
все альтернативы.
Это рассуждение будет правильным
лишь в том случае, если у нас есть
веские основания не рассматривать
в качестве возможных похитителей
кораллов Малыша или кого-то ещё.
21. Условно-разделительные силлогизмы
Условно-разделительный(лемматический) силлогизм –
силлогизм, в котором первые посылки
являются условными, а последняя –
разделительным суждением.
Правила условно-разделительного силлогизма
В условно-разделительном силлогизме можно умозаключать от
утверждения основания к утверждению следствия или от отрицания
следствия к отрицанию основания, но нельзя умозаключать от
утверждения следствия к утверждению основания или от отрицания
основания к отрицанию следствия.
В разделительном суждении совокупность членов суждения должна
исчерпывать все альтернативы.
В разделительном суждении союз «или» должен употребляться в
чисто разделительном значении.
22.
Условно-разделительные силлогизмыВ зависимости
от числа
условных посылок
В зависимости от
В зависимости
характера умозаключения
от тождественности
(от утверждения основания
или различия
к утверждению следствия
оснований (или следствий)
или от отрицания следствия
условных посылок
к отрицанию основания)
Дилеммы
Конструктивные
Простые
Трилеммы
Деструктивные
Тетралеммы
Сложные
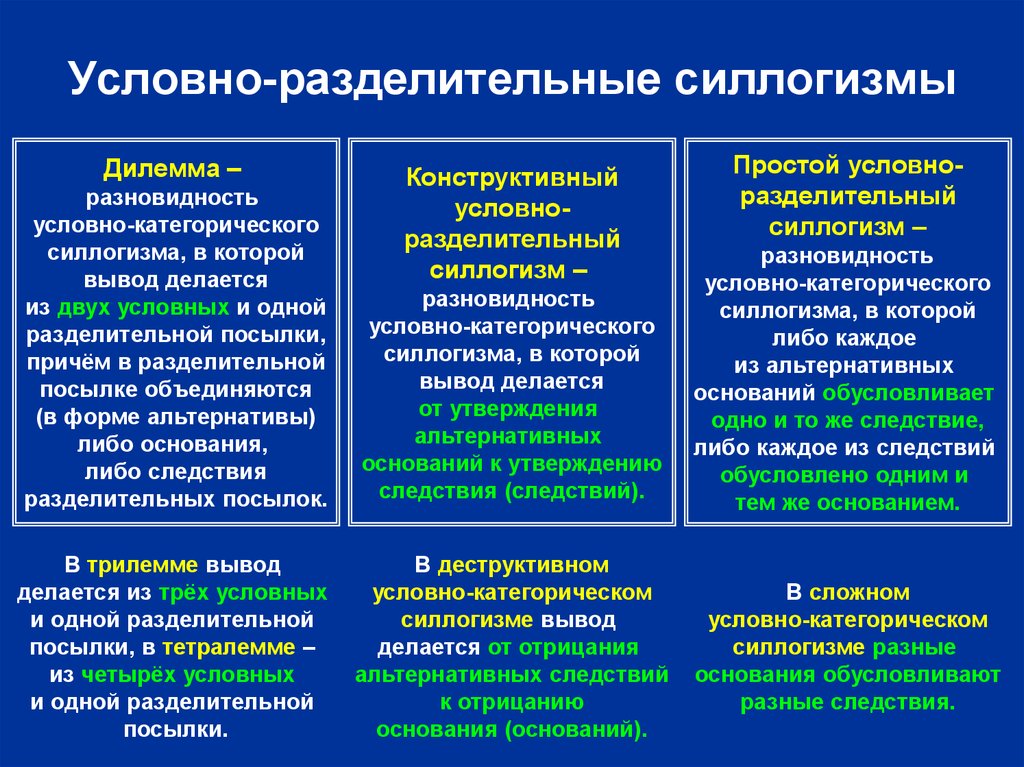
23. Условно-разделительные силлогизмы
Дилемма –Конструктивный
условноразделительный
силлогизм –
разновидность
условно-категорического
силлогизма, в которой
вывод делается
из двух условных и одной
разделительной посылки,
причём в разделительной
посылке объединяются
(в форме альтернативы)
либо основания,
либо следствия
разделительных посылок.
разновидность
условно-категорического
силлогизма, в которой
вывод делается
от утверждения
альтернативных
оснований к утверждению
следствия (следствий).
В трилемме вывод
делается из трёх условных
и одной разделительной
посылки, в тетралемме –
из четырёх условных
и одной разделительной
посылки.
В деструктивном
условно-категорическом
силлогизме вывод
делается от отрицания
альтернативных следствий
к отрицанию
основания (оснований).
Простой условноразделительный
силлогизм –
разновидность
условно-категорического
силлогизма, в которой
либо каждое
из альтернативных
оснований обусловливает
одно и то же следствие,
либо каждое из следствий
обусловлено одним и
тем же основанием.
В сложном
условно-категорическом
силлогизме разные
основания обусловливают
разные следствия.
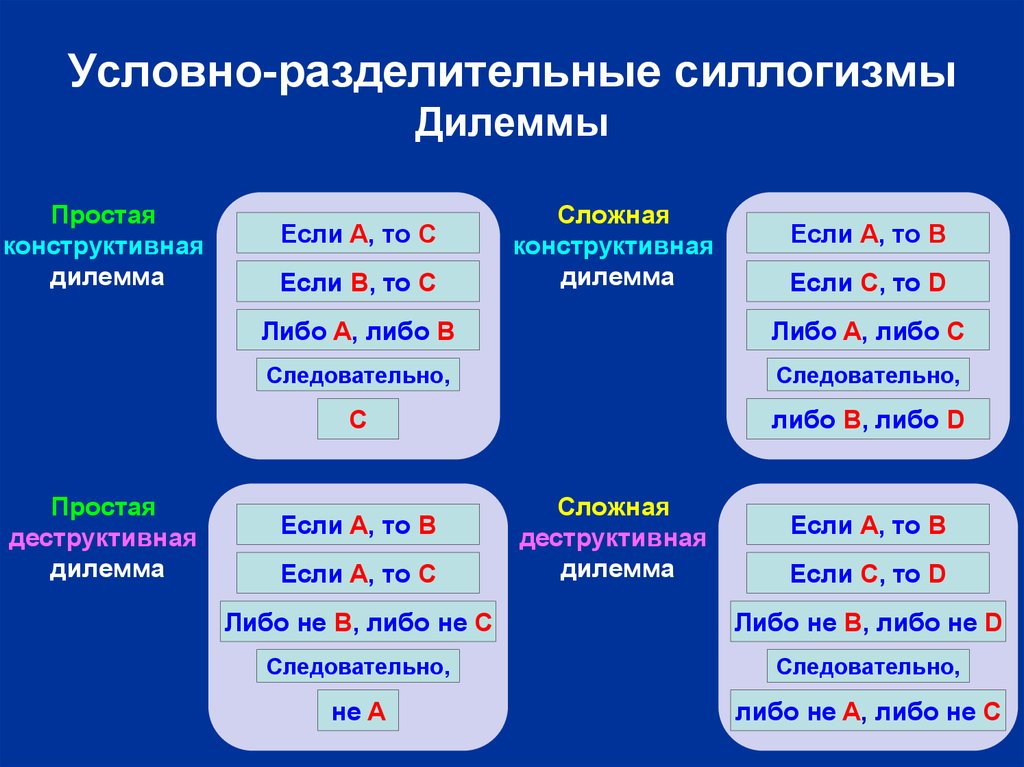
24. Условно-разделительные силлогизмы Дилеммы
Простаяконструктивная
дилемма
Простая
деструктивная
дилемма
Если A, то C
Если B, то C
Сложная
конструктивная
дилемма
Если A, то B
Если C, то D
Либо A, либо B
Либо A, либо C
Следовательно,
Следовательно,
С
либо B, либо D
Если A, то B
Если A, то C
Сложная
деструктивная
дилемма
Если A, то B
Если C, то D
Либо не B, либо не C
Либо не B, либо не D
Следовательно,
Следовательно,
не A
либо не A, либо не C
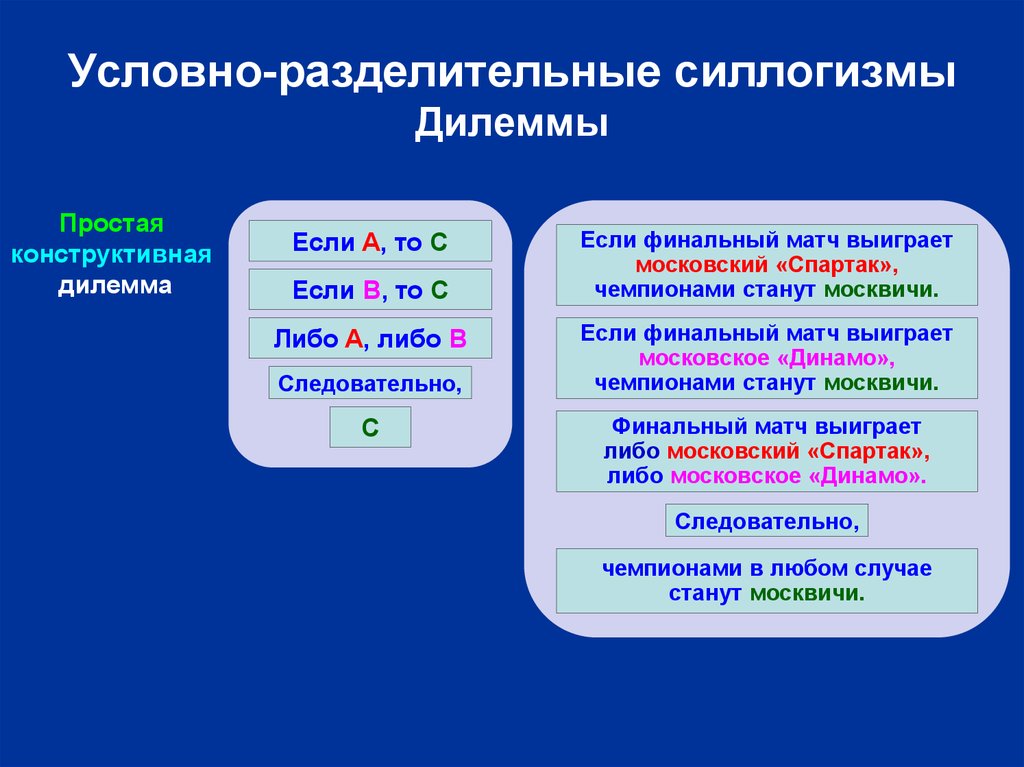
25. Условно-разделительные силлогизмы Дилеммы
Простаяконструктивная
дилемма
Если A, то C
Если B, то C
Либо A, либо B
Следовательно,
С
Если финальный матч выиграет
московский «Спартак»,
чемпионами станут москвичи.
Если финальный матч выиграет
московское «Динамо»,
чемпионами станут москвичи.
Финальный матч выиграет
либо московский «Спартак»,
либо московское «Динамо».
Следовательно,
чемпионами в любом случае
станут москвичи.
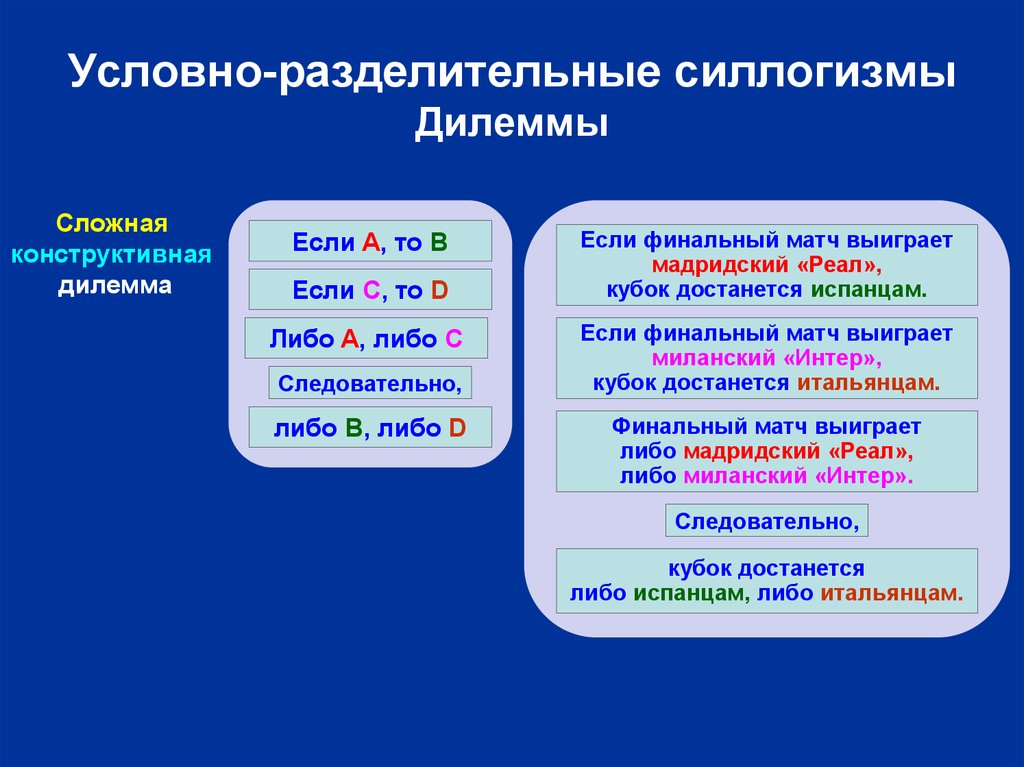
26. Условно-разделительные силлогизмы Дилеммы
Сложнаяконструктивная
дилемма
Если A, то B
Если C, то D
Либо A, либо C
Следовательно,
либо B, либо D
Если финальный матч выиграет
мадридский «Реал»,
кубок достанется испанцам.
Если финальный матч выиграет
миланский «Интер»,
кубок достанется итальянцам.
Финальный матч выиграет
либо мадридский «Реал»,
либо миланский «Интер».
Следовательно,
кубок достанется
либо испанцам, либо итальянцам.
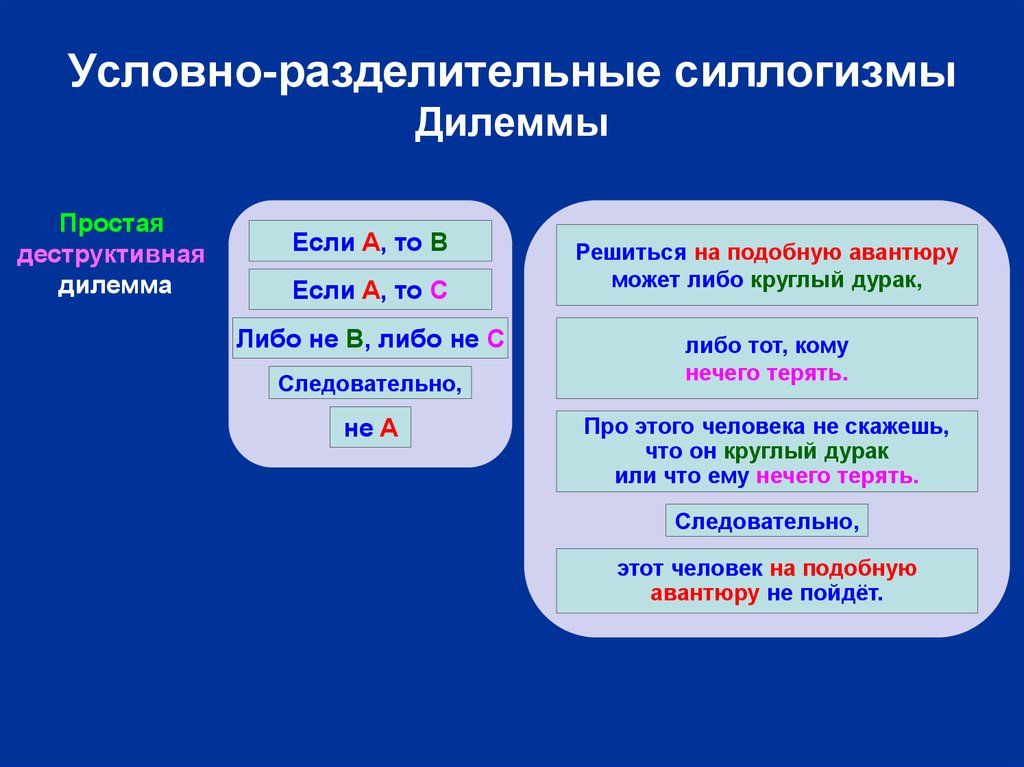
27. Условно-разделительные силлогизмы Дилеммы
Простаядеструктивная
дилемма
Если A, то B
Если A, то C
Либо не B, либо не C
Следовательно,
не A
Решиться на подобную авантюру
может либо круглый дурак,
либо тот, кому
нечего терять.
Про этого человека не скажешь,
что он круглый дурак
или что ему нечего терять.
Следовательно,
этот человек на подобную
авантюру не пойдёт.
28. Условно-разделительные силлогизмы Дилеммы
Сложнаядеструктивная
дилемма
Если A, то B
Если C, то D
Либо не B, либо не D
Следовательно,
либо не A, либо не C
Если бы
«Спартак» выиграл у «Динамо»,
«Спартак» вышел бы в финал.
Если бы
«Торпедо» выиграло у «Зенита»,
«Торпедо» вышло бы в финал.
Но «Спартак» и «Торпедо»
так и не встретились в финале.
Следовательно,
либо «Спартак» не выиграл у
«Динамо», либо «Торпедо» не
выиграло у «Зенита».













 philosophy
philosophy








