Similar presentations:
Формирование языка античной науки. Логика Аристотеля. (Тема 4)
1. История и философия науки
Тема 4Формирование языка античной науки
Логика Аристотеля
2. Логика Аристотеля Орудие и язык теоретического мышления
Принципы логики (законы мышления)• Закон [запрета] рротиворечия
• Закон исключённого третьего
Формы мышления
• Понятие
• Суждение
• Умозаключение
Непосредственные умозаключения
Простой категорический силлогизм
o Правила простого категорического силлогизма
o Фигуры простого категорического силлогизма
o Модусы простого категорического силлогизма
Условные и разделительные силлогизмы
Модальная логика
3. Логика Аристотеля Орудие и язык теоретического мышления
Основные сочинения• Органон
Категории
Об истолковании
Первая аналитика
Вторая аналитика
Топика
О софистических опровержениях
Аристотель
(384 – 322 до н. э.)
4. Логика Аристотеля Орудие и язык теоретического мышления
Логика(греч. λογική, наука о мышлении,
от λόγος, слово, понятие) –
наука о законах, формах и приёмах
мыслительной познавательной деятельности.
Термин «логика» ввели, по-видимому, стоики.
Сам Аристотель своё логическое учение
называл «аналитикой»).
5. Принципы логики (законы мышления)
Законы логикиЗакон
тождества
Закон [запрета]
противоречия
Логические выводы
Не могут быть
надёжны лишь при условии, одновременно истинными
что все понятия (термины)
два противоречащих
в пределах рассуждения
высказывания об
имеют один и тот же смысл. одном и том же предмете.
Закон исключённого
третьего
Не могут быть
одновременно ложными
два противоречащих
высказывания об
одном и том же предмете.
6. Принципы логики Принцип тождества
Несомненно, что те,кто намерен участвовать в беседе,
должны сколько-нибудь
понимать друг друга.
Если это не достигается, то
как можно беседовать друг с другом?
Поэтому каждое слово должно быть
понятно и обозначать что-то,
и именно не многое, а только одно;
если же оно имеет несколько значений,
то надо разъяснять,
в каком из них оно употребляется.
Аристотель.
«Метафизика».
7. Принципы логики Принцип запрета противоречия
А самое достоверное из всех начал –то, относительно которого невозможно ошибиться,
ибо такое начало должно быть наиболее очевидным
(ведь все обманываются в том, что не очевидно)
и свободным от всякое предположительности.
Действительно, начало, которое необходимо знать
всякому постигающему что-либо из существующего,
не есть предположение; а то, что необходимо
уже знать тому, кто познаёт хоть что-нибудь,
он должен иметь, уже приступая к рассмотрению.
Таким образом, ясно, что именно такое начало есть
наиболее достоверное из всех; а что это за начало,
укажем теперь. А именно: невозможно, чтобы одно и
то же в одно и то же время было и не было присуще
одному и тому же в одном и том же отношении (и всё
другое, что мы могли бы ещё уточнить, пусть будет
уточнено во избежание словесных затруднений) –
это, конечно, самое достоверное из всех начал,
к нему подходит данное выше определение.
Аристотель.
«Метафизика».
8. Принципы логики Принцип запрета противоречия
А самое достоверное из всех начал –
то, относительно которого невозможно ошибиться,
ибо такое начало должно быть наиболее очевидным
(ведь все обманываются в том, что не очевидно)
и свободным от всякое предположительности.
Действительно, начало, которое необходимо знать всякому
постигающему что-либо из существующего, не есть предположение;
а то, что необходимо уже знать тому, кто познаёт хоть что-нибудь,
он должен иметь, уже приступая к рассмотрению.
Таким образом, ясно, что именно такое начало есть наиболее
достоверное из всех; а что это за начало, укажем теперь. А именно:
невозможно, чтобы одно и то же
в одно и то же время
было и не было присуще
одному и тому же
в одном и том же отношении
(и всё другое, что мы могли бы ещё уточнить, пусть будет уточнено
во избежание словесных затруднений) –
это, конечно, самое достоверное из всех начал, к нему подходит
данное выше определение.
9. Принципы логики Принцип запрета противоречия
Невозможно, чтобыодно и то же
в одно и то же время
было и не было присуще
одному и тому же
в одном и том же отношении.
Аристотель.
«Метафизика».
10. Принципы логики Принцип исключённого третьего
Равным образомне может быть ничего
промежуточного между
двумя членами противоречия,
а относительно чего-то одного
необходимо что бы то ни было одно
либо утверждать, либо отрицать.
Аристотель.
«Метафизика».
11. Принципы логики Принцип исключённого третьего
Если же ложноеесть не что иное, как
отрицание истины, то
всё не может быть ложным,
ибо один из двух членов
противоречия
должен быть истинным.
Аристотель.
«Метафизика».
12. Формы мышления
Формы мышленияПонятие
Лошадь
Человек
Животное
Смертный
Суждение
Лошадь
Человек
животное
смертен
Умозаключение
Все
животные
смертны
Лошади
животные
Все
лошади
смертны
13. Формы мышления
Суждение –Понятие –
форма мышления,
отражающая предметы
в их общих, необходимых
и существенных признаках.
форма мысли, в которой
утверждается или отрицается
что-либо относительно
предметов и явлений,
их свойств, связей и отношений.
Умозаключение –
логическое действие, в результате
которого из одного или нескольких
суждений (именуемых посылками)
получается новое суждение
(именуемое выводом), в котором
содержится новое знание.
14.
Понятие как форма мышленияСодержание и объём понятия
В понятии, по Аристотелю, мыслятся общие свойства предметов
какого-то вида или рода.
Понятие применяется, таким образом, к множеству предметов.
На языке логики это множество именуется классом; мощность
множества (число элементов) характеризует объём понятия.
Если с точки зрения объёма, понятие относится к совокупности
предметов (предицируется им), то с точки зрения содержания, его
можно охарактеризовать как совокупность признаков (общих,
необходимых и существенных), предицируемых данному
понятию).
15.
Понятие как форма мышленияСодержание и объём понятия
Содержание понятия –
Объём понятия –
множество признаков,
характеризующих
данное понятие.
множество понятий,
признаком которых
является данное понятие.
Содержание понятия
можно охарактеризовать
как множество понятий,
предицируемых
данному понятию
(как логическому субъекту).
Объём понятия
можно охарактеризовать
как множество понятий,
которым
(как логическим субъектам)
предицируется данное понятие.
Операция предицирования лежит в основе формы мышления,
именуемой суждением.
16.
Понятие как форма мышленияСодержание и объём понятия
В понятии, по Аристотелю, мыслятся общие свойства предметов
какого-то вида или рода.
Понятие применяется, таким образом, к множеству предметов.
На языке логики это множество именуется классом; мощность
множества (число элементов) характеризует объём понятия.
Если с точки зрения объёма, понятие относится к совокупности
предметов (предицируется им), то с точки зрения содержания, его
можно охарактеризовать как совокупность признаков (общих,
необходимых и существенных), предицируемых данному
понятию).
Чем больше признаков мыслится в понятии, тем меньше его объём,
т. е. тем меньше элементов в классе, обозначаемом данным понятием,
и наоборот.
Отвлекаясь (абстрагируясь) от каких-то признаков, мы получаем
более общее понятие; эта операция называется «обобщением».
Обратная операция, заключающаяся в добавлении признаков к
общему понятию, именуется «ограничением понятия».
Операция предицирования лежит в основе формы мышления,
именуемой суждением.
17.
Понятие как форма мышленияЛогические отношения между понятиями
Логические отношения между понятиями
определяются наличием или отсутствием
общих элементов в их объёмах.
Логические отношения между понятиями следует отличать
от одноимённых логических отношений между суждениями.
Хотя по содержанию (смыслу) эти два понятия, а именно:
логическое отношению между понятиями и одноимённое
логическое отношение между суждениями – в чём-то между
собой сходны, их объёмы общих элементов не имеют, т. е.
сами понятия несовместимы.
18.
Понятие как форма мышленияЛогические отношения между понятиями
Понятия
Совместимые
Несовместимые
Соподчинённые
Равнозначащие
Несоподчинённые
несовместимые
Подчинённые и
подчиняющие
Противоположные
Перекрещивающиеся
Соподчинённые
перекрещивающиеся
Контрадикторные
Контрарные
19.
BAA
BB
Равнозначащие понятия –
понятия, объёмы которых полностью совпадают.
A
Перекрещивающиеся понятия –
понятия, объёмы которых частично совпадают.
A
B
B
A
Несовместимые
понятия
B
Подчинённое и подчиняющее понятия –
понятия, объём одного из которых (подчинённого) целиком
входит в объём другого (подчиняющего), не исчерпывая его.
C
A ~A
A B
A
B C
Противоположные
понятия
Совместимые
понятия
A
Несовместимые понятия –
понятия, объёмы которых не имеют общих элементов.
Соподчинённые понятия – понятия, объёмы которых
составляют разные (несовпадающие или частично
совпадающие) части объёма общего подчиняющего понятия.
Контрадикторные (противоречащие) понятия –
пара несовместимых соподчинённых понятий, совокупный
объём которых исчерпывает объём подчиняющего понятия.
Контрарные (противные) понятия –
пара несовместимых соподчинённых понятий, совокупный
объём которых не исчерпывает объём подчиняющего понятия.
20.
AB
Несовместимые понятия:
политическая партия
число, кратное трём
AB
Равнозначащие понятия:
равносторонний треугольник
равноугольный треугольник
A
Перекрещивающиеся понятия:
француз
шахматист
A
B
B
A
B
Подчинённое и подчиняющее понятия:
кошка
животное
C
A
B C
Соподчинённые понятия:
спутник Земли
пианист
спутник Марса
скрипач
A ~A
Контрадикторные (противоречащие) понятия:
красное
некрасное
A B
Контрарные (противные) понятия:
красное
зелёное
21.
Суждение как форма мышленияСуждение – это такая форма мысли, в которой утверждается
или отрицается что-либо относительно предметов и явлений,
их свойств, связей и отношений.
22.
Суждение как форма мышленияПосылка есть речь,
утверждающая или отрицающая
что-то относительно чего-то.
Аристотель.
«Первая аналитика».
23.
Суждение как форма мышленияСуждение – это такая форма мысли, в которой утверждается
или отрицается что-либо относительно предметов и явлений,
их свойств, связей и отношений.
Элементарное суждение можно представить в виде формулы:
A
(не) присуще
B
S
(не) еcть
P
субъект
Субъект суждения –
то, о чём высказывается
суждение
(та часть суждения
которая обозначает
предмет мысли).
связка
предикат
Логическая связка –
элемент суждения,
который соединяет
субъект и предикат.
Предикат суждения –
то, что высказывается
(утверждается
или отрицается)
о предмете
(субъекте суждения).
24.
Суждение как форма мышленияСуждение – это такая форма мысли, в которой утверждается
или отрицается что-либо относительно предметов и явлений,
их свойств, связей и отношений.
Элементарное суждение можно представить в виде формулы:
A
(не) присуще
B
Суждение выражает (с точки зрения соответствия его содержания
действительности) либо истину, либо ложь.
25.
Суждение как форма мышленияИмена же и глаголы сами по себе
подобны мысли без связывания
или разъединения,
например «человек» или «белое»;
когда ничего не прибавляется,
нет ни ложного, ни истинного,
хотя они и обозначают что-то:
ведь и «козлоолень» что-то обозначает,
но ещё не истинно и не ложно,
когда не прибавлен [глагол]
«быть» или «не быть» –
либо вообще,
либо касательно времени.
Аристотель.
«Об истолковании».
26. Суждение как форма мышления Виды суждений
Суждение – это такая форма мысли, в которой утверждается
или отрицается что-либо относительно предметов и явлений,
их свойств, связей и отношений.
Элементарное суждение можно представить в виде формулы:
A
(не) присуще
B
Суждение выражает (с точки зрения соответствия его содержания
действительности) либо истину, либо ложь.
С точки зрения формы, Аристотель делит суждения на:
утвердительные и отрицательные (классификация по качеству);
общие, частные и неопределённые (классификация по
количеству);
категорические (безусловные), условные и разделительные
(классификация по отношению);
аподиктические (необходимости), ассерторические
(действительности) и проблематические (возможности)
(классификация по модальности).
27. Суждение как форма мышления Виды суждений
Всякая же посылка есть посылкаили о том, что присуще,
или о том, что необходимо присуще,
или о том, что возможно присуще;
и из них в соответствии с каждым
способом сказывания
одни утвердительные,
другие отрицательные;
и далее,
из утвердительных и отрицательных
одни – общие,
другие – частные,
третьи – неопределенные.
Аристотель.
«Первая аналитика».
28. Суждение как форма мышления Виды суждений
Общей я называю [посылку]о присущем всем
или не присущем ни одному,
частной – о присущем
или не присущем некоторым
или присущем не всем,
неопределённой – о присущем или
не присущем без указания того,
общая ли она или частная,
как, например, <…>
удовольствие не есть благо.
Аристотель.
«Первая аналитика».
29. Логические отношения между понятиями и основные типы категорических суждений
PS
S
S
S
P
P
SS
PP
Общеутвердительное суждение
Все S суть P
P
Общеотрицательное суждение
Все S не суть P
S
SP
P
S
P
(Всякое S есть P)
(Ни одно S не есть P)
Частноутвердительное суждение
Некоторые S суть P
(Существуют S, которые суть P)
Частноотрицательное суждение
Некоторые S не суть P
(Существуют S, которые не суть P)
30. Логические отношения между понятиями и основные типы категорических суждений
PS
S
S
S
P
P
SS
PP
P
S
Общеутвердительное суждение
S – подчинённое, P – подчиняющее понятие
S и P – равнозначащие понятия
Общеотрицательное суждение
S и P – несовместимые понятия
Частноутвердительное суждение
SP
P
S и P – перекрещивающиеся понятия
S – подчиняющее, P – подчинённое понятие
S
Частноотрицательное суждение
P
S и P – перекрещивающиеся понятия
S – подчиняющее, P – подчинённое понятие
31. Логические отношения между суждениями
Логические отношения между суждениямиопределяются сочетанием их истинности и ложности.
Логические отношения между суждениями следует отличать
от одноимённых логических отношений между понятиями.
Хотя по содержанию (смыслу) эти два понятия, а именно:
логическое отношению между суждениями и одноимённое
логическое отношение между понятиями – в чём-то между
собой сходны, их объёмы общих элементов не имеют, т. е.
сами понятия несовместимы.
32. Логические отношения между суждениями
Логические отношения между суждениямиопределяются сочетанием их истинности и ложности.
Отдельное суждение является либо истинным, либо ложным.
Суждения не находятся ни в каком логическом отношении, если
истинность или ложность одного никак не связана с истинностью
или ложностью другого.
Если же истинность или ложность одного связана с истинностью
или ложностью другого, возможны пять вариантов сочетания их
истинности и ложности, а именно:
o они могут быть либо оба истинными, либо оба ложными;
o они не могут быть оба ни истинными, ни ложными;
o они не могут быть оба истинными, но могут быть оба ложными;
o они могут быть оба истинными, но не могут быть оба ложными;
o наконец, истинность одного может означать истинность другого
(соответственно, ложность этого другого будет означать и
ложность первого), но ложность первого не обязательно будет
означать ложность другого (соответственно, истинность этого
другого не обязательно будет означать истинность первого).
33. Логические отношения между суждениями
Отношениеравнозначности –
Отношение
контрадикторности –
логическое отношение
между двумя суждениями,
заключающееся в том, что
данные суждения
могут быть или оба истинными,
или оба ложными.
логическое отношение
между двумя суждениями,
заключающееся в том, что
данные суждения
не могут быть ни оба
истинными, ни оба ложными.
Традиционная логика отношение
равнозначности специально
не рассматривала, но без его
выделения обзор логических
отношений между суждениями
и видов непосредственных
умозаключений будет неполным.
34. Логические отношения между суждениями
Отношениеконтрарности –
Отношение
субконтрарности –
логическое отношение
между двумя суждениями,
заключающееся в том, что
данные суждения
не могут быть оба истинными,
но могут быть оба ложными.
логическое отношение
между двумя суждениями,
заключающееся в том, что
данные суждения
не могут быть оба ложными,
но могут быть оба истинными.
35. Логические отношения между суждениями
Отношениеподчинения –
логическое отношение
между двумя суждениями, при котором
из истинности одного
(именуемого подчиняющим) суждения
следует истинность другого
(именуемого подчинённым) суждения
(соответственно, из ложности подчинённого
следует ложность подчиняющего),
но из ложности подчиняющего суждения
не следуют ни ложность, ни истинность
подчинённого (соответственно,
из истинности подчинённого не следуют
ни истинность, но ложность подчиняющего).
36. Логические отношения между суждениями Отношение равнозначности
Слонбольше
Моськи
Равнозначные
суждения
могут быть
или оба
истинными,
или оба
ложными.
Таяние
снегов –
причина
паводка
Филипп –
отец
Александра
равнозначность
Моська
меньше
слона
равнозначность
Паводок –
следствие
таяния
снегов
равнозначность
Александр –
сын
Филиппа
Если одно
равнозначное
суждение
истинно,
то и другое
истинно, если
одно ложно, то
и другое ложно.
37. Логические отношения между суждениями Логический квадрат
контрарностьподчинение
I
E
субконтрарность
O
Общеотрицательное
суждение
NEGO
Частноутвердительное
суждение
A
подчинение
AFFIRMO
Общеутвердительное
суждение
Частноотрицательное
суждение
Логический квадрат иллюстрирует логические отношения между суждениями
«с одинаковой материей» (т. е. с одинаковыми субъектами и одинаковыми
предикатами), различающимися лишь по качеству и/или количеству).
38. Логические отношения между суждениями Отношение контрадикторности
Общеутвердительноесуждение
Контрадикторные
суждения
не могут быть
ни оба истинными,
ни оба ложными,
т. е. одно из них
обязательно
истинно, а другое
обязательно
ложно.
Частноутвердительное
суждение
Все
яблоки
суть
красные
Ни одно
яблоко
не есть
красное
Общеотрицательное
суждение
Если одно из
контрадикторных
суждений истинно,
другое ложно,
и наоборот:
если одно ложно,
другое истинно.
Некоторые
яблоки
суть
красные
Некоторые
яблоки
не суть
красные
Частноотрицательное
суждение
39. Логические отношения между суждениями Отношение контрарности
Общеутвердительноесуждение
Все
яблоки
суть
красные
контрарность
Ни одно
яблоко
не есть
красное
Если одно
из контрарных
суждений истинно,
другое ложно, но
если одно ложно,
другое может быть
как истинным,
так и ложным.
Контрарные
суждения
не могут быть
оба истинными,
но могут быть
оба ложными.
Частноутвердительное
суждение
Общеотрицательное
суждение
Некоторые
яблоки
суть
красные
Некоторые
яблоки
не суть
красные
Частноотрицательное
суждение
40. Логические отношения между суждениями Отношение субконтрарности
Общеутвердительноесуждение
Все
яблоки
суть
красные
Ни одно
яблоко
не есть
красное
Если одно из
субконтрарных
суждений ложно,
другое истинно, но
если одно истинно,
другое может быть
как истинным,
так и ложным.
Субконтрарные
суждения
не могут быть
оба ложными,
но могут быть
оба истинными.
Частноутвердительное
суждение
Общеотрицательное
суждение
Некоторые
Некоторые
яблоки
яблоки
субконтрарность
суть
не суть
красные
красные
Частноотрицательное
суждение
41. Логические отношения между суждениями Отношение подчинения
Общеутвердительноесуждение
Все
яблоки
суть
красные
подчинение
Частноутвердительное
суждение
яблоки
суть
красные
Если
подчинённое
суждение ложно,
подчиняющее
также ложно, но
если подчинённое
суждение истинно,
подчиняющее
может быть
как истинным,
так и ложным.
Некоторые
подчинение
Если
подчиняющее
суждение истинно,
подчинённое
также истинно, но
если подчиняющее
суждение ложно,
подчинённое
может быть
как истинным,
так и ложным.
Некоторые
Ни одно
яблоко
не есть
красное
Общеотрицательное
суждение
яблоки
не суть
красные
Частноотрицательное
суждение
42. Умозаключение как форма мышления
Умозаключение – это такое логическое действие, в результате
которого из одного или нескольких – определённым образом
связанных – суждений (именуемых посылками) получается новое
суждение (вывод), в котором содержится новое знание.
Умозаключения подразделяются на индуктивные (от частного к
общему) и дедуктивные (от общего к частному). Поскольку
необходимое связано с общим, логически безупречные
(необходимые) выводы можно получить лишь путём дедукции,
индуктивные выводы лишь предположительны.
43. Умозаключение как форма мышления
ДедукцияИндукция
(лат., deductio, выведение) –
процесс логического вывода,
т. е. перехода по тем или иным
правилам логики, от некоторых
данных положений (посылок)
к их следствиям (заключениям).
(лат., inductio, наведение) –
форма мышления, посредством
которой мысль наводится на
общее правило, общее
положение, присущее всем
предметам какого-либо класса.
Дедуктивное умозаключение
1) представляет собой переход
от общего к частному и
2) даёт логически безупречный
необходимый вывод.
Индуктивное умозаключение
1) представляет собой переход
от частного к общему и
2) даёт (исключая
тривиальные случаи) лишь
вероятностный вывод.
44. Умозаключение как форма мышления
Умозаключение – это такое логическое действие, в результате
которого из одного или нескольких – определённым образом
связанных – суждений (именуемых посылками) получается новое
суждение (вывод), в котором содержится новое знание.
Умозаключения подразделяются на индуктивные (от частного к
общему) и дедуктивные (от общего к частному). Поскольку
необходимое связано с общим, логически безупречные
(необходимые) выводы можно получить лишь путём дедукции,
индуктивные выводы лишь предположительны.
В зависимости от того, выводится заключение из одной или
нескольких посылок, дедуктивные умозаключения
подразделяются на непосредственные и силлогизмы.
o Примером непосредственного умозаключения является
превращение: замена связки на противоположную с
одновременной заменой предиката контрадикторным
понятием.
Цезарь смертен
Цезарь не бессмертен
45. Умозаключение как форма мышления
Умозаключение – это такое логическое действие, в результате
которого из одного или нескольких – определённым образом
связанных – суждений (именуемых посылками) получается новое
суждение (вывод), в котором содержится новое знание.
Умозаключения подразделяются на индуктивные (от частного к
общему) и дедуктивные (от общего к частному). Поскольку
необходимое связано с общим, логически безупречные
(необходимые) выводы можно получить лишь путём дедукции,
индуктивные выводы лишь предположительны.
В зависимости от того, выводится заключение из одной или
нескольких посылок, дедуктивные умозаключения
подразделяются на непосредственные и силлогизмы.
o Другим примером непосредственного умозаключения
является обращение: перестановка субъекта и предиката.
Ни один гусь не лебедь
Ни один лебедь не гусь
Все гуси – птицы
Некоторые птицы – гуси
46. Умозаключение как форма мышления Распределённость терминов
Поскольку дедуктивный вывод есть вывод от общего к частному,
его обоснованность зависит от распределённости терминов.
“Распределённым” называется термин, взятый в суждении во всём
объёме.
47. Умозаключение как форма мышления Распределённость терминов
Распределённый термин –термин, взятый в суждении
в полном объёме.
Соответственно, термин,
взятый в суждении
лишь в части объёма
называется
нераспределённым.
Распределёнными являются
субъекты общих
и предикаты отрицательных
категорических суждений.
Субъекты частных категорических суждений не распределены,
предикаты утвердительных категорических суждений могут быть распределены,
если объём предиката меньше или равен объёму субъекта.
48. Умозаключение как форма мышления Распределённость терминов
Поскольку дедуктивный вывод есть вывод от общего к частному,
его обоснованность зависит от распределённости терминов.
“Распределённым” называется термин, взятый в суждении во всём
объёме.
Субъекты распределены в общих суждениях (утвердительных и
отрицательных) по определению: в общих суждениях что-либо
утверждается (или отрицается) о каждом элементе класса субъекта.
Предикаты распределены в отрицательных суждениях (общих и
частных): отрицая принадлежность предиката субъекту, мы
утверждаем непринадлежность субъекту любого элемента класса
предиката.
Таким образом распределёнными оказываются:
в общеотрицательном суждении (A) – и субъект, и предикат;
в общеутвердительном (E) – только субъект;
в частноотрицательном (O) – только предикат;
в частноутвердительном (I) – ни субъект, ни предикат.
49. Умозаключение как форма мышления Правило распределённости
Если терминне распределён в посылке,
он не может быть
распределён в выводе.
Ни один гусь не лебедь
Ни один лебедь не гусь
Все гуси – птицы
Некоторые птицы – гуси
Некоторые гуси белые
Некоторые белые гуси
Некоторые птицы не гуси
Некоторые гуси не птицы
Частноотрицательные суждения не обращаются.
50. Умозаключение как форма мышления
Умозаключение – это такое логическое действие, в результате
которого из одного или нескольких – определённым образом
связанных – суждений (именуемых посылками) получается новое
суждение (вывод), в котором содержится новое знание.
Умозаключения подразделяются на индуктивные (от частного к
общему) и дедуктивные (от общего к частному). Поскольку
необходимое связано с общим, логически безупречные
(необходимые) выводы можно получить лишь путём дедукции,
индуктивные выводы лишь предположительны.
В зависимости от того, выводится заключение из одной или
нескольких посылок, дедуктивные умозаключения
подразделяются на непосредственные и силлогизмы.
o Противопоставление предикату сочетает превращение с
обращением.
Все матери – женщины
Ни одна мать не мужчина
Ни один мужчина не мать
Ни одна мать не мужчина
Все матери – женщины
Некот. женщины – матери
51. Умозаключение как форма мышления
Умозаключение – это такое логическое действие, в результате
которого из одного или нескольких – определённым образом
связанных – суждений (именуемых посылками) получается новое
суждение (вывод), в котором содержится новое знание.
Умозаключения подразделяются на индуктивные (от частного к
общему) и дедуктивные (от общего к частному). Поскольку
необходимое связано с общим, логически безупречные
(необходимые) выводы можно получить лишь путём дедукции,
индуктивные выводы лишь предположительны.
В зависимости от того, выводится заключение из одной или
нескольких посылок, дедуктивные умозаключения
подразделяются на непосредственные и силлогизмы.
o Противопоставление предикату сочетает превращение с
обращением.
Но ядро аристотелевской логики составляет силлогистика.
o Наиболее детально была разработана теория простого
категорического силлогизма.
52. Умозаключение как форма мышления Простой категорический силлогизм
Простой категорический силлогизм(греч. συλλογισμός) –
умозаключение,
посредством которого
устанавливается
логическое отношение
между двумя понятиями
на основании их отношения
к некоему третьему понятию.
53. Умозаключение как форма мышления Структура простого категорического силлогизма
Среднийтермин
M
есть
Меньшая
посылка
S
есть
P
Бóльшая
посылка
M
Средний
термин
P
Бóльший
термин
(предикат
вывода)
Следовательно,
Меньший
термин
(субъект
вывода)
S
есть
54. Простой категорический силлогизм Структура простого категорического силлогизма
Крайние терминыМеньший термин –
Бóльший термин –
субъект (подлежащее)
вывода (заключения)
силлогизма.
предикат (сказуемое)
вывода (заключения)
силлогизма.
Средний термин –
общий для обеих посылок
термин силлогизма, служащий
посредствующим элементом
между крайними (меньшим
и бóльшим) терминами.
Бóльшая посылка –
Меньшая посылка –
посылка,
устанавливающая
логическое отношение
бóльшего термина
к среднему.
посылка,
устанавливающая
логическое отношение
меньшего термина
к среднему.
55.
Простой категорический силлогизмАксиома силлогизма
Всё, что утверждается (или отрицается)
относительно каждого элемента
данного множества (класса),
утверждается (или отрицается)
относительно каждого элемента
любого подмножества (подкласса)
данного множества (класса).
В основе аксиомы силлогизма лежит логическое отношение подчинения.
Хотя в самой аксиоме эта мысль напрямую не формулируется, следует помнить, что
из истинности подчинённого суждения истинность подчиняющего не следует, поэтому
утверждать (или отрицать) относительно каждого элемента множества (класса) то, что
утверждается (или отрицается) относительно всех (или некоторых) элементов
какого-то из его подмножеств (подклассов), некорректно.
Другими словами, аксиома силлогизма не обратима.
56. Простой категорический силлогизм Правила простого категорического силлогизма
Правила терминов:• Правило трёх терминов: в силлогизме должно быть три термина –
не больше и не меньше.
• Правило среднего термина: средний термин должен быть
распределён хотя бы в одной из посылок.
• Правило крайних терминов: термины, не распределённые в
посылках, не могут быть распределены в выводе.
Правила посылок:
• Правило утвердительной посылки: по меньшей мере одна из
посылок должна быть утвердительным суждением, так как из двух
отрицательных посылок нельзя получить никакого вывода.
• Правило отрицательной посылки: если одна из посылок –
отрицательное суждение, то и вывод должен быть отрицательным.
• Правило общей посылки: по меньшей мере одна из посылок
должна быть общим суждением, так как из двух частных посылок
нельзя получить никакого вывода.
• Правило частной посылки: если одна из посылок – частное
суждение, то и вывод может быть только частным.
57. Простой категорический силлогизм Правила простого категорического силлогизма
Правило трёх терминов вытекает из определения силлогизма.
Правило среднего термина вытекает из правила трёх терминов: если
средний термин не распределён ни в одной из посылок, крайние
термины могут оказаться связанными с такими частями объёма
среднего термина, которые не имеют общих элементов, что
равносильно отсутствию среднего термина (учетверению терминов).
58. Простой категорический силлогизм Правило среднего термина
Вселандыши
суть
белые
Некоторые
растения
суть
белые
Все
сосны
суть
деревья
Все
сосны
суть
растения
Следовательно (?),
все
сосны
суть
белые
Следовательно (?),
все
сосны
суть
белые
59. Простой категорический силлогизм Правила простого категорического силлогизма
Правило трёх терминов вытекает из определения силлогизма.
Правило среднего термина вытекает из правила трёх терминов: если
средний термин не распределён ни в одной из посылок, крайние
термины могут оказаться связанными с такими частями объёма
среднего термина, которые не имеют общих элементов, что
равносильно отсутствию среднего термина (учетверению терминов).
Правило крайних терминов вытекает из аксиомы силлогизма, вернее –
из её необратимости.
Правило утвердительной посылки вытекает из определения
силлогизма: средний термин, связь которого с обоими крайними
отрицается, не может связать друг с другом крайние термины каким-то
определённым образом, так как отсутствие опосредования не является
достаточным основанием ни для утверждения, ни для отрицания связи
между ними, поскольку понятия, не связанные посредством одного
термина, могут оказаться связанными посредством другого.
60. Простой категорический силлогизм Правило утвердительной посылки
5не есть
4
5
не есть
2+2
3
не есть
5
7–3
не есть
5
Следовательно (?),
3
не есть
Следовательно (?),
4
7–3
не есть
2+2
61. Простой категорический силлогизм Правило утвердительной посылки
5не есть
2+2
4
есть
2+2
7–3
не есть
5
7–3
есть
4
Следовательно (?),
7–3
не есть
2+2
Следовательно (?),
7–3
есть
2+2
62. Простой категорический силлогизм Правила простого категорического силлогизма
Правило трёх терминов вытекает из определения силлогизма.
Правило среднего термина вытекает из правила трёх терминов: если
средний термин не распределён ни в одной из посылок, крайние
термины могут оказаться связанными с такими частями объёма
среднего термина, которые не имеют общих элементов, что
равносильно отсутствию среднего термина (учетверению терминов).
Правило крайних терминов вытекает из аксиомы силлогизма (вернее –
из обратной аксиомы).
Правило утвердительной посылки вытекает из определения
силлогизма: средний термин, связь которого с обоими крайними
отрицается, не может связать друг с другом крайние термины каким-то
определённым образом, так как отсутствие опосредования не является
достаточным основанием ни для утверждения, ни для отрицания связи
между ними, поскольку понятия, не связанные посредством одного
термина, могут оказаться связанными посредством другого.
Правило отрицательной посылки вытекает из характера логических
связей между терминами: если связь одного из крайних терминов со
средним – отрицательная, отрицательной будет и его – опосредованная
средним термином – связь с другим крайним термином.
63. Простой категорический силлогизм Правила простого категорического силлогизма
При доказательстве правила общей посылки следует рассмотреть два
случая: 1) когда обе посылки – утвердительные суждения, 2) когда одна
из посылок – утвердительное, а другая – отрицательное суждение.
Если обе частные посылки будут утвердительными суждениями, в
посылках не будет ни одного распределённого термина, что
противоречит правилу среднего термина.
Если одна из частных посылок будет утвердительным, а другая
отрицательным суждением, в посылках будет только один
распределённый термин – предикат отрицательной посылки, и
нераспределённым окажется
o либо средний термин, что противоречит правилу среднего
термина,
o либо бóльший термин , что противоречит правилу крайних
терминов (поскольку он распределён в выводе – отрицательном
по правилу отрицательной посылки).
64. Простой категорический силлогизм Правила простого категорического силлогизма
При доказательстве правила частной посылки следует рассмотреть те
же два случая: 1) обе посылки – утвердительные суждения, 2) одна из
посылок – утвердительное, другая – отрицательное суждение.
Если обе посылки будут утвердительными суждениями (одна –
общим, другая – частным),
o в посылках будет только один распределённый термин –
субъект общей посылки;
o это должен быть средний термин – по правилу среднего
термина;
o но тогда меньший термин в посылке распределён не будет,
o следовательно, он не будет (по правилу крайних терминов)
распределён и в выводе,
o а значит вывод – при нераспределённом субъекте – будет
частным суждением.
65. Простой категорический силлогизм Правила простого категорического силлогизма
При доказательстве правила частной посылки следует рассмотреть те
же два случая: 1) обе посылки – утвердительные суждения, 2) одна из
посылок – утвердительное, другая – отрицательное суждение.
Если одна из посылок будет отрицательным суждением,
o в посылках будут только два распределённых термина –
субъект общей и предикат отрицательной посылки,
o и это должны быть средний и бóльший термины:
средний термин – по правилу среднего термина,
бóльший термин – по правилу крайних терминов (поскольку
он распределён в выводе – отрицательном по правилу
отрицательной посылки);
o но тогда меньший термин в посылке распределён не будет,
o следовательно, он не будет (по правилу крайних терминов)
распределён и в выводе,
o и вывод – при нераспределённом субъекте – будет частным
суждением.
66. Простой категорический силлогизм Фигуры простого категорического силлогизма
Фигура силлогизма –форма силлогизма,
определяемая
положением среднего
термина в посылках.
Поскольку средний термин присутствует в обеих посылках и в
каждой может занимать одну из двух позиций: субъекта или
предиката, – всего возможны четыре варианта его расстановки
(2х2).
Соответственно, имеются четыре фигуры силлогизма: первая,
вторая, третья и четвёртая.
o
Из них самим Аристотелем рассматривались только первые три.
67. Простой категорический силлогизм Модусы простого категорического силлогизма
Фигура силлогизма –
Модус силлогизма –
форма силлогизма,
определяемая
положением среднего
термина в посылках.
разновидность силлогизма,
определяемая качеством
и количеством суждений
(посылок и вывода).
Каждое из трёх суждений, составляющих простой категорический
силлогизм (две посылки и вывод), может быть либо
общеутвердительным, либо общеотрицательным, либо
частноутвердительным, либо частноотрицательным.
Всего возможны 64 сочетания суждений (4х4х4) для каждой из
четырёх фигур силлогизма, т. е. в общей сложности 256 вариантов.
Из них только 24 не противоречат правилам силлогизма и
считаются модусами.
o
Если из их числа вычесть 5 так называемых «ослабленных» модусов,
останется 19, из которых Аристотелем были описаны и
проанализированы 14 относящихся к первым трём фигурам.
68. Простой категорический силлогизм Фигуры простого категорического силлогизма
IM
P
P
M
S
M
S
M
S
P
S
P
В первой фигуре оба крайних
термина занимают в посылках
те же позиции, что и в выводе.
III
M
P
M
S
II
Во второй фигуре средний
термин является предикатом
в обеих посылках.
P
M
S
M
S
P
S
P
В третьей фигуре средний
термин является субъектом
в обеих посылках.
IV
К четырём модусам первой фигуры
ученик Аристотеля Теофраст добавил ещё
пять модусов, впоследствии выделенных
в самостоятельную, четвёртую, фигуру.
69. Простой категорический силлогизм Первая фигура
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Все
M
(не) суть
P
есть
M
Правила первой фигуры
Меньшая посылка должна быть
утвердительным суждением.
Бóльшая посылка должна быть
общим суждением.
S
Следовательно,
S
(не) есть
P
70. Простой категорический силлогизм Доказательства правил первой фигуры
• Меньшая посылка должна быть утвердительным суждением.Допустим, что меньшая посылка – отрицательное суждение.
Тогда (по правилу отрицательной посылки) отрицательным будет и
вывод.
Следовательно, бóльший термин (по определению – предикат
вывода) в выводе будет распределён.
В этом случае он должен (по правилу крайних терминов) быть
распределён и в посылке (по определению – бóльшей).
Но в первой фигуре бóльший термин является (по определению
фигуры) предикатом бóльшей посылки, предикаты же
распределены в отрицательных суждениях.
Следовательно, бóльшая посылка должна быть отрицательным
суждением.
Но тогда обе посылки окажутся отрицательными суждениями, что
противоречит правилу утвердительной посылки.
Следовательно, исходное допущение неверно и меньшая посылка
не может быть отрицательным суждением.
71. Простой категорический силлогизм Доказательства правил первой фигуры
• Бóльшая посылка должна быть общим суждением.Поскольку доказано, что меньшая посылка – утвердительное
суждение, средний термин (по определению первой фигуры –
предикат меньшей посылки) в ней не распределён.
Следовательно, он должен (по правилу среднего термина) быть
распределён в бóльшей посылке.
В бóльшей посылке средний термин является (по определению
первой фигуры) субъектом, субъекты же распределены в общих
суждениях.
Следовательно, бóльшая посылка должна быть общим суждением.
72. Простой категорический силлогизм Первая фигура
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Все
M
(не) суть
P
есть
M
Правила первой фигуры
Меньшая посылка должна быть
утвердительным суждением.
Бóльшая посылка должна быть
общим суждением.
Назначение первой фигуры –
обоснование подчинения,
в том числе правомерности
подведения отдельного случая
под определённое правило:
в бóльшей (общей) посылке это
правило формулируется, меньшая
(утвердительная) подведение
(подчинение) обосновывает.
S
Следовательно,
S
(не) есть
P
73. Простой категорический силлогизм Первая фигура
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Все
M
(не) суть
P
есть
M
Модусы первой фигуры
BARBARA
CELARENT
DARII
FERIO
S
Следовательно,
Сочетание общей бóльшей посылки
(утвердительной или отрицательной)
с утвердительной меньшей посылкой
(общей или частной).
S
(не) есть
P
74. Простой категорический силлогизм Первая фигура, модус Barbara
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Все
M
суть
P
суть
M
Модусы первой фигуры
BARBARA
CELARENT
DARII
FERIO
Все
S
Следовательно,
Сочетание общеутвердительной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
общеутвердительный вывод.
Все
S
суть
P
75. Простой категорический силлогизм Первая фигура, модус Celarent
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Ни одно
M
не есть
P
суть
M
Модусы первой фигуры
BARBARA
CELARENT
DARII
FERIO
Все
S
Следовательно,
Сочетание общеотрицательной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
общеотрицательный вывод.
Ни одно
S
не есть
P
76. Простой категорический силлогизм Первая фигура, модус Darii
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Все
M
суть
P
суть
M
Модусы первой фигуры
BARBARA
CELARENT
DARII
FERIO
Некоторые
S
Следовательно,
Сочетание общеутвердительной
бóльшей посылки
с частноутвердительной меньшей
посылкой даёт
частноутвердительный вывод.
Некоторые
S
суть
P
77. Простой категорический силлогизм Первая фигура, модус Ferio
Оба крайних терминазанимают в посылках те же
позиции, что и в выводе.
Ни одно
M
не есть
P
суть
M
Модусы первой фигуры
BARBARA
CELARENT
DARII
FERIO
Некоторые
S
Следовательно,
Сочетание общеотрицательной
бóльшей посылки
с частноутвердительной меньшей
посылкой даёт
частноотрицательный вывод.
Некоторые
S
не суть
P
78. Простой категорический силлогизм Модусы первой фигуры
BARBARACELARENT
Все M суть P
Все S суть M
→ Все S суть P
P
M
M
S
Ни одно M не есть P
Все S суть M
→ Ни одно S не есть P
DARII
S
M
P
S
FERIO
P
Все M суть P
Некоторые S суть M
→ Некоторые S суть P
M
Ни одно M не есть P
Некоторые S суть M
→ Некоторые S не суть P
S
P
79. Простой категорический силлогизм Модусы первой фигуры
BARBARAСмертные
Люди
CELARENT
Все люди смертны
Все греки – люди
→ Все греки смертны
Люди
Жираф
Греки
Греки
Ни один человек не жираф
Все греки – люди
→ Ни один грек не жираф
DARII
Греки
Афиняне
Поэты
FERIO
Все афиняне – греки
Некоторые поэты – афиняне
→ Некоторые поэты – греки
Греки
Поэты
Ни один грек не немец
Некоторые поэты – греки
→ Некоторые поэты не немцы
Немцы
80. Простой категорический силлогизм Вторая фигура
Одна из посылок должна бытьотрицательным суждением.
Следовательно, и вывод
будет отрицательным.
Бóльшая посылка должна
быть общим суждением.
P
(не)
не суть
суть
S
M
средний
термин
Правила второй фигуры
Все
не есть
Средний термин
является предикатом
в обеих посылках.
(не)
не есть
есть
M
Следовательно,
S
не есть
P
81. Простой категорический силлогизм Доказательства правил второй фигуры
• Одна из посылок должна быть отрицательным суждением.Средний термин должен быть распределён хотя бы в одной из
посылок (правило среднего термина).
Но в обеих посылках второй фигуры средний термин является (по
определению фигуры) предикатом, предикаты же распределены в
отрицательных суждениях.
Следовательно, одна из посылок должна быть отрицательным
суждением.
Соответственно, отрицательным должен быть и вывод (по правилу
отрицательной посылки).
• Бóльшая посылка должна быть общим суждением.
Раз вывод – отрицательное суждение, бóльший термин (по
определению – предикат вывода) в выводе будет распределён.
В этом случае он (по правилу крайних терминов) должен быть
распределён и в посылке (по определению – бóльшей).
Но во второй фигуре бóльший термин является (по определению
фигуры) субъектом бóльшей посылки, субъекты же распределены в
общих суждениях.
Следовательно, бóльшая посылка должна быть общим суждением.
82. Простой категорический силлогизм Вторая фигура
Одна из посылок должна бытьотрицательным суждением.
Следовательно, и вывод
будет отрицательным.
Бóльшая посылка должна
быть общим суждением.
Назначение второй фигуры –
отвержение ложного подчинения,
в том числе обоснование
неправомерности подведения
данного случая под определённое
правило: в бóльшей (общей)
посылке правило формулируется,
меньшая (качеством отличающаяся
от бóльшей) обосновывает
неправомерность подведения.
P
(не) суть
S
M
средний
термин
Правила второй фигуры
Все
не есть
Средний термин
является предикатом
в обеих посылках.
(не) есть
M
Следовательно,
S
не есть
P
83. Простой категорический силлогизм Вторая фигура
CESARE
CAMESTRES
FESTINO
BAROKO
P
(не) суть
S
M
средний
термин
Модусы второй фигуры
Все
не есть
Средний термин
является предикатом
в обеих посылках.
(не) есть
M
Следовательно,
Сочетание общей бóльшей посылки
(отрицательной или утвердительной)
с противоположной по качеству
меньшей посылкой
(общей или частной).
S
не есть
P
84. Простой категорический силлогизм Вторая фигура, модус Cesare
CESARE
CAMESTRES
FESTINO
BAROKO
P
не есть
Все
S
M
средний
термин
Модусы второй фигуры
Ни одно
не суть
Средний термин
является предикатом
в обеих посылках.
суть
M
Следовательно,
Сочетание общеотрицательной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
общеотрицательный вывод.
Ни одно
S
не есть
P
85. Простой категорический силлогизм Вторая фигура, модус Camestres
CESARE
CAMESTRES
FESTINO
BAROKO
P
суть
Ни одно
S
M
средний
термин
Модусы второй фигуры
Все
не есть
Средний термин
является предикатом
в обеих посылках.
не есть
M
Следовательно,
Сочетание общеутвердительной
бóльшей посылки
с общеотрицательной меньшей
посылкой даёт
общеотрицательный вывод.
Ни одно
S
не есть
P
86. Простой категорический силлогизм Вторая фигура, модус Festino
CESARE
CAMESTRES
FESTINO
BAROKO
P
не есть
Некоторые
S
M
средний
термин
Модусы второй фигуры
Ни одно
не суть
Средний термин
является предикатом
в обеих посылках.
суть
M
Следовательно,
Сочетание общеотрицательной
бóльшей посылки
с частноутвердительной меньшей
посылкой даёт
частноотрицательный вывод.
Некоторые
S
не суть
P
87. Простой категорический силлогизм Вторая фигура, модус Baroko
CESARE
CAMESTRES
FESTINO
BAROKO
P
суть
Некоторые
S
M
средний
термин
Модусы второй фигуры
Все
не суть
Средний термин
является предикатом
в обеих посылках.
не суть
M
Следовательно,
Сочетание общеутвердительной
бóльшей посылки
с частноотрицательной меньшей
посылкой даёт
частноотрицательный вывод.
Некоторые
S
не суть
P
88. Простой категорический силлогизм Модусы второй фигуры
CESAREM
P
S
FESTINO
M
S
CAMESTRES
Ни одно P не есть M
Все S суть M
→ Ни одно S не есть P
M
S
Все P суть M
Ни одно S не есть M
→ Ни одно S не есть P
Ни одно P не есть M
Некоторые S суть M
→ Некоторые S не суть P
P
Все P суть M
Некоторые S не суть M
→ Некоторые S не суть P
P
BAROKO
M
P
S
89. Простой категорический силлогизм Модусы второй фигуры
CESAREПтица
Ни одна рыба не птица
Все галки – птицы
→ Ни одна галка не рыба
Рыба
Галка
FESTINO
Немцы
CAMESTRES
Рыба
Галка
Щука
Все щуки – рыбы
Ни одна галка не рыба
→ Ни одна галка не щука
Ни один грек не немец
Некоторые поэты – немцы
→ Некоторые поэты не греки
BAROKO
Греки
Поэты
Поэты
Греки
Все афиняне – греки
Некоторые поэты не греки
→ Некоторые поэты не афиняне
Афиняне
90. Простой категорический силлогизм Третья фигура
Меньшая посылка должнабыть утвердительным
суждением.
Вывод – частное суждение.
(не) есть
M
P
(не) суть
Правила третьей фигуры
M
средний
термин
Средний термин
является субъектом
в обеих посылках.
есть
S
Следовательно,
Некоторые
S
(не) суть
P
91. Простой категорический силлогизм Доказательства правил третьей фигуры
• Меньшая посылка должна быть утвердительным суждением.Допустим, что меньшая посылка – отрицательное суждение.
Тогда (по правилу отрицательной посылки) отрицательным будет и
вывод.
Следовательно, бóльший термин (по определению – предикат
вывода) в выводе будет распределён.
В этом случае он должен (по правилу крайних терминов) быть
распределён и в посылке (по определению – бóльшей).
Но в третьей фигуре бóльший термин является (по определению
фигуры) предикатом бóльшей посылки, предикаты же
распределены в отрицательных суждениях.
Следовательно, бóльшая посылка должна быть отрицательным
суждением.
Но тогда обе посылки окажутся отрицательными суждениями, что
противоречит правилу утвердительной посылки.
Следовательно, исходное допущение неверно и меньшая посылка
не может быть отрицательным суждением.
92. Простой категорический силлогизм Доказательства правил третьей фигуры
• Вывод – частное суждение.Поскольку доказано, что меньшая посылка – утвердительное
суждение, меньший термин (по определению третьей фигуры –
предикат меньшей посылки) в ней не распределён.
В таком случае он не может (по правилу крайних терминов) быть
распределён и в выводе.
Коль скоро субъект вывода не распределён, вывод – суждение
частное.
93. Простой категорический силлогизм Третья фигура
Меньшая посылка должнабыть утвердительным
суждением.
Вывод – частное суждение.
Назначение третьей фигуры –
доказательство исключений из
общего правила и необоснованности тех или иных обобщений:
меньшая (утвердительная)
посылка приписывает субъекту
предикат, отличный от того, что
приписывается (или отрицается)
бóльшей, тем самым либо выводя
часть объёма меньшего термина
из подчинения бóльшему, либо
утверждая исключительно частный
характер такого подчинения.
(не) есть
M
P
(не) суть
Правила третьей фигуры
M
средний
термин
Средний термин
является субъектом
в обеих посылках.
есть
S
Следовательно,
Некоторые
S
(не) суть
P
94. Простой категорический силлогизм Третья фигура
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание общей бóльшей посылки
(утвердительной или отрицательной)
с утвердительной меньшей посылкой
(общей или частной)
и частной бóльшей посылки
(утвердительной или отрицательной)
с общеутвердительной меньшей.
(не) есть
M
P
(не) суть
Модусы третьей фигуры
M
средний
термин
Средний термин
является субъектом
в обеих посылках.
есть
S
Следовательно,
Некоторые
S
(не) суть
P
95. Простой категорический силлогизм Третья фигура, модус DARAPTI
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание общеутвердительной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
(с учётом правила частного вывода)
частноутвердительный вывод.
M
суть
Все
M
P
суть
Модусы третьей фигуры
Все
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
суть
P
96. Простой категорический силлогизм Третья фигура, модус DISAMSIS
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание частноутвердительной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
частноутвердительный вывод.
M
суть
Все
M
P
суть
Модусы третьей фигуры
Некоторые
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
суть
P
97. Простой категорический силлогизм Третья фигура, модус DATISI
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание общеутвердительной
бóльшей посылки
с частноутвердительной меньшей
посылкой даёт
частноутвердительный вывод.
M
суть
Некоторые
M
P
суть
Модусы третьей фигуры
Все
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
суть
P
98. Простой категорический силлогизм Третья фигура, модус FELAPTON
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание общеотрицательной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
(с учётом правила частного вывода)
частноотрицательный вывод.
M
не есть
Все
M
P
не суть
Модусы третьей фигуры
Ни одно
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
не суть
P
99. Простой категорический силлогизм Третья фигура, модус BOCARDO
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание частноотрицательной
бóльшей посылки
с общеутвердительной меньшей
посылкой даёт
частноотрицательный вывод.
M
не суть
Все
M
P
не суть
Модусы третьей фигуры
Некоторые
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
не суть
P
100. Простой категорический силлогизм Третья фигура, модус FERISON
DARAPTI
DISAMIS
DATISI
FELAPTON
BOCARDO
FERISON
Сочетание общеотрицательной
бóльшей посылки
с частноутвердительной меньшей
посылкой даёт
частноотрицательный вывод.
M
не есть
Некоторые
M
P
не суть
Модусы третьей фигуры
Ни одно
средний
термин
Средний термин
является субъектом
в обеих посылках.
суть
S
Следовательно,
Некоторые
S
не суть
P
101. Простой категорический силлогизм Модусы третьей фигуры
DARAPTIS
P
M
DISAMIS
P
DATISI
P
M
S
FELAPTON
S
BOCARDO
S
Некоторые M не суть P
Все M суть S
→ Некоторые S не суть P
Все M суть P
Некоторые M суть S
→ Некоторые S суть P
P
M
Ни одно M не есть P
Все M суть S
→ Некоторые S не суть P
Некоторые M суть P
Все M суть S
→ Некоторые S суть P
S
M
Все M суть P
Все M суть S
→ Некоторые S суть P
M
P
FERISON
Ни одно M не есть P
Некоторые M суть S
→ Некоторые S не суть P
S
M
P
102. Простой категорический силлогизм Модусы третьей фигуры
DARAPTIСмертные
Люди
Греки
DISAMIS
Люди
Греки
Поэты
DATISI
Белые
Птицы
Гуси
Все греки люди
Все греки смертны
→ Некоторые смертные – люди
FELAPTON
Цветы
Розы
Ни одна роза не лютик
Все розы – цветы
→ Некоторые цветы не лютики
Некоторые поэты – греки
Все поэты – люди
→ Некоторые люди – греки
BOCARDO
Люди
Некоторые греки не поэты
Все греки – люди
→ Некоторые люди не поэты
Все гуси – птицы
Некоторые гуси белые
→ Некоторые белые – птицы
Лютики
Поэты
Греки
FERISON
Ни один гусь не слон
Гуси
Некоторые гуси белые
→ Некоторые белые не слоны
Белые
Слоны
103. Простой категорический силлогизм Четвёртая фигура
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Все
P
P
(не)
неесть
есть
есть
M
(не)
не есть
есть
S
Правила четвёртой фигуры
Если бóльшая посылка –
утвердительное суждение,
то меньшая посылка должна
быть общим суждением.
Если одна из посылок –
отрицательное суждение,
то бóльшая посылка должна
быть общим суждением.
Все
M
M
Следовательно,
S
(не) есть
P
104. Простой категорический силлогизм Доказательства правил четвёртой фигуры
• Если бóльшая посылка – утвердительное суждение, то меньшаяпосылка должна быть общим суждением.
Если бóльшая посылка – утвердительное суждение, то средний
термин (по определению четвёртой фигуры – предикат бóльшей
посылки) в ней не распределён.
Следовательно, он должен быть распределён в меньшей посылке.
Но в меньшей посылке средний термин является субъектом (по
определению четвёртой фигуры), субъекты же распределены в
общих суждениях.
Следовательно, меньшая посылка должна в этом случае (если
бóльшая посылка – не отрицательное суждение) быть общим
суждением.
105. Простой категорический силлогизм Доказательства правил четвёртой фигуры
• Если одна из посылок – отрицательное суждение, то бóльшаяпосылка должна быть общим суждением.
Если одна из посылок – отрицательное суждение, отрицательным
будет (по правилу отрицательной посылки) и вывод.
Раз вывод – отрицательное суждение, бóльший термин (по
определению – предикат вывода) в выводе распределён.
В этом случае он (по правилу крайних терминов) должен быть
распределён и в посылке (по определению – бóльшей).
Но в четвёртой фигуре бóльший термин является (по определению
фигуры) субъектом бóльшей посылки, субъекты же распределены в
общих суждениях.
Следовательно, бóльшая посылка должна в этом случае (если одна
из посылок – отрицательное суждение) быть общим суждением.
106. Простой категорический силлогизм Четвёртая фигура
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Все
P
P
(не)
неесть
есть
есть
M
(не)
есть
не есть
S
Правила четвёртой фигуры
Если бóльшая посылка –
утвердительное суждение,
то меньшая посылка должна
быть общим суждением.
Если одна из посылок –
отрицательное суждение,
то бóльшая посылка должна
быть общим суждением.
Назначение четвёртой фигуры –
обоснование умозаключений
в тех случаях, когда «связь идей»
обратна «связи вещей» (например,
обоснование целесообразности).
Все
M
M
Следовательно,
S
(не) есть
P
107. Простой категорический силлогизм Четвёртая фигура
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
P
(не) есть
M
M
(не) есть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Следовательно,
Сочетание утвердительной бóльшей
посылки (общей или частной)
с общей меньшей посылкой
(утвердительной или отрицательной)
и общеотрицательной бóльшей
посылки с утвердительной меньшей
(общей или частной).
S
(не) есть
P
108. Простой категорический силлогизм Четвёртая фигура, модус BRAMANTIP
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Все
P
суть
M
суть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Все
M
Следовательно,
Сочетание общеутвердительной
бóльшей посылки)
с общеутвердительной меньшей
посылкой даёт
(с учётом нераспределённости
меньшего термина)
частноутвердительный вывод.
Некоторые
S
суть
P
109. Простой категорический силлогизм Четвёртая фигура, модус CAMENES
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Все
P
суть
M
не есть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Ни одно
M
Следовательно,
Сочетание общеутвердительной
бóльшей посылки)
с общеотрицательной меньшей
посылкой даёт
общеотрицательный вывод.
Ни одно
S
не есть
P
110. Простой категорический силлогизм Четвёртая фигура, модус DIMARIS
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Некоторые
P
суть
M
суть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Все
M
Следовательно,
Сочетание частноутвердительной
бóльшей посылки)
с общеутвердительной меньшей
посылкой даёт
частноутвердительный вывод.
Некоторые
S
суть
P
111. Простой категорический силлогизм Четвёртая фигура, модус FESAPO
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Ни одно
P
не есть
M
суть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Все
M
Следовательно,
Сочетание общеотрицательной
бóльшей посылки)
с общеутвердительной меньшей
посылкой даёт
(с учётом нераспределённости
меньшего термина)
частнотрицательный вывод.
Некоторые
S
не суть
P
112. Простой категорический силлогизм Четвёртая фигура, модус FRESISON
Крайние термины занимаютв посылках позиции,
противоположные тем, что
они занимают в выводе.
Ни одно
P
не есть
M
суть
S
Модусы четвёртой фигуры
BRAMANTIP
CAMENES
DIMARIS
FESAPO
FRESISON
Некоторые
M
Следовательно,
Сочетание общеотрицательной
бóльшей посылки)
с частноутвердительной меньшей
посылкой даёт
частнотрицательный вывод.
Некоторые
S
не суть
P
113. Простой категорический силлогизм Модусы четвёртой фигуры
BRAMANTIPS
M
P
DIMARIS
S
P
Все P суть M
Все M суть S
→ Некоторые S суть P
CAMENES
M
Все P суть M
Ни одно M не есть S
→ Ни одно S не есть P
Некоторые P суть M
Все M суть S
→ Некоторые S суть P
FESAPO
Ни одно P не есть M
Все M суть S
→ Некоторые S не суть P
M
FRESISON
Ни одно P не есть M
Некоторые M суть S
→ Некоторые S не суть P
S
M
S
P
P
S
P
M
114. Простой категорический силлогизм Модусы четвёртой фигуры
BRAMANTIPСмертные
Люди
Греки
DIMARIS
Цветы
Алые
Розы
Все греки – люди
Все люди смертны
→ Некоторые смертные – греки
CAMENES
Люди
Все греки – люди
Ни один человек не слон
→ Ни один слон не грек
Некоторые алые – розы
Все розы – цветы
→ Некоторые цветы алые
FESAPO
Крылатые
Ни одна оса не птица
Все птицы крылаты
→ Некоторые крылатые не осы
FRESISON
Поэты
Греки
Ни один турок не грек
Некоторые греки – поэты
→ Некоторые поэты не турки
Слоны
Греки
Турки
Птицы
Осы
115. Простой категорический силлогизм Фигуры простого категорического силлогизма
IM
P
P
M
S
M
S
M
S
P
S
P
Назначение первой фигуры –
обоснование подчинения, в том числе
правомерности подведения
данного случая под данное правило.
III
M
P
M
S
II
Назначение второй фигуры –
отвержение ложного подчинения, в том числе
обоснование неправомерности подведения
данного случая под данное правило.
P
M
S
M
S
P
S
P
Назначение третьей фигуры –
доказательство исключений
из общего правила и необоснованности
тех или иных обобщений.
IV
Назначение четвёртой фигуры –
обоснование умозаключений в тех случаях,
когда «связь идей» обратна «связи вещей»
(например, обоснование целесообразности).
116. Умозаключение как форма мышления Условно-категорический силлогизм
Modus ponensModus tollens
Если A, то B
Если A, то B
A
Не B
Следовательно,
Следовательно,
B
не A
Закон контрапозиции
Если A, то B
Следовательно,
если не B, то не A
117. Условно-категорический силлогизм Modus ponens
Если A, то BA
Следовательно,
B
От утверждения основания
к утверждению следствия
Если A, то B
Не A
Следовательно,
не B
От отрицания основания
к отрицанию следствия
Modus ponens –
разновидность условнокатегорического умозаключения
(силлогизма), в которой
первая (бóльшая) посылка –
невыделяющее условное суждение
(т. е. суждение, устанавливающее
логическое отношение подчинения
между основанием и следствием),
вторая (меньшая) посылка –
категорическое суждение,
утверждающее
истинность основания
(т. е. подчиняющего суждения),
а заключение утверждает
истинность следствия
(т. е. подчинённого суждения).
118. Условно-категорический силлогизм Modus ponens
Если A, то BЕсли идёт дождь, то крыши мокрые.
A
Идёт дождь.
Следовательно,
Следовательно,
B
крыши мокрые.
От утверждения основания
к утверждению следствия
Правильное умозаключение:
modus ponens
Если A, то B
Если идёт дождь, то крыши мокрые.
Не A
Дождя нет.
Следовательно,
Следовательно,
не B
крыши не мокрые.
От отрицания основания
к отрицанию следствия
Неправильное умозаключение:
отрицание основания
119. Условно-категорический силлогизм Modus tollens
Если A, то BModus tollens –
Не B
разновидность условнокатегорического умозаключения
(силлогизма), в которой
первая (бóльшая) посылка –
невыделяющее условное суждение
(т. е. суждение, устанавливающее
логическое отношение подчинения
между основанием и следствием),
вторая (меньшая) посылка –
категорическое суждение,
отрицающее
истинность следствия
(т. е. подчинённого суждения),
а заключение отрицает
истинность основания
(т. е. подчиняющего суждения).
Следовательно,
не A
От отрицания следствия
к отрицанию основания
Если A, то B
B
Следовательно,
A
От утверждения следствия
к утверждению основания
120. Условно-категорический силлогизм Modus tollens
Если A, то BЕсли идёт дождь, то крыши мокрые.
Не B
Крыши не мокрые.
Следовательно,
Следовательно,
не A
дождя нет.
От отрицания следствия
к отрицанию основания
Правильное умозаключение:
modus tollens
Если A, то B
Если идёт дождь, то крыши мокрые.
B
Крыши мокрые.
Следовательно,
Следовательно,
A
идёт дождь.
От утверждения следствия
к утверждению основания
Неправильное умозаключение:
утверждение следствия
121. Разделительно-категорический силлогизм
Modus ponendo tollensS
либо
есть
P
либо
Modus tollendo ponens
Q
S
есть
либо
либо
P
S
есть
P
S
не есть
P
S
не есть
Q
S
есть
Q
Q
Правила разделительно-категорического силлогизма
Правило модуса ponendo tollens: союз «или» должен употребляться в
чисто разделительном значении.
Правило модуса tollendo ponens: в предикате разделительной посылки
должны быть перечислены все альтернативы.
122. Разделительно-категорический силлогизм Modus ponendo tollens
Modus ponendo tollens –S
есть
либо
P
либо
S
есть
P
S
не есть
Q
В модусе ponendo tollens
союз «или» должен
употребляться в чисто
разделительном значении.
Q
разновидность разделительнокатегорического умозаключения
(силлогизма), в которой
первая посылка –
разделительное суждение,
(т. е. суждение, утверждающее,
что данному предмету присущ
только один из признаков,
перечисленных в предикате
суждения),
вторая посылка –
категорическое суждение,
утверждающее один
из альтернативных признаков,
а заключение
отрицает на этом основании
все другие признаки.
123. Разделительно-категорический силлогизм Modus ponendo tollens
Sесть
либо
P
либо
Q
Мужем Людмилы станет
либо Руслан, либо Фарлаф.
S
есть
P
Мужем Людмилы
станет Руслан.
S
не есть
Q
Фарлаф не станет
мужем Людмилы.
В модусе ponendo tollens
союз «или» должен
употребляться в чисто
разделительном значении.
Это рассуждение будет
правильным лишь в том случае,
если обычаи страны не
допускают двоемужия.
124. Разделительно-категорический силлогизм Modus tollendo ponens
Modus tollendo ponens –S
есть
либо
P
либо
S
не есть
P
S
есть
Q
Q
В модусе tollendo ponens
совокупность признаков,
перечисленных в предикате
разделительной посылки, должна
исчерпывать все альтернативы.
разновидность разделительнокатегорического умозаключения
(силлогизма), в которой
первая посылка – разделительное
суждение, (т. е. суждение,
утверждающее, что данному
предмету присущ только один
из признаков, перечисленных
в предикате суждения),
вторая посылка – категорическое
суждение, отрицающее один
из альтернативных признаков
(или, если признаков больше
двух, все альтернативные
признаки, кроме одного),
а заключение утверждает на этом
основании оставшийся признак.
125. Разделительно-категорический силлогизм Modus tollendo ponens
Sесть
либо
P
либо
Q
Кораллы у Клары украл
либо Карл, либо Карлсон.
S
не есть
P
Карл кораллов у Клары не крал.
S
есть
Q
Кораллы у Клары украл Карлсон.
В модусе tollendo ponens
совокупность членов
разделительной посылки
должна исчерпывать
все альтернативы.
Это рассуждение будет правильным
лишь в том случае, если у нас есть
веские основания не рассматривать
в качестве возможных похитителей
кораллов Малыша или кого-то ещё.
126. Умозаключение как форма мышления Модальная логика
Модальная логика Аристотеля связана с его учением о возможности
и действительности.
Эта логика (именуемая в наше время алетической) использует три
модальных оператора, а именно: необходимо, действительно
(фактически), возможно. Соответствующие суждения называются
аподиктическими, ассерторическими и проблематическими.
Алетические суждения той же материи и одного качества находятся
друг с другом в отношении подчинения.
Это значит, что если аподиктическое суждение истинно, истинным
будет и ассерторическое суждение той же материи и того же
качества, а значит и соответствующее проблематическое суждение.
S необходимо есть P
S есть P
S может быть P
Если же проблематическое суждение ложно, ложными будут также
ассерторическое и аподиктическое суждение.
S не может быть P
S не есть P
S не необходимо есть P











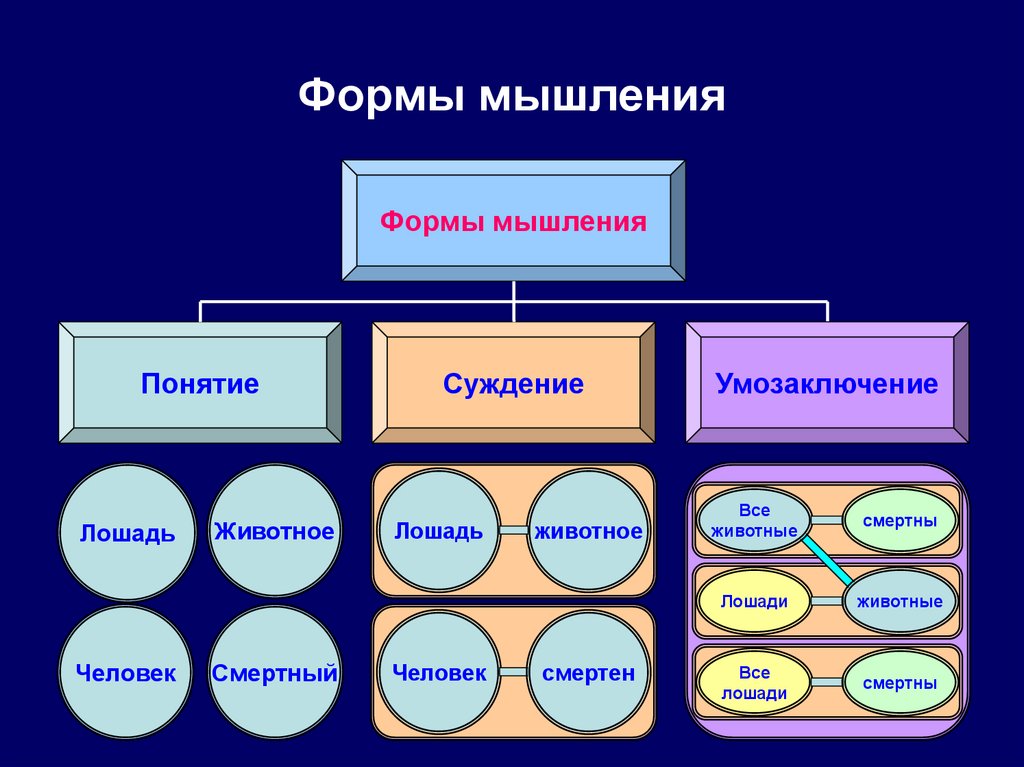
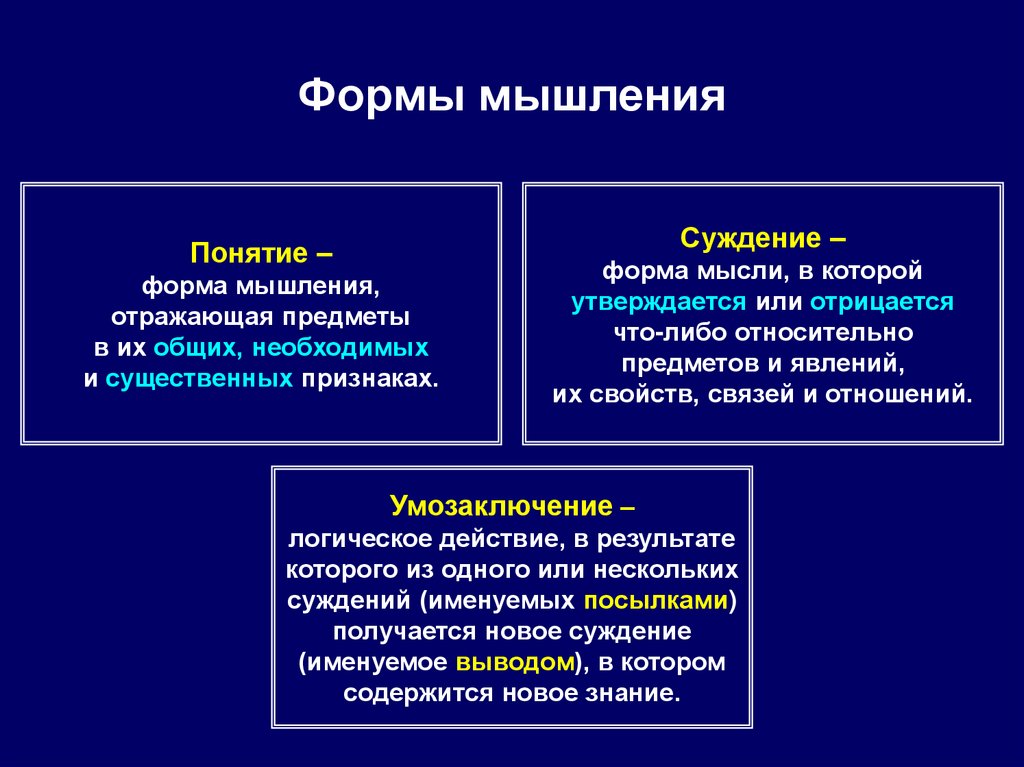

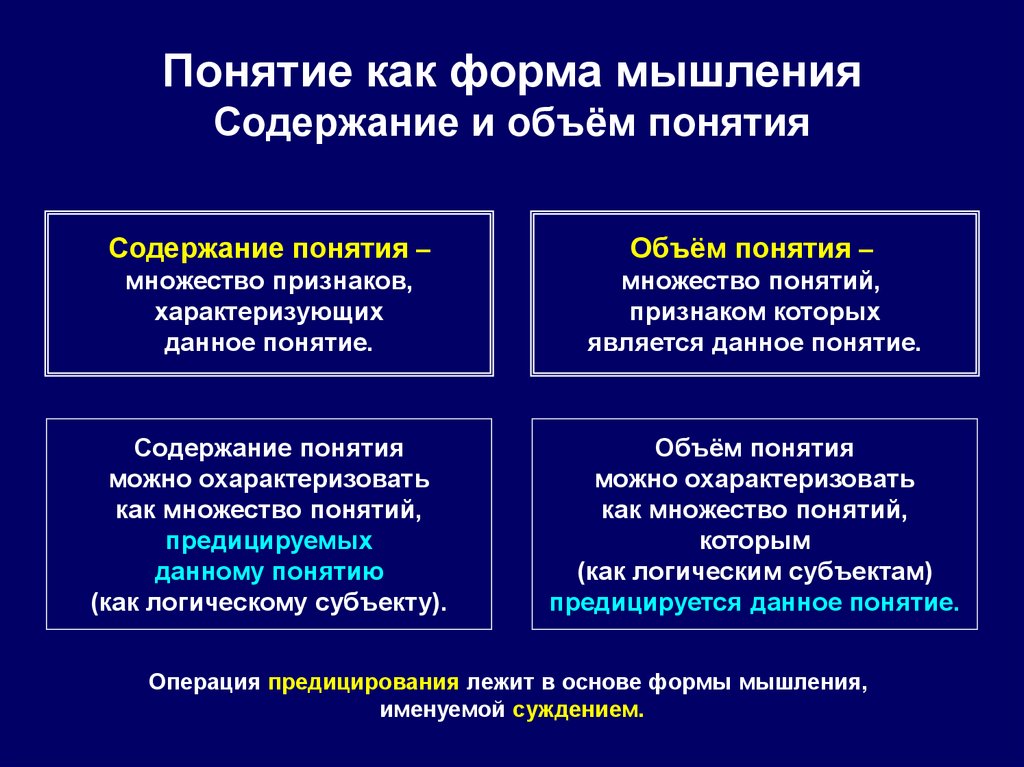


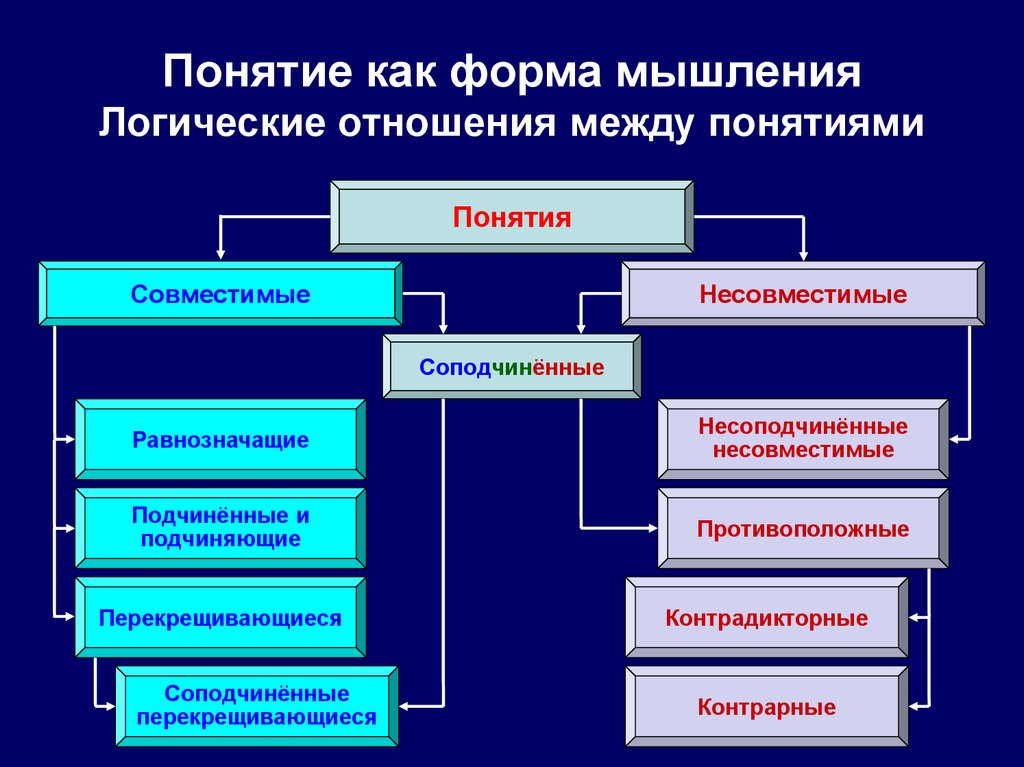

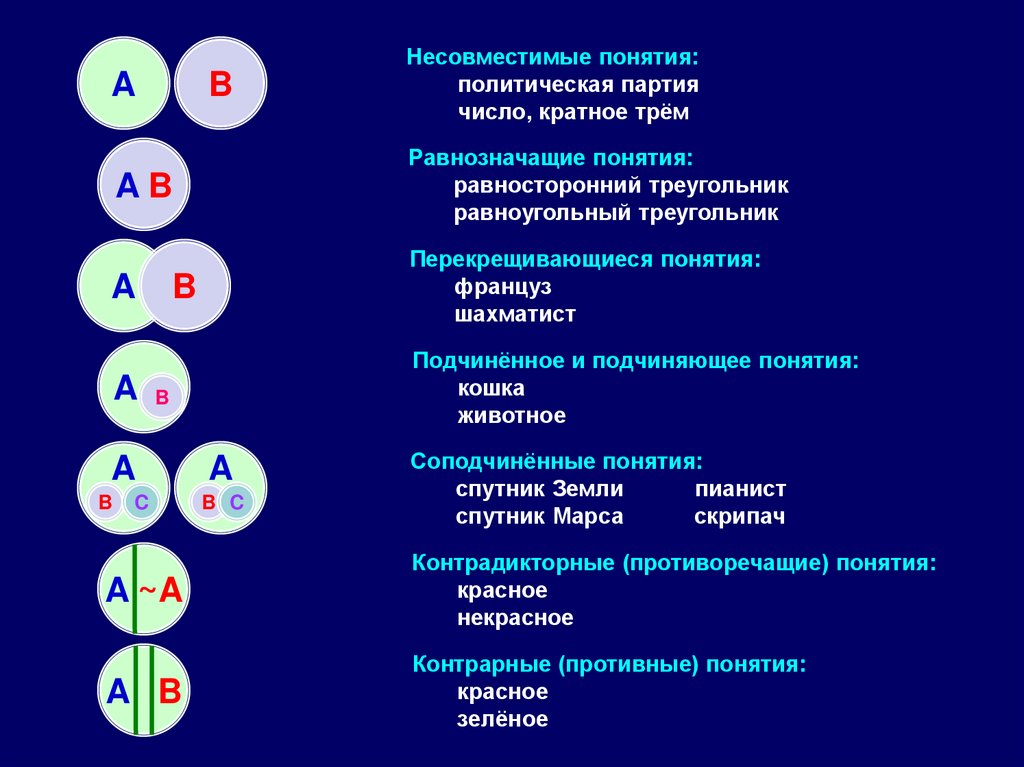








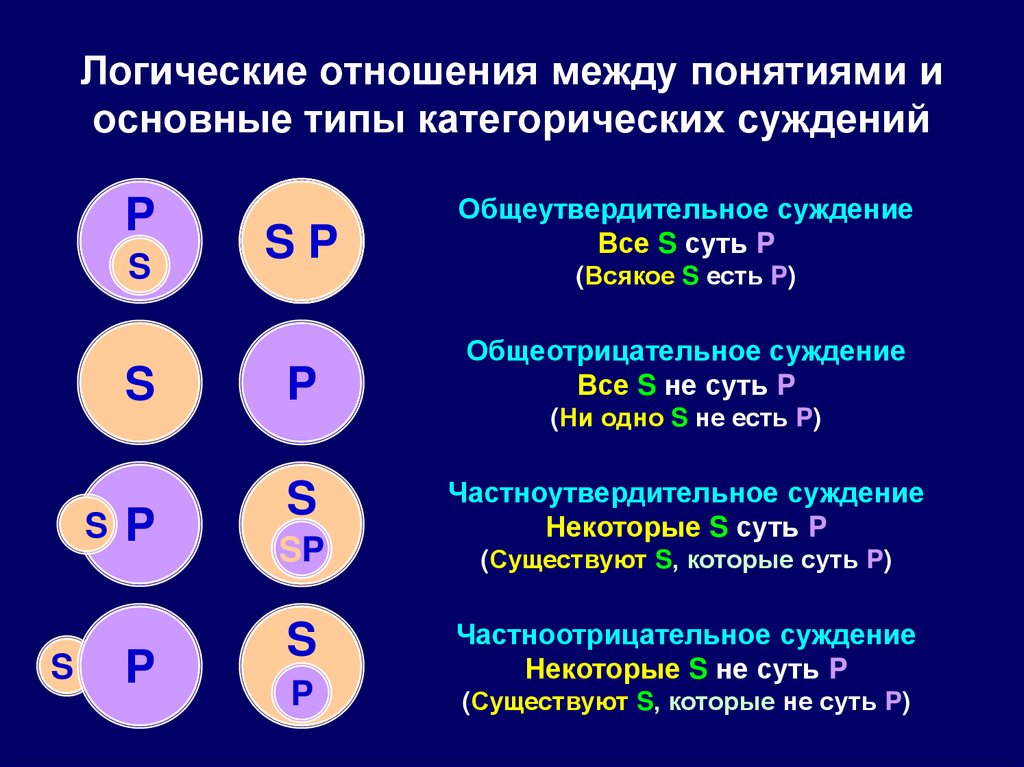






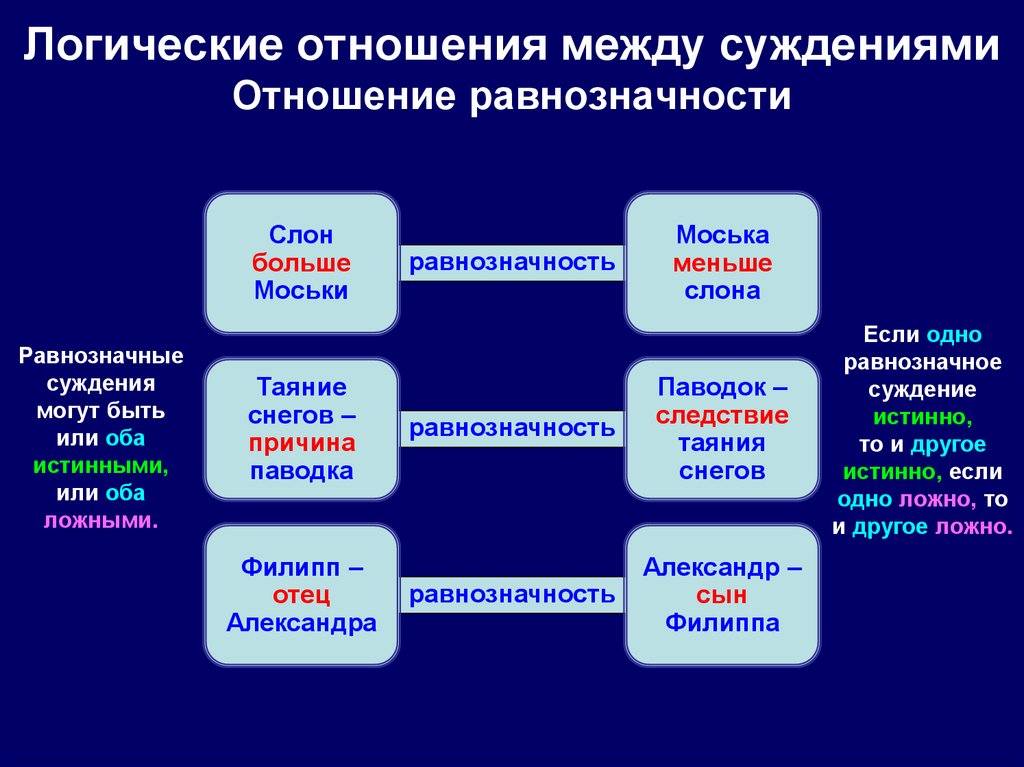
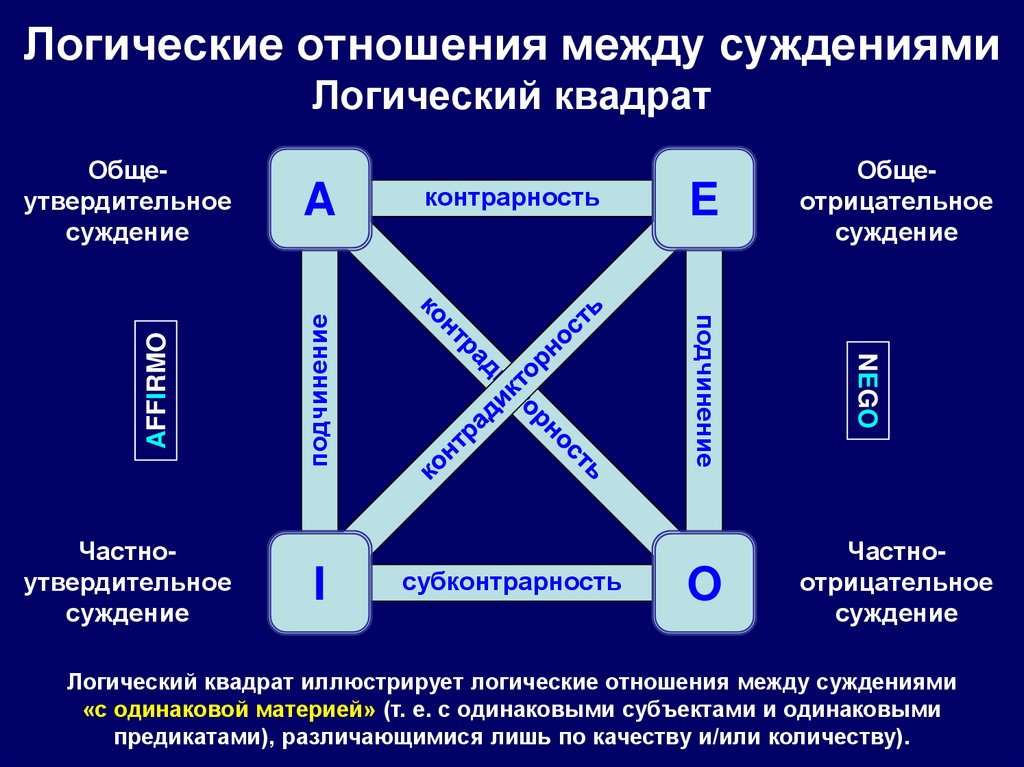
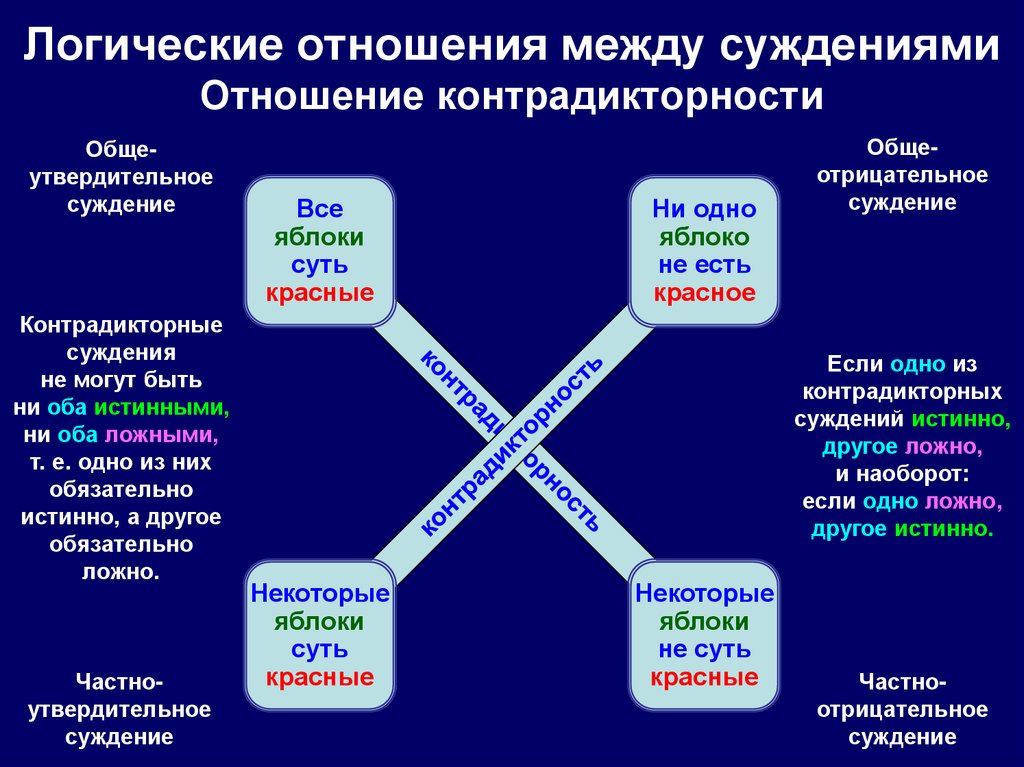
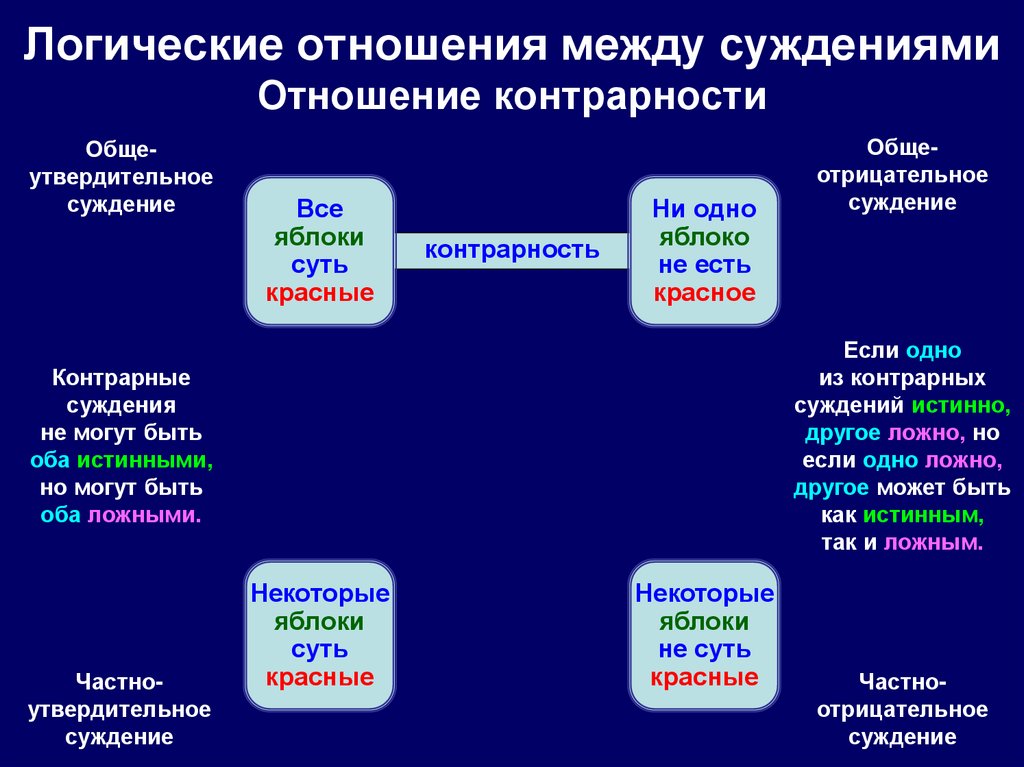
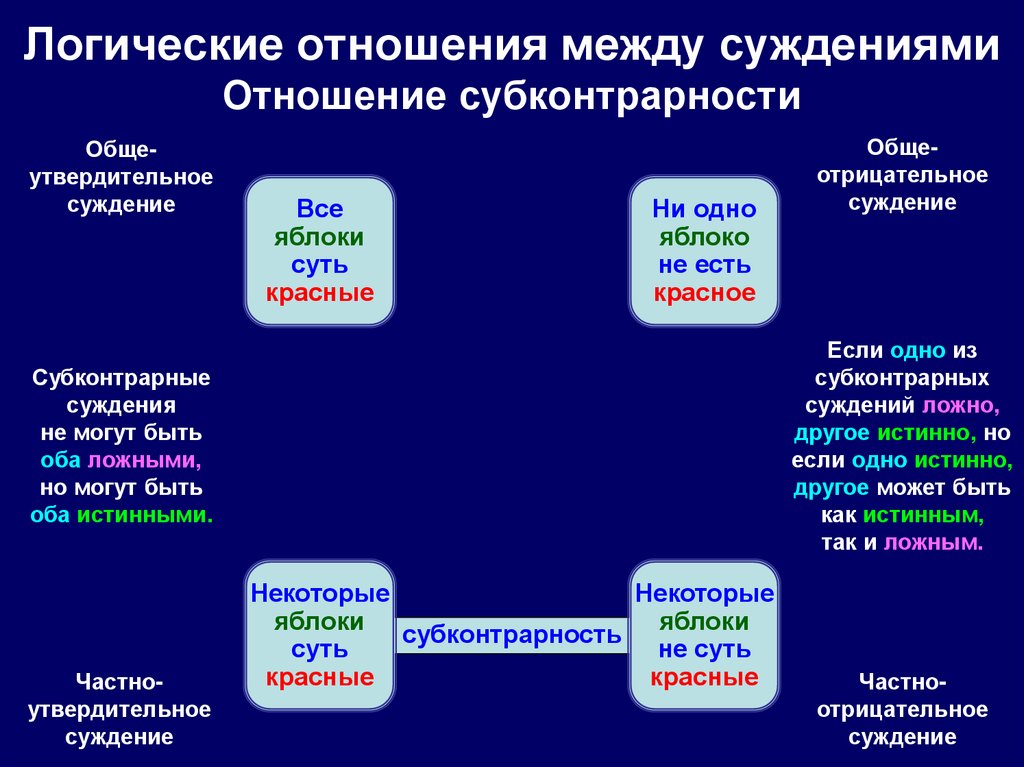
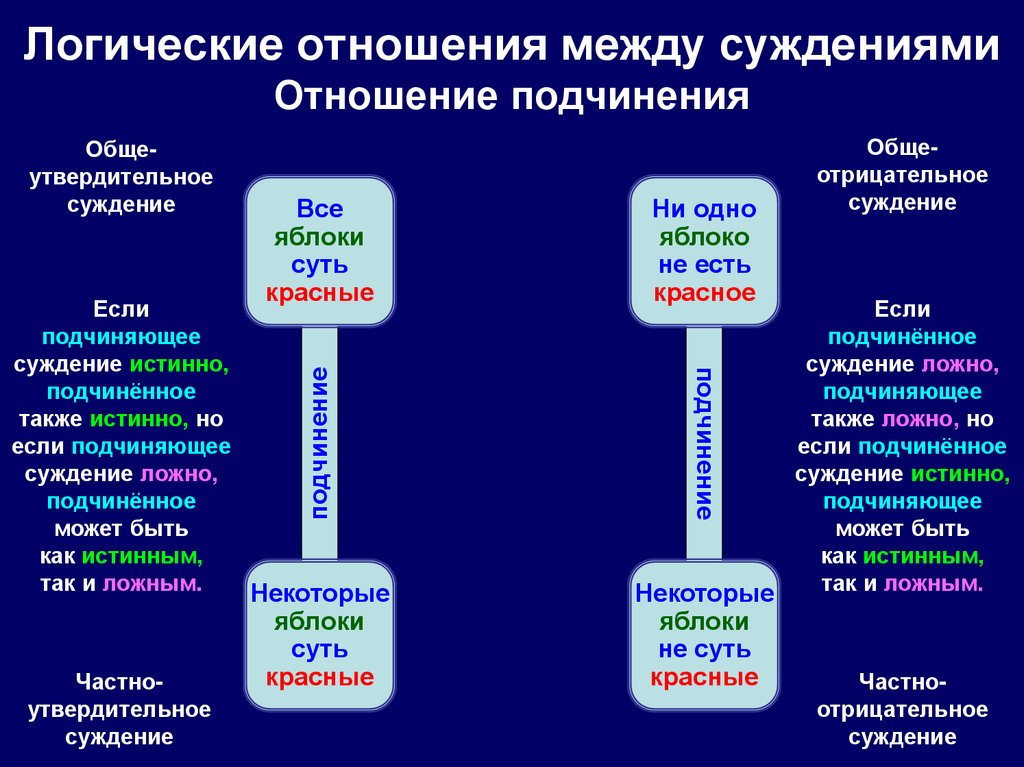







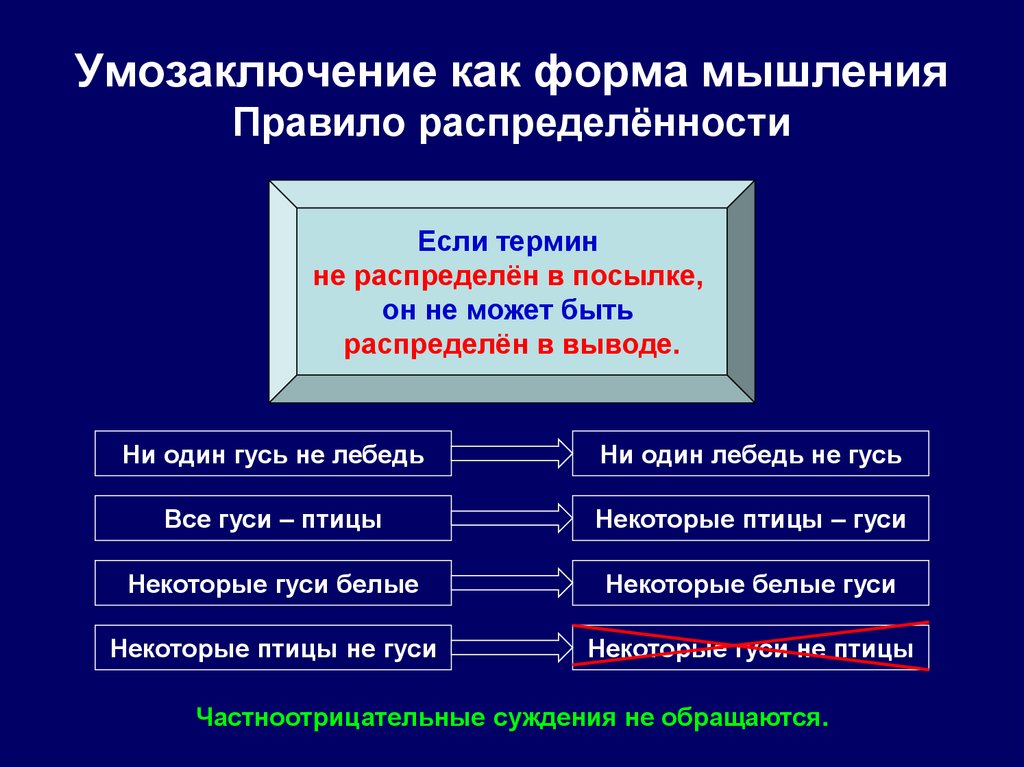



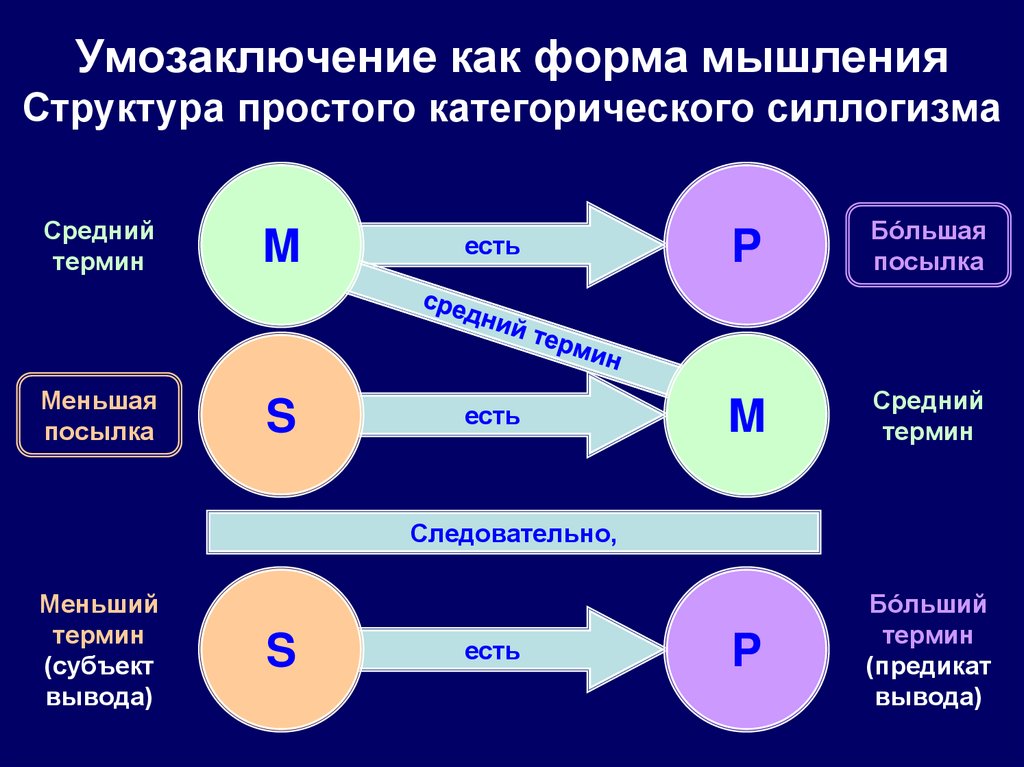
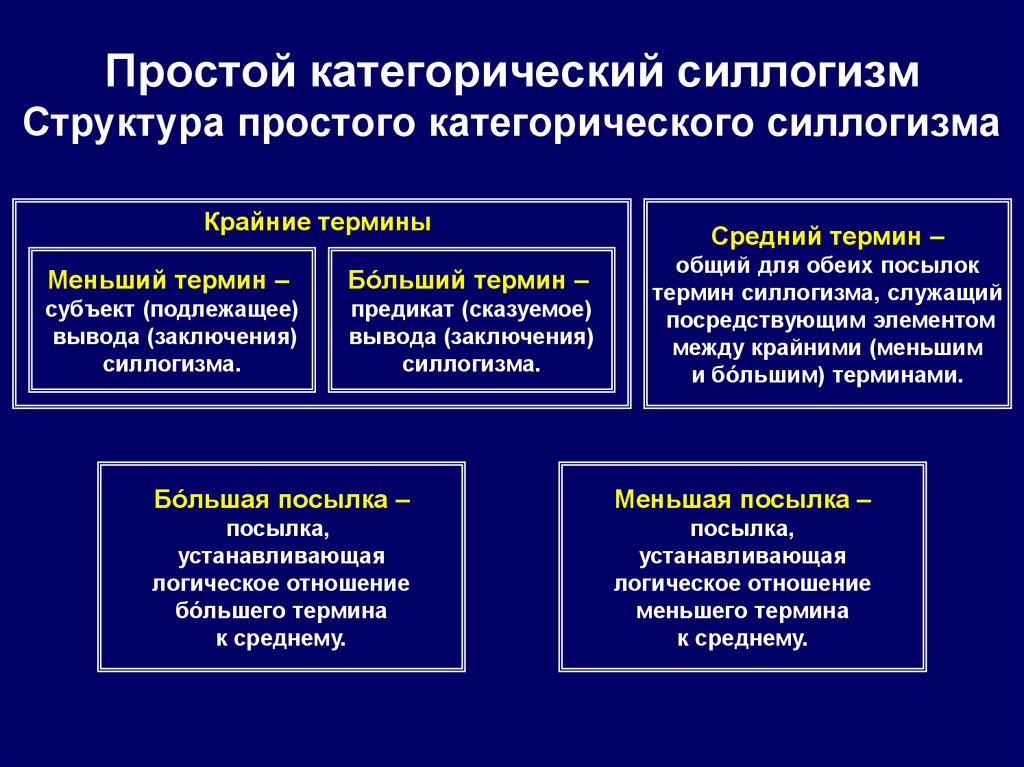



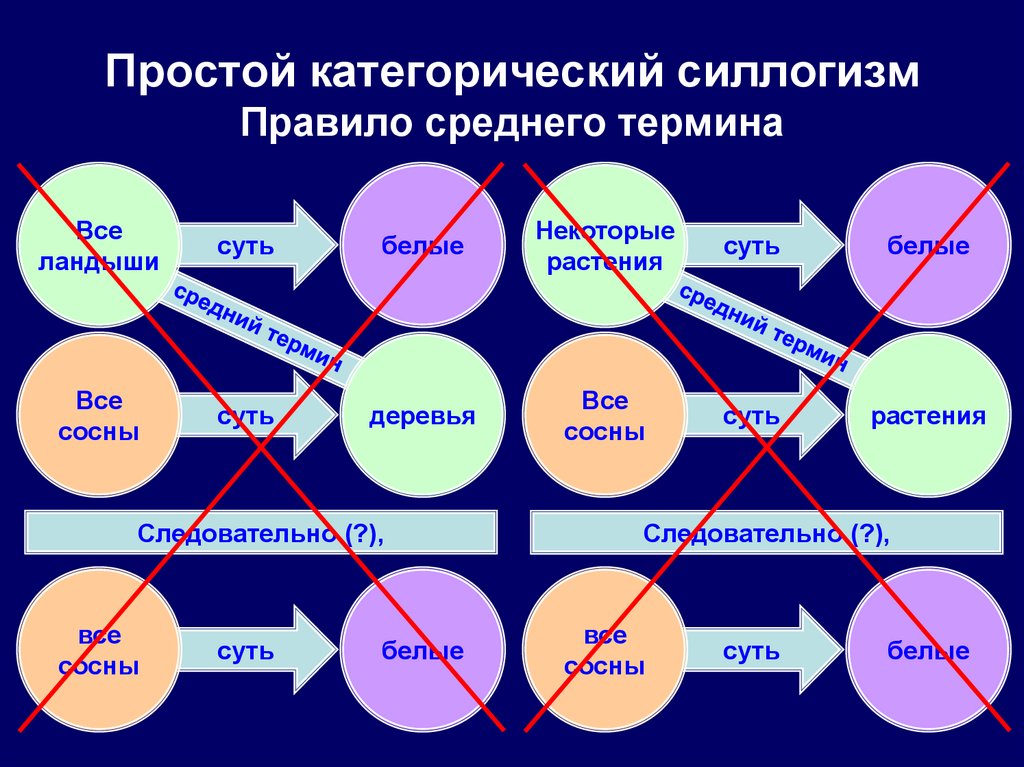

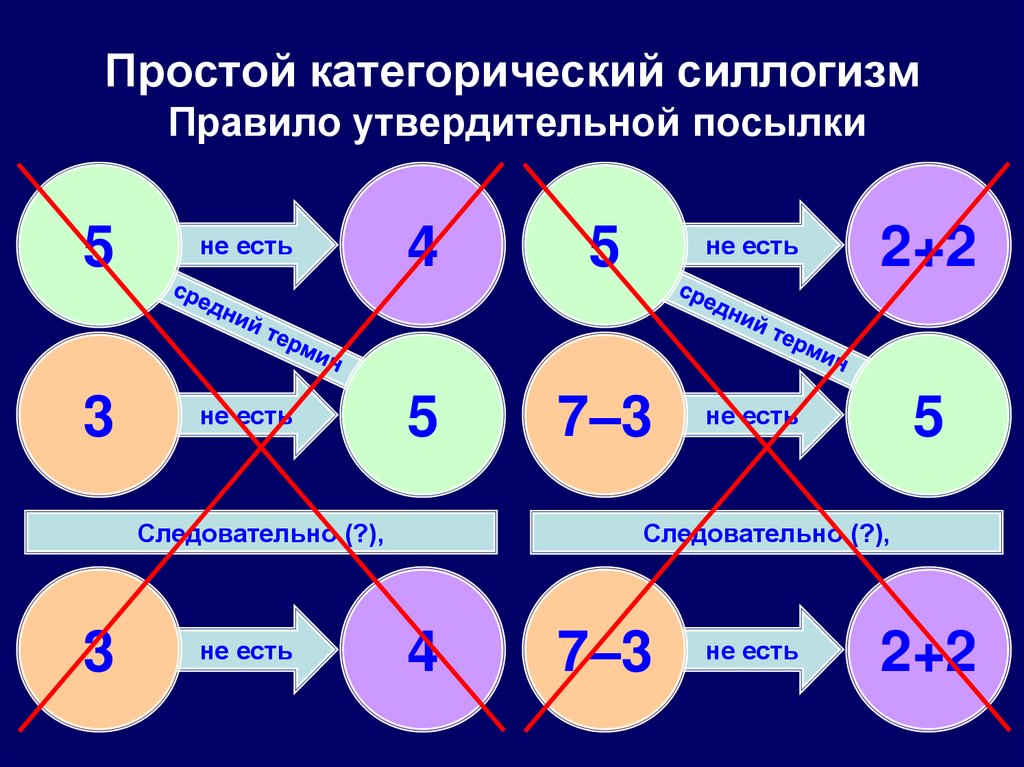
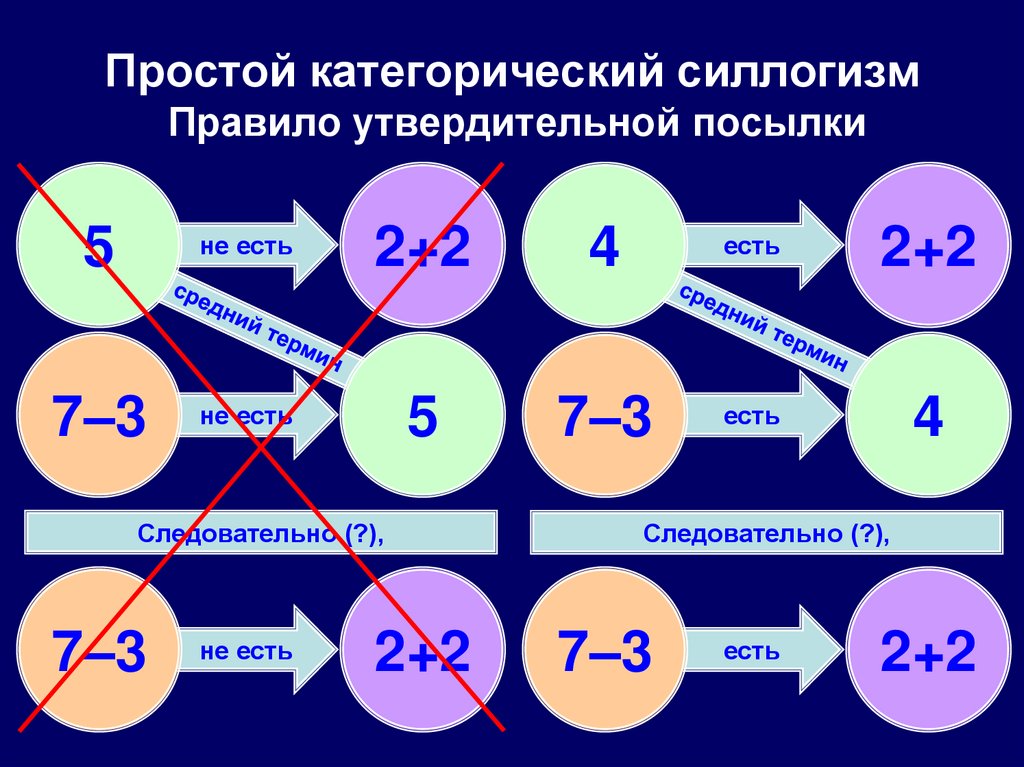






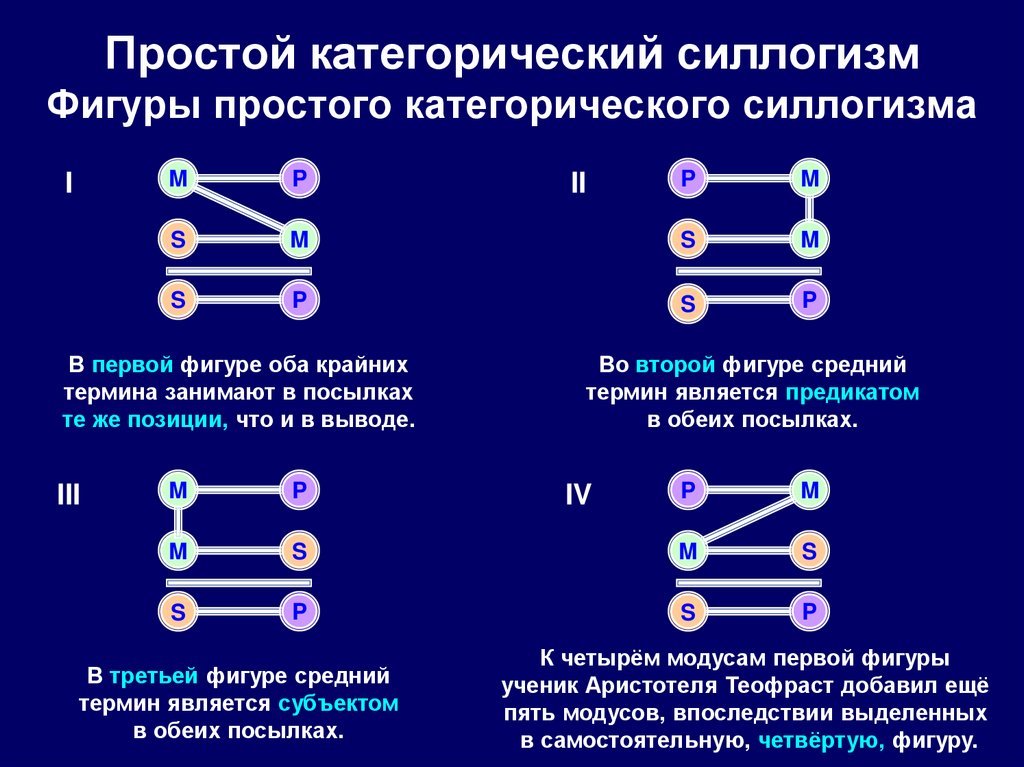
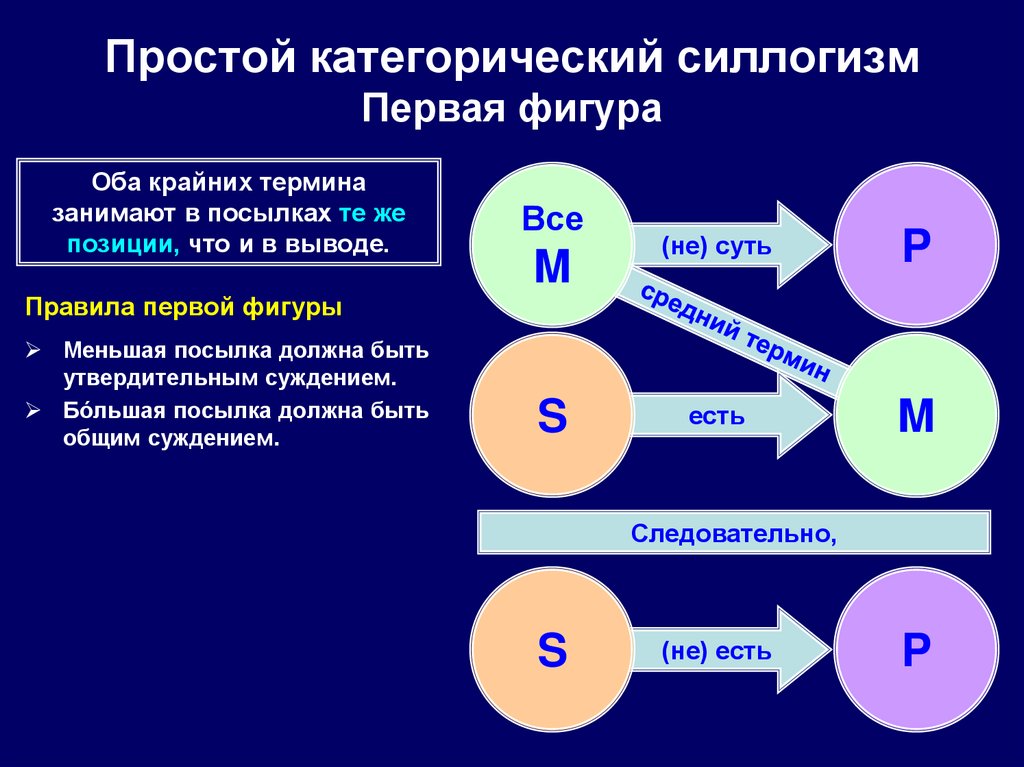


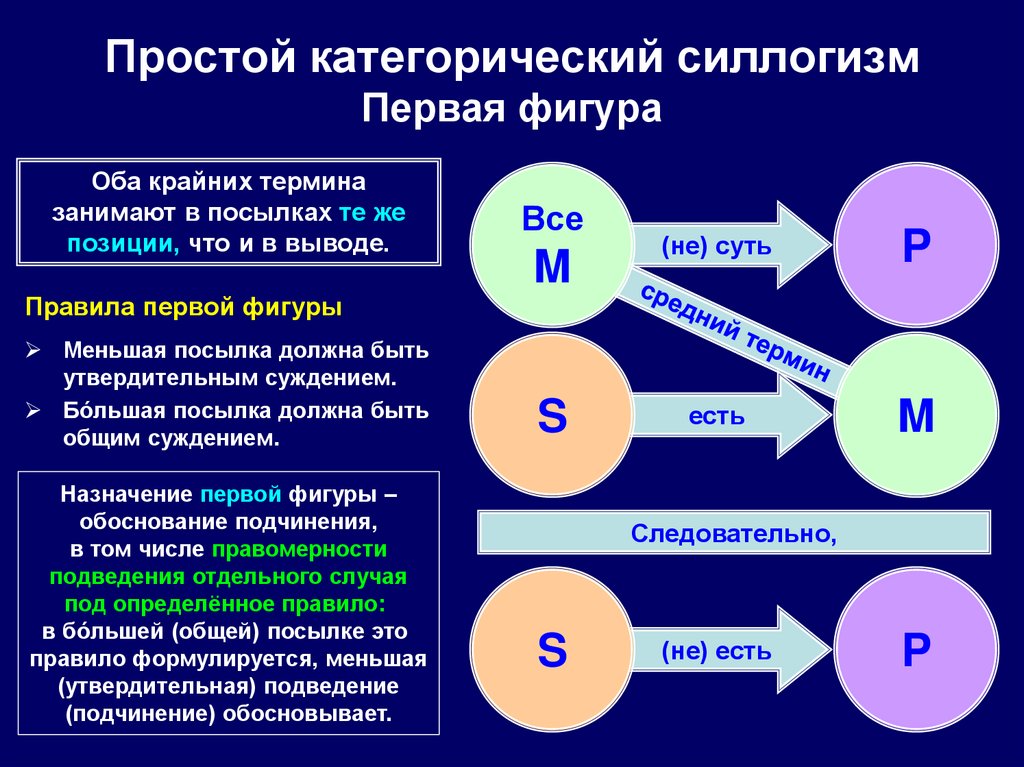
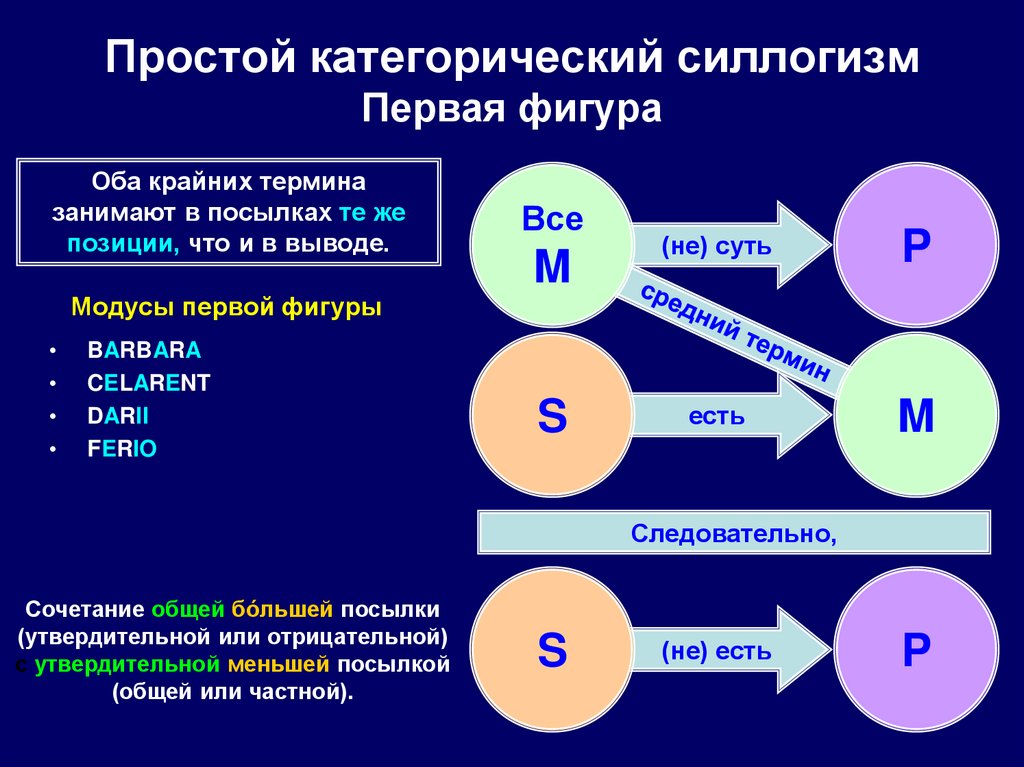
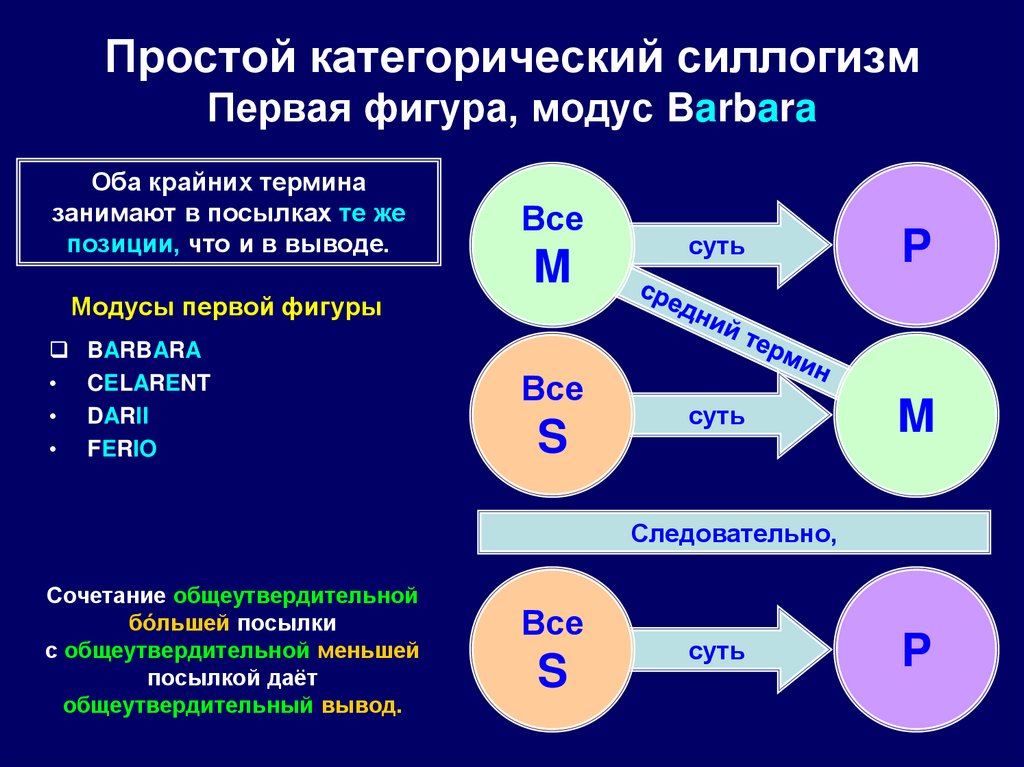
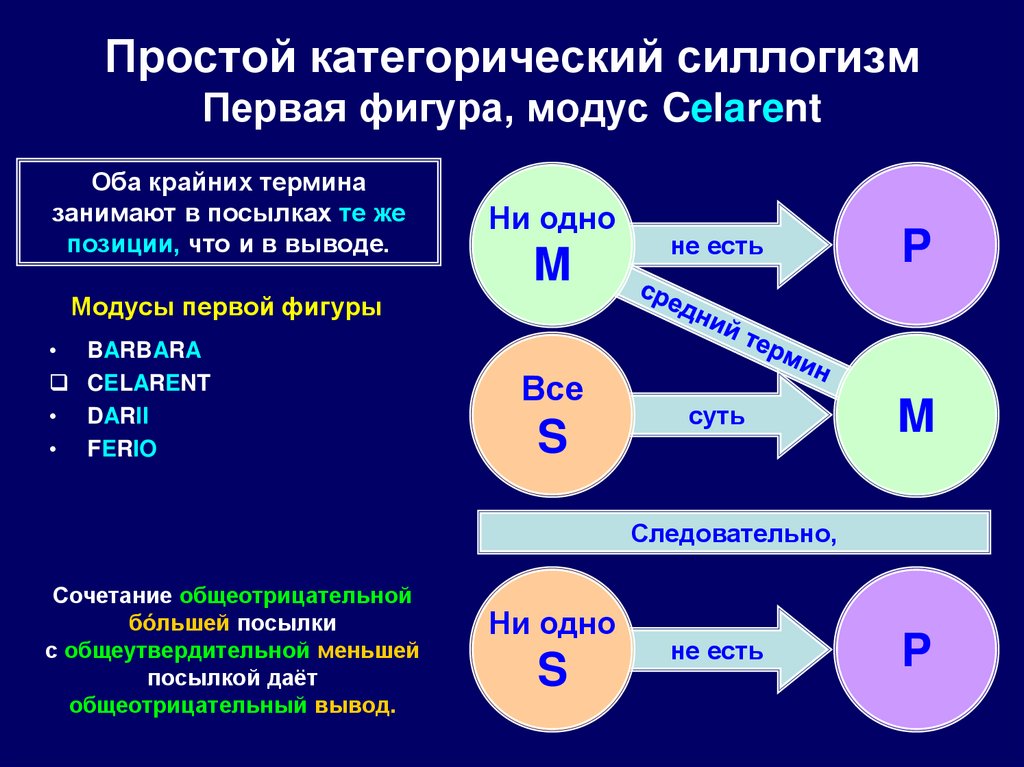
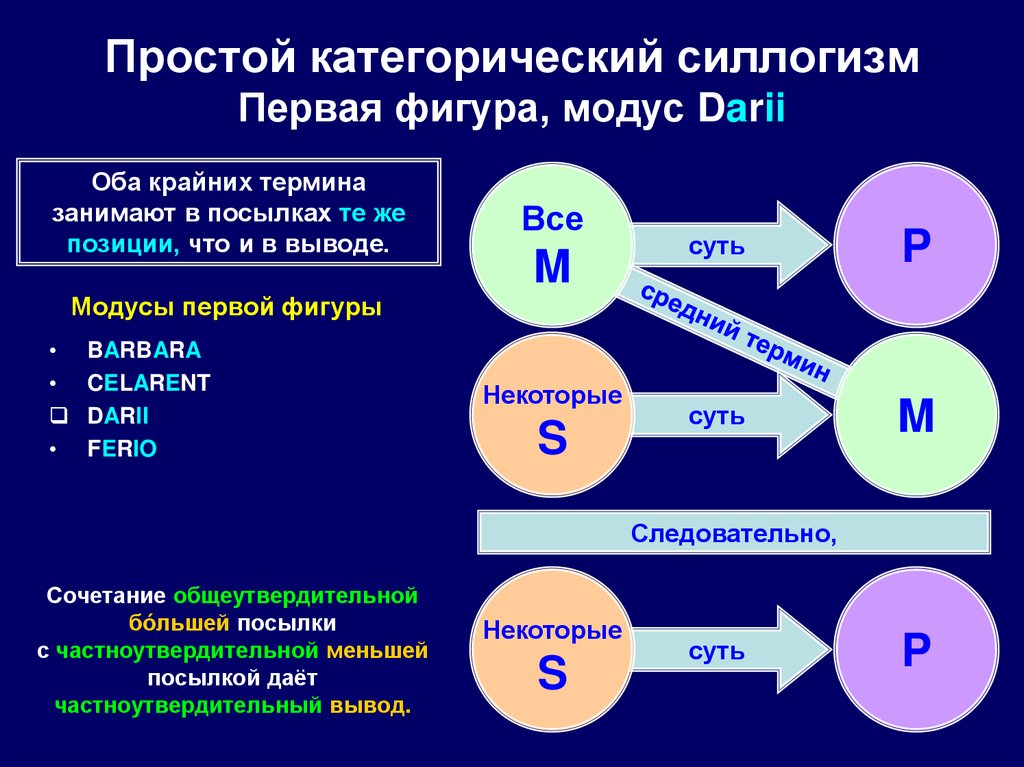
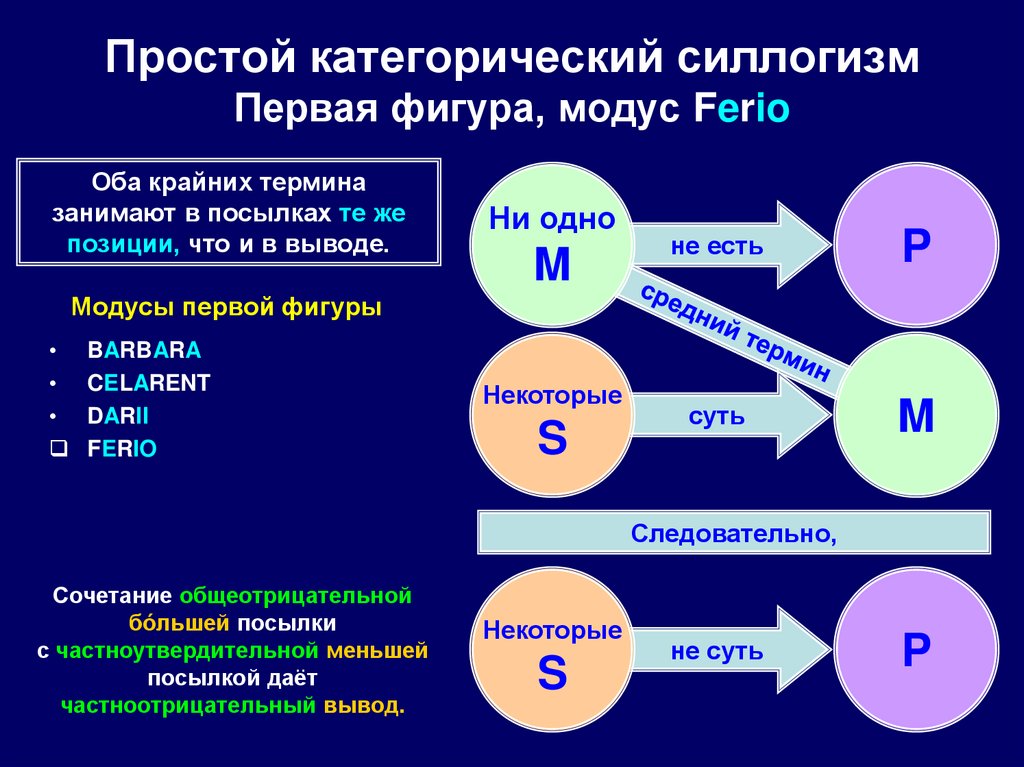
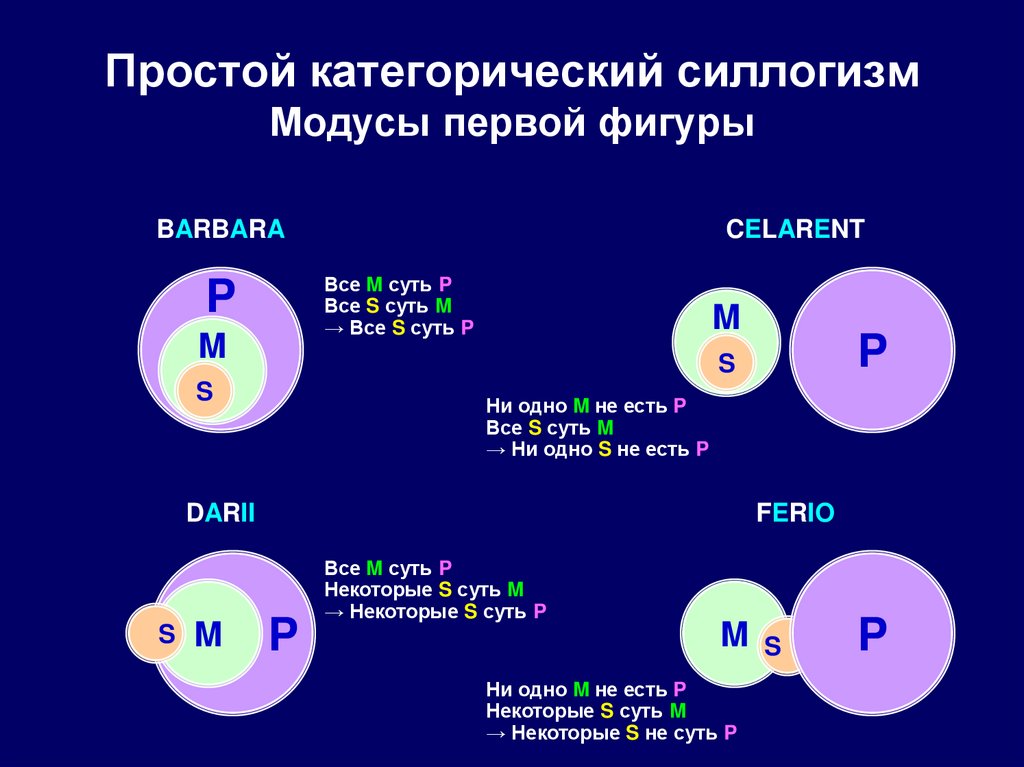
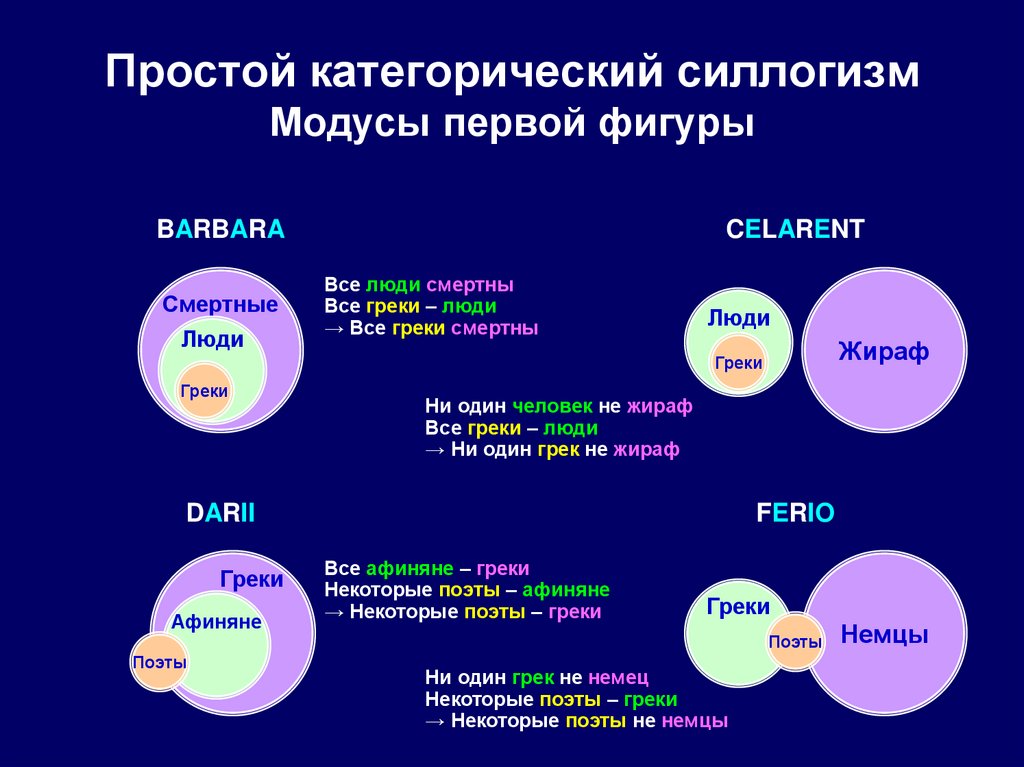
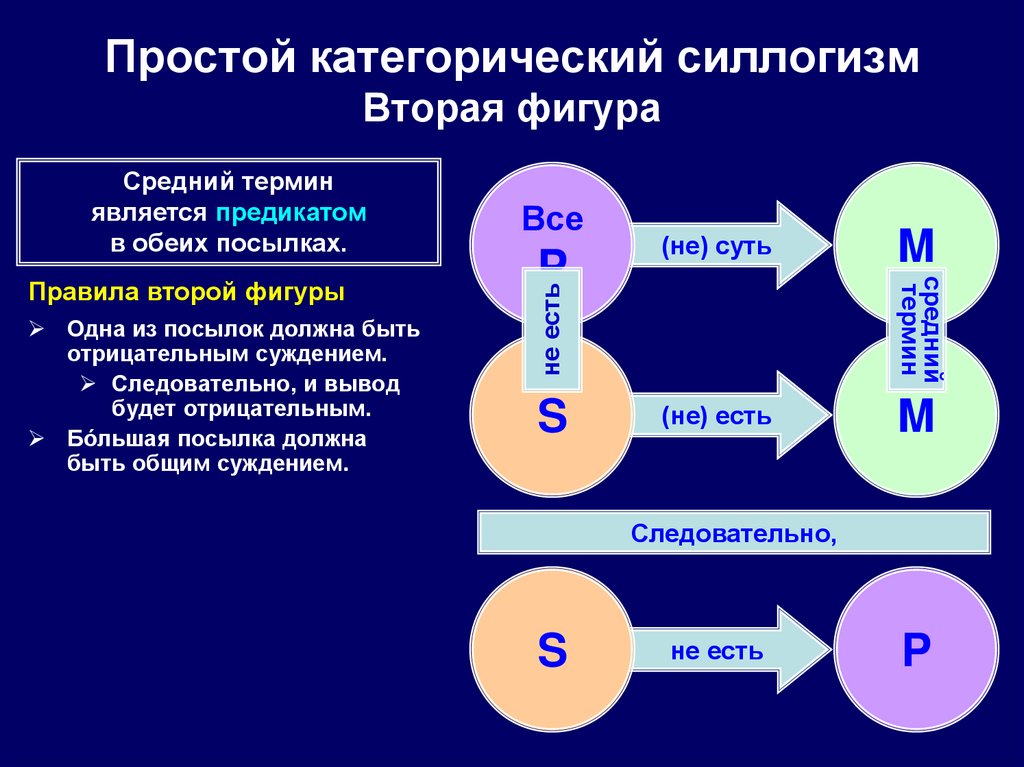


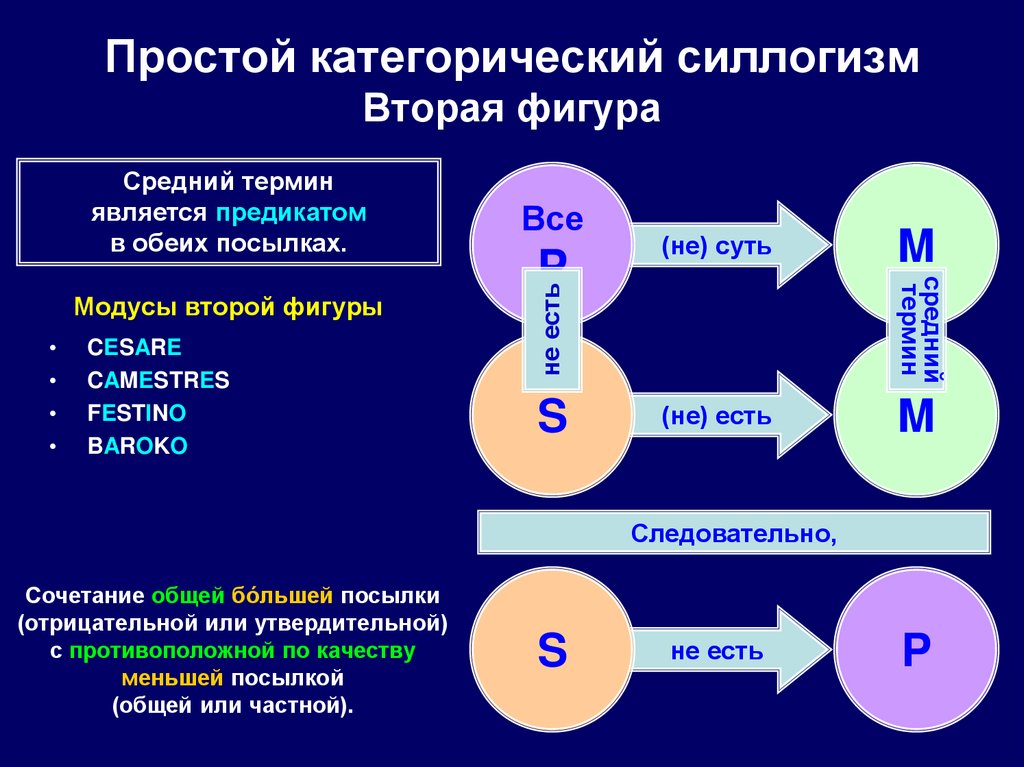
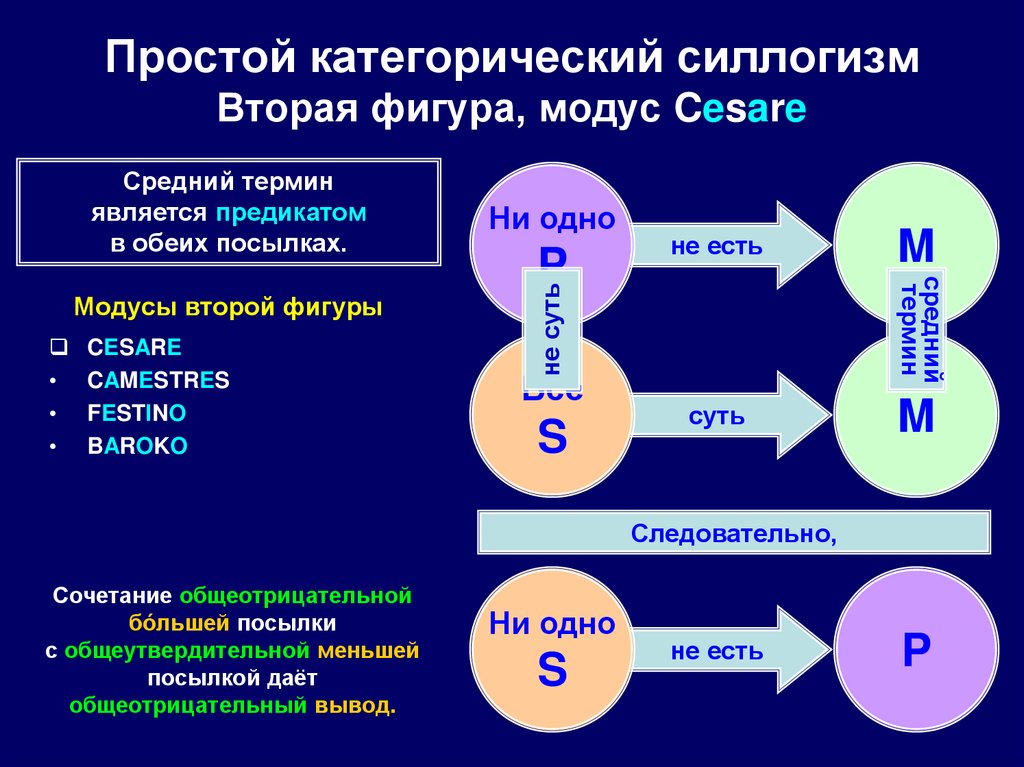
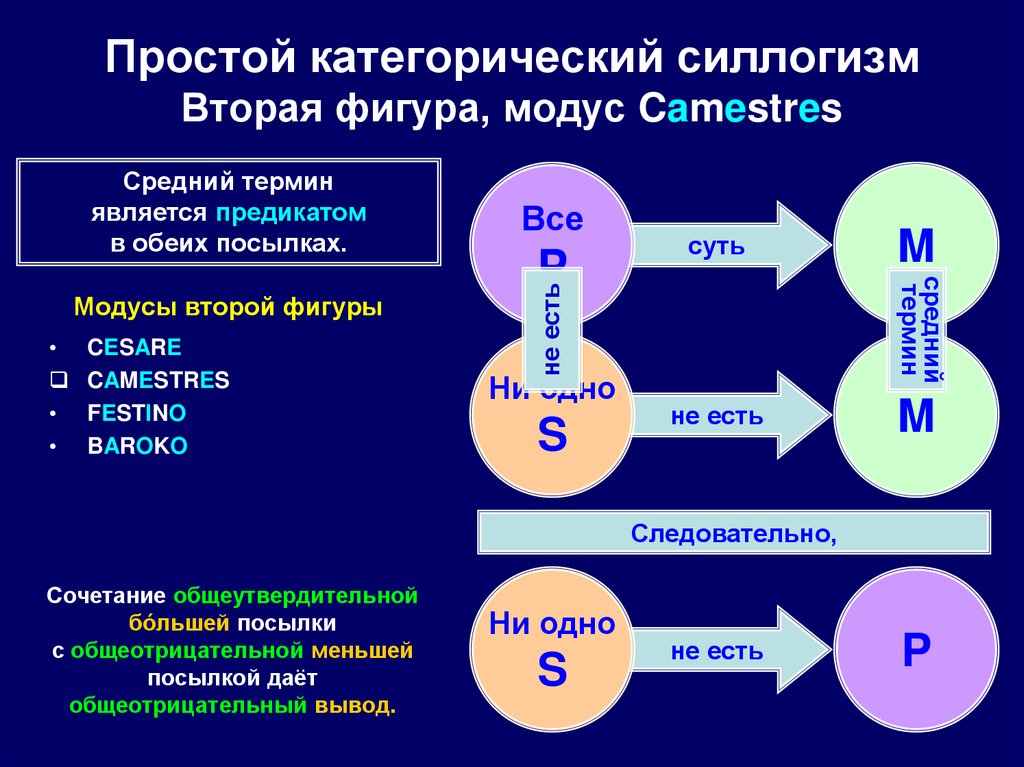
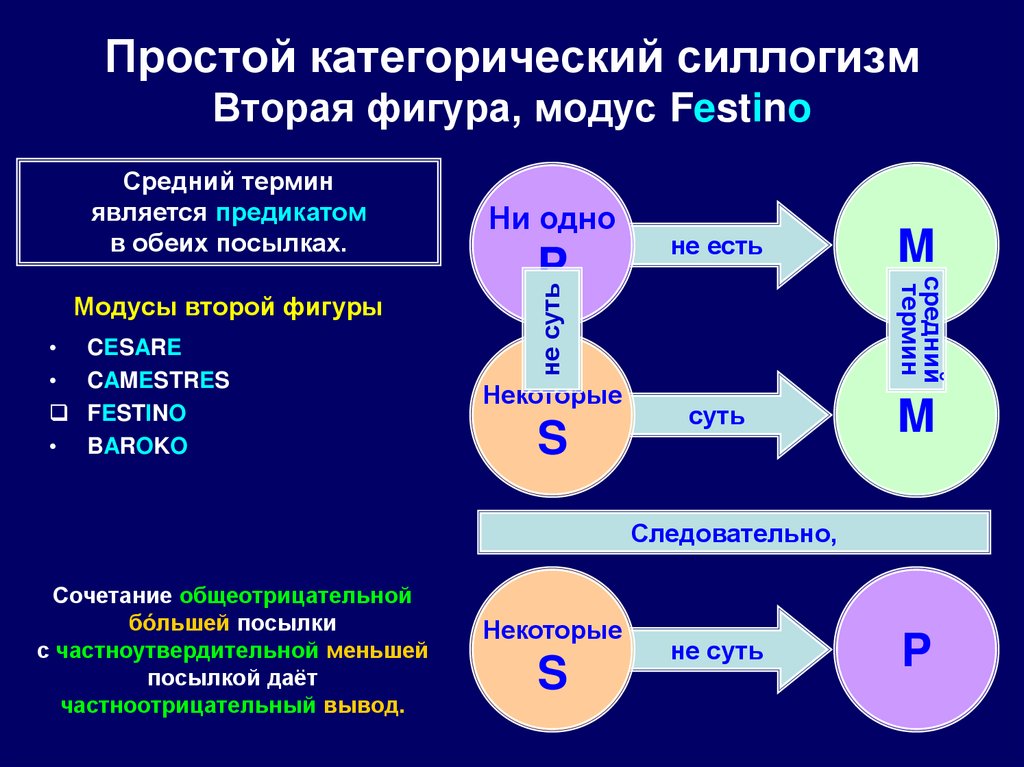
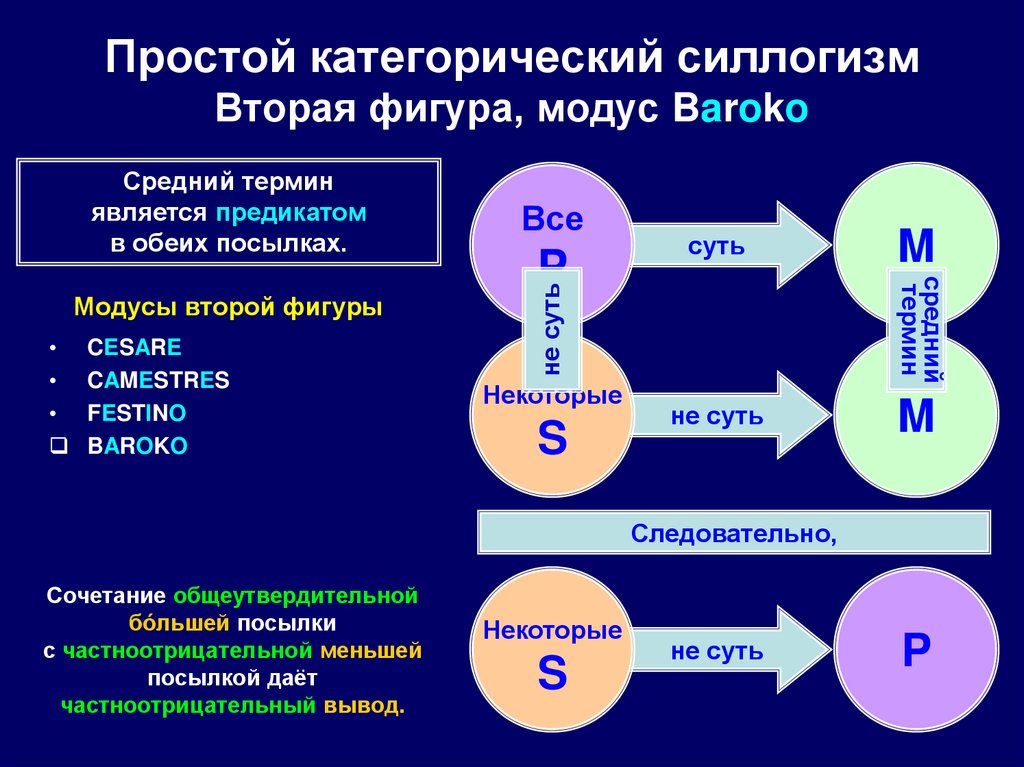
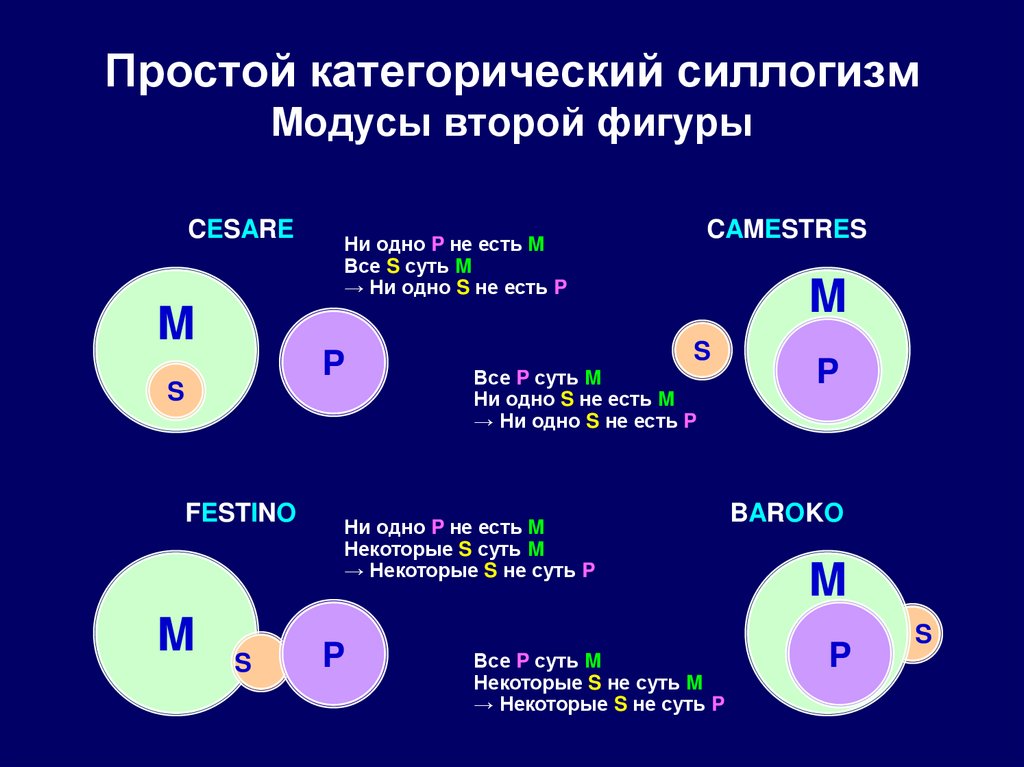
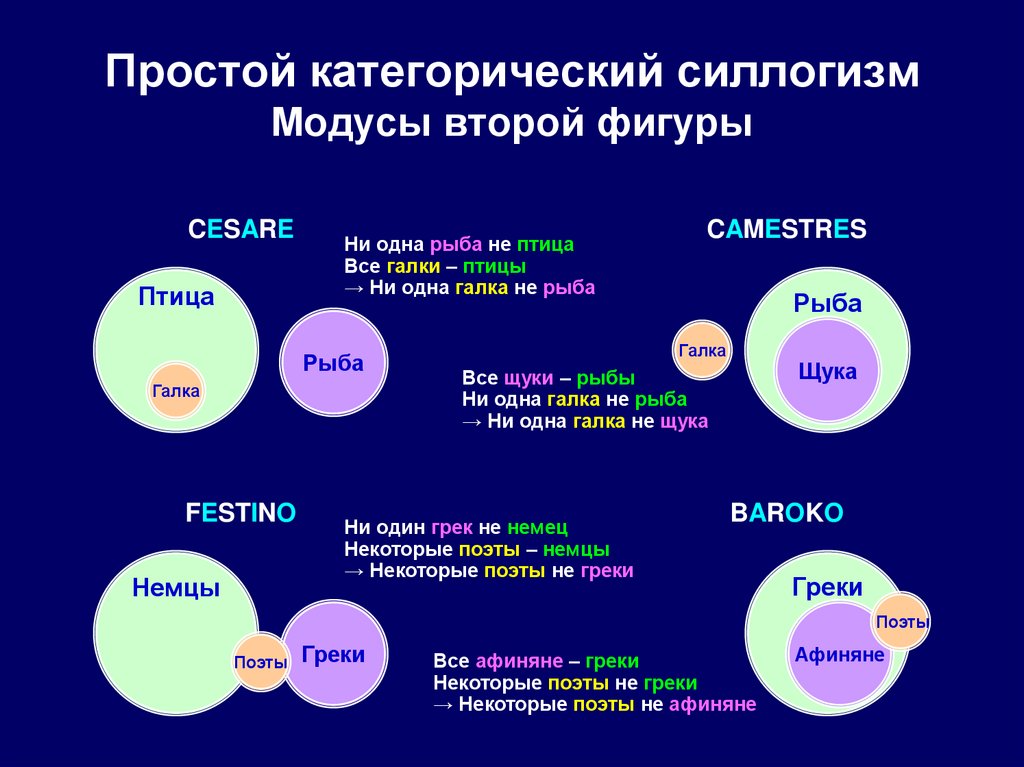
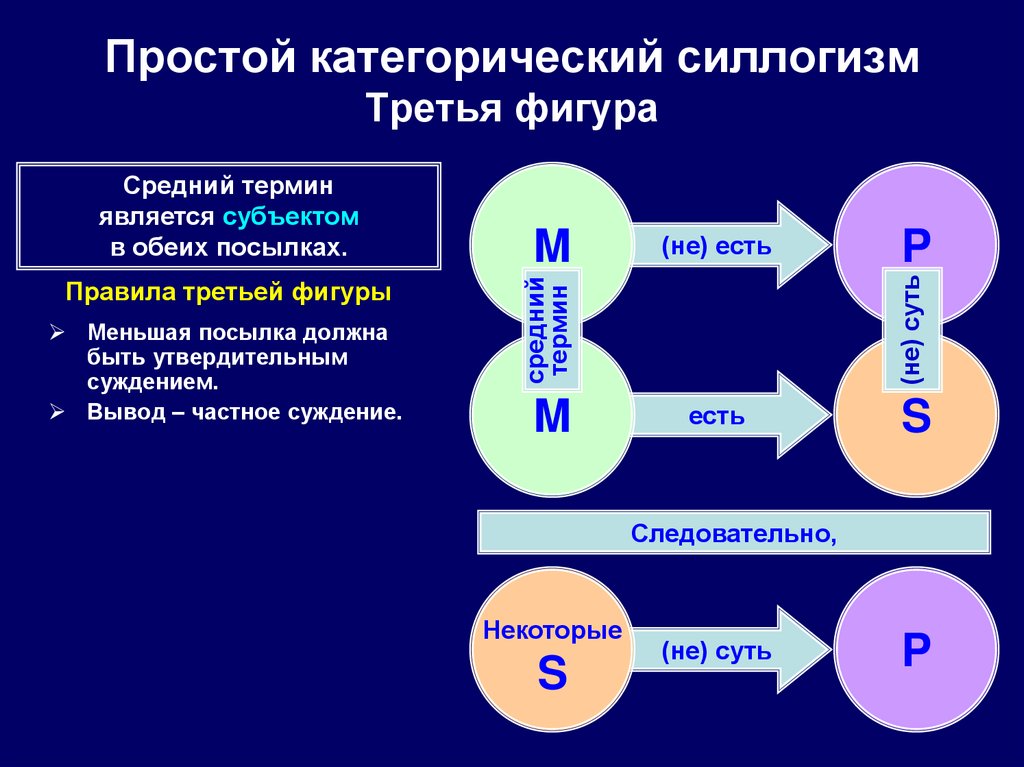


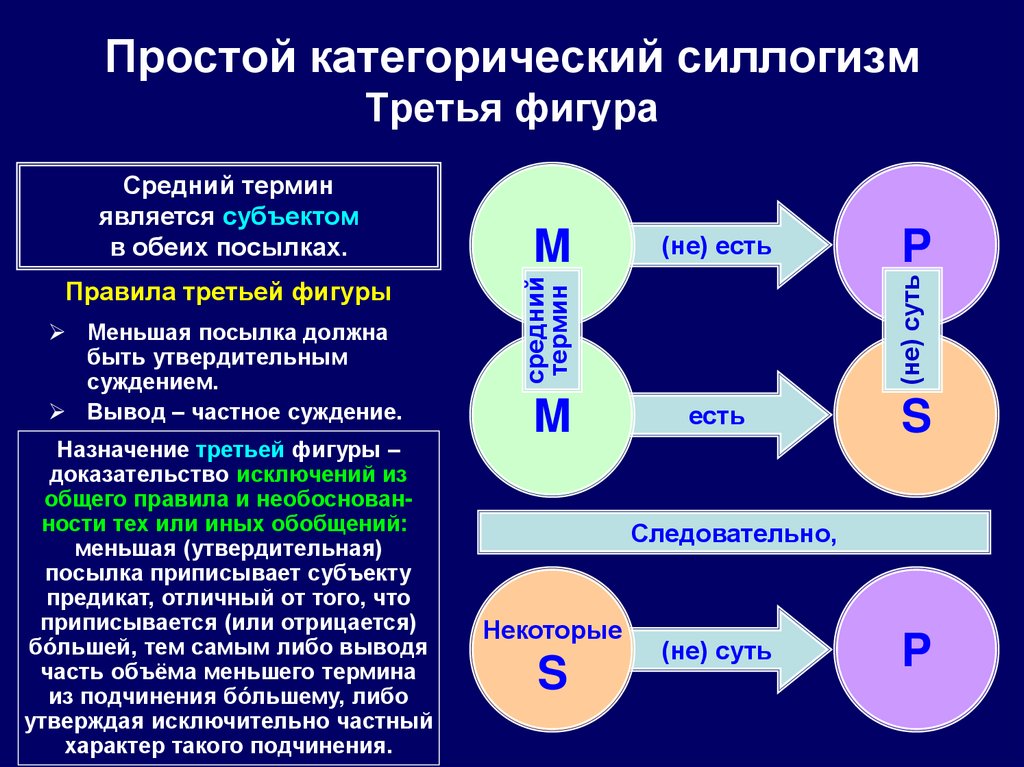
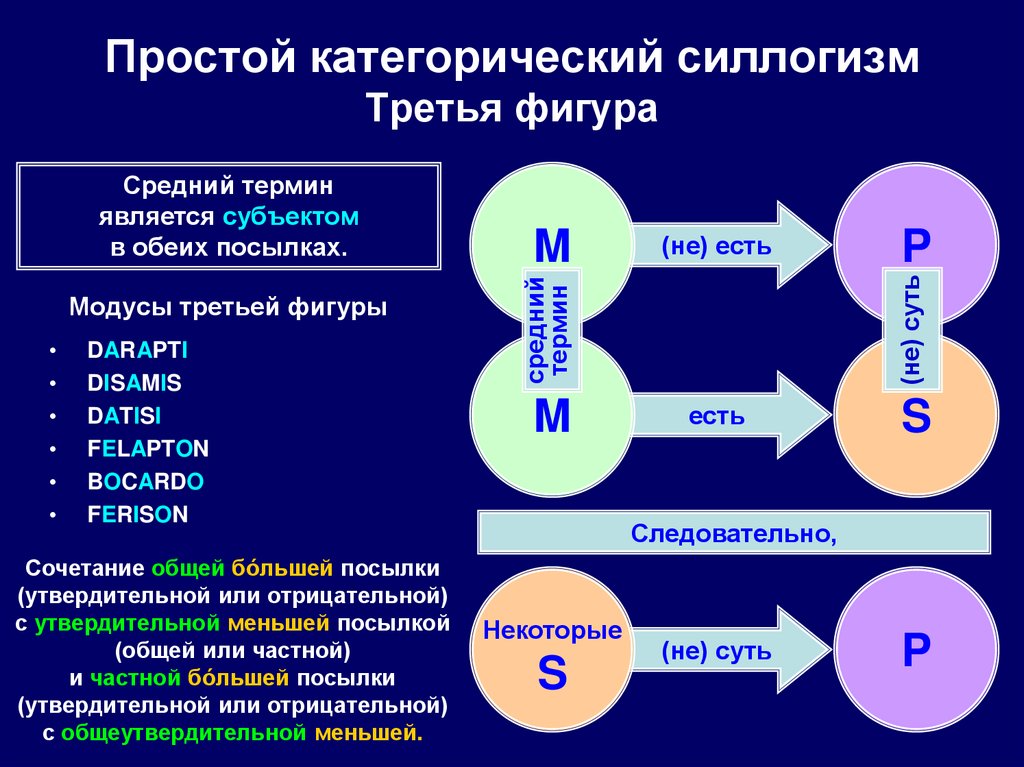



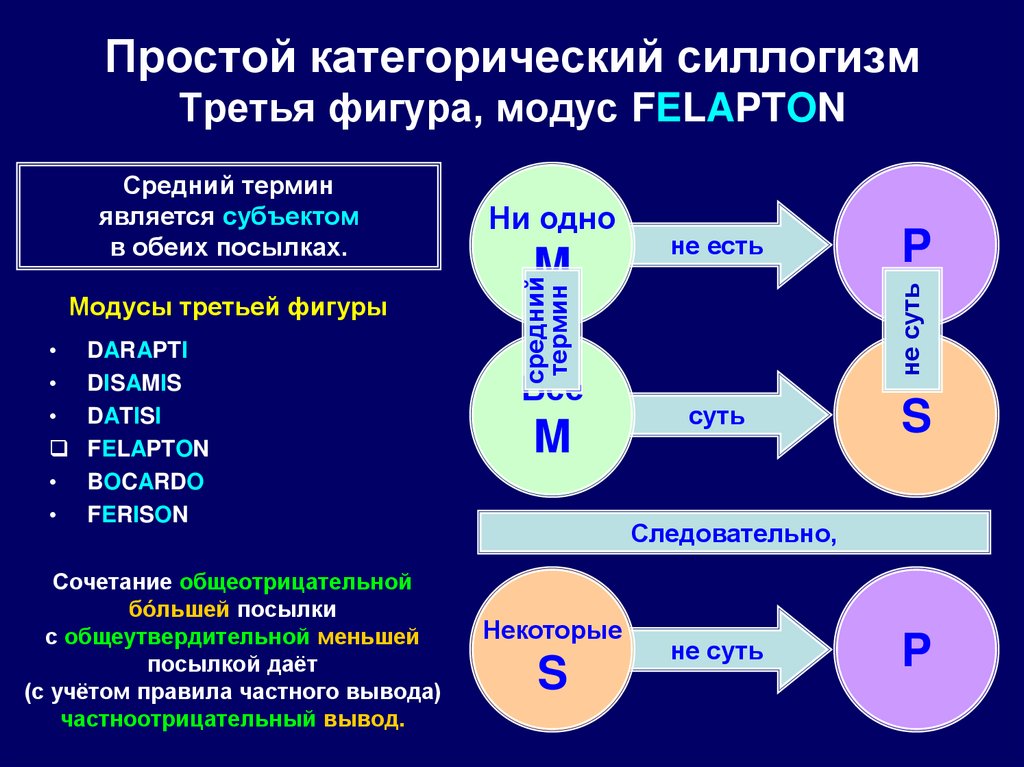
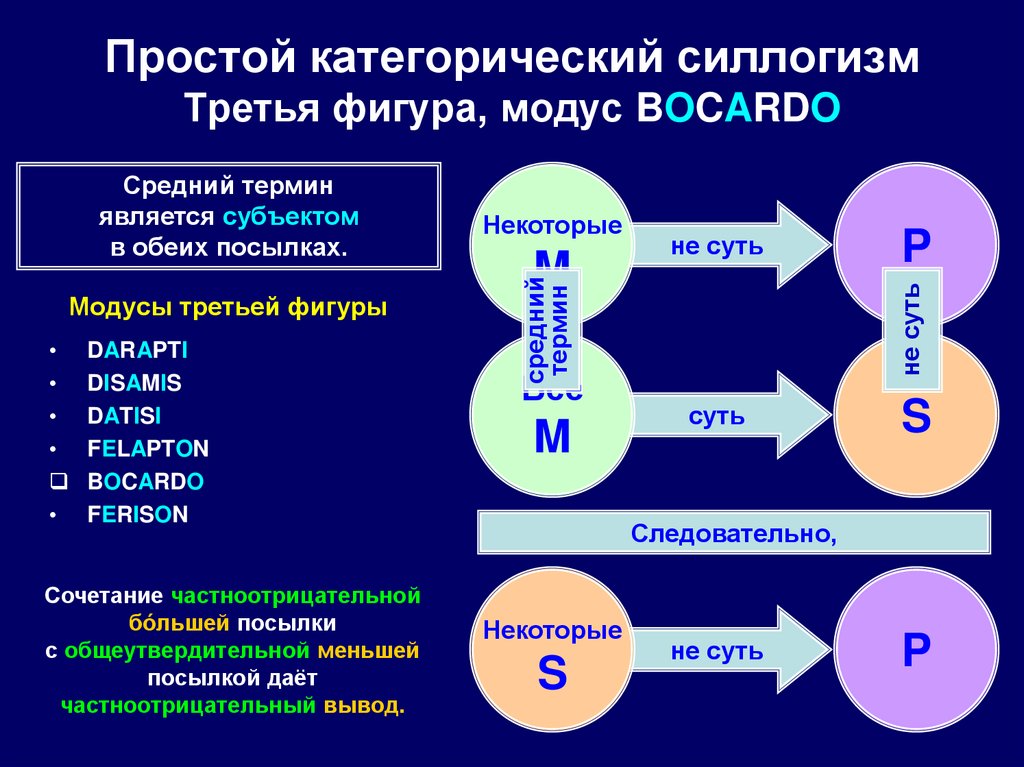
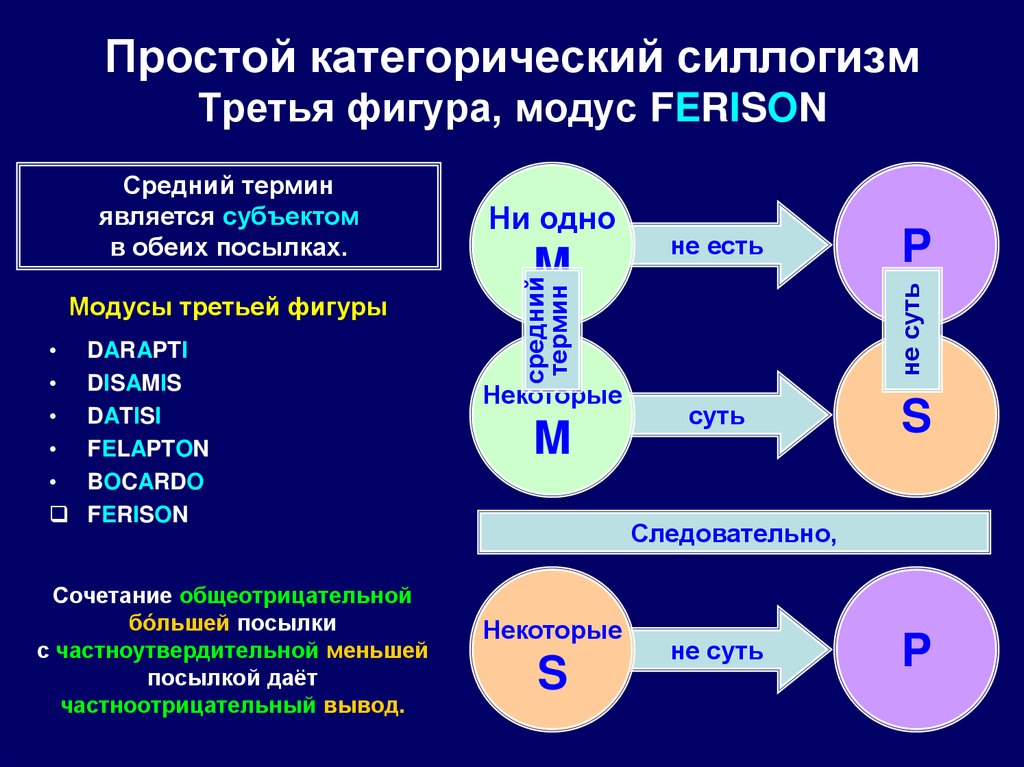
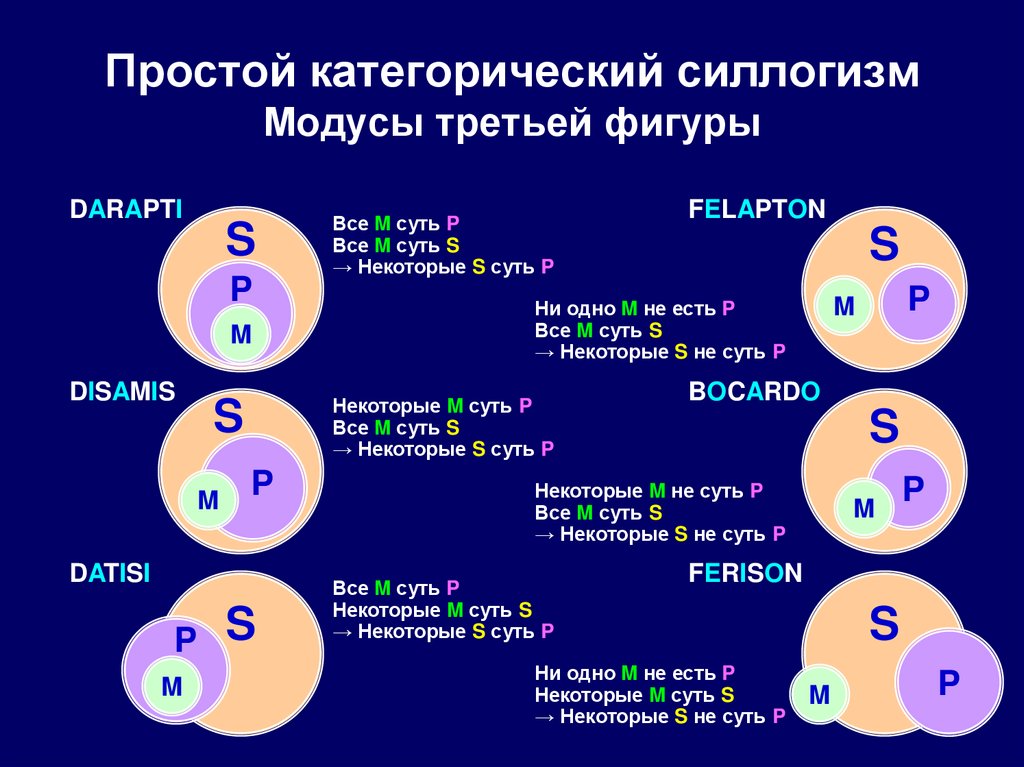
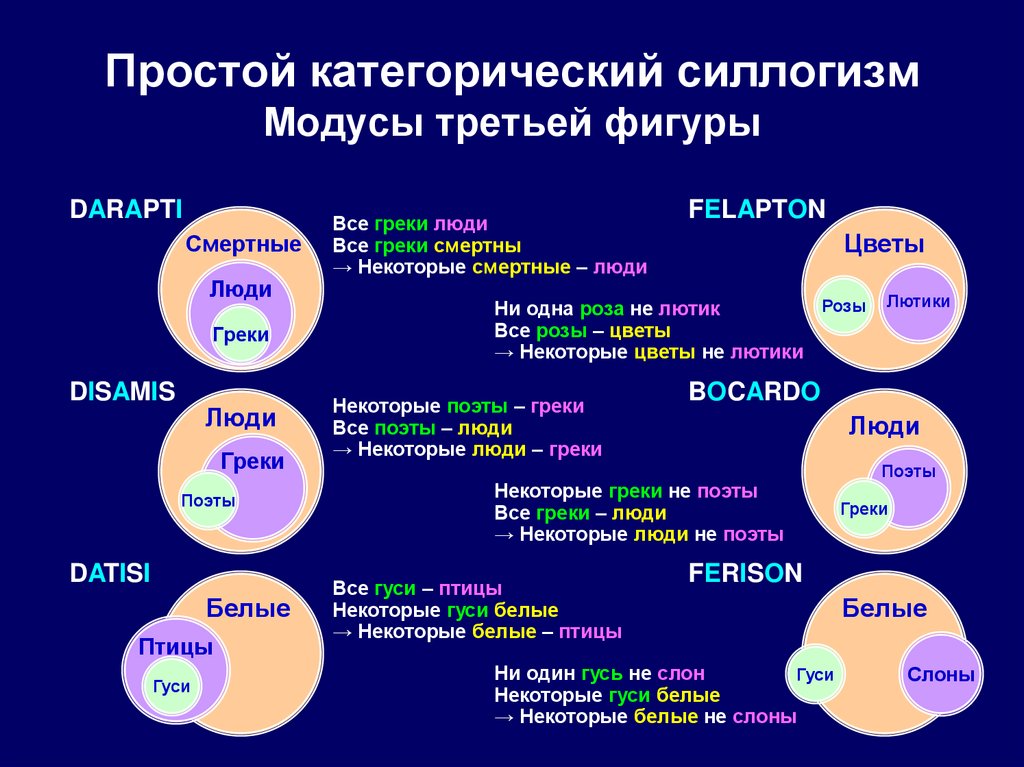
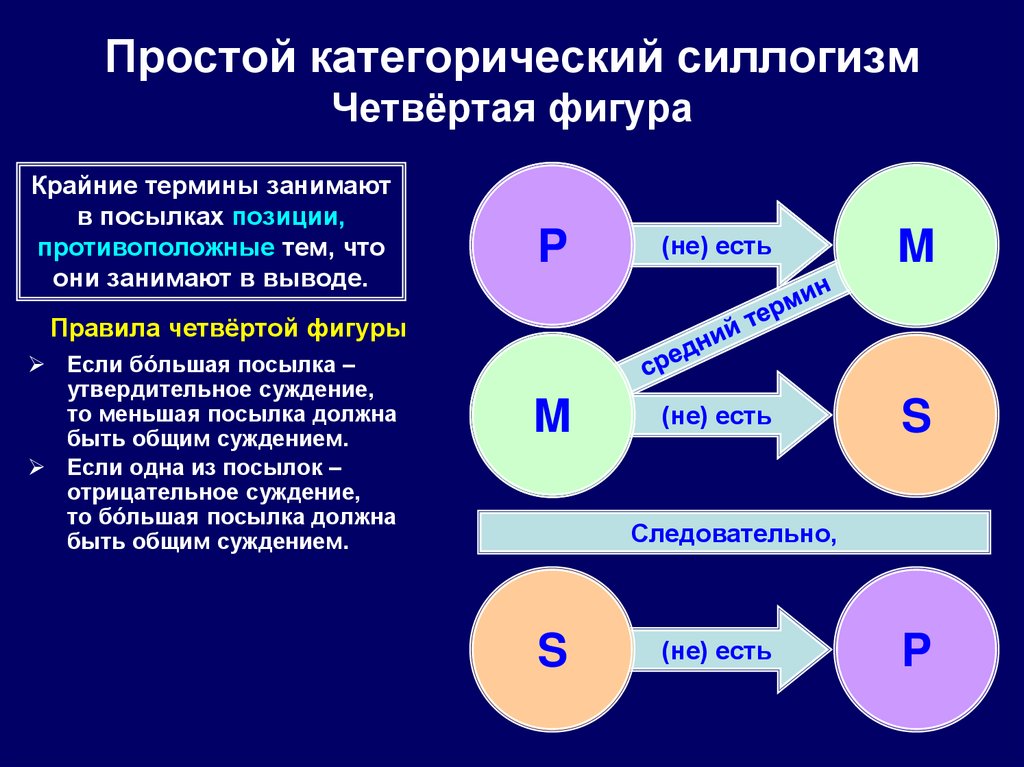


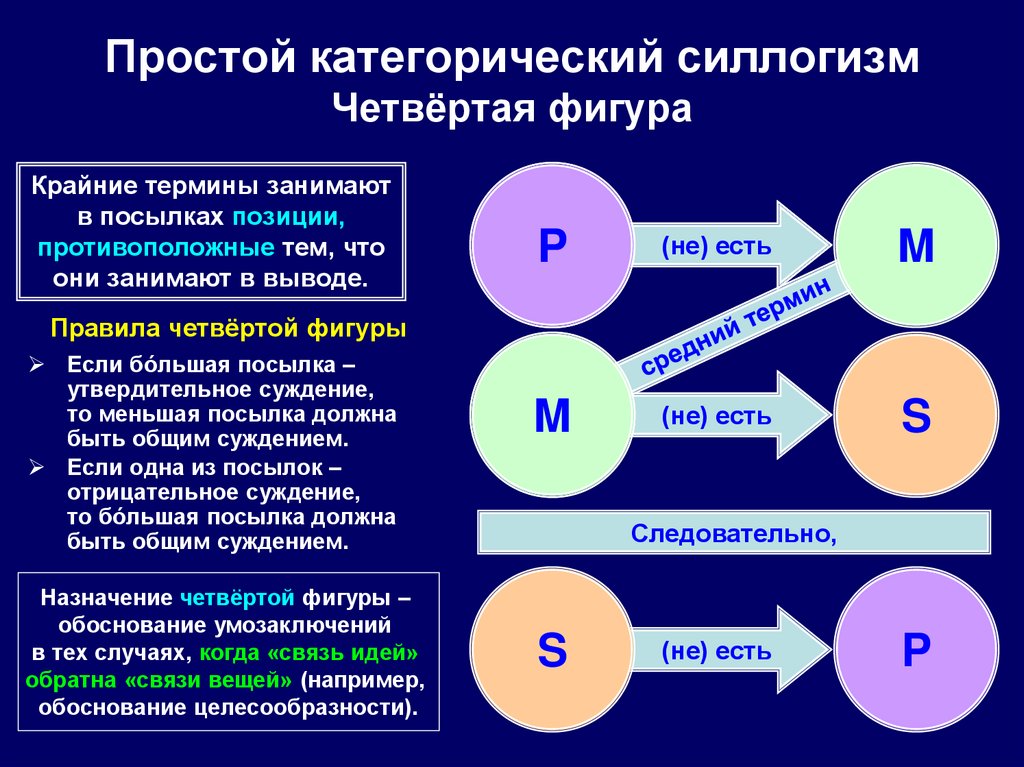
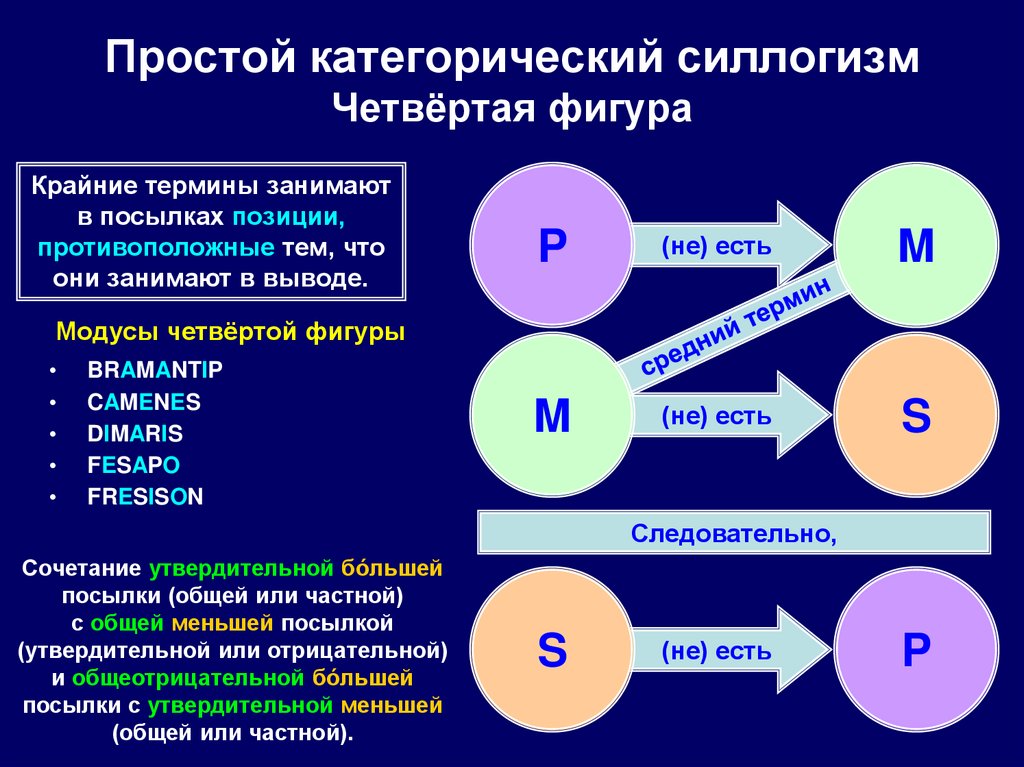

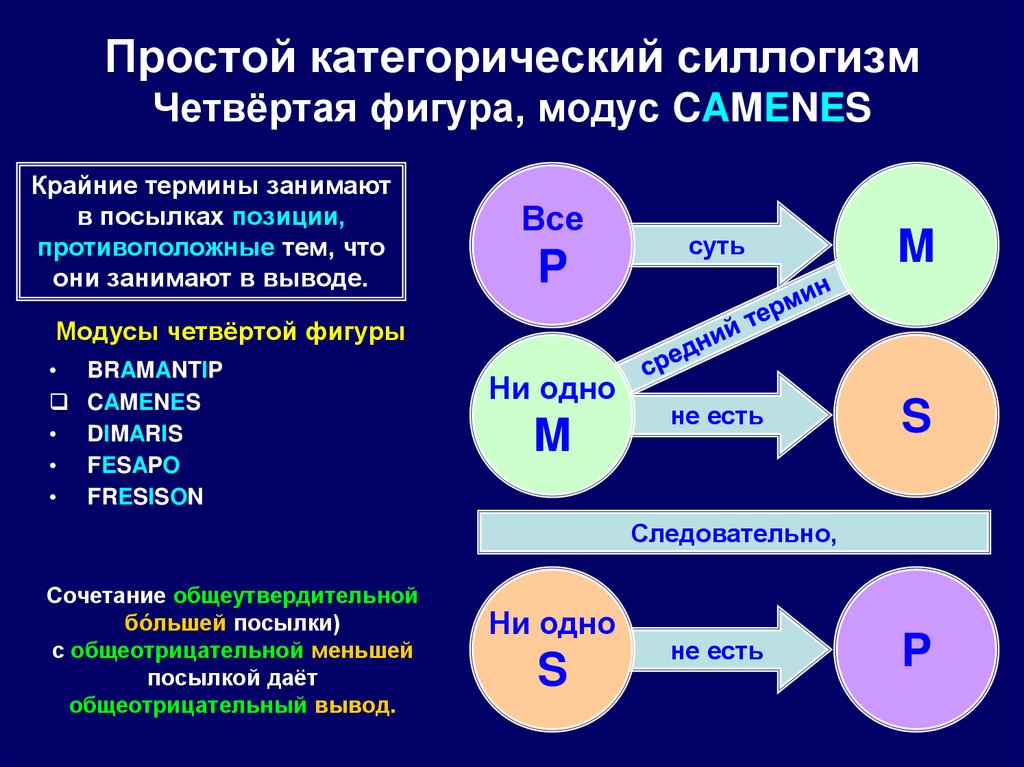

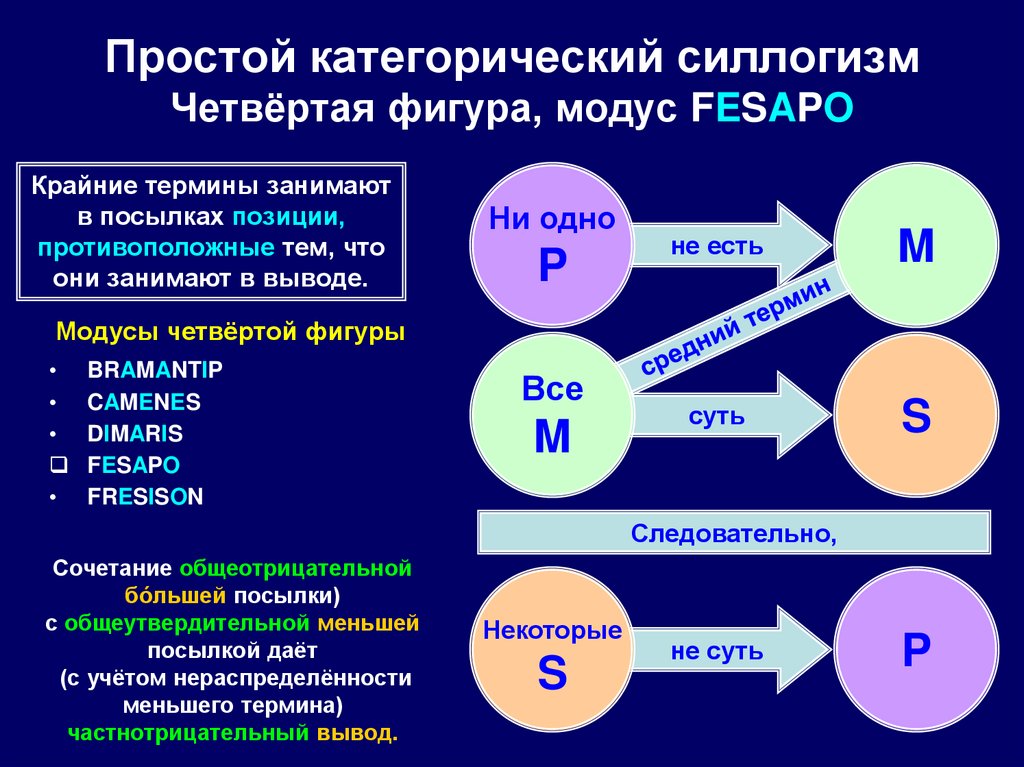
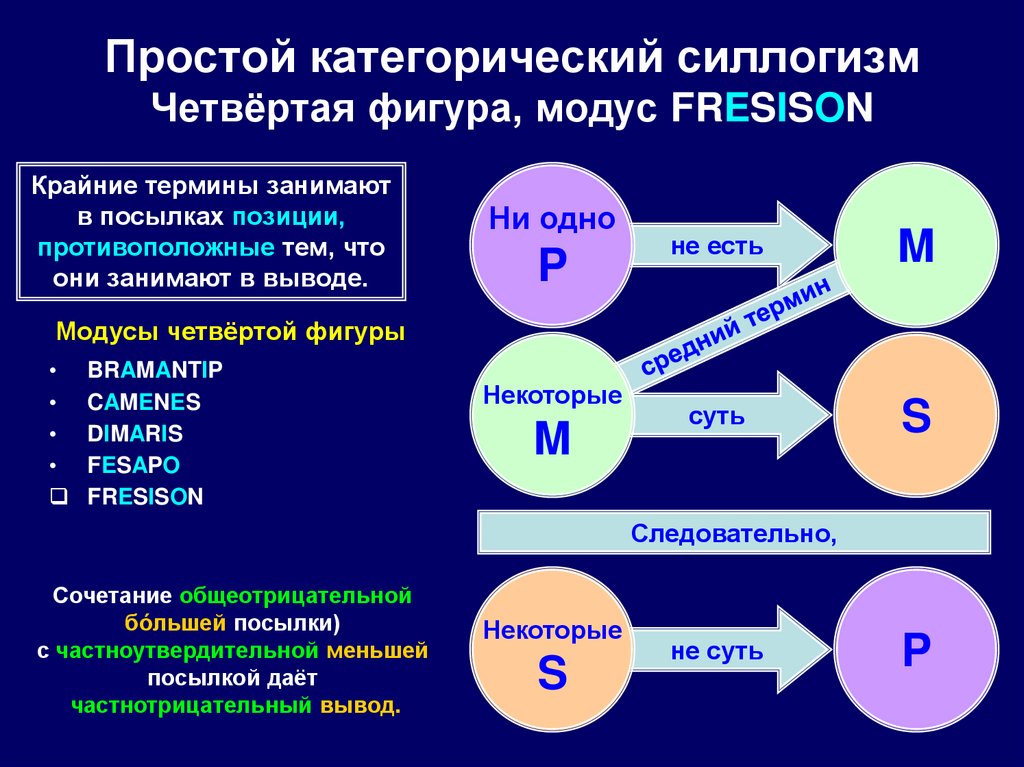


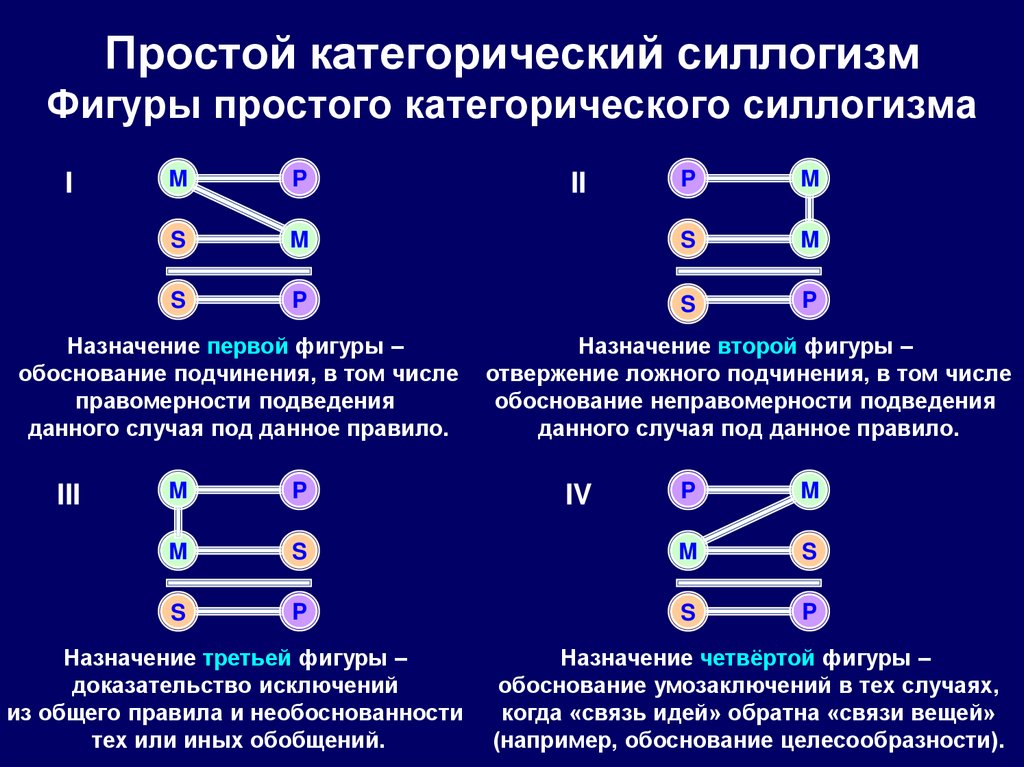
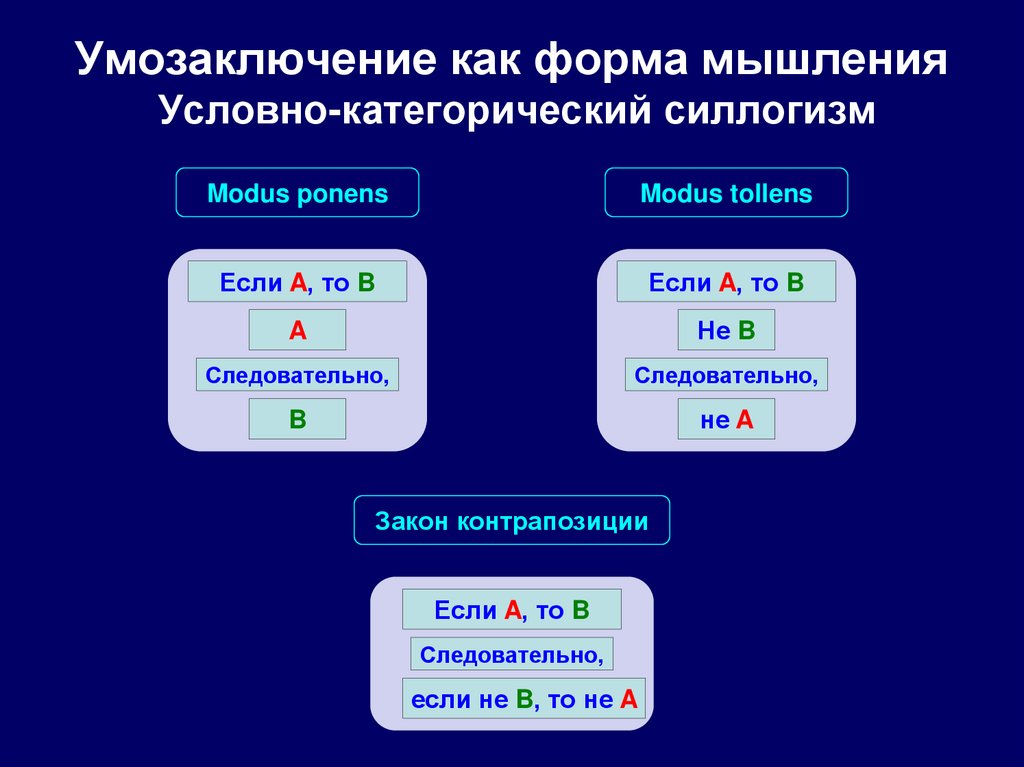
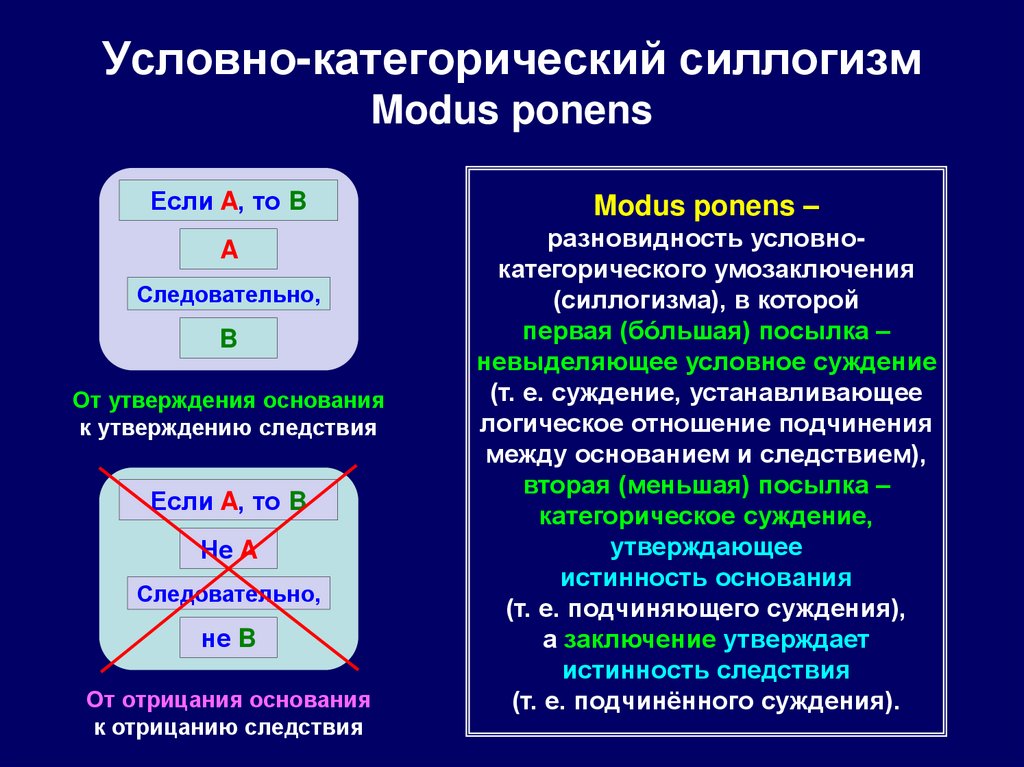
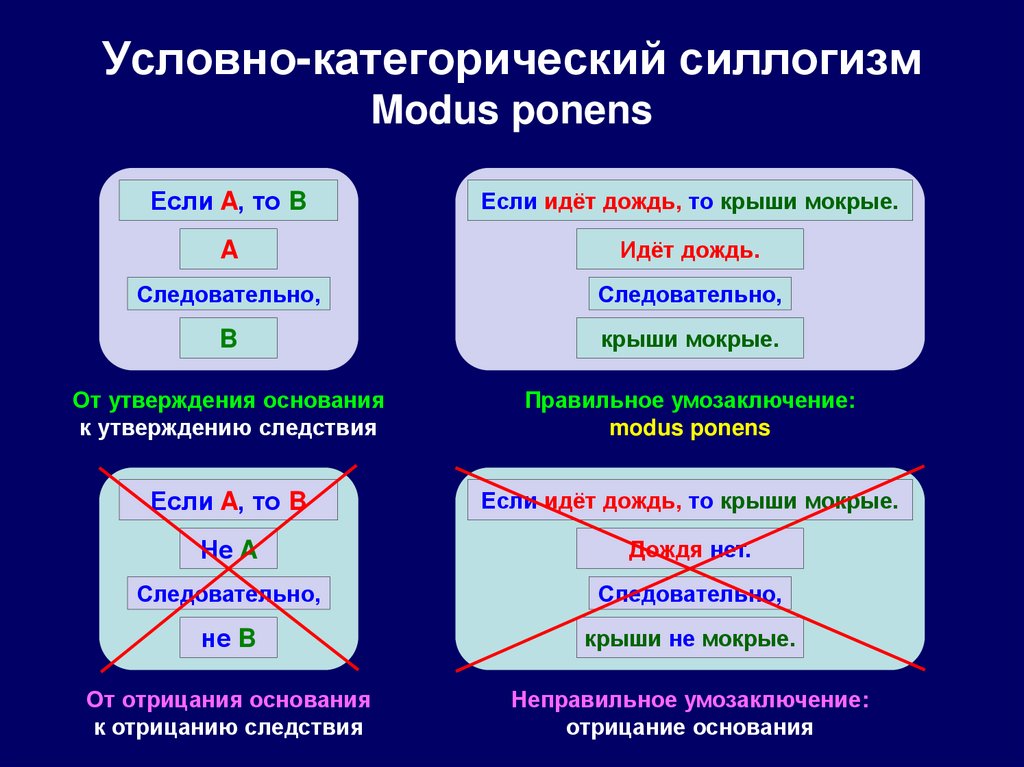
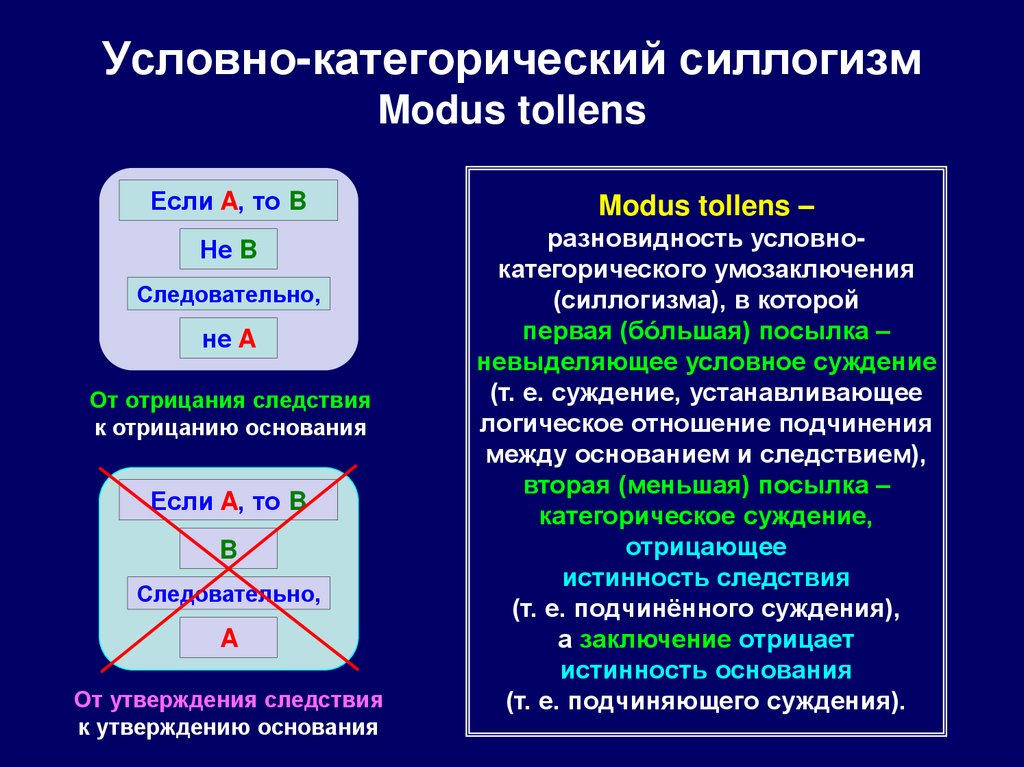
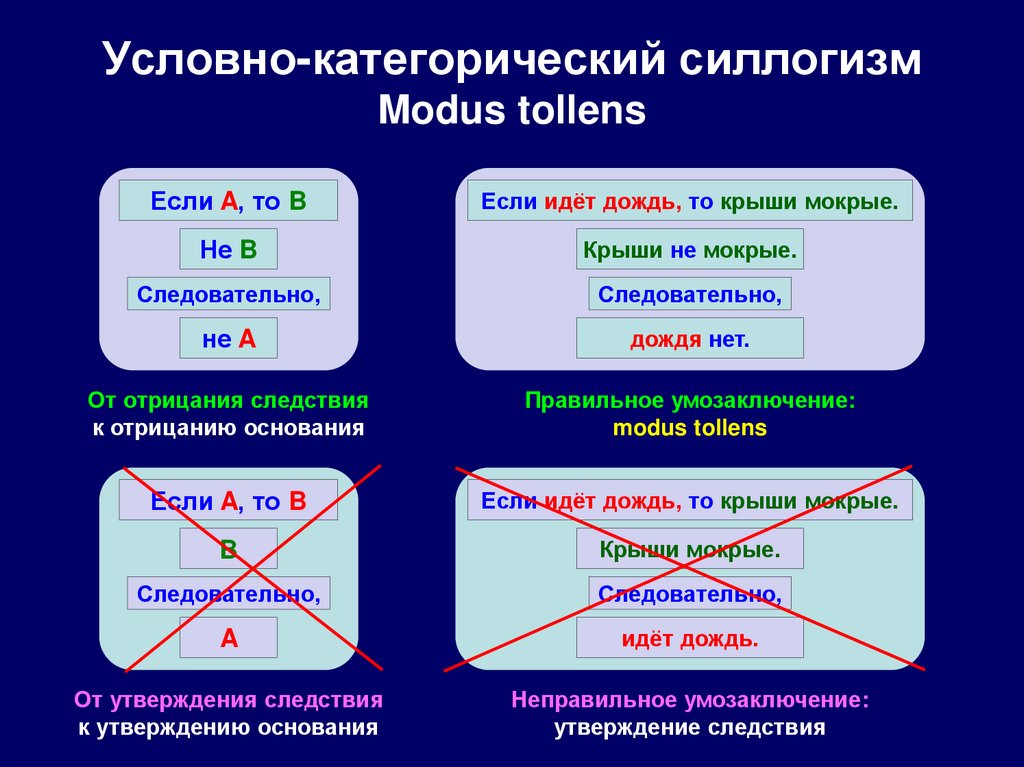
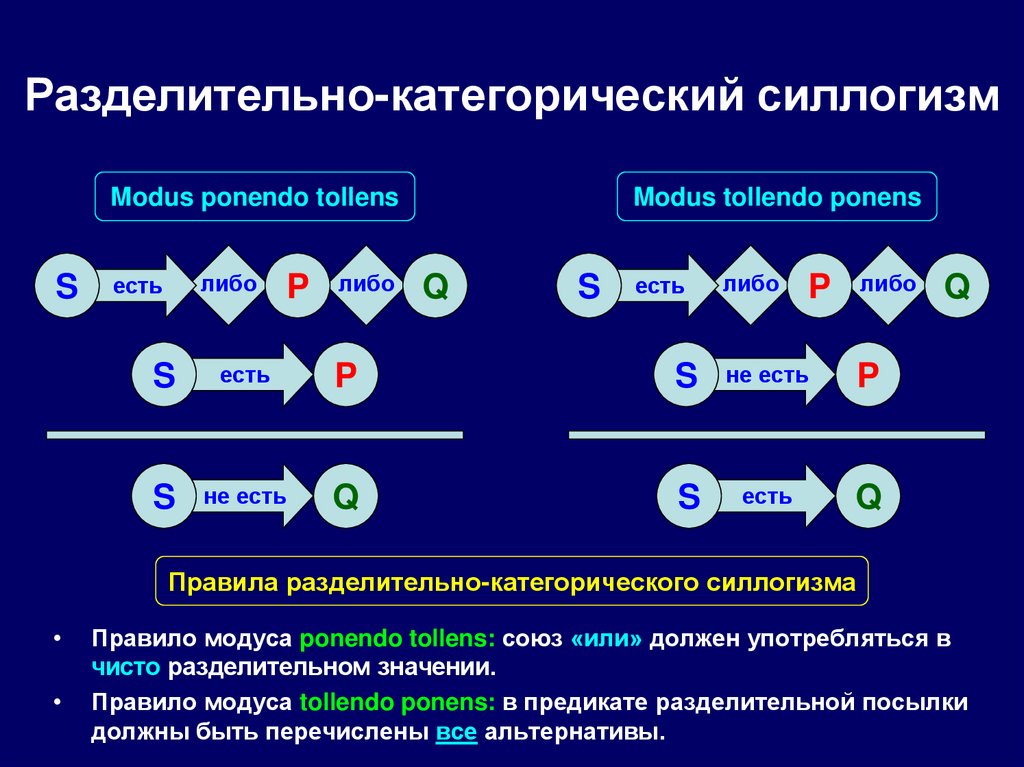
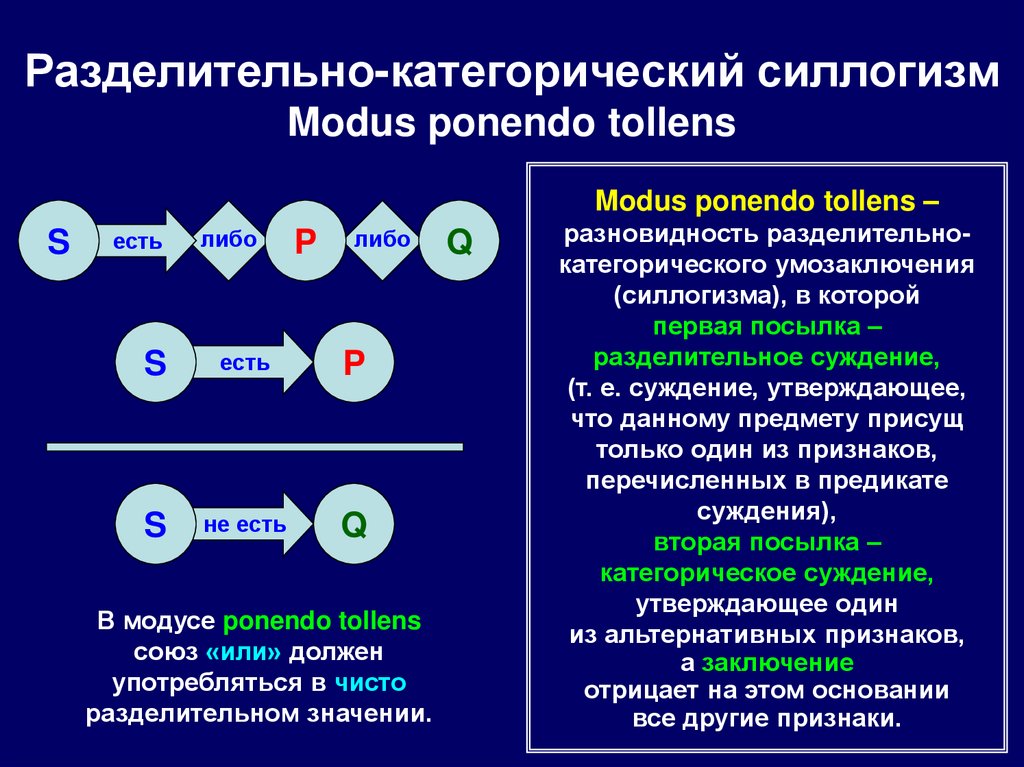
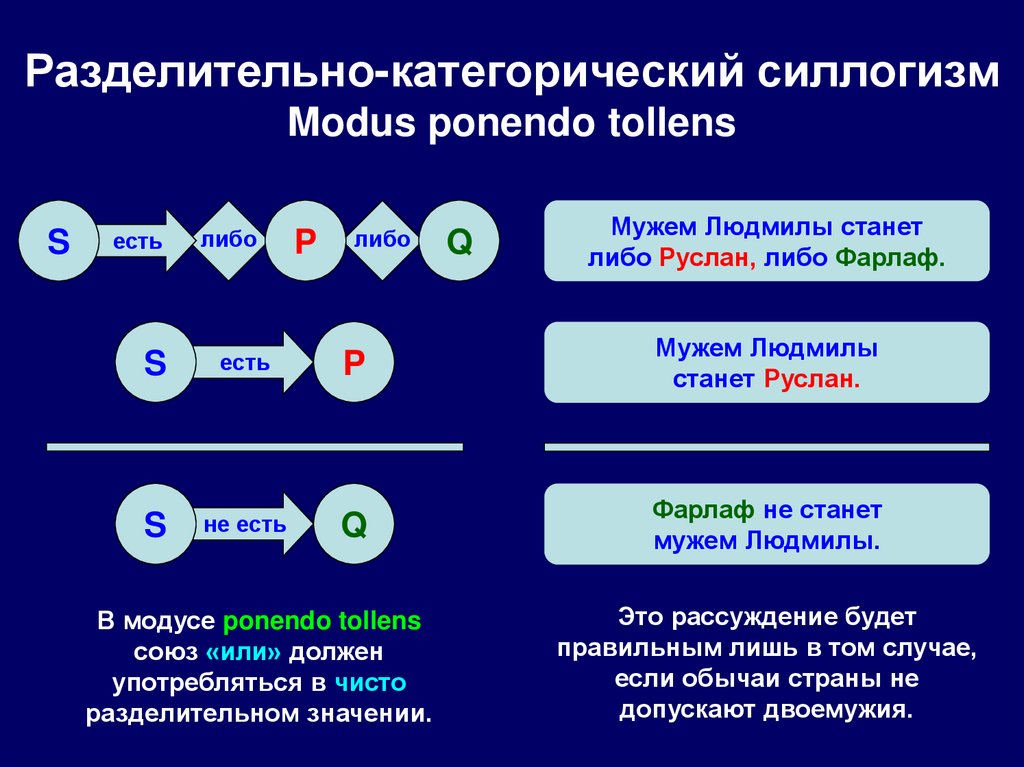
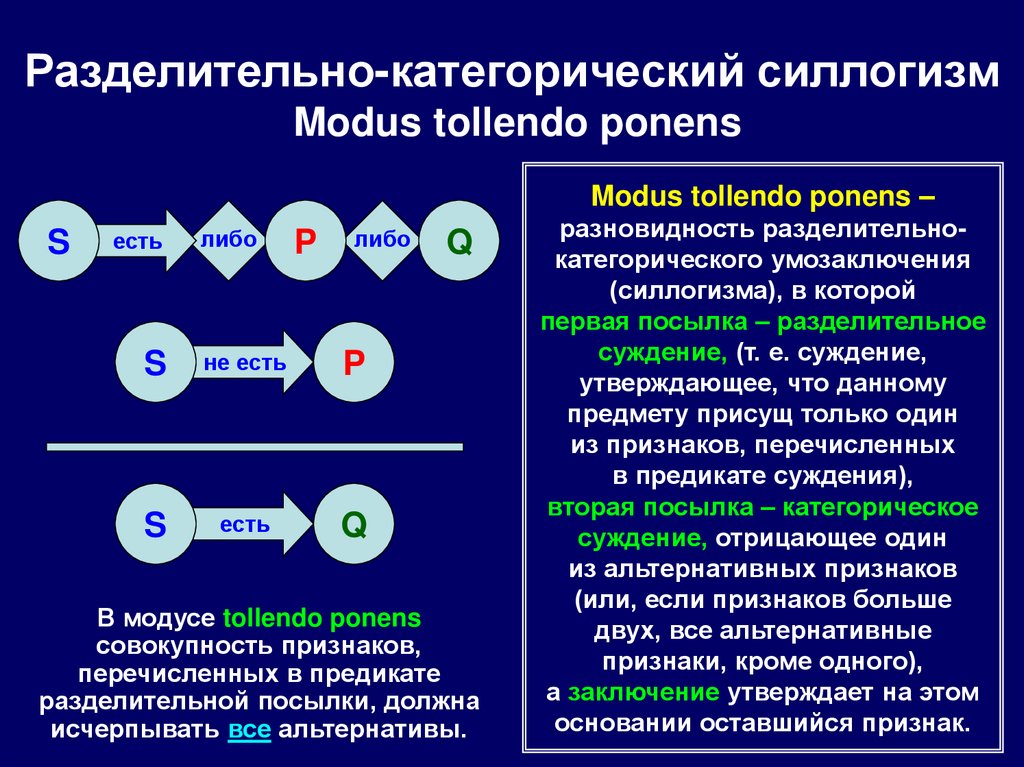
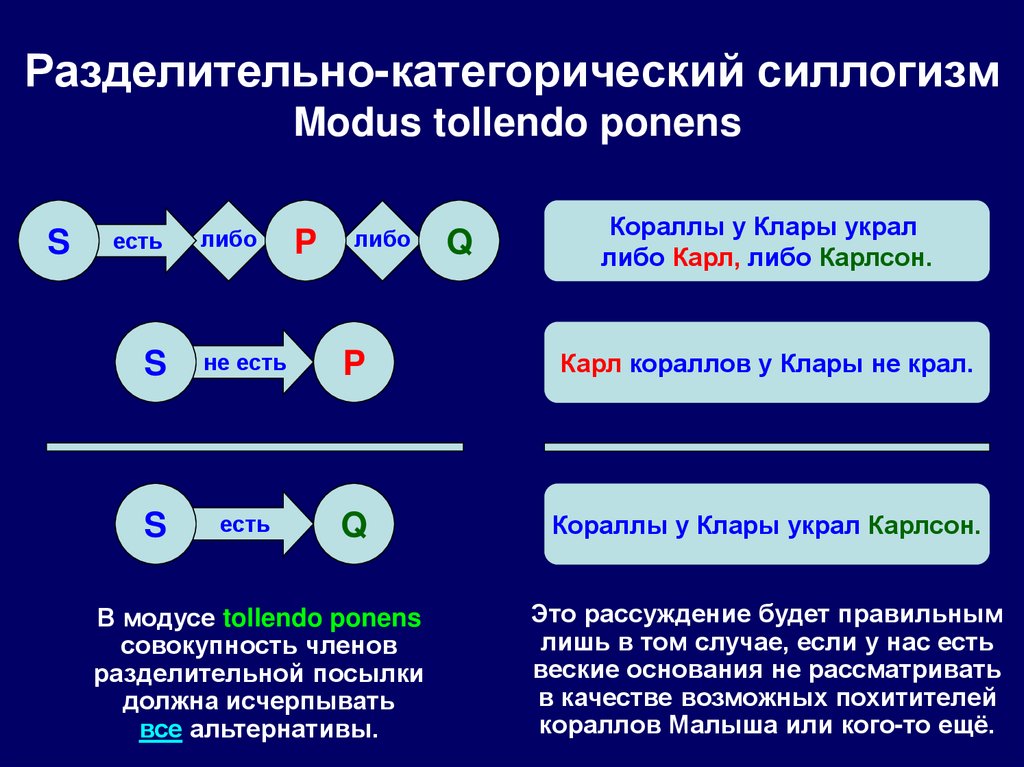
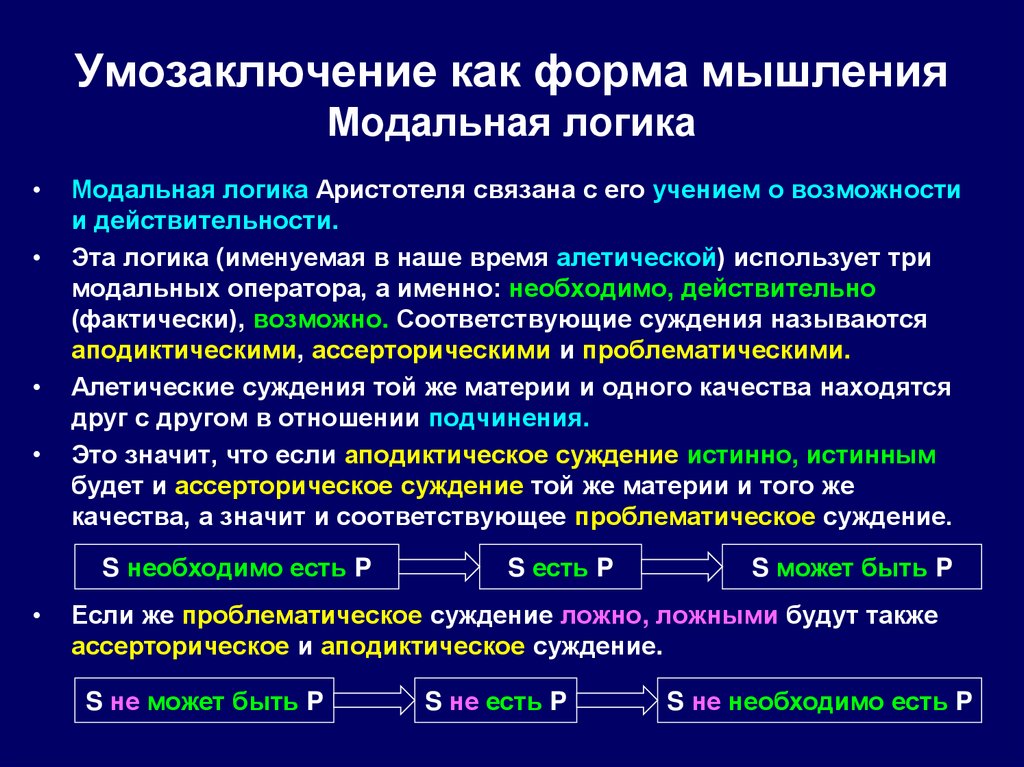

 philosophy
philosophy








