Similar presentations:
Логика. Умозаключение
1. Логика
V. Умозаключение2. Умозаключение
Умозаключением называется такой приемрассуждения, посредством которого мы
из некоторого исходного знания
получаем новое, выводное знание.
MaP
Беспокойства и волнения истощают жизненные силы
S aполна
M беспокойств и волнений
Современная жизнь
Современная жизнь
силы
S aистощает
P
посылки
заключение
Правило следования
3. Виды умозаключения
По характеру направленности процессавывода умозаключения делятся на:
дедуктивные
индуктивные
традуктивные (аналогия)
(от латинского traductio перемещение)
Кроме того, умозаключения делятся на
непосредственные и
опосредствованные.
4. Непосредственные умозаключения
Умозаключения по логическому квадратуПревращение
Обращение
Противопоставление предикату
5. Непосредственные умозаключения
ПревращениеSaP
S e не-P
SiP
S o не-P
SeP
S a не-P
S
S
S
P
P
P
SoP
S i не-P
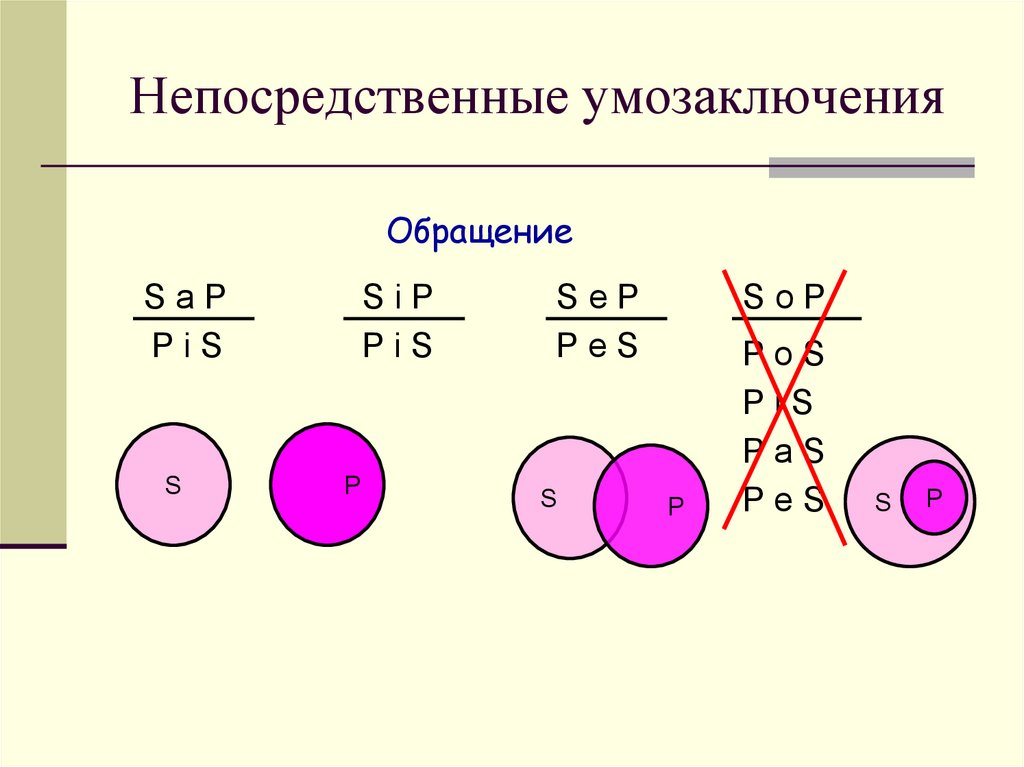
6. Непосредственные умозаключения
ОбращениеSaP
PiS
S
SiP
PiS
P
SeP
PeS
S
SoP
P
PoS
PiS
PaS
PeS
S
P
7. Непосредственные умозаключения
Противопоставление предикатуSaP
S e не-P
не-P e S
SiP
S o не-P
SeP
S a не-P
SoP
S i не-P
не-P i S
не-P i S
Все слоны боятся мышей
Ни один не боящийся мышей не есть слон
8. Простой категорический силлогизм
M a PВсякий, кто работает на лекции, сдает экзамен без проблем.
Sнаaлекции
M
Сидоров работает
Сидоров сдаст экзамен
S a Pбез проблем
Средний термин - M
Крайние термины – S и P
Меньший - S
Меньшая посылка – S a M
Больший - P
Большая посылка – M a P
9. Аксиома силлогизма
Если объем одного термина полностьювходит в объем другого, а объем другого
полностью входит в объем третьего, то и
объем первого полностью входит в
объем третьего. А если объем одного
термина полностью входит в объем
другого, а объем другого полностью
исключается из объема третьего, то и
объем первого полностью исключается
из объема третьего.
10. Фигуры и модусы категорического силлогизма
Всякий, кто работает на лекции, сдает экзамен без проблем.Сидоров работает на лекции
Сидоров сдаст экзамен без проблем
M a P
S a M
S a P
M
S
P
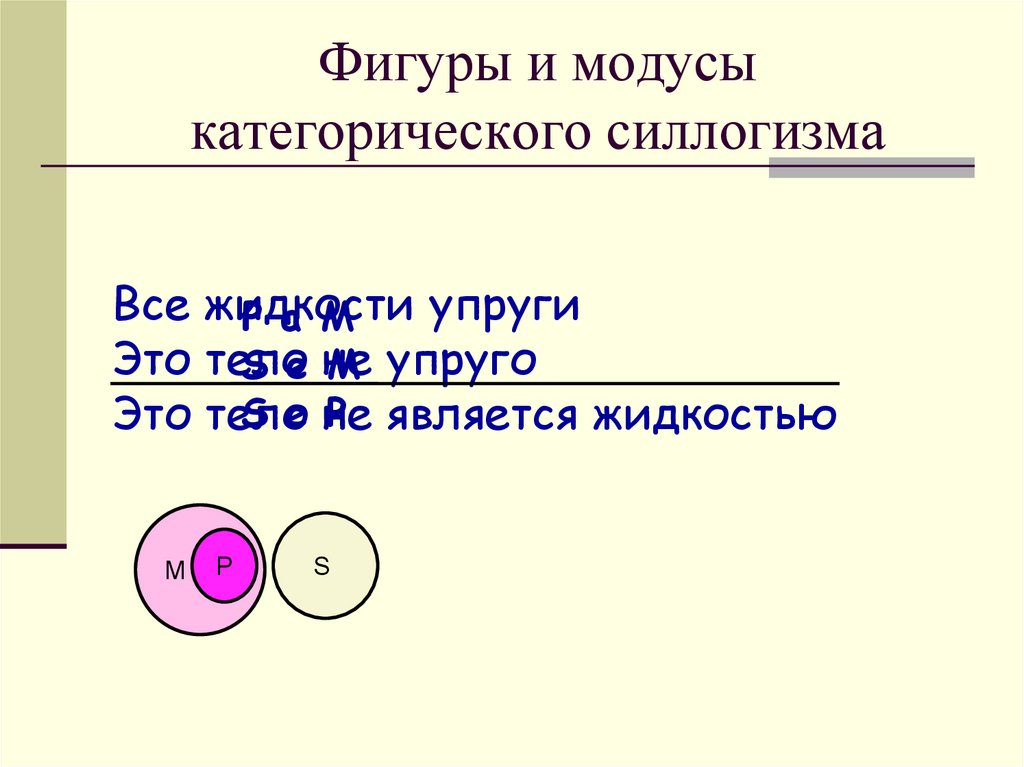
11. Фигуры и модусы категорического силлогизма
Все жидкостиупруги
P a M
Это тело
S е не
M упруго
S e не
P является жидкостью
Это тело
M
P
S
12. Фигуры и модусы категорического силлогизма
Бόльшаяпосылка
Мéньшая
посылка
Заключение
M
S
P P
M S
M M
M M
S–P
S–P
I фигура
II фигура
P P
S M
M
S
S–P
S–P
III фигура
IV фигура
Некоторые птицы не летают
Все птицы имеют крылья
Некоторые имеющие крылья не летают
13. Фигуры и модусы категорического силлогизма
Бόльшаяпосылка
Мéньшая
посылка
Заключение
M
S
P P
M S
M M
M M
S–P
S–P
I фигура
II фигура
P P
S M
M
S
S–P
S–P
III фигура
IV фигура
Некоторые студенты 1 курса отличники.
Все отличники сдали экзамен по логике на «5».
Некоторые сдавшие экзамен по логике на «5» студенты
1 курса.
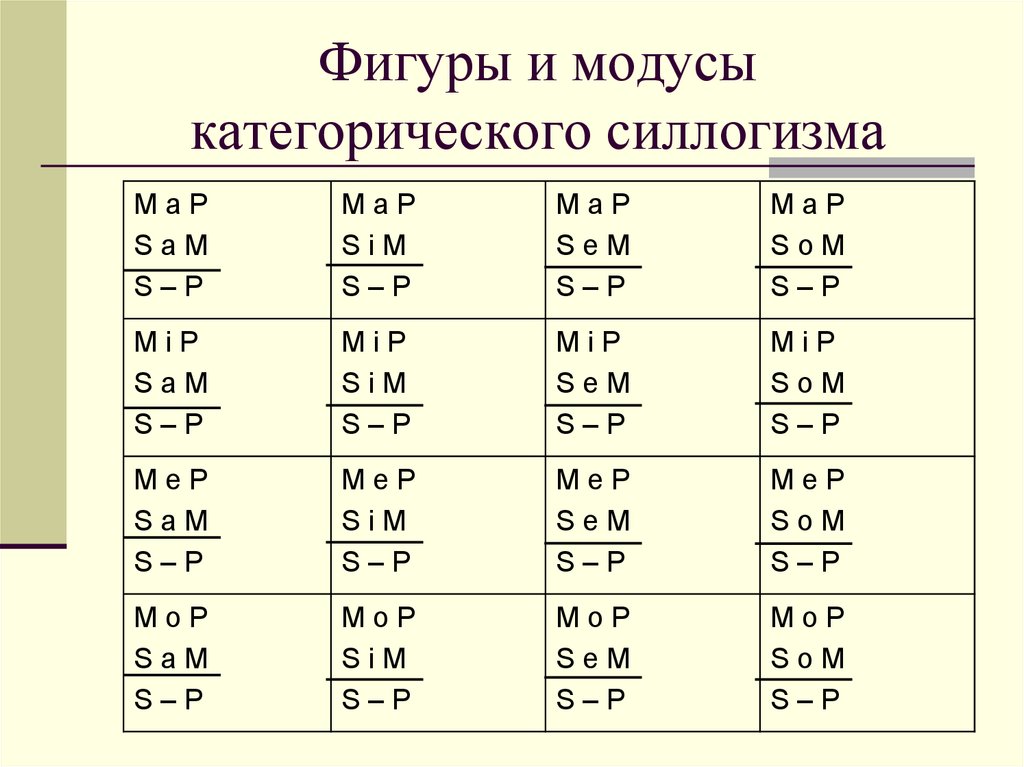
14. Фигуры и модусы категорического силлогизма
MaPSaM
S–P
MaP
SiM
S–P
MaP
SeM
S–P
MaP
SoM
S–P
MiP
SaM
S–P
MiP
SiM
S–P
MiP
SeM
S–P
MiP
SoM
S–P
MeP
SaM
S–P
MeP
SiM
S–P
MeP
SeM
S–P
MeP
SoM
S–P
MoP
SaM
S–P
MoP
SiM
S–P
MoP
SeM
S–P
MoP
SoM
S–P
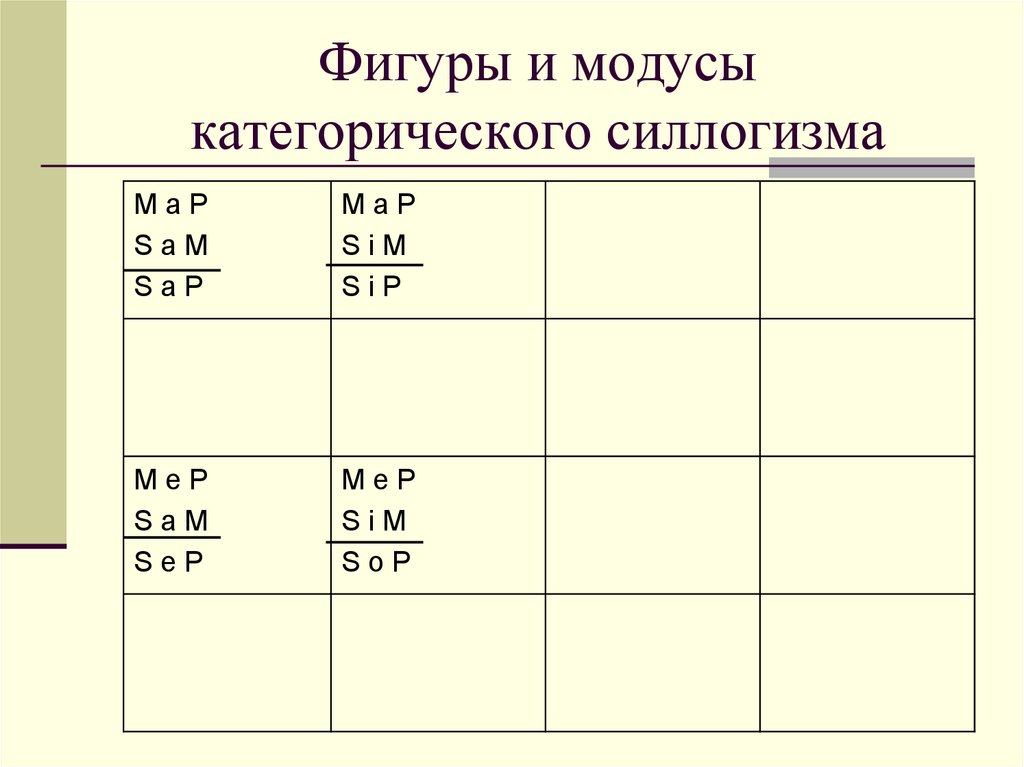
15. Фигуры и модусы категорического силлогизма
MaPSaM
SaP
MaP
SiM
SiP
MeP
SaM
SeP
MeP
SiM
SoP
16. Фигуры и модусы категорического силлогизма
Правильные модусы.I фигура
Barbara, Celarent, Darii, Ferio;
II фигура
Cesare, Camestres, Festino, Baroko;
III фигура
Darapti, Disamis, Datisi, Felapton,Bokardo, Feriso
IV фигура
Bramantip, Camenes, Dimaris, Fesapo, Fresison.
17. Фигуры и модусы категорического силлогизма
I фигураBarbara,
M a P
S a M
S a P
M
S
Celarent,
M e P
S a M
S e P
P
M
S
Darii,
Ferio;
M a P
S i M
S i P
M e P
S i M
S o P
P
18. Фигуры и модусы категорического силлогизма
M a PS o M
S o P
S a P
S i P
S e P
S
S
M
P
S
S
19. Правила категорического силлогизма
Общие правилаПравила фигур
Правила терминов
Правила посылок
20. Правила категорического силлогизма
Правила терминов1. В категорическом силлогизме должно
быть три и только три термина.
21. Упражнение 1
“Ни одна война не бывает в течениедолгого времени популярной, так как
всякая война увеличивает налоги; а
популярность всего, что затрагивает
карман, - непродолжительна.”
Ни одно М 1 не есть Р
Все S суть М 2
Celarent
Ни одно S не есть Р
22. Упражнение 1
Ни одно М1 не есть РВсе М2 суть М1
Ни
одно
М2 не
Все
S суть
М2есть Р
M1
P
M2 S
Ни одно S не есть Р
Ни одно М2 не есть Р
M2 S
P
23. Упражнение 1
ПолисиллогизмНи одно М1 не есть Р
Все М2 суть М1
Ни одно М2 не есть Р
Ни одно М2 не есть Р
Все S суть М2
Ни одно S не есть Р
M1
P
M2
M2 S
P
24. Упражнение 1
СоритПолисиллогизм
Ни одно М1 не есть Р
Все М2 суть М1
Ни одно М2 не есть Р
Все S суть М2
Ни одно S не есть Р
25. Правила категорического силлогизма
Правила терминов1. В категорическом силлогизме должно
быть три и только три термина.
2. Термин, не распределенный в
посылках, не может быть распределен в
заключении
26. Правила категорического силлогизма
Все люди, имеющие повышенную температуру,Все
больные имеют повышенную температуру
больны.
Петров не имеет повышенной температуры.
Петров не болен.
M a P
S е M
S е P+
-
P a M
S е M
S е P
Camestres
?
27. Правила категорического силлогизма
Правила терминов1. В категорическом силлогизме должно
быть три и только три термина.
2. Термин, не распределенный в
посылках, не может быть распределен в
заключении
3. Средний термин должен быть
распределен по крайней мере в одной
из посылок.
28. Правила категорического силлогизма
1.2.
3.
4.
5.
Правила посылок.
Из двух отрицательных посылок нельзя
сделать никакого заключения.
Если одна из посылок отрицательная, то
заключение – отрицательное.
Из двух частных посылок нельзя сделать
никакого заключения.
Если одна из посылок частная, то заключение
– частное.
Из двух утвердительных посылок нельзя
сделать отрицательного заключения.
29. Правила категорического силлогизма
Правила фигурПравила I фигуры.
M - P
S - M
S - P
P - M
S - M
S - P
M - P
M - S
S - P
Большая посылка обязательно общее суждение,
а меньшая посылка – утвердительная.
Правила II фигуры.
Большая посылка всегда общее суждение, одна из
посылок – отрицательная.
Правила III фигуры.
Меньшая посылка всегда утвердительное
суждение, заключение – частное.
30. Правила категорического силлогизма
P - MM - S
S - P
Правила IV фигуры.
Если большая посылка утвердительная, то меньшая
должна быть общей. И это понятно почему. Если
большая посылка является утвердительной, то это
означает нераспределенность среднего термина в
большей посылке, поэтому он должен быть
распределен в меньшей, следовательно, меньшая
посылка должна быть общей.
Если одна из посылок - отрицательное суждение, то
большая посылка должна быть общим суждением.
При наличии отрицательной посылки заключение было
бы отрицательным, что означает распределенность
большего термина в заключении. Следовательно, он
должен быть распределен и в большей посылке,
которая должна быть общей.
31. Упражнение 2
“Невозможно преуспевать в предмете не работая над ним”.Можно ли утверждать, что раз выполняется условие, то и
заключение необходимо подразумевается в нем? Логически
обосновать ответ.
Никто, кто не работает, не может преуспевать.
M
Ни одно не-М не есть Р
Всякий, кто преуспевает, работает над предметом.
Всякий, кто преуспевает, работал над предметом.
Петров работал над предметом
Петров преуспевает
Всякий, кто преуспевает, работал над предметом
Петров не работал над предметом
Петров не преуспевает.
P
?
Camestres
32. Упражнение 3
“Неприятные вещи иногда бывают полезными, так как огорченияиногда приносят пользу, а ни одно огорчение нельзя назвать
приятным”.
Некоторые огорчения полезны
Все огорчения неприятны__________
Некоторые неприятные вещи полезны
(Disamis)
Третья фигура часто используется в том случае, когда в споре
приводятся примеры для опровержения какого-либо положения.
“Всякий умный человек обладает тонким чувством юмора”
Нет, N, например. (1) N умен, а (2) чувством юмора не обладает.
Если ваш противник согласен с (1) и (2), то он вынужден отказаться от
высказанного положения.
Петров не обладает чувством юмора
Петров умен_________________________________
Некоторые умные люди не обладают чувством юмора
(Felapton)
33. Энтимема
Все лжецы трусыКай – лжец
Кай – трус
P
Все лжецы
M
трусы
Ma P
S a M
S a P
34. Энтимема
Работа не волк, в лес не убежит.Все, убегающие в лес, – волки.
Работа не волк
Работа в лес не убежит
Mв лес
Все, что убегает
P волк
P a M
S e M
S e P





























 philosophy
philosophy








