Similar presentations:
Умозаключение. Виды умозаключений
1. Умозаключение
2. Умозаключение
• Df. Умозаключение – это формамышления, в которой из данных суждений
(называемых посылками) выводится новое
суждение (называемое заключением).
3. Виды умозаключений
• Умозаключения делятся надедуктивные и индуктивные.
• В дедуктивных умозаключениях
вывод совершается от общих посылок к
менее общему или же к частному
заключению.
• В индуктивных умозаключениях
вывод совершается от частных посылок
к общему заключению.
4. Виды умозаключений
Прямые умозаключения имеют вид:А1, А2 …Аn
Т
Косвенные умозаключения (или
заключения от противного) имеют
вид:
┐Т → В & ┐В
Т
5. Непосредственные умозаключения
Df. Непосредственное умозаключение– это вывод из одной посылки.
• Непосредственными умозаключениями
являются операции:
превращения,
обращения,
противопоставления предикату,
противопоставления субъекту.
6. Превращение
• Df. Превращение – это логическаяоперация, в которой качество посылки
меняется на противоположное, а
предикат заменяется на понятие,
противоречащее исходному.
7. Превращение для А
• А. Все S есть РВсе S не есть не-Р
не-Р
не-Р
РР
S=P
S
S
8. Превращение
А. Все S есть РВсе S не есть не-Р
I. Некоторые S есть Р
Некоторые S не есть не-Р
E. Все S не есть Р
Все S есть не-Р
O. Некоторые S не есть Р
Некоторые S есть не-Р
9. Задача: провести превращение
Все студенты людиВсе студенты не есть не-люди
А. Все S есть Р
Все S не есть не-Р
10. Задача: провести превращение
Некоторые студенты не есть отличникиНекоторые студенты есть не-отличники
О. Некоторые S не есть Р
Некоторые S есть не-Р
11. Обращение
• Df. Обращение – это логическая операция,в которой субъект и предикат посылки
меняются местами в соответствии со
следующими формулами:
12. Обращение
А. Все S есть РНекоторые Р есть S
I. Некоторые S есть Р
Некоторые Р есть S
E. Все S не есть Р
Все Р не есть S
O. Некоторые S не есть Р
?
13. Обращение для А
А. Все S есть РНекоторые Р есть S
P
S=P
SS
14. Обращение для I
I. Некоторые S есть РНекоторые Р есть S
S
P
P
S
S=P
S
P
15. Обращение для Е
E. Все S не есть РВсе Р не есть S
S
P
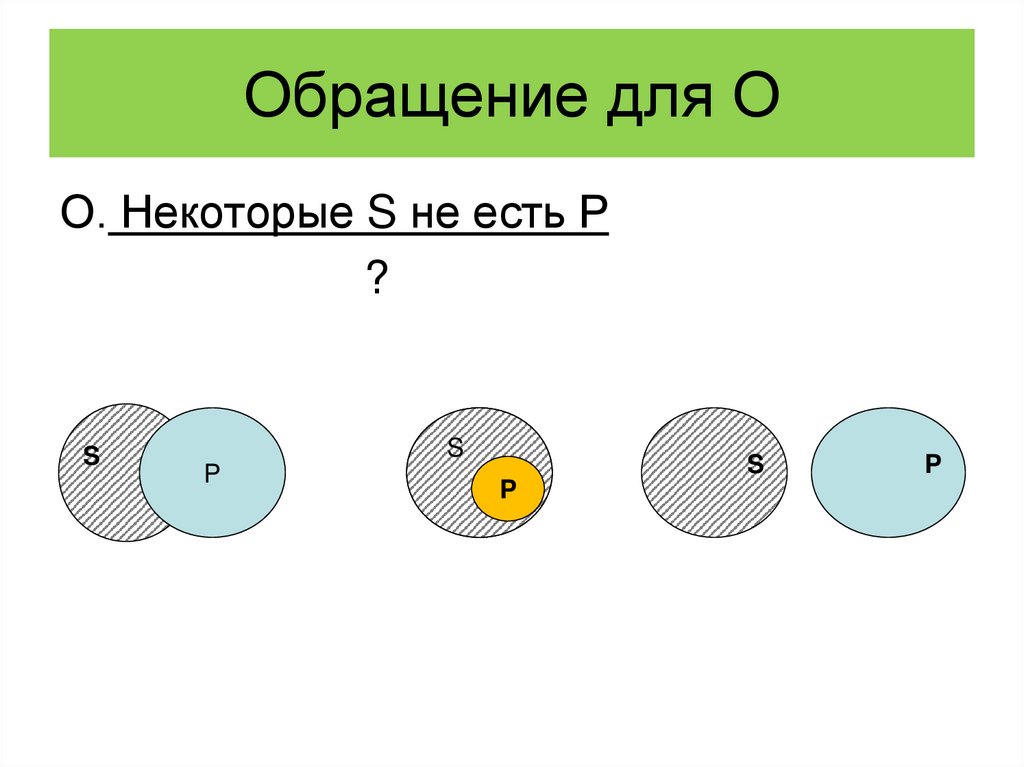
16. Обращение для О
О. Некоторые S не есть Р?
S
P
P
S
S
S
P
P
17. Задача: провести обращение
Некоторые студенты есть отличникиНекоторые отличники есть студенты
О. Некоторые S есть Р
Некоторые Р есть S
18. Противопоставление предикату
• Df. Противопоставление предикату –это логическая операция, в которой
сначала проводится превращение
исходной посылки, а затем обращение
полученного суждения.
19. Противопоставление предикату для А
• А. Все S есть РВсе S не есть не-Р
Все не-Р не есть S
20. Задача: провести противопоставление предикату
• Все курицы – птицы• Все не-птицы не есть курицы
• А. Все S есть Р
Все S не есть не-Р
Все не-Р не есть S
21. Противопоставление субъекту
• Df. Противопоставление субъекту –это логическая операция, в которой
сначала проводится обращение
исходной посылки, а затем
превращение полученного суждения.
22. Противопоставление субъекту для А
• А. Все S есть РНекоторые Р есть S
Некоторые Р не есть не-S
23. Простой категорический силлогизм
• Df.1. Простой категорическийсиллогизм – это дедуктивное
умозаключение из двух посылок, где и
посылки, и заключение представляют
собой простые суждения, а в их состав
входят три различные понятия,
каждое из которых встречается дважды.
24.
• Df.2. Простой категорическийсиллогизм – это умозаключение, в
котором от наличия некоторых
отношений между терминами S и М и
терминами Р и М, фиксируемых в
посылках, приходят к заключению о
наличии определенного отношения
между терминами S и Р.
25. Простой категорический силлогизм: пример
посылкиВсе люди смертны
Все преподаватели – люди
Все преподаватели смертны
заключение
26. Структура силлогизма
• В силлогизм входятБольший (Р),
крайние термины
меньший (S)
и средний (M) термины.
27. Термины силлогизма
• Df. Большим термином силлогизмабудем называть понятие, играющее в
заключении роль предиката (Р).
• Df. Меньшим термином силлогизма
будем называть понятие, играющее в
заключении роль субъекта (S).
• Df. Средним термином (М) силлогизма
будем называть понятие, которое входит в
обе посылки, но не входит в заключение.
28. Посылки
• Df. Большей посылкой будемназывать ту, куда входит больший
термин.
• Df. Меньшей посылкой будем
называть ту, куда входит меньший
термин.
29. Выявление терминов силлогизма
Все люди смертныВсе преподаватели – люди
Все преподаватели смертны
30. Больший термин
Больший термин определяется позаключению.
Все люди смертны
Все преподаватели – люди
Все преподаватели смертны
31. Больший термин
Больший термин является взаключении предикатом:
Все люди смертны
Все преподаватели – люди
Р
Все преподаватели смертны
32. Больший термин
РВсе люди смертны
Все преподаватели – люди
Р
Все преподаватели смертны
33. Меньший термин
Меньший термин является взаключении субъектом
Р
Все люди смертны
Все преподаватели – люди
S
Р
Все преподаватели смертны
34. Меньший термин
РВсе люди смертны.
S
Все преподаватели – люди.
S
Р
Все преподаватели смертны.
35. Средний термин
Средний термин входит в обепосылки и не входит в заключение
М
Р
Все люди смертны.
S
М
Все преподаватели – люди.
S
Р
Все преподаватели смертны.
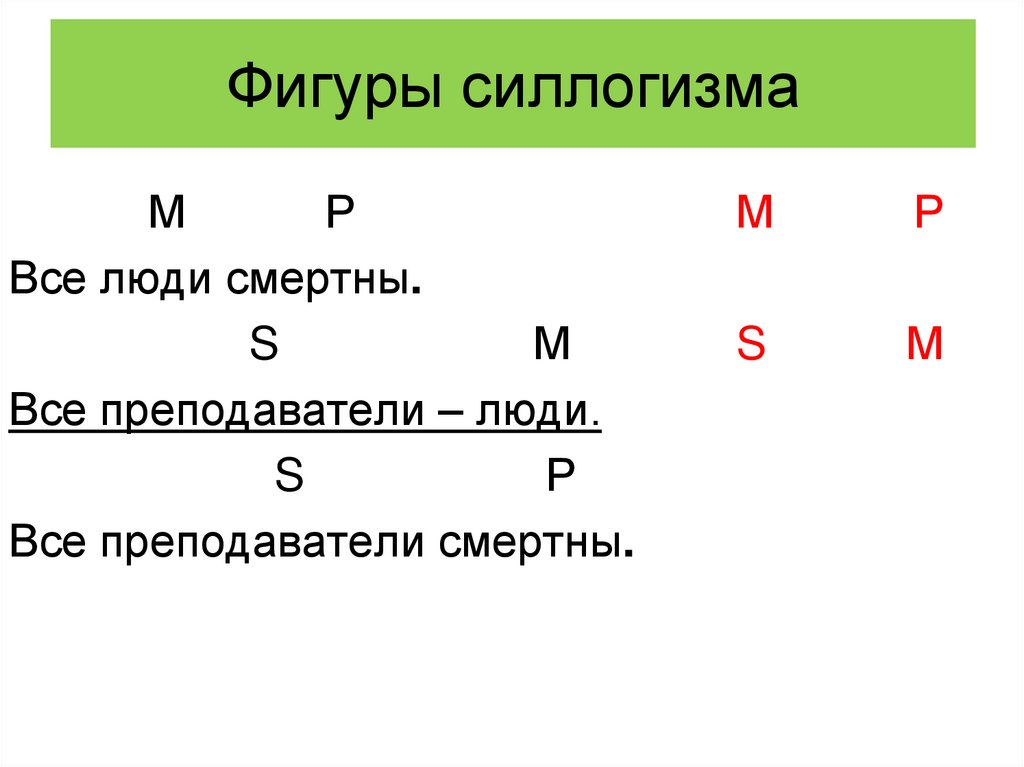
36. Фигуры силлогизма
МР
Все люди смертны.
S
М
Все преподаватели – люди.
S
Р
Все преподаватели смертны.
М
Р
S
М
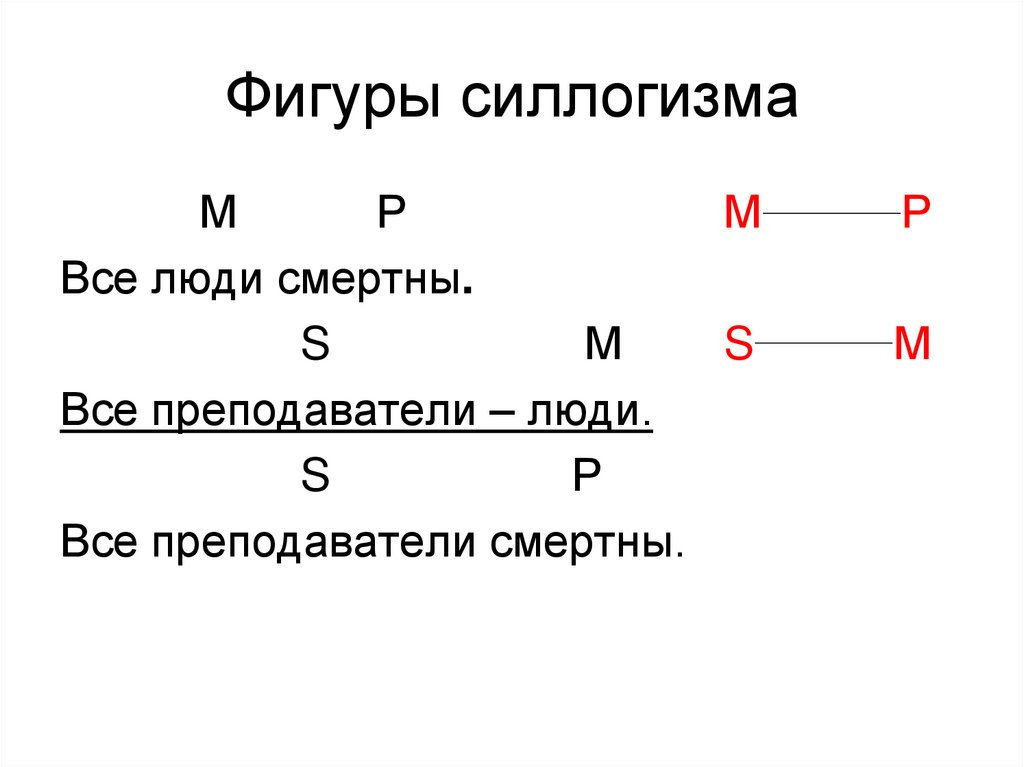
37. Фигуры силлогизма
МР
М
Все люди смертны.
S
М
S
Все преподаватели – люди.
S
Р
Все преподаватели смертны.
Р
М
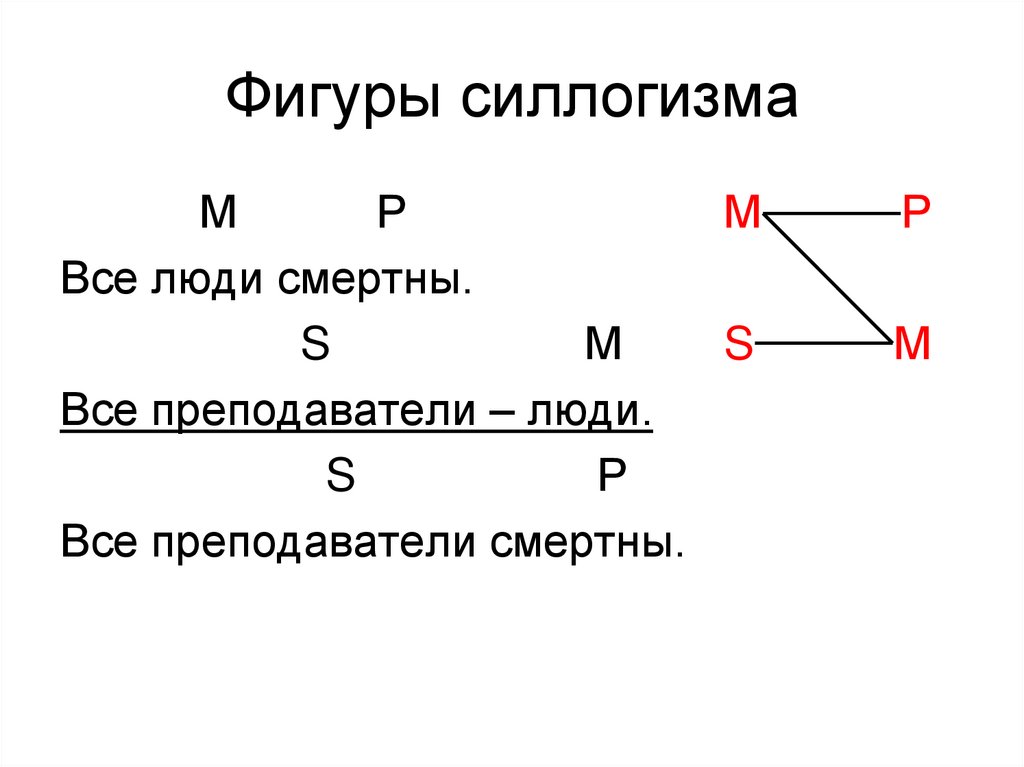
38. Фигуры силлогизма
МР
М
Все люди смертны.
S
М
S
Все преподаватели – люди.
S
Р
Все преподаватели смертны.
Р
М
39. Четыре фигуры силлогизма
1-я фигура3-я фигура
2-я фигура
4-я фигура
40. Уточнение
• При определении 1 и 4 фигурнеобходимо, чтобы большая посылка
стояла первой.
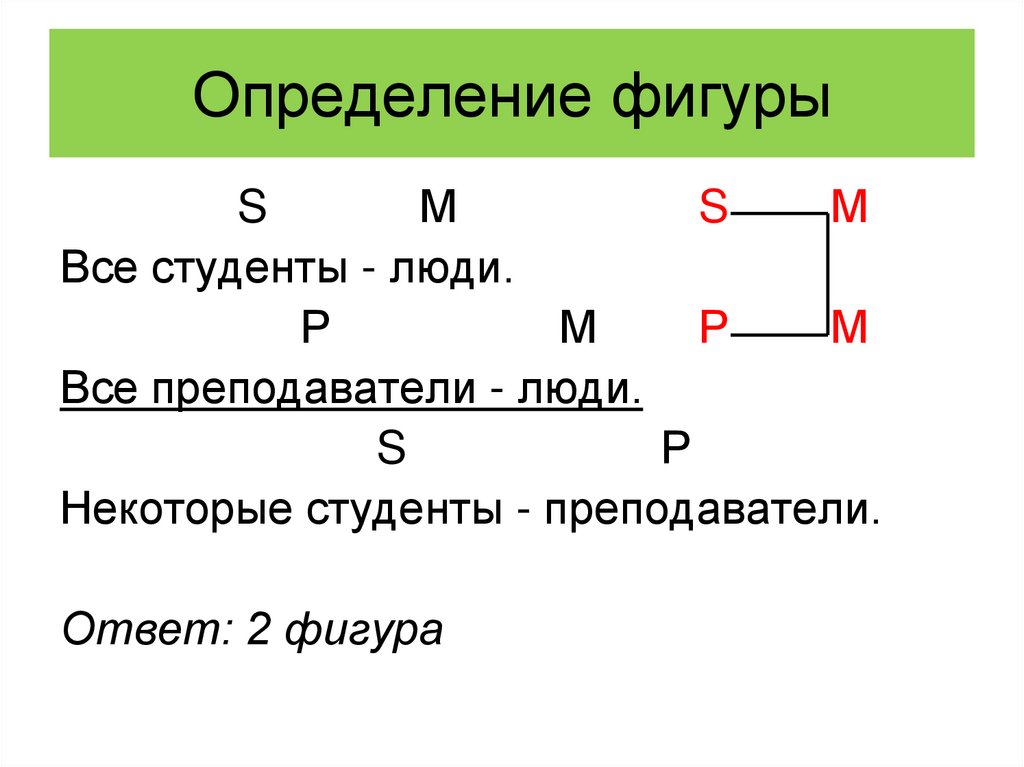
41. Определение фигуры
• Пример 1:Все студенты - люди.
Все преподаватели - люди.
Некоторые студенты - преподаватели.
42. 1.Определение большего термина
Все студенты - люди.Все преподаватели - люди.
Р
Некоторые студенты - преподаватели.
43. Определение большего термина
Все студенты - люди.Р
Все преподаватели - люди.
Р
Некоторые студенты - преподаватели.
В данном примере во второй посылке
больший термин силлогизма играет
роль субъекта!!!
44. Определение меньшего термина
Все студенты - люди.Р
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
45. Определение меньшего термина
SВсе студенты - люди.
Р
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
46. Определение среднего термина
SМ
Все студенты - люди.
Р
М
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
47. Определение фигуры
SМ
S
М
Все студенты - люди.
Р
М
Р
М
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
48. Определение фигуры
SМ
S
М
Все студенты - люди.
Р
М
Р
М
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
49. Определение фигуры
SМ
S
М
Все студенты - люди.
Р
М
Р
М
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
Ответ: 2 фигура
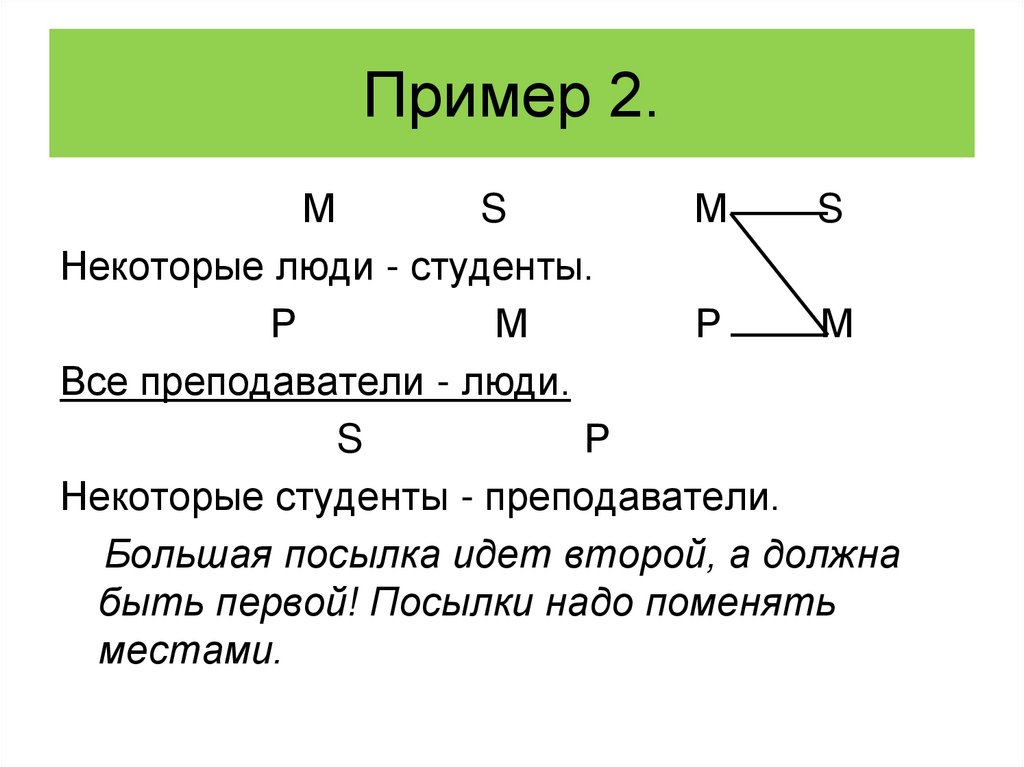
50. Пример 2.
МS
М
S
Некоторые люди - студенты.
Р
М
Р
М
Все преподаватели - люди.
S
Р
Некоторые студенты - преподаватели.
Большая посылка идет второй, а должна
быть первой! Посылки надо поменять
местами.
51. Ответ
Р
М
М
S
• Ответ: 4-я фигура.
52. Модусы силлогизма
• Модус (вид) силлогизма определяетсяпо типу входящих в него суждений.
А. Все преподаватели – люди
А. Все люди смертны
А. Все преподаватели смертны
Модус: ААА (Барбара)
53. Модусы силлогизма
Е. Все люди – не марсианеА. Все студенты – люди
Е. Все студенты не марсиане
Модус: ЕАЕ (Celarent)
54. Модусы силлогизма
• В каждой фигуре существует 64 модуса,т.е. всего – для всех четырех фигур –
256,
из них 24 являются правильными
(по шесть на каждую фигуру).
55. Способы проверки правильности силлогизма
1. Традиционный2. На кругах Эйлера
3. Современный – по пяти правилам
56. 1. Традиционный
Алгоритм проверки:а) проверить общие правила,
б) найти больший, меньший и средний
термины,
в) определить фигуру,
г) проверить специальные правила фигуры.
Правила фигур не всегда гарантируют
правильный вывод!!!
57. 2. На кругах Эйлера
Алгоритм проверкиа). найти больший, меньший и средний
термины,
б) нарисовать круговые схемы для
каждого из суждений в силлогизме,
в) сравнить каждый случай из первой
посылки с каждым случаем из второй
посылки, совмещая М и М.
58.
• Силлогизм является правильным,если и только если в результате
совмещения круговых схем каждого
случая из первой посылки с каждым
случаем из второй посылки, мы
получим вариант, имеющийся в
заключении.
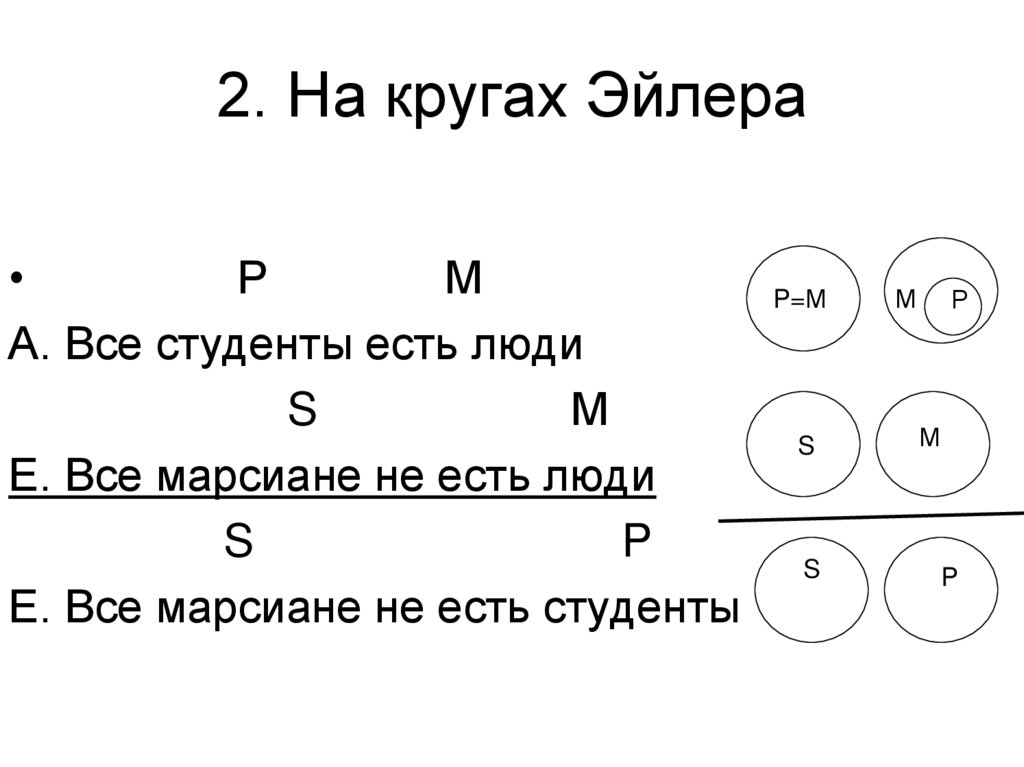
59. 2. На кругах Эйлера
А.Все студенты есть людиЕ.Все марсиане не есть люди
Е.Все марсиане не есть студенты
60. 2. На кругах Эйлера
Р
М
А. Все студенты есть люди
S
М
Е. Все марсиане не есть люди
S
P
Е. Все марсиане не есть студенты
61. 2. На кругах Эйлера
Р
М
А. Все студенты есть люди
S
М
Е. Все марсиане не есть люди
S
P
Е. Все марсиане не есть студенты
P=М
S
S
М
Р
М
P
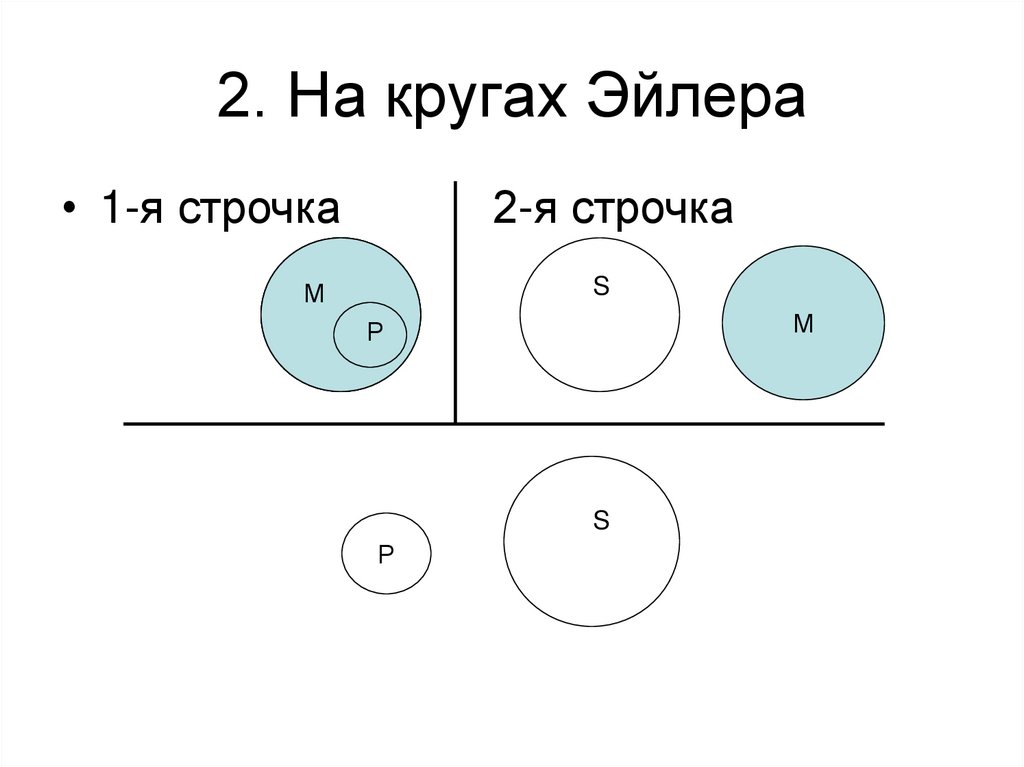
62. 2. На кругах Эйлера
• 1-я строчка2-я строчка
Р=М
S
Р=М
S
М
М
63. 2. На кругах Эйлера
• 1-я строчка2-я строчка
Р=М
S
Р
S
М
М
64. На кругах Эйлера
• 1-я строчка2-я строчка
S
М
Р
М
S
Р
М
65. 2. На кругах Эйлера
• 1-я строчка2-я строчка
S
М
Р
S
Р
М
М
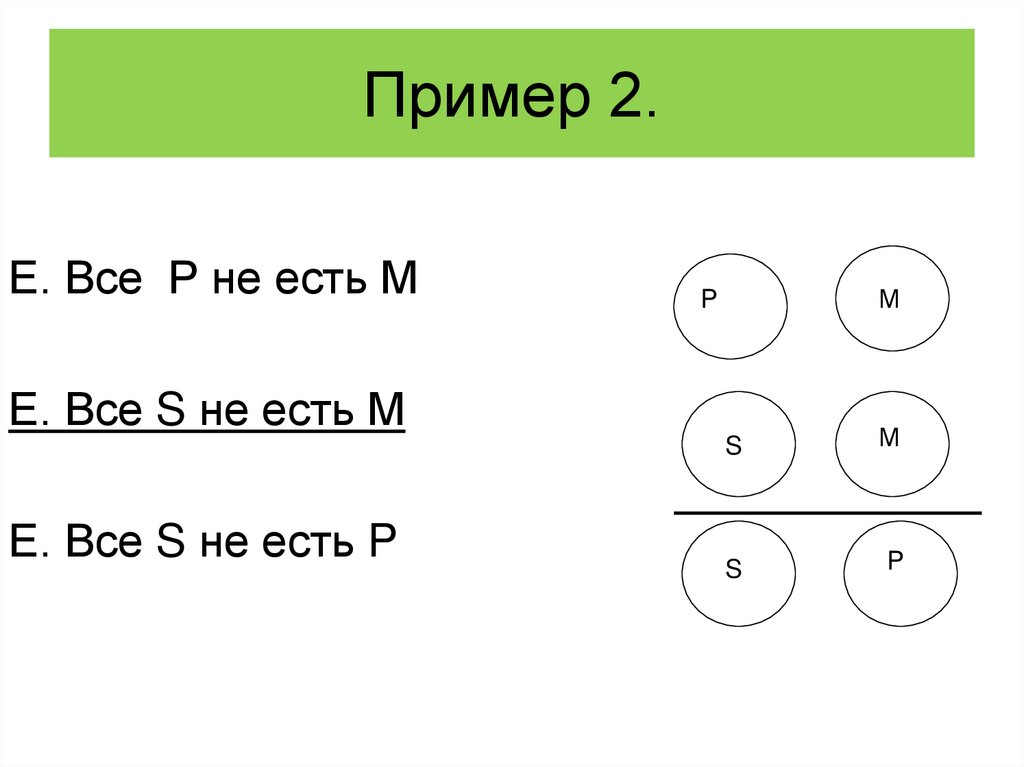
66. Пример 2.
Е. Все Р не есть ММ
P
Е. Все S не есть М
Е. Все S не есть P
S
М
S
P
67. 2. На кругах Эйлера
• 1-я строчкаР
P
2-я строчка
М
М
S
S
М
68. 2. На кругах Эйлера
SP
S
Р
М
P=S
P
S
69. 3. Современный
• Силлогизм является правильным, еслии только если в нем выполняются все
пять правил.
70. Правила силлогизма
Правила посылок1. По крайней мере одна посылка должна
быть утвердительной.
2. Если есть отрицательная посылка, то и
заключение должно быть отрицательным.
3. Если обе посылки утвердительные, то и
заключение должно быть утвердительным.
71. Правила силлогизма
Правила посылок1. По крайней мере одна посылка должна
быть утвердительной,
т.е. утвердительной может быть:
одна посылка
обе посылки
правило 2
правило 3
72. Правила силлогизма
Правила терминов4. Средний термин должен быть
распределен (М+) хотя бы в одной из
посылок.
5. Термин, распределенный (S+, P+) в
заключении, должен быть распределен
(S+, P+) и в посылке. (К термину, не
распределенному (S-, P-) в заключении,
правило не применяется!)
73. Алгоритм проверки силлогизма:
а). выявить больший, меньший и среднийтермины силлогизма;
б). установить распределённость терминов;
в). проверить правила.
74. Пример 1.
Все студенты есть людиНекоторые марсиане не есть люди
Некоторые марсиане не есть студенты
75. Выявление большего термина
РВсе студенты есть люди
Некоторые марсиане не есть люди
Р
Некоторые марсиане не есть студенты
76. Выявление меньшего термина
РВсе студенты есть люди
S
Некоторые марсиане не есть люди
S
Р
Некоторые марсиане не есть студенты
77. Выявление среднего термина
РМ
Все студенты есть люди
S
М
Некоторые марсиане не есть люди
S
Р
Некоторые марсиане не есть студенты
78. Распределённость субъектов
Р+М
Все студенты есть люди
SМ
Некоторые марсиане не есть люди
SР
Некоторые марсиане не есть студенты
Df. Субъект распределён в общих суждениях и
не распределён в частных.
79. Распределённость предикатов
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
Df. Предикат распределен в отрицательных
суждениях и не распределен в
утвердительных
80. Проверка 1-го правила
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
Правило 1.По крайней мере одна посылка
должна быть утвердительной.
1.+ (первая посылка утвердительная)
81. Проверка 2-го правила
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
Правило 2. Если есть отрицательная
посылка, то и заключение должно быть
отрицательным.
1. + 2.+ (есть отрицательная посылка и
заключение отрицательное)
82. Проверка 3-го правила
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
Правило 3. Если обе посылки
утвердительные, то и заключение должно
быть утвердительным.
1. + 2.+ 3.не применяется (нет двух
утвердительных посылок)
83. Проверка 4-го правила
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
Правило 4. Средний термин должен быть
распределён (М+) хотя бы в одной из
посылок
1. + 2.+ 3.не пр. 4.+ (средний термин
распределен во второй посылке)
84. Проверка 5-го правила
Р+МВсе студенты есть люди
SМ+
Некоторые марсиане не есть люди
SР+
Некоторые марсиане не есть студенты
5. Термин, распределённый в заключении (S+, P+),
должен быть распределен и в посылках.
1. + 2.+ 3.не применяется. 4.+ 5. для S не
применяется (так как S-), для Р + (так как Р+ в
посылке).
Общий ответ: силлогизм правильный
85.
Р+a МS- e М+S- o Р+
1.+; 2.+; 3. не прим.; 4.+; 5.+
86. Пример 2.
• Все студенты не марсиане• Некоторые преподаватели не марсиане
• Некоторые студенты не преподаватели
87. 1-й шаг: выявление терминов
S
М
• Все студенты не марсиане
P
М
• Некоторые преподаватели не марсиане
S
P
• Некоторые студенты не преподаватели
88. 2-й шаг: установление распределённости субъектов
S+М
Все студенты не марсиане
PМ
Некоторые преподаватели не марсиане
SP
Некоторые студенты не преподаватели
89. 2-й шаг: установление распределённости предикатов
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
90. 3-й шаг:проверка 1-го правила
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
1.-
91. 3-й шаг:проверка 2-го правила
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
1.- 2.+
92. 3-й шаг:проверка 3-го правила
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
1.- 2.+ 3.не пр.
93. 3-й шаг: проверка 4-го правила
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
1.- 2.+ 3.не пр.4.+
94. 3-й шаг: проверка 5-го правила
S+М+
• Все студенты не марсиане
PМ+
• Некоторые преподаватели не марсиане
SP+
• Некоторые студенты не преподаватели
1.- 2.+ 3.не пр.4.+ 5. для S – не пр., для Р Ответ: силлогизм неправильный, так как
нарушены правила 1. и 5.
95. Полисиллогизм
• Df. Полисиллогизм – это цепочкасиллогизмов, где заключение одного
силлогизма является посылкой другого
силлогизма.
Полисиллогизм правильный, если и
только если все силлогизмы в его
составе правильные.
96. Пример полисиллогизма
Все люди смертныВсе студенты люди
Все студенты смертны
Все марсиане не студенты
Некоторые марсиане не смертны
97. Первый силлогизм в полисиллогизме
Все люди смертныВсе студенты люди
Все студенты смертны
Все марсиане не студенты
Некоторые марсиане не смертны
98. Второй силлогизм в полисиллогизме
Все люди смертныВсе студенты люди
Все студенты смертны
Все марсиане не студенты
Некоторые марсиане не смертны
99. Пример полисиллогизма
Все люди смертныВсе студенты люди
Все студенты смертны
Все марсиане не студенты
Некоторые марсиане не смертны
100. Проверка правильности полисиллогизма. Вариант 1.
• Разбить полисиллогизм на отдельныесиллогизмы и проверить их
правильность.
101.
S+М+
Все рыбы не летают
РМНекоторые птицы летают
SР+
Некоторые рыбы не есть птицы
1. +; 2.+; 3. не пр.; 4. +; 5. – (для P);
102.
РМ+Некоторые рыбы не есть птицы
МSОтдельные птицы - лебеди
SP+
Некоторые лебеди не есть рыбы
1. +; 2.+; 3. не пр.; 4. +; 5. – (для P);
103.
• Ответ:• Полисиллогизм неправильный, так как
неправильный первый силлогизм –
нарушено правило 5., и неправильный
второй силлогизм – тоже нарушено
правило 5.
104. Проверка правильности полисиллогизма. Вариант 2.
S+М+
Все рыбы не летают
РМНекоторые птицы летают
S- РР+ М+
Некоторые рыбы не есть птицы
МSОтдельные птицы - лебеди
SP+
Некоторые лебеди не есть рыбы
1. +; 2.+; 3. не пр.; 4. +; 5. -;
1. +; 2.+; 3. не пр.; 4. +; 5. -;
105.
• Ответ:• Полисиллогизм неправильный, так как
неправильный первый силлогизм –
нарушено правило 5., и неправильный
второй силлогизм – тоже нарушено
правило 5.
106. Виды полисиллогизмов
• Если вывод предыдущего силлогизмастал большей посылкой последующего,
то получившийся полисиллогизм
называется прогрессивным.
• Если же вывод предыдущего
силлогизма становится меньшей
посылкой следующего, то
полисиллогизм
называется регрессивным.
107. Прогрессивный полисиллогизм
Все, что развивает мышление, полезно.Все интеллектуальные игры развивают
мышление.
Все интеллектуальные игры полезны.
Шахматы – интеллектуальная игра.
Шахматы полезны.
108. Регрессивный полисиллогизм
Все звезды – это небесные тела.Солнце – это звезда.
Солнце – это небесное тело.
Все небесные тела участвуют в
гравитационных взаимодействиях.
Солнце участвует в гравитационных
взаимодействиях.
109. Энтимема
• Энтимема – это сокращенныйсиллогизм, где пропущена одна из
посылок или заключение.
110. Примеры энтимемы
1. Все люди смертны, следовательно,все преподаватели смертны.
2. Все преподаватели смертны, потому
что все люди смертны.
3. Все люди смертны. Все преподаватели
смертны.
111. Найти посылку и заключение. Пример 1.
АВсе люди смертны, следовательно,
В
все преподаватели смертны.
А→В
112. Восстановление силлогизма: пример 1
Все люди смертны.…
________________________
Все преподаватели смертны.
113. Найти посылку и заключение: пример 2.
АВсе преподаватели смертны, потому
В
что все люди смертны.
В→А
114. Восстановление силлогизма: Пример 2
• Все люди смертны• …
• ___________________
• Все преподаватели смертны
115. Найти посылку и заключение: пример 3.
3. Все люди смертны. – АВсе преподаватели смертны. - В
Варианты:
3.1. А → В ; 3.2. В → А ;
3.3. А,В → С
116. Найти посылку и заключение. Пример 3 – возможные варианты.
3.1. Все люди смертны…
__________________
Все преподаватели смертны
________________________________________
3.2. Все преподаватели смертны
…
__________________________
Все люди смертны
117.
3.3. Все преподаватели смертныВсе люди смертны
_____________________________
…
118. Восстановление энтимемы. Пример 3.1: А→В
1. Все люди смертны…
__________________
Все преподаватели смертны
119. Восстановление энтимемы. 3.1: А→В.
M+PВсе люди смертны
…
есть …
__________________
S+
PВсе преподаватели смертны
1.+, 2.не пр., 3.+, 4.+, 5. для S?, для Р не
пр.
120. 3.1: А→В. Вариант 1
M+PВсе люди смертны
S
Mпреподаватели есть люди
S+
PВсе преподаватели смертны.
1.+, 2+, 3.+, 4.+, 5. для S? , для Р не пр.
121. 3.1: А→В. Вариант 1
M+PВсе люди смертны
S+
Mпреподаватели - люди
S+
PВсе преподаватели смертны.
1.+, 2+, 3.+, 4.+, 5. +
122. 3.1: А→В. Вариант 1
M+PВсе люди смертны
S+
MВсе преподаватели - люди
S+
PВсе преподаватели смертны.
1.+, 2+, 3.+, 4.+, 5.+
123. 3.1: А→В.Вариант 2
M+PВсе люди смертны
М
Sлюди есть преподаватели
S+
PВсе преподаватели смертны
1.+, 2. не пр., 3.+, 4.+, 5. для S -, для Р не
пр.
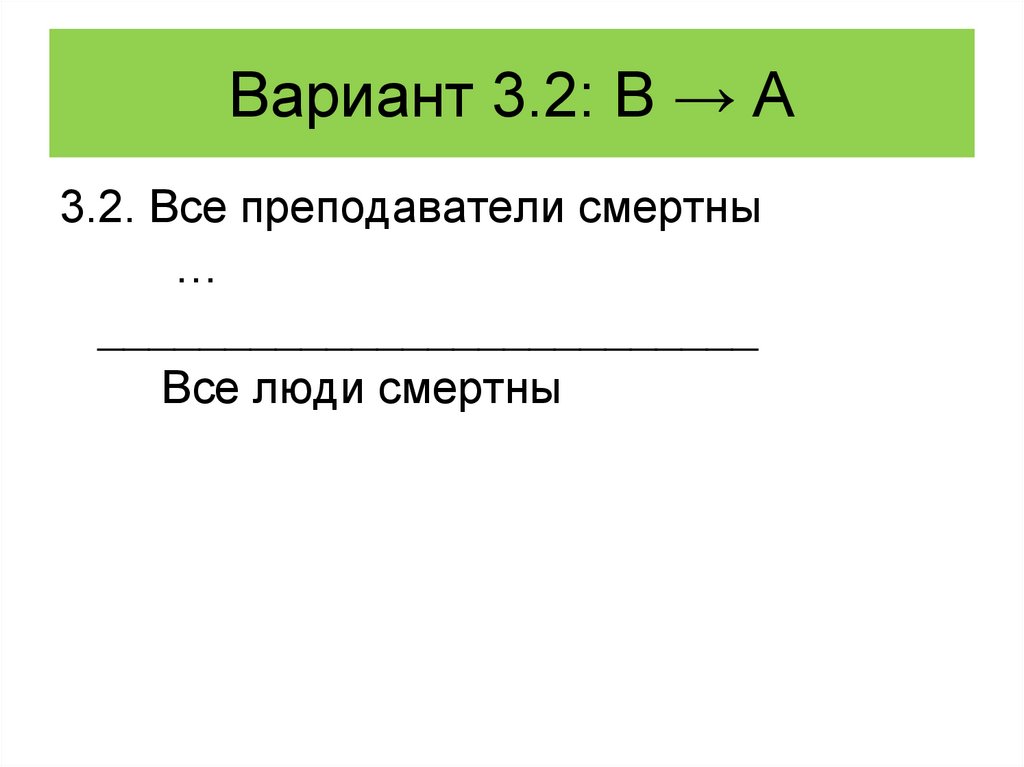
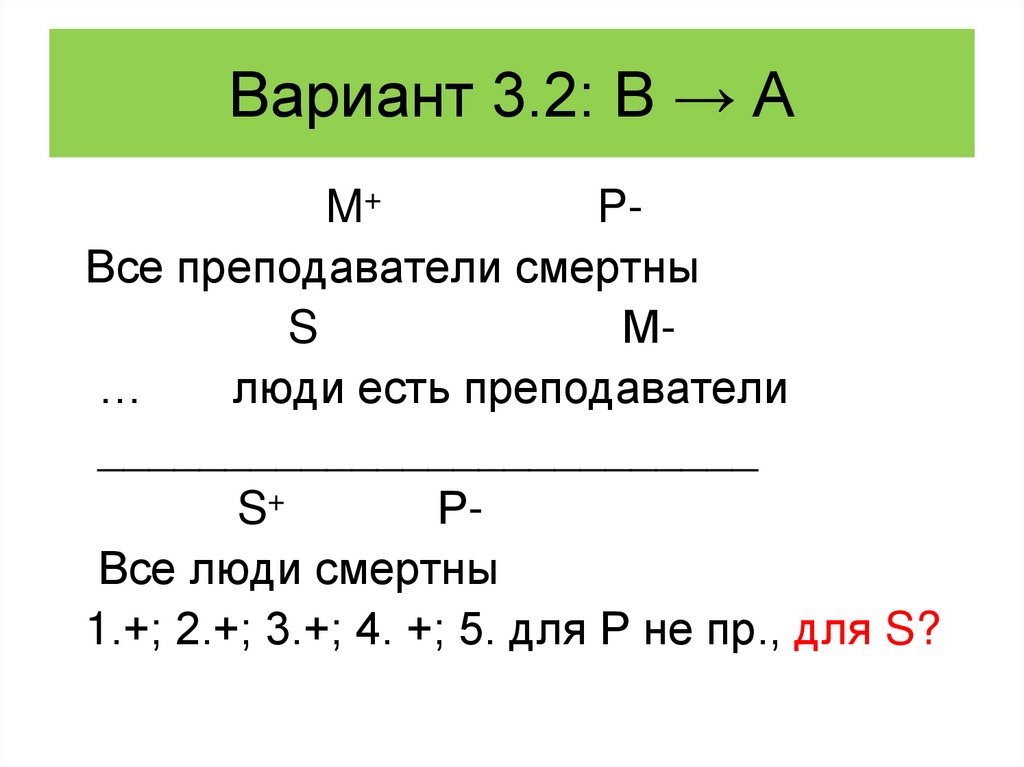
124. Вариант 3.2: В → А
3.2. Все преподаватели смертны…
__________________________
Все люди смертны
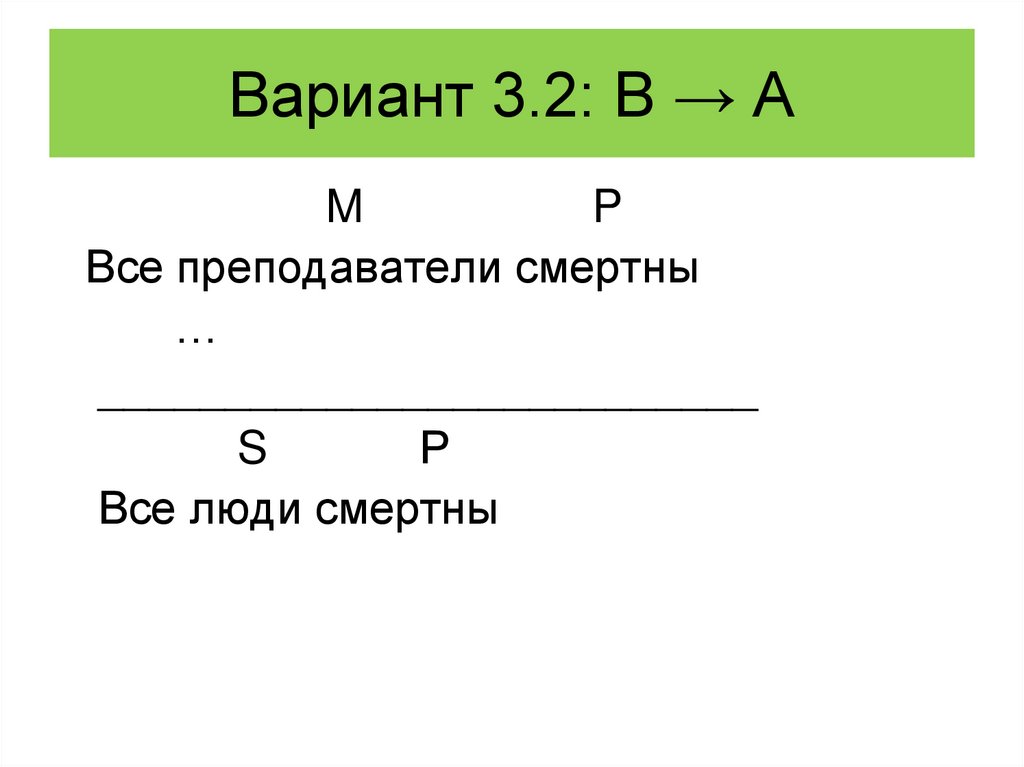
125. Вариант 3.2: В → А
MP
Все преподаватели смертны
…
__________________________
S
Р
Все люди смертны
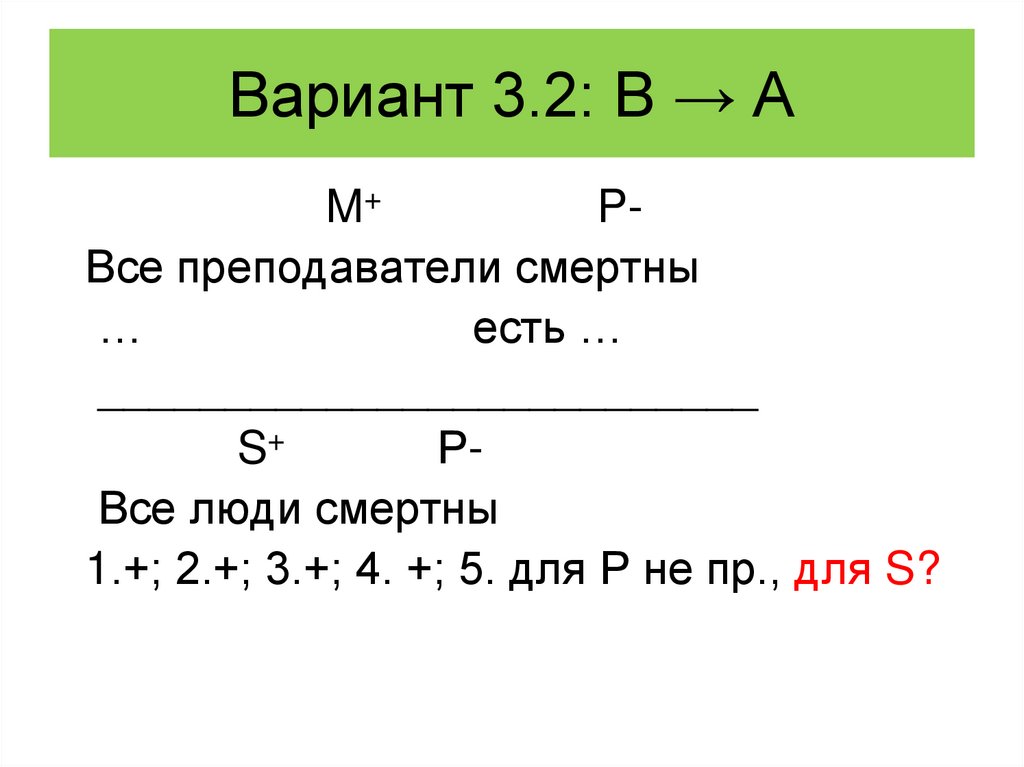
126. Вариант 3.2: В → А
M+PВсе преподаватели смертны
…
есть …
__________________________
S+
РВсе люди смертны
1.+; 2.+; 3.+; 4. +; 5. для Р не пр., для S?
127. Вариант 3.2: В → А
M+PВсе преподаватели смертны
S…
есть люди
__________________________
S+
РВсе люди смертны
1.+; 2.+; 3.+; 4. +; 5. для Р не пр., для S?
128. Вариант 3.2: В → А
M+PВсе преподаватели смертны
S
М…
люди есть преподаватели
__________________________
S+
РВсе люди смертны
1.+; 2.+; 3.+; 4. +; 5. для Р не пр., для S?
129. Вариант 3.2: В → А
M+PВсе преподаватели смертны
S+
МВсе люди есть преподаватели - ложь
__________________________
S+
РВсе люди смертны
1.+; 2.+; 3.+; 4. +; 5. для Р не пр., для S+
130. Вариант 3.3
М3. Все преподаватели смертныМВсе люди смертны
_____________________________
…
4. -
131. Задача
• По возможности восстановить даннуюэнтимему в правильный силлогизм или
показать, что это нельзя сделать.
Все рыбы умеют плавать.
Следовательно, все дельфины –
рыбы.
132. Задача
• По возможности восстановить даннуюэнтимему в правильный силлогизм или
показать, что это нельзя сделать.
Все рыбы умеют плавать. (A)
Значит, все дельфины – рыбы. (B)
A →B
133.
М-/S… есть …P+
MВсе рыбы умеют плавать
S+
PВсе дельфины – рыбы.
1.+; 2.не пр.; 3.+; 4.-;5.для S-, для Р не пр.
Ответ: нельзя восстановить.
134. Эпихейрема
• Эпихейрема – это простой силлогизм, вкотором обе посылки являются
энтимемами.
• Возьмем, два силлогизма и выведем из
них энтимемы.
135. 1 силлогизм
Все, что приводит общество к бедствиям,есть зло.
Социальная несправедливость приводит
общество к бедствиям.
Социальная несправедливость – это зло.
136.
• Пропуская в этом силлогизме большуюпосылку, получаем энтимему:
Социальная несправедливость – это
зло, так как она приводит общество к
бедствиям.
137. 2 силлогизм
Все, что способствует обогащениюодних за счет обнищания других, – это
социальная несправедливость.
Частная собственность способствует
обогащению одних за счет обнищания
других.__________________________
Частная собственность – это
социальная несправедливость.
138.
• Пропуская в этом силлогизме большуюпосылку, получаем энтимему:
Частная собственность – это
социальная несправедливость, так как
она способствует обогащению одних за
счет обнищания других.
139.
Если расположить эти две энтимемыдруг за другом, то они станут
посылками нового, третьего
силлогизма, который и будет
эпихейремой:
140.
• Частная собственность – это зло.• Социальная несправедливость – это
зло, так как оно приводит общество к
бедствиям.
• Частная собственность – это
социальная несправедливость, так как
она способствует обогащению одних
за счет обнищания других.
141.
• В составе эпихейремы можно выделитьтри силлогизма: два из них являются
посылочными, а один строится из
выводов посылочных силлогизмов.
Этот последний силлогизм
представляет собой основу для
окончательного вывода.
142. Сорит
Сорит или сложносокращенныйсиллогизм – это полисиллогизм, в
котором пропущена посылка
последующего силлогизма, являющаяся
выводом предыдущего.
143. Сорит
• Вернемся к рассмотренному вышепримеру прогрессивного
полисиллогизма и пропустим в нем
большую посылку второго силлогизма,
которая представляет собой вывод
первого силлогизма. Получится
прогрессивный сорит:
144. Сорит на базе прогрессивного полисиллогизма
• Все, что развивает мышление, полезно.• Все интеллектуальные игры развивают
мышление.
• Шахматы – это интеллектуальная игра.
• Шахматы полезны.
145. Сорит на базе регрессивного полисиллогизма
• Все звезды – это небесные тела.• Солнце – это звезда.
• Все небесные тела участвуют в
гравитационных взаимодействиях.
• Солнце участвует в гравитационных
взаимодействиях.
146. Условно-категорический силлогизм
• Df.Условно-категорическийсиллогизм – это силлогизм, где одна
посылка является условным
суждением, а вторая посылка и
заключение – простыми
категорическими суждениями.
147. Пример
Если идет дождь, то на небе тучи.Дождь идет.
На небе тучи.
A→ B
modus ponens
А
_____
B
148. Правильные модусы
A→ BA
______
B
modus ponens
A→ B
не-B
______
не-А
modus tollens
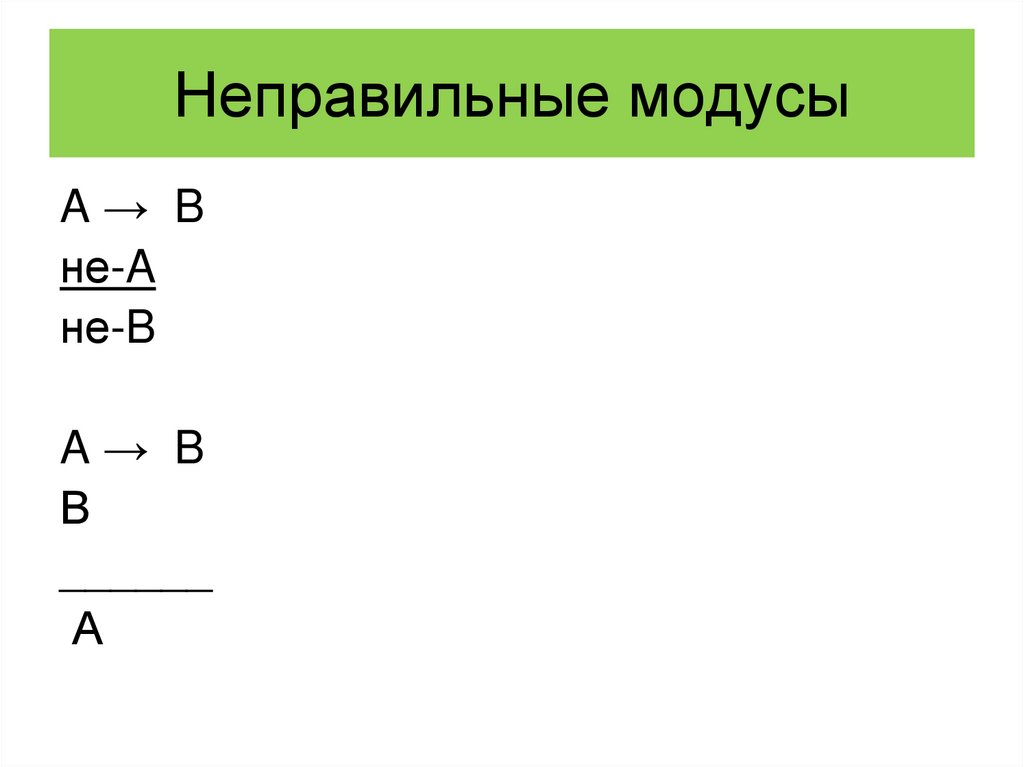
149. Неправильные модусы
A→ Bне-A
не-B
A→ B
В
______
А
150. Загадка
• «Идите сюда, – сказал я как-то тремстудентам. – Вот у меня здесь 5 шапок: 3
белые и 2 черные. Закройте глаза, и я надену
на каждого из вас шапку. Когда вы откроете
глаза, то сможете увидеть, какого цвета
шапки на ваших товарищах. Свою
собственную шапку вы увидеть не сможете и
не увидите, какие шапки остались у меня.
Тот, кто догадается, какого цвета на нем
шапка, сразу же получит зачет по логике».
151. Разделительно-категорический силлогизм
• Df. Разделительно-категорическийсиллогизм – это силлогизм, одна из
посылок которого разделительное
суждение, а вторая посылка и
заключение – простые категорические
суждения.
152. Пример
Я пойду на лекцию или в кино.Я не пошел на лекцию
Я пошел в кино
АvВ
не-А
В
АvВ
не-В
А










































































































































 philosophy
philosophy








