Similar presentations:
Метрические задачи
1.
Лекция 3Метрические задачи
Проф. Пиралова О.Ф.
1
2. Пример определения расстояния способом прямоугольного треугольника
A0Натуральная
величина
βº
∆y = yB – yA
B2
∆z = zB – zA
zB
A2
zA
X2,1
yA
A1
αº
∆z = zB – zA
yB
A0
αº
B1
Угол наклона
прямой к
горизонтальной
плоскости
проекций П1
βº Угол наклона
прямой к фронтальной
плоскости проекций П2
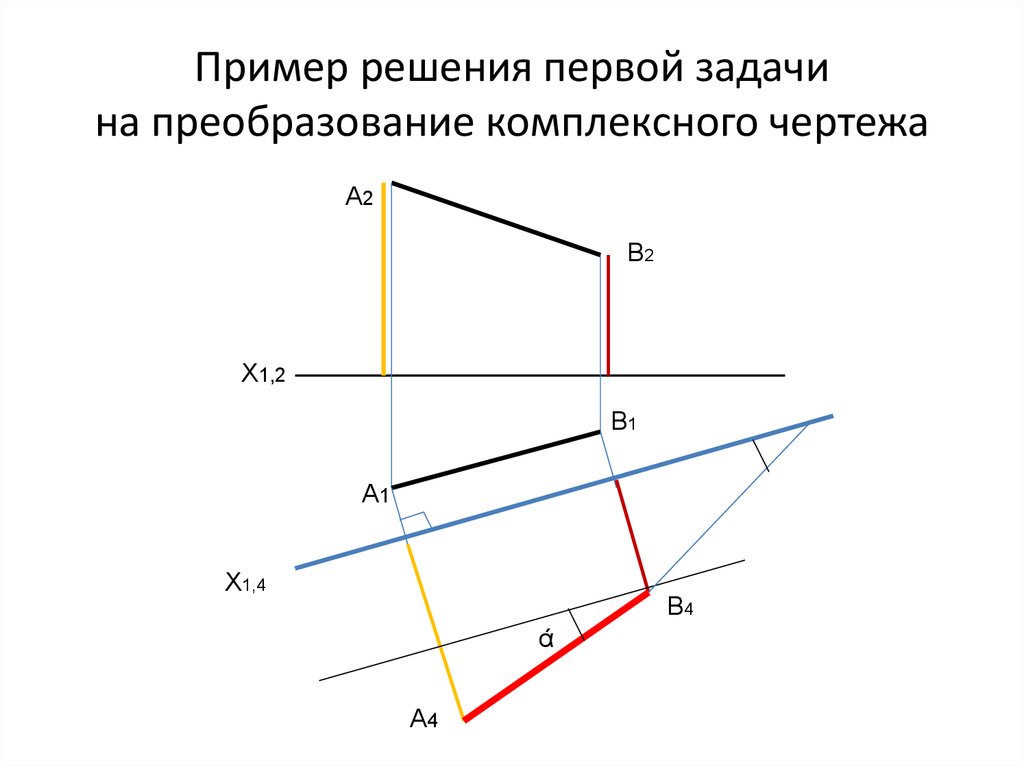
3. Пример решения первой задачи на преобразование комплексного чертежа
А2В2
Х1,2
В1
А1
Х1,4
В4
ά
А4
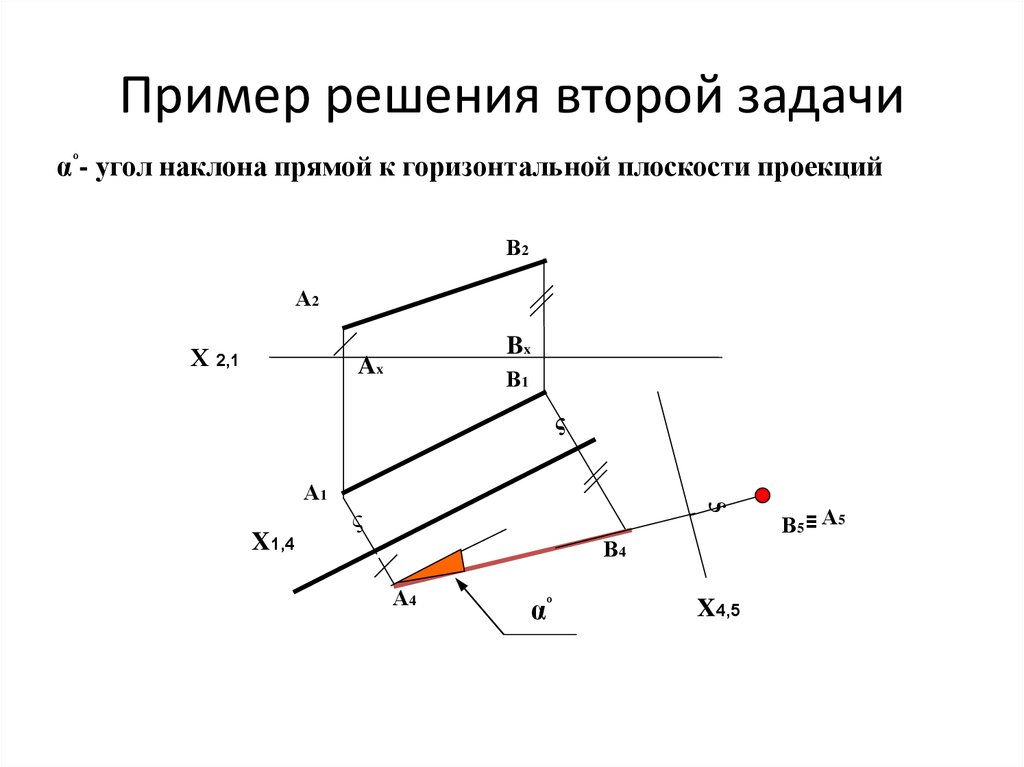
4. Пример решения второй задачи
αº- угол наклона прямой к горизонтальной плоскости проекцийВ2
А2
Х 2,1
Bx
Ax
В1
А1
X1,4
ς
ς
ς
В4
А4
αº
X4,5
В5 ≡ А5
5. Алгоритм решения третьей задачи
С212
А2
h2
В2
Х 2,1
В1
В4
αº
А1
11
h1
А4
С1
С4
X1,4
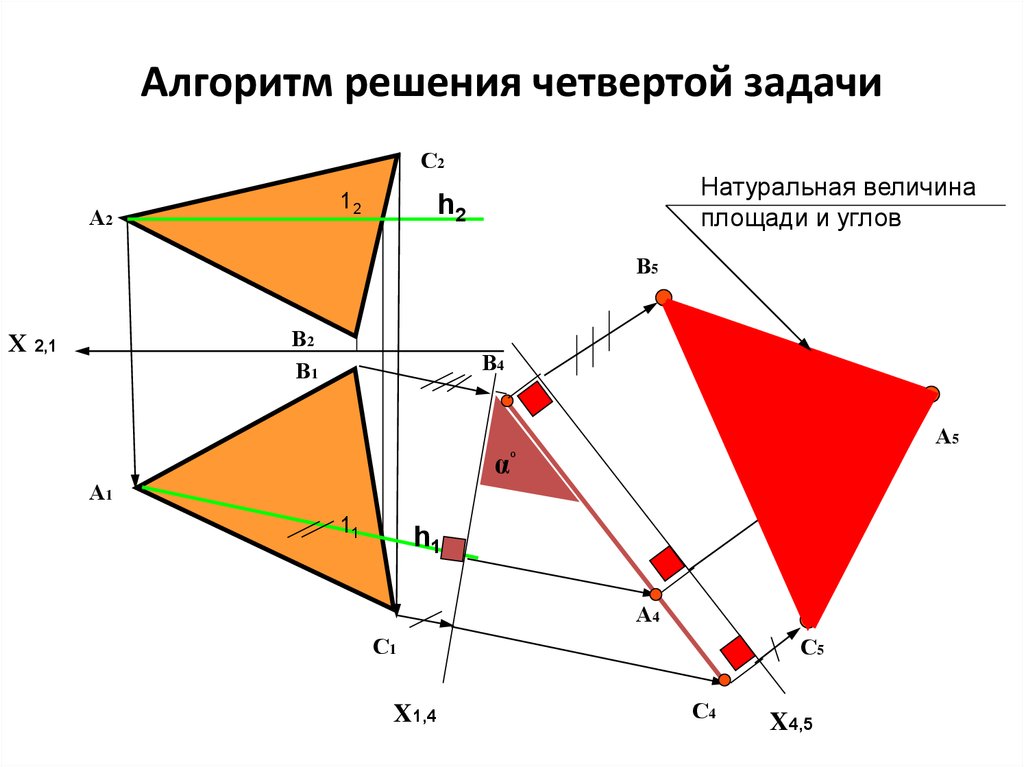
6. Алгоритм решения четвертой задачи
С212
А2
Натуральная величина
площади и углов
h2
В5
В2
В1
Х 2,1
В4
А5
αº
А1
11
h1
А4
С1
X1,4
С5
С4
X4,5
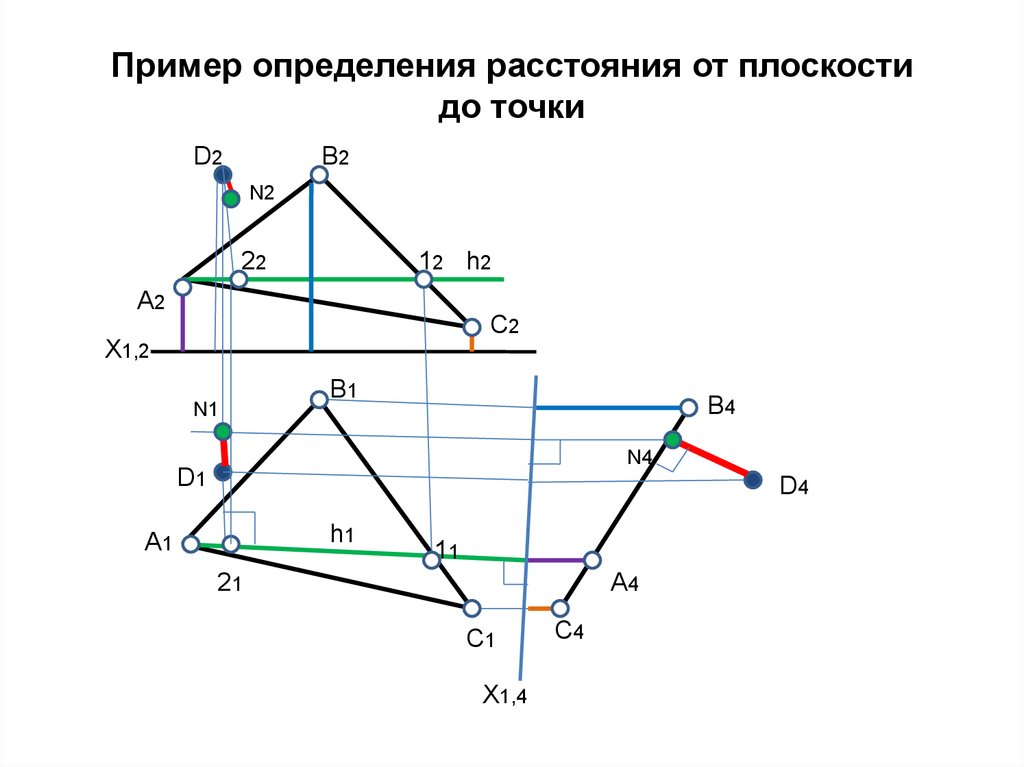
7.
Пример определения расстояния от плоскостидо точки
В2
D2
N2
22
12 h2
А2
С2
X1,2
N1
В1
В4
N4
D1
D4
h1
А1
11
А4
21
С1
X1,4
С4
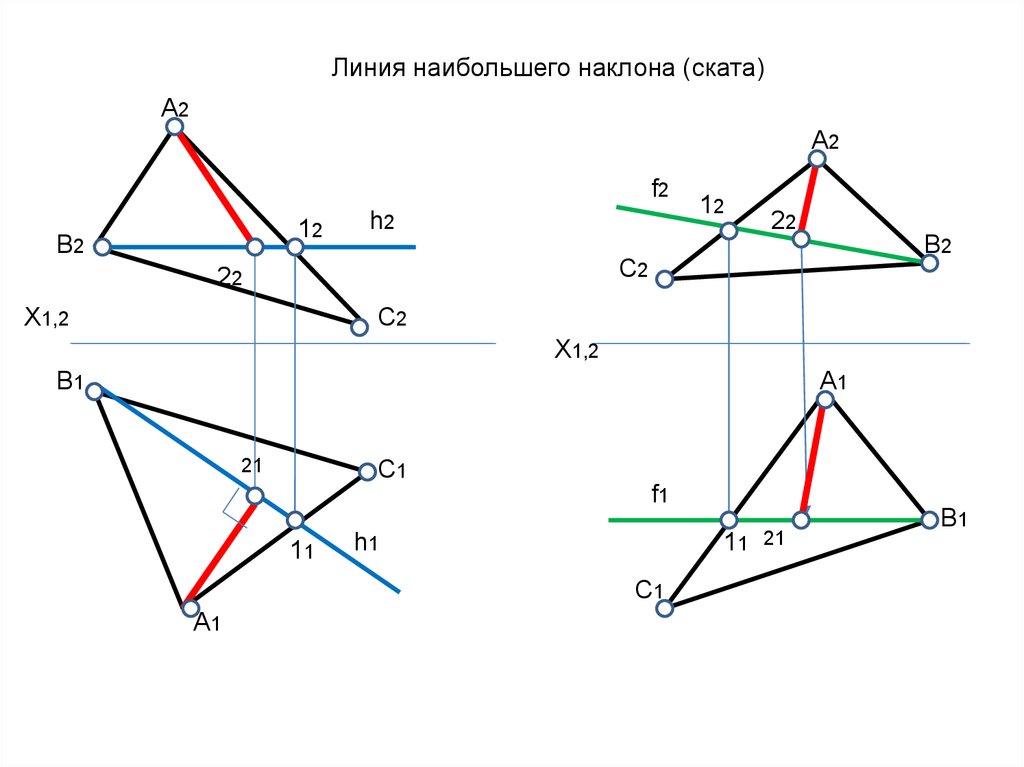
8.
Линия наибольшего наклона (ската)А2
А2
f2
12
В2
h2
12
22
В2
С2
22
С2
X1,2
X1,2
В1
А1
С1
21
f1
11
11 21
h1
С1
А1
В1
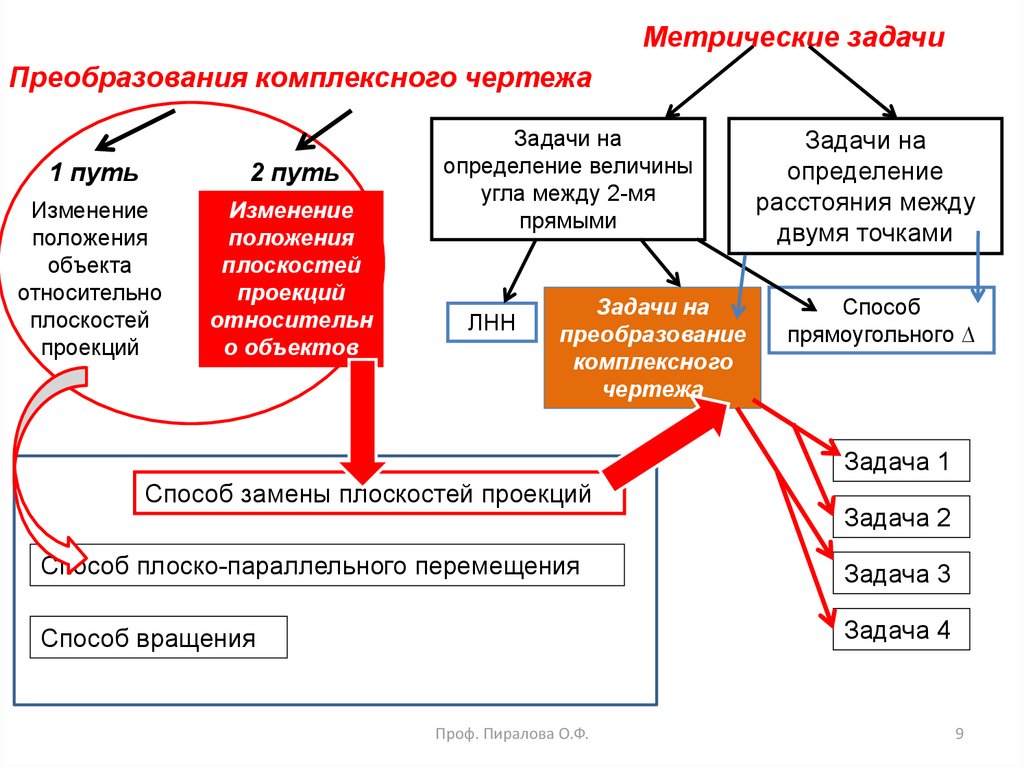
9.
Метрические задачиПреобразования комплексного чертежа
1 путь
2 путь
Изменение
положения
объекта
относительно
плоскостей
проекций
Изменение
положения
плоскостей
проекций
относительн
о объектов
Задачи на
определение величины
угла между 2-мя
прямыми
ЛНН
Задачи на
преобразование
комплексного
чертежа
Задачи на
определение
расстояния между
двумя точками
Способ
прямоугольного ∆
Задача 1
Способ замены плоскостей проекций
Задача 2
Способ плоско-параллельного перемещения
Задача 3
Способ вращения
Задача 4
Проф. Пиралова О.Ф.
9
10.
Спасибо завнимание!!!




 drafting
drafting








