Молекулярна динаміка з врахуванням обертових ступенів вільності

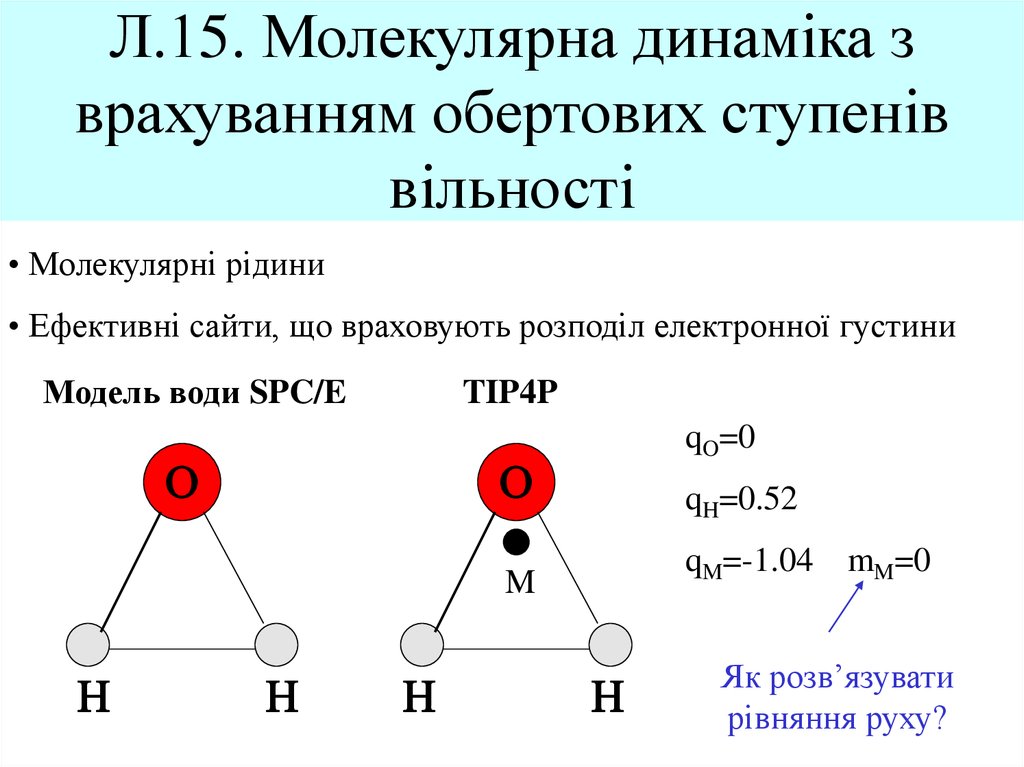
1. Л.15. Молекулярна динаміка з врахуванням обертових ступенів вільності

• Молекулярні рідини
• Ефективні сайти, що враховують розподіл електронної густини
Модель води SPC/E
TIP4P
O
qO=0
O
qH=0.52
qM=-1.04
M
H
H
H
H
mM=0
Як розв’язувати
рівняння руху?

2. Рівняння руху динаміки жорстких тіл

Жорстке тіло є набором точкових атомів, локальна геометрія
яких є інваріантна в часі. Розв’язування рівнянь руху
ітеративними иетодами типу SHAKE є часто пробематичним,
або і неможливим (наприклад лінійні молекули).
Жорстке тіло можна задати за допомогою тензора
моментів інерції I з компонентами
I
1
mr r
2 sites
rα- відстань від центру мас Rcm
Завжди можна вибрати таку систему координат, щоб тензор інерції
був діагональним і компоненти, щоб задовольняли умові:

3. Рівняння руху динаміки жорстких тіл

I xx I yy I zz
Тоді орієнтація локальної системи координат по
відношенню до загальної фіксованої системи координат
задається чотирикомпонентним вектором (кватерніоном)
Q (q0 , q1 , q2 , q3 )
Умова нормування
q02 q12 q22 q32 1

4. Кватерніони

q0 cos( ) cos(
)
2
2
q2 sin( ) sin(
)
2
2
, ,
-кути Ейлера
q1 sin( ) cos(
)
2
2
q3 cos( ) sin(
)
2
2
Матриця переходу від локальної системи координат до
фіксованої є така:
q02 q12 q22 q32
R 2(q1q2 q0 q3 )
2(q1q3 q0 q2 )
2(q1q2 q0 q3 )
q02 q12 q22 q32
2(q2 q3 q0 q1 )
2(q1q3 q0 q2 )
2(q2 q3 q0 q1 )
2
2
2
2
q0 q1 q2 q3

5. Рівняння руху динаміки жорстких тіл

Якщо di є положенням і-го вузла в жорсткому тілі
відносно центру мас, то його розтащування в фіксованій
системі координат задається
di Rdi
fix
Нехай тепер на жорстке тіло діє загальна сила F , яка є
сумарною сило, що діє на всі вузли :
F fi
i

6. Рівняння руху динаміки жорстких тіл

Рух жорсткого тіла розбивається на трансляційний та
обертовий. Трансляційний інтегрується за допомогою
стандартних алгоритмів, наприклад leapfrog чи Верле.
t
t
F (t )
v (t ) v (t ) t
2
2
M
t
r (t t ) r (t ) tv (t )
2
Повна сила
Обертовий момент, що діє на тіло у фіксованій системі є:
T fix di fix fi
i
Повна маса

7. Рівняння руху динаміки жорстких тіл

В локальній системі координат:
T RT T fix
де
x ( I yy I zz ) y z
та інші циклічні перестановки
Кутова швидкість в локальній системі координат може також
бути проінтегрована алгоритмом leapfrog
t
t
1
(t ) (t ) tI T (t )
2
2

8. Рівняння руху динаміки жорстких тіл

Однак, тепер треба знайти значення кватерніонів у новий
момент часу. Для цього існує алгоритм кватерніонів Фінчема
t
Q(t t ) Q(t ) ( (t )W (t ) (t t )W (t t ))
2
де
а матриця
W (0, )T
є означена наступним чином
q0 q1 q2 q3
q
q
q
q
1 1
0
3
2
q0 q1
2 q2 q3
q1
q0
q3 q2
Проблема !!!

9. Рівняння руху динаміки жорстких тіл

Рівняння для розв’язується ітеративно використовуючи як
нульове наближення
Q(t t ) Q(t ) t (t )W (t )
Звичайно використовуються 3-4 ітерації.
На кожному часовому кроці накладається додаткова умова, що
| Q | 1
Термостати та баростати: окремі термостати під’єднуються
для контролю температури до трансляційних та обертових
швидкостей. Баростат взаємодіє лише з трансляційними
ступенями вільності.

10. Рівняння руху динаміки зв’язаних жорстких тіл

Інколи бувають два або більше жорстких тіл пов’язані між
собою зв’язком по відстані. Для цього використовується
алгоритм QSHAKE, який узагальнює алгоритм SHAKE з
кватерніоніми
При інтегруванні рівнянь динаміки жорстких тіл додатковий
зв’язок буде приводити до додаткової сили та обертового
моменту, що діють на жорсткі тіла, пов’язані між собою
зв’язком по відстані – аналогічно як в SHAKE.